Modelling of Efficient Graph-aware Data Storage using DNA
Asad Usmani
a
and Lena Wiese
b
Institute of Informatics, Goethe University, Bockenheim Campus, Frankfurt, Germany
Keywords:
Dna Storage, Big Data Archives, Data Management, Data Modelling, Data Compression, Simple Graph.
Abstract:
The global demand for massive data archival with a yearly exponential growth rate is near to outpacing the
capability of the conventional world storage media. Fortunately, DNA (Deoxyribonucleic acid) storage has
made a substantial breakthrough for archiving such vast data for a long time. Though many scientists have
made remarkable efforts to use DNA storage as a promising emergent solution for archiving raw data, not
anyone has exploited it to store graph-aware encoded data. Desirably, the exploitation of graph-aware data
archiving has notable advantages over raw data. That supports data portability and significantly reduces the
concerned data size for DNA storage in terms of nucleotides. Hence, it benefits us in database operational
cost reduction. We present a theoretical model for efficient DNA storage of simple graph-based scientific data.
Furthermore, some simple graph-based datasets, particularly from the biological domain, have been used for
experimental results and analysis. That revealed a compression ratio between 1.18 to 1.53.
1 INTRODUCTION
Long term scientific data archives (Doorn and
Tjalsma, 2007; Buneman et al., 2004; Whitlock et al.,
2010) have become a foundation of science and future
research advancements. Researchers in various fields
such as biology, life sciences, ecology and medicine,
working exclusively on network data, need historical
data archives for practical experiments. For instance,
six prominent public databases have adapted to store
and retrieve existing data about the protein-protein
interaction (PPI) network (Lehne and Schlitt, 2009).
Typically, a graph model is used to represent such net-
work data. For convenient modelling of the PPI net-
work, we denote proteins as nodes and interactions
between them as edges within a simple undirected
graph. Likewise, various other applications from so-
cial networks, biological networks, community detec-
tion etc., are also strong candidates for simple graph-
based modelling. Needfully, the gigantic graph-aware
data archival wants a low cost and durable storage
medium. Fortunately, DNA storage has been estab-
lished and functional for offering such data archival.
Since the 60s, scientists have dreamed about the
data storage capabilities of DNA (Neiman, 1964),
but this field has significantly evolved during the last
decade. In 2012 and 2013, almost a megabyte of data
a
https://orcid.org/0000-0001-5579-6980
b
https://orcid.org/0000-0003-3515-9209
was stored in DNA and then successfully recovered
by two groups guided by Church (Church et al., 2012)
and Goldman (Goldman et al., 2013), respectively.
Prominently, (Organick et al., 2018) stored and recov-
ered data at a large scale comprised of 35 files (over
200MB in size) using millions of DNA nucleotides.
Thus, synthetic DNA storage is potentially a next-
generation data storage medium (Clelland et al., 1999;
Bancroft et al., 2001; Church et al., 2012; Goldman
et al., 2013; Bornholt et al., 2016), which is a low
cost, highly dense, immutable, durable and energy-
efficient storage solution for rapidly growing archived
data. The half-life of DNA is approximately 520 years
(Allentoft et al., 2012), which reveals its high durabil-
ity. Despite that DNA storage ensures the longevity
of the data archival at a low cost, the concerned ac-
cessibility cost makes its usage slightly impractical.
However, the accessibility cost is exponentially de-
creasing every year with the rapid advancements in
the biotechnology industry (Carlson, 2014; Eid et al.,
2009). Since DNA writing (synthesis) and reading
(sequencing) methods are gradually upgrading, thus
economical DNA storage is evolving with anticipa-
tion. Evidently, DNA storage has made great strides
in preserving huge data seemingly forever hence sim-
ple graph-aware data archival is a must use-case.
The simple graph-aware data storage using DNA
would be comparatively more efficient than raw data
archival. We will see in a later section that it re-
180
Usmani, A. and Wiese, L.
Modelling of Efficient Graph-aware Data Storage using DNA.
DOI: 10.5220/0011355400003269
In Proceedings of the 11th International Conference on Data Science, Technology and Applications (DATA 2022), pages 180-189
ISBN: 978-989-758-583-8; ISSN: 2184-285X
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Graph
Database
AATGCCATGA
DNA
Storage
AATGCCATGA
1.Convert
6.Reproduce
5.Decode
2.Encode
3.Synthesis
4.Sequencing
A Simple
Graph G
Figure 1: DNA end to end process for reading and writing a simple graph data.
duces the number of nucleotides that need to be stored
in DNA. This compact data leads toward more eco-
nomical DNA storage as the synthesis process costs
up to almost $0.05–0.15 per nucleotide (Kosuri and
Church, 2014). Additionally, it also resolves the
data portability concern as a by-product. Due to
this, graph-aware encoded data archival is convinc-
ingly encouraged rather than raw data archival. We
start this article by explaining the DNA background
and defining the simple graph and compression tech-
niques in Section 2. Then we proceed to Section 3
to discuss our methodology, where we propose a the-
oretical model for simple graph-aware data storage
using DNA. In section 4, the experimental results,
provisioning diverse real-world datasets, illustrate the
worthwhile compression ratio obtained.
2 BACKGROUND AND RELATED
WORK
2.1 DNA Storage System and Database
Engine
Deoxyribonucleic acid or DNA (Seeman, 2003) is
a composition of four nucleotides: adenine (A),
thymine (T), cytosine (C), and guanine (G) and a
sequence of these nucleotides is called an oligonu-
cleotide (oligo) or a DNA strand. Generally, the
DNA molecules are the carrier of genetic informa-
tion, which is functionally essential for all living or-
ganisms. Moreover, a DNA strand has two ends: 5
0
and 3
0
and its structure is composed of a double helix
in nature with two (“reverse complement”) strands in
opposite directions. In contrast, a single DNA strand
is sufficient for data storage. Primarily, DNA storage
deals with nucleotides rather than bits for traditional
storage media such as magnetic tape, HDD, SSD etc.
Therefore, digital data must be in a sequence of qua-
ternary (A, G, T, C) characters for DNA storage com-
patibility. For instance, a binary string of length n
can be encoded into an equivalent oligo of size n/2
by mapping 00, 01, 10, 11 to A, G, T and C, respec-
tively. Optionally, one of the suggested DNA encod-
ing schemes (Heinis and Alnasir, 2019) can also be
used as appropriate. Overall, any digital data of clas-
sic objects like PDF, JPEG or a graphical representa-
tion etc., can be encoded and then decoded to retrieve
the original information using DNA. An end-to-end
DNA storage process is abstractly expressed in Fig-
ure 1 to read and write a simple graph data.
(Appuswamy et al., 2019) proposed a DNA stor-
age system architecture for a relational database as
OligoArchive. They replaced traditional data storage
tape with a DNA storage device as oligos had to be
stored instead of binary data. The presented DNA
storage system has three components: a synthesizer, a
sequencer, and a storage container. The DNA synthe-
sizer encodes the digital data and then stores them in
DNA as oligos. Conversely, the DNA sequencer reads
oligos and converts them into original digital data.
Both synthesis and sequencing methods in the DNA
storage system support PUT and GET operations of
the database engine, respectively. The storage con-
tainer can be conceived as an object for the DNA stor-
age device. This object is also called DNA Storage
Library: a collection of “DNA pools”. Knowingly,
an oligo is the basic unit of DNA storage, which can
roughly store at most 100-200 nucleotides. There-
fore, many DNA strands are needed to map a classic
data object in partitions. The limitation of one-on-
one mapping of oligos and DNA pools leads to re-
serving several DNA pools to contain single object
Modelling of Efficient Graph-aware Data Storage using DNA
181

DBMS
DNA
Synthesizer
PCR
thermocycler
DNA
Sequencer
DNA Storage System
DNA Library
{ PUT,
{ID: AG},
{Address: TAG},
{Payload: AGTCTAGC}
}
{
{Payload: AGTCTAGC}
}
{ GET,
{ID: AG},
{Address: TAG}
}
DNA pool
Figure 2: Demonstrates an abstraction of the database engine and DNA storage system interfacing proposed in the
OligoArchive architecture. Both GET and PUT methods are used to read and write encoded relational data, respectively.
data. Unlikely, a “DNA pool” does not allow an or-
ganized address for indexing as a traditional storage
medium. So, a unique address itself must be embed-
ded in every DNA strand with payload data. A DNA
sequencing primer as a unique object identifier is re-
sponsible for retrieving all the corresponding oligos
from the DNA Storage Library for a particular ob-
ject. The PCR (polymerase chain reaction) thermo-
cycler facilitates retrieving data from the DNA Stor-
age Library when a template DNA strand provides in-
put in the sequencing process. This template DNA
strand includes the sequencing primers to locate the
exact oligo from where the data are to be retrieved
and populates itself with output data. In conclusion,
both GET and PUT methods can be utilised in read-
ing and writing oligo(s) from/to DNA storage system
using the same database engine for the relational data
as shown in Figure 2.
2.2 Simple Graph Model and
Representation
To gain efficiency for simple graph-aware DNA data
storage in terms of nucleotides, the impact of differ-
ent representations for a simple graph model needs
to evaluate quantitatively. (Besta et al., 2019) com-
prehensively described a few graph models from the
perspective of graph databases. In this regard, we are
mentioning only a simple graph underneath.
Definition: A (simple) graph G is modeled using a set
of two objects V and E, where V is a set of vertices
(or nodes) and E denotes a set of edges (or links).
The set V consists of a non-empty finite number of
n vertices, e.g. V = {v
1
, v
2
, v
3
, . . . , v
n
} and E ⊆
V × V is a set of m paired vertices, e.g. E = {e
1
, e
2
,
e
3
, . . . , e
m
} | ∀ e
k
∈ E (1 ≥ k ≤ m) = {(x, y) — x, y
∈ V and x 6= y}. For an undirected G, an edge e
k
=
(x,y) ∈ E is a set of two nodes while e
k
represents a
tuple (or directed edge) of two nodes from x towards
y in case of directed graph G, where x stands for the
out-vertex (or source node) and y stands for the in-
vertex (or dest node).
The selection of a simple graph representation
technique must be optimal for efficient DNA stor-
age. Primarily, one of the four techniques (Davoudian
et al., 2018) can be used for a simple graph represen-
tation: adjacency matrix (AM), adjacency list (AL),
edge list (EL) and compressed sparse row (CSR). We
briefly describe only AM and AL as followings:
Adjacency Matrix: Usually, AM is used to repre-
sent G in memory. In this representation, a matrix
M ∈ {0, 1}
n,n
shows the presence of all the edges in
G such that M
x,y
= 1 ⇔ (x, y) ∈ E if (x,y) is directed,
otherwise M
x,y
= 1 and M
y,x
= 1. The AM represen-
tation is not recommended for large scale graphs.
Adjacency List: For the AL representation of G,
we maintain an array A for n vertices such that |A| = n.
Each index of the array A corresponds to a vertex’s
ID. In addition, for each vertex x, a list A
x
is associ-
ated with it, which only contains IDs of other vertices
such that y ∈ A
x
⇔ (x, y) ∈ E if (x, y) is directed, oth-
erwise y ∈ A
x
and x ∈ A
y
. The AL format minimizes
the storage overhead for sparse graphs.
2.3 Compression Techniques
Researchers have developed various compression
techniques (Boldi and Vigna, 2004; Apostolico and
Drovandi, 2009) to optimize a graph representation
by exploiting compression for AM, AL and EL etc.
Despite that, (Simecek, 2009) used the quadtree com-
pression strategy for simple graph storage; a more
compact representation of AM presented by (
´
Alvarez
et al., 2010) is called k
2
-tree.
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
182

2.3.1 k
2
-tree Compression Technique
For k
2
-tree construction (
´
Alvarez et al., 2010), an AM
M of size n × n is recursively partitioned based on an
input value k such that n is in k’s power. For each par-
tition, a node symbolizing a parent contains one bit
and k
2
pointers to its children (sub-partitions) in the
tree. At the first level, the M is split equally into k
2
submatrices. The root node holds these k
2
submatri-
ces using its k
2
pointers. For each node of k
2
children,
its bit is enabled to 0 if the corresponding partition
contains only 0s, or 1 otherwise. A node with a bit
value 0 reveals that its affiliated submatrix is empty.
Hence, there is no need to make a recursive call for
that particular partition anymore. Otherwise, the sub-
matrix further breaks continually until the base case
finds. Concisely, the k
2
-tree technique generates a bi-
nary string as an output. That optimally represents
a simple graph compared to AM. The k
2
-tree takes
advantage of a matrix’s sparsity, especially when a
sparse matrix would have multiple large regions con-
taining only 0s. Where applicable, this technique is
valuable in getting significant data compression.
2.3.2 Re-Pair Algorithm
Furthermore, (Claude and Navarro, 2010) adapted
a grammar-based compression technique for the
AL compression of a simple graph using Re-
Pair algorithm (RA). Using this technique, a
single array list L(G) is composed by including
all the adjacency lists of a graph G: L(G) =
¯v
1
v
1,1
v
1,2
...v
1,m
1
¯v
2
v
2,1
v
2,2
...v
2,m
2
... ¯v
n
v
n,1
v
n,2
...v
n,m
n
so that v
j,k
< v
j,k+1
where 1 ≤ j ≤ n and 1 ≤ k ≤ m
j
.
There, each delimiter ¯v
j
= −v
j
is essentially incor-
porated in the list L(G) to distinguish the adjacency
list of the node v
j
from the previous one.
Without going into details for the algorithmic ex-
planation, the Re-Pair algorithm runs various steps on
input list L(G) and then produces three objects as out-
put: a remaining adjacency list C(G), a dictionary T
for grammar rules and two bitmaps B
1
and B
2
. The
list C(G) contains a subset of L(G). The dictionary
T occupies several dictionary rules. For tracing the
beginning and size of each adjacency list in the C(G),
two bitmaps B
1
[1...n] and B
2
[1...|C(G)|] can be ad-
vantageously used rather than keeping pointers to ev-
ery adjacency list especially for sparse graphs. If the
adjacency list of node V
i
is empty then B
1
[i] = 0 oth-
erwise B
1
[i] = 1. The bitmap B
2
marks the starting
place of every adjacency list in C(G). Where the func-
tion rank(B
1
,i) returns the number of 1s until index i
inclusively in B
1
. Given that if B
1
[i] = 1 then function
select(B
2
,rank(B
1
,i)) returns the starting index of i
th
node’s adjacency list otherwise it is empty.
3 PROPOSED GRAPH-AWARE
DATA STORAGE MODELLING
FOR DNA
A model is an abstract but informative representation
of a system. That reveals the entities or objects and
relationships among those present within that system.
Furthermore, we can gain a comprehensive under-
standing of the overall workflow of the entire process
while using a model (Epstein, 2008).
3.1 Model using k
2
-tree Technique
Here we suggest an efficient theoretical model for
storing a simple directed graph into DNA. For that,
four recommended steps are illustrated in Figure 3.
Firstly, a simple directed graph is represented in
AM format and subsequently compressed in a binary
string using the k
2
-tree technique. The size of that
compressed binary string depends on the input graph
size and its compression ratio. Due to the limited ca-
pacity, accommodation of an entire binary sequence
into one DNA strand is not permissible. So, in the
third step, the single binary object is divided into
multiple fixed-length segments. The size of a DNA
strand determines the number of blocks of the input
binary string. For instance, a binary string with a
length of 900 bits will be partitioned into three chunks
only if a DNA strand consists of 150 nucleotides
in addition to primers and considering the encoding
method presented by Church (Lee et al., 2018), which
maps 2 bits to one nucleotide. Accordingly, a re-
lation with three attributes: GraphID, BlockID and
Data, is created within a database system to store ev-
ery graph’s equivalent binary configuration. The at-
tribute GraphID denotes a graph number in a rela-
tion and identifies all the chunks associated with this
graph. The attributes BlockID and Data specify the
order of each block and its corresponding binary data
of a graph, respectively. Any relational database may
contain such fixed-length data of all given attributes
within a relation. Finally, that relation replicates into
another nucleotides-based shadow relation such that
each tuple containing binary data maps to an equiv-
alent nucleotides-based tuple by encoding. Hence,
each nucleotides-based tuple will fit into an indepen-
dent DNA strand for systematic DNA storage. Con-
clusively, more compacted graph data will demand
fewer DNA strands. It, in turn, benefits in overall cost
reduction of synthesis and sequencing processes.
In general, how much compression ratio can be
obtained using the k
2
-tree format? To answer it, let
us assume that we exactly find as many 0s as 1s at
each level of the tree. Thus, if we have n children on
Modelling of Efficient Graph-aware Data Storage using DNA
183

3
2
6
5
4
1
1
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
1
1
0
0
.
.
0
1
0
1
GraphID BlockID Data
1 1 101110100110110
1 2 100011000100101
1 3 10110101111
2 1 101010101111010
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
ID Address Payload
AG TAG AGTCTAGC
AG TAT TCGCATAT
AG TAC GCTATG
AT TAG GCAGACTC
A simple
graph G
1.Convert
Adjacency Matrix
2.Compress
k
2
-tree output: a
binary string
3.Segment and
Store
4.Encode
A relation in databaseNucleotide-based mirror relation in database
8.Regenerate
7.Decompress
5.Decode
6.Combine
Figure 3: Illustrates the step by step database storage process of a simple graph by using the k
2
-tree compression technique.
i
th
level then there will be
n
2
× k
2
children on i + 1
th
level. A formula T (i) =
(k
2
)
(i−1)
2
i−2
|i ≥ 3 to find the
number of child nodes at any i
th
level can easily be
determined using this recurrence T (i) =
T (i−1)
2
× k
2
,
where T (2) = k
2
and T (1) = 1. If d = log
k
n de-
notes the last level of k
2
-tree then total bits required to
represent an AM into k
2
-tree format will be equal to
S = (
∑
d
i=3
(k
2
)
(i−1)
2
i−2
) + k
2
+ 1. Finally, the compression
ratio calculates using this
n
2
S
formula as AM needs n
2
bits to represent a graph. For n = 1024 and k = 4, it
produces a compression ratio almost 64 times better
than AM. Theoretically, we acknowledge a consid-
erable reduction in the nucleotide counts needed for
DNA storage. However, in the next section, we will
evaluate the experimental results for better compari-
son. In conclusion, we have not obtained any antici-
pated graph-aware data exploitation for efficient DNA
storage using this technique rather than compression
only.
3.2 Model using Re-Pair Algorithm
The theoretical model for DNA storage of graph-
based data using the RA is presented below in Fig-
ure 4. Firstly, a graph G representation transforms
into an AL instead of to AM in Figure 3. A compos-
ite edge list: a concatenation of all edges-list into a
single edge list; is then provided with an input to the
RA during the second step. For data compression,
we already know that the Re-Pair algorithm gener-
ates a triplet of objects as output: 1) a dictionary of
rules T , 2) a remaining edges list C(G), and 3) two
bitmaps B
1
and B
2
. This triplet is a core to recon-
struct the original graph again in AL representation
after its perfect restoration from DNA storage. Ide-
ally, this triplet requires fewer bits than direct storage
of a single identical edges list into DNA. A mecha-
nism must be established for the careful handling of
such triplets in DNA storage. Specifically, the parts
of a triplet must be concatenated to obtain a binary
string and then restored again correctly when needed.
Thirdly, each triplet’s elements are successively inte-
grated in addition to their cardinalities as prefixes to
make a composite string. Indeed, each triplet’s fac-
tor will be split again from its composite object with
the help of its prefix. Afterwards, the binary sequence
is partitioned into multiple fixed-length chunks and
stored in a database table. Furthermore, a nucleotides-
based shadow relation is synchronized from binary to
nucleotides format after encoding data similar to the
previous process.
We consider and evaluate the AL representation of
a simple directed graph G for DNA storage. Suppos-
edly, we store it as a concatenated sequence of n +
m + 1 integers with p bits each such that |V |k
n
i=1
V
i
=
|V
i
|ke
i,1
ke
i,2
k...ke
i,|V
i
|
, where n = |V |, m =
∑
n
i=1
|V
i
|,
p = log
2
|V | and xky = xy. The compound sequence of
all adjacency lists of G will result in a binary string of
a total D = (n +m+1)× p bits in length. Importantly,
how would the integers be reproduced from this com-
posite binary sequence? For this, a fixed-size integer
of 2 bytes has to append with the binary string as a
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
184

3
2
6
5
4
1
1
0
0
0
0
0
0
1
0
3
4
5
0
1
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
.
.
1
0
1
1
GraphID BlockID Data
1 1 011110100110110
1 2 100011000100101
1 3 10110101111
2 1 101010101111011
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
ID Address Payload
AG TAG CATCTAGC
AG TAT TCGCATAT
AG TAC GCTATG
AT TAG GCAGACTA
A simple
graph G
1.Convert
Adjacency List
2.Compose: a
single edges list
Use Re-Pair algorithm
4.Segment and
Store
5.Encode
A relation in database
Nucleotide-based mirror relation
3.Concate: a single
binary string
Re-Pair output
1
Dictionary rules
2
Remaining edges
list
3
Corresponding
two bitmaps
2
6
2
4
1
2
3
4
5
6
7
8
9
10.Regenerate 9.Decompose: an
array of edges list
6.Decode
7.Combine
8.Split
Figure 4: Illustrates the step by step database system storage process of a simple graph by using the Re-Pair algorithm.
prefix. This prefix will contain the value of p and aid
in splitting all the integers and regenerating the orig-
inal AL correctly. Hence, a total of D + 16 bits are
enough for AL storage as raw data in DNA.
Arguably, we find a significant compression ra-
tio for a simple directed graph G using Re-Pair al-
gorithm. As indicated above, let us say l = |C(G)|,
d = max(C(G)), n = |L(G)|, p = log
2
|V | and r = |T |
then l, d, n, p and r accumulatively determine the
total bits sufficient to compress a graph configration
list L(G) using this technique, where |B
1
| = l and
|B
2
| = n. Assuming each dictionary rule in T is a
triplet of integers, which can be stored in an array R.
Hence, |R| = 3 × |T |. Apparently, a total S
1
= (3r +
l) × p + n + l bits are required to store a compressed
form of L(G) in this case. Moreover, we know that
each dictionary rule comprises one non-terminal and
two terminals. For optimization, a pattern exists in the
numeric values of non-terminals of dictionary rules in
T , which starts from |V | + 1 and then increments by
one for every succeeding rule. Since we store a tu-
ple of terminals with a non-terminal value |V | + i at
i
th
index of the array R for i ≥ 1, an index value of
every tuple of terminals in R in addition to |V | equals
the value of its non-terminal. Therefore, this numeric
pattern advantageously omits the storage demand for
the non-terminal integers in the array R. Desirably,
apart from compression, we have found substantial
exploitation in graph-aware data for DNA storage us-
ing this strategy. Accordingly, a composite binary
string including C(G), R, B
1
and B
2
objects with their
cardinalities as prefixes can be structured as follows:
pklkC(G)k2rkRklkB
1
knkB
2
. Remember, a fixed-size
2 bytes integer containing the value p is used to dis-
tinguish all the integers from each other. Optimally,
now a total of S
2
= (2r + l + 4) × p + n + l + 16 bits
(equals to
S
2
2
nucleotides) is necessary to store a com-
pressed graph representation using DNA in this case.
Therefore, the compression ratio can be calculated as
D+16
S
2
for the Re-Pair algorithm.
Of course, the experimental analysis will reveal
what proportion of compression would be achieved.
However, assuming that the fraction value of
D+16
S
2
would be significantly greater than 1 to deliver a valu-
able compression ratio. Then, using this, fewer nu-
cleotides would be needed for simple graph storage
in DNA to AL requirements considering the same en-
coding scheme. Since, a = d
D+16
m
e ≥ b = d
S
2
m
e when
D+16
S
2
≥ 1, hence, fewer DNA strands with each size
m would be synthesised and sequenced using PUT
and GET methods offered in the database engine (Ap-
puswamy et al., 2019). Eventually, an efficient DNA
storage mechanism demonstrated above will profit us
by saving a cost of at least (a − b) × m × $0.05. It
also assists in data portability because the nucleotide-
based relation keeps track of the primer addresses re-
quired to fetch the corresponding data from DNA in
future. So, an existing graph data can be retrieved
randomly from DNA using the GET method to re-
fill the concerned nucleotide relation in the database.
We can reconstruct a simple graph once all its rel-
evant tuples would recover appropriately. Formerly,
the reengineering process should be followed by or-
derly attending to steps from 6 to 10 in Figure 4.
Modelling of Efficient Graph-aware Data Storage using DNA
185

4 EXPERIMENTAL EVALUATION
This section shows experimentally that the Re-Pair
compressor produces significant compression ratios
over other graph representations like AL and AM. The
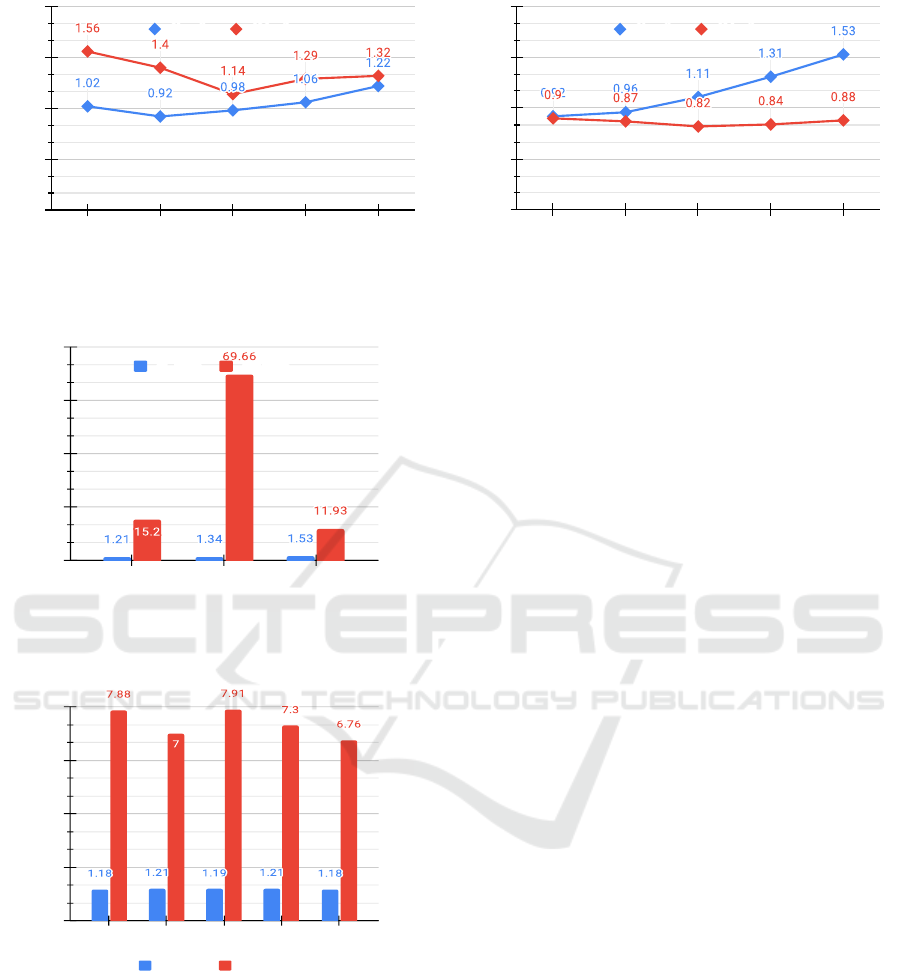
results shown in the Figure 5 are based on simple
graphs with randomly generated edge-lists. Where
both of the Figures 5(a) and 5(b) illustrate the com-
pression ratio (y-axis) with respect to various number
of nodes (x-axis) for different graphs with an aver-
age E pV (edges per vertex) ratios of 10% and 20%
respectively. As we know, the AM representation
of a graph needs |V |
2
+ 16 bits hence the compres-
sion ratio using the RA over AM can be calculated
as
|V |
2
+16
S
2
, where a total
S
2
2
nucleotides are required
to represent a graph using the Re-Pair algorithm in
DNA. The blue and red lines in the Figure 5 act for
RA compression ratio achieved over AL and AM rep-
resentations respectively. Intuitively, the Re-Pair al-
gorithm should be compared only with AL. Instead,
it reveals in the Figure 5(b) that AL behaves worse
than AM representation if the average E pV ratio of
any simple graph inclined over 20%. This argument
can be proved by using a mathematical relation that
0.20 × |V |
2
× log
2
|V | ≥ |V |
2
for all V ≥ 32, where
log
2
|V | is the total bits to store a single integer value.
Therefore, the potential compression ratio gain of the
RA algorithm over AL representation does not guar-
antee us a real benefit in terms of data compression
because it may still be lower than either AM repre-
sentation or not significantly greater enough. Hence,
the k
2
-tree compression should be an obvious choice
if a graph has an average E pV ratio above 20%. Oth-
erwise, the Re-Pair algorithm compression technique
performs better, as depicted in Figure 5(a). However,
our experimental study reveals that the average E pV
ratio for most of the graphs does not accede over 20%
in practice which recommends utilisation of the Re-
Pair algorithm generically for all simple graphs. Two
exemplary datasets have been compressed using the
RA. Moreover, the results are shown graphically in
Figures 6 and 7. To pick the best compression tech-
nique for a graph to take maximum advantage of DNA
storage, we will evaluate all potential compression
techniques for that candidate graph data. Then, that
graph data will compress accordingly. Certain bits
as compressor ID should append to the final com-
pressed binary string as a prefix because graph data
will reconstruct according to its specific compression
technique. For instance, a two bits prefix is enough
to distinguish four different compression techniques.
Generically, the additional eight bits as a prefix to
the final compressed binary string should be reserved
only for this purpose. Conclusively, for graphs in the
metabolic dataset, a minimum compression ratio be-
tween 1.21 to 1.53 has been achieved using the RA.
The data size compresses to at least 18% for all simple
graphs in the case of the PPI (protein-protein interac-
tions) network dataset. In summarizing, the compres-
sion ratio obtained would eventually benefit in worth-
while cost reduction of DNA storage. The implemen-
tation code for the Re-Pair compressor is available on
our GitHub repository
1
in Python language.
4.1 Datasets
4.1.1 Metabolic and Protein Networks
This dataset
2
is about the network of metabolic reac-
tions of (Escherichia coli) bacteria. In the metabolic
network, each node represents a metabolite and each
directed edge X −→ Y denotes the reaction between
metabolites X and Y , where X is given as input and
Y is a product of the reaction (e.g. X + A −→ Y + B).
The sizes of simple graphs data in this dataset are be-
tween 26-45 KB.
4.1.2 Students Network
This dataset
3
is about the students cooperation social
network. In the students network, each node repre-
sents a student and each directed edge X −→ Y denotes
an interaction or friendship between two students X
and Y . The size of this simple directed graph data is
only 6 KB.
4.1.3 Protein-Protein Interactions Network
This dataset
4
is about the normal and cancerous cell
network with respect to protein-protein interaction. In
this network data, each node symbolises a protein,
and each directed edge X −→ Y represents the physical
connection between proteins X and Y in the cell. The
sizes of simple graphs data in this dataset are between
8-46 KB.
The main features of the above datasets are spec-
ified quantitatively in Table 1. Noticeably, the EpV
ratio remains between 1.99 to 7.11. We have not illus-
trated the experimental results for the graph datasets
about the cancerous category rather than the normal
category in the PPI network.
1
https://github.com/asadru90/
DNA-simpleGraphRACompressor.git
2
http://networksciencebook.com/translations/en/
resources/data.html
3
https://data4goodlab.github.io/dataset.html
4
https://rahmanidashti.github.io/PPINetworkAnalysis/
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
186

Number of nodes = |V|
0.0
0.5
1.0
1.5
2.0
16 32 64 128 256
AL ratio AM ratio
(a) Compression of G with average E pV = 10% × |V |.
Number of nodes = |V|
0.0
0.5
1.0
1.5
2.0
16 32 64 128 256
AL ratio AM ratio
(b) Compression of G with average E pV = 20% × |V |.
Figure 5: Compression ratio achieved using Re-Pair algorithm for different G with various |V | as compared to AM and AL.
Compression ratio (times)
0
20
40
60
80
students.
protein.
metaboli
AL ratio AM ratio
Figure 6: Compression ratio achieved using Re-Pair algo-
rithm as compared to AL and AM representation for some
graphs in metabolic and students network datasets.
Compression ratio (times)
0
2
4
6
8
Bone-
Breast-
Liver-
Colon-
Kidney-
AL ratio AM ratio
Figure 7: Compression ratio achieved using Re-Pair com-
pared to AL and AM representation for various exemplary
graphs in PPI network dataset of normal category only.
5 DISCUSSION
Given the high cost of DNA data storage but its abil-
ity to replace tape, potential data must be compressed
in advance. Considering simple graph data archival
demand, we have noticed that exploitation of graph-
aware data storage has an advantage over raw data
storage using DNA besides compression. Optionally,
we can use the k
2
-tree compression technique to re-
duce the relevant input data size for optimal DNA
storage, but this does not support additional data com-
paction benefits using graph-aware data exploitation.
However, the Re-Pair compressor claims a substan-
tial edge of graph-aware data utilization over raw data
for DNA storage. Furthermore, due to potential er-
rors in synthesis and sequencing methods (Schwarz
et al., 2020) of a DNA storage system, the reconstruc-
tion of the original graph seems to be impossible after
retrieving the data from DNA storage based on the
k
2
-tree compression technique. Anticipatedly, even
a single bit error will completely disturb the decom-
pression step in Figure 3. Subsequently, the expected
adjacency matrix would not be appropriate for recon-
structing the original graph. In contrast, errors caused
by biological constraints could have a little impact
on overall graph reconstruction from DNA data stor-
age based on the Re-Pair compressor unless certain
critical bits, such as prefixes, are damaged. As ex-
pected, archived data should be retrieved from DNA
precisely, even after a century. Therefore, a stan-
dard protocol must also be developed and globally
followed by a corresponding DBMS regarding pre-
fixes sizes. Aside from that, we observed that the
Re-Pair algorithm takes too much time to produce the
output, especially for large graph datasets. For in-
stance, it finished execution in more than 10 hours to
produce the final results for the (Breast-Cancer.csv)
dataset that we run on a system with the specifica-
tions of i5-7300U CPU @ 2.60GHz and 32GB RAM.
Therefore, promptly compression of such datasets
will require a high-performance computing environ-
ment. Regarding implementation, we know that the
GET and PUT operations for a relational DBMS have
already been enforced practically by OligoArchive to
read and write oligo(s) within a DNA storage system,
so those can be used straightforwardly as an interface
in our proposed theoretical model implementation.
Modelling of Efficient Graph-aware Data Storage using DNA
187

Table 1: Shows some characteristics of corresponding exemplary graphs in the PPI network and other datasets from the
biological domain. Further, it reveals the representation requirements of these simple graphs data using the Re-Pair algorithm
compared to the AL and AM in terms of bits.
Dataset Nodes Edges EpV Plain size (KB) AM(bits) AL(bits) RA(bits)
Kidney-Normal.csv 315 1347 4.27 17 99225 14958 12581
Colon-Normal.csv 305 1487 4.87 18 93025 16128 13275
Liver-Normal.csv 302 1227 4.06 15 91204 13761 11520
Breast-Normal.csv 331 1694 5.11 21 109561 18225 14997
Bone-Normal.csv 192 618 3.21 8 36864 6480 5449
Kidney-Cancer.csv 491 3135 6.38 38 241081 32634 27301
Breast-Cancer.csv 541 3847 7.11 46 292681 43880 36263
Bone-Cancer.csv 351 1781 5.07 22 123201 19188 16107
protein.edgelist.txt 2018 5047 2.5 26 4072324 77715 58454
metabolic.edgelist.txt 1039 6399 6.15 45 1079521 81818 68203
studentsNetwork.csv 184 367 1.99 6 33856 4408 2878
6 FUTURE WORK
In future work, we want practical implementation of
our proposed model. While working on this research,
an idea about merging multiple graphs to make a com-
posite or aggregate graph (Liu et al., 2016) followed
by its compression and then DNA storage got our at-
tention. It could be another optimization if we suc-
ceed after the exploration that way. We also intend
to exploit other complex graph models, like property
graphs and RDF graphs (Das et al., 2014; Angles,
2018) for efficient DNA storage. With data archives
assistance of these graphs, many emergent databases
and big graph processing frameworks supply persis-
tent, highly scalable, diversified, and efficient analyti-
cal and query processing capabilities for future appli-
cation demands (Sakr et al., 2021; Cai et al., 2018).
Due to this, complex graph-based data should also be
exploited for archival using DNA. It could be chal-
lenging to deal with such vibrant data. However, it
seems to have more potential for compaction due to
the repetition of labelling data. Additionally, we want
to explore other storage media like Peptide sequences
(Ng et al., 2021) similar to DNA.
7 CONCLUSIONS
We presented a theoretical model for DNA storage
of simple graph-based data. The overall vision for
defining this model was to provide a key idea for sim-
ple graph-aware data storage in DNA rather than raw
data storage and show the potential benefit of reduc-
ing the number of nucleotides that need to be stored.
With that concern, a comparative analysis of two tech-
niques: k
2
-tree and the Re-Pair algorithm, was per-
formed experimentally. Moreover, the model focused
on the simple graph-aware data exploitation using the
Re-Pair compressor and accomplished at least 18%
compaction of input data size for DNA storage be-
forehand. A comprehensive description and illustra-
tion of the proposed modelling will contribute to the
optimal implementation of simple graph-aware DNA
data storage.
ACKNOWLEDGEMENTS
I want to thank both (DAAD-Germany and HEC-
Pakistan) organizations for financially supporting me
during my PhD studies at GUF under the “Overseas
Scholarships for PhD in Selected Fields, Phase III,
Batch-1, 2020” program.
REFERENCES
Allentoft, M. E., Collins, M., Harker, D., Haile, J., Oskam,
C. L., Hale, M. L., Campos, P. F., Samaniego, J. A.,
Gilbert, M. T. P., Willerslev, E., et al. (2012). The
half-life of dna in bone: measuring decay kinetics in
158 dated fossils. Proceedings of the Royal Society B:
Biological Sciences, 279(1748):4724–4733.
´
Alvarez, S., Brisaboa, N. R., Ladra, S., and Pedreira,
´
O.
(2010). A compact representation of graph databases.
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
188

In Proceedings of the Eighth Workshop on Mining and
Learning with Graphs, pages 18–25.
Angles, R. (2018). The property graph database model. In
AMW.
Apostolico, A. and Drovandi, G. (2009). Graph compres-
sion by bfs. Algorithms, 2(3):1031–1044.
Appuswamy, R., Le Brigand, K., Barbry, P., Antonini, M.,
Madderson, O., Freemont, P., McDonald, J., and Hei-
nis, T. (2019). Oligoarchive: Using dna in the dbms
storage hierarchy. In CIDR.
Bancroft, C., Bowler, T., Bloom, B., and Clelland, C. T.
(2001). Long-term storage of information in dna. Sci-
ence, 293(5536):1763–1765.
Besta, M., Peter, E., Gerstenberger, R., Fischer, M., Pod-
stawski, M., Barthels, C., Alonso, G., and Hoefler, T.
(2019). Demystifying graph databases: Analysis and
taxonomy of data organization, system designs, and
graph queries. arXiv preprint arXiv:1910.09017.
Boldi, P. and Vigna, S. (2004). The webgraph framework
i: compression techniques. In Proceedings of the 13th
international conference on World Wide Web, pages
595–602.
Bornholt, J., Lopez, R., Carmean, D. M., Ceze, L., Seelig,
G., and Strauss, K. (2016). A dna-based archival stor-
age system. In Proceedings of the Twenty-First Inter-
national Conference on Architectural Support for Pro-
gramming Languages and Operating Systems, pages
637–649.
Buneman, P., Khanna, S., Tajima, K., and Tan, W.-C.
(2004). Archiving scientific data. ACM Transactions
on Database Systems (TODS), 29(1):2–42.
Cai, H., Zheng, V. W., and Chang, K. C.-C. (2018). A com-
prehensive survey of graph embedding: Problems,
techniques, and applications. IEEE Transactions on
Knowledge and Data Engineering, 30:1616–1637.
Carlson, R. (2014). Time for new dna synthesis and se-
quencing cost curves. Synthetic Biology News.
Church, G. M., Gao, Y., and Kosuri, S. (2012). Next-
generation digital information storage in dna. Science,
337(6102):1628–1628.
Claude, F. and Navarro, G. (2010). Fast and compact web
graph representations. ACM Transactions on the Web
(TWEB), 4(4):1–31.
Clelland, C. T., Risca, V., and Bancroft, C. (1999). Hiding
messages in dna microdots. Nature, 399(6736):533–
534.
Das, S., Srinivasan, J., Perry, M., Chong, E. I., and Baner-
jee, J. (2014). A tale of two graphs: Property graphs
as rdf in oracle. In EDBT, pages 762–773.
Davoudian, A., Chen, L., and Liu, M. (2018). A survey
on nosql stores. ACM Computing Surveys (CSUR),
51(2):1–43.
Doorn, P. and Tjalsma, H. (2007). Introduction: archiving
research data. Archival science, 7(1):1–20.
Eid, J., Fehr, A., Gray, J., Luong, K., Lyle, J., Otto, G.,
Peluso, P., Rank, D., Baybayan, P., Bettman, B., et al.
(2009). Real-time dna sequencing from single poly-
merase molecules. Science, 323(5910):133–138.
Epstein, J. M. (2008). Why model? Journal of artificial
societies and social simulation, 11(4):12.
Goldman, N., Bertone, P., Chen, S., Dessimoz, C., LeP-
roust, E. M., Sipos, B., and Birney, E. (2013).
Towards practical, high-capacity, low-maintenance
information storage in synthesized dna. nature,
494(7435):77–80.
Heinis, T. and Alnasir, J. J. (2019). Survey of informa-
tion encoding techniques for dna. arXiv preprint
arXiv:1906.11062.
Kosuri, S. and Church, G. M. (2014). Large-scale de novo
dna synthesis: technologies and applications. Nature
methods, 11(5):499–507.
Lee, H. H., Kalhor, R., Goela, N., Bolot, J., and Church,
G. M. (2018). Enzymatic dna synthesis for digital in-
formation storage. bioRxiv, page 348987.
Lehne, B. and Schlitt, T. (2009). Protein-protein inter-
action databases: keeping up with growing interac-
tomes. Human genomics, 3(3):1–7.
Liu, Y., Safavi, T., Dighe, A., and Koutra, D. (2016). Graph
summarization methods and applications: A survey.
arXiv: Information Retrieval.
Neiman, M. S. (1964). Some fundamental issues of micro-
miniaturization. Radiotekhnika, 1(1):3–12.
Ng, C. C. A., Tam, W. M., Yin, H., Wu, Q., So, P.-K.,
Wong, M. Y.-M., Lau, F., and Yao, Z.-P. (2021). Data
storage using peptide sequences. Nature Communica-
tions, 12(1):1–10.
Organick, L., Ang, S. D., Chen, Y.-J., Lopez, R., Yekhanin,
S., Makarychev, K., Racz, M. Z., Kamath, G.,
Gopalan, P., Nguyen, B., et al. (2018). Random access
in large-scale dna data storage. Nature biotechnology,
36(3):242–248.
Sakr, S., Bonifati, A., Voigt, H., Iosup, A., Ammar, K.,
Angles, R., Aref, W., Arenas, M., Besta, M., Boncz,
P. A., et al. (2021). The future is big graphs: a com-
munity view on graph processing systems. Communi-
cations of the ACM, 64(9):62–71.
Schwarz, M., Welzel, M., Kabdullayeva, T., Becker, A.,
Freisleben, B., and Heider, D. (2020). Mesa: auto-
mated assessment of synthetic dna fragments and sim-
ulation of dna synthesis, storage, sequencing and pcr
errors. Bioinformatics, 36(11):3322–3326.
Seeman, N. C. (2003). Dna in a material world. Nature,
421(6921):427–431.
Simecek, I. (2009). Sparse matrix computations using the
quadtree storage format. In 2009 11th International
Symposium on Symbolic and Numeric Algorithms for
Scientific Computing, pages 168–173.
Whitlock, M. C., McPeek, M. A., Rausher, M. D., Riese-
berg, L., and Moore, A. J. (2010). Data archiving.
The American Naturalist, 175(2):145–146.
Modelling of Efficient Graph-aware Data Storage using DNA
189