Linear Programming: A Diet Problem with Methane Emission

Xunzi Xie

1,*

, Shi Zhang

, Yizhe Chen

and Yifan Pan

University of California, Los Angeles, 90024, U.S.A.

Shanghai Pinghe School, Shanghai, 201206, China

Hangzhou Foreign Language School, Hangzhou, 310000, China

Villanova Preparatory School, Ojai, 93023, U.S.A.

Keywords: Linear Programming, Optimization, Diet Problem, Methane Emissions.

Abstract: Cattle diet problems are concerned with finding the optimal diet for cattle. Classical diet problems are linear

programming problems. This paper considers a complication of diet problem, adding to the traditional setting

the extra component of methane emission. We find that under proper assumptions this complicated model is

yet another linear programming problem. We then realize our model with empirical data and obtain the

optimal diet for cattle via the simplex method. Sensitivity analysis is run against selected parameters. We

conclude that our model is mostly successful, yielding many practical considerations.

1 INTRODUCTION

Diet, by its definition, is the food and drink that a

person or animal drinks and eats regularly.

Researches have been done on optimizing the diet of

cattle in a limited range or within a specific area. To

generalize, we developed an adaptable model which

aims at balancing between the cost of a diet and

maintaining the animal’s basic conditions. The

general goal of this process is getting the maximum

nutritional requirements for the least amount of

money. A unique feature of our model is the added

goal of reducing methane emissions.

In building the model, we have made

assumptions, gathered data for nutrition intake

required for cattle, formulated functions, and gained

results by utilizing linear programming.

2 BACKGROUND AND

PROBLEM SET-UP

First we present a quick summary of our problem

scenario. Our model starts with a cattle representative

which is bought in at an initial weight. This cattle

gains weight daily. The cattle is fed with a diet of N

types of food. That cattle is also assumed to have a

realistic eating habit, where it eats only a certain

amount of food every day determined by its weight.

This value is known as the dry matter intake of the

cattle.

For each type of food, a set of nutrient

concentrations are obtained from laboratory and

empirical estimations. 4 nutrient requirements are

checked every day to ensure that the cattle is growing

healthily. The daily growth in weight of the cattle

depends on how much food the cattle consumes, and

in particular we assume that the growth in weight

depends on the total energy intake of the cattle.

Ultimately the main source of income of the cattle

owner comes from selling the finishing cattle. The

sale price is per unit weight.

Finally, IPCC estimated the daily methane

emission of cattle as a linear function of its total

energy intake (Dong, Mangino, & McAllister 2006).

We then imagine that the government imposes

environmental policies so that an emission fine is

charged for every unit of excessive methane emission

(amount that exceeds an emission threshold).

We move on to formulate the above scenario into

an optimization problem. First, recall that our

objectives are to increase the sale price of cattle, to

reduce methane emission, and to reduce the diet cost.

We then translate these into the following equation:

𝑚𝑎𝑥. 𝑝 ∙ ∆𝑊 − 𝑐



∙𝑥−𝑓∙𝑀



(1)

where ∆𝑊 is the daily increase of weight, 𝑐



(Rankin, 2021, Halopka, 2020, Livestock, Poultry, &

Grain, University of Missouri Extension,

IndexMundi, Alibaba 2021) is a vector of diet food

Xie, X., Zhang, S., Chen, Y. and Pan, Y.

Linear Programming: A Diet Problem with Methane Emission.

DOI: 10.5220/0011361000003438

In Proceedings of the 1st International Conference on Health Big Data and Intelligent Healthcare (ICHIH 2022), pages 295-301

ISBN: 978-989-758-596-8

295

cost, 𝑓 is the unit fine charged on methane emission

𝑀



, 𝑝 (Ag Decision Maker 2021) is the unit sell price

of cattle, and 𝑥 is a vector of the weight of each food

type in the diet. The given question requires us to vary

𝑥 to achieve the maximum of the objective function

of 𝑥 defined above.

To ensure that this problem is realistic, we set up

six constraints with respect to the food vector 𝑥 .

First, obviously entries of 𝑥 should be positive:

𝑥≥0 (2)

We introduce the term 𝐷 to represent the daily

dry matter intake of a cattle, which is estimated using

the linear equation 𝐷 = 1.8545 + 0.01937 ∙ 𝑊



where 𝑊



is the initial weight (Ag Decision Maker

(2021). 𝐷 then equals the total weight of the food

provided:

𝑒



∙ 𝑥 = 𝐷, 𝑒 =



1, 1, … ,1





(3)

We require that our diet should satisfy the daily

nutrient requirements of cattle. We introduce the

matrix 𝐴 (National Academy of Science,

Engineering, and Medicine (2000), whose columns

correspond to each food type and rows correspond to

the different types of nutrients. We further introduce

the term 𝑏 National Academy of Science,

Engineering, and Medicine (2000) to represent the

minimum nutrients required by the cattle for

sustenance. Hence,

𝐴∙𝑥≥𝑏 (4)

We also require that the cattle are always gaining

weight. This ensures that the farmer is always making

profit. According to NASEM, the daily increase in

weight can be estimated as ∆𝑊 = 13.91 ∙

(

𝐸



−

𝐸



)

∙𝑊

.

, where 𝑊 is the daily weight, 𝐸



the total energy intake, and 𝐸



is the energy required

to maintain a cattle’s activities. 𝐸



and 𝐸



can

further be estimated by 𝐸



=𝐶



∙𝑥 and 𝐸



=𝑠∙

𝑊

.

, where 𝐶 National Academy of Science,

Engineering, and Medicine (2000) is an energy vector

specifying the energy concentration in each type of

food and 𝑠 National Academy of Science,

Engineering, and Medicine (2000) is a scaling factor

depending on the cattle’s breed, sex, and cattle’s

nutritional conditions etc. These equations then allow

us to write ∆𝑊 as a function of 𝑥 , and we obtain

another constraint:

∆𝑊

(

𝑥

)

= 13.91 ∙

(

𝐶



∙𝑥 −𝑠∙𝑊

.

)

∙𝑊

.

≥0(5)

According to IPCC, the total methane emission

𝑀 is estimated as 𝑀=





∙∙



, w h e r e 𝑘 is a unit

conversion factor, 𝑚 is a methane conversion factor,

and 𝑚𝑒𝑐 is the methane energy constant (Dong,

Mangino, & McAllister, 2006). We then set an

emission threshold 𝑀



and define the corresponding

excessive methane emission 𝑀



=𝑀−𝑀



. Our

problem is meaningful only if 𝑀



is positive:

𝑀



≥0 (6)

We also want to ensure that 𝑀



follows IPCC’s

empirical estimation:

𝑀



≥





∙∙



−𝑀



∙



∙𝐶



∙𝑥−𝑀



(7)

Combining these estimates, we obtain the

following optimization problem:

(*) 𝑚𝑎𝑥. 𝑝 ∙ ∆𝑊(𝑥) − 𝑐



∙𝑥−𝑓∙𝑀



(8)

𝑠. 𝑡. 𝑥 ≥ 0, 𝑒



∙𝑥=𝐷,𝐴∙𝑥≥𝑏,∆𝑊

(

𝑥

)

≥0,𝑀



≥0,𝑀



≥

∙



∙𝐶



∙𝑥−𝑀



(9)

A summary of all variables and their symbols can

be found in table 1.

Table 1: Symbols

Symbol Uni

Description

𝑥

kg N-dimensional vector specifying how much kg of each food types a cattle eats per day.

𝑀

kg Estimated kg of methane emitted by a cattle per day

𝑐



$/kg N-dimensional vector specifying how much a kg of each food type costs

𝐴

unit MN matrix specifying how much nutrient each food type contains

𝑏

kg M-dimensional vector specifying daily requirement of a specific nutrient

𝐶

J/kg N-dimensional vector specifying energy concentration in each food type

𝑒



unit N-dimensional vector of ones

ICHIH 2022 - International Conference on Health Big Data and Intelligent Healthcare

296

𝑝

$/kg Selling price of cattle meat

𝑊

kg Daily weight of a cattle

𝑓

$/kg Amount of capital punishment per kg of excessive methane emission

𝐷

kg Daily dry matter intake of a cattle

𝐸



MCal Daily energy of maintenance for a cattle

𝑠

J/kg0.75 Correlation factor between Emand W, which depends on breed, nutritional state, and sex etc.

𝑘

MJ/MCal Unit conversion factor

𝐸



MCal Total energy intake of a cattle per day

𝑚

unit Methane conversion factor

𝑚𝑒𝑐

MJ/kg Methane energy constant

𝑀



kg Methane emission threshold

3 DATA AND METHODOLOGY

3.1 Data

Our primary data sources are IPCC and NASEM.

Other data (mainly market prices of diet food and

cattle) are quoted from various Internet sources. We

manually assign values to some parameters, such as

the fine placed on excessive methane emissions. See

table 2-4 for a full presentation of data and their

sources.

Table 2: Nutritional/Energy concentration and Cost (A/C

and c):

Food Type

(Mcal/kg)

(%)

Cost

($/ton)

ALFALFA

Fresh

1.38 18.90 1.29 0.26 167

Hay 1.31 18.6 1.40` 0.28 171

Straw 0.6 4.40 0.30 0.07 70

Gluten

meal

2.20 66.3 0.07 0.61 700

Seed 2.24 24.4 0.17 0.62 370

Barley

Grain

2.06 13.2 0.05 0.35 114

Sugar beets 1.76 9.8 0.68 0.1 125

Cotton

hulls

0.68 4.2 0.15 0.09 230

Wheat

midds

1.6 18.7 0.17 1.01 220

Cottonseed

Meal

1.79 46.1 0.02 0.02 370

Distiller’s

grains

dried

2.18 30.4 0.26 0.83 271

Oat hulls 0.41 4.1 0.16 0.15 129

Table 3: Nutritional requirement (b): (assume W_0 = 400

kg; breed code “1 Angus”; W_T = 890 kg).

Type Measurement/Unit (per day) Value

Energy Net Energy (NE) / Mcal 6.38

Table 4: Data Sources.

Protein

Metabolizable protein

(MP) /kg

(CP = MP/0.64)

0.274

C/Calciu

C / kg 9/1000

P/Phosphorus P / kg 7/1000

Paramete

Estimated Value/Unit Source

Linear Programming: A Diet Problem with Methane Emission

297

𝑐



See table 2

𝐴

See table 2 NASEM

2000, 134

𝑏

See table 3 NASEM

2000, 106

𝐶

See table 2 NASEM

2000, 134

𝑝

2.9548/$/kg

𝑊



400/kg NASEM

2000, 106

𝑓

88644/1000000 30% of

sell

rice

𝑠

0.077 NASEM

2000, 6

𝑘

4184000/1000000

𝑚

3% IPCC

2006,

4 ,10.30

𝑚𝑒𝑐

55.65 IPCC

2006, 4,

10.31

𝑀



0.125 Assume

𝐸



=𝐸



then

compute

IPCC’s

uation

3.2 Methodology

Simplex Method is an iterative algorithm, which aims

to find the optimal solution of x. Its main steps are:

1) find a basic feasible solution;

2) judge whether the solution is the optimal

according to the optimality theory;

3) if it is the optimal, then stop the process;

4) if it is not, then try to generate a new feasible

solution which better minimizes the objective

function; and

5) judge its optimality again.

This loop is continued until an optimal solution is

found.

However, in different cases, there are distinct

results of the simplex method. In some cases, the LP

problem would degenerate. This happens when one

of basic feasible variables has zero value. Infinite

iterations would appear, and this prevents the

algorithm from converging.

If no degeneracy appears, the simplex method

would converge after certain iterations. Two results

would appear: an optimal feasible solution, which

leads to a minimum value of objective; or an infinite

amount of feasible solutions where the objective has

no lower bound.

Simplex method only works for optimization

problems in their canonical forms. To convert (*) into

its canonical form, we define the canonical variables

as follows:

Table 5: Canonical Variables.

Slack

Variable

Definition

(where v is a vector of slack

variables

)

These canonical variables define an optimization

problem as follows:

(**) 𝑚𝑖𝑛. 𝑐̂



∙𝑥

𝑠. 𝑡. 𝑥≥0,𝐴



∙𝑥=𝑏



(10)

And it is easy to check that (**) is equivalent with

(*). We then run the simplex method to obtain a

ICHIH 2022 - International Conference on Health Big Data and Intelligent Healthcare

298

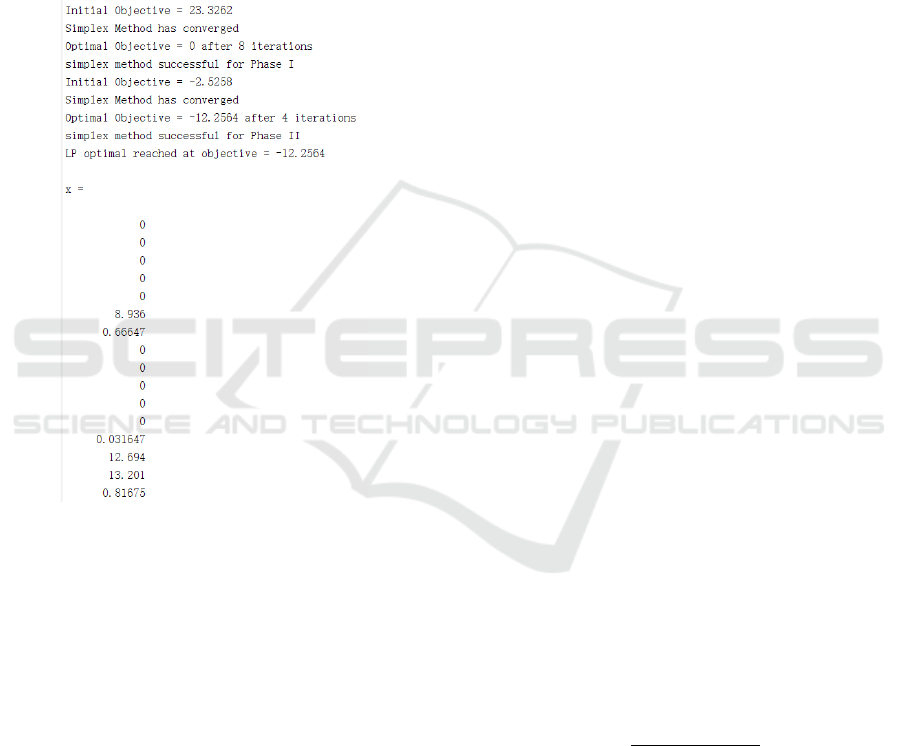
solution to (**), from which we obtain a solution to

(*).

3.3 Results and Analysis

The algorithm run on the data apparently converges

and outputs an optimal diet with two non-zero

components: about 8.9 kg of barley grains and 0.67

kg of sugar beets. The program also reports an

optimal objective of -12.2564, meaning that the

maximum profit for the cattle owner on the first day

is about 12 dollars.

Figure 1: Simplex Method Status and Optimal 𝒙



A couple of remarks on the result are in place.

First, only two types of food are included in the

optimal diet. Usually one should worry when the

number of non-zero outputs is small. In particular, it

may mean that the problem is degenerate if the

number of non-zero outputs is significantly lower

than the number of constraints. However, for our

problem we only have one equality constraint in our

original diet problem:

𝑒



∙ 𝑥 = 𝐷 (11)

Hence if the other inequality constraints are

merciful, then potentially we only need to allow one

or a few degrees of freedom in the diet vector x to

meet all the constraints. This intuition is justified.

Observe that 𝑥 has five other non-zero components.

One of these corresponds to 𝑀



, and the other four are

slack variables. Indeed, 𝐴



in the canonical form is a

rank 7 matrix. Hence, it makes sense for us to obtain

exactly seven non-trivial components in our solution.

The fact that only two components of the diet vector

are non-trivial is a direct consequence of the way the

constraints are formulated. Therefore,

mathematically the result is consistent.

There are two zero slack variables. This indicates

that two constraints have reached the boundaries on

the feasibility plane. When we plug in our vector x

back to the optimization problem, we can see that the

requirement of Calcium (C) is exactly reached. If the

cattle may require slightly more protein, phosphorus,

and energy, the diet given above is still suitable and

effective. But if calcium (C) requirement increases,

then the boundary is pushed outwards and the

optimum diet above no longer satisfies the nutrient

requirements.

Another legitimate concern is that compared with

the nutrient requirements specified in vector 𝑏, some

reasonably priced food types are simply too nutritious

so that the nutrient requirements are easily met. This

intuition can be backed up by a simple sensitivity

analysis on the parameter 𝑏 . Indeed, apparently

doubling 𝑏 only increases the maximum profit by

about 0.1 dollars. The new optimal diet is still

composed of sugar beets and barley grains where

barley grains. This pattern persists as we impose

stricter nutrient requirements, until when the nutrient

requirements are about four times stricter than the

original one and the linear program then becomes

infeasible. Therefore, the objective function is

apparently insensitive to the nutrient requirements

(wherever the problem is feasible). This then supports

the intuition that when the cattle owner is choosing

between different types of diet food with the hope of

maximizing net profit, nutrient requirements turn out

to be a rather insignificant factor.

Next, observe that the thirteenth component (of

which corresponds to 𝑀



) is closed to 0. This means

that the optimal methane emission is very closed to

the emission threshold (𝑀



). Recall that methane

emission and growth in weight both depend linearly

on energy intake:

(***) 𝑓=

.∙∙

.

∙

∙

(12)

So, changing 𝑥 should result in comparable

changes in the profit generated by growth in weight

𝑝∙𝑊 and the cost resulted from excessive methane

emission −𝑓 ∙ 𝑀



. Sensitivity analysis on 𝑝 a n d 𝑓

confirms a part of this intuition. The objective is

sensitive to 𝑝 but quite stable with respect to 𝑓 ,

unless f is multiplied to be quite large. This makes

sense intuitively, since 𝑓 is per kg charge on

Linear Programming: A Diet Problem with Methane Emission

299

methane emission. As we all know methane is a gas,

and hence kg is a rather misleading dimension of

weight for methane.

Furthermore, when the profit generated by growth

in weight matches with the cost from emission (the

exact 𝑓 that makes this happen can be obtained from

solving the equation (***) above) the farmer is not

making any real profit out of the cattle business. This

is perhaps a useful fact for governors to decide how

much fine should be in place (with respect to the sale

price of cattle) in order to economically effectively

affect the cattle owner’s behaviors.

Finally, sensitivity analysis on the food cost 𝑐

and 𝐷 are also conducted. The food cost is

apparently very low in comparison with sale price 𝑝

and methane emission fine. Hence, apparently the

objective is quite insensitive to the food cost unless

the sale price of cattle diet food becomes comparable

to the sale price of cattle itself. 𝐷 acts as an upper

bound for the diet vector 𝑥 . Should D increase

drastically, it is expected that under our problem set

up the cattle grows in weight indefinitely. The

objective indeed shoots off as D increases

indefinitely.

4 RESULTS AND ANALYSIS

In this paper, we have considered a revised cattle diet

problem with the added component of methane

emissions. We formulate the problem as an

optimization problem and solve it through the

simplex method. In general, our problem is easy to

construct and solve. Sensitivity analysis proves that

the methane emission fee is an effective way to affect

the cattle business. In addition, our model is also

adaptable to different species of animals and different

nutrition requirements, by simply changing several

parameters in our model. Within reasonable range,

we expect our method to still converge to an optimal.

Any model has to give way to simplifications. We

now turn to point out some issues and suggestions for

future improvements. To begin with, there are a

couple of assumptions that can be avoided by

considering more complicated models. First, in our

model we assume that the weight gain of the cattle is

a constant. Our model can naturally be extended to a

dynamic programming problem by introducing a

weight function that evolves over discrete time.

Moreover, we assume that the same nutrient

requirements apply to cattle among all age groups. In

reality, it requires more nutrients when cattle are

young and in the process of growth. Hence the

constraint for nutrient requirements should depend on

time as well, and this can be incorporated with the

growth in weight in a dynamic programming version

of our simply model.

Also, note that the methane emission fee we put

on is regarded as fixed regardless of the amount of

excessive emissions. However, as in the case of

taxation capital punishments are typically piecewise

functions. This can be potentially a more complex

constraint for our problem.

Finally, in our optimal diet only two types of food

are selected. This is because our constraints and

nutritional estimations are simple and we pay no

attention to digestion processes and finer nutritional

requirements. For example, our system is based on an

assumption that the cattle will take in all the nutrition

the food supplies them. However, in the real world it

is definitely not the truth. The cattle may require other

food to help them fully absorb the nutrients. Future

studies of cattle diet problems should take these into

the account and consider, for example, a more

intricate mechanistic model of cattle’s nutrition.

5 CONCLUSIONS

Our group formulates a revised diet problem, which

considers sell price of cattle, cost of the diet, the fine

charged on methane emission, and the weight growth

of cattle. We obtain formulas mainly from NASEM

and IPCC and collect data of parameters on the

Internet. This could then be solved by Simplex

Method in Matlab. We conclude with a suggested

optimal diet and suggest for future research that a

dynamic version of our problem to be developed.

REFERENCES

Ag Decision Maker (2021). Historical Cattle Prices.

https://www.extension.iastate.edu/agdm/livestock/pdf/

b2-12.pdf

Alibaba.com (2021). Organic Price Sugar Pellets Beet Pulp.

https://ua1335743999cerh.trustpass.alibaba.com/produ

ct/62006362618-

810718723/Organic_Price_Sugar_Pellets_Beet_Pulp.h

tml

AMS Livestock, Poultry, & Grain Market News. US

(2021). Hay Auction Weighted Average Report For

June 23,

2021.https://www.ams.usda.gov/mnreports/ams_1725.

pdf

Dong, H., Mangino, J., & McAllister, T. (2006). Emissions

from Livestock and Manure Management. In: IPCC

(Ed.), 2006 Guidelines for National Greenhouse Gas

Inventories. The Institutes for Global Environmental

ICHIH 2022 - International Conference on Health Big Data and Intelligent Healthcare

300

Strategies, Japan. volume 4.10: pp. 31-

32.https://www.ipcc-

nggip.iges.or.jp/public/2006gl/pdf/4_Volume4/V4_00

_Cover.pdf

Halopka, R. US (2020). Hay Market Demand and Price

Report for the Upper Midwest For January 13,

2020.https://fyi.extension.wisc.edu/forage/files/2020/0

1/01-13-20.pdf

IndexMundi (2021). Barley Monthly Price.

https://www.indexmundi.com/commodities/?commodi

ty=barley&months=60

National Academy of Science, Engineering, and Medicine

(2000). Nutrient Requirements of Beef Cattle: Seventh

Edition. National Academy Press. p.6, pp.106-134.

Rankin, M. US (2021). USDA Hay Market.

https://hayandforage.com/articles.sec-7-1-

Markets.html

University of Missouri Extension. US (2021). By-Product

Feed Price Listing.

http://agebb.missouri.edu/dairy/byprod/bplist.asp

Linear Programming: A Diet Problem with Methane Emission

301