Control Strategy of Upper Limb Rehabilitation Exoskeleton based on

Impedance Control and Position Feedback

Yan Bo

and Wei Wei

b, *

School of Electrical and Electronic Engineering, Changchun University of Technology,

Yanan Main Street, Changchun, China

Keywords: Rehabilitation Robot, Impedance Control, Human Body Impedance Model.

Abstract: The upper limb rehabilitation exoskeleton was designed based on the human movement mode, and the

kinematics and dynamics of the exoskeleton were modeled by simulink. The double closed-loop control

system composed of impedance controller and position feedback was designed according to the control

requirements. Based on the movement requirements, The parameters were adjusted adaptively to meet the

design needs, and the conclusion was proved through simulation experiments.

https://orcid.org/0000-0001-5781-6025

https://orcid.org/0000-0001-8760-7400

1 INTRODUCTION

At present, with the improvement of living standards

and the increase of average life expectancy, the

number of people with movement disorders caused

by strokes and other causes is increasing

rapidly(Cheng 2019). Rehabilitation training is an

important recovery method for people with

movement disorders (Zhuo 2003), but traditional

rehabilitation training is highly dependent on

professionals (Sun 2019). The training method

assisted by rehabilitation robots has developed

rapidly in recent years (Lo 2010, Klamroth-

Marganska 2014). Studies have shown that

rehabilitation robots such as exoskeleton can play a

very helpful role in the rehabilitation training of

patients with movement disorders caused by stroke

(Connell 2014). The rehabilitation exoskeleton can

realize different types of rehabilitation training, such

as active and passive, through the cooperation of

man and machine. By simulating the daily motion

behavior of the human body, it helps patients to

realize the recurrence of daily activities, and helps

users to achieve muscle and nervous system

recovery by providing impedance or exercise

assistance, and restore the corresponding motor

functions (Yao 2019). In this regard, scholars have

conducted a lot of researches on rehabilitation

exoskeleton, the focus of which is the human-

computer interaction control method of exoskeleton

(Li 2008).

Due to the non-linear characteristics of the man-

machine coupling system, many scholars have

proposed different control strategies based on

different control theories. According to the extracted

human-computer interaction information, it can be

divided into two types: bio-signal-based human-

computer interaction and force/position information-

based human-computer interaction (Du 2018). Since

human body signals are difficult to extract and

susceptible to interference, signal processing in this

way is relatively cumbersome. The human-computer

interaction method based on force/position

information has the advantages of simple extraction

and clear physical meaning. The current research is

relatively mature. For example, Saglia et al. used

impedance control to adjust the compliance of the

ankle rehabilitation robot to achieve patient-assisted

training (Saglia 2013). However, the traditional

impedance control control method has fixed control

parameters and is effective for a single training

target, but it is difficult to meet different training

requirements. Aiming at the above problems, this

paper designs an exoskeleton control system that

adaptively adjusts impedance control parameters.

Bo, Y. and Wei, W.

Control Strategy of Upper Limb Rehabilitation Exoskeleton based on Impedance Control and Position Feedback.

DOI: 10.5220/0011370500003438

In Proceedings of the 1st International Conference on Health Big Data and Intelligent Healthcare (ICHIH 2022), pages 379-384

ISBN: 978-989-758-596-8

379

2 EXOSKELETON MODEL

2.1 Exoskeleton Kinematics Model

In order to ensure the coordination of human-

machine movement, the exoskeleton and the human

body should adopt similar movement patterns and

structural designs. The upper limb exoskeleton

model with 2 rigid bodies and 4 free in series is used

as the research object. The shoulder joint and elbow

joint are used as the main joints for exercise

assistance. The four degrees of freedom of shoulder

internal rotation/external rotation, forward

flexion/posterior extension, outward

swing/adduction, and elbow joint flexion/posterior

extension are the design degrees of freedom. The

schematic diagram is shown in Fig 1. Among them,

the X

-Y

-Z

coordinate system is the base

coordinate system, and its coordinate origin

coincides with the shoulder joint point.

The exoskeleton uses flat extension to the right

as the initial state of motion, and the joint angle θ

1-4

represents the angle between it and the initial state,

where θ

1-4

corresponds to the flexion/extension,

extension/adduction, and rotation of the shoulder

joint, respectively. Internal/external rotation, elbow

flexion/extension four degrees of freedom. Since

there are two rotating shafts that coincide with the

joints, it is difficult to model with the D-H parameter

method. The kinematics model is established

directly by the principle of coordinate change. The

transformation method is shown in Table 1.

Figure 1: Schematic diagram of exoskeleton.

Table 1: Coordinate system change table.

Coordinate

system

0→1 1→2

Coordinate

system

change

method

Rotate around

the X-axis

square -pi/2 →

rotate around the

Z-axis square θ

Rotate around the Y-axis

square -pi/2→

rotate around the X-axis

square pi/2→

rotate around the Z-axis

square θ2

Table 1 (CONTINUED)

Coordinate

system

2→3 3→4

Coordinate

system

change

method

Rotate around the

Z-axis square -

pi/2→

rotate around the

X-axis square -

pi/2→

translate along the

Z-axis square l1→

rotate around the

Z-axis s

uare θ3

Rotate square

around Y axis -

pi/2→

rotate pi/2

around X axis→

rotate square

around Z axis

θ4

𝑇=𝑅𝑜𝑡

(

𝑋,−𝑝𝑖 2

⁄)





𝑅𝑜𝑡

(

𝑍,𝜃



)(

)

𝑇=𝑅𝑜𝑡

(

𝑌,−𝑝𝑖 2

⁄)





𝑅𝑜𝑡

(

𝑋,𝑝𝑖 2

⁄)

𝑅𝑜𝑡

(

𝑍,𝜃



)(

)

𝑇=𝑅𝑜𝑡

(

𝑍,−𝑝𝑖 2

⁄)





𝑅𝑜𝑡

(

𝑋,−𝑝𝑖 2

⁄)

∙

𝑇𝑟𝑎𝑛𝑠(𝑍,𝑙



)𝑅𝑜𝑡

(

𝑍,𝜃



)(

)

𝑇=𝑅𝑜𝑡

(

𝑌,−𝑝𝑖 2

⁄)

𝑅𝑜𝑡

(

𝑋,𝑝𝑖 2

⁄)





𝑅𝑜𝑡

(

𝑍,𝜃



)(

)

Where, 𝑇





represents the coordinate

transformation matrix from the coordinate to the nth

coordinate in the n+1 coordinate system. 𝑅𝑜𝑡

(

𝑎,𝜃

)

represents the transformation matrix that rotates θ

degrees around the coordinate axis a, and

𝑇𝑟𝑎𝑛𝑠(𝑍,𝑙



) represents the transformation matrix

that translates l1 toward the Z axis. Then the spatial

coordinates of the elbow joint and wrist joint in the

base coordinate system are



𝑋



,𝑌



,𝑍







=𝑇





𝑇





𝑙



,0,0,1



(

)



𝑋



,𝑌



,𝑍







=𝑇





𝑇𝑇𝑇













𝑙



,0,0,1



(

)

Where, [X

] is the coordinate of the elbow

joint, [X

] is the coordinate of the wrist joint,

and the speed of the joint points is

𝑉 = 𝜕𝑋 𝜕𝜃

⁄

∙𝑑𝜃 𝑑𝑡

⁄(

)

2.2 Exoskeleton Dynamic Model

In this paper, Lagrangian equations are used to

establish the exoskeleton dynamics model. The

model ignores the joint friction damping and the

movement deviation caused by the mechanism

mismatch. At the same time, the exoskeleton is

regarded as a pure rigid mechanism. Take the

shoulder joint as the origin of motion, and the o-xy

plane of the base coordinate system as the zero

potential energy surface. Assuming that the weight

of the boom mechanism is m1, the center of mass

and the origin of motion are l

, the weight of the

forearm mechanism is m

, and the distance between

ICHIH 2022 - International Conference on Health Big Data and Intelligent Healthcare

380

the center of mass and the elbow joint is l

. From the

Lagrangian equation

𝑇=

𝑑

𝑑𝑡

𝜕𝐿

𝜕𝜃



−

𝜕𝐿

𝜕𝜃

(

)

Among them, T is the joint torque and L is the

Lagrangian function, which is the difference

between the kinetic energy and the potential energy

of the system, namely

𝐿𝜃



,𝜃=𝐾𝜃



,𝜃−𝑃

(

𝜃

)(

)

Among them, K is the total kinetic energy of the

system, and P is the total potential energy of the

system. The exoskeleton is regarded as a

homogeneous rigid body to reduce the complexity of

the system. Then the rigid body can be equivalent to

the mass point at the center of mass of the rigid

body. From equation (7), the speed of the mass point

in various directions can be known, and the negative

semi-axis direction of the base coordinate Z axis is

taken as the gravity direction. Then

𝐿𝜃



,𝜃=(𝑚



𝑉





𝜃



,𝜃+𝑚



𝑉



(𝜃



,𝜃)) 2

⁄

−𝑚



𝑍



(

𝜃

)

+𝑚



𝑍



(

𝜃

)

𝑔

(

)

The standard form of its kinetic equation can be

expressed as

𝑀

(

𝜃

)

𝜃



+𝐶𝜃



,𝜃𝜃



+𝐺

(

𝜃

)

=𝑇

(

)

Among them, 𝑀

(

𝜃

)

represents the moment of

inertia of the exoskeleton, 𝐶𝜃



,𝜃 represents the

Geese force and centrifugal force terms of the

system, and 𝐺

(

𝜃

)

represents the gravity term

2.3 Human Body Impedance Model

The paper (Duchaine 2009) uses a spring model to

describe the human body impedance, and proposes a

human body impedance model. The concept is that

when the human body remains stationary in space,

the distance between the moving unit and the force

is linear. Namely

𝐹=𝐾𝑥+𝑏

(

)

This article uses this method to obtain the contact

force between the human body and the exoskeleton.

In the preliminary work of this research group, the

repeatability of human motion was verified, and the

results proved that for the same moving target, the

human body's multiple motion trajectories have a

high degree of similarity. The movement was

planned. Based on the above assumptions, it can be

considered that during movement, when the actual

route of the human body deviates from the

movement intention, a force will be applied in the

opposite direction of the deviation direction. Based

on the results of literature (Duchaine 2009), it is

assumed that the force of the device has a linear

relationship with the actual route and the size of the

motion intention, thereby simulating the human-

machine contact force in actual motion.

3 EXOSKELETON

CONTROLLER DESIGN

3.1 Design Requirements

The control design of the human rehabilitation

exoskeleton should meet the active and passive

training requirements of rehabilitation training, that

is, when the user is completely or partially disabled,

the exoskeleton provides additional torque to help

the patient complete the exercise goal. When the

user has active exercise ability, he should follow the

user's movement. At the same time, safety

requirements should be met, and when the contact

force is large, stop in time to ensure the safety of

users. In addition, it should have a certain degree of

flexibility to meet the needs of human-computer

interaction.

3.2 Impedance Control

Impedance control is a way to achieve indirect force

control by controlling the movement of the robot. Its

ultimate goal is neither to directly control the

movement of the system nor the contact force

between the system and the outside world, but the

dynamic relationship between the two. Make the

motion joints of the mechanical system exhibit the

dynamic characteristics of the second-order system

composed of spring-damping-mass, namely:

𝑀



𝜃





+𝐷



𝜃





+𝐾



𝜃



=𝜏



(

)

Among them, 𝑀



,𝐷



,𝐾



correspond to the set

mass, damping, and elastic coefficient respectively.

In order to make the impedance characteristics of

each joint independent of each other, 𝑀



,𝐷



,𝐾



are

generally designed as diagonal arrays, and 𝜃



is the

movement deviation angle. Combine it with

equation (11) to obtain a motion model including

impedance control.

Control Strategy of Upper Limb Rehabilitation Exoskeleton based on Impedance Control and Position Feedback

381

𝜏=𝑀

(

𝜃

)

𝜃





+𝐶𝜃



,𝜃𝜃



+𝐺

(

𝜃

)

+𝑀

(

𝜃

)

𝑀







𝐷



𝜃





+𝐾



𝜃





+𝐼−𝑀

(

𝜃

)

𝑀





𝜏



(14)

Among them, 𝜃



is the set joint angle, θ is the actual

joint angle, and I is the identity matrix.

3.3 Position Feedback

Because the feedback torque of the impedance

control part of the design controller is determined by

the actual joint angle and the user's own planned

joint angle. For the set trajectory and the actual

trajectory, it is actually an open-loop control. In this

case, in order to improve the controllability of the

exoskeleton, the joint angle and joint angular

velocity feedback are used to realize the position

feedback of the controller.

𝜏



=𝐾



𝜃



+𝐾



𝜃

(

)

The controller block diagram is shown as in Fig.

Figure 2. System control block diagram

3.4 Control Parameter Design

Based on the design function realization

requirements, the designed control model should

satisfy different motion feedback under different

motion assistance requirements. The overall system

feedback can be divided into impedance control

feedback based on contact force and position

feedback based on position information, namely

𝜏



=𝜏+𝜏



+𝜏



(

)

Where,

𝜏



is the total input of the controlled

torque, τ is the input of the calculation based on the

kinematics model,

𝜏



is the position feedback, and

𝜏



is the equivalent feedback of impedance

control. Based on the principle of impedance

control, under the influence of 𝜏



, the motion

trajectory will have an offset that tends to the human

body motion intention, and 𝜏



will cause the motion

trajectory to have an offset close to the set value.

Therefore, the feedback of 𝜏



can be controlled by

increasing the coefficient K. Control the strength of

the position feedback to affect the overall control

effect, thereby meeting the design requirements.

4 EXPERIMENT

Assuming that the length l1 of the exoskeleton arm

part is 0.35m, the weight is 4kg, the length l1 of the

forearm part is 0.25m, the weight is 4kg, and the

human body impedance coefficient is 6000N/m, the

exoskeleton model is established. Use simulink to

establish a dynamic model, as shown in Fig.3, build

a control model from the control structure shown in

Fig.2, as shown in Fig. 4

Figure 3. Exoskeleton dynamic model.

Figure 4. Overall control model.

The result of setting a larger position feedback

coefficient is shown in Fig 5. The actual motion

curve is close to the set value, and the contact force

is larger. The result of setting a smaller position

feedback coefficient is shown in Fig 6. The actual

motion curve is close to the intention curve, and the

contact force is small. The result of setting the

ICHIH 2022 - International Conference on Health Big Data and Intelligent Healthcare

382

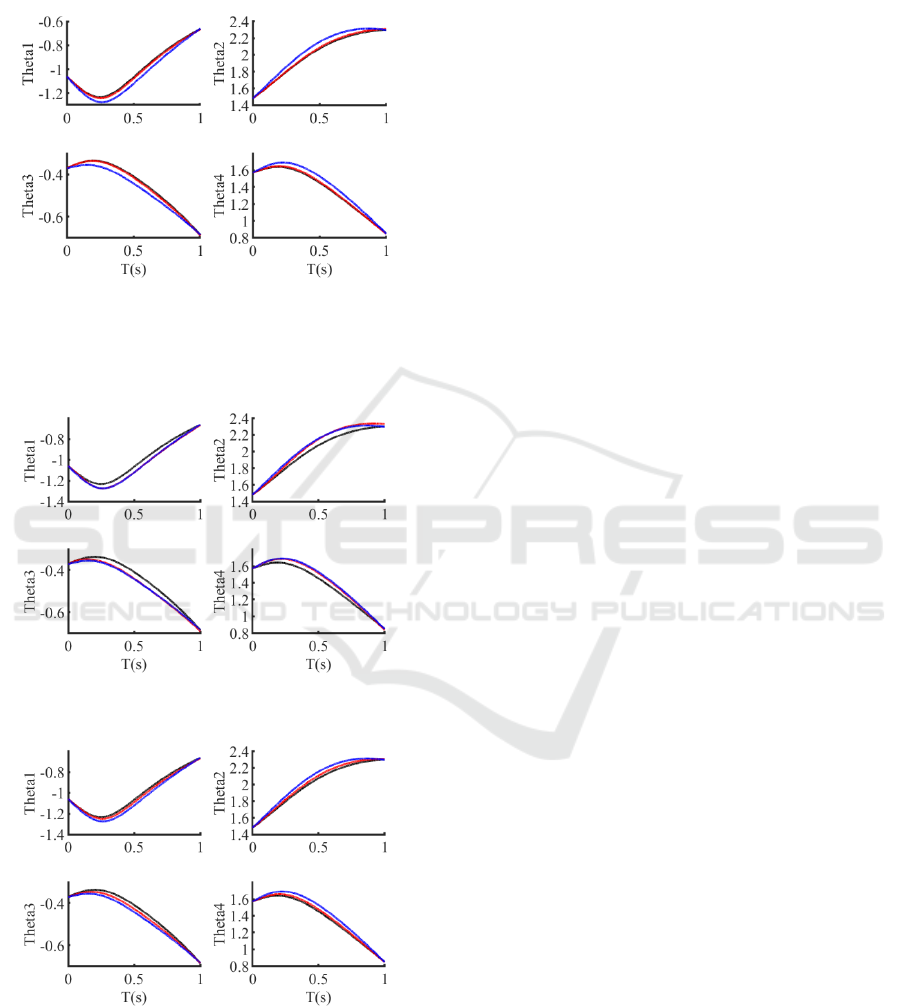
position feedback coefficient in the middle is shown

in Fig 7. The actual motion curve is between the

intention curve and the set curve, and the contact

force is moderate.

Figure 5. Oscilloscope waveform (from top to bottom are

θ1-4, the black curve is the set rotation angle, the red is the

actual rotation angle, and the blue line is the intention of

the human body)

Figure 6. Oscilloscope waveform

Figure 7. Oscilloscope waveform

5 CONCLUSIONS

The simulation experiment proves that by adjusting

the position feedback coefficient, the control can be

switched between different performances. The

impedance control coefficient determines the upper

limit of the closeness between the actual motion

curve and the human body intention curve. The

position feedback coefficient can be adjusted to

adjust the closeness between the actual curve and the

intention curve or the set curve to achieve different

human-computer interaction requirements.

REFERENCES

Cheng Siyuan, Chen Guangfeng. Research and Simulation

of fuzzy PID control for lower limb rehabilitation

exoskeleton robot [J]. Measurement and control

technology, 2019, 038 (012): 22-28.Chinese

Connell L A, McMahon N E, Harris J E, et al. A formative

evaluation of the implementation of an upper limb

stroke rehabilitation intervention in clinical practice: a

qualitative interview study[J]. Implementation

Science, 2014, 9(1): 1-12.

Du Yihao, Qiu Shi, Xie Ping, et al. Adaptive Human-

Computer Interaction Control Strategy for lower limb

rehabilitation robot [J]. Journal of automation, 2018,

44 (4): 743-750 Chinese

Duchaine V, Gosselin C. Safe, stable and intuitive control

for physical human-robot interaction[C]//2009 IEEE

International Conference on Robotics and Automation.

IEEE, 2009: 3383-3388.

Klamroth-Marganska V , Blanco J , Campen K , et al.

Three-dimensional, task-specific robot therapy of the

arm after stroke: a multicentre, parallel-group

randomised trial.[J]. The Lancet Neurology, 2014,

13(2):159-166.

Li Qingling, sun lining, Du Zhijiang. Analysis and

Research on the development status of upper limb

rehabilitation robot [J]. Mechanical design, 2008 (09):

1-3 Chinese

Lo A C, Guarino P D, Richards L G, et al. Robot-assisted

therapy for long-term upper-limb impairment after

stroke[J]. New England Journal of Medicine, 2010,

362(19): 1772-1783.

Saglia J A , Tsagarakis N G , Dai J S , et al. Control

Strategies for Patient-Assisted Training Using the

Ankle Rehabilitation Robot (ARBOT)[J].

IEEE/ASME Transactions on Mechatronics, 2013,

18(6):1799-1808.

Sun dingyang, Shen Hao, Guo Chao, et al. Design and

control of rope driven flexible upper limb exoskeleton

robot [J]. Robot, 2019, 41 (6): 834-841.Chinese

Tu Yao, Zhu aibin, song Jiyuan, et al. Human computer

interaction force adaptive admittance control of lower

limb exoskeleton rehabilitation robot [J]. Journal of

Control Strategy of Upper Limb Rehabilitation Exoskeleton based on Impedance Control and Position Feedback

383

Xi'an Jiaotong University, 2019, 053 (006): 9-16

Chinese

Zhuo Dahong. Chinese rehabilitation medicine [M].

Huaxia publishing house, 2003.Chinese

ICHIH 2022 - International Conference on Health Big Data and Intelligent Healthcare

384