Determination of Half-Life in Mutation Process of Polymerase Basic

Protein 1 Family from Influenza a Virus

Shaomin Yan

and Guang Wu

National Engineering Research Center for Non-Food Biorefinery, State Key Laboratory of Non-Food Biomass and Enzyme

Technology, Guangxi Academy of Sciences, 98 Daling Road, Nanning, 530007, Guangxi, China

Keywords: Bioinformatics, Amino-Acid Pair Predictability, Differential Equation, Evolution, Influenza A Virus,

Polymerase Basic Protein 1.

Abstract: The evolutionary process of a protein family is usually an up and down fluctuating curve when it presents in

the x, y coordinates, where the x-axis is time and y-axis is an evolutionary feature of proteins. This irregular

curve characterizes its patterns with various periodicities and unexplainable time frames. In the past, we

used the fast Fourier transform (FFT) to find these periodicities in hemagglutinin, a surface protein from

influenza A virus. However, FFT cannot distinguish the up and down fluctuations without periodicity. In

this study, we employ the analytical solution of a system of differential equations from our previous studies

to determine the half-life of evolution of the polymerase basic protein 1 (PB1) from influenza A virus from

1918 to 2009. We (i) converted 2352 PB1 into the predictable portion, (ii) presented these predictable

portions according to their sampling times with respect to subtypes, (iii) employed the analytical solution to

fit the predictable portions versus time profile, (iv) used several statistical measures to determine the

goodness-of-fit, and (v) obtained the half-life of evolutions with respect to subtypes. Although our study

sheds some insight onto the PB1evolution, much work is needed to better understand the virus evolution.

1 INTRODUCTION

It is widely acceptable and well known that

mutations in protein push the protein evolution

forward (Levine, 2020, Lyons, Lauring, 2018,

Bloom, Arnold. 2009). In the x, y coordinates, the x-

axis and y-axis are time and a protein feature, which

represents its evolution. Based upon this evolution-

time profile, one can easily perceive some particular

aspects of a protein evolution. In this x, y

coordinates, the y-axis is can be any protein feature

subject to mutations. In other words, a mutation

changes a given protein feature, which leads to a

different value in the y-axis.

In such x, y coordinates, the evolutionary process

can be a line up and down irregularly, no matter

whether it presents in alphabets, which are form of

protein, or in numeric values, which are converted

using any of 540-plus conversion methods

(Kawashima et al., 2008, Wu, Yan, 2008).

https://orcid.org/0000-0001-7642-3972

https://orcid.org/0000-0003-0775-5759

It is useful and meaningful to find the patterns in

such irregular up and down evolution-time profile.

In the past, our research group used the fast Fourier

transform to find the periodicity in the evolution of

hemagglutinins from influenza A virus (Wu, Yan,

2005, 2006). However, the evolution of

hemagglutinins does not have a unique periodicity,

but many periodicities, because the fast Fourier

transform can decompose a combined periodicity

into many components. Therefore, it would be more

useful and meaningful to pursue another aspect of

evolution, the half-life of irregular up and down

evolutionary line in the x, y coordinates.

In the past, our research group developed a

system of differential equations to describe the

evolution of influenza A virus hemagglutinins (Wu,

Yan, 2009), matrix protein 2 (Yan et al., 2009),

matrix protein 1 (Yan et al., 2010), polymerase

acidic protein (Yan, Wu, 2010), nucleoprotein (Yan,

Wu, 2011), and neuraminidase (Yan, Wu, 2021). We

prefer three terms of the analytical solution as y(t) =

-k1t

cos(

1) + A

-k2t

cos(

) + A

k3t

cos(

) + C, where y is the protein feature of

Yan, S. and Wu, G.

Determination of Half-Life in Mutation Process of Polymerase Basic Protein 1 Family from Inﬂuenza A Virus.

DOI: 10.5220/0011377200003443

In Proceedings of the 4th International Conference on Biomedical Engineering and Bioinformatics (ICBEB 2022), pages 1051-1056

ISBN: 978-989-758-595-1

1051

evolution, A,

and k are parameters, t is the time,

is a phase difference, and C is a constant.

In this study, we are interested in the polymerase

basic protein 1 (PB1) from influenza A virus. PB1 is

a subunit of RNA-dependent RNA polymerase

complex, which is associated with the transcription

and replication of the influenza A viral genome

(Engelhardt, Fodor, 2006, Nayak et al., 2004). PB1

is important for the efficient propagation of the virus

in the host and for its adaptation to new hosts

(Brower-Sinning et al., 2009) and considered as a

determinant of the pathogenicity of the 1918

pandemic virus (Watanabe et al., 2009). Besides,

PB1 is the major target for both CD4(+) and CD8(+)

T-cell responses (Assarsson et al., 2008). Because of

this importance, we wish to find some patterns in

PB1 evolution.

2 MATERIALS AND METHODS

2.1 Data

5125 full-length PB1s of influenza A virus sampled

from 1918 to 2009 were obtained from the influenza

virus resources (Influenza virus resources, 2021).

After excluded identical sequences (Furuse et al.,

2009), 2352 PB1s were used in this study.

2.2 PB1 Evolution

In x, y coordinates, we use the time in the x-axis and

the amino-acid pair predictability (AAPP) of each

PB1 as protein evolution feature in the y-axis, and

AAPP was computed with the following example.

ABL31752 PB1 from human H5N1 influenza virus,

strain A/Indonesia/CDC836/2006(H5N1), comtains

757 amino acids. The first and second amino acids

can be counted as an adjacent amino-acid pair, the

second and third as another pair, the third and fourth,

until the 756th and 757th, thus there are totally 756

adjacent amino-acid pairs.

This PB1 has 51 serines (S) and 59 threonines

(T), if the permutation can predict the appearance of

amino-acid pair ST: it must appear 4 times

(51/757×59/756×756=3.97). Actually it does appear

four times, so the pair ST is predictable. In contrast,

this PB1 has 33 phenylalanines (F) and 50 glutamic

acids (E), if the permutation can predict the

appearance of amino-acid pair FE: it must appear

twice (33/757×50/756×756=2.18). But, it appears

six times in realty, so the pair FE is unpredictable. In

this way, all amino-acid pairs in ABL31752 PB1 can

be classified as predictable and unpredictable, which

are 26.98% and 73.02%.

In the second example, ABL31774 PB1 from

human influenza virus isolated in 2006 has only one

amino acid different from ABL31752 PB1 at

position 598. However, its predictable and

unpredictable portions are 25.40% and 74.60%.

Thus, AAPP distinguishes one PB1 from another in

terms of numbers rather than alphabets that represent

amino acids.

In this manner, we can use 26.98% to represent

ABL31752 PB1 and 25.40% to represent ABL31774

PB1 in the y-axis of x, y coordinates. This method is

applied to all 2352 PB1 in this study.

2.3 Half-Life of Evolution and

Statistics

We use the analytical solution shown in Introduction

to fit the AAPP-time profile to get the half-life. The

t-test was employed to compare the difference

between uphill and downhill half-life, and P < 0.05

is considered significant. The fitting was conducted

using SigmaPlot (SPSS Inc., 2002).

3 RESULTS AND DISCUSSION

Figure 1 shows the evolution of 2352 PB1s over 90

year for the NA subtypes. Graphically, Figure 1 has

the following meanings: the solid curve in the top

panel presents the evolution of 2352 PB1s from

1918 to 2009, and each point is the mean value of

predictable portions of all PB1s in a given year with

its standard deviation (vertically grey line). The

dotted line is the fitting by three-term of analytical

solution. Similarly, the same meanings can be

applied to other panels. In top panel, the time starts

from 1918, when the Spanish pandemic occurred,

for N1 subtype. However, this is not the case for the

rest NA subtypes. Therefore, the imbalanced data

may compromise us to use the analytical solution to

fit these AAPP-tine profiles to find out the half-life

of evolution. Thus, we conducted three statistical

tests to determine the goodness-of-fit when we use a

three-term analytical solution to treat these

evolutionary curses.

ICBEB 2022 - The International Conference on Biomedical Engineering and Bioinformatics

1052

Figure 1: Evolution of influenza A virus PB1 family from

1918 to 2009 in terms of predictable portion of AAPP in

different NA subtypes. The data present as mean±SD. The

dotted lines are fitted curves using analytical solution.

Figure 2: Residual over time for different NA subtypes.

Figure 2 demonstrates the goodness-of-fit for

fitting of data in Figure 1 by observing whether there

is a trend in plotting residual over time. Actually, we

cannot see any monotonic trend in any panel in

Figure 2 although there is a tendency that the longer

the time involved, the more the fluctuations.

Nevertheless, we observed the relatively large

fluctuations around 1980s.

Figure 3: Evolution of influenza A virus PB1s from 1918

to 2009 in terms of predictable portion of AAPP in all

PB1s and different HA subtypes. The data present as

mean±SD. The dotted lines are fitted curves using

analytical solution.

Figure 3 illustrates the evolution of 2352 PB1s

over 90 year for the HA subtypes. Graphically,

Figure 3 is completely similar to Figure 1, therefore,

all the implications in Figure 1 are applicable to

Figure 3. In Figure 3, we can see several

dramatically sharp decreases in AAPP while there is

only one such fall in Figure 1, suggesting the

difference between HA and NA subtypes.

Figure 4 exactly is the same as Figure 2, i.e. to

observe any trend of residuals over time for the

goodness-of-fit. Similarly, we cannot notice any

monotonic trend in all the panels in Figure 4,

suggesting a goodness-of-fit. Again, we can see

some fluctuations around 1980s. Both Figures 3 and

4 ran our first statistical test.

Determination of Half-Life in Mutation Process of Polymerase Basic Protein 1 Family from Inﬂuenza A Virus

1053

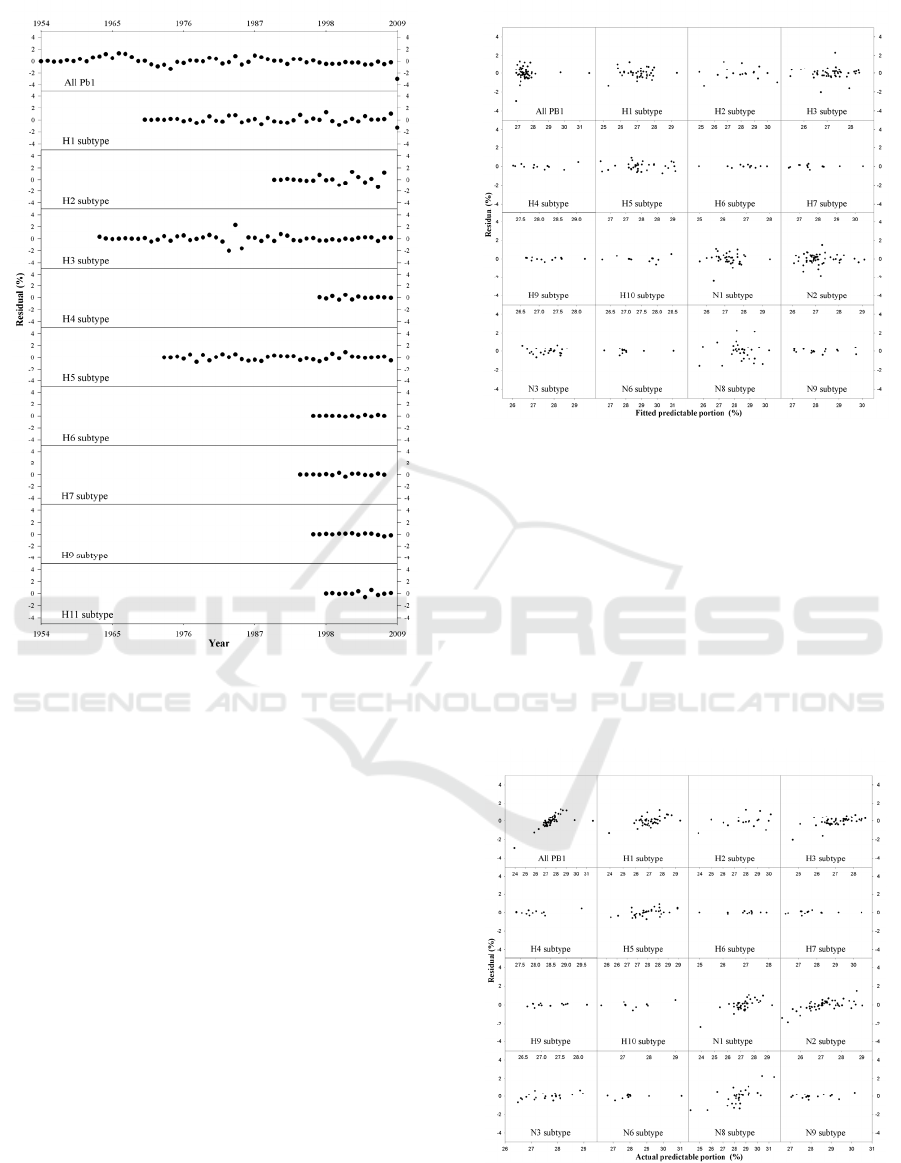
Figure 4: Residual over time in all and different HA

subtypes.

Figure 5 pictures the second statistical test, that

is, residuals versus fitted values. Here, we are still

looking for whether there is any trend between two

variables. Indeed, there is no any visible trend

although sometimes clusters formed.

Figure 6 manifests the third statistical test, say,

residuals versus actual values. Similarly, we wish to

find whether there is any trend in these panels. In

good agreement with the above two statistical tests,

we cannot find out any monotonic trend although the

residual increases as actual value increases in some

cases, which are generally attributed to the

unbalanced data because of difficulty in collecting

samples of influenza A virus. Collectively, these

three statistical tests confirmed goodness-of-fit when

using three exponential terms of analytical solution.

Figure 5: Residual versus fitted value of predictable

portion for all and different subtypes of PB1.

The solid curves in Figures 1 and 2 present the

change in predictable portions of the PB1s over

time. Their fluctuation renders us to find the

downhill and uphill half-life, which then serves as

initial values for fitting. With decaying exponential,

the half-life is t

=ln(2)/k=0.696/k, where k=(ln

ypeak

ytrough

)/t

interval

, which is the downhill half-life.

Hereafter, we can compute the uphill half-life in the

similar way. Consequently, we can find the

parameters in the three terms of analytical solution

in Table 1.

Figure 6: Residual versus actual value of predictable

portion for all and different subtypes of PB1.

ICBEB 2022 - The International Conference on Biomedical Engineering and Bioinformatics

1054

In Table 1, the third term in the analytical

solution cannot be found by fitting for H4, H6, H9

and H11. This phenomenon may not be surprising

because the samples of those subtypes are quite

imbalanced. On the other hand, this also indicates

the limitation in fitting although the goodness-of-fit

looks good. In reality, these parameters lack physical

meanings in biological sense. This is the drawback

of application of mathematical methods in biological

and medical fields because it is always very hard to

relate a model parameter to a biological and medical

meaningful indicator.

Table 1: Parameters for analytical solution.

Subtype A

C R

All -15.28 0.97 0.55 1.80 -0.28 0.00 2.01 -5.96 -0.23 0.00 0.89 6.75 27.41 0.53

H1 5.67 0.00 -0.04 0.52 -8.17 0.87 1.36 -3.56 0.40 0.00 1.04 -1.53 21.95 0.69

H2 13.48 0.35 0.45 3.94 2.22 0.00 0.58 6.48 -1.19 0.00 1.78 1.93 27.78 0.85

H3 -0.67 0.02 0.68 4.76 -1.52 0.04 -0.25 3.35 0.57 0.02 0.90 4.13 27.14 0.60

H4 1.13 0.13 1.71 -1.84 1.95 0.15 0.39 4.10 27.63 0.84

H5 3.75 0.17 1.52 -0.82 -2.37 0.11 0.42 0.85 3.34 0.12 1.32 -3.08 27.32 0.71

H6 4.10 0.33 2.02 -0.70 0.27 0.00 1.31 -1.57 26.91 0.98

H7 -14.93 0.86 2.02 -3.36 -2.18 0.00 0.49 1.78 -1.58 0.00 0.72 3.09 28.02 0.98

-0.60 0.03 2.35

14.1

-5.35 0.81 1.26 0.61 27.10 0.92

H11 -3.80 0.12 0.19 4.94 -0.92 0.00 1.27 -0.38 29.07 0.84

-0.46 0.00 1.08 1.07 -0.39 0.00 0.63 0.16

11.2

0.53 5.59 -0.54 27.25 0.54

N2 2.38 0.22 1.95 -2.76 2.82 0.07 -0.26 -4.15 0.31 0.03 1.21 -8.55 26.97 0.60

N3 -2.74 0.00 0.64 7.03 2.55 0.00 0.68 6.51 2.04 0.15 -1.21 -6.86 27.71 0.76

N6 -29.25 0.99 1.99 -0.31 -0.26 0.00 2.08 1.69 27.80 0.98

N8 2.17 0.06 1.08 0.30 1.01 0.04 1.55 8.05 1.88 0.05 0.46 -0.22 28.40 0.52

N9 0.73 0.00 1.50 -0.40 -0.81 0.00 -0.31 3.37 0.66 0.02 0.87 1.82 28.40 0.94

Table 2. Half-life between uphill and downhill in influenza A virus PB1.

Subtype U

hill half-life (

ears) Downhill half-life (

ears) t test

P value

Number Mean SD Number Mean SD

All PB1 11 50.34 15.94 12 38.34 16.25 0.09

H1 11 46.64 19.90 13 41.82 19.28 0.55

H2 10 36.73 15.45 8 36.73 15.45 0.64

H3 6 44.83 31.65 6 39.30 19.13 0.72

H4 3 30.42 18.69 5 49.72 22.93 0.27

H5 7 42.67 16.68 10 54.99 22.18 0.23

H6 7 36.76 15.51 7 41.66 25.39 0.67

H7 5 32.68 18.57 6 44.19 18.30 0.33

H9 4 52.40 26.01 6 56.27 19.33 0.79

H11 6 38.21 13.15 4 36.63 14.85 0.86

N1 10 50.74 19.01 11 40.19 15.97 0.18

N2 8 34.09 15.07 10 38.09 12.77 0.55

N3 6 64.18 29.62 6 42.95 13.58 0.14

N6 8 56.55 20.38 7 58.74 28.13 0.87

N8 5 23.63 16.89 7 26.79 19.00 0.77

N9 6 48.69 21.35 7 45.96 24.09 0.83

Table 2 lists the half-life with statistical

comparison, As no statistical difference was found

between uphill and downhill half-lives, we can see

that the half-life is ranged smaller in HA subtype

than that in NA subtype, especially for the uphill

half-life. Yet, the standard deviations (SD) are

actually quite large, suggesting the sampling number

is not large. This demonstrates another difficulty in

modeling, that is, the experimental data always do

not meet the demand from modelers. Therefore, do

we need to design an experiment according to

experimenters or modelers?

The pandemic/epidemic mechanism is extremely

complicated, and the current Covid-19 is the best

proof that we know too little to implement any

efficient and effective measures to stop the spread of

coronavirus. Because of rich data in influenza virus,

the detailed and comprehensive studies on influenza

virus nevertheless can enrich our knowledge on

Determination of Half-Life in Mutation Process of Polymerase Basic Protein 1 Family from Inﬂuenza A Virus

1055

influenza virus, which can extrapolate to

coronavirus.

4 CONCLUSIONS

In this study, we attempted to determine the half-life

of PB1 from influenza A virus in terms of its

evolutionary process. This is accomplished by using

a three-term analytical solution of a system of

differential equations obtained in our previous

studies. In this way, we hope to reveal another

aspect of virus evolution, however how to interpret

the meaning of model parameters still requires more

studies in the future.

ACKNOWLEDGEMENTS

Scientific Development Fund of Guangxi Academy

of Sciences (2021YFJ1203) was kindly

acknowledged.

REFERENCES

Assarsson, E. Bui, H. H., Sidney, J., Zhang, Q. J. Glenn,

Q., Oseroff, C., Mbawuike, I. N., Alexander, J.,

Newman, M. J., Grey, H, & A. Sette, (2008).

Immunomic analysis of the repertoire of T-cell

specificities for influenza A virus in humans. J. Virol.

82, 12241–12251.

Bloom, J. D. & F. H. Arnold, (2009). In the light of

directed evolution: pathways of adaptive protein

evolution. Proc Natl Acad Sci. 106 Suppl 1, 9995–

10000.

Brower-Sinning, R., Carter, D. M., Crevar, C. J., Ghedin,

E., Ross, T. M. & P. V. Benos, (2009). The role of

RNA folding free energy in the evolution of the

polymerase genes of the influenza A virus. Genome

Biol. 10, R18.

Engelhardt, O. G. & E. Fodor, (2006). Functional

association between viral and cellular transcription

during influenza virus infection. Rev. Med. Virol. 16,

329–345.

Furuse, Y., Suzuki, A., Kamigaki, T. & H. Oshitani,

(2009). Evolution of the M gene of the influenza A

virus in different host species: large-scale sequence

analysis. Virol. J. 6, 67–79.

Influenza virus resources. (2021).

https://www.ncbi.nlm.nih.gov/genome/viruses/

Kawashima, S., Pokarowski, P., Pokarowska, M.,

Kolinski, A., Katayama, T. & M. Kanehisa, (2008).

AAindex: amino acid index database, progress report

2008. Nucleic Acids Res. 36, D202–D205.

Levine, A. J., (2020). p53: 800 million years of evolution

and 40 years of discovery. Nature Rev. Cancer. 20,

471-480.

Lyons, D. M. & A. S. Lauring (2018). Mutation and

epistasis in influenza virus evolution. Viruses. 10, 407.

Nayak, D. P., Hui, E. K. & S. Barman (2004) Assembly

and budding of influenza virus. Virus Res. 106, 147–

165.

SPSS Inc., (2002). SigmaPlot for Windows Version 8.02.

Watanabe, T., Watanabe, S., Shinya, K., Kim, J. H., Hatta,

M. & Y. Kawaoka (2009) Viral RNA polymerase

complex promotes optimal growth of 1918 virus in the

lower respiratory tract of ferrets. Proc. Natl. Acad. Sci.

106, 588–592.

Wu, G & S. Yan, (2005). Timing of mutation in

hemagglutinins from influenza A virus by means of

unpredictable portion of amino-acid pair and fast

Fourier transform. Biochem. Biophys. Res. Commun.

333, 70–78.

Wu, G & S. Yan, (2006). Timing of mutation in influenza

a virus hemagglutinins by means of amino-acid

distribution rank and fast Fourier transform. Protein

Pept. Lett. 13, 143–148

Wu, G & S. Yan, (2009). Describing evolution of

hemagglutinins from influenza A viruses using a

differential equation. Protein Pept. Lett. 16, 794–804.

Wu, G & S. Yan. 2008. Lecture notes on computational

mutation, Nova Science Publishers. New York.

Yan, S. & G. Wu, (2010). Fitting evolutionary process of

polymerase acidic protein family from influenza A

virus with analytical solution of system of differential

equations. Guangxi Sci. 17, 247–254.

Yan, S. & G. Wu, (2011). Fitting evolutionary process of

influenza A virus nucleoproteins using analytical

solution of differential equation. Interdis. Sci. Comput.

Life Sci. 3, 128–137.

Yan, S. & G. Wu, (2021). Description of evolution of

neuraminidase from influenza A virus. Proceedings of

2nd International Conference on Computer Vision,

Image, and Deep Learning, SPIE 11911.

Yan, S. Li, Z., & G. Wu, (2010). Fitting evolution of

matrix protein 1 from influenza A virus using

analytical solution of differential equation. Protein

Pept. Lett. 17, 530–541.

Yan, S., Li, Z. C. & G. Wu, (2009). Fitting evolutionary

process of matrix protein 2 family from influenza A

virus using analytical solution of differential equation.

J. Biomed. Sci. Engineer. 2, 587–593.

ICBEB 2022 - The International Conference on Biomedical Engineering and Bioinformatics

1056