MAJORITY VOTING IN STABLE MARRIAGE PROBL
EM WITH
COUPLES
Using a monotone systems based tournament approach
Tarmo Veskioja, Leo Võhandu
Institute of Informatics, Tallinn Technical University, Raja 15, Tallinn, 12618, Estonia
K
eywords: GDSS, stable matching, voting, tournament, monotone systems, intransitivity
Abstract: Providing centralised matching services can be viewed as a group decision support system (GDSS) for the
participants to reach a stable matching solution. In the original stable marriage problem all the participants
have to rank all members of the opposite party. Two variations for this problem allow for incomplete
preference lists and ties in preferences. If members from one side are allowed to form couples and submit
combined preferences, then the set of stable matchings may be empty (Roth et al., 1990). In that case it is
necessary to use majority voting between matchings in a tournament. We propose a majority voting
tournament method based on monotone systems and a value function for it. The proposed algorithm should
minimize transitivity faults in tournament ranking.
1 INTRODUCTION
Stable marriage problem has attracted a considerable
amount of interest after the problem was first
formulated by Gale and Shapley (Gale et al., 1962).
Many centralized two-sided markets can be
described as variants of the stable marriage problem.
An instance of the original stable marriage
problem (SM) consists of N men and N women,
with each person having a preference list that totally
orders all members of the opposite sex. A man and a
woman form a blocking pair in a matching if both
prefer each other to their current partners. A
matching is stable if it contains no blocking pair. In
every instance of SM there is at least one stable
matching (Gale et al., 1962).
A variant of SM allows for incomplete
preferences. This problem is denoted SMI (Stable
Marriage with Incomplete preferences). The
definition of a blocking pair is extended, so that each
member of the pair prefers the other instead of the
current partner or is currently single and acceptable.
Every instance of SMI has at least one stable
matching, although it may not always be a maximum
cardinality matching. If a player is single in one
stable matching, then that player is single in any
other stable matching.
Another variant of SM allows for ties in the
preferences. This problem is denoted SMT (Stable
Marriage with Ties). In this case the definition of
stability needs to be extended. A man and a woman
form a blocking pair if each strictly prefers the other
to his/her current partner. A matching without such a
blocking pair is called weakly stable. Every instance
of SMT has at least one stable matching.
A variant of SM that allows for both incomplete
preferences and ties in the preferences is denoted
SMTI. In this problem there always exists a weakly
stable matching (Iwama et al., 1999), but the sizes of
stable matchings may vary. Finding maximum
cardinality matching in SMTI is NP-complete
(Iwama et al., 1999) and even the approximation is
APX-hard (Halldórsson et al., 2002).
A hospital-residents assignment (HR),
sometimes also called stable admissions problem or
many-to-one matching, is a variant of SM, where
many residents can be assigned to one hospital and
one resident can fill in only one vacancy. HR
problem can also have relaxations of preferences,
allowing for incomplete preferences and/or ties.
These subproblems are denoted HRI and HRTI
accordingly. Most of the properties of SM, SMI and
SMTI carry over to the HR, HRI and HRTI
problems and algorithms.
Matching is a majority assignment (best-voted
matching) if there is no other matching that is
442
Veskioja T. and Võhandu L. (2004).
MAJORITY VOTING IN STABLE MARRIAGE PROBLEM WITH COUPLES - Using a monotone systems based tournament approach.
In Proceedings of the Sixth International Conference on Enterprise Information Systems, pages 442-447
DOI: 10.5220/0002655904420447
Copyright
c
 SciTePress

preferred by a majority of participants to the original
matching. Gärdenfors (Gärdenfors, 1975) observed
that, when the preferences are strict, the set of
majority assignments comprises the set of stable
matchings, thus showing that the notion of majority
assignment is a relaxation of stability (Klijn et al.,
1999). Weakly stable matching is a matching,
possibly having a blocking pair undermining the
stability of a matching, but this blocking pair is not
credible in the sense that one of the partners may
find a more attractive partner with whom he forms
another blocking pair for the original matching
(Klijn et al., 1999). In other words, Klijn and Masso
define an individually rational matching to be
weakly stable if every blocking pair is - in the sense
discussed above - not credible. Clearly, weak
stability is also a relaxation of stability.
Many markets also require taking into account
some additional constraints - for example in HR a
pair of residents may have formed a couple and
prefer to find a placement at the same hospital, or at
least work in the same city. In this case, the couple
submits rank ordered preferences over acceptable
pairs of hospitals. After acceptable pairs of hospitals
the couple can give rank ordered preferences over
single pairs of hospital – couple member, where one
of the members of the couple is left without a pair.
In this article these mentioned constraints will be
called couple constraints.
Matching markets with couple constraints may
not have any stable matchings (Roth et al., 1990). In
that case it is natural to use majority voting to find
the best matching. We propose a heuristical majority
voting tournament method based on monotone
systems and a value function for it. The proposed
algorithm should minimize transitivity faults in
tournament ranking. Preliminary results (described
in more detail in a paper submitted to a conference
CAISE’04) show that our proposed method
successfully minimizes transitivity faults on all
possible tournament tables of size 5x5. It is feasible
to check the performance of the proposed method on
all tables up to size 7x7 or 8x8, but beyond that it is
only feasible to compare it against other heuristical
methods and on selected tournament tables.
In the next chapter we give the definitions of
domination and the core of a game (Roth et al.,
1990; pages 54-55, 166-167). The definitions are
needed to understand the importance of stability and
the core. Then we use an example of a matching
model with couple constraints from Roth (Roth et
al., 1990) to show that it has intransitivities and
every dominance path of matchings leads to the
cycle of unstable matchings.
In the third chapter we give a simple definition
of a ranking algorithm based on a monotone system,
we describe a specific tournament algorithm and
show that it works on the example.
The fourth chapter is for the conclusions.
2 THE CORE OF A MARRIAGE
GAME
The following are the definitions of domination and
the core of a game (Roth et al., 1990; pages 54-55,
166-167).
Definition 1. For any two feasible game
outcomes x and y, x dominates y if and only if there
exists a coalition of players S such that
(a) every member of the coalition S prefers x to
y; and
(b) the rules of the game give the coalition S the
power to enforce x (over y).
For this reason, if x dominates y, we might
expect that y will not be the outcome of the game.
This leads us to consider the set of undominated
outcomes.
Definition 2. The core of a game is the set of
undominated outcomes.
We can relax the domination conditions of
definition 1, assuming that the coalition can make
side-payments to those players that are indifferent
between outcomes x and y.
Definition 3. For any two feasible game
outcomes x and y, x weakly dominates y if and only
if there exists a coalition of players S such that
(a) every member of the coalition S prefers x at
least as much as y; and
(b) at least one member of the coalition S prefers
x to y; and
(c) the rules of the game give the coalition S the
power to enforce x (over y).
Definition 4. The core of a game defined by
weak domination is the set of weakly undominated
outcomes.
According to the first two definitions the core of
the one-to-one matching market equals the set of
stable matchings (Roth et al., 1990, chapter 3.1,
theorem 3.3). When preferences are strict, the two
cores coincide in the one-to-one matching model,
but not in the many-to-one model. However, when
hospital preferences are responsive (as defined in
Roth et al., 1990, definition 5.2, page 128), and
when preferences over individuals are strict, the set
MAJORITY VOTING IN STABLE MARRIAGE PROBLEM WITH COUPLES
443

of stable matchings coincides with the core defined
by weak domination (Roth et al., 1990; proposition
5.36, page 167). In the many-to-one (or one-to-one)
matching model with couples, the set of stable
matchings and consequently the core may be empty
(Roth et al., 1990, theorem 5.11, page 141). Lets
look at the example that Roth & Sotomayor gave to
illustrate this problem.
2.1 An empty core example of many-
to-one model with couples
The following example is taken from Roth &
Sotomayor (Roth et. al., 1990; theorem 5.11, page
141).
Consider the market with hospitals H = {H
1
, H
2
,
H
3
, H
4
} each of which offers exactly one position
and each of which has strict preferences over
students S = {s
1
, s
2
, s
3
, s
4
} as given in Table 1. The
students consist of two married couples, {s
1
, s
2
} and
{s
3
, s
4
}. Each couple has strict preferences over
ordered pairs of hospitals, as given in Table 1.
Table 1: Preferences of hospitals and couples
Hospitals' rank
orders
Couples' rank
orders
H
1
H
2
H
3
H
4
{s
1
,s
2
} {s
3
,s
4
}
s
4
s
4
s
2
s
2
H
1
H
2
H
4
H
2
s
2
s
3
s
3
s
4
H
4
H
1
H
4
H
3
s
1
s
2
s
1
s
1
H
4
H
3
H
4
H
1
s
3
s
1
s
4
s
3
H
4
H
2
H
3
H
1
H
1
H
4
H
3
H
2
H
1
H
3
H
3
H
4
H
3
H
4
H
2
H
4
H
3
H
1
H
2
H
1
H
3
H
2
H
2
H
3
H
2
H
3
H
1
H
2
H
2
H
4
H
1
H
4
H
2
H
1
H
1
H
3
Thus couple {s
1
, s
2
} has as its first choice that s
1
be matched with H
1
and s
2
with H
2
, and has its last
choice that s
1
be matched with H
2
and s
2
with H
1
.
The 24 individually rational matchings of students to
hospitals are listed in Table 2, along with the reason
that each such matching is unstable.
Table 2: Every matching is unstable
Matching H
1
H
2
H
3
H
4
Unstable with
respect to
1 s
1
s
2
s
3
s
4
s
4
,H
2
2 s
1
s
2
s
4
s
3
s
4
,H
2
3 s
1
s
3
s
2
s
4
s
2
,H
4
4 s
1
s
3
s
4
s
2
s
4
,H
1
5 s
1
s
4
s
2
s
3
s
2
,H
4
6 s
1
s
4
s
3
s
2
s
4
,H
1
7 s
2
s
1
s
3
s
4
s
4
,H
1
8 s
2
s
1
s
4
s
3
s
4
,H
2
9 s
2
s
3
s
1
s
4
s
2
,H
4
10 s
2
s
3
s
4
s
1
s
4
,H
1
11 s
2
s
4
s
1
s
3
s
2
,H
4
12 s
2
s
4
s
3
s
1
s
4
,H
1
13 s
3
s
1
s
2
s
4
s
4
,H
2
14 s
3
s
1
s
4
s
2
s
2
,H
3
15 s
3
s
2
s
1
s
4
s
2
,H
4
16 s
3
s
2
s
4
s
1
s
2
,H
3
17 s
3
s
4
s
1
s
2
s
1
,H
1
18 s
3
s
4
s
2
s
1
s
2
,H
1
19 s
4
s
1
s
2
s
3
s
4
,H
2
20 s
4
s
1
s
3
s
2
s
2
,H
3
21 s
4
s
2
s
1
s
3
s
2
,H
4
22 s
4
s
2
s
3
s
1
s
2
,H
3
23 s
4
s
3
s
1
s
2
s
3
,H
3
24 s
4
s
3
s
2
s
1
s
4
,H
4
Thus matching 1, which assigns student s
i
to
hospital H
i
, i=1,…,4, is unstable because both
hospital H
2
and couple {s
3
, s
4
} would prefer that
student s
4
be matched with H
2
. (This follows since
H
2
prefers s
4
to s
2
, and {s
3
, s
4
} prefers H
3
H
2
to
H
3
H
4
.)
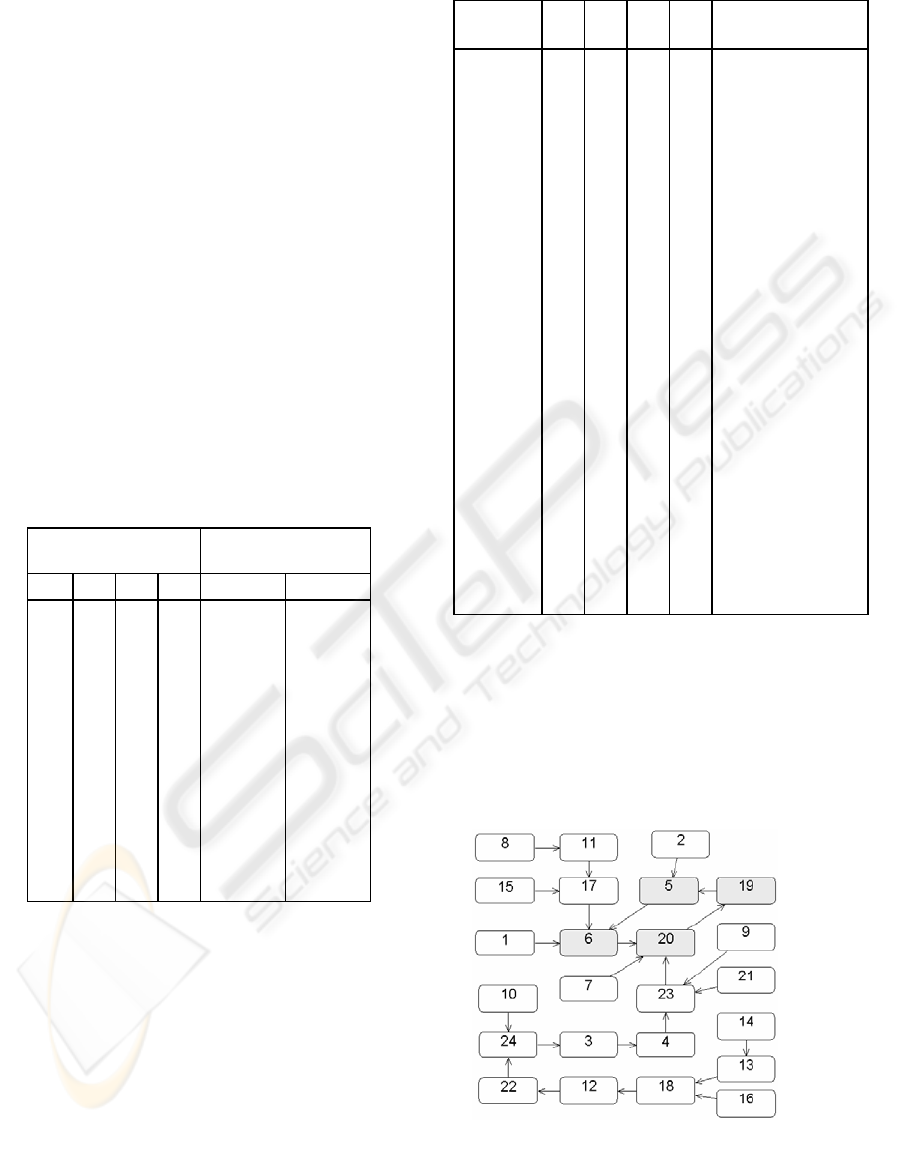
The domination graph between matchings is
shown on Figure 1.
If we study the dominance between these
matchings, it becomes clear that every dominance
path leads to the following cycle of unstable
Figure 1: Domination graph
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
444

matchings {6, 20, 19, 5} (in the order of
dominance), entering the cycle from one of the
matchings 6, 20 or 5.
Roth & Sotomayor (Roth et al., 1990, page 142)
formulated an open question whether there exist
plausible restrictions on the preferences of the
couples that would insure that stable matchings
always exist. We suggest that studying these
restrictions in the context of minimizing transitivity
faults is a more fruitful approach. If there are few
enough transitivity faults left in the tournament
ranking, then at some point stable matchings should
emerge.
As soon as the players of the marriage game
realize that there is no stable outcome, they start
looking for a way out of this vicious cycle, at least in
a cooperative game. In doing that the players will
start seeking coalitions to reach an outcome through
majority voting. The existence of cyclic domination
also means the existence of intransitivity. So to
reach an outcome, the players have to vote between
pairwise matchings as in a tournament.
Note that the only way to avoid a tournament is
to not let the existence of the cycle to become
common knowledge. The blocking pair (or one of
them) to the last matching in the cycle can choose to
not form a pair by themselves, but to seek coalition
partners to seek out the best matching in the cycle
for the coalition and to dominate over other
matchings.
Lets look at the tournament between the
matchings. An algorithm based on monotone
systems is used for the tournament.
3 FINDING BEST SOLUTIONS
WITH A TOURNAMENT
The aim of the tournament method is to minimize
transitivity inconsistencies in a ranking. Transitivity
requires that if solution a is better than solution b
and solution b is better than solution c, then solution
a must be better than solution c. With special
constraints (for example permitting couples to
submit combined preferences) this transitivity may
not always hold in a marriage model.
The first criterion for ranking is to minimize the
number of transitivity faults. If there are several
different rankings with the same minimal number of
transitivity faults, then a second-order criterion must
be used. The minimal transitivity inconsistency
ranking in a tournament problem is NP-hard, that is
why an efficient heuristic tournament method is
needed. One class of good heuristic methods for this
problem is based on monotone systems (Mullat,
1976; Võhandu, 1989, 1990).
3.1 An algorithm based on a
monotone system
Definition 5. (A weakly) monotone system is a
system built on a set of objects, such that
(a) objects are weighted by a value function
(b) after removal of one object from the set all
the weights of other objects still in the set
change monotonically in one direction
(increase or decrease) or stay on the same
level.
Algorithms based on such a simple monotone
system work as follows:
Step 1. Evaluate all objects in the set.
Step 2. Find the weakest object (with the
smallest (largest) weight), and remove it from the
set. If there are several weakest objects, then
recursively apply the tournament algorithm to the set
of weakest objects. If at any stage of the recursion
any object was removed from the set of weakest
objects, then backtrack. If the set of weakest objects
still contains more than one object, then compare the
weights from the previous iteration and choose an
object that is more similar to the previously removed
object. If the weights in all the previous iterations
are the same, then according to the value function
these objects are equivalent and we can remove any
one of those (usually the first object will be
removed).
Step 3. If there are still objects in the set, then
continue from Step 1.
Any given algorithm always removes the object
with the smallest weight, or the largest weight.
Algorithm cannot change the choice function (min,
max) during the course of action. Value function can
be chosen relatively freely, as long as it satisfies
monotonicity condition. The sequence of removal of
objects constitutes object ranking.
3.2 Tournament method based on a
monotone system
To construct a tournament method for the stable
marriage problem we need to define a value function
and an ordered set of object removal criteria.
In a majority voting, all the players have to vote
(pairwise) between the matchings. Voting results
MAJORITY VOTING IN STABLE MARRIAGE PROBLEM WITH COUPLES
445

constitute the voting table v. Voting table for the
cycle of unstable matchings {6, 20, 19, 5} is given
in Table 3.
Table 3: Voting table
v 5 6 19
20
5 3 5 6
6 3 4 3
19 1 4 5
20 2 3 1
The tournament table t is computed based on the
voting table v. We compare votes of all pairs of
matchings v
rc
and v
cr
and make the following
transformations:
If v
rc
< v
cr
then t
rc
=0, t
cr
=1;
If v
rc
> v
cr
then t
rc
=1, t
cr
=0;
If v
rc
= v
cr
then t
rc
=0, t
cr
=0.
The tournament table for the cycle of unstable
matchings {6, 20, 19, 5} is given in Table 4.
Our proposed method makes use of both the
number of wins (rowsums) and losses (column
sums). The method iteratively finds the weakest
object, removes it from the tournament table and
adds it to the ranking. If we were to remove one
matching, then the winning points (and also the
losing points) of all the other matchings will
decrease or stay on the same level, so the system is a
(weakly) monotone one.
The process of finding the weakest object to
remove is also iterative. In one iteration the number
of wins and losses in the remaining subset of the
weakest objects are calculated at first. The weakest
objects are selected by the minimum number of wins
and then by the maximum number of losses. This
iterative minimax selection is used until either only
one weakest object remains or the last minimax
selection was not able to reduce the number of
weakest objects. In the latter case the last remaining
weakest object in the original ranking is removed.
The last remaining object in the tournament table is
the winner.
Table 4: Tournament table
t 5 6 19 20 Iter1 Iter2 Iter3 Iter4
5 0 1 1 2 1 0 0
6 0 0 0 0 0 0
19 0 0 1 1 0
20 0 0 0 0 Wins
Iter1 0 0 1 2
Iter2 0 0 1
Iter3 0 0
Iter4 0 Losses
In the first iteration matchings 6 and 20 have no
wins, but the number of losses are 0 and 2
accordingly. Matching 20 is removed first based on
the number of losses. Values from column 20 are
subtracted from the winning points (row sums) of
remaining matchings. Values from row 20 are
subtracted from the losses (column sums) of
remaining matchings.
In the second iteration matchings 6 and 19 have
no wins. Based on the number of losses (0 and 1)
matching 19 will be removed. Wins and losses of the
remaining matchings are recalculated.
In the third iteration matchings 5 and 6 have no
wins. Voting between them gave a draw. Both have
no losses, since voting between them gave a draw.
One way to differentiate between the two matchings
is to look at the wins (and then losses) before the
first iterations. Matching 5 had one win in the
previous iteration, so matching 6 has to be removed
first and matching 5 will be removed last.
The obtained tournament ranking is (5, 6, 19, 20)
and matching 5 is the best matching. Note that
simple majority voting does not always produce
transitivity faults in the cycle of unstable matchings,
since even if one matching is dominated by the other
in the sense of stability, the voting between the two
matchings may still be a draw. One can, however,
define a rule that if voting between two matchings
gives a draw then the second criterion to decide the
better one is the domination. Clearly, such a rule
introduces intransitivities inside the cycle of
unstable matchings.
The proposed method has been tested to give a
ranking with minimum number of transitivity faults
on all tournament tables (including ties) up to size
5x5 (results described in more detail in a paper
submitted to a conference CAISE’04). The proposed
method has a maximum time complexity of O(N
3
)
and average time complexity between O(N
2
) and
O(N
3
), thus enabling to use it on tournament tables
of up to (tens of) thousands of objects.
3.3 How to select matchings for the
tournament
When using majority voting in a full tournament one
has to have a relatively small set of matchings (up to
thousands or tens of thousands). Since the number of
individually rational matchings is combinatorial, the
selection of matchings for majority voting
tournament becomes critical.
One solution is to hold a tournament between the
set of matchings in the cycle of unstable matchings.
A stable matching searching algorithm can be used
to find the cycle.
It would be interesting to know whether the
outcome of the majority voting tournament depends
ICEIS 2004 - ARTIFICIAL INTELLIGENCE AND DECISION SUPPORT SYSTEMS
446

on the subset of individually rational matching,
which always includes the cycle of unstable
matchings. If we look at the following dominance
path {18; 12; 22; 24; 3; 4; 23; 20; 19; 5; 6}, then the
minimum number of transitivity faults is 2 and there
are several rankings with that number of faults. Our
tournament method gives a following ranking (12;
24; 22; 6; 5; 3; 18; 23; 19; 20; 4). There are only two
transitivity faults. As we can see, if the matching 12
is included (and all subsequent matchings along the
dominance path to the cycle) in the tournament, it
always wins.
In the complete information game the matchings
need not even be restricted to the cycle and the path
leading to the cycle, but all the matchings in the
majority voting are “fair game”. If we were to
include all matchings in the tournament, then the
ranking order in our example would be (12; 24; 5; 2;
18; 22; 6; 11; 20; 1; 3; 23; 10; 17; 9; 21; 19; 7; 4; 15;
13; 16; 14; 8). The number of transitivity faults is
13.
If the stable marriage model includes couples,
then the complexity of finding if there exists a stable
matching is NP-complete and “logspace P-hard”
(Ronn 1986, 1987). So for large markets with
couples it may not always be practical to find a
stable matching even when one exists. In this case a
probabilistic matching algorithm can be used to find
a stable matching or a cycle of unstable matchings.
One promising approach would also be using a
genetic algorithm together with majority voting
tournaments to search for the best matching.
4 CONCLUSION
We have described a matching model, where
intransitivities may arise and for this situation we
have proposed using majority voting in a
tournament.
We have also proposed a tournament method
based on monotone systems and a value function for
it. The proposed algorithm should minimize
transitivity faults in tournament ranking and
experimental results show that it does that on tables
up to size 5x5. The proposed method has a
maximum time complexity of O(N
3
) and average
time complexity between O(N
2
) and O(N
3
), thus
enabling to use it on tournament tables of up to (tens
of) thousands of objects.
One open question regarding our proposed
solution is how to select matchings for the
tournament. We have formulated several alternative
answers for that question.
ACKNOWLEDGEMENT
This work was partially supported by ESF Grant
4844.
REFERENCES
Gale, D., Shapley, L., 1962. College Admissions and the
Stability of Marriage. In American Mathematical
Monthly, 69(1), pp.9-15.
Gusfield, D., Irwing, R. W., 1989. Stable Marriage
Problem: Structure and Algorithms, MIT Press Series
in the Foundations of Computing, MIT Press,
Cambridge, Massachusetts.
Gärdenfors, P., 1975. Match Making: Assignments Based
on Bilateral Preferences, In Behavioral Science, 20,
pp.166-173.
Halldórsson, M., Iwama, K., Miyazaki, S., Morita, Y.,
2002. Inapproximability results on stable marriage
problems, In Proceedings of LATIN 2002: the Latin-
American Theoretical INformatics symposium, volume
2286 of Lecture Notes in Computer Science, pp. 554-
568. Springer-Verlag.
Iwama, K., Manlove, D., Miyazaki, S., Morita, Y., 1999.
Stable marriage with incomplete lists and ties, In Proc.
ICALP'99, pp.443-452.
Klijn,F., Masso,J., 2003. Weak stability and a bargaining
set for the marriage model, in Games and Economic
Behavior, 42, pp. 91-100.
Mullat, I., 1976. Extremal Subsystem of Monotone
Systems. In Automation and Remote Control, 5, pp.
130-139; 8, pp. 169-178 (in Russian)
Ronn, E., 1986. On the complexity of stable matchings
with and without ties, Ph.D. diss., Yale University.
Ronn, E., 1987. NP-complete stable matching problems,
Computer Science Department, Technion – Israel
Institute of Technology. Mimeo
Roth, A., Sotomayor, M., 1990. Two-sided matching : a
study in game-theoretic modeling and analysis,
Cambridge University Press, Econometric Society
Monographs, no.18, Cambridge, Massachusetts, USA.
Võhandu, L., 1989. Fast Methods in Exploratory Data
Analysis, In Proceedings of Tallinn Technical
University, Tallinn, No. 705, pp. 3-13.
Võhandu, L., 1990. Best Orderings in Tournaments, In
Proceedings of Tallinn Technical University, Tallinn,
No. 723, pp. 8-14.
MAJORITY VOTING IN STABLE MARRIAGE PROBLEM WITH COUPLES
447