AN IMPROVED HIGH-DENSITY KNAPSACK-TYPE PUBLIC
KEY CRYPTOSYSTEM
Zhang Yunpeng, Lin Xia and Liu Xi
College of Software and Microelectronics, Northwestern Polytechnic University, 710072 Xi’an, China
Keywords: Cryptography, Public key cryptosystem, Fast public key algorithm.
Abstract: Almost all knapsack-type public key cryptography has been proven unsafe. To solve this problem, more
secure public key cryptographic algorithms are urgently needed. This article first discusses the basic theory
of knapsack-type public key and methods that used to attack the knapsack public key. Then, it analysis the
literature (Wang & Hu 2006, p.2930), and points out the potential defects of its cryptography safety.
Meanwhile, the article gives out an improved algorithm, and discusses the safety and efficiency of the
algorithm. The analysis of the algorithm shows that the improved algorithm is better than the original one in
security.
1 INTRODUCTION
There are many insecure factors on the file
transformation or e-mail business dealings on the
Internet , the computer security has thus become a
very important research area.
But, the key transmission and custody issues
of symmetric cryptography can not be solved
today.
Public key encryption algorithm separates the
public key and the private key, so that it
successfully resolved the key transmission and
custody issues. However, the speed of public key
cryptographic algorithm is a serious constraint
bottlenecks in their applications (Yasuyuki,
Masao & Takeshi 2008, p. 357).
In response to these issues, this article did a
useful exploration and research on the fast public
key encryption system and the chaotic system
used in the public key algorithm.
2 THE CORRELATION THEORY
OF KNAPSACK PUBLIC KEY
Description of knapsack problem: Given a bunch
of objects with different mass, is it possible if we
get a portion of these objects and put them in a
knapsack, in order to make the mass of the
knapsack equals to a given value?
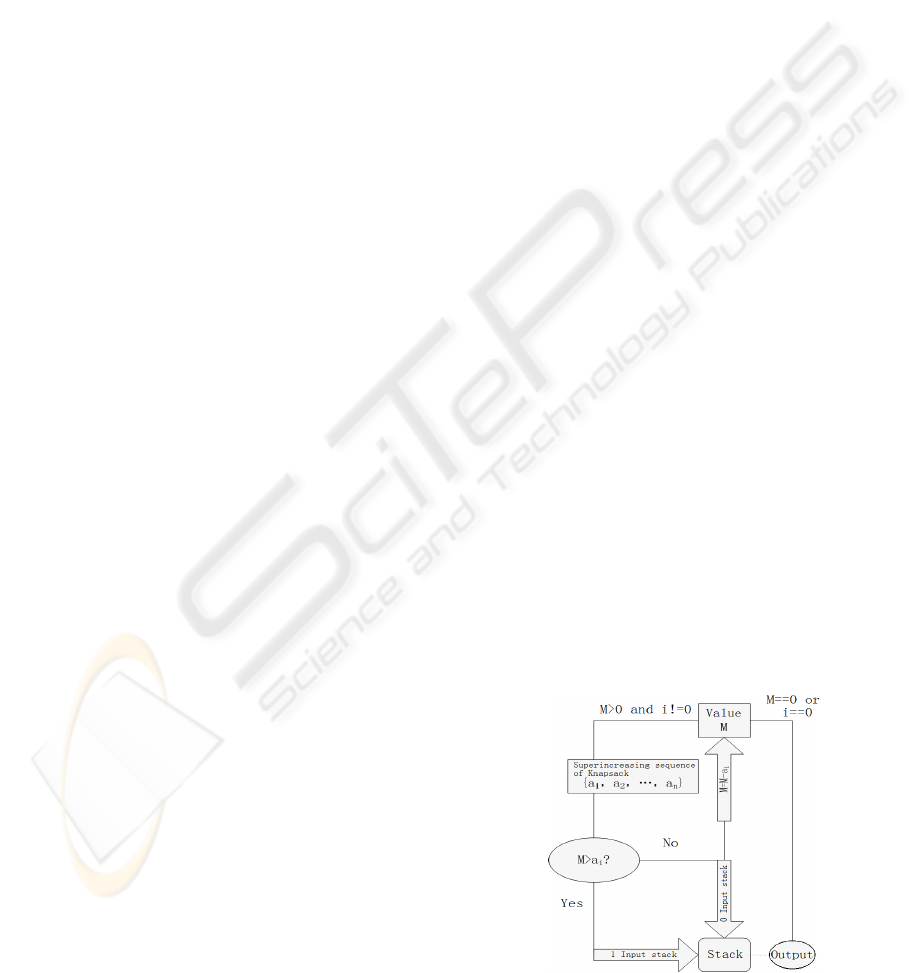
2.1 Problem
The solution to the super increasing knapsack
problem can be easily found, that compare the
total mass with the largest number in the sequence,
if the total mass is smaller than this number, it is
out of the knapsack; if the total mass is lager than
this number, and it belongs to the knapsack. Then,
make the mass of knapsack minus this number,
and afterwards study the second largest number in
the sequence. Repeat the process till the end. If
the total mass becomes 0, then there exists one
solution, otherwise, there is no solution. Here is a
simple flow chart show in Fig1:
Figure1: The flow chart which solve the Super-increasing
sequence of Knapsack.
127
Yunpeng Z., Xia L. and Xi L. (2010).
AN IMPROVED HIGH-DENSITY KNAPSACK-TYPE PUBLIC KEY CRYPTOSYSTEM.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 127-132
DOI: 10.5220/0002923701270132
Copyright
c
SciTePress

At present, most of the public key algorithms
are constructed based on sum of the set problem,
due to that this structure is simple, with lower
complexity in computation, and can efficiently
solve the problem of the efficiency of algorithm.
Merkle-Hellman encryption algorithm in
Knapsack has many deformations. Besides, there
is also a Chor-Rivest encryption in Knapsack,
which is the only known public encryption
algorithm without using the AB mod form to
disguise as a easy sum of the set problem.
2.2 Decipher of Knapsack Public Key
Algorithm
The strongest attack to the encryption algorithm
in knapsack that known is
L
3
-Lattice base
reduction algorithm which was first proposed by
A.Shamir and had been improved by many
scientists. This method reduces the subset sum
problem by making it into to find a short vector in
a lattice.
Definition of subset sum density: Let us
suppose that
},,,{
21
sss
S
n
is a Knapsack
set. The density of Knapsack set is defined as
2
max{l o g |1 }
i
n
d
in
s
Let
R
bbb
n
n
,,,
21
, then
11
{|}k
kk
nn
ii
ii
ii
LZ
bb
is the subset of
n-dimensional space
R
n
.
Among them, R is the real number set, and Z
is integer set, and we call L a lattice.
R
bbb
n
n
,,,
21
is a set of bases of lattice L.,
n is the rank of lattice L. A lattice can have many
different bases, among which the vector included
has relatively shorter length is called reduced.
Here is any n linear independence
vectors
R
bbb
n
n
,,,
21
, and constructs a set of
bases of lattice L:
bbb
n
**
2
*
1
,,, , among which
)1(;
*
1
1
**
*
*
1
*
1
ib
bb
bb
bbbb
j
i
j
jj
ji
ii
.
Let
*
**
()
ij
ij
jj
bb
ij
bb
, if a set of
bases
R
bbb
n
n
,,,
21
of lattice L
simultaneously satisfies the following two
conditions:
1)
2
1
||
ij
,
j
i ;
2)
||
||
*
1
4
3
*
1
1,
*
2
2
b
bb
i
i
ii
i
, ( 1i );
Then we call
R
bbb
n
n
,,,
21
a set of
reduction bases of lattice L. And the
L
3
-lattice
base reduction algorithm gradually constructs a
set of reduction bases
bbb
n
**
2
*
1
,,,
through
bbb
n
,,,
21
. It is an algorithm of
polynomial time.
Here is the method that cracks the knapsack
problem using the
L
3
-lattice base reduction
algorithm. Let us suppose
Csss
n
,,,,
21
are
positive integers, now we solve the 0-1 vector
)(
n
xxxx ,,,
21
whose length is n and
makes
Csx
n
i
ii
1
.
Step1. Take a set of bases of lattice L:
112 2
1
(1,0,0, ,0, ), (0,1,0, ,0, ), , (0,0,0, ,1, ),
(0,0,0, ,0, )
nn
n
bsbsbs
bC
Step2. Seek the reduction
base
bbbb
nn
*
1
**
2
*
1
,,,,
of L using
the
L
3
-algorithm;
Step3. If for any
),,,,
(
*
1,
*
,
*
2,
*
*
1,
bbb
b
b
ninii
i
i
that all 0
*
b
ij
, or
there exists a constant
)1(, nj
making
it has a solution of
*
,
1
j
ij
x
b
ji , then
stops, otherwise turn to Step 4;
Step4.
n
i
i
C
a
C
1
, repeat Step 1 to Step 3, and
get the solution
)(
n
xxxx ,,,
21
, then the
solution of the original knapsack problem
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
128

is )1,,1,1(
21
xxx
n
.
Because the knapsack set density of
super-increasing sequence in knapsack must less
than 1, or there will be multiple solutions. And
when the knapsack set density of super-increasing
sequence in knapsack
0.94d
, the success rate of
cracking the knapsack using the
L
3
-lattice base
reduction algorithm is very high. Lagrias-Odlyzko
and Brickellwill both independently proved that it
is completely possible to crack the knapsack
problem when
64.0d
(Fleshwound 2009.10).
For the multiple iterated knapsack encryptions,
each time it iterated will lower the density of
knapsack set, when it reaches a certain times, the
success rate of the
L
3
-lattice base reduction
algorithm be greatly improved. So, it is not
advisable to use the multiple iterated methods.
3 IMPROVE THE ALGORITHM
3.1 Analysis of the Original Algorithm
In the literature (Wang & Hu 2006, p.2930), the
author proposed a tractable knapsack problem.
The author used this knapsack problem to
design the limit of the door knapsack public-key
algorithms. The basic idea is to produce backpack
sequence which meets the above conditions.
Certain degree of transformations is used for the
sequence, such as modular multiplication
transformation. And such sequence after the
transformation can be considered as the public
key. Through the author's analysis, the efficiency
and safety of this public key algorithm were very
high.
But, we need to explain that, first, the essence
of tractable knapsack problem, which is proposed
by the author, is still based on the
super-increasing knapsack problem, nothing but
the author conceals the super-increasing sequence
di. There are no essential differences between
releasing the knapsack as a public key directly
and MH public key algorithm; second, it is not
easy for the algorithm to produce the knapsack
vector. The author puts forward a method: pick up
(repeatable) n numbers g
1
,…g
n
, randomly from
U= {14, 17,19,22,23,26,28,29,30,31,34,37,38, 39,
40,41,42,43,44,46,47,48}, let
n
ik
ki
dg
,
then randomly select n-1 numbers h
2
,…,h
n
which are all relatively prime to
g
1
,…g
n
.
Let
a
1
=d
1
,a
i
=h
i
d
i
,i=2 , …, n. The a
1
we get meets
the requirements. But, the author uses octal
plaintext when construct the algorithm (That is
why the elements of U are no larger than 49),
because we select
g
i
from U only, the variation of
the parameters is limited, this may bring
potentially risk to secret key.
3.2 The Flow Chart of the Improved
Algorithm
Figure 2: The flow chart of the improved algorithm.
3.3 Produce the Secret Key
Select knapsack vector S=(s
1
,…,s
n
) randomly,
which meets the requirements that d
1
=s
1
, d
i
=gcd(s
i
,
d
i-1
), d
n
=gcd(s
n
, d
n-1
)=1, select a random
replacement f to replace the knapsack vector S,
AN IMPROVED HIGH-DENSITY KNAPSACK-TYPE PUBLIC KEY CRYPTOSYSTEM
129

and we get the replaced knapsack vector S`.
Randomly select vector a=( a
1
,…,a
n
),
b=( b
1
,…,b
n
), which makes s`
i
= a
i
+ b
i
. Randomly
select mode number p>
1
n
i
i
a
, q>
1
n
i
i
b
, and
produce secret parameters v, w which meets the
requirements gcd(v,p)=1,gcd(w,q)=1, that makes
v and w have inverse element of modulo p and
modulo q.
Let α
i
= v a
i
(modp), β
i
= w b
i
(modq)
The public key and private key we get are as
follows:
Public key: α=(α
1
,…,α
n
),β=(β
1
,…,β
n
)
Private key: s,v,w,p,q,a,b,f
4 ANALYSIS OF ALGORITHM
4.1 Computational Complexity
Analysis
Let us suppose the binary length of the plaintext
M is k, the binary length of vector α and β are
approximately k. We need to calculate Ep =
1
n
ii
i
m
,Eq =
1
n
ii
i
m
to encrypt. But the
computation of encryption is linear, so the
computation’s complexity of encryption is 0 (k).
The complexity of encrypt time is 20 (k). We
know that the complexity of encryption’s
computation of the traditional public key
encryption algorithm RSA(Rivcs, Gau &
Adlcman 1978, p.120),ElGamal(Guan 1987, p.51)
are 3 powers.
During the decryption process, the improved
algorithm needs to calculate Mp =
1
(mod )vEp p
and Mq=
1
wq(modq)E
,and
respectively used one degree modular
multiplication and one degree computation of
inversion. That is to say, the complexity of this
section is O (k
2
). Besides, according to
1
1
1
[( ) / ]( / ) (mod / ),
n
ijjiiiii
ji
x
saxdad dd
we also need to make n-times multiplication and
n-times division, the complexity of these
computations is one degree, which is O (n k). In
addition, we also need to carry out n-times
modular multiplication, whose complexity is O (n
k
2
). Finally, the complexity of f’s inverse
replacement is linear, and it can be ignored. The
strict complexity of decryption’s computation is O
(nk)+ O(k
2
)+ O(n k
2
). So, the complexity
of decryption’s computation is O(n k
2
), which
is still smaller when it compared to O(k
3
).
Meanwhile, the complexity of the improved
decrypt computation is at the same index level of
that in the original text.
4.2 Security Analysis
1) Secret key security: according to s = a + b,at
least we can randomly get a complete random
sequence from a and b. Assume that a is generated
totally randomly, then b = s-a.
Public key α and β
are created from two irrelevant modules. A is
completely random, which implies that α and β
are completely random sequence for the attacker.
We can say that the attacker can not get s through
α and β. Then we can avoid the potentially risk
that the knapsack vector would be released
directly as a public key.
2) Defend low-density subset sum attack (Coster,
Joux, LaMacchia, et al 1992, p.111):
In the knapsack problem, the knapsack density of
knapsack vector S is usually defined as the
followings:
2
max(l o g s |1 )
i
n
d
in
According to the L
3
– lattice base reduction
algorithm, if this algorithm can always get a base
that includes the shortest non-zero lattice vector,
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
130

and when d<0.9408, the rate of effective attack is
very high. The attack can use lattice as follows:
1
1...
...
... 1
11
...
22
n
Oms
Oms
mS
Among them, select the suitable integer m,
satisfies m>
1
2
n . The dimension lattice of the
matrix is (n+ 1),
S=
1
n
ii
i
sx
. Considering the
infinite extension: Let’s make it that the size of s
i
is L bits, suppose the size of a is similar with s,
which is also L bits. According to p>
1
n
i
i
a
, the
size of modulus p is L + log
2
n, when L>n-log
2
n,
then d>1, that is Cp can defend LDA attack; For
the similar reason, Cq can defend LDA attack.
4.3 Some Comparison to the Original
Algorithm
1) The original algorithm has some restrictive
conditions to produce a certain backpack vector:
select n parameters from U = (14,17,19,
22,23,26,28,29,30,31,34,37,38,39,40, 41,42,43,44,
46,47,48)
to further generate backpack vector.
This brought the key space so small, although
the parameters selected from the U should be
multiplied with the random parameter h before
it's used to be the knapsack vector S, it can not be
eliminated that the key constraints on U, because
the elements of S will be the multiples of the
corresponding elements of U. In the improved
algorithm, knapsack vector is generated from the
multiplication of two completely random numbers,
so the key security issues of original algorithm is
well solved.
2) The improved algorithm is based on the ease of
solution of the original algorithm knapsack
problem, so the efficiency of encryption and
decryption are equal to the original
algorithm.
There is a problem
that the speed of decryption is
slow
in this algorithm and the original one. We
can see the efficiency between this algorithm and
the traditional RSA(Rivcs, Gau & Adlcman 1978,
p.120) and other mode refers to operation is more
or less the same, which is made by the complexity
of making knapsack problem. In addition, the
original algorithm generates knapsack vector
quickly at the expense of the key security.
Although the security of the key algorithm has
been required higher in the improved algorithm,
the terms 0 ≤ x ≤ k-1 should be met still, so there
are still some limitations during the key
generating.
5 CONCLUSION AND PROSPECT
This paper introduces the basic theory of
knapsack-type public key cryptography, and the
strongest attacking method to this public key
cryptography. Then, the article analysis the
literature(Wang & Hu 2006, p.2930), pointing out
the potential defects of the security of secret key,
and gives the improved method, discusses its
safety and efficiency, and finally obtains the
conclusion that on the premise of same efficiency,
the safety is better than the original algorithm.
ACKNOWLEDGEMENTS
This work is supported by Aero-Science Fund of
China (2009ZD53045), and Innovation Project of
Northwestern Polytechnic University (W016141).
AN IMPROVED HIGH-DENSITY KNAPSACK-TYPE PUBLIC KEY CRYPTOSYSTEM
131

REFERENCES
Wang, BC, Hu, YP 2006, ‘Knapsack-type public-key
cryptosystem with high density’, Journal of
Electronics & Information Technology, Vol. 28, No. 12,
pp. 2390-2393.
Yasuyuki, M, Masao, K & Takeshi, N 2008, ‘A new
trapdoor in knapsack public-key cryptosystem with
two sequences as the public key’, Convergence and
Hybrid Information Technology, pp. 357 - 362.
Fleshwound 2009.10, ‘Encryption-algorithm based on
multiple knapsack-type’, <www.smatrix.org.>.
Rivcst, R L, Gau, M J & Adlcman, L M 1978, ‘A method
for obtaining digital signature and public key
cryptosystems’, Communications of the ACM, vol.
21(2), pp. 120-126.
Guan, P H 1987, ‘Cellular automaton public-key
cryptosystem’, Complex Systems, vol. 1, pp.51- 57.
Coster, M J, Joux, A, LaMacchia, B A, et al 1992,
‘Improved low-density subset sum algorithms’,
Computational Complexity, vol. 2(2), pp.111-128.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
132
