
EXPLORING THE COMPLEXITY OF A PROPOSED
RECURSIVE MEASURE OF RECOMBINATIONAL DISTANCE
Robert Collier and Mark Wineberg
Department of Computing and Information Science, University of Guelph, Guelph, Ontario, Canada
Keywords: Genetic Algorithms, Distance Measurement, Complexity Analysis.
Abstract: When studying evolutionary systems, either from the natural world or artificially constructed using
simulated populations, researchers must be able to quantify the genotypic differences that are observed.
With the simple genetic algorithm employing both a unary mutation operator and a binary recombination
operator to maintain variation in the population, it is exceedingly difficult to quantify the distance between
elements of the chromosome space with an approach that is truly representative of the distance that would
need to be traversed by the evolutionary mechanism. Although evaluation function dependence and the
binary arity of the recombination operator both contribute to this difficulty, it is possible to redefine the
function of recombination in such a way as to facilitate the computation of a more representative
measurement of the distance the genetic algorithm would need to traverse to create a specific chromosome
from a given population. The recursive approach presented here entails the definition of unary
recombination operators and ultimately results in a technique for calculating the recombinational distance
between chromosomes with a time complexity that is improved logarithmically over a simplistic approach.
1 INTRODUCTION
Whether conducting scientific studies on organisms
that have been observed in the natural world, or
developing simulations with which to analyze forms
of artificial life, every scientist investigating the
underlying mechanisms that govern the processes of
evolution recognizes the need for scientific
taxonomy and, ultimately, the importance of being
able to quantify any distinguishing differences
observed between organisms. However, where
researchers of the natural world are largely restricted
to collecting observations about the phenotypes of
living organisms, often employing structures such as
pedigree charts to trace evolutionary processes, for
those researchers investigating the population
simulations employed by the genetic algorithm it is
possible to compute an accurate measurement of the
distance between simulated chromosomes in terms
of the actual genetic operators that are in use by the
algorithm. Not only are these same measurements of
distance essential for calculating population
diversity, any attempt to visualize the movement of a
population through a search space of possible
structures requires accurate and representative
measures of interchromosomal distance.
As there are numerous applications for
representative measures of interchromosomal
distance (Stadler, 2002; Jones, 1995a; Wineberg and
Oppacher, 2003), it is the objective of this paper to
introduce and thoroughly explore an approach to the
measurement of these distances with respect to the
function of the recombination operator. Furthermore,
as the incurrence of computational expense is often
used in the justification of excessively simplistic
methodologies, this paper places a strong emphasis
on the complexity of the proposed approach. The
details surrounding any one specific application of
this measure largely exceed the scope of this paper
and are only briefly addressed.
2 GENETIC OPERATORS
With the substitutional mutation process observed in
natural world biology representing one of the
simplest processes by which a new feature can be
introduced into the phenotype of an organism, it is
not surprising that most attempts to quantify the
distance between chromosomes focus upon the
distance that would be traversed by a point mutation
operator. Mitchell (1998) offered the simple
85
Collier R. and Wineberg M..
EXPLORING THE COMPLEXITY OF A PROPOSED RECURSIVE MEASURE OF RECOMBINATIONAL DISTANCE.
DOI: 10.5220/0003085800850094
In Proceedings of the International Conference on Evolutionary Computation (ICEC-2010), pages 85-94
ISBN: 978-989-8425-31-7
Copyright
c
2010 SCITEPRESS (Science and Technology Publications, Lda.)

operational definition of the mutation operator of the
genetic algorithm as the act of randomly changing
the values of some alleles of a simulated
chromosome. As it is technically possible, though
highly unlikely, for every allele of a simulated
chromosome to be mutated in a single generation of
a typical genetic algorithm, it follows that it is then
also possible for any chromosome to be entirely
transformed into any other chromosome in a single
generation. However, as the mutation operator is
typically applied to each allele probabilistically and
independently, the likelihood of one chromosome
transforming into another decreases exponentially
with the number of alleles that differ between the
chromosomes in question. Consequently, the widely
known Hamming distance metric often used in
quantifying the distance between two strings is
frequently employed by researchers of the genetic
algorithm as a measurement of the distance between
the chromosomes in the population simulation.
Although the widespread use of the Hamming
distance (Jones, 1995a) as a measure of the distance
between simulated chromosomes is not
inappropriate, it is important to acknowledge that
Hamming distance alone is only representative of
the developments facilitated by a mutation operator
and, thus, should only be considered the sole source
of variation in a population that employs asexual
reproduction alone. With sexual reproduction
becoming the predominant form of reproduction for
the majority of the non-microscopic organisms
observed in the natural world (Merrell, 1994), the
genetic algorithm, seeking to emulate populations
observed in the natural world as closely as possible,
typically also employs a binary recombination
operator that is often referred to as the crossover
operator.
This recombination operator used by the genetic
algorithm can be defined simply as an operator that
exchanges data between the encoded chromosomes
of two population members, in emulation of the
biological process (Mitchell, 1998). Typically the
operator randomly selects a set of alleles from one
chromosome to be exchanged with the
corresponding alleles of another. A uniform
recombination operation will exchange each allele of
a simulated chromosomes probabilistically and
independently which, although similar to the manner
in which the typical mutation operator is applied,
entails that the range of possible offspring that can
be created through recombination is directly
proportional to the genetic difference between the
simulated chromosomes selected to act as parents.
Although k-point recombination operations,
which randomly select a set number of substrings
from a simulated chromosome for exchange, are also
employed by genetic algorithm researchers with
great frequency, since the set of possible offspring
that can be created through the application of a
uniform recombination operation contains all sets of
possible offspring that can be created through the
application of any number of fixed k-point
recombination operations, for the sake of
generalizability all subsequent references to
recombination refer to uniform recombination.
3 DISTANCE MEASUREMENT
The significance of distance functions to the genetic
algorithm is most apparent when considering a
formal definition of the fitness landscape (Stadler,
2002) that the genetic algorithm traverses in search
of an optimum. Stadler defined the three-part
composition of a fitness landscape to include an
evaluation function to be optimized, the set of
possible candidate solutions, that are represented by
the genetic algorithm as simulated chromosomes,
and a conceptualization of distance or
neighbourhood that induces a topology on the
solution set to create a solution space. Furthermore,
knowing the distance between two chromosomes
that must be traversed by the operators of the genetic
algorithm is a reasonable indicator of the smallest
number of generations it will take before the
transformation of one chromosome to another is
possible. Although the application of this
information to optimization is apparent, by
computing the distance between all possible pairs of
chromosomes in the population, it is possible to get
an impression of the actual diversity of the
population as well.
For a function whose domain is a pair of
simulated chromosomes and whose range is a real
value to be considered a true measure of distance
(or, equivalently, a metric), there are four conditions
that must be satisfied. Firstly, the function must
never report the distance between two elements of
the solution set as a negative value, a condition
known as non-negativity. The function must also
comply with the identity of indiscernibles condition
that states that the distance between two elements
can and will only be considered zero if the two
elements are identical. The third condition that must
be observed, symmetry, states that the distance to be
traversed from element x to element y must be the
same as the distance that would be traversed from
ICEC 2010 - International Conference on Evolutionary Computation
86

element y to element x. Finally, the function must
also comply with the triangle inequality, which
states that the distance from element x to element y
must always be less than or equal to the sum of the
distance from x to z and the distance from z to y.
Since it is often the case that the mechanism of an
operator cannot be described using a function that
satisfies each of the four metric conditions presented
above, a more generalized measure can be created
by relaxing one or more conditions. Pseudometrics,
semimetrics, and quasimetrics each observe three of
the four conditions, failing to observe the identity of
indiscenibles, the triangle inequality, and the
symmetry conditions, respectively.
3.1 Recombinational Distances
The binary arity of the recombination operator, in
contrast with the unary arity of the typical mutation
operator, poses the most significant barrier to the
introduction of an accurate measure of distance
between chromosomes as would be traversed by
recombination. Since recombination requires two
arguments, the notion of two chromosomes being
separated by any finite number of recombinations is
undefined without the composition of the
population. Consequently, when considering
traversal of the search space using only
recombination, the population must be explicitly
considered, as in Figure 1.
Figure 1: Populations P and P', shaded, from the space S
of binary chromosomes of length 2. It is observed that
while recombination in population P {, , } of
(a) is capable of producing , indicated by the edges
between and the shaded area, if member is
removed, as in population P' of (b), all edges incident on
disappear, demonstrating that the presence of an edge
between members is dependent upon the entire population.
It was noted by both Jones (1995a, 1995b) and
Culberson (1994) that considering each point in the
search space to be a single chromosome does not
permit researchers to explicitly connect them
through a recombination operator. They proposed
that points in the search space represent possible
chromosome pairs between which connections exist
when one pair could be recombined to produce the
other pair as offspring, as depicted in Figure 2.
Figure 2: It is possible to depict recombination operations
in a simple graph if vertices represent pairs, rather than
individual chromosomes. Although the space S of binary
chromosomes remains unchanged from Figure 1, there are
three unique pairings of the two members of population P,
shaded and denoted P'' in the figure. The edge that
connects pair (, ) with (, ) indicates that
recombination between one pair could produce the other
pair as offspring.
Similarly, in Altenberg's (1997) development of
an evaluation function for his fitness distance
correlation counterexample, a measure termed
"crossover distance" was defined as the number of
single point recombination operations that must be
applied to transform one pair of complementary
chromosomes into another complementary pair.
However, as recombination operations applied to
complementary chromosomes can produce offspring
of any configuration, this definition need not
consider pairs separated by infinite distances.
Although this was sufficient for the construction of
Altenberg's function, it was also acknowledged that
the recombination of complementary chromosomes
is a rare occurrence during the operation of an actual
instance of the genetic algorithm.
A contrasting alternative proposed by Gitchoff
and Wagner (1996) employs a hypergraph topology
wherein chromosomes are connected by as many
hyperedges as there are offspring that could be the
result of recombining hyperconnected chromosomes,
as depicted in Figure 3 on the following page.
EXPLORING THE COMPLEXITY OF A PROPOSED RECURSIVE MEASURE OF RECOMBINATIONAL
DISTANCE
87

Figure 3: Under the other paradigm proposed, possible
recombination operations can be depicted in a hypergraph
if vertices depict individual chromosomes connected by as
many hyperedges as possible offspring, as demonstrated
by the complementary pair (, ) in (b) having twice
as many hyperedges as pair (, ) in (a).
4 RECOMBINATION ARITY
Although either of the aforementioned techniques
successfully captures some notion of the distance
between possible chromosomes, a third alternative
might suggest that the set of all possible binary
recombination operations in a given population
could instead be expressed using a set of unary
operations. As a clarifying example, for a population
of three simulated chromosomes, the set of possible
binary operations recombine(A,B), recombine(A,
C), and recombine(B, C), could be equivalently
expressed using the three unary operators
recombineWithA, recombineWithB, and
recombineWithC. Under this paradigm, the distance
between two simulated chromosomes with respect to
traversal by the recombination operator would be the
smallest number of unary recombination operations
available within the current population. It is
important to recognize, however, that the symmetry
property normally associated with true measures of
distances cannot be upheld when each binary
recombination operation between two chromosomes
is treated as a unary operation. Consider, as a
clarifying example, three sample chromosomes A =
{0,0,0,0}, B = {1,1,1,1}, and C = {0,0,1,1} with the
binary recombination operation redefined as two
distinct unary operations. Although it is true that the
operation recombineWithA(B) is capable of
producing an offspring chromosome C under
uniform recombination, it does not follow that
recombineWithA(C) could produce B as an
offspring. Since the distance (measured in terms of
unary recombination operation recombineWithA)
between B to C is finite while the distance from C to
B is infinite, the recombination distance measure
would, in fact, be more accurately defined as a
quasimetric.
Although it is known that the search space of
possible simulated chromosomes can only be
depicted as a simple graph in two dimensions (with
one vertex for each possible chromosome) if the
undirected edges are representative of a unary
operator such as mutation (Stadler, 2002), with the
replacement of the binary recombination operator
with a set of unary recombination operators, a
graphical representation becomes possible.
However, since it has been demonstrated that the
unary recombination operator is not symmetric, a
directed graph representation would be more
accurate.
4.1 Unary Recombination Definition
In order to define a unary recombination operator it
is first necessary to establish a definition of the
space of possible chromosomes in terms of a single
fixed chromosome, here denoted α, as was done
with the recombineWithA operator example of the
previous section. With the recombination operators
of the genetic algorithm defined for chromosome
operands of a fixed length λ, the set of possible
chromosomes of the same length with which the
fixed chromosome α could be recombined is
referred to as the set β, of cardinality 2
λ
. Within the
set β there are C(λ, δ) unique chromosomes at a
Hamming distance of δ from α, ∀δ where 0 ≤ δ ≤
λ. From the binomial theorem it is established that
δ=0
Σ
λ
C(λ, δ) = 2
λ
and, consequently, the subsets of β
associated with each possible Hamming distance
value of δ, for 0 ≤ δ ≤ λ, are mutually exclusive and
exhaustive. Any chromosome β
i
belonging to set β
can be uniquely identified as the chromosome of
length λ that has values complementary to those of α
at the set of indices χ, where the cardinality of set χ
can range from 0 (for chromosome β
1
at Hamming
distance 0 from α) to λ (for chromosome β
2
λ
,
complementary to chromosome α, at a Hamming
distance of λ).
It is stressed that any binary string of length λ
could be assigned to chromosome α provided that
the set of chromosomes β is the set of all binary
ICEC 2010 - International Conference on Evolutionary Computation
88

strings of length λ, ordered such that β
0
for χ = {}
will be the binary string that is identical to α, having
a Hamming distance of 0, β
1
for χ = {1} will be the
binary string that is identical to α except at index 1
for which it will be complementary, having a
Hamming distance of 1, etc. It is now possible to
define a unary recombination operator such that the
domain is a single chromosome and the range is a
set of possible offspring chromosomes. The set of
possible offspring chromosomes ε of a uniform
recombination operation between parent
chromosomes α and β
i
is the set of chromosomes
having values complementary to those of α at any
set of indices that is a member of the power set P(χ).
Equivalently, it could be stated that every element of
the set of possible offspring chromosomes ε is
contained within the highest order schema that
contains both parent chromosomes α and β
i
. This
schema would only contain wildcard characters at
indices where chromosomes α and β
i
differ and,
thus, the set of wildcard character indices would be
equivalent to the set χ. For recombination between
parent chromosomes α and β
i
between which there
is a Hamming distance value of δ, the cardinality of
set χ will be δ, and thus the cardinality of the power
set P(χ) will be 2
δ
, as is evident in the example from
Figure 4.
Figure 4: For uniform recombination between the pair of
parent chromosomes and , where is
defined relative to as having complementary index
set χ = {2, 3}, there exists exactly one possible offspring
defined relative to with a complementary index set
that is a unique member of the power set of the
complementary index set between α and β
i
.
It should be noted that since every chromosome
β
i
is described relative to chromosome α using a
complementary index set χ, the actual configuration
() for the chromosome α need not have been
explicitly noted. Had α been a different fixed
chromosome (, for example), the
complementary index set χ ={2,3} would change the
configuration of chromosome β
i
(into if α
was configuration ). The possible offspring
would remain the configurations defined by
complementary index sets {}, {2}, {3}, and {2,3}.
With every chromosome β
i
described relative to α, it
is sufficient to associate each set of possible
offspring chromosomes, denoted ε, with the parent
chromosome β
i
which, when recombined with α,
could produce those chromosomes as offspring.
With the newly established approach for
redefining the space of possible chromosomes with
respect to a single, fixed chromosome using
complementary index sets, the set of unary
recombination operators necessary to replace the
binary recombination operator can be constructed.
For every unique chromosome α in the population
that could act as one operand of the binary
recombination operator, there exists a unary operator
(upon the chromosome space defined in terms of α)
that takes a single operand chromosome and
generates a set of possible offspring chromosomes
equal to the set of possible offspring for a binary
recombination operation between the operand
chromosome and the fixed chromosome α.
The associations present between chromosomes
from set β and the set ε that represents the set of
possible offspring of a recombination operation
between a member of β and the chromosome α can
be stored as an adjacency matrix that would define a
directed graph structure representative of the
recombination operations possible. Although similar
to the matrix employed by Vose (1990) to encode
mixing information (the probability that a pair of
chromosomes, through both unary mutation and
binary recombination, can produce a specific
offspring), the adjacency matrix for the digraph
representation of recombination would encode
boolean values for whether or not each chromosome
could produce any other in the space solely through
the act of recombining with a member of the
population. Furthermore, as it was Vose's intention
to employ the mixing probabilities in tandem with
the selection probabilities (which cannot be
computed without the evaluation function and a
corresponding decrease in generality), for the
present task of determining whether or not a given
chromosome can be created through the
recombination of elements of the current population,
the proposed adjacency matrix of boolean values
would incur a lesser computational expense.
4.2 Digraph Representation
Since the recombination operations discussed herein
probabilistically determine whether or not each
allele of a chromosome will be exchanged
EXPLORING THE COMPLEXITY OF A PROPOSED RECURSIVE MEASURE OF RECOMBINATIONAL
DISTANCE
89

independently, the adjacency matrix used to define
the directed graph representation for recombination
between chromosomes of length λ can be
constructed recursively from adjacency matrices for
chromosomes of length λ−1. Under the temporary
assumption that chromosome α is the binary string
of length λ comprised entirely of zero bits, there
exists a 2
λ
× 2
λ
matrix of Boolean values where
entry φ
ij
indicates whether or not recombination
between α and the i
th
member of the chromosome
space can yield the j
th
member of the chromosome
space as an offspring. The matrix that would
function as the basis for a recursive construction
would be used for a chromosome length of 1 and,
thus, entry φ
00
would indicate whether or not
chromosome α (which is '0') and the zeroth member
of the chromosome space (which is also '0') can be
recombined to produce the zeroth member of the
chromosome space (which is also '0') as an
offspring. Entry φ
01
, on the other hand, would
indicate whether or not chromosome α (which is '0')
and the zeroth member of the chromosome space
(which is also '0') can be recombined to produce the
first member of the chromosome space (which is '1')
as an offspring. For single bit chromosome
recombination, the entries φ
00
, φ
01
, φ
10
, and φ
11
would be assigned the boolean values true, false,
true, and true, respectively.
For the recursive step in the construction of an
adjacency matrix of the digraph representation for a
chromosome of length λ, assume that the adjacency
matrix of the digraph representation for a
chromosome of length λ - 1 is complete and
accurate. For entry φ
ij
of the adjacency matrix for a
chromosome of length λ to have a value of true, it
must be possible to recombine the i
th
member of the
chromosome space of length λ, denoted "i
1
i
2
i
3
...
i
λ
", with a chromosome of length λ of only zero bits,
such as "0 0 0 ... 0", and produce the j
th
member of
the chromosome space of length λ, denoted "j
1
j
2
j
3
... j
λ
" as an offspring. In the case where i
1
= "1" this
recombination is possible if and only if "i
2
i
3
... i
λ
"
and "0 0 ... 0" can be recombined to produce "j
2
j
3
...
j
λ
", since an i
1
of "1" can be recombined with a "0"
from α to produce either possible value of j
1
.
Consequently, the 2
λ -1
× 2
λ -1
entries φ
ij
of the
adjacency matrix for length λ for i from [2
λ -1
+1...2
λ
]
and j from [1...2
λ -1
] and the 2
λ -1
× 2
λ -1
entries φ
ij
of
the adjacency matrix for length λ for i from [2
λ -
1
+1...2
λ
] and j from [2
λ -1
+1...2
λ
] will both be precise
copies of the adjacency matrix associated with
chromosomes of length λ - 1. In the alternative case,
where i
1
= "0", recombination between "i
1
i
2
i
3
... i
λ
"
and "0 0 0 ... 0" can only produce "j
1
j
2
j
3
... j
λ
" as an
offspring chromosome if and only if j
1
= "0" and "i
2
i
3
... i
λ
" and "0 0 ... 0" can be recombined to produce
"j
2
j
3
... j
λ
" as an offspring. Consequently, the 2
λ -1
×
2
λ -1
entries φ
ij
of the adjacency matrix for length λ
for i from [1...2
λ -1
] and j from [1...2
λ -1
] will also be
a precise copy of the adjacency matrix associated
with chromosomes of length λ - 1 and the 2
λ -1
× 2
λ -1
entries φ
ij
of the adjacency matrix for length λ for i
from [1...2
λ -1
] and j from [2
λ -1
+1...2
λ
] will have a
value of false.
For demonstrative purposes, consider the
construction of the 4 × 4 adjacency matrix for
chromosome length 2. Under the continued
assumption that chromosome α is comprised entirely
of zero bits (in this case, chromosome "00"),
recombination with the 1
st
chromosome, "00", can
produce only "00" as an offspring. Thus, the first
row of the adjacency matrix will be [true false false
false]. Recombination between α and the second
chromosome, "01", can produce either "00" or "01"
as an offspring and, thus, the second row of the
adjacency matrix will be [true true false false].
Similarly, the third and fourth rows of the adjacency
matrix will be [true false true false] and [true true
true true], respectively. The adjacency matrices for
the digraph representations of recombination
operations applied to chromosomes of length 1 and 2
are depicted in Figure 5 (a) and (b), respectively.
Figure 5: The adjacency matrices used to define the
digraph representation of recombination between
chromosomes of length 1, (a), and length 2, (b). The
recursive construction approach for these adjacency
matrices is evidenced by the top left, bottom left, and
bottom right quadrants of the matrix in (b) being identical
to the matrix in (a).
As expected from the structural induction proof
of the preceding paragraph, if the adjacency matrix
for chromosome length 2 is bisected vertically and
horizontally into exactly 4, 2 × 2 adjacency matrices,
the top-left, bottom-left and bottom-right matrices
are copies of the basis matrix, and the top right is a 2
× 2 matrix comprised entirely of zeros.
It also follows that if the adjacency matrix for
chromosome length 3 is bisected vertically and
ICEC 2010 - International Conference on Evolutionary Computation
90
horizontally into exactly 4, 4 × 4 adjacency matrices,
the top-left and bottom matrices are copies of the
adjacency matrix for the digraph representation of
recombination between chromosomes of length 2,
and the top right is a 4 × 4 matrix comprised entirely
of zeros. Figure 6 clearly depicts the presence of the
digraph associated with recombination for
chromosomes of length 2 within the digraph
associated with recombination for chromosomes of
length 3.
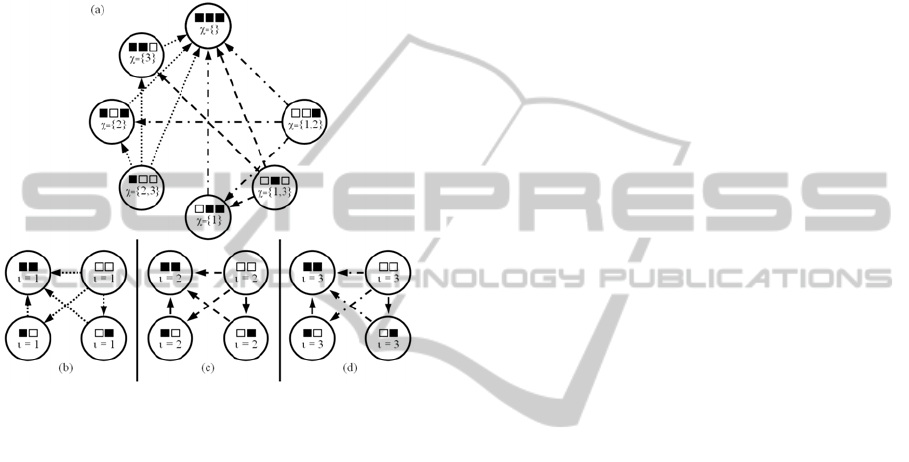
Figure 6: For β
i
separated from α by Hamming distance δ
< λ, the chromosomes must share at least one allele,
making any recombination between these configurations
equivalent to a recombination applied to configurations of
length λ-1. In (a) above, since λ = 3, configuration β
i
and
α must share the symbol at index ι = 1, 2 or 3. If the index
ι = 1, then the digraph representation (b) of recombination
for length 2 can be consulted, and the edges mapped to the
nodes in (a) by inserting the symbol shared by β
i
and α at
index ι. For example, if β
i
and α share the symbol at ι = 1,
the arc from to in (b) corresponds to the arc
from to . If the symbol at ι = 2 is shared, the
arc from to in (c) corresponds to the arc
to . Thus, every arc in a digraph representation for
λ, except for those that originate in the node
complementary to α, can be determined from the digraph
representation for λ-1.
5 POSSIBLE OFFSPRING
It can be concluded, from the proof and discussion
contained in the previous section, that if the first
parent chromosome α of a recombination operation
is a binary string of zero digits, there is a trivially
simple recursive algorithm that will determine
whether the chromosome ε
i
can be produced as an
offspring of a recombination operation between the
first parent chromosome α and the second parent
chromosome β
i
. This algorithm, in order to
determine whether the i
th
member of the
chromosome space can produce the j
th
member of
the chromosome space as an offspring through
recombination with a chromosome comprised
entirely of zero bits, entails determining whether the
entry φ
ij
of the adjacency matrix lies in the top right
quadrant of the adjacency matrix. If so, it can be
concluded that a recombination operation between
the i
th
member of the chromosome space and the
zero bit chromosome cannot produce the j
th
member
of the chromosome space as an offspring. If,
however, the entry φ
ij
lies in any other quadrant, the
same algorithm is recursively applied to the 2
nd
through the λ
th
bits of chromosomes i and j until the
chromosome length is 1.
5.1 Fixed Parent General Case
As an alternative to the development of a similar
proof for every other possible value of the simulated
first parent chromosome α, it would suffice to
demonstrate that there exists a reversible
transformation that, when applied to both the parent
and offspring chromosomes, would convert one of
the parent chromosomes into the binary string
comprised entirely of zeros. Under this
transformation, denoted τ, the boolean value
describing whether or not recombination between a
pair of chromosomes β
i
and β
j
can yield
chromosome ε
k
as an offspring would be equivalent
to the boolean value describing whether or not a
recombination operation applied to a chromosome α
that is comprised entirely of zero bits and
chromosome τ(β
j
) can yield the chromosome τ(ε
i
) as
an offspring.
Vose (1990) noted such a transformation in the
second lemma of his technical report on the
formalization of the genetic algorithm to be the
application of the bitwise exclusive disjunction
operator. This section will demonstrate that the use
of this operator allows a single digraph
representation of a recombination operation with a
chromosome comprised entirely of zero bits to serve
as a sufficient representation for any recombination
operator.
If the previously mentioned adjacency matrix has
already been constructed, wherein the boolean value
of entry φ
ij
indicates whether or not recombination
between a chromosome α comprised entirely of zero
bits can be recombined with the i
th
member of the
chromosome space to yield the j
th
member of the
EXPLORING THE COMPLEXITY OF A PROPOSED RECURSIVE MEASURE OF RECOMBINATIONAL
DISTANCE
91

chromosome space as an offspring, then the question
of whether uniform recombination between the pair
of simulated chromosomes β
i
and β
j
can yield
chromosome ε
k
as an offspring is equivalent to the
question of whether recombination between a
chromosome α comprised entirely of zero bits and
τ(β
j
) can yield chromosome τ(ε
i
) as an offspring.
This boolean value, in turn, can be read directly
from the adjacency matrix.
If transformation τ is the application of a bitwise
exclusive disjunction operation (represented with the
symbol ⊕) between the operand and the k
th
member
of the chromosome space, then τ("i
1
i
2
i
3
... i
λ
")
would be equivalent to "k
1
⊕ i
1
k
2
⊕ i
2
k
3
⊕ i
3
... k
λ
⊕ i
λ
". Since exclusive disjunction results in a value
of false if and only if the two operands are either
both true or both false, then "τ(k)1 τ(k)2 ... τ(k)λ"
would be equivalent to "k
1
⊕ k
1
k
2
⊕ k
2
... k
λ
⊕ k
λ
",
also equivalent to "0 0 0 ... 0".
To solve for the boolean value of whether
recombination between the k
th
and i
th
member of the
chromosome space, denoted "k
1
k
2
k
3
... k
λ
" and "i
1
i
2
i
3
... i
λ
" respectively, can produce the jth member,
denoted "j
1
j
2
j
3
... j
λ
", as an offspring, the
application of a bitwise exclusive disjunction
operations with "i
1
i
2
i
3
... i
λ
" will transform the k
th
,
i
th
, and j
th
members of the chromosome space into
configurations "0 0 0 ... 0", "τ(i)
1
τ(i)
2
τ(i)
3
... τ(i)
λ
",
and "τ(j)
1
τ(j)
2
τ(j)
3
... τ(j)
λ
", respectively. It then
suffices to prove that the boolean value describing
whether uniform recombination between
configurations "0 0 0 ... 0" and "τ(i)
1
τ(i)
2
τ(i)
3
...
τ(i)
λ
" can produce configuration "τ(j)
1
τ(j)
2
τ(j)
3
...
τ(j)
λ
" as an offspring is equivalent to the boolean
Table 1: The fact that the fourth column, j
x
= k
x
∨ i
x
, and
the eighth column, τ(j)
y
= 0 ∨ τ(i)
y
, are equivalent
demonstrates that recombination can produce offspring j
from parent configurations i and k if and only if
recombination between a chromosome comprised entirely
of zeros and one equal to i ⊕ k can produce j ⊕ k as an
offspring.
k
x
i
x
j
x
j
x
= k
x
∨ i
x
k
x
⊕ k
x
≡ τ(k)
x
k
x
⊕ i
x
≡ τ(i)
x
k
x
⊕ j
x
≡ τ(j)
x
τ(j)
y
=
0 ∨ τ(i)
y
0 0 0 true 0 0 0 true
0 0 1 false 0 0 1 false
0 1 0 true 0 1 0 true
0 1 1 true 0 1 1 true
1 0 0 true 0 1 1 true
1 0 1 true 0 1 0 true
1 1 0 false 0 0 1 false
1 1 1 true 0 0 0 true
value describing whether uniform recombination
between the k
th
and i
th
member of the chromosome
space can produce the j
th
member of the
chromosome space. For this to be true it must be
shown that, for all values of x, τ(j)
y
= 0 ∨ τ(i)
y
will
be true if and only if j
x
= k
x
∨ i
x
is also true. This
particular fact can be most easily demonstrated
through the use of a simple truth table, and has been
included as Table 1.
5.2 Digraph Representation Properties
Since the set of possible offspring chromosomes that
can be produced by the application of uniform
recombination operations to chromosomes of length
λ is equivalent to the set of possible chromosomes β
with which chromosome α could be recombined to
create offspring chromosomes, and since both sets
are present in the digraph representation of
recombination, the number of possible resultant
offspring chromosomes is 2
λ
. Furthermore, since the
C(λ, δ) unique chromosomes at a Hamming distance
of δ, where 0 ≤ δ ≤ λ, represent every possible
chromosome with which chromosome α could be
recombined, and the cardinality of the set of possible
offspring that could be produced from a
recombination operation applied to chromosomes
between which there is a Hamming distance of δ is
2
δ
, the number of arcs present in the offspring
digraph is
δ=0
Σ
λ
C(λ, δ)⋅2
δ
= (1+2)
λ
= 2
λ
.
6 COMPLEXITY ANALYSES
6.1 Impressions of Complexity
If the set of all possible chromosomes to be searched
by the genetic algorithm is denoted R, it was
explicitly observed by Jones (1995a, 1995b) and
Culberson (1994) that binary recombination would
then act on an element of R
2
to produce elements of
R. This function could be accurately depicted using
bipartite directed graph G = (U, V, E) where, for
every vertex of U representative of a pair of
chromosomes, there exists an arc in E whose direct
successor is a vertex in V representative of a
chromosome that might be created by recombining
the pair of chromosomes at the direct predecessor of
the arc in U. While it is obvious that the cardinality
of set V is the cardinality of the entire chromosome
space S being searched, where |S| = 2
λ
, depending
upon whether or not the recombination operator is
permitted to recombine a chromosome with itself,
the cardinality of set U is, for a population
ICEC 2010 - International Conference on Evolutionary Computation
92

containing exactly ρ unique chromosomes, either
(ρ+1)! / (2!⋅(ρ-1)!) or (ρ)! / (2!⋅(ρ-2)!) respectively.
It might then be concluded that determining
whether or not (from the set B of Boolean values) a
specified chromosome (belonging to set V) can be
produced by the application of a single
recombination operation to a pair of chromosomes
from the population (belonging to set U), and thus
evaluating the solution for the function f:(U,V) → B,
is equivalent to searching the previously defined
bipartite directed graph and must then have a
complexity of the order O(ρ
2
2
λ
).
The contrasting representation of binary
recombination investigated by Gitchoff and Wagner
(1996) employed a hypergraph wherein exactly one
vertex exists for each possible chromosome, and a
hyperedge between any two vertices would exist for
each possible offspring that could be the result of a
recombination operation between the
hyperconnected vertices. Although this hypergraph
would have only P vertices, the set of hyperedges
that would connect a single pair of complementary
vertices would have the cardinality of the entire
chromosome space S. With binary recombination
being possible between any two chromosomes in the
population, this would be a complete graph of n(n-
1)/2 edges, also suggesting a complexity of the order
O(ρ
2
2
λ
).
6.2 Actual Complexity Analysis
With the proposed methodology, determining
whether a given chromosome can be produced by a
population through a single application of a binary
recombination operator is equivalent to determining
whether a given chromosome can be produced from
any pair of chromosomes in the population,
necessitating the O(ρ
2
) component of the complexity
associated with examining all possible chromosome
pairs. Although it remains true that recombination
between a pair of complementary chromosomes
could theoretically result in any chromosome in the
search space S as an offspring, determining whether
or not a matrix entry is located in the top right
quadrant, at most λ times, has time complexity O(λ).
Overall, the time complexity of the proposed
recursive algorithm is the sum of the complexity of
locating the appropriate matrix entries for all
possible chromosome pairings, O(ρ
2
λ), and the
complexity of the application of the bitwise
exclusive or operations necessary to redefine the
chromosomes of the current population in terms of
each possible fixed parent, also O(ρ
2
λ), for a total
worst case time complexity of O(ρ
2
λ). Thus, the
time complexity has been reduced from O(ρ
2
2
λ
) to
O(ρ
2
λ), which constitutes a logarithmic speedup.
Furthermore, for each of the λ determinations of
whether the associated matrix entry lies in the top
right adjacency matrix quadrant, the 25% likelihood
that the algorithm can terminate early at every step
of the recursion also indicates a very fast average
case time complexity of the algorithm as well.
7 DISCUSSION
It was previously noted that the notion of
interchromosomal distances in the genetic algorithm
is central to both the established adaptive landscape
visualization technique and measures of population
diversity. It was noted by Wineberg and Oppacher
(2003) that every measure of population diversity in
common usage is essentially an aggregating function
of the Hamming distances between all possible pairs
of chromosomes that are present in the population
(or a slight variant thereof). Furthermore, when
constructing a three-dimensional adaptive landscape
visualization, the chromosome space must first be
represented as a two-dimensional plane from which
the landscape can be extruded. Since the
dimensionality of the chromosome space employed
by a genetic algorithm is typically in excess of two,
if researchers do not wish to limit their own usage of
this visualization technique to instances where the
evaluation function is of two dimensions or less the
chromosome space dimensionality should be
reduced by multidimensional scaling technique for
which an accurate interchromosomal distance
measure has been defined. Although some
researchers might consider the Hamming distance
metric sufficient for calculating interchromosomal
distances, it must be explicitly observed that the
chromosome space is traversed by the genetic
algorithm with both a mutation operator and a
recombination operator, simultaneously. Since it has
been previously demonstrated that recombination
operations are more likely to assemble higher order
building blocks than mutation operations (Spears,
1998), the set of approaches to interchromosomal
distance measurement in the genetic algorithm
would be remiss if a technique for measuring
recombinational distance were not included.
8 CONCLUSIONS
Although previous approaches to the depiction of the
binary recombination operator would seem to
EXPLORING THE COMPLEXITY OF A PROPOSED RECURSIVE MEASURE OF RECOMBINATIONAL
DISTANCE
93

suggest a time complexity O(ρ
2
2
λ
), this paper has
demonstrated that a logarithmic speedup can be
achieved. By first defining a set of unary
recombination operators that are equivalent to the
function of the binary recombination operator,
followed by the application of a bitwise
transformation on the operands, the time complexity
associated with the process of determining whether a
certain chromosome can be produced from a given
population through a single recombination can be
improved to O(ρ
2
λ). The recursive approach
presented in this paper affords researchers an
opportunity to include consideration for the traversal
of the chromosome space by both mutational and
recombinational operations, which will ultimately
result in more representative visualizations and
calculations of population diversity.
ACKNOWLEDGEMENTS
The authors wish to acknowledge partial funding for
this research by the Natural Sciences and
Engineering Research Council of Canada (NSERC).
REFERENCES
Altenberg, L. 1997. Fitness Distance Correlation Analysis:
An Instructive Counterexample. Proceedings of the
7th International Conference on Genetic Algorithms,
pp. 57--64.
Culberson, J. C. 1995. Mutation-Crossover Isomorphisms
and the Construction of Discriminating Functions.
Evolutionary Computation, 2, pp. 279--311.
Dybowski, R., Collins, T. D. and Weller, P. R. 1996.
Visualization of Binary String Convergence by
Sammon Mapping. Proceedings of the 5th Annual
Conference on Evolutionary Programming, pp. 377--
383.
Gitchoff, P. and Wagner, G. P. 1996. Recombination
Induced Hypergraphs. Complexity, 2(1), pp. 37--43.
Goldberg, D. E. 1989. Genetic Algorithms in Search,
Optimization and Machine Learning. Addison-Wesley
Longman Publishing Co., Inc.
Hamming, R. 1950. Error Detecting and Error Correcting
Codes. Bell System Technical Journal, 29(2), pp. 147--
160.
Jones, T. 1995. Evolutionary Algorithms, Fitness
Landscapes, and Search. Thesis Document. The
University of New Mexico, Albuquerque, New
Mexico, USA.
Jones, T. 1995. One Operator, One Landscape. Working
Paper. Santa Fe Institute.
Merrell, D. J. 1994. The Adaptive Seascape: The
Mechanism of Evolution. pp. 59.
Mitchell, M. 1996. An Introduction To Genetic
Algorithms. Cambridge, MA, USA: MIT Press.
Sammon, J. W. 1969. A Nonlinear Mapping for Data
Structure Analysis. IEEE Transactions on Computers,
18(5), pp. 401--409.
Spears, W. M. 1998. The Role of Mutation and
Recombination in Evolutionary Algorithms. Thesis
Document. George Mason University, Fairfax, VA,
USA.
Stadler, P. F. 2002. Fitness Landscapes. Biological
Evolution and Statistical Physics, pp. 183--204.
Van Wijk, J. J. 2005. The Value of Visualization. IEEE
Visualization Conference, 0, pp. 11.
Vose, M. D. 1990. Formalizing Genetic Algorithms.
Proceedings of Genetic Algorithms, Neural Nets, and
Simulated Annealing Applied to Problems in Signal
and Image Processing.
Wineberg, M. and Oppacher, F. 2003. The Underlying
Similarity of Diversity Measures Used in Evolutionary
Computation. Proceedings of the 5th Genetic and
Evolutionary Computation Conference, pp. 1493--
1504.
Wright, S. 1932. The Roles of Mutation, Inbreeding,
Crossbreeding and Selection in Evolution.
Proceedings of the 11th International Congress of
Genetics, 8, pp. 209--222.
ICEC 2010 - International Conference on Evolutionary Computation
94
