
A STRATEGIC SIMULATION TOOL FOR CAPABILITY-BASED
JOINT FORCE STRUCTURE ANALYSIS
Cheryl Eisler and Dave Allen
Centre for Operational Research and Analysis, Defence R&D Canada, 101 Colonel By Drive, Ottawa, Canada
Keywords: Discrete Event Simulation, Monte Carlo, Force Structure Analysis, Fleet Mix, Capability-Based Planning.
Abstract: This paper describes a stochastic discrete event simulation model for scheduling of joint military force
structures. The model employs capability-based methods to link scenario requirements to force structure
assets. Assignment of assets to scenarios is designed to attempt to mimic the decisions of a military
scheduler. Force structure performance is evaluated based on how well and how often scenario capability
requirements are met. The model output permits options analysis, capability gap analysis, determination of
optimal force structure composition, and evaluation of force structure performance in the face of changing
requirements and policies (such as readiness and sustainment, operations tempo, and personnel tempo
constraints).
1 INTRODUCTION
Determining the size and composition of a future
military force structure
1
is a problem that can be
approached from many different directions, and is
often driven by nation-specific policies, processes,
and objectives. It is also a question of the depth and
breadth of exploration required; depth in terms of
the level of fidelity that is used to model the force
structure, and breadth across military services.
In practice, quantitative evaluation of force
structures range from “back-of-the-envelope” type
calculations (e.g., with two bases, two ships are
required at each so that one is always available when
one is in maintenance) or subject matter expert
(SME) opinion, to detailed theatre level combat
modelling (e.g., Bulut, 2001, Gallagher and Kelly,
1991) or campaign analysis (Taylor and Lane,
2004). Low fidelity models are easy to generate, but
tend to rely on broad-ranging assumptions and are
subject to significant criticism regarding objectivity.
Ideally, high fidelity models would be used to
determine the performance of the total force against
high-fidelity models are very data intensive and/or
use physics-based approaches that are time-various
threats across multiple scenarios (Farr et al., 1994).
While they are significantly less subjective,
consuming to evaluate and difficult to extrapolate
for future capability. Taking a moderated approach,
medium fidelity models focus on resource allocation
(how many are needed) rather than resource
effectiveness (how likely the mission can be
accomplished). This is a specialized application of
general scheduling and routing problems, for which
many customized models have been developed.
Service-specific scheduling models abound.
Logistic problems such as sealift (Salmeron et al.,
2009), airlift (Wu et al., 2009, Wesolkowski and
Billyard, 2008, Baker et al., 2002) – to name but a
few, or a combined mobility problem (Mattock et
al., 1995) are well developed, but difficult to expand
for use across services. If not focused on airlift, air
force structure models tend to be driven by
maintenance requirements and facilities (Mattila et
al., 2008). Army force structure analysis is highly
separated between personnel-driven models
(Klerman et al., 2008) and vehicle fleet mixes
(Whitacre et al., 2008, Abbass et al., 2007,
Walmsley and Hearn, 2004, Brown et al., 1991).
Naval deployment scheduling applications are
common (Zadeh, 2009, Horn et al., 2007, Dugan,
2007, and others). Five naval fleet planning
applications (Gauthier et al., 2008, Fildes, 2006,
Greer et al., 2005, Crary et al., 2002, Cortez and
1
“Force structure” is a term used to designate the set o
f
assets within a military unit and the inter-dependence
b
etween these assets, as well as their home base. Fo
r
example, a naval force structure could include all the ships
and crews, as well as the infrastructure supporting them.
Eisler, C. and Allen, D.
A STRATEGIC SIMULATION TOOL FOR CAPABILITY-BASED JOINT FORCE STRUCTURE ANALYSIS.
DOI: 10.5220/0003727800210030
In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES 2012), pages 21-30
ISBN: 978-989-8425-97-3; ISSN: 2184-4372
Copyright
c
2023 by His Majesty the King in Right of Canada as represented by the Minister of National Defence and SCITEPRESS – Science and Technology Publications, Lda. Under
CC license (CC BY-NC-ND 4.0)
21

Kaiser, 1991) exhibit properties that may be useful if
applied to joint force structure scheduling. Only two
references (Davis, 2002, Farr et al., 1994) were
found that attempt to tackle joint force structure
problems. The first leaves much of the methodology
undefined, and the second is a deterministic model
that does not optimize over a range of requirements.
Selection of a force structure must balance
strategic policies and objectives, while maintaining
realism at the operational and tactical levels – and
still provide answers in a timely fashion. To achieve
a measure of balance among these conflicting
drivers, Defence R&D Canada’s Centre for
Operational Research and Analysis (DRDC CORA)
has developed a strategic level simulation tool,
known as Tyche. Tyche takes a moderate-fidelity
approach to joint force structure analysis that utilizes
capability-based planning. The next section
describes the Tyche model, including novel features
and modelling limitations. Section 3 provides a
sample joint force structure case study. Conclusions
are given in Section 4.
2 THE SIMULATION MODEL
Tyche is a stochastic simulation model that
schedules the deployment of assets within a force
structure to address a set of missions. The
assignment of assets to missions is based on a set of
predefined rules that attempt to reproduce the
decisions made by a military scheduler. Scheduling
assignment is capability-based; meaning each
mission requires a set of capabilities for success, and
each asset type provides a set of capabilities that
may or may not overlap with the required mission
capabilities. The force structure measure of
performance (MOP) is evaluated based on how well
and how often the missions’ capability requirements
are met.
When it was originally developed in 2004, Tyche
was designed to model naval force structures. It was
later adapted to accommodate joint asset types;
however, a number of assumptions within the
program affect the range of detailed joint military
applications. These limitations will be discussed in
the following subsections, and are slated for future
development.
Tyche is divided into three interconnected
environments: a data entry environment where the
data required to perform simulations are entered; a
run environment where the specifics of the desired
simulations are entered; and a data exploration
environment where the MOP and run output can be
visualized and further investigated. The function of
these three environments is described.
2.1 Data Structure
There are five fundamental data structures employed
within the Tyche model to build a simulation:
capabilities, asset types, bases/theatres, scenarios,
and force structures.
2.1.1 Capabilities
While capabilities simply refer to any ability to
perform a task, they provide a flexible way to link
mission requirements to force structures. Most force
structure analysis models are either platform-based
(meaning requirements are defined in terms of the
number and type of platforms for mission success)
or physics-based (specifying physical characteristics,
such as dimensional capacity for air or sea lift).
Tyche is unique in that the user can define
capabilities to suit the simulation model
requirements. Typical capabilities used for military
simulations simulation include command and control
(C2), surveillance, firing, jamming, transportation,
etc. Quality and quantity factors are associated with
each capability. Quality is a scale on (0,1] for
relative comparison; quantity is a positive integer
(
Z
∈
). This permits objective comparison of often
subjective evaluations (e.g., the higher C2 capability
of a destroyer compared to a frigate is modelled
model by a higher numerical quality), as well as
encompassing the physical characteristics in a
single, broader definition of capability (e.g., lane
meters of sea lift is associated to a numerical
quantity).
2.1.2 Asset Types
Asset types are defined to allow for modelling of
equipment, personnel, weapons, modules, etc., and
include both dynamic and static assets (static assets
cannot travel to theatre on their own, such as
maritime helicopters). Various levels of fidelity in
the modelling of assets are possible, which positions
the tool well to cross between coarse strategic-level
studies and more detailed operational-level analysis.
One limitation that the user must bear in mind when
defining asset types is the timescale within Tyche.
The smallest unit of time is one day, and simulations
are intended to run over multiple years (an
assumption that was suitable for naval applications).
A user-selectable timescale is planned for future
versions of the software to accommodate force
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
22

structures that commonly operate on smaller
timescales.
Tyche also allows for modelling of external
assets; those that could be chartered or assumed
available (based on a given probability) from
another source. This allows for simple modelling of
assets about which little knowledge is available.
The concept of “level” is introduced as a key
element in the modelling of assets. Levels are used
to model the different states or working conditions
of the assets such as the readiness states,
breakdowns, maintenance, training, and leave. In
essence, the levels allow the modelling of variations
of the capability supplied by the assets under user-
defined circumstances. An asset type’s levels are
prioritized, so that critical tasks can override (or
bump) less important tasks. Associated with each
prioritization instruction between two given levels
are a bump time, a bump penalty, and rescheduling
instructions for the bumped level.
In addition, levels are characterized by type, a set
of capability supply and demand, and the optional
inclusion of constraints with regards to the possible
asset assignment. Level types include random (e.g.,
to model unforeseen breakdowns), scheduled (e.g.,
to model maintenance periods), on-demand (e.g., to
model mission assignment), and follow-on (e.g., to
model a quality of life break following a long
mission assignment). The set of capability supply
and demand associated with the asset type is specific
to each level. For example, a user may model levels
of readiness with different degrees of capability and
response time associated with each. Synergistic
effects can also be captured; as when two assets are
assigned together to produce a higher level
capability of either alone (e.g., a helicopter
embarked on a frigate to increase the effectiveness
of the frigate’s surveillance capability).
The association of capability demand to assets
leads to the ability to model multi-layer and co-
dependent capability demand chains. An asset may
demand capability, just as a scenario would. This is
common with static assets requiring transportation
into theatre. Co-dependent demand arises when a
demanded asset requires capability supplied by the
asset requiring it. For example, a helicopter requires
transportation to theatre which can be provided by a
frigate, and in reverse the frigate requires a
helicopter to provide surveillance.
A distinction between capability supply and
capability demand is in the number of associated
attributes. Capability supplies have only an assigned
quantity and quality which specify the number and
the degree to which the capability is provided. On
the other hand, in addition to a quantity, capability
demands have two quality values specified: the
required and marginal quality levels. The required
quality determines the degree of desired quality for
satisfactory performance, and the marginal quality
provides the degree needed for minimum
performance standards. The quantity determines the
number of requested capabilities to support a single
asset type at the level being defined. In addition to
the quality and quantity, the capability demand also
requires a weight, which is used to quantify the
importance of this capability demand with regard to
other capability demands. Finally, a capability
demand can be deemed “essential”. If an essential
capability demand cannot be satisfied at the required
quality with a capability supply from another asset,
then this asset will not be able to go to this level. For
example, for a ship to leave a port, it needs to be
manned by a crew. If there is no crew available, then
the ship will stay alongside. Thus, the crew provides
a capability that is essential to the ship when it is
requested to leave the port.
Constraints on maximum or minimum duration
or on the number of occurrences of one or more
levels over a given period of time can also be
imposed to mimic scheduling limitations such as
maximum time used (e.g., annual flight hours for
aircraft), or frequency of usage in long-term high-
intensity missions to maintain personnel tempo.
2.1.3 Bases and Theatres
Bases are locations where assets are stationed when
not assigned to a mission and theatres are locations
where missions occur. Neither is given physical
coordinates, merely relative distances to one
another. No units of distance are specified, allowing
the user to determine a physical route for travel that
is compatible with the speed unit that will be
associated with the assets using these locations. For
example, two bases could be used to represent a
single location from which air and sea assets depart.
An over-land great circle arc distance would be used
for the distance that air assets travel, while an over-
water distance (often much larger, when taking into
account land mass detours) would be used for the
sea assets.
In this formulation, a simple model of one home
base for each asset, which then travels to a single
theatre for a scenario, is used. Waypoints for
intermediate activities (such as resupply), and
forward stationing of assets, are more complex
behaviours that are under consideration to better
model aspects of joint force operation.
A STRATEGIC SIMULATION TOOL FOR CAPABILITY-BASED JOINT FORCE STRUCTURE ANALYSIS
23

2.1.4 Scenarios
Scenarios represent missions (or a group of
missions) to which assets are assigned. A scenario is
defined in terms of phases, which represent the
variation of capability demand required over time
(e.g., pre-crisis a scenario might require more
diplomatic and economic intervention and a show of
force, while later phases may demand combat
capabilities and non-combatant evacuation). Each
scenario also has a number of possible theatres, each
having a probability of assignment. Each phase can
be independent, or linked to one or more other
phases. Consequently, activities of varying
capability demand, duration, and location can be
modelled.
In terms of associated attributes, the phases of a
scenario show many similarities with the levels of an
asset. There are three types of phases: scheduled,
random, or follow-on. As with the level, a scheduled
phase requires a start date and frequency that set the
precise dates the phase will occur. For the random
phases, only the frequency must be specified; a
Poisson distribution is used to determine the
occurrence of these scenarios (see Section 2.2.1).
The main difference between levels and phases is
the absence of the timing constraints and capability
supply for the latter, as well as the appearance of
more complex scoring criteria. The scoring criteria
determine how to select assets for the phase, by
means of a cost function for various choices of
assets and selecting the best additive score of all the
possibilities.
2
The cost function will be defined in
Section 2.2.2.
2.1.5 Force Structures
A force structure stores all the assets from the
different asset types that would be used for a given
simulation run, including possible external assets.
The term “fleet” was used but the assets are not
limited to naval types. Assets are defined by
specifying type, home base, and a scheduling offset.
The offset is a number that specifies the number of
days by which the start date of the scheduled levels
of the asset will be shifted with respect to other
assets of the same type. Currently, many force
structures can be defined, but each must be run
individually. The possibility of incorporating the
model inside an optimization routine is under
consideration, so as to determine the optimal force
structure to meet a set of requirements.
2.2 Simulation Procedure
At its core, Tyche is a discrete-event scheduling
program. For every iteration, the force structure data
are initialized, a list of events is generated where
each event requires assets to be assigned, and the
“best” available assets are then assigned to these
events. Data is then output in the form of an
operational schedule for each iteration. Data for
reinitializing the random number generator are also
output to allow for continuation of simulation runs at
a subsequent time (this can be useful in the event of
computer issues).
2.2.1 Event Generation
The list of events is generated at the start of every
iteration, and updated as the clock progresses in the
simulation. An event occurs every time a scenario
phase begins or an asset changes level. To build the
list of events, Tyche first selects a random date,
which is the initial date at which the simulation
starts. All scheduled events are created in relation to
this date (where day 0 is the first day of the calendar
year). Random phases and levels are determined
from a Poisson distribution with a frequency of
occurrence per year of λ. For an iteration of n years,
the number of events (N) is determined by selecting
a random number, r uniformly distributed on [0,1],
and applying Eq. (1).
()
()
()
()
∑
−
∑
−
=
−
=
≤<∈=
i
j
j
i
j
j
j
n
n
j
n
n
ereiiN
0
1
0
!
*
!
|with
λ
λ
λ
λ
Z
(1)
Note that the sum over the integer j from 0 to i-1
is set to 0 in the case i=0. The start date of each
random event is then selected from the set of days
inside the time window using a uniform distribution.
The duration of events that cross the number of
years simulated are reduced to fit completely inside
the time window. Events that are too short to have
any assets assigned (based on minimum preparation
and travel time) are removed from the simulation.
As a result, the first and last year of all simulation
iterations are not counted in the statistics generation
(see Section 2.3.1) to eliminate this burn-in effect.
There are times during the simulation run when
the event list can be modified. While follow-on
phases are generated immediately after their
preceding phase, follow-on levels are only added to
the event list when the asset goes to the level that
precedes the follow-on level. In addition,
2
The reader might wonder why scoring criteria are required fo
r
the phases, but not for the levels. In fact, Tyche employs har
d
coded scoring criteria for the levels. The capability and conflic
t
criterion, with constant weights, scales, and thresholds, are use
d
to assign assets to meet the level’s capability demands.
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
24

rescheduling of an asset from one event to another
(bumping) alters the event list. Based on the
rescheduling rules selected with the bumped event, it
may be added again later in the event list.
Once a list of events for the iteration has been
built, Tyche will assign assets to each event in a
chronological order. The flow chart in Figure 1
illustrates how Tyche processes each Nth event in
the event list.
Figure 1: Event logic flow chart.
2.2.2 Asset Scoring Criteria
The method by which assets are selected for
assignment is based on an additive cost function.
While this is a myopic policy for meeting a single
requirement by selecting from a list of assets based
on information that is known now and actionable
now (MP:R-AL/KNAN) (Wu et al., 2009), it
provides a great deal of flexibility to mimic the
decisions made by a military scheduler. Additional
model development is planned to include
optimization of asset assignment over the entire
requirements list (events) at a given point in time
and implementing a rolling time-horizon policy for
forecasted demand.
The cost function is calculated for a set of assets
using four scoring criteria that are described in Table
1; each criterion is defined separately for every
scenario phase (for events with an asset source,
levels use a predefined subset of these criteria). The
first set of assets computed that has the highest score
based on the scoring criteria is assigned to the
mission. In the case of a tied score, the first
computed with the score is selected – hence, entry
order is important.
Table 1: Scoring criteria composition.
Criteria Description
Capability
(mandatory)
Number of capability demands that are met at
the required or marginal level.
Capability
Excess
(optional)
Sum of the quality of the capabilities
supplied by the assigned assets that exceed
the capability demand of the scenario phase.
Timeliness
(optional)
Sum of the time delay for all capabilities
provided after the desired response time.
Conflict
(optional)
Sum of the penalties for every asset bumped
to go to the scenario phase.
The cost function for a single asset is simply the
weighted sum of the scores obtained for all selected
scoring criteria. Weights for each criterion are
subjectively established by the user and can be
tailored to try to reproduce the asset selections made
by a military scheduler. A tool is included in the
software to allow the user to preview the ideal asset
selections (assuming unlimited assets and no
timeliness or scheduling conflict) to tune the weights
before a simulation is run. Consider a scenario (s)
with a set of capability demands {D}. An asset with
a set of capability supply {S} will have the cost (C)
components defined in Eqs. (2)-(5), with the
subsequent scaling factors (Sc). The scaling factors
are also weights that are subjectively established by
the user, different from the cost component weights
used in the overall cost function.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+=
∑∑
)()(
5.0
MD
D
RD
DCC
WWScC
(2)
∑
∉
−=
}{
(S)
DS
ECEC
QScC
(3)
(
)( )
[
]
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−Θ−
−=
∑
∑
∈
∉
}{
}{
1
)(*)(
DS
DS
RR
TT
TSTTST
ScC
(4)
∑
≠
−=
DC
LALA
CDSCSC
,LLScC
)(:
)Penalty( Bump
(5)
The capability score (Eq. 2) is obtained by
summing over the capability demands that are met at
the required level (D(R)) and over those met only at
the marginal level (D(M)). The arbitrary factor 0.5
multiplying the second sum indicates that the
capability met at the required level provides a higher
contribution to the capability score than those only
A STRATEGIC SIMULATION TOOL FOR CAPABILITY-BASED JOINT FORCE STRUCTURE ANALYSIS
25

met at the marginal level. Furthermore, since the
capability score is obtained from the sum of the
capability weights (W(D), indicating the importance
of the capability to the success of the scenario
phase), capabilities with higher weights will
contribute more to the score.
The excess capability score in Eq. (3) is obtained
by summing over all the capability supplies (S) that
are not requested by the capability demand (
∉
D).
This excess score prevents Tyche from sending too
much capability (too many assets or too capable
assets) to the scenario phase. Excess quality of a
capability that is required by a scenario and provided
by an asset is not taken into account (i.e., if two
assets supply the same capability at different
qualities, both greater than the required quality level,
there is no penalty for selection of the one asset that
exceeds the required level more than the other).
Eq. (4) defines the timeliness score, where T
R
is
the desired response time and Θ(T(S)-T
R
) is the
Heaviside step function. The timeliness score is
obtained by computing the overall delay (T(S)-T
R
)
required to get all of the capability supplies (S) that
are requested by the capability demand (
∈
D) into
theatre. The summation is normalized by the number
of supplied capabilities.
Finally, the conflict score is obtained by
summing the penalties of all bumped assets in Eq.
(5). The penalty given for bumping the asset is
specified by the user in the asset type definition for
bumping the asset from its current level (L
c
) to the
desired level (L
D
). The sum is over all selected assets
(A) for which the current level (L
c
(A)) is not the
default level. This conflict score favours the
selection of available assets rather than bumping
non-available ones.
The cost function for a group of assets is then the
additive score for each individual asset; it is also a
function of the order in which the assets are
assigned. This will be discussed further in Section
2.2.3.
In addition, a threshold is also established for
each scoring criteria. The threshold is used to reject
poor groups of assets. In other words, if the best
group of assets has an unacceptably low score
component, it is possible to reject it and not send any
assets at all. The threshold allows the user, for
example, to prevent assets from being sent to a six-
month mission to arrive only two days before the
end of the mission. The effect of the thresholds
(Thr) can be summarized as follows. If, for a given
mission, the set of assets with the highest cost
function is a set of k assets, σ(A
1
,…,A
k
), then the set
of assets assigned to the mission, σ*, is given in Eq.
(6).
()
⎪
⎩
⎪
⎨
⎧
<∃
=
otherwise ,...,
*)( | Criterion if 0
*
1 k
x
x
x
AA
ThrScSign
Sc
C
x
σ
σ
(6)
Where “0” is the empty set of assets and “Sign”
is a function that returns -1, 0, or 1 based on the
value of the argument (<0,=0,>0).
2.2.3 Asset Assignment Algorithm
The assignment problem consists of matching the
capability demand with the capability supply in an
optimal way, with the objective of maximizing the
cost function. This problem is thus equivalent to
finding an optimal matching on a bipartite weighted
graph. This equivalence follows from the following
definitions (Diestel, 2005):
A graph is a set of nodes and a set of edges
between nodes. For the assignment problem,
the nodes are given by the set of capability
supplies and capability demands while the
edges are determined from the search domain;
A weighted graph has a scalar value associated
with every edge. For the assignment problem,
the weight associated with the edge is
computed using the capability and timeliness
scoring criteria as described in Eqs. (2) and
(4);
A bipartite graph is a graph for which the set of
nodes can be divided into two subsets such
that there is no edge between nodes pertaining
to the same group. For the assignment
problem, the nodes can be divided into the set
of capability demand and the set of capability
supply. Since every edge is between a
capability and a capability demand, the graph
is bipartite;
A matching on a graph is obtained by selecting
a subset of edges such that no selected edge
has a common node. The assignment of assets
is done by matching each capability demand
with one, and only one, capability supply. It
thus corresponds to selecting a matching on
the graph. Every asset for which at least one
capability supply is adjacent to an edge
pertaining to the matching belongs to the set
of selected assets.
Only the capability score and timeliness score
can be assigned as a weight associated with the
edges. This is possible because these two scores are
given as a sum over the capability demands that are
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
26

matched. The excess and conflict score cannot be
obtained through a distributed sum along the edges
pertaining to the matching. Thus, if the excess and
conflict score do not belong to the selected scoring
criteria then the optimal matching corresponds
directly to the highest weight matching, which is a
well-known problem in graph theory (Diestel, 2005).
In particular, the backtracking and backjumping
algorithm has been applied successfully to this type
of problem (Wolf, 2006). Because the weights for
the excess and conflict scoring criteria are typically
small, this algorithm should produce solutions that,
while not optimal, are “good enough”.
Because there are typically few asset types that
can satisfy a given set of capabilities, the user can
exploit this information to define a restricted search
domain. An enumerated search is then performed to
determine which assets to assign. Tailoring of the
search domain adds a significant amount of
flexibility for assignment selection, increasing the
capability of the program. The enumerated search is
guaranteed to select the best available asset when
only one asset is required for a scenario. If more
than one asset is required, it is possible that the
highest ranked combination of available assets is not
assigned, because the search is conducted on an
asset-by-asset basis. The next asset that adds the
most to the total score, based on the remaining
capability demand, is assigned.
The selection of assets is also done in a multi-
layered way. At each layer, assets are selected to
meet the capability demands that were introduced at
the previous layer. If, at some layer, the capability
demands cannot be met, then the algorithm
backtracks to the previous layer and selects a
different group of assets. At each layer, after a group
of assets has been selected, the algorithm checks for
redundancy. If redundant assets are found, then the
redundant asset is removed and replaced by the new
asset that can provide the capability that the
redundant asset was providing and the algorithm
backjumps to the layer where the redundant asset
was selected.
2.3 Output and MOP
The results of the Monte Carlo simulation are output
so that operational schedules from individual
iterations can be viewed in text or graphical format.
This allows for detailed examination of asset
assignment, scheduling conflicts, and mission
timing. Upon completion of the simulation run,
statistics are generated for asset usage, scenario
assignments, and capability fulfillment. A
capability-based risk measure is introduced to
aggregate the results into a single MOP for force
structure comparisons.
2.3.1 Statistical Information
Asset statistics collect information on the
assignment of individual force structure assets in
terms of average duration and standard deviation of
the duration spent at a given level. While the user
must reconstruct which levels correspond to which
scenario phases, the data output is generalized for
use across all military services.
Scenario statistics indicate the average frequency
of occurrence of scenario phases and the percentage
of time that particular combinations of assets (or no
assets) are being sent.
Capability statistics are the primary indicator of
the ability of a force structure to meet scenario
demand. For each scenario phase, the percentage of
time that capabilities are not met at the required and
marginal levels are reported.
2.3.2 Capability-based Risk Assessment
Maintaining the focus on capability-based planning,
an assessment of the risk associated with a particular
force structure can be derived using the probability
that capabilities are not met, and frequency of
scenario occurrence. The risk is defined in Eq. (7),
where the mean yearly political risk (R) for a given
scenario (s) is defined as the product of the annual
frequency of occurrence (f), the impact (I) of failure
to provide capability, and the probability the
capability supply deployed is inadequate (P). The
risk is then summed over all scenarios.
∑
=
s
sss
PIf R
(7)
The first factor is assessed by averaging the
number of times the scenario occurs yearly across all
iterations. The second factor, known as impact
score, can be provided as a subjective input by
SME’s. This allows the risk assessment to
incorporate military judgement, often critical to
balance the perceived effect of low impact-high
frequency and high impact-low frequency scenarios.
The third and final factor (P
s
) is calculated from Eq.
(8). The probability that the capability supply is
inadequate can be defined in several ways,
depending on how risk-averse the assessment should
be. In general, it is a weighted summation of the
percentage of time (P
Tyche
) that the scheduler fails to
provide capability to a scenario with a given asset
assignment (A).
A STRATEGIC SIMULATION TOOL FOR CAPABILITY-BASED JOINT FORCE STRUCTURE ANALYSIS
27
∑
=
A
TycheAs
APwP )(*
(8)
Given that the Tyche scheduler can assign assets
to meet capability at different levels, one highly risk-
averse method would be to utilize three categories:
where, due to force structure limitations, Tyche fails
to assign assets altogether (A=0), and where at least
one capability demand is not met at the required
(A=R’) and marginal level (A=M’). The weights for
each of the categories of capability failure can also
be provided by SME input. In the case study, it will
be assumed that w
0
= 1.0, w
R’
= 0.5 and w
M’
= 0.1.
The statistical nature of the risk measure also
implies that there is an error on the estimation of the
average. It is reported as twice the standard
deviation (σ) of the mean distribution, where σ is
estimated by the square root of the sample variance
of the risk distribution divided by the number of
iterations.
3 A CASE STUDY
Utilizing a simple case study, it is possible to
illustrate the kinds of results Tyche can produce, as
well as the types of problems that can be analysed.
The case study is built around hypothetical asset
types and scenarios, and the capabilities attributed to
these assets are not intended to model capabilities of
real force assets.
In this example, five generic capabilities (A, B,
C, D, E) were created, along with two crewing and
one transport capabilities for modelling
dependencies. Five asset types (Air Asset, Air Crew,
Sea Asset, Sea Crew, and Special Operations Force)
can supply these capabilities, at various levels
shown in Table 2. The Air Asset requires an Air
Crew with a quantity of 3 persons, and can provide
transport for up to 10 persons. The Sea Asset
requires a Sea Crew, with a quantity of 70, and can
provide transport for 100 persons. The Special
Operations Force (SOF) is composed of 6 persons,
and can be transported on either Air or Sea Assets.
Table 2: Asset capability supply.
Asset Type Capability Quality Quantity
Air Asset A
B
C
0.8
0.7
0.2
1
6
1
Sea Asset A
C
D
0.7
0.6
0.9
1
1
1
SOF E 1.0 1
Air Assets were modelled to have a 50% chance
of requiring maintenance after use in a scenario,
with a duration determined from a triangular
distribution with minimum, most likely and
maximum values of 1, 2, and 10 days. They were
also restricted for use in 100 of every 365 days. The
Sea Asset has a Short Work Period of 18-20-25 days
5 times per year. It also has a Docking Work Period
of 100-180-365 days once every 5 years. Both Air
and Sea Crews were constrained to take a quality-of-
life break after every scenario for 5-5-10 days.
There were two bases: Air 1 and Sea 1,
collocated together. There were four possible
theatres, some favouring the assignment of air assets
and others that are unbiased. Three scenarios (S1-
S3) were defined to occur at two or more possible
theatres, with requirements from Table 3. The
scenario search domain was the same for all,
including Air Assets from Air 1, Sea Assets from
Sea 1, and SOF from Air 1.
Six force structures were tested. It was assumed
that there was one crew per platform, and force
structures are labelled according to the number of
[Air Assets, Sea Assets, SOF]. The first three
structures, [6,4,6], [3,2,3] and [1,1,1] looked at
decreasing fleet sizes across all assets. Three
additional structures reduced a single asset type from
the largest, [6,2,6], [3,4,6], and [6,4,3]. The risk
measure was computed using three for impact score,
with values of 1.0 for S1, 1.5 for S2, and 5.0 for S3,
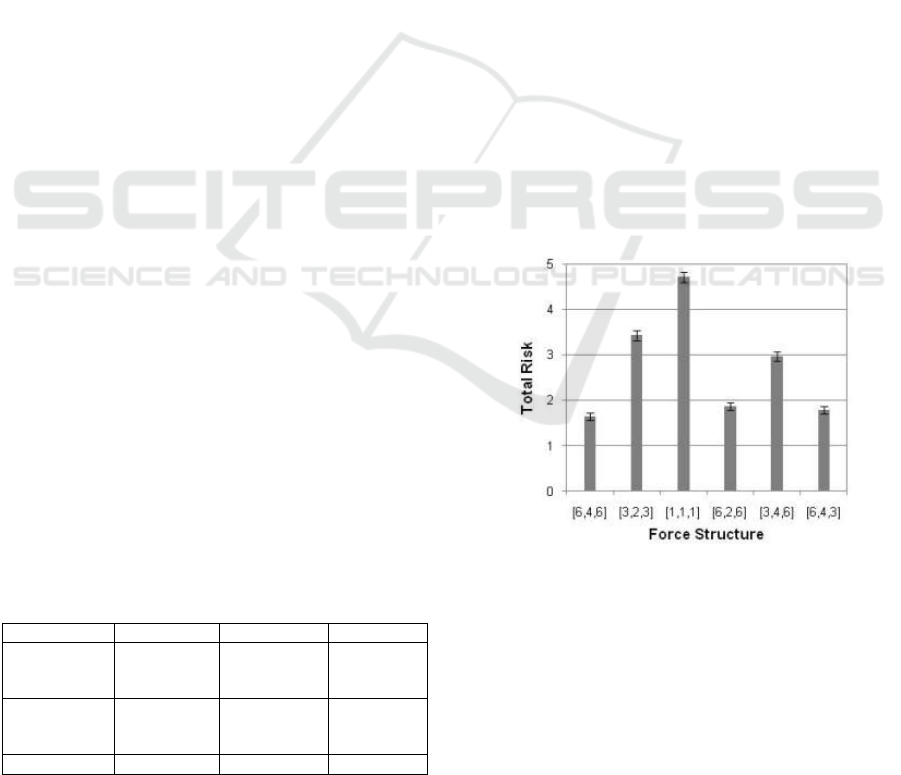
and is shown in Figure 2.
Figure 2: Case study results.
As illustrated, the risk of not being able to fulfil
scenario capability requirements increases with
decreasing fleet size. The simple parametric
decrease in assets of a given type indicates that force
structure [6,2,6] and [6,4,3] do not have a
statistically significant difference in performance,
and are near the large [6,4,6] structure. However,
when Air Assets are removed [3,4,6], the risk
increases sharply.
This case study is representative of the force
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
28
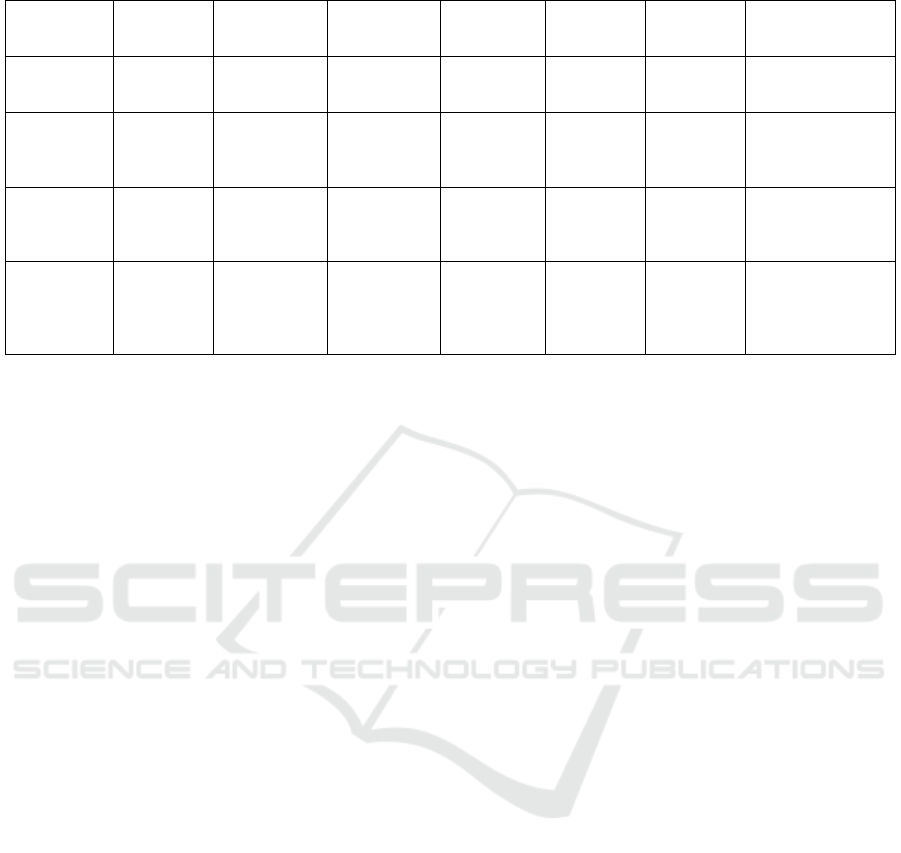
Table 3: Scenario timing and capability demand.
Scenario:
Phase
Type,
Frequency
Theatre,
Probability
Duration,
Response
Time (Days)
Capability,
Quantity
Required,
Marginal
Quality
Weight (All
Non-
Essential)
Scoring Criteria,
Weight, Scale,
Threshold
S1:P1 Random
3.0 / year
1, 0.2
2, 0.8
20-30-60
25
A, 1
B, 15
C, 2
0.8, 0.4
0.7, 0.2
0.4, 0.1
2
4
1
Capability,10,1,1
Conflict,1,1,100
S2:P1 Scheduled
1.0 / year
Starting on
Day 30
1, 0.25
2, 0.25
3, 0.25
4, 0.25
30-60-90
15
A, 1
C, 2
E, 2
0.6, 0.4
0.4, 0.1
1.0, 1.0
2
1
2
Capability,10,1,1
Conflict,1,1,100
Timeliness,1,1,20
S3:P1 Random
0.33 / year
3, 0.8
4, 0.2
90-150-180
30
A, 1
B, 15
C, 2
E, 4
0.9, 0.4
0.7, 0.2
0.4, 0.1
1.0, 1.0
2
4
1
2
Capability,10,1,1
Conflict,1,1,100
Timeliness,5,1,8
S3:P2 Follow-on,
With P1
duration ≥
150 days
Same as P1 90-150-180
30
No overlap
with P1
A, 1
B, 15
C, 2
D, 1
E, 4
0.9, 0.4
0.7, 0.2
0.4, 0.1
0.5, 0.3
1.0, 1.0
2
4
1
1
2
Capability,10,1,1
Conflict,1,1,100
Timeliness,5,1,8
structure analysis that can be performed with Tyche,
as well as options analysis around force structures of
interest. While Tyche is not integrated into an
optimization framework, simulation optimization to
determine the optimal fleet with respect to some
objective (minimum risk, structure size, cost, etc.)
can still be performed, albeit in a less efficient way.
Tyche is also useful for performing options
analysis, capability gap analysis, testing new
capability architectures, and evaluating force
structure performance in the face of changing
requirements. As well, the rate of usage of assets can
be examined to determine the effects of readiness
and sustainment policies on performance in
operations. For example, in the case study, the Sea
Asset goes through a number of work periods. The
length and frequency can be varied to determine the
effect on risk. Similarly, with crews, operations and
personnel tempo constraint policies can be varied.
4 CONCLUSIONS
This paper described a Monte Carlo discrete event
simulation for joint force structure analysis. The
Tyche tool is currently used by DRDC CORA and,
while it has not yet been employed for a formal joint
force structure study, it exhibits potential advantages
for strategic level capability-based planning.
Development is already underway to rectify known
modelling limitations. Additional research avenues
include optimization of asset assignment over the
entire requirements list at a given point in time and
implementing a rolling time-horizon policy for
forecasted demand.
ACKNOWLEDGEMENTS
The authors would like to thank Alex Bourque,
Pawel Michalowski, Carolyn Augusta, Dave
Heppenstall, Alain Forget, Debbie Blakeney, Evan
DeCorte, R.M.H. Burton, and Geordie MacDonald
for their roles in the development of Tyche.
REFERENCES
Abbass, H., Bender, A., Baker, S. , Sarker, R. A. Year.
Anticipating future scenarios for the design of
modularised vehicle and trailer fleets. In: SimTecT,
2007 Brisbane, Australia.
Baker, S. F., Morton, D. P., Rosenthal, R. E. , Williams, L.
M. 2002. Optimizing Military Airlift. Operations
Research, 50, 582-602.
Brown, G. G., Clemence, R. D., Teufert, W. R. , Wood, R.
K. 1991. An optimization model for modernizing the
army’s helicopter fleet. INTERFACES, 21, 39-52.
Bulut, G. 2001. Robust Multi-Scenario Optimization of an
Air Expeditionary Force Force Structure Applying
Scatter Search to the Combat Forces Assessment
Model. Air Force Institute of Technology.
Cortez, L. A. , Kaiser, T. J. 1991. U.S. Coast Guard Fleet
Mix Planning: A Decision Support System Prototype.
Master of Science in Information Systems, Naval
Postgraduate School.
Crary, M., Nozick, L. K. , Whitaker, L. R. 2002. Sizing
the US destroyer fleet. European Journal of
Operational Research, 136, 680-695.
Davis, P. K. 2002. Analytic architecture for capabilities-
based planning, mission-system analysis, and
transformation. Santa Monica, CA: RAND
Corporation.
A STRATEGIC SIMULATION TOOL FOR CAPABILITY-BASED JOINT FORCE STRUCTURE ANALYSIS
29

Diestel, R. 2005. Graph Theory. Graduate Texts in
Mathematics, Vol. 173. 3rd ed. Heidelberg: Springer-
Verlag.
Dugan, K. 2007. Navy Mission Planner. Master of Science
in Operations Research, Naval Postgraduate School.
Farr, J. V., Nelson, M. S. , Diaz, A. A. 1994. Resource
Allocation Methodology to Support Mission Area
Analysis. West Point, NY: United States Military
Academy.
Fildes, L. 2006. A Decision Support Tool for the
Procurement and Planning of Royal Naval Ships.
Master of Science in Operational Research, University
of Southampton.
Gallagher, M. A. , Kelly, E. J. 1991. A New Methodology
for Military Force Structure Analysis. Operations
Research, 39, 877-885.
Gauthier, Y., Wardrop, W., Price, A. , Lawrence, A. 2008.
The size of MARS: quantifying requirements for the
Royal Navy’s future afloat support fleet. 25th
International Symposium on Military Operational
Research. Cranfield University.
Greer, W. L., Kaufman, A. I., Levine, D. B., Nakada, D.
Y. , Nance, J. F. 2005. Exploration of Potential Future
Fleet Architectures. Alexandria, VA: Institute for
Defense Analyses.
Horn, M. E. T., Jiang, H. , Kilby, P. 2007. Scheduling
patrol boats and crews for the Royal Australian Navy.
Journal of the Operational Research Society, 58,
1284-1293.
Klerman, J. A., Ordowich, C., Bullock, A. M. , Hickey, S.
2008. The RAND SLAM program. RAND National
Defense Research Institute.
Mattila, V., Virtanen, K. , Raivio, T. 2008. Improving
Maintenance Decision Making in the Finnish Air
Force Through Simulation. INTERFACES, 38, 187-
201.
Mattock, M., Schank, J., Stucker, J. , Rothenberg, J. 1995.
New capabilities for strategic mobility analysis using
mathematical programming, RAND Corporation.
Salmeron, J., Wood, R. K. , Morton, D. P. 2009. A
Stochastic Program For Optimizing Military Sealift
Subject To Attack. Military Operations Research, 14,
19-39.
Taylor, B. , Lane, A. 2004. Development of a Novel
Family of Military Campaign Simulation Models. The
Journal of the Operational Research Society, 55, 333-
339.
Walmsley, N. S. , Hearn, P. 2004. Balance of Investment
in Armoured Combat Support Vehicles: An
Application of Mixed Integer Programming. The
Journal of the Operational Research Society, 55, 403-
412.
Wesolkowski, S. , Billyard, A. 2008. The Stochastic Fleet
Estimation (SaFE) model. Proceedings of the 2008
Spring simulation multiconference.
Ottawa, Canada:
Society for Computer Simulation International.
Whitacre, J. M., Bender, A., Baker, S., Fan, Q., Sarker, R.
A. , Abbass, H. Year. Network Topology and Time
Criticality Effects in the Modularised Fleet Mix
Problem. In: SimTecT, 2008 Melbourne, Australia.
Wolf, A. 2006. Intelligent Search Strategies Based on
Adaptive Constraint Handling Rules. Theory and
Practice of Logic Programming, 6, 213-224.
Wu, T. T., Powell, W. B. , Whisman, A. 2009. The
optimizing-simulator: An illustration using the
military airlift problem. ACM Transactions on
Modeling and Computer Simulation, 19, 1-31.
Zadeh, H. S. 2009. NaMOS; Scheduling Patrol Boats and
Crews for the Royal Australian Navy. 2009 IEEE
Aerospace Conference. Big Sky, MT.
ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems
30
