
A Fuzzy-stochastic Inventory Model without Backorder under
Uncertainty in Customer Demand
Pankaj Dutta and Madhukar Nagare
SJM School of Management, Indian Institute of Technology Bombay, Mumbai-400076, India
Keywords: Inventory, Fuzzy Random Demand, Possibilistic Mean Value, Optimization.
Abstract: In the current business scenario, a vital aspect of a realistic inventory model is to accurately estimate the
customer demand especially in uncertain environment. Keeping this fact in mind recent trend of research
includes uncertain demand, either random or fuzzy. In this paper, we amalgamate both random behavior and
fuzzy perception into the optimization setting in modeling an inventory model without backorder. Treating
customer demand as fuzzy random variable, we aim at providing an approach of modeling uncertainty that
is closer to real situations. In addition, a distinct characteristic of this study is that the decision maker’s
degree of optimism is incorporated in this model using possibilistic mean value approach. The objective is
to determine the optimal order quantity associated with cost minimization. An illustrative numerical
example is presented to clarify the reality of the model.
1 INTRODUCTION
Decision-making environment of inventory
management in retail supply chain is full of
uncertainties especially when dealing with end
customer demand of innovative and style goods. The
uncertainty is mainly because of vague, uncertain
and volatile demand for these products coupled with
short selling season. Shrinking product lifecycles
and intensifying competitive pressure add to the
difficulty. Therefore, it is a real challenge for the
retailers or the decision-makers to determine
customer demand for a plan period T. Again,
inventory problems in realistic situation are too
complex to be represented in mathematical models.
On this view, many researchers have developed
fuzzy inventory models for situations where the
customer demand is described linguistically like
“demand is about d” ((Chen and Wang, 1996);
(Hsieh, 2002); (Dutta et al., 2007a); (Dutta and
Chakraborty, 2010); (Dutta et al., 2012)). Jing-Shing
Yao and his group have presented several papers on
fuzzy inventory without backorders. For instance,
Lee and Yao (1999a, b) fuzzified the order quantity
using triangular and trapezoidal fuzzy numbers and
obtained the fuzzy total cost. They used centroid
method to defuzzify the total cost to determine the
economic order quantity. Again, Yao et al. (2000)
fuzzified the order quantity and total demand with
triangular fuzzy numbers and obtained total cost
using extension principle and centroid method. Yao
and Chiang (2003) presented a fuzzy inventory
model without backorders where they fuzzified the
total demand and storing cost and defuzzified the
total inventory cost using centroid and signed
distance method.
In all these papers, the authors have addressed
the customer demand as a fuzzy number which is
characterized by the phrase “demand is about d”.
But, problem arises when this linguistic information
varies randomly. For example, the prediction of the
future demand forecast varies from expert to expert
and is described by the phrases “demand is about
d
1
”, “demand is about d
2
”, etc. Stochastic variation
is presented due to the difficulty to predict with
precision and fuzzy sets enter into the figure because
the above mentioned phrases are subjective and only
partially quantifiable. In this case, fuzzy random
variable (FRV) provides an appropriate
mathematical tool to handle such situations. The
concept and characteristics of FRV are available in
Lopez-Diaz and Gil (1998), Feng et al. (2001) and
Luhandjula (2004). An application of FRV in the
field of inventory system can be found in Dutta et al.
(2005, 2007b), Chang et al. (2006), Dutta and Roy
(2007) and Nagare and Dutta (2012).
However, an inventory model without backorder
307
Dutta P. and Nagare M..
A Fuzzy-stochastic Inventory Model without Backorder under Uncertainty in Customer Demand.
DOI: 10.5220/0004342801090114
In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems (ICORES-2013), pages 109-114
ISBN: 978-989-8565-40-2
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

under customer demand uncertainty arising out of
both fuzziness and randomness under one roof is yet
to receive attention. The purpose of this paper is to
redefine the fuzzy inventory model without
backorders (Yao and Chiang, 2003) in a mixed
fuzzy-stochastic environment by incorporating
customer demand as FRV. Moreover, in addition to
the synergistic approach of demand, a decision-
maker’s (DM) attitudinal scale is employed in
defuzzifying the cost function. Main thrust of this
paper is to determine the optimal order quantity that
minimizes associated total cost. The model is
designed using possibilistic mean value of a fuzzy
number proposed by Carlsson and Fuller (2001).
The rest of the paper is organized as follows. In
Section 2, we present the mathematical model
without backorder in presence of FRV. A detailed
solution methodology is developed in Section 3. A
sensible numerical example is provided in Section 4
to illustrate the model. Finally, Section5 summarizes
the work done.
2 MATHEMATICAL MODEL
The following notations have been adopted to
develop the inventory model without backorder
under fuzzy-stochastic environment.
T length of the finite planning period (in days) in
which the inventory system operates
h the cost of storing one unit per day
A the cost of placing an order
d total customer demand over the planning time
period [0,T]
length of the cycle
order quantity per cycle
The model is developed for a single item which
is replenished, stored and consumed. Therefore,
from Figure 1 it can have
or
The total cost in the planning time period [0, T]
consists of inventory holding cost, ordering cost and
it can be written in the following form
2
,0
(1)
Using the classical approach, one can obtain the
optimal order quantity
and total
minimum cost
√
2. The Figure 1
shows the inventory without backorder.
Figure 1: Inventory without backorder.
Many a times, due to uncertainty or vagueness,
customer demand is prescribed in linguistic
expressions like “demand is about d” and it can be
characterized as a fuzzy number
(say). In such
cases, optimization is attained using centroid or
signed distance method as proposed by Yao and
Chiang (2003). When subjective demand
expressions vary from expert to expert randomly,
demand can be aptly described as fuzzy random.
Restated, the customer demand is treated as FRV.
This paper assumes all the (fuzzy) observations of
FRV as triangular fuzzy numbers. This consideration
does not restrict the solution procedures for other
fuzzy numbers.
The customer demand denoted as
assumes
values on set of all triangular fuzzy numbers.
Suppose
s (1) are the fuzzy observations
of
with the given probability p
i
, i.e.;
,
,
,
,….,
,
Let μ
denote the membership function of
where
μ
,
,
,
,
0,
with
,
as the support of each
. Here
is the
modal of fuzzy number
;
,
:→0,1 are the
left and right shape continuous functions.
Thus, incorporating customer demand as FRV
in
equation (1), the total cost in the fuzzy sense is given
by
1
2
(2)
Following proposition flows from this equation:
Proposition 1. Total cost function defined in
equation (2) itself is a FRV.
T
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
308

Proof. It can be recalled that a FRV associated with
a random experiment is an appropriate formulization
of a process assessing a fuzzy value to each
experimental outcome. Here the total cost is a
function of uncontrollable variable
. Again, the
expert’s opinions about
are linguistic, i.e., fuzzy.
Therefore, for each values of
of
there is a
corresponding fuzzy value of
with probability
. Consequently,
becomes a fuzzy valued
random variable. Restated,
is also a FRV.
3 SOLUTION PROCEDURE
Corresponding to the crisp expected value of a
positive classical random variable, the expectation of
FRV is a unique fuzzy number. In other words, the
fuzzy expected value summarizes central tendency
of FRV. Therefore, total expected cost of
becomes a fuzzy quantity on . Let
=
be
the fuzzy expected value of
.
The main problem is to determine the optimal
policy under the synergetic approach of customer
demand into the optimization setting. Decision
policy is to find the optimal order quantity
∗
that
minimizes the associated total inventory cost. Since
the total expected cost is a fuzzy quantity, we first
find out several level set of
and then using
possibilistic mean value method the fuzzy quantity
is ranked.
Let us introduce the following lemma.
Lemma 1. For
∈, let
and
be the
lower and upper endpoints of level set
,
respectively. Then
i)
is a left continuous nondecreasing
function on (0,1] and right continuous at 0,
ii)
is a left continuous non-increasing
function on (0,1] and right continuous at 0,
iii)
;01.
Proof. Since the expected total cost
is a fuzzy
number belonging to F (set of fuzzy numbers) and a
fuzzy number is a fuzzy set with a normal, convex
and continuous membership function of bounded
support, the proof is straightforward.
Then, we get the following proposition.
Proposition 2. If
be the fuzzy expected value
of
then for each values of ∈
0,1
,
,
is a closed bounded interval and
we have
i) the lower end point of
as
∑
ii) the upper end point of
as
∑
Proof. Since
is a fuzzy quantity, using Lemma
1, we obtain the level set of
as
=
,
=
,
;01.
At0,
,
is the support of
fuzzy expected value
Now,
,
;01 is a FRV,
therefore, from the properties of FRV,
and
are the crisp random variables (i.e.; measurable
functions) for each ∈
0,1
and are respectively
given by
1
2
and
1
2
Thus according to the crisp probability theory,
and
can easily be found for
different values of01. The exact
expressions obtained for
and
, are
given below:
1
2
,
1
2
1
2
(3)
and
1
2
,
∑
(4)
This completes the proof.
Now, we calculate the possibilistic mean value of
as a function of order quantity , say
,
and then optimize
to determine the optimal
AFuzzy-stochasticInventoryModelwithoutBackorderunderUncertaintyinCustomerDemand
309

order quantity
∗
.
Thus, using (3) the lower possibility-weighted
average of the minima of the sets of
is
given by
∗
2
1
2
2
6
3
and using (4) the upper possibility-weighted average
of the maxima of the sets of
is given by
∗
2
1
2
2
6
3
Therefore, the interval-valued possibilistic mean
of total expected annual cost is defined as
∗
,
∗
.
As
is a fuzzy quantity and its expected
representative depends on the attitude (viz. optimism
or pessimism) of the DM. In order to calculate a
defuzzified value or mean value of fuzzy ‘expected
total cost’, starting from a subjective assignation
related to the relative importance of the lower and
upper possibilistic mean of total expected cost, one
could define a parameter ∈
0,1
, which reflects
DM’s degree of optimism.
Therefore, the expected representative of
as
a function of order quantity is obtained by
∗
1
∗
,
1
2
2
3
3
1
where the parameter is selected by a DM. Between
the two extreme values of 0 and 1 there is
an attitude scale for the uncertainty for each DM.
Using the attitudinal values, the optimal
∗
is
computed that minimizes the associated total cost in
fuzzy sense. Equating the first order derivatives of
with respect to to zero, we obtain
∗
2
1
(5)
Since,
2
3
2
1
is positive, so
∗
is the minimum and is given
by
∗
1
2
∗
2
3
∗
∗
∑
1
(6)
Equation (6) is the predicted total inventory cost
in the possibilistic sense with an index of
optimism∈
0,1
.
4 NUMERICAL EXAMPLE
The numerical example pertains to an Indian retailer
of ethnic fashion apparels for women that combine
the ethnic tastes with western styles making it
attractive to educated Indian Women. The product is
a style good-pair of salwar kameez with V-Neck and
introduced every season.
The demand for this product is rather vague and
uncertain for reason of its newness. Monetary unit is
changed from rupee into Pound sterling with
exchange rate of Rs 80/£. Required information is
provided in Table 1.
Table 1: Input values of model parameters.
Parameter Value
Selling Price (P) 100£
Inventory holding cost (h) 0.08 £/unit/day
Ordering cost (A) 125£/order
Planned season duration (T) 120 days
Average daily demand 20 units (approx.)
Demand estimation is obtained from thirty two
experts. These estimates were in the form of
linguistic expressions or in numerical form
(minimum, mean and maximum). The linguistic
expressions like “demand around 2400” were
transformed into numerical data and segregated in
five classes and probability is calculated. Table 2
provides the feature of
.
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
310
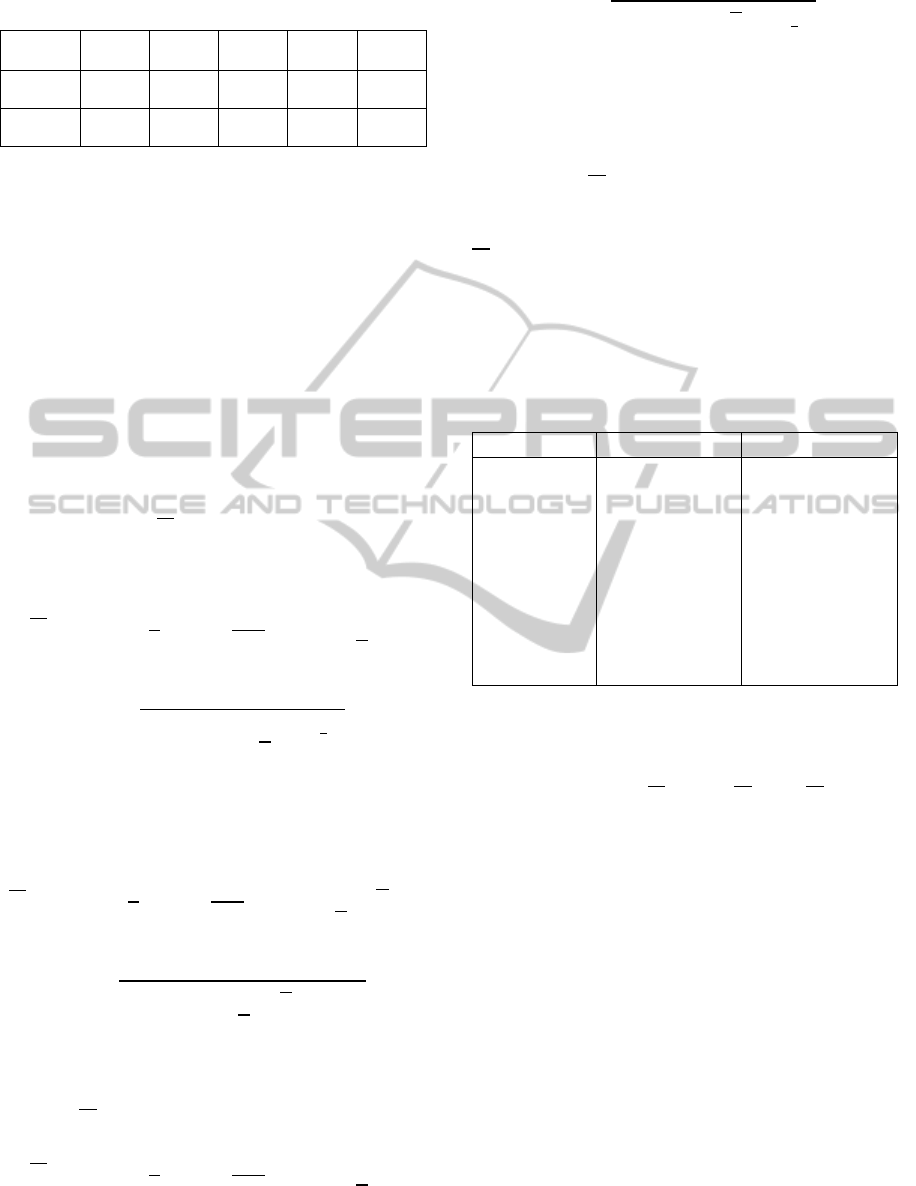
Table 2: Input data of customer demand D
.
Demand
around
1800
around
2100
around
2400
around
2700
around
3000
Experts
5 6 11 7 3
Prob.
0.16 0.19 0.34 0.22 0.09
These fuzzy observations are transformed in to
triangular fuzzy numbers as follows:
“around 1800” =
= (1500,1800,2100)
“around 2100” =
= (1800,2100,2400)
“around 2400” =
= (2100,2400,2700)
“around 2700” =
= (2400,2700,3000)
“around 3000” =
= (2700,3000,3300)
In the following paragraphs, we first discuss
variations of order quantity and expected cost as a
function of the DM attitude parameter and then the
optimal solutions as presented in Table 2.
(1) Optimistic Scenario (.): In this
situation, the DM is absolutely optimistic for the
estimation of expected total cost, which reflects the
least possible cost
.
∗
and using the results
of equations (5) and (6), we get the optimal decision
as follows:
.
∗
1
2
∗
3
∗
2
along with
∗
∑
2
.
(2) Moderate Scenario (.5): In this situation,
the DM is moderately optimistic for the estimation
of expected total cost reflecting in a crisp
representative of
provided by
.
∗
1
2
∗
6
∗
4
along with
∗
∑
4
⁄
.
(3) Pessimistic Scenario (.): This situation
provides an absolutely pessimistic decision
viewpoint. In this case, the choice of the expected
total cost
.
∗
can be put forth as
.
∗
1
2
∗
3
∗
2
along with
∗
∑
2
.
From above results, it is clear that for an
absolutely optimistic (1) DM, the expected total
cost is the lowest and hence the optimistic scenario
should be selected. In this case, the optimal order
quantity works to
∗
= 242.97 and minimum total
expected cost
.
= 2332.55. On the other hand,
for a pessimistic DM (0), the optimal order
quantity is
∗
= 253.46 along with expected cost of
.
= 2433.27.
For a DM with moderate attitudinal scale,
optimal order quantity and expected cost are 248.27
and 2383.44 respectively. Results for different
values of are given in Table 3.
Table 3: Optimal solutions for different values of
∗
Expected cost
0.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
253.46
252.43
251.40
250.36
249.32
248.27
247.22
246.17
245.10
244.04
242.97
2433.26
2423.38
2413.46
2403.49
2393.49
2383.44
2373.35
2363.21
2353.04
2342.81
2332.55
The percentage change in expected total cost
(PCEC) with extreme values of as compared with
the moderate scenario is computed as
100
∈
,
.
/
.
It yields -2.13% changes at 1 and +2.09%
changes at 0.
5 CONCLUSIONS
The current paper has considered a common
inventory model without backorder and presented a
fuzzy-stochastic inventory model where both
fuzziness and randomness are considered under one
roof. Since the expected value of a FRV is a fuzzy
quantity, a method of ranking fuzzy numbers using
their possibilistic mean values is adopted to find the
optimal order quantity that minimizes associated
cost. It is observed that results obtained in
comparable situations are numerically closer to the
well-known classical results. The paper consider all
fuzzy observations of customer demand as triangular
AFuzzy-stochasticInventoryModelwithoutBackorderunderUncertaintyinCustomerDemand
311

fuzzy numbers and on that basis the model is
developed as an interactive decision making
problem. It is important to note that the proposed
methodology is capable of providing optimal
solution even for fuzzy observations represented by
trapezoidal fuzzy numbers or by s-curves. Moreover,
incorporating the attitudinal parameter ∈
0,1
reflecting DM’s degree of optimism offers more
flexibility in decision making to a DM, required in a
real world.
REFERENCES
Carlsson, C., Fuller, R., 2001. On possibilistic mean value
and variance of fuzzy numbers, Fuzzy Sets and
Systems 122, 315-326.
Chang, H. C., Yao, J. S., Ouyang, L. Y., 2006. Fuzzy
mixture inventory model involving fuzzy random
variable lead-time demand and fuzzy total demand,
European Journal of Operational Research 169, 65-
80.
Chen, S. H., Wang, C. C.,1996. Backorder fuzzy inventory
model under functional principle, Information
Sciences 95, 71-79.
Dutta, P., Chakraborty, D.,2010. Incorporating one-way
substitution policy into the newsboy problem with
imprecise customer demand, European Journal of
Operational Research 200, 99-110.
Dutta, P., Chakraborty, D., Roy, A. R. 2005. A single
period inventory model with fuzzy random variable
demand, Mathematical and Computer Modeling41,
915-922.
Dutta, P., Chakraborty, D., Roy, A. R. 2007a. An
inventory model for single period products with
reordering opportunities under fuzzy demand,
Computers and Mathematics with Applications
53,1502-1517.
Dutta, P., Chakraborty, D., Roy, A. R., 2007b. Continuous
review inventory model in mixed fuzzy and stochastic
environment, Applied Mathematics and Computation
188, 970-980.
Dutta, P., Roy, A. R. 2007. Decision on back order
inventory model under mixed uncertainty, Tamsui
Oxford Journal of Management Sciences 23, 59-70.
Dutta, P., Chakraborty, D.,Roy, A. R., 2012. Uncertain
Demand in (Q, r) inventory systems: A fuzzy
optimization approach, The Journal of Fuzzy
Mathematics 20, 501-514.
Feng,Y., Hu, L., Shu, H., 2001.The variance and
covariance of fuzzy random variables and their
applications, Fuzzy Sets and Systems 120, 117-127.
Hsieh, C. H., 2002. Optimization of fuzzy production
inventory models, Information Sciences 146, 29-40.
Lee, H. M., Yao, J. S., 1999a. Economic order quantity in
fuzzy sense for inventory without backorder model,
Fuzzy Sets and Systems 105, 12-31.
Lee, H. M., Yao, J. S.,1999b. Fuzzy inventory with or
without backorder order quantity with trapezoid fuzzy
number, Fuzzy Sets and Systems 105, 311-337.
Lopez-Diaz, M., Gil, M. A. 1998. The -average value of
the expected value of a fuzzy random variable, Fuzzy
Sets and Systems 99, 347-391.
Luhandjula, M. K. 2004. Fuzzy random variable: A
mathematical tool for combining randomnessand
fuzziness, Journal of Fuzzy Mathematics 12,755-764.
Nagare, M., Dutta, P. 2012. On solving single-period
inventory model under hybrid uncertainty,
International Journal of Economics and Management
Sciences 6, 290-295.
Yao, J. S., Chang, S. C., Su, J. S., 2000. Fuzzy inventory
without backorder for fuzzy order quantity and fuzzy
total demand quantity,
Computers and Operations
Research 27, 935-962.
Yao, J. S., Chiang, J., 2003. Inventory without backorder
with fuzzy total cost and fuzzy storing cost defuzzified
by centroid and signed distance, European Journal of
Operational Research 148, 401-409.
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
312
