Modelling Complex Systems using the Pliant Cognitive Map
J´ozsef D. Dombi
1
and J´ozsef Dombi
2
1
Department of Software Engineering, University of Szeged, Arpad ter 2., Szeged, Hungary
2
Department of Computer Algorithms and Artificial Intelligence, University of Szeged, Arpad ter 2., Szeged, Hungary
Keywords:
Dynamic System, Pliant System, Cognitive Map, Fuzzy Operators.
Abstract:
Here, we present a tool for describing and simulating dynamic systems. Our starting point is the aggregation
concept, which was developed for multicriteria decision making. Using a continuous logic operator and a
proper transformation of the sigmoid function, we build positive and negative effects. From the input data we
can calculate the output effect with the help of the aggregation operator. Our approach is similar to that of the
Fuzzy Cognitive Map. We shall introduce a new technique that is more efficient than the FCM method. The
applicability of PCM is discussed and simulation results are presented.
1 INTRODUCTION
When we have to deal with a sophisticated system,
we are confronted by certain difficulties as we have
to represent it as a dynamic system. Using a dy-
namic system model can be hard computationally. In
addition, formulating a system using a mathematical
model may be difficult, or even impossible. Devel-
oping a model requires effort and specialized knowl-
edge. Usually a system involves complicated causal
chains, which might be non-linear. It should also be
mentioned that numerical data may be hard to obtain,
or it may contain certain errors, noise and incomplete
values. Our approach seeks to overcome the above-
mentioned difficulties. It is a qualitative approach
where it is sufficient to have a rough description of the
system and deep expert knowledge is not necessary.
A similar approach was proposed by Kosko (Kosko,
1986; Kosko, 1994; Kosko, 1992), and it is called
the Fuzzy Cognitive Map (FCM). FCMs are hybrid
methods that lie in some sense between fuzzy systems
and neural networks (Glykas, 2010; Salmeron et al.,
2012; Yaman and Polat, 2009; Salmeron and Lopez,
2012; Maio et al., 2011). Knowledge is represented
in a symbolic way using states, processes and events.
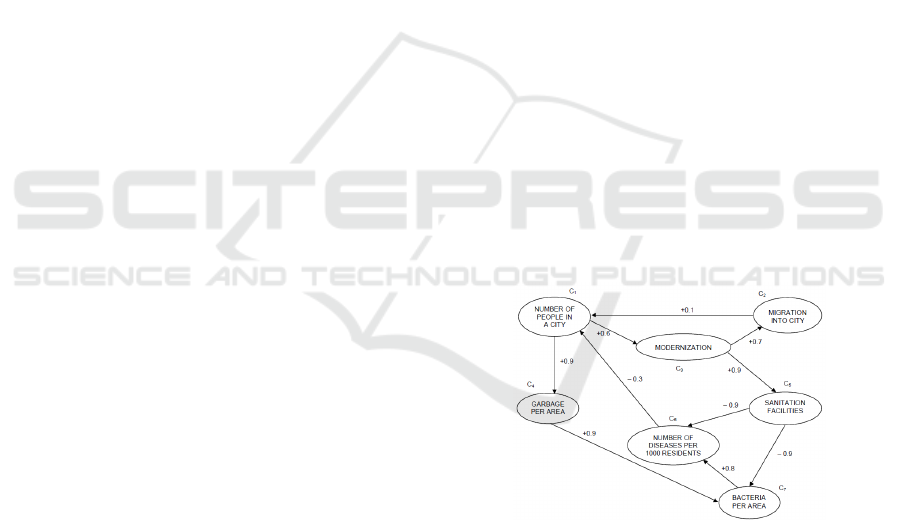
Every piece of information has a numerical value. In
Figure 1 we can see a typical FCM model, which is a
directed graph.
The FCM approach allows us to perform qual-
itative simulations and experiment with a dynamic
model. It has better properties than expert systems
or neural networks, since it is relatively easy to use,
Figure 1: The FCM model.
it represents structured knowledge and inferences can
be computed by numeric matrix operations instead of
applying rules. In this paper, we will use a modifica-
tion of the FCM concept so that ours better matches
real-world modeling, which we call Pliant Cognitive
Maps (Jozsef Dombi, 2005) (J. Dombi, 2005). We
use cognitive maps to represent knowledge and to
model decision making, which was first introduced by
Axelrod (Axelrod, 1976). Kosko used fuzzy values
and matrix multiplication to calculate the next state
of a system. Here instead of values, we use time-
dependent functions that are similar to impulse func-
tions to represent positive and negative influences.
Another improvement is that we drop the concept of
matrix multiplication. On the one hand, matrix mul-
tiplication is not well suited in continuous logic (or
fuzzy logic), where the true value is one and the false
value is zero. On the other hand, general operators are
more efficient for calculating the next step of a simu-
lation. Logic and the cognitivemap model correspond
506
D. Dombi J. and Dombi J..
Modelling Complex Systems using the Pliant Cognitive Map.
DOI: 10.5220/0004478205060512
In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 506-512
ISBN: 978-989-8565-59-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

to each other in the PCM case. It is easier to construct
a PCM and after we have run PCM simulations and
compared them with the real world, extracting knowl-
edge is much easier. Combining cognitive maps with
logic helps us to extract knowledge more efficiently,
in contrast to when we use rule-based systems. The
standard knowledge representation in expert systems
is achieved through a decision tree. This form of
knowledge representation in most cases cannot model
the dynamic behaviour of the real world. The cog-
nitive map describes the whole system by a graph
showing the cause-effects that connect concepts. It
is a directed graph with feedback that describes the
real world concepts and the causal influences between
them. From a logic point of view, causal concepts are
unary operators of a continuous valued logic contain-
ing negationoperators in the case of inhibition effects.
The value of the node reflects the degree of system ac-
tivity at any given time. Concept values are expressed
on a normal [0,1] range. Values do not denote exact
quantities, but the degree of activation. The inverse
of the normalization might express the values com-
ing from the real world, i.e. using a sigmoid func-
tion. Unlike the Fuzzy Cognitive Map, we do not use
thresholds to force it to take values between zero and
one. The mapping is a variation of the ”fuzzification”
process in fuzzy logic, and it always hinders our de-
sire to get quantitative results. In Pliant logic we map
the real world into the logical model. These maps are
continuous, strictly monotonous increasing functions,
and so the inverse of these functions yields data about
the real world. This paper is organized as follows.
Section II describes the representation and mathemat-
ical formulation of the PCM concept compared to the
FCM concept. Section III describes the components
of the PCM, while Section IV describes how to create
the PCM model. In Section V we discuss the develop-
ment of a FCM model for the heat exchanger system
that is common in the process industry. Section VI
presents the features and potential use of the PCM for
modeling complex systems. Lastly, in Section VII.,
we summarize our findings.
2 PLIANT COGNITIVE MAPS
In the FCM, a causal relationship is expressed by ei-
ther positive or negative functions that have differ-
ent weights. As we mentioned earlier, this will be
replaced by unary operators in the PCM. First, let
{C
1
, . . . ,C
m
} be a set of concepts. Define a directed
graph over the concepts. A directed edge has a weight
w
ij
from conceptC
i
to concept C
j
. This weight mea-
sures the influence of C
i
on C
j
, where
• 0.5 is the neutral value,
• 0 is the maximum negative and
• 1 is the maximal positive influence or causality.
In the FCM, the weight value w
ij
∈ [−1, 0, 1] . In
our case,
• w
ij
> 0.5 means there is a direct (positive) causal
relationship between concepts C
i
and C
j
. That is,
the increase (decrease) in the value of C
i
leads to
an increase (decrease) in the value of C
j
.
• w
ij
< 0.5 means there is an inverse (negative)
causal relationship between concepts C
i
and C
j
.
That is, the increase (decrease) in the value of C
i
leads to a decrease (increase) in the value of C
j
.
• w
ij
= 0.5 means there is no causal relationship be-
tween C
i
and C
j
.
During the simulation, the activation level a
i
of
concept C
i
is calculated in an iterative way. In the
FCM, the calculation rule that was initially introduced
to calculate the value of each concept based only on
the influence of the interconnected concepts is
A
t
i
= f
∑
i6= j
A
t−1
j
·W
ji
!
,
where A
t
i
is the value of concept C
i
for time step t,
A
t−1
j
is the value of conceptC
j
for time step t − 1, W
ji
is the weight of the causal interconnection from the
jth concept toward the ith concept and f is a threshold
function. One of the most popular threshold functions
is the sigmoid function, where λ > 0 determines the
steepness of the continuous function f and squashes
the contents of the function into the interval [0,1]:
f(x) =
1
1+ e
−λx
. A more general FCM formula was proposed By
Stylios et al. (Stylios and Groumpos, 2004) to calcu-
late the valuesof concepts for each time step. Namely,
A
t
i
= f
k
i
1
∑
i6= j
A
t−1
j
·W
ji
+ k
i
2
A
t−1
i
!
The coefficients k
i
1
and k
i
2
must satisfy the condi-
tions 0 ≤ k
i
1
≤ 1 and 0 ≤ k
i
2
≤ 1. The coefficient k
i
1
ex-
presses the influence of the interconnected concepts in
the configuration of the new value of concept A
i
. The
coefficient k
i
2
represents the proportion of the contri-
bution of the previous value of the concept in the com-
putation of the new value. The FCM approach has the
advantage that we get a new state vector by multiply-
ing the previous state vector a by the edge matrix W,
which shows the effect of the change in the activation
ModellingComplexSystemsusingthePliantCognitiveMap
507
level of one concept on another. In the Pliant con-
cept, we aggregate the influences instead of summing
up the values. The result always lies between 0 and
1, so we do not need normalization as an additional
step. Aggregation in Pliant logic is a general oper-
ation, which contains conjunctive operators and dis-
junctive operators as well. Depending on the param-
eter called the neutral value of the aggregation opera-
tor, we can build logical operators like Dombi opera-
tors. Using PCMs (Pliant Cognitive Maps) we answer
”what if” questions based on an initial scenario. Now
let A
i
be the initial state vector. The new state is cal-
culated repeatedly with the aggregation operator until
the system converges
A
t
i
− A
t−1
i
< ε. Eventually we
get the equilibrium vector, which provides a set of an-
swers to our ”what-if” questions. The PCM approach
can be used in every area covered by the FCM ap-
proach.
3 COMPONENTS OF THE PCM
Now we will introduce the components of the Pliant
Cognitive Maps.
3.1 Aggregator Operator
Besides the logical operatorsconstructed in fuzzy the-
ory, a non-logical operator also appears. The reason
for this is the insufficiency of using either conjunc-
tive or disjunction operators for real-world situations
(Zimmermann and Zysno, 1980). The rational form
of an aggregation operator is (Dombi, 1982):
a(x
1
, . . . , x
n
) =
1
1+
1−ν
0
ν
0
·
ν
1−ν
∑
w
i
−1
·
∏
n
i=1
(
1−x
i
x
i
)
w
i
We can model conjunctive and disjunctive opera-
tors with the aggregation operator. If v is close to 0
then the operation has a disjunctive characteristic and
if v is close to 1 then the operation has a conjunctive
characteristic. From this property it can be seen that
by using aggregation we have more possibilities than
by simply using the sum function in FCM. By varying
the neutral values at the nodes, different operations
can be performed.
3.2 Creating Influences
In the Pliant Cognitive Map, we define influences.
The sigmoid function naturally maps the values to the
(0,1) interval. Positive (negative) influences can be
built with the help of two sigmoid functions and the
conjunctive operator. Hence we get the generalized
positive impulse function
c(t, u, v, a, b) =
1
1+ u∗ e
−λ
1
(t−a)
+ v∗ e
−λ
2
(t−b)
,
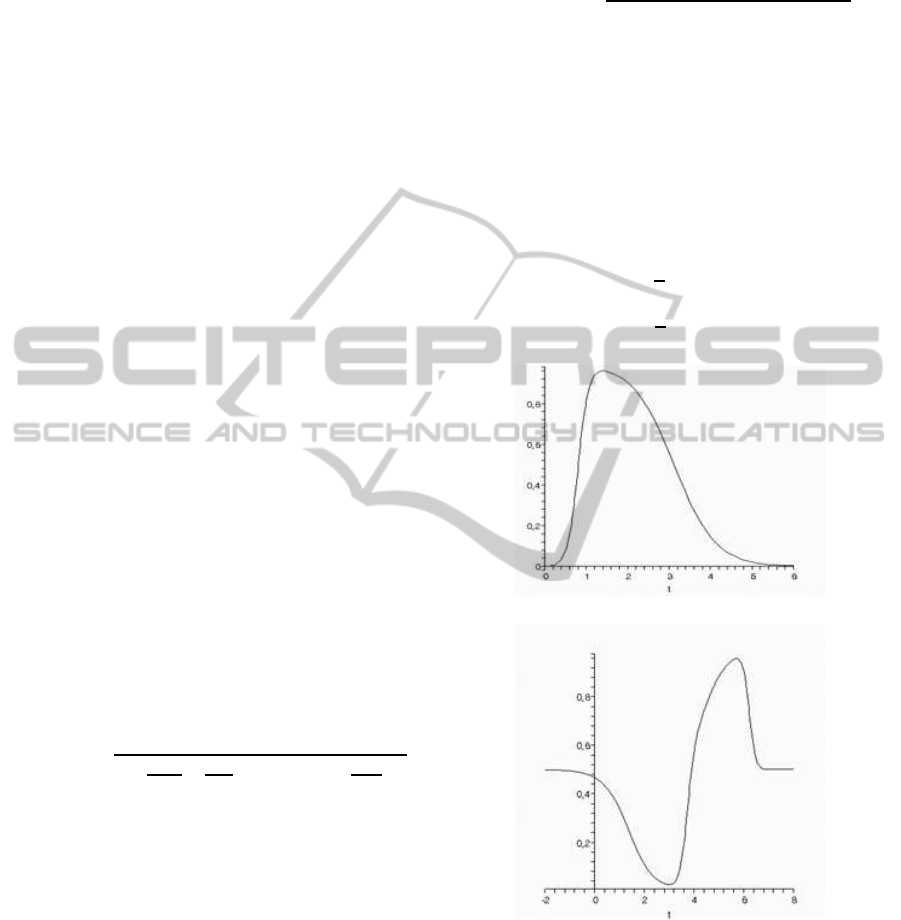
where u and v are weights. In Figure 2 we can see
a basic influence, as mentioned in (Jozsef Dombi,
2005). If the influence is neutral, we can represent
it by a 1/2 value. If there are no influences, then we
continuously order 1/2 values in the system. If we
want to model positive influences, we order a value
which is larger than 1/2, and whose maximal value is
1. The negative influence is the negation of the posi-
tive influence. To create these influences, we use the
following transformations:
P(t, u, v, a, b) =
1
2
(1+ c(t, u, v, a, b))
N(t, u, v, a, b) =
1
2
(1− c(t, u, v, a, b))
Figure 2: An average influence.
Figure 3: The aggregation of two influences.
In Figure 3, we have plotted the aggregation of a
positive and a negative effect.
4 CONSTRUCTION OF THE PCM
To simulate the system, the only thing we have to do
is to aggregate the influences. The aggregation oper-
ator is a guarantee that we will use influences in the
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
508
right way. The following steps should be carried out
to simulate the system:
1. Collect the concepts.
2. Define the expectation values of the nodes (i.e.
threshold values of the aggregations).
3. Build a cognitive map (i.e. draw a directed graph
for the concepts).
4. Define the influences (i.e. whether they are posi-
tive or negative)
In the iterative method we
1. Use the proper function or supply a data list for
the input nodes.
2. Calculate the positive and negative influences us-
ing step 4.
3. Aggregate the positive and negative influences,
where the aggregation parameter ν
0
value is the
previous value of the concept C
j
.
5 HEAT EXCHANGER
APPLICATIONS
A heat exchanger is a standard device in the chemi-
cal and process industries (M. Fischer and Isermann,
2000). In this task, the temperature control is still a
major challenge as the heat exchanger is used over a
wide range of operating conditions. The behaviour of
the system, which is non-linear, strongly depends on
the flow rates and on the temperature of the medium.
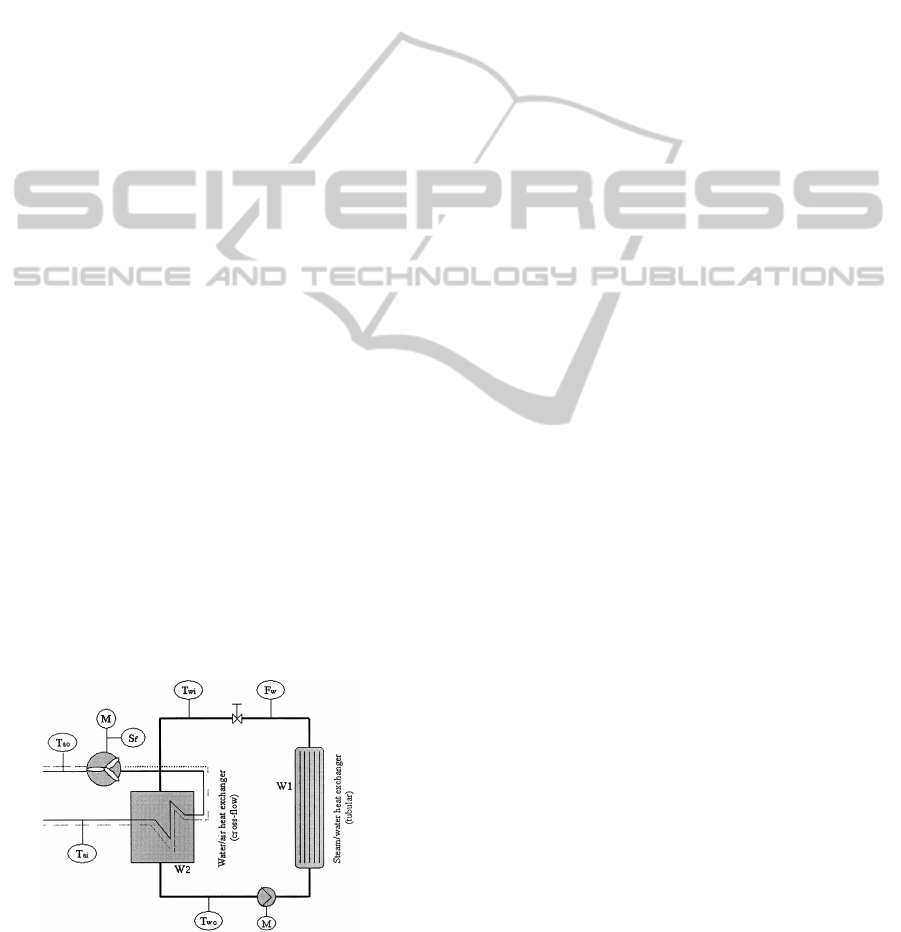
A cross-flow water/air heat exchanger is envisaged,
which is subject to immeasurable or non-modeleddis-
turbances that require the use of knowledge-based
techniques. In this problem, we wish to develop a be-
havioural model for the heat exchanger system, that
will control the water outlet temperature by manipu-
lating the flow rate of the air.
Figure 4: Typical heat exchanger system.
Here, in Figure 4 we can see a typical set-up for
the system. It is well known that the FCM can be
used to model and control the heat exchanger process
(Stylios and Groumpos, 2004). In most process indus-
tries the thermal plant comprises two heat exchangers,
but in our example (see Figure 2) we will just con-
sider the secondary circuit. Our system contains two
circuits W
1
and W
2
. W
1
is a circuit, which is a tubular
steam/water heat exchanger, and W
2
is the cross-flow
water/air exchanger. The water in this circuit is heated
by means of W
1
. On the left hand side, the water is
cooled in the cross-flow water/air heat exchanger W
2
.
A fan sucks in cold air from the environment (temper-
ature Tai). After passing through the heat exchanger
and the fan, the air is blown back out into the envi-
ronment. The water temperature Two is controlled by
manipulating the fan speed S f. The control variable
Two depends on the manipulated variable Sf and the
measurable disturbances: the inlet water temperature
Twi, air temperature Tai and water flow rate Fw. In
most systems, the water flow rate is usually regulated
by a PI-controlled pneumatic valve which strongly in-
fluences the behaviour of the heat exchanger W2 and
it is a major challenge to design a temperature con-
troller for Two when the flow rates vary over a wide
range (Bittanti and Piroddi, 1997), (Ernst and Hecker,
1996). The operators of the heat exchanger gather
experience that can be used to build a model. To
construct an FCM system, we have to determine the
concepts. Here, concepts stand for the input and out-
put variables of the process. Earlier the thermal plant
was described, and the concepts of the FCM were de-
rived from a Stylios analysis (Stylios and Groumpos,
2004). Experts define five concepts for this situation:
• Concept1: The fan speed Sf, which is the manip-
ulated variable.
• Concept2: The water flow rate Fw.
• Concept3: The water inlet temperature Twi.
• Concept4: The air inlet temperature Tai. The en-
vironmental temperature cannot be manipulated
as it depends on the weather and season.
• Concept5: The water outlet temperature Two,
which is the output of the model.
In the next step, the causal interconnectionsfor the
concepts have to be determined. Experts can describe
the relation between any two concepts based on the
system. The connections for the concepts are
• Linkage1: It connects concept1 (fan speed S f)
with concept5 (water outlet temperature Two).
When the value of Sf increases, the value of Two
decreases.
• Linkage2: It connects concept2 (flow rate Fw)
with concept5 (water outlet temperature Two).
ModellingComplexSystemsusingthePliantCognitiveMap
509

When the value of Fw increases, the value of Two
increases.
• Linkage3: It connects concept2 (flow rate Fw)
with concept1 (fan speed Sf ). When the value
of Fw increases, the value of Sf increases.
• Linkage4: It connects concept3 (water inlet tem-
perature Twi) with concept5 (water outlet temper-
ature Two). When the value of Twi increases, the
value of Two increases.
• Linkage5: It connects concept3 (water inlet tem-
perature Twi) with concept1 (fan speed S f ).
When the value of Twi increases, the value of S f
increases.
• Linkage6: It connects concept3 (water inlet tem-
perature Twi) with concept2 (flow rate Fw).
When the value of Twi increases, the value of Fw
decreases.
• Linkage7: It connects concept4 (air inlet tempera-
ture Tai) with concept5 (water outlet temperature
Two). When the value of Tai increases, the value
of Two increases.
• Linkage8: It connects concept4 (air inlet tempera-
ture Tai) with concept1 (fan speed Sf ). When the
value of Tai increases, the value of S f decreases.
• Linkage9: It connects concept5 (water outlet
temperature Two) with concept2 (flow rate Fw).
When the value of Two increases, the value of Fw
decreases.
• Linkage10: It connects concept5 (water outlet
temperature Two) with concept1 (fan speed S f ).
When the value of Two increases, the value of Sf
increases.
Figure 5: The FCM model for the heat exchanger system.
Figure 5 shows our system which describes, mod-
els and controls the heat exchanger system. The FCM
model for the heat exchanger is in accordance with the
models and experiments described in (M. Fischer and
Isermann, 2000) (Ernst and Hecker, 1996). It is also
possible to create an influence matrix for the system
like that in Table 1.
Table 1: The weighted matrix of the model.
Sf Fw Twi Tai Two
0 0.625 0.75 -0.25 0.625
0 0 -0.75 0 -0.75
0 0 0 0 0
0 0 0 0 0
-0.75 0.125 0.25 -0.75 0
Table 2: Simulation results for the FCM.
Iteration Sf Fw Two Improvement:
1 0,77 0,52 0,56 0,8577
2
0,85 0,44 0,54 0,1906
3 0,85 0,43 0,51 0,0419
4
0,85 0,43 0,5 0,0107
5 0,85 0,43 0,5 0,0036
To simulate a real environment in the FCM, the
values of concepts correspond to real measurements
that have been transformed to the interval [0,1]. A
corresponding mechanism is needed that will trans-
form the measures of the system to their represen-
tative values of concepts in the FCM model and
vice versa. The initial measurements of the heat
exchanger system were transformed to concept val-
ues and the initial vector of the FCM is A
0
=
[0.3 0.65 0.45 0.15 0.3]. In Figure 5, it also shows
the initial values of each concept and the interconnec-
tions with their weights. With these initial values of
concepts, the FCM starts to simulate the behaviour of
the process. For the FCM area, a running step is de-
fined as the time step during which the values of the
concepts are calculated. The value of each concept is
defined by taking all the causal linkage weights point-
ing to this concept and multiplying each weight by
the value of the concept that causes the linkage, and
adding the last value of each concept. Then the sig-
moid function with λ = 1 is applied and the result falls
into the range [0,1]. The results of the simulation are
listed below.
This table does not contain input node values
where the value is the same all time. Evaluating the
results, we see that the value of fan speed Sf has in-
creased, the value of flow rate Fw has decreased, and
after the third step, the water outlet temperature Two
falls below the value of 0.50. We also see that the
value between any two simulation steps decreases, but
this decrease is not uniform, which is not as good as
we first thought. Because concepts control physical
devices, we should vary the values as smoothly as
possible.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
510
6 EVALUATE WITH THE PCM
Our method works with real data measurements,
which means that we do not need to transform real
values between [0,1] in order to run the simulation. In
our model we use the same concepts and connections,
and the initial values of the concepts are the same as
before. So first of all to evaluate our method we need
to identify the range values of the concepts. Because
previous articles do not mention these values, we will
choose the following values:
Table 3: The range values of the concepts.
Concept Minimum Maximum Default
Sf 100 500 250
Fw 2 20 6
Twi 20 50 30
Tai 18 35 24
Two 20 40 30
The default value is used to specify the real values
of the first step. Using the above-mentioned ranges
we define a sigmoid function that will be used for the
calculations. For example, the initial value of the Sf
concept is 0.3, and we apply the following sigmoid
function:
S
f
(x) =
1
1+ e
−
4
500
(x−250)
In this case, the real value of Sf should be 144.08.
Based on these calculations, we can compute the ini-
tial values of the concepts:
Table 4: The initial values of the concepts.
Sf Fw Twi Tai Two
144.08 3.7 27.5 8.8 21.52
This method also shows that with each simula-
tion step it is easy to recover the real value. In the
classical FCM method, the influence does not change
during the simulation. In order to compare it with
our method, we will also define a constant influence.
Hence in a simulation step we calculate the new con-
cept value in the following way. For each node in
the set we create a set that contains all the incoming
nodes. Also, we will use the following expression to
calculate the strength of the incoming node:
1− x
i
x
i
w
ij
,
where x
i
is the actual value of the node and w
ij
is the
value of the influence between concept C
i
and C
j
. Af-
ter, we calculate this method for each node in the set,
then we use the aggregation operator to calculate the
Table 5: Simulation results for the PCM.
Iteration
Sf Fw Two Improvement:
1 0.53 0.68 0.75 0.7262
2 0.81 0.33 0.59 0.7870
3
0.52 0.46 0.31 0.7024
4 0.42 0.67 0.57 0.5787
5
0.71 0.47 0.67 0.5881
6 0.66 0.40 0.42 0.3810
7
0.46 0.59 0.46 0.4327
8 0.60 0.56 0.63 0.3492
9 0.69 0.43 0.53 0.3310
10
0.54 0.51 0.44 0.3176
11 0.54 0.58 0.56 0.1951
12
0.65 0.48 0.57 0.2203
13 0.60 0.47 0.47 0.1590
14
0.54 0.55 0.51 0.1829
15 0.61 0.52 0.57 0.1602
16
0.63 0.47 0.51 0.1224
17 0.56 0.52 0.49 0.1266
18
0.58 0.53 0.55 0.0833
19 0.62 0.49 0.54 0.0908
20
0.59 0.50 0.50 0.0734
21 0.57 0.53 0.52 0.0712
22
0.60 0.51 0.54 0.0675
23 0.60 0.50 0.52 0.0405
24
0.58 0.52 0.51 0.0462
25 0.59 0.52 0.54 0.0337
26
0.60 0.50 0.53 0.0380
27 0.59 0.51 0.51 0.0336
28
0.59 0.52 0.53 0.0256
29 0.60 0.51 0.53 0.0264
30 0.60 0.51 0.52 0.0174
31
0.59 0.51 0.52 0.0191
32 0.59 0.51 0.53 0.0155
33
0.60 0.51 0.52 0.0148
34 0.59 0.51 0.52 0.0141
35
0.59 0.51 0.53 0.0084
new value of the concept. For example, the new value
of Fw is obtained by computing
1
1+
1−0.45
0.45
−0.75
1−0.3
0.3
−0.75
Now we can run the simulation until it exceeds a
limit. The following table shows the results of our
simulation.
Evaluating the results we notice that they are dif-
ferent from those got by using the FCM method. In
Figure 6, we see how the values vary.
The value of the fan speed Sf has decreased, the
value of flow rate Fw has decreased and the water
outlet temperature Two is below the value of 0.50.
We also see that the differences between two simu-
lation steps decreases (see Figure 7), but this decrease
ModellingComplexSystemsusingthePliantCognitiveMap
511
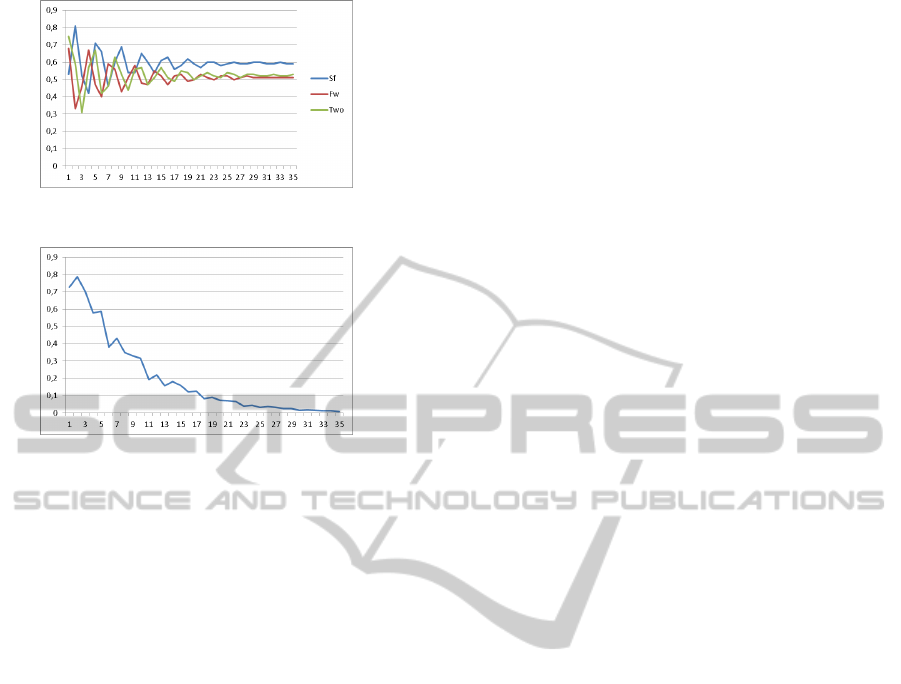
Figure 6: Results for the PCM model.
Figure 7: Sum of value change for each step.
is smooth, and this is why it requires more simulation
steps.
7 CONCLUSIONS
In this paper, we made use of numerical methods to
model complex systems based on positive and nega-
tive influences. This concept is similar to the FCM
concept, but the functions and the aggregation proce-
dures are quite different. It is based on a continuous-
valued logic and all the parameters have a semantic
meaning. Here, we showed that we can apply this
method in a real environment. The values of the sim-
ulation steps smoothly decrease, but it requires more
simulation steps. In this example, we used the same
influence for each concept all the time, but it is also
possible to vary the strength of the influence, and then
we can model a real-world situation better.
REFERENCES
Axelrod, R. (1976). Structured of Decision: the cognitive
maps of political elites. Princeton University press,
New Jersey.
Bittanti, S. and Piroddi, L. (1997). Nonlinear identification
and control of a heat exchanger: a neural network ap-
proach. J. Franklin Inst., page 135153.
Dombi, J. (1982). A general class of fuzzy operators, the De
Morgan class of fuzzy operators and fuzziness mea-
sures induced by fuzzy operators. Fuzzy Sets and Sys-
tems, 8:149–163.
Ernst, E.-J. and Hecker, O. (1996). Predictive control of a
heat exchanger. Proc. Seminar Theory Applications
Model Based Predictive Control, pages 1–18.
Glykas, M. (2010). Fuzzy Cognitive Maps Advances in The-
ory, Methodologies, Tools and Applications. Springer-
Verlang.
J. Dombi, J. D. D. (2005). Pliant cognitive map using con-
junctive operator. Proceedings of IEEE International
Workshop on Soft Computing Applications, page 11.
Jozsef Dombi, J. D. D. (2005). Cognitive maps based on
pliant logic. 16TH European Simulation Symposium,
page 63.
Kosko, B. (1986). Fuzzy entropy and conditioning. Infor-
mation Sciences, 40:165–174.
Kosko, B. (1992). Neural Networks and Fuzzy Systems.
Prentice Hall, Englewood Cliffs.
Kosko, B. (1994). Fuzzy Thinking. Flamingo. hardcopy.
M. Fischer, O. N. and Isermann, R. (2000). Knowledge-
based adaptation of neurofuzzy models in predictive
control of a heat exchanger. Soft Computing and In-
telligent Systems, page 469489.
Maio, C. D., Fenza, G., Gaeta, M., Loia, V., and Orciuoli, F.
(2011). A knowledge-based framework foremergency
DSS. Knowl.-Based Syst, 24(8):1372–1379.
Salmeron, J. L. and Lopez, C. (2012). Forecasting risk im-
pact on ERP maintenance with augmented fuzzy cog-
nitive maps. IEEE Trans. Software Eng, 38(2):439–
452.
Salmeron, J. L., Vidal, R., and Mena, A. (2012). Rank-
ing fuzzy cognitive map based scenarios with TOP-
SIS. Expert Syst. Appl, 39(3):2443–2450.
Stylios, C. D. and Groumpos, P. P. (2004). Modeling com-
plex systems using fuzzy cognitive maps. IEEE Trans-
actions on Systems, Man, and Cybernetics, Part A,
34:155–162.
Yaman, D. and Polat, S. (2009). A fuzzy cognitive map
approach for effect-based operations: An illustrative
case. Inf. Sci, 179(4):382–403.
Zimmermann, H. J. and Zysno, P. (1980). Latent connec-
tives in human decision making. Fuzzy Sets and Sys-
tems, 4(1):37–51.
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
512
