
Adaptive LQG/LTR Control; Discontinuity Issue
Dariusz Horla and Andrzej Krolikowski
Poznan University of Technology, Institute of Control and Information Engineering, ul. Piotrowo 3a, 60-965 Poznan, Poland
Keywords:
LQG Control, Loop transfer Recovery, Adaptive Control.
Abstract:
An adaptive LQG control with no control cost is considered. In such case the loop transfer recovery (LTR)
effect can be obtained. The control problem is handled using discrete-time state-space model and the parameter
estimation is performed for corresponding ARMAX model which can be represented in innovation state-space
form. Thus the direct estimation of model parameters is possible by means of standard ERLS procedure and
the adaptive control is implemented through certainty equivalence principle. In such a situation the problem
of solution continuity of Riccati equation can arise for nonminimum-phase systems. Computer simulations of
third-order systems modeled by a second-order minimum-phase and nonminimum-phase models are given to
illustrate the robustness and performance properties of the adaptive controller, particularly with respect to the
modelling error parameter η.
1 INTRODUCTION
The problem of adaptive LQG/LTR control is not
much investigated in the literature. It is known that
even without LTR an adaptive LQG control itself is
difficult to solve in optimal manner. Adaptive LQG
control has been discussed e.g. in (Kumar, 1983;
Bitmead et al., 1990; Tay and Moore, 1991; Kro-
likowski, 1995; M¨akil¨a et al., 1984; Duncan and
B.Pasik-Duncan, 1999), where in (Tay and Moore,
1991) an adaptiveLQG/LTR problem was solvedaug-
menting the basic estimator-based controller with a
stable proper linear system feeding back the estima-
tion residuals. This idea was also used for non-
adaptive continuous-time systems in (Tay and Moore,
1989) using the H
∞
/H
2
optimization technique. The
LQG/LTR problem for continuous-time systems was
considered in (A. Saberi and Sannuti, ) where the
analysis of loop transfer recovery is given for not nec-
essarily left invertible and not necessarily minimum-
phase (mph) systems.
The key issue in adaptive LQG control is the
closed-loop identifiability. For example in (Kumar,
1983) a discrete-time system and a cost-biased least-
squares parameter estimation was used in order to
achieve overall asymptotic system optimality. In
(Duncan and B.Pasik-Duncan, 1999) a continuous-
time system was considered and a modified weighted
least-squares parameter estimation algorithm was
used to obtain good properties of estimates. In both
papers only a fully state observation case was consid-
ered.
In this paper, LQG adaptive control with LTR ef-
fect is considered. The adaptive discrete-time LQG
control with no control cost (cheap control) is pro-
posed when the full LTR effect, at least for mph sys-
tems can be obtained. The controller/filter parameters
are tuned on-line based on parameter identification
of ARMAX model. This can sometimes lead to dis-
continuous behaviour of solution to Riccati equation
depending on system parameters (Saberi and Stoor-
vogel, 1996). Asymptotic performance and robust-
ness properties are analyzed and simulations for third-
order system considered as a second-order model are
given. The impact of modelling error parameter η on
performance, robustness and solution discontinuity of
corresponding Riccati equation is underlined.
2 LQG/LTR PROBLEM FOR
DISCRETE-TIME SYSTEMS
The state-space discrete-time system is given by
x
t+1
= Fx
t
+ Gu
t
+ w
t
(1)
y
t
= Hx
t
+ v
t
(2)
where n,m,r are dimensions of the state, control and
output vectors, respectively and where {w
t
} and {v
t
}
are sequences of independentrandom vector variables
802
Horla D. and Krolikowski A..
Adaptive LQG/LTR Control; Discontinuity Issue.
DOI: 10.5220/0005121408020807
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 802-807
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

with zero mean and covariances Ew
t
w
T
s
= Σ
w
δ
t,s
,
v
t
v
T
s
= Σ
v
δ
t,s
.
The Kalman predictor for (1), (2) in steady-state is
given by
ˆx
t+1/t
= Fˆx
t/t−1
+ Gu
t
+ K
p
˜y
p
t
(3)
where ˜y
p
t
= y
t
− H ˆx
t/t−1
is an innovation of output at
time t. The predictor gain is given by
K
p
= FP
f
H
T
[HP
f
H
T
+ Σ
v
]
−1
(4)
where P
f
is the solution of Riccati equation
P
f
= FP
f
F
T
+ Σ
w
− FP
f
H
T
[HP
f
H
T
+ Σ
v
]
−1
HP
f
F
T
(5)
The filtered estimate ˆx
t/t
in terms of ˆx
t/t−1
is
ˆx
t/t
= ˆx
t/t−1
+ K
f
˜y
p
t
(6)
and its recursive version is
ˆx
t+1/t+1
= Fˆx
t/t
+ (I − K
f
H)Gu
t
+ K
f
˜y
f
t+1
(7)
where ˜y
f
t+1
= y
t+1
− HF ˆx
t/t
and the filter gain
K
f
= P
f
H
T
[HP
f
H
T
+ Σ
v
]
−1
, (8)
so K
p
= FK
f
in view of (4). An alternative equation
for (7) is
ˆx
t+1/t+1
= Fˆx
t/t
+ Gu
t
+ K
f
˜y
p
t+1
(9)
The Kalman filter-based control law
u
t
= K
c
ˆx
t/t
(10)
aims to minimize the cost function
J = E
∞
∑
t=0
y
T
t
Qy
t
. (11)
where the gain K
c
is given by
K
c
= −[G
T
P
c
G]
−1
G
T
P
c
F (12)
and P
c
is the solution of Riccati equation
P
c
= F
T
P
c
F − F
T
P
c
G[G
T
P
c
G]
−1
G
T
P
c
F + Q (13)
When the weighting matrix is Q = H
T
H and assum-
ing that the system (1), (2) is stabilizable, detectable
and mph then it can be shown (Tadjine et al., 1994),
(Maciejowski, 1985) that K
c
takes very simple form
K
c
= −(HG)
−1
HF. (14)
and the optimal cost function is
J
opt
= trH
T
H[Σ
w
+ FP
f
F
T
]. (15)
If G(z) = H(zI − F)
−1
G is mph and K
c
takes a form
(14) then the perfect recovery takes place, that is
∆(z) = G(z)G
f
(z) − Φ(z) = 0, (16)
where the transfer function G
f
(z) of compensator de-
fined by (7) and (10) can be manipulated into the form
G
f
(z) = −zK
c
[zI − (I − K
f
H)(F + GK
c
)]
−1
K
f
=
= −zK
c
[zI − F − GK
c
]
−1
K
f
, (17)
and the filter’s open-loop return ratio is
Φ(z) = H(zI − F)
−1
K
p
. (18)
Putting (14) into (16) it can be seen that ∆(z) = 0 so
the recovery takes place. When G(z) is nonminimum-
phase (nmph) then the perfect recovery is in general
not possible, however is recommended because the
partial recovery is frequently achieved in closed-loop
bandwidth.
The robustness in the presence of additive modeling
error i.e. G
∗
= G+ ηG
p
, can be measured by means
of the ||H||
∞
norm of sensitivity transfer function
S(z) = (I + G(z)G
f
(z))
−1
, (19)
by checking up the inequality
η||G
p
(z)||
∞
||G
f
(z)S(z)||
∞
≤ 1, (20)
where η||G
p
(z)||
∞
is an upper bound of additive mod-
eling error.
It can be noted that for the Kalman predictor-based
feedback control u
t
= K
c
ˆx
t/t−1
the perfect recovery
cannot in general be possible.
3 ADAPTIVE CONTROL
The SISO ARMAX model is given by
A(q
−1
)y
t
= B(q
−1
)u
t
+C(q
−1
)e
t
(21)
where A(q
−1
),B(q
−1
) and C(q
−1
) are polynomials
in the backward shift operator q
−1
, i.e. A(q
−1
) =
1 + a
1
q
−1
+ ... + a
n
q
−n
,B(q
−1
) = b
1
q
−1
+ ... +
b
n
q
−n
,C(q
−1
) = 1 + c
1
q
−1
+ ... + c
n
q
−n
and y
t
is the
output , u
t
is the control input, and { e
t
} is assumed
to be a sequence of independent variables with zero
mean and variance σ
2
e
. Unknown system parameters
θ
= (a
1
,..., a
n
,b
1
,..., b
n
,c
1
,..., c
n
)
T
are estimated on-
line to obtain an updated model at time t, i.e.
ˆ
θ
t
.
ARMAX model (21) has an equivalent innovation
state-space representation
x
t+1
= Fx
t
+ g
u
t
+ k
e
e
t
(22)
y
t
= h
T
x
t
+ e
t
(23)
where g
= (b
1
,..., b
n
)
T
, k
e
= (c
1
− a
1
,..., c
n
−
a
n
)
T
, h
T
= (1,0,..., 0)
F =
−a
1
1 ... 0
. . ... 0
−a
n−1
. ... 1
−a
n
. ... 0
.
AdaptiveLQG/LTRControl;DiscontinuityIssue
803

For ARMAX system different forms of Kalman fil-
ter can be proposed. One of them takes the Kalman
predictor (3) associated with eq.(22) as
ˆx
t+1/t
= F ˆx
t/t−1
+ g
u
t
+ k
p
˜y
p
t
(24)
where ˜y
p
t
= y
t
− h
T
ˆx
t/t−1
and σ
2
˜y,p
is the variance of
˜y
p
t
for which it holds σ
2
˜y,p
= σ
2
e
. The predictor gain is
now given by
k
p
= (FP
f
h
+ σ
2
e
k
e
)[h
T
P
f
h
+ σ
2
e
]
−1
(25)
where P
f
is the solution of Riccati equation
P
f
= FP
f
F
T
+ k
e
k
T
e
σ
2
e
− (FP
f
h
+ k
e
σ
2
e
) ×
×[h
T
P
f
h+ σ
2
e
]
−1
(FP
f
h+ k
e
σ
2
e
)
T
(26)
The actual model used for control is obtained for cur-
rent parameter estimates
ˆ
θ
t
. The LTR control law (14)
is especially useful for adaptive control because there
is no need solving the Riccati equation (13) for ev-
ery model
ˆ
θ
t
, and the feedback gain K
c
can be tuned
directly, however this holds only for mph systems.
The investigatedproblem is to check up how the mod-
eling error influences the performance,robustness and
parameter estimation quality of adaptive control.
4 THE DISCONTINUITY ISSUE
The stability of the proposed adaptive control sys-
tem depends not only on the magnitude of modeling
error but also on the asymptotic convergence of pa-
rameter estimates. The parameter estimation in LQG
adaptive control does not in general assure the con-
vergence to the true parameters, even in the lack of
modelling error. Moreover, it is known that the so-
lutions of Riccati equation may have discontinuities
as a function of system parameters. This can oc-
cur for non left-invertible and nmph systems (Saberi
and Stoorvogel, 1996). Obviously, possible discon-
tinuities have impact on certainty equivalence-based
control and the closed-loop global stability cannot be
guaranteed. The concept of left-invertibility plays
here a crucial role. System (1) with r ≥ m is said to
be left-invertible if it satisfies
max
z
rankP
l
(z) = n+ m (27)
where
P
l
(z) =
zI − F −G
H 0
.
If the system is not left-invertible then it is almost
always possible to find parameter perturbations that
cause discontinuity (Saberi and Stoorvogel, 1996).
Even if the system is left-invertible discontinuity
problems can occur when the system is nmph.
5 SIMULATIONS
Consider an example of a third-order actual system
G
∗
(s) =
s+ 2
(s+ 1)(s+ 3)
+ η
1
s+ 2
whose nominal model G(s) is mph, so the case η = 0
corresponds to the lack of modeling error and η =
1 is the case of undermodeling. Discretizing the
continuous-time system with ZOH and sampling pe-
riod T
s
= 0.5s yields the following transfer function
in q
−1
operator
G
∗
(q
−1
) =
−0.3262q
−1
− 0.1224q
−2
1− 0.8297q
−1
+ 0.1535
−2
+ η
0.3101q
−1
1− 0.3679q
−1
.
(28)
As already mentioned, a second-order model was
taken for identification and certainty equivalence
principle was used to implement the adaptive control
system to demonstrate the robustness of adaptive con-
troller with respect to undermodeling.
The corresponding RLS parameter estimates of
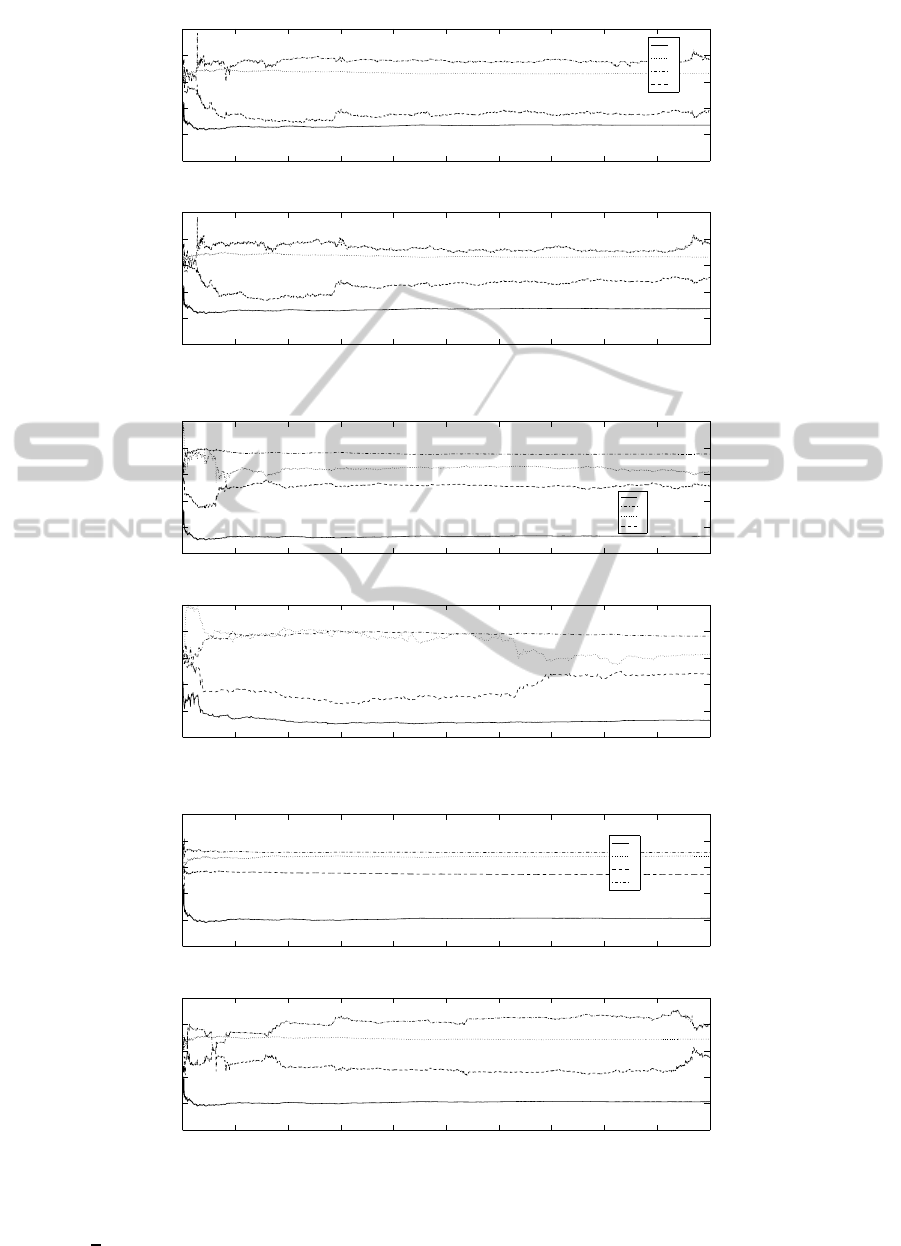
the nominal model are shown in Fig.1, for η = 0 and
in Fig.2 for η = 1 where the noise variance σ
2
e
was
set at 0.1. From Fig.1 one can see that for η = 0
parameter estimates converge to the true parameters
of second-order nominal model. It is to observe that
when η = 1 as in Fig.2 the parameter estimates con-
verge to some stationary points, however different
from the true ones.
As a second example consider a third-order actual
system
G
∗
(s) =
−s+ 1
(s+ 1)(s+ 2)
+ η
1
s+ 3
whose nominal model is nmph. Discretizing the
continuous-time system with ZOH and sampling pe-
riod T
s
= 0.5s yields the following transfer function
operator
G
∗
(q
−1
) =
−0.1612q
−1
+ 0.2856q
−2
1− 0.9744q
−1
+ 0.223q
−2
+ η
0.259q
−1
1− 0.223q
−1
.
(29)
From Fig.3 one can see that for η = 0 parameter
estimates again converge to the true parameters of
second-order nominal model. The case with η = 0.5
is shown in Fig.4. Again the parameter estimates
converge to some stationary points, however different
from true values.
Fig.5 shows the gain k
c
versus η obtained in
adaptive control for mph and nmph nominal systems
where both the formula (12) based on the Riccati
equation (13) and the formula (14) are used for cal-
culation of k
c
. This is illustrated by left and right col-
umn, respectively. In the mph case the result is the
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
804
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
−1.5
−1
−0.5
0
0.5
1
samples
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
−1.5
−1
−0.5
0
0.5
1
samples
a
1
a
2
b
1
b
2
Figure 1: MPH: estimates for η = 0.
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
−1.5
−1
−0.5
0
0.5
1
samples
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
−1.5
−1
−0.5
0
0.5
1
samples
a
1
a
2
b
1
b
2
Figure 2: MPH: estimates for η = 1.
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
−1.5
−1
−0.5
0
0.5
1
samples
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
−1.5
−1
−0.5
0
0.5
1
samples
a
1
a
2
b
1
b
2
Figure 3: NMPH: estimates for η = 0.
same for both formulae while for nmph nominal sys-
tem the gain k
c
calculated according to (12) and (14)
gives instability. The discontinuous jumps in nmph
case can be caused by discontinuity in solutions of the
Riccati equation (13) that can follow from parameter
estimates convergence to wrong values when η > 0.
AdaptiveLQG/LTRControl;DiscontinuityIssue
805

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
−1.5
−1
−0.5
0
0.5
1
samples
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
−1.5
−1
−0.5
0
0.5
1
samples
a
1
a
2
b
1
b
2
Figure 4: NMPH: estimates for η = 0.5.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−3
−2.5
−2
−1.5
−1
−0.5
K
c
(MPH, LQG)
η
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−3
−2.5
−2
−1.5
−1
−0.5
K
c
(MPH, (14))
η
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−7
−6
−5
−4
−3
−2
−1
K
c
(NMPH, LQG)
η
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
−10
−5
0
5
10
15
20
25
30
35
K
c
(NMPH, (14))
η
Figure 5: Plot of k
c
versus η.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0.18
0.2
0.22
0.24
0.26
0.28
0.3
0.32
J
MPH
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0.18
0.2
0.22
0.24
0.26
0.28
0.3
J
last est.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.2
0.4
0.6
0.8
1
||ηG
f
G
p
S||
η
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.2
0.4
0.6
0.8
1
J
NMPH
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.2
0.4
0.6
0.8
1
J
last est.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0
0.2
0.4
0.6
0.8
1
||ηG
f
G
p
S||
η
Figure 6: Plot of J and norms versus η.
This happens only when the system is nmph, more-
over the results obtained on the base of (14) give un-
stable gains k
c
.
In the case of η > 0 a deterioration of cost function
is to be expected. This is illustrated in Fig.6 where
the simulated cost function (11) is plotted versus η for
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
806

adaptive control and for nonadaptive control with sys-
tem parameters taken as their final estimates. The cost
function values for η = 0 are J
0
= 0.1848, 0.1828, and
J
0
= 0.2998, 0.2665 for mph and nmph nominal sys-
tems, respectively. Again, some jumps of cost func-
tion are observed in adaptive case for η > 0.
The norm condition of robust stability (20), for
both mph and nmph systems with known parameters
is also illustrated in Fig.6 for η = [0,2]. It can be ob-
served that robust stability margin for nmph system is
even larger than for mph system, i.e. the value of η
at which the norm attains 1 is greater in the case of
nmph system.
The RLS algorithm was applied for parameter
identification of a considered ARX model and as al-
ready has been shown in Figures 1, 3 the estimates
converge to the true nominal values for both mph and
nmph systems.
For general ARMAX models, the recursive pseu-
dolinear regression (RPLR) or recursiveprediction er-
ror (RPEM) algorithms should be applied. The results
shown in (Nilsson and Egardt, 2010), confirm that
RPEM is then more suitable in the considered under-
modelled situation taking into account the asymptotic
properties of the algorithms.
6 CONCLUSIONS
Simple adaptive discrete-time LQG control in the
context of LTR is presented. Parameter estimation of
ARMAX model is used for tuning the discrete-time
compensator. The interplay between robustness, per-
formance and estimation convergence with respect to
the modeling error is underlined. Examples of third-
order actual systems described by a second-order mph
and nmph nominal models are taken for simulation.
Simulation results show an effectivness of the adap-
tive LQG control with possible LTR effect as a way
for robustifying the adaptive control especially for
mph systems. On the other hand, problems with dis-
continuous solution of Riccati equation may occur for
nmph systems.
REFERENCES
A. Saberi, B. C. and Sannuti, P. Theory of ltr for non-
minimum systems, recoverable target loops, and re-
covery in a subspace. Int. J. Control.
Bitmead, R., Gevers, M., and Wertz, V. (1990). Adaptive
Optimal Control. Prentice Hall International.
Duncan, T. and B.Pasik-Duncan (1999). Adaptive
continuous-time linear quadratic gaussian control.
IEEE Trans. Automat. Contr., 44(9):1653–1665.
Krolikowski, A. (1995). Amplitude constrained
adaptive LQG control of first order systems.
Int.J.Adapt.Contr.Sign.Proc., 9(3):285–299.
Kumar, P. (1983). Optimal adaptive control of linear-
quadratic-gaussian systems. SIAM J. Control and Op-
timization, 21(2):163–178.
Maciejowski, J. (1985). Asymptotic recovery for discrete-
time systems. IEEE Trans. Automat. Contr.,
30(6):602–605.
M¨akil¨a, P., Westerlund, T., and Toivonen, H. (1984). Con-
strained linear quadratic gaussian control with process
applications. Automatica, 20(1):15–29.
Nilsson, M. and Egardt, B. (2010). Comparing recursive
estimators in the presence of unmodeled dynamics. In
Proc. IFAC Symp. ALCOSP, pages 135–149, Antalya,
Turkey.
Saberi, A. and Stoorvogel, A. A. (1996). Continuity prop-
erties of solutions to h
2
and h
∞
riccati equations. Sys-
tems and Control Letters., 27(4):209–222.
Tadjine, M., M’Saad, M., and Dugard, L. (1994). Discrete-
time compensators with loop transfer recovery. IEEE
Trans. Automat. Contr., 39(6):1259–1262.
Tay, T. and Moore, J. (1989). Loop recovery via h
∞
/h
2
sensitivity recovery. Int.J.Control, 49(4):1249–1271.
Tay, T. and Moore, J. (1991). Adaptive LQG controller with
loop transfer recovery. Int.J.Adapt.Contr.Sign.Proc.,
5(2):135–149.
AdaptiveLQG/LTRControl;DiscontinuityIssue
807
