
On using Pollard’s p-1 Algorithm to Factor RPrime RSA Modulus
Maya Silvi Lydia
1
, Mohammad Andri Budiman
1
and Dian Rachmawati
1
1
Departemen Ilmu Komputer, Fakultas Ilmu Komputer dan Teknologi Informasi, Universitas Sumatera Utara, Medan,
Indonesia
Keywords: Public Key Cryptography, Cryptanalysis, Factorization, RPrime RSA, Pollard’s p-1
Abstract: RPrime RSA is a variant of RSA public key algorithm that uses the multiplication of two or more prime
numbers to construct its modulus. The larger the prime numbers are being used, the better the security of the
RPrime RSA becomes. Thus, the security of RPrime RSA depends on the hardness of factoring one big integer
into its prime factors. In this study, we attempt to factorize the modulus of RPrime RSA using a modified
version of Pollard’s p-1 algorithm, an exact algorithm used to factor an integer into its factors. The modified
version of Pollard’s p-1 algorithm makes use of Fermat’s algorithm in order to make sure that all of the factors
are primes. The results show that the correlation between RPrime RSA modulus and the factoring time is
directly proportional, but the value of RPrime RSA modulus does not always reflect the number of iterations
the Pollard’s p-1 algorithm is going through.
1 INTRODUCTION
The concept of public key cryptography (Diffie and
Hellman, 1976) was introduced in 1976 and the
Rivest-Shamir-Adleman (RSA) algorithm (Rivest,
Shamir, and Adleman, 1978) is one of the oldest
algorithms that implement the concept. Nowadays,
the use of RSA is still very popular since the RSA is
easy to implement and it can also be utilized in both
encryption scheme and digital signature scheme
(Verma, Dutta, and Vig, 2018).
The RSA has a lot of variants; one of them is the
RPrime RSA (Paixao and Filho, 2003). Both the RSA
and the RPrime RSA base their security on the
hardness of factoring a very large integer into its
prime factors. The difference is that there are exactly
two prime factors that make the modulus of the RSA;
while in the case of RPrime RSA, there can be two or
more prime factors. Therefore, it is intuitively clear
that the RPrime RSA is harder to cryptanalyze than
the original RSA.
The Pollard’s p-1factorization algorithm (Pollard,
1974) is an exact algorithm studied in the field of
number theory whose purpose is to factorize an
integer into its two factors. This algorithm makes use
of Fermat’s Little Theorem (Beatty, Barry, and
Orsini, 2018), B-smooth integers (Monaco and
Vindiola, 2017), and Euclidean GCD (Marouf, 2017)
to quicken its process. Pollard’s rho algorithm, which
is the other Pollard’s factorization algorithm, has
been known to be more efficient to factorize the RSA
modulus than random restart hill-climbing, a
metaheuristic algorithm (Budiman and Rachmawati,
2017).
In our study, we use the Pollard’s p-1 algorithm to
factor the modulus of the RPrime RSA. Factoring the
RPrime RSA modulus can be expected to be harder
and slower than factoring the RSA modulus since the
RPrime RSA modulus can have more than two prime
factors. Therefore, the Pollard’s p-1 algorithm should
be modified so it can factor a large integer into infinite
numbers of prime factors. The graphical relationships
amongst factoring time, the size of the modulus, and
the size of its prime factors will be shown as a result.
2 METHODS
In this section we give explanations about the RPrime
RSA key generation, the original Pollard’s p-1
algorithm, and the modified version of Pollard’s p-1
to factor the RPrime RSA modulus in Python
programming language. The example of each
algorithm is explained.
Lydia, M., Budiman, M. and Rachmawati, D.
On using Pollard’s p-1 Algorithm to Factor RPrime RSA Modulus.
DOI: 10.5220/0010083618951899
In Proceedings of the International Conference of Science, Technology, Engineering, Environmental and Ramification Researches (ICOSTEERR 2018) - Research in Industry 4.0, pages
1895-1899
ISBN: 978-989-758-449-7
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
1895

2.1 RPrime RSA Key Generation
As with any other public key cryptography algorithm
(Batten, 2013), the RPrime RSA has three stages: key
generation, encryption, and decryption. In this study,
the key generation of the modulus is the most
relevant, and, therefore, it is put forward as follows
(Paixao and Filho, 2003):
1. Choose k, the number of prime numbers
which will be used in forming the modulus.
2. Generate k random prime numbers, namely,
p1, p2, ..., pk, so that gcd(p1 – 1, p2 – 1, …
pk – 1) = 2.
3. Compute n = p1 × p2 × … × pk.
As an example, let us select k = 3. We then
generate 3 random prime numbers, p1 = 37, p2 = 47,
p3 = 71, and we check that gcd(37 – 1, 47 – 1) =
gcd(47 – 1, 71 – 1) = gcd(37 – 1, 71 – 1) = 2, so they
all can be used as the prime numbers for the RPrime
RSA. Lastly, we compute n = 37 × 47 × 71 = 123469.
2.2 Pollard’s p-1 Algorithm
The Pollard’s p-1 algorithm works as follows (see
Pollard (1974), Batten (2013), and Yan (2009)):
1. Get n, an odd integer to be factored.
2. Let a = 2 and i = 2.
3. Compute a = a
i
mod n.
4. Compute d = gcd(a – 1, n).
5. If 1 < d < n, then output d as a factor of n.
6. If d = 1, then i = i + 1, and go to step 3.
For example, let us factor n = 209. Let a = 2 and i
= 2. Compute a = 2
2
mod 209 = 4. Compute d = gcd(4
– 1, 209) = 1. Since d = 1, compute i = 2 + 1 = 3, and
go to step 3. Compute a = 4
3
mod 209 = 64. Compute
d = gcd(64 – 1, 209) = 1. Since d = 1, compute i = 3
+ 1 = 4, and go to step 3. Compute a = 64
4
mod 209
= 159. Compute d = gcd(159 – 1, 209) = 1. Since d =
1, compute i = 4 + 1 = 5, and go to step 3. Compute a
= 159
5
mod 159 = 144. Compute d = gcd(144 – 1,
209) = 11. Since 1 < d < 209, d = 11 is a factor of 209.
The other factor of 209 is 209/11 = 19.
2.3 A Modified Version of Pollard’s p-1
Algorithm to Factor the RPrime
RSA Modulus
The original Pollard’s p-1 algorithm can handle
factorization of an integer into its two factors. In order
to factor RPrime RSA modulus, the Pollard’s p-1
algorithm has to be modified so that it can handle
factorization of an integer into two or more factors
and it can ensure that all of these factors are primes
(by using Fermat’s algorithm to test the primality of
those factors). Our modified version of Pollard’s p-1
algorithm to factor the RPrime RSA modulus is
shown as a Python code as follows.
iterations = 1
def Pollard(n):
global iterations
a = 2
i = 2
factor = [1]
while (n % 2 == 0):
factor.append(2)
n = n // 2
while (n != 1):
print "Factoring ", n
if Fermat(n):
print n, "is already a
prime, thus it is a factor"
factor.append(n)
factor.sort()
return factor
a_old = a
a = modexp(a, i, n)
print "iterations =",
iterations
print "a =", a_old, "^", i,
"mod", n, "=", a
d = gcd(a - 1, n)
n_old = n
if 1 < d < n:
factor.append(d)
n = n // d
ICOSTEERR 2018 - International Conference of Science, Technology, Engineering, Environmental and Ramification Researches
1896

i = 1
if d == 1:
print "d = gcd(", a, "-
1,", n_old, ") =", d
else:
print "d = gcd(", a, "-
1,", n_old, ") =", d, "is a factor"
print "Now, factoring ",
n_old, "/", d, "=", n_old / d
print
iterations += 1
i += 1
The above code assumes that we have a function
gcd(m, n) to compute the greatest common divisor
of m and n, a function
modexp(a, i, n) to compute
a
i
mod n and a function Fermat(n) that returns True
if n is prime and
False if n is composite.
3 RESULTS AND DISCUSSIONS
Let us run the code to factor RPrime RSA modulus, n
= 123469 we got from Section 2.1. When the code
runs, it produces the following output.
Factoring 123469
iterations = 1
a = 2 ^ 2 mod 123469 = 4
d = gcd( 4 - 1, 123469 ) = 1
Factoring 123469
iterations = 2
a = 4 ^ 3 mod 123469 = 64
d = gcd( 64 - 1, 123469 ) = 1
Factoring 123469
iterations = 3
a = 64 ^ 4 mod 123469 = 108901
d = gcd( 108901 - 1, 123469 ) = 1
Factoring 123469
iterations = 4
a = 108901 ^ 5 mod 123469 = 32697
d = gcd( 32697 - 1, 123469 ) = 1
Factoring 123469
iterations = 5
a = 32697 ^ 6 mod 123469 = 41441
d = gcd( 41441 - 1, 123469 ) = 37 is
a factor
Now, factoring 123469 / 37 = 3337
Factoring 3337
iterations = 6
a = 41441 ^ 2 mod 3337 = 2801
d = gcd( 2801 - 1, 3337 ) = 1
Factoring 3337
iterations = 7
a = 2801 ^ 3 mod 3337 = 1883
d = gcd( 1883 - 1, 3337 ) = 1
Factoring 3337
iterations = 8
a = 1883 ^ 4 mod 3337 = 1820
d = gcd( 1820 - 1, 3337 ) = 1
Factoring 3337
iterations = 9
a = 1820 ^ 5 mod 3337 = 900
d = gcd( 900 - 1, 3337 ) = 1
Factoring 3337
On using Pollard’s p-1 Algorithm to Factor RPrime RSA Modulus
1897
iterations = 10
a = 900 ^ 6 mod 3337 = 2593
d = gcd( 2593 - 1, 3337 ) = 1
Factoring 3337
iterations = 11
a = 2593 ^ 7 mod 3337 = 1563
d = gcd( 1563 - 1, 3337 ) = 71 is a
factor
Now, factoring 3337 / 71 = 47
Factoring 47
47 is already a prime, thus it is a
factor
Thus, our code shows that the factors of RPrime
RSA modulus n = 123469 are 37, 47, and 71, and
these are the prime numbers we have generated in
Section 2.1.
The code is then tested with RPrime RSA moduli
of different sizes. The result is pictured in Table 1 and
Table 2.
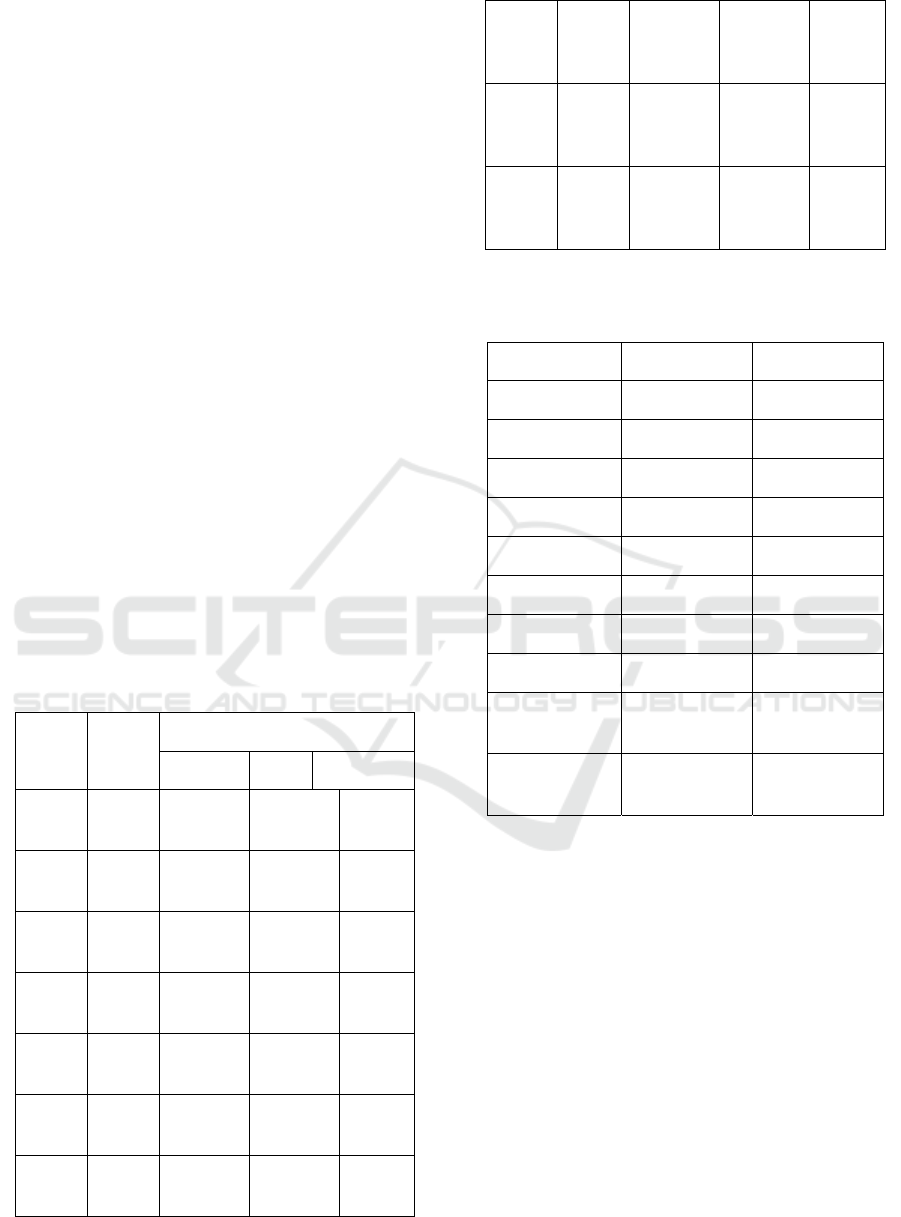
Table 1: Factoring different RPrime RSA modulus n with
modified version of Pollard’s p-1 algorithm into p1, p2, p3
n digit factors
p1 p2 p3
604
21 5 23 37 71
251
905 6 5 83 607
482
353 6 19 53 479
353
1581 7 23 233 659
194
585749 9 563 577 599
229
858861 9 499 557 827
539
715601 9 547 653
151
1
309
1706464
9 11 1471 2393
878
3
841
4353423
21699 15 92251 94847
961
67
152
0587019
820740 16 47303 49811
645
353
Table 2: Iterations and time to factor different RPrime RSA
modulus
n time (seconds) iterations
60421 0.125804186 11
251905 0.452283144 43
482353 0.197597027 17
3531581 0.474875927 38
194585749 0.315865994 27
229858861 1.497702837 140
539715601 1.726655006 162
30917064649 0.375844002 35
841435342321
699 12.35400701 1048
152058701982
0740 7.281822205 644
In Table 1, it is shown that the various sizes of n
have been successfully factorized into p1, p2, and p3
which are the RPrime RSA prime numbers. One may
check that n = p1× p2 × p3 for every n shown in that
table. The trend shown in Table 2 shows that while it
is intuitively true that the larger the value of the
RPrime RSA modulus, the longer it takes time to
factorize it, sometimes irregularities do happen. One
example of the irregularities is that factoring n =
539715601 (9 digits) takes 1.726655006 seconds,
while factoring n = 30917064649 (11 digits) takes
0.375844002 seconds. This irregularity is due to the
fact that factoring n = 539715601 takes 162 iterations,
while factoring n = 30917064649 only takes 35
iterations. The number of iterations depends on the
relationship amongst the prime numbers that form the
RPrime RSA modulus.
ICOSTEERR 2018 - International Conference of Science, Technology, Engineering, Environmental and Ramification Researches
1898

4 CONCLUSIONS
The conclusions of our study are as follows. First, the
modified version of Pollard’s p-1 algorithm which
makes use of Fermat’s algorithm is able to factor
RPrime RSA modulus into its all its prime factors.
Second, the correlation between RPrime RSA
modulus and the time to factor it with Pollard’s p-1
tends to be directly proportional. Third, the value of
RPrime RSA modulus does not always reflect the
number of iterations the Pollard’s p-1 algorithm is
going through.
ACKNOWLEDGEMENTS
We gratefully acknowledge that this research is
funded by Kemenristekdikti Republik Indonesia via
Lembaga Penelitian Universitas Sumatera Utara. The
support is under the research grant DRPM
Kemenristekdikti of Year 2018 Contract Number:
59/UN5.2.3.1/PPM/KP-DRPM/2018.
REFERENCES
Batten L M 2013 Public key cryptography applications and
attacks (Hoboken, N.J: Wiley-Blackwell)
Beatty T, Barry M and Orsini A 2018 A Geometric Proof
of Fermat’s Little Theorem Advances in Pure
Mathematics 08 41–4
Budiman M A and Rachmawati D 2017 On factoring RSA
modulus using random-restart hill-climbing algorithm
and Pollard’s rho algorithm Journal of Physics:
Conference Series 943 012057
Diffie W and Hellman M 1976 New directions in
cryptography IEEE Transactions on Information
Theory 22 6 pp 644-654
Marouf I 2017 Reviewing and Analyzing Efficient
GCD/LCM Algorithms for Cryptographic Design
International Journal of New Computer Architectures
and their Applications 7 1–7
Monaco J V and Vindiola M M 2017 Integer factorization
with a neuromorphic sieve 2017 IEEE International
Symposium on Circuits and Systems (ISCAS)
Paixao C A M and Filho D L G 2003 An efficient variant
of the RSA cryptosystem IACR Cryptology ePrint
Archive
Pollard J M 1974 Theorems on factorization and primality
testing Mathematical Proceedings of the Cambridge
Philosophical Society 76 521
Rivest R L, Shamir A and Adleman L 1978 A method for
obtaining digital signatures and public-key
cryptosystems Communications of the ACM 21 2 pp
120-126
Verma R, Dutta M and Vig R 2018 RSA Cryptosystem
Based on Early Word Based Montgomery Modular
Multiplication Services – SERVICES 2018 Lecture
Notes in Computer Science 33–47
Yan S Y 2009 Primality testing and integer factorization in
public-key cryptography (Boston: Springer)
On using Pollard’s p-1 Algorithm to Factor RPrime RSA Modulus
1899
