A Search Space Strategy for Pedestrian Detection and Localization in
World Coordinates
Mikael Nilsson
1
, Martin Ahrnbom
1
, H˚akan Ard¨o
1
and Aliaksei Laureshyn
2
1
Centre of Mathematical Sciences, Lund University, Lund, Sweden
2
Traffic and Roads, Department of Technology and Society, Lund University, Lund, Sweden
Keywords:
Pedestrian, Detection, World Coordinates, Machine Learning, Camera Cali bration.
Abstract:
The focus of this work is detecting pedestrians, captured in a surveillance setting, and locating them in world
coordinates. Commonly adopted search strategies operate in the image plane to address the object detection
problem with machine learning, for example using scale-space pyramid with the sliding windows methodo-
logy or object proposals. In contrast, here a new search space i s presented, which exploits camera calibration
information and geometric priors. The proposed search strategy will facilitate detectors to directly estimate
pedestrian presence in world coordinates of interest. Results are demonstrated on real world outdoor collected
data along a path in dim light conditions, with the goal to locate pedestrians in world coordinates. The pro-
posed search strategy indicate a mean error under 20 cm, while image plane search methods, with additional
processing adopted for l ocalization, yielded around or above 30 cm in mean localization error. This while only
observing 3-4% of patches required by the image plane searches at the same task.
1 INTRODUCTION
Extracting relevant information from images is a key
goal in many camera based applications. For exam-
ple, pedestrian detection is o ne important and well-
studied area of research (Doll´ar et al., 2012). Despite
the extensive research on pedestrian detection, recent
papers still show significant improvements, sugges-
ting that a saturation point has not yet been reached
(Doll´ar et al., 2014; Zhang et al., 2016b; Zha ng et al.,
2016a ). T hese methods typically adopt a scale-space
pyramid with sliding windows search or are combi-
ned with object proposal methods (Cheng et al., 2014;
Zitnick and Doll´ar, 2014; van de Sande et al., 2011).
However, this endeavor of detecting pedestrians is
mainly focused on an imag e as the only input, and
output as coordinates in the image plane.
Research has been conducted that focused on fin-
ding world information as a post-processing step fol-
lowing image plane d etection (A ndriluka et al., 2010;
Xiang et al., 2014; Choy et al., 2015). While other
works have exploited more explicit world, or three di-
mensional, reasoning, but only as a means of speeding
up im a ge plane search (Sudowe and Leibe, 2011; Be-
nenson et al., 2012). Note that these me thods a ll uti-
lize an image plane search as a basis.
Other methods have exploited a mo re explicit
use of 3D information for detection. For example,
by prior camera calibration and geometric priors in
sports tracking (Carr et al., 2012) and car detection
(Nilsson and Ard¨o, 2014). However, those approa-
ches make use of foregroun d/background segmenta-
tion rather than utilizing machine learning.
A key observation here is that there is a gap be-
tween exploiting directly available 3D information
and machine learning, where state-of-the-art detec-
tors work only in the image plane. In this paper, a
core insight is that, with addition al camera calibration
informa tion and geometric priors, one can prod uce a
new search strategy, suitable for machine learning, to
directly address the 3D localization pro blem. Thus
what is proposed can be seen as a “glue” that ties 3D
informa tion together with patch based mach ine lear-
ning tools. Or, to put this in another light, what is pro-
posed can be viewed as a specialized object proposal
method re sulting in rotated rectangles. Note though,
that the “proposal part” here is directly formed using
camera calibration, geometric priors and a world sam-
pling grid. Furthermore, each object proposed h a s a
correspo nding world co ordinate location.
The paper is organized as follows. The following
section presents th e real-world collected data and c a -
libration used for evaluations. Section 3 presents how
the framework proposed is formed from the image,
Nilsson, M., Ahrnbom, M., Ardö, H. and Laureshyn, A.
A Search Space Strategy for Pedestrian Detection and Localization in World Coordinates.
DOI: 10.5220/0006511800170024
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages
17-24
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17

camera calibration and geometric prior to a search
strategy resulting in patc hes that can be f ed to a ma-
chine lea rning fra mework. Section 4 p resents the ma-
chine learning used in the paper. Section 5 presents
experiments comparing ima ge plane search methodo-
logies to the one proposed. Finally, conclusions are
made in Section 6.
2 DATA COLLECTION AND
CAMERA CALIBRATION
In an outdoor setup, using an Axis F41 camera with a
F1015 lens mounted on top of a lamppo st, pedestrians
can be viewed on a piece of a pa th approximatively
four meters wide.
A requirement for the proposed methodology is
the existence of a calibrated camera. Note that the
focus of this paper is not that of the camera cali-
bration, it is on the design of search space utilizing
a calibrated camera that can be f eed to a patch ba-
sed machine learning system. Due to the availability
of a h igh precision GPS, a Leic a GX1230 GG, the
fixed camera could be calibrated with goo d re sults
by marking twelve world reference positions, mar-
ked by spraying the ground at positions on the side of
the path and measuring the world coordinates a t each
point. The points were then m anually positioned in
the camera image, see Fig. 1. Camera calibration was
then performed using Tsai calibration (Tsai, 1987).
In a general description, let Θ denote all the Tsai
calibration parameters, then a world point p
world
=
[x
w
,y
w
,z
w
]
T
can be projected as
p
image
= f (p
world
,Θ) (1)
where f is a vector valued function involving all the
world to image point operations in the Tsai method
(Tsai, 1987) and p
image
= [x,y]
T
is the resulting image
point. Furthermore, if N points are stacked into a ma-
trix P of size 3 × N then the ope ration f (P,Θ) is one
world to image mapping per column in P and the out-
put a matrix of size 2 × N.
A dataset composed of ten im ages fo r each of
twelve persons when passing the camera results in
120 images. Each ped e stria n had their feet location
Figure 1: World position of camera (white), field of view
(red) and calibration points (yellow) sprayed on the ground
and measured with high precision GPS.
annotated in world coordinates in each im age. These
will b e explored for exper imentation o f pedestrian lo-
calization in world coordinates. Note that the vie-
wpoint here is from a higher angle than usually ap-
pear in existing databases such as Caltech pedestrians
(Doll´ar et al., 2009; Doll´ar et al., 20 12) and INRIA
pedestrians (Dala l a nd Triggs, 2005), where an eye le-
vel camera is typically applied, see examples in Fig. 2.
Figure 2: Examples of pedestrians from the outdoor scene.
3 IMAGE SEARCH STRATEGY
AROUND 3D MODELS
The p roposed searc h strategy works by transf orming
3D models, here a 3D box, in the world to a sam-
pling grid in the image plane. This samplin g grid in
the image is a rotated rectangle since camera rotation,
roll in particular, as well as le ns distortio ns produce
tilted pedestrians, making an axis a ligned rectangle
less suitable. Furthermore, note that the method pre-
sented here can, in prin c iple, be utilized w ith any 3D
model in general. A general overview of the process
for a given world point can be found in Fig. 3 and a
specific example can be found in Fig. 4. The specifics
for each step will follow.
With p rior knowledge one can consider th e pre-
sence of a pedestrian on several world coordinates of
interest, as we will see later, a grid on the path f or ex-
ample, see Fig.6a. As will be seen later, such a grid,
which utilize prior knowledge and a camera calibra-
tion, can produce far fewer patches to explore compa-
red to a brute force image plane search. What follows
is the proposed processing pipeline to get a classifier
score from one such world point.
Given world coordinates for the feet of a pede-
strian, a box is calculated around it. In general, a box
of size width × depth × height is used to capture pe-
destrians in the world coordinate system. In this p aper
a standard box is considered to be 0.5 × 0.5 × 1.8
meters. However, due to taller persons, and the
desire to captur e some context, an e nlarged box of
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
18

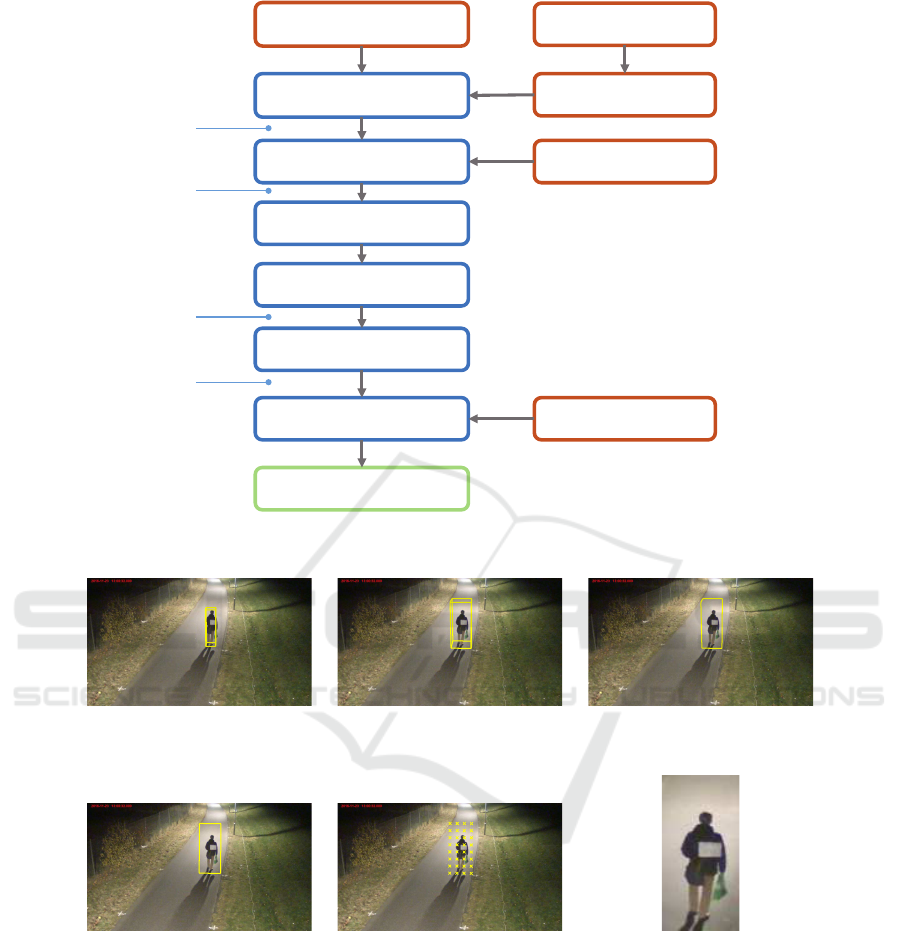
Point in 3D to evaluate object
presence
3D point to box (model) in 3D
Vetrices from 3D model mapped to
image points
Camera calibration
Convex Hull of image points
Rotating caliper to get rotated
rectangle and ordering of points
Image
Sample points for patch from rotated
rectangle
Patch creation using sample grid and
image
Patch for classification, standard box
as output if positive
Standard Box in 3D
Enlarged Box in 3D
P
Q
R
S
Figure 3: Principle for getting a rotated rectangle given a 3D point, an image, the camera calibration and a 3D shape.
(a) Standard box, 0.5 × 0.5 ×
1.8 meter.
(b) Enlarged box, 1.0 × 1.0 ×
2.2 meter.
(c) Convex hull of points map-
ped to image plane.
(d) Minimum rotate rectangle
around the points.
(e) Sampling or rotated rec-
tangle. Sampled with 64 × 128
points, here shown as 4 × 8 for
clarity.
(f) Patch
sampled
on a
64 × 128
grid.
Figure 4: Steps a) to f) for creation of patches from a world coordinate box.
size 1.0 × 1.0 × 2.2 me te rs is employed . Thus, if a
detection is found from the larger box, then the stan-
dard one is considered as the output detection box,
see Fig. 4a and Fig. 4b for the different boxes. More
formally, le t W, D and H denote width, depth and
height of the enlarged box, respectively. Then a ma-
trix containing eight vertices, on e at eac h column, of
the box can be foun d as
A Search Space Strategy for Pedestrian Detection and Localization in World Coordinates
19

P =


x
w
−
W
2
x
w
−
W
2
x
w
+
W H
2
x
w
+
W
2
x
w
−
W
2
x
w
−
W
2
x
w
+
W
2
x
w
+
W
2
y
w
−
D
2
y
w
+
D
2
y
w
−
D
2
y
w
+
D
2
y
w
−
D
2
y
w
+
D
2
y
w
−
D
2
y
w
+
D
2
z
w
z
w
z
w
z
w
z
w
+ H z
w
+ H z
w
+ H z
w
+ H


. (2)
The next step involves finding the corresponding
vertices in the image plan e . Let
Q = f (P,Θ) (3)
contain the eight poin ts in th e image plane. These
points are now the main input towards finding a ro -
tated rectangle in the image plane. The way this ro-
tated rectangle is formed involves finding the mini-
mum rotated rectangle enclosing all the points. This
is achieved by first finding the convex h ull and then
finding the smallest-are a enclosin g rectangle of a po-
lygon that has a side collinear with one of the edges
of this c onvex hull. This method ology is known as
the ro ta ting calipers algorithm (Fr e eman and Shapira,
1975; Toussaint, 1983). See an example of finding the
convex hull from Q in Fig. 4c and from the convex
hull finding the minimum rota te d rectangle in Fig. 4d.
The output from the r otating calipers algorithm is four
image points. To keep the order o f these points in a
consistent manner, they are ordered following the pro-
cedure outlined in Algorithm. 1. Th is process enfor-
ces a top-left, top-right, bottom-left and bottom-right
ordering of the points. Note that the points of the ro-
tated r e ctangle can be outside the image at times, ex-
amples of this can be seen in Fig. 5b. The result, in
Algorithm 1: Order selection.
Input: A set of four image points. W
image
and H
image
being the width and height of the image, respecti-
vely.
Output: Four ordered i ma ge points
1: select point one as the one with minimum Eucli-
dian distance to the point [−W
image
,−H
image
]
T
from
the four points, remove this point from the set
2: select point two as the one with minimum Eucli-
dian distance to the point [2W
image
,−H
image
]
T
from
the three remaining points, r e move this point from
the set
3: select point three as the one with minimum Eucli-
dian distance to the point [−W
image
,2H
image
]
T
from
the two remaining points, remove this point from
the set
4: select the last point as the one left in the set
form of four ordered points, are stored in colum ns of
a matrix
R =

p
1
p
2
p
3
p
4

=

x
1
x
2
x
3
x
4
y
1
y
2
y
3
y
4

.
(4)
The next step involves prod ucing a sam pling grid
matching a desired patch size. The four points in R,
and a given patch size f ormed by S
width
and S
height
,
are now used to produce a samp ling gr id in the im age
plane. This sampling grid is stored in matrix
S =

s
1
s
2
s
3
.. . s
S
width
·S
height

(5)
of size 2 ×S
width
·S
height
and the construction of it can
be found in Algorithm. 2.
Algorithm 2: Sampling rotated rectangle.
Input: p
1
, p
2
, p
3
and p
4
are the ordered points, see
Eq. (4). Chosen S
wid th
and S
height
being the desired
width and height of the patc h, respectively.
Output: The matrix S containing S
wid th
· S
height
sam-
pling points in the image, see Eq. (5)
1: k = 0
2: C = (S
wid th
− 1) (S
height
− 1)
3: for i = 1,2,.. . ,S
height
do
4: for j = 1,2,. .. ,S
wid th
do
5: k = k +1
6: w
1
= (S
height
− i) (S
wid th
− j)/C
7: w
2
= (S
height
− i) ( j −1)/C
8: w
3
= (i − 1)(S
wid th
− j)/C
9: w
4
= (i − 1)( j − 1)/C
10: s
k
= w
1
p
1
+ w
2
p
2
+ w
3
p
3
+ w
4
p
4
11: end for
12: end for
Finally, the patch for classification is formed using
the sampling points S. Examp le of a resulting patch
can be found in Fig. 4f.
In the im age view, boxes mapped from the world
may become too small or heavily cropped at image
borders to be useful. For this reason, three thresholds
are enforced allowing a rotated rectangle to be used
for processing only if it passes all three. The first and
second threshold are on the width and height in pixels
of the rotated rectangle, θ
width
and θ
height
, respecti-
vely. Anoth er feature to threshold is the ratio of the
sample points inside the image, denoted θ
ratio
. Choi-
ces of thresholds used in the paper can be found in
Table. 1. Examples of reje cted boxes can be found in
Fig. 5b.
4 CLASSIFICATION OF PATCH
FROM ROTATED RECTANGLE
Given the po ssibility to produce patches from a gi-
ven world position described in th e previous section,
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
20

it is now possible for pro duce training and test data for
machine learning tools. In the dataset collected there
are twelve unique individuals, each contributing with
ten samples resulting in 120 tagged samples. Each
sample conta ins o nly one single pedestrian in a given
frame. Since only one ped estrian is visible in a gi-
ven scene, both positive and negatives samples can b e
created with the following process: around the po int,
eight samples for the radii 5 c m and 10 cm, are col-
lected, resulting in 17 positive patches for one tag -
ging. For an initial negative sample set the radius of
40, 80 and 120 centimeters are used to collect eight
samples for each, resulting in 24 negative patch sam-
ples. Hence, with this type of jittering one get 17 po-
sitive and 24 negative samples per annotated frame.
The negative set will later be b ootstrapped on images
containing no pedestrians. All patches created here
from a point in world coordinates are of size 64 × 128
from the gr id in the rotated rectangle following propo-
sed procedure, see Fig. 3 and Fig. 4. Note that there
might be negative samples containing pedestrians to
some degree using this approach, but those are not
properly positioned to yield a go od world localiza-
tion, see Fig. 5a.
This collection of p atches, as de scribed above, can
now be fed to basically any machine learning tool at
one’s disp osal. For example, HOG-SVM (Dalal and
Triggs, 2005), ACF (Doll´ar e t al., 2014), HSC (Ren
and Ramanan, 2013), Roerei (Benenson et al., 2013),
VGG-16 (Simonyan and Zisserman, 2014) and vari-
ous others (Zhang et al., 2016b). Note that the focus
of this paper is not that of the the specific machine le-
arning tools used, it is o n the design of search space
utilizing a calibrated c amera that can be feed to a pa-
tch based machine learnin g system. Thus, while in-
teresting, it is out of the scope of this paper to ex-
plore various meth ods for this task. Rath e r, the aim is
to indicate the usefulness of the search strategy pro-
posed. For this reason, a single method, inspired by
HSC (Ren and Ramanan, 2013), employing a sparse
coding and logistic regression framework is adop-
ted. In par ticular, a sparse cod ing, with ability to in-
corporate su pervised infor mation ( N ilsson, 2016), is
used to build a discriminative dictionary from all non-
overlapping 8 × 8 patche s from all samples. This was
done by forming a discriminate matrix with K = 32
atoms, where eight atoms was allocate d for positive,
16 for negative and eight as a do-not-care region. For
more in-depth details on this discriminative dictionary
learning, the read e r is referred to the work by Nilsson
(Nilsson, 2016). Then, u sing this dictio nary, codes
are extracted from all training samples and feed to lo-
gistic regression with elastic net regularization (Nils-
son, 2014).
In this setup a twelve-fold cross validation is used,
implying that all samples from one person is lef t out
in training and evaluated in a full search. During de-
tection this full search is composed of a samplin g grid
produced with ten centimeter distances between the
points on the path of interest, this resultin g in 7047
patches to evaluate after rejecting rotated rectangles
with θ
width
= 32, θ
height
= 64 and θ
ratio
= 0.9. Ex-
amples of rejected boxes with these thresholds can be
found in Fig. 5b.
In image p la ne searches the I ntersection over
Union (IoU) is a c ommonly adop ted measure in a
Non-Maximum Suppression (NMS) method to prune
detections. The results produced here can utilize the
classifier scores on the grid in world coordinate s, and
could benefit from this knowledge. Hence, a World
NMS (WNMS) is introduced instead. This WNMS
is using Euclidian distance betwee n points, in meters,
and a thr eshold on this distance as a measur e to decide
overlap. In general, this WNMS have three parame-
ters γ
det
, γ
radius
and γ
count
where γ
det
is the classifier
threshold for detection, γ
radius
the radius in meters to
define overlap and γ
count
is the number of detections
that are pruned into the maximum one. In all exam-
ples in this paper γ
det
= 0.5 ( on the logistic regres-
sion o utput), γ
radius
= 0 .5 and γ
count
= 3. An exam-
ple of detection scores and the final WNMS output vs
ground truth can be foun d in Fig. 6.
5 EXPERIMENTS
The experiments focus on investigating the world lo-
calization of pedestrians. First, baselines are formed
by utilizing ima ge plane searches. The goal is to see
how far one can come by first running an image plane
detector and then, as a second step, aim to find the
world coordinates. Then the proposed sampling stra-
tegy is investigated. Finally, a comparison between
the baselines and the proposed method is performed.
The core parameters introduced thro ughout the
paper has been stated and described previously. A
summary of them can be fou nd in Table. 1, th ese va-
lues are used throughout the paper.
5.1 Image Plane Localization Baselines
5.1.1 Image Plane Detection
As a first step, an image plane scanning is perfor-
med. Three different methods are adopted as baseli-
nes. First, the same sparse coding a nd logistic regres-
sion framework, using twelve-fold cross validation,
adopted for the proposed methods is u sed here. The
A Search Space Strategy for Pedestrian Detection and Localization in World Coordinates
21

(a) One positive sample out of the 17 shown as red, and eight
negative out of the 24 shown as yellow. Note that some ne-
gatives contain the pedestrian but are not aligned for proper
localization.
(b) Examples of ignored boxes due to thresholds.
Figure 5: Positive and negative samples and examples of i gnored boxes.
(a) Sampling grid and classifier scores. Yellow indicates low
scores and red high scores.
(b) Final detection after WNMS.
Figure 6: From scores on the grid in the ground-plane to detction box aft er WNMS.
Table 1: Parameter choices.
parameter
S
width
S
height
θ
width
θ
height
θ
ratio
γ
det
γ
radius
γ
count
value 64 128 32 64 0.9 0.5 0.5 3
difference is th a t axis aligned patches, formed from
the same poin ts th at were used for rotated boxes in the
proposed method, are used for training and a scale-
space and sliding window search is adopted instead.
This method used scaling 1.25 in the scale space and
jumped three pixels, resulting in 187769 patches to
eva luate. This method is d enoted SCLR2D and resul-
ted in 112 true positives and 30 false positives on the
120 images. A true positive was indicated if the Inter-
section over Union (IoU) with a ground truth boun-
ding box was over 0.65.
In addition, the Aggregated Channel Features
(ACF) method (Doll´ar et al., 2014) is employed on the
120 images contain ing one pedestrian each. Using an
ACF detector trained on the INRIA database (Dalal
and Triggs, 2005) resulted in 113 true positives and
64 false positives. The ACF, trained on the Caltech
dataset (Do ll´ar et al., 2009; Do ll´ar e t al., 2012), resul-
ted in 97 true positives and ten false positives.
5.1.2 Image Plane Detection Box to World
Coordinates
Note that the goal here is to do localization in world
coordinates using the calibration. Theref ore, conver-
sion from the image plane detectio n box to world
coordinates is required as a secon d step for image
plane searches. A method positioning a fixed point
in a norma lize d box in the image p lane (width an d
height equal to one and top left position at (0, 0))
was employed. For a given bounding box this fixed
point, in nor malized coordinates, is then mapped back
to the detected bounding box, resultin g in a point in
the image. This point is then transformed to world
coordinates at the ground plane using the camera cali-
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
22

0
0.5
1
1.5
2
proposed ACF Caltech ACF INRIA SCLR2D
Localization Error in Meters [m]
(a) Box-Whisker plots of the localization errors.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6
0
0.5
1
1.5
2
2.5
3
3.5
4
Localization Error in Meters [m]
Estimated pdf [%]
proposed
ACF Caltech
ACF INRIA
SCLR2D
(b) Parzen window density estimation of localization er-
rors with bandwidth of 0.05.
Figure 7: Evaluation metrics on localization. B est viewed in color.
bration. In order to decide this fixed point in the n or-
malized box, an optimization finding the be st mean
localization error in the world from all the detections
was performed. Note that th is is a optimistic loca-
lization done here, sin ce the p oint in the normalized
box is found on the same boxes as it is evaluated on.
Nevertheless, this resulted in world localization errors
for the ACF INRIA, ACF Caltech detector and locali-
zation baselines.
5.2 Direct Localization using Sampling
Strategy
Here the world localization employing th e propo -
sed search strategy is employed. Hence, a resulting
hypothesis for each of the points in a sam pled grid,
with ten centimeter distances, in the world coordi-
nates are produced and detections follows the World
NMS (WNMS), see Fig. 6. This detector resulted in
103 true positives and 11 false p ositives. A positive
was con sidered to be a detection point located within
a radius of two meters from the manual annotation.
This choice of 2 m was to match some of the errors re-
ceived using the baselines with an IoU choice of 0.65
in the image plane as detection choice, and co uld in
practice been lower. M ore importa ntly, this localiza-
tion was achieved by exploring only 7047 patches due
to the exploitation of the camera calibration an d p rior
knowledge. This to compare to 312977 patches ex-
plored by the ACF methods and 187769 patc hes by
SCLR2D using only the image.
5.3 Comparisions
A set of 74 detections, those detections that all were
detected by all three me thods, were used for localiza-
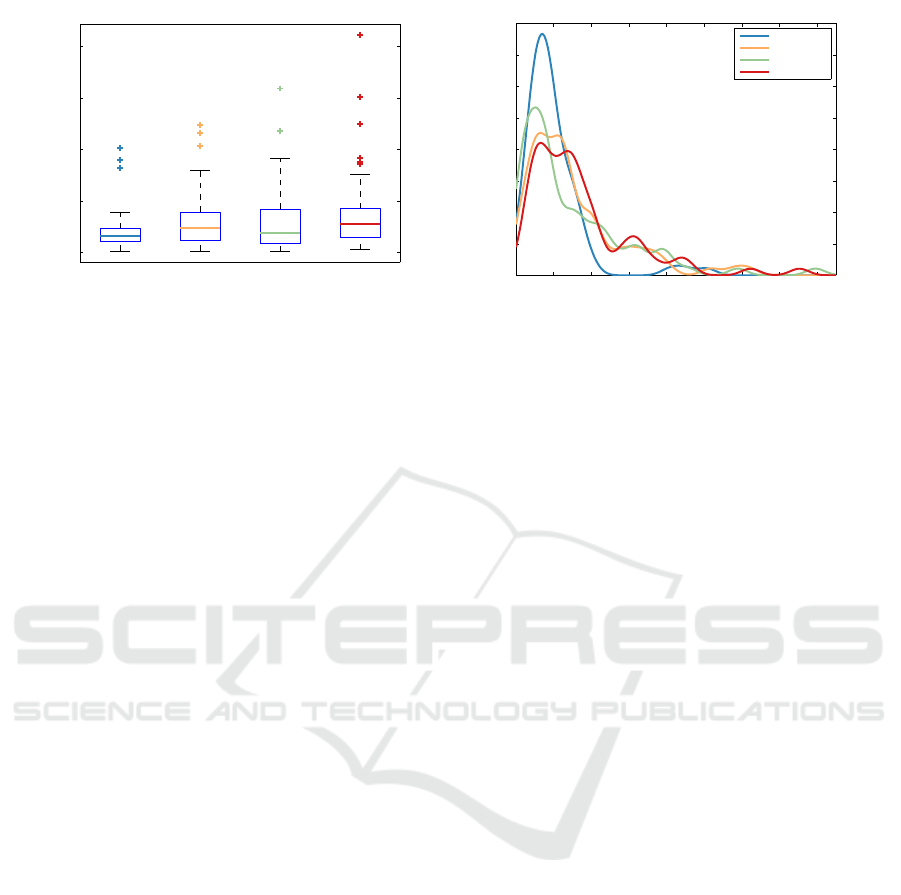
tion evaluation. The results gave mean error of 19.9
cm for the proposed method, 30.5 cm f or ACF trained
on Caltech, 29 .4 cm for ACF trained on INRIA and
36.3 cm for SCLR2D. For a more detailed study of
the statistics of the errors in meter s, the Box-Whisker
plot (Tukey, 1977) and density estima tion using a Par-
zen window (Parzen, 1962) can be found in Fig. 7a
and Fig. 7b, respectively. Note that the method pro-
posed has far fewer ou tliers, in form of errors over 0.5
m. The main takeaways fr om these experiments and
the proposed search space a re:
• With a given cam e ra calibration, it is possible to
design a search space with no n e ed for additional
processing for world localization.
• The number of patches needed to be explor ed can
be far fewer compared to image plane search.
• The localization accuracy can actually benefit in
the proc ess.
6 CONCLUSIONS
A search strategy producing a rotated rectangle fr om
a camera calibration a nd prior 3D shape has been pro-
posed and investigated. By explo iting camera calibra-
tion infor mation it has been shown that the sampling
method c an be used to facilitate machine learning that
can directly produce classification scores in world lo -
cations of interest. This approach le a d to accurate lo-
calization of pedestrians in world c oordina te s with a
mean error of 19.9 cm, while three image plane de -
tectors, adopte d for the localization task, resulted in
mean errors of 29.4 cm, 30.5 cm and 36.3 cm. This
while only o bserving less than 3-4% of patches nee-
ded in the image plane search. Future work involves
exploring the methodology proposed on more views,
more crowded scenarios, investigating various other
A Search Space Strategy for Pedestrian Detection and Localization in World Coordinates
23

machine learning methods for the task and applying
the method on other objects.
REFERENCES
Andriluka, M., Roth, S., and Schiele, B. (2010). Monocular
3d pose estimation and tracking by detection. In 2010
IEEE Computer Society Conference on Computer Vi-
sion and Pattern Recognition, pages 623–630.
Benenson, R., Mathias, M., Timofte, R., and Van Gool, L.
(2012). Fast stixels estimation for fast pedestrian de-
tection. In ECC V, CVVT workshop.
Benenson, R., Mathias, M., Tuytelaars, T., and Gool, L. V.
(2013). Seeking the strongest rigid detector. In 2013
IEEE Conference on Computer Vision and Pattern Re-
cognition, pages 3666–3673.
Carr, P., Sheikh, Y., and Matthews, I. (2012). Monocular ob-
ject detection using 3d geometric primitives. In Pro-
ceedings of the 12th European Conference on Compu-
ter Vision - Volume Part I, ECCV’12, pages 864–878,
Berlin, Heidelberg. S pringer-Verlag.
Cheng, M. M., Z hang, Z., Lin, W. Y., and Torr, P. (2014).
Bing: Binarized normed gradients for objectness esti-
mation at 300fps. In 2014 IEEE Conference on Com-
puter Vision and Pattern Recognition, pages 3286–
3293.
Choy, C. B. , Stark, M., Corbett-Davies, S., and Savarese, S.
(2015). Enriching object detection with 2d-3d regis-
tration and continuous viewpoint estimation. In 2015
IEEE Conference on Computer Vision and Pattern Re-
cognition (CVPR), pages 2512–2520.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. I n 2005 IEEE Compu-
ter Society Conference on Computer Vision and Pat-
tern Recognition (CVPR’05), volume 1, pages 886–
893 vol. 1.
Doll´ar, P., Wojek, C., Schiele, B., and Perona, P. (2009).
Pedestrian detection: A benchmark. In CVPR.
Doll´ar, P., Wojek, C., Schiele, B., and Perona, P. (2012).
Pedestrian detection: An evaluation of the state of the
art. PAMI, 34.
Doll´ar, P., Appel, R., Belongie, S., and Perona, P. (2014).
Fast feature pyramids f or object detection. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 36(8):1532–1545.
Freeman, H. and Shapira, R. (1975). Determining the
minimum-area encasing rectangle for an arbitrary clo-
sed curve. Commun. ACM, 18(7):409–413.
Nilsson, M. (2014). Elastic net regularized logistic regres-
sion using cubic majorization. In Proceedings of the
IEEE International Conference on Pattern Recogni-
tion (ICPR), pages 3446–3451.
Nilsson, M. (2016). Sparse coding with unity range co-
des and label consistent discriminative dictionary lear-
ning. In Proceedings of the IEEE International Con-
ference on Pattern Recognition (ICPR).
Nilsson, M. and Ard¨o, H. (2014). In search of a car uti-
lizing a 3d model with context for object detection.
In The International Conference on Computer Vision
Theory and Applications (VISAPP), volume 2, pages
419–424.
Parzen, E. (1962). On estimation of a probability density
function and mode. Ann. Math. Statist., 33(3):1065–
1076.
Ren, X. and Ramanan, D. (2013). Histograms of sparse
codes for object detection. In 2013 IEEE Conference
on Computer Vision and Pattern Recognition, pages
3246–3253.
Simonyan, K. and Zisserman, A. (2014). Very deep con-
volutional networks for large-scale image recognition.
CoRR, abs/1409.1556.
Sudowe, P. and Leibe, B. (2011). Efficient Use of Geome-
tric Constraints for Sliding-Window Object Detection
in Video. In International Conference on Computer
Vision Systems (ICVS’11).
Toussaint, G. ( 1983). Solving geometric problems with the
rotating calipers. I n Proc. IEEE MELECON ’83, pa-
ges 10—02.
Tsai, R. Y. (1987). A versatile camera calibration technique
for high-accuracy 3d machine vision metrology using
off-the-shelf TV cameras and lenses. IEEE J. Robotics
and Automation, 3(4):323–344.
Tukey, J. (1977). Exploratory Data Analysis. Behavioral
Science: Quantitative Methods. Addison-Wesley, Re-
ading, Mass.
van de Sande, K. E. A., Uijlings, J., Gevers, T., and Smeul-
ders, A. (2011). Segmentation as Selective S earch for
Object Recognition. In ICCV.
Xiang, Y., Mottaghi, R., and Savarese, S. (2014). Beyond
pascal: A benchmark for 3d object detection in the
wild. In IEE E Winter Conference on Applications of
Computer Vision (WACV).
Zhang, L., Lin, L., Liang, X., and He, K. (2016a). Is Faster
R-CNN Doing Well for Pedestrian Detection?, pages
443–457. Springer International Publishing, Cham.
Zhang, S., B enenson, R., Omran, M., Hosang, J., and
Schiele, B. (2016b). How far are we from solving
pedestrian detection? In CVPR.
Zitnick, C. L. and Doll´ar, P. (2014). Edge Boxes: Locating
Object Proposals from Edges, pages 391–405. Sprin-
ger International Publishing, Cham.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
24