Effects of Age, BMI, Anxiety and Stress on the Parameters of a Stochastic
Model for Heart Rate Variability Including Respiratory Information
Rachele Anderson
1
, Peter J
¨
onsson
2
and Maria Sandsten
1
1
Mathematical Statistics, Centre for Mathematical Sciences, Lund University, Sweden
2
School of Education and Environment, Centre for Psychology, Kristianstad University, Sweden
Keywords:
HRV, Chirp Respiratory Frequency, Locally Stationary Chirp Processes, Time-varying Signals, Time-series
Modelling, Linear and Logistic Regression.
Abstract:
Recent studies have focused on investigating different factors that may affect heart rate variability (HRV),
pointing especially to the effects of age, gender and stress level. Other findings raise the importance of consid-
ering the respiratory frequency in the analysis of HRV signals. In this study, we evaluate the effect of several
covariates on the parameters of a stochastic model for HRV. The data was recorded from 47 test participants,
whose breathing was controlled by following a metronome with increasing frequency. This setup allows for
a controlled acquisition of respiratory related HRV data covering the frequency range in which adults breathe
in different everyday situations. A stochastic model, known as Locally Stationary Chirp Process, accounts
for the respiratory signal information and models the HRV data. The model parameters are estimated with
a novel inference method based on the separability features possessed by the process covariance function.
Least square regression analysis using several available covariates is used to investigate the correlation with
the stochastic model parameters. The results show statistically significant correlation of the model parameters
with age, BMI, State and Trait Anxiety as well as stress level.
1 INTRODUCTION
Heart rate variability (HRV) is the physiological phe-
nomenon of the variation in the time interval be-
tween heartbeats. Especially parameters related to
high frequency HRV (HF-HRV) are increasingly used
as a proxy of cardiac parasympathetic nervous sys-
tem regulation (Billman, 2011). However, since many
variables influence the measure, the use of HF-HRV
power could be difficult and sometimes unreliable.
Recent studies have focused on investigating the
different factors that may affect the HRV. In partic-
ular, several publications have highlighted the im-
pact of gender and age differences on HRV. Voss et.
al. (Voss et al., 2015) have investigated the gender-
specific development of HRV indices for different cat-
egories of age. A decrease in HF-HRV power was
found with increasing age for women as well as for
men, but females had an increased HF power for ages
25-54 years in comparison to males. In (J
¨
onsson et al.,
2015), HF-HRV power is found to be decreasing with
age.
Reduced HF-HRV power is related to atten-
tion deficits, depression, various anxiety disor-
ders, long-term work related stress and burnout,
(Davari Dolatabadi et al., 2017; Hernando et al.,
2016; Lennartsson et al., 2016; Woo and Kim, 2015;
Gates et al., 2015). In (Woo and Kim, 2015), the cor-
relation between subjective ratings of stress and HRV
in healthy adults is investigated, showing that stress is
negatively correlated with HF-HRV power. Reduced
HF-HRV power is also found for individuals suffering
from clinical burnout (Lennartsson et al., 2016).
Another aspect is the phenomenon of Respiratory
Sinus Arrythmia (RSA), i.e. the heart rate variabil-
ity in synchrony with respiration, by which the heart
rate increases during inspiration and decreases during
expiration (Billman, 2011). Recent studies claim that
the actual respiratory frequency is the main informa-
tion to be considered in analysis of HRV (Hernando
et al., 2016; Choi and Gutierrez-Osuna, 2011; Weip-
pert et al., 2015). These findings have also increased
the interest of estimating the respiratory frequency
from the HRV signal, e.g., (Khan et al., 2017) and ref-
erences therein. Joint analysis of respiration and HRV
obtains a more reliable characterization of autonomic
nervous response to stress, even if classical frequency
domain HRV indices scarcely show statistical differ-
Anderson, R., Jönsson, P. and Sandsten, M.
Effects of Age, BMI, Anxiety and Stress on the Parameters of a Stochastic Model for Hear t Rate Variability Including Respiratory Information.
DOI: 10.5220/0006512900170025
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 4: BIOSIGNALS, pages 17-25
ISBN: 978-989-758-279-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17

ences during stress (Hernando et al., 2016). Similar
results are found in (Choi and Gutierrez-Osuna, 2011)
where the HRV is decomposed into a component that
is correlated with the respiratory frequency and one
residual component. The residual HRV is used to
discriminate mental stress conditions from relaxation
conditions. In (Weippert et al., 2015), metronome
guided breathing during rest is used to investigate ef-
fects on HRV indices. The results show that respira-
tion frequency needs to be considered as a contributor
when analysing HRV measures.
In this work, we apply a stochastic model suitable
for HRV to measurements recorded from 47 subjects.
The test participants were told to breathe following
a metronome with slowly increasing frequency. This
allows for the acquisition of respiratory related HRV-
data covering the frequency range in which adults
breathe in different everyday situations. Compared
to a usual resting measure with spontaneous breath-
ing, this chirp breathing task allows for examination
of the dynamics of peripheral nervous system (PNS)
mediated cardiac regulation, from slower to faster res-
piratory related HF-HRV.
The considered stochastic model falls into the
practical strand of addressing the non-stationarity of
data by assuming stationarity on local scale. This
popular approach has led to the several available def-
initions of locally stationary processes in literature.
We will refer to Silverman’s definition, (Silverman,
1957). Locally Stationary Processes (LSPs) in Silver-
man’s sense are stochastic processes resulting from a
modulation in time of a stationary covariance func-
tion. Thanks to the flexibility of the definition, LSPs
are suitable for modelling a wide range of time-
varying signals and especially physiological signals
(Anderson and Sandsten, 2017). We consider an ex-
tension of the LSP definition that accounts for the
presence of a chirp in the signals, enabling the in-
clusion of the respiratory frequency information, and
we will refer to these kind of processes as Locally
Stationary Chirp Processes, as in (Hansson-Sandsten,
2011; Wahlberg and Hansson, 2007).
The final purpose of our work is to investigate the
correlation of the model parameters, estimated with
a novel inference method, with several available co-
variates, including Age, Gender, Weight, Body-Mass-
Index (BMI), Spielberg State-Trait Anxiety Inventory
(STAI) (Spielberger and Gorsuch, 1983) and Shirom-
Melamed Burnout Questionnaire (SMBQ) (Shirom,
1989; Melamed et al., 1992; Melamed et al., 2006).
State Anxiety refers to a temporary emotional state, as
a transient level of physiological arousal and feelings
of vigilance, dread and tension, whereas Trait Anxiety
reflects a consistent personality attribute, such as the
individual disposition to experience anxious feelings,
thoughts or behaviours, (Spielberger and Gorsuch,
1983). The SMBQ is a multidimensional measure for
burnout consisting of a combination of physical fa-
tigue, emotional exhaustion, and cognitive weariness.
According to this conceptualization, burnout repre-
sents a separate construct not interchangeable with
depression and anxiety (Shirom, 2003), (Lundgren-
Nilsson et al., 2012). Therefore, it is of interest to
consider both STAI and SMBQ. Previous studies have
validated the Swedish version of the STAI (Hansen
et al., 2006; Persson and Ørbæk, 2003; Persson et al.,
2005) and the SMBQ (Grossi et al., 2003; Lundgren-
Nilsson et al., 2012).
The paper is structured as follows. In section 2 test
description, data acquisition and preprocessing are
presented. Section 3 includes the mathematical back-
ground for the general stochastic model, an outline
of the novel inference method, the specific stochas-
tic model introduced for this study case and remarks
on the regression approach. Results from the fitted
regression models are presented and discussed in sec-
tion 4, followed by the conclusions in section 5.
2 DATA DESCRIPTION
2.1 Test Description
The test participants are 21 women and 26 men with
ages in the range 20-65 years old, at different stages
of work related burnout. They were told neither to
ingest food, caffeine, or tobacco during 2 hours before
the experiment, nor alcohol the day before. Patients
using medicines or suffering from any disease known
to affect the cardiovascular system were not included
in the study.
To obtain respiratory related HRV-data covering
the frequency range in which adults normally breathe,
the recordings were made while the test participants
were breathing following a metronome starting at
0.12 Hz and slowly increasing to 0.35 Hz.
Additionally, for each test participant informa-
tion on general health and stress level has been col-
lected. The available information includes age, gen-
der, height, weight, STAI and SMBQ.
2.2 Data Acquisition and Preprocessing
The heart rate has been recorded through electrocar-
diography (ECG) using disposable electrodes. Mea-
sure of the respiration has been obtained using a strain
gauge over the chest. ECG and respiration were
recorded at 1 kHz using the ML866 Power Lab data
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
18

acquisition system and analysed using its software
LabChart8 (ADInstruments Pty Ltd.) and MATLAB
(Math-Works, Inc., Natick, MA, USA). The R-waves
were detected with LabChart8 and the HRV data are
obtained from the HR data, as the time difference be-
tween two consecutive heartbeats.
The raw data sequences, consisting of 5 minutes
of recording of heart rate and respiratory data, were
down-sampled to 4 Hz. After adjusting to zero mean,
the middle 960 samples were used, corresponding to
4 minutes of recording. An example of HRV and res-
piratory data measured from one subject is presented
in Figure 1.
3 METHODS
3.1 Locally Stationary Processes
Even though theory of stationary stochastic processes
is well developed, the assumption of stationarity is too
restrictive for most measured signals, which usually
exhibit changes in the behavior over time. Several ap-
proaches have been considered, often involving split-
ting the data into shorter segments for the estimation
of time-varying parameters.
An alternative approach revolves around classes
of processes with desirable properties extending the
stationary case. This is the case for Locally Station-
ary Processes (LSPs) (Silverman, 1957), assuming
stationarity on local scale. This definition of LSPs
avoids time-varying parameters and is based on the
modulation in time of an ordinary stationary covari-
ance function. More precisely, a zero mean stochastic
process X (t), t ∈ [T
0
, T
f
] ⊆ R, is a LSP if its covari-
ance C(s,t) = E[X(s)X(t)
∗
] can be written as
C(s, t) = q

s + t
2

· r (s −t) (1)
with s, t ∈ [T
0
, T
f
] ⊆ R, where q is a non-negative
function and r is a normalized (r(0) = 1) stationary
covariance function. When q is a constant, Eq. (1)
reduces to a stationary covariance, therefore this defi-
nition includes stationary processes as a special case.
The wide range of possibilities for the choice of
the functions q and r makes LSPs a flexible tool to
model time-varying data. For instance, in (Anderson
and Sandsten, 2017), LSPs are used to model elec-
troencephalography data sequences collected within
a study on human memory retrieval.
For this application on HRV data, we consider
an extension of the model that allows us to include
the respiratory frequency information. The covari-
ance matrix of an underlying chirp is included in the
model covariance as a multiplicative factor, similarly
to the definition of Locally Stationary Chirp Process
(LSCP) found in (Hansson-Sandsten, 2011; Wahlberg
and Hansson, 2007).
3.2 Inference Method
A novel inference methodology, based on the sepa-
rability properties of the model covariance, is used
to estimate the model parameters for each data se-
quence. In the following we present an outline of the
inference method.
In the sampled data framework, denote with x a
data sequence, consisting of n observations x
k
, k =
1. . . n, sampled at equidistant times t
k
= T
0
+ (k −
1)∆t, in the time interval [T
0
, T
f
] ⊆ R, where ∆t =
t
k
−t
k−1
is the constant sampling interval.
To account for the differences among individuals
in the interpretation of the task of breathing accord-
ingly to the metronome, the chirp covariance matrix is
estimated from the respiratory signal of each subject
in the study. Unfortunately, the classical estimator of
a non-stationary covariance, the Sample Covariance
Matrix (SCM)
ˆ
C
SCM
= x · x
T
(2)
is known to be extremely unreliable if it is based on a
single realization (Smith, 2005). Therefore we make
use of a surrogate respiratory signal, based on the in-
stantaneous frequency (IF) estimate from the spectro-
gram of the measured single realization respiratory
signal. Using the estimated IF, a number of 1000 sur-
rogate respiratory realizations with different phases
are simulated, and the resulting SCMs are averaged.
We denote the estimated covariance matrix of the res-
piratory signal with
ˆ
K .
Let Q ∈ M
n×n
be the matrix Q(k, l)
.
= q(
t
k
+t
l
2
), cor-
responding to the function q, and R ∈ M
n×n
be the
matrix R(k, l)
.
= r(
|
t
k
−t
l
|
), corresponding to the sta-
tionary covariance function r . Clearly, from the defi-
nition, it follows that Q is a Hankel matrix, which car-
ries the information about the power schedule, while
R is a symmetric Toeplitz matrix.
The function q describes the power schedule of
the process X(t), as can be deduced by taking s = t in
Eq. (1), C(t,t) = E[X (t)
2
] = q(t) · r (0) = q(t). Con-
sequently, an estimate of the parameters determining
q can be obtained through a least squares fitting of
the parametric curve to the instantaneous power of a
single realization of the HRV data, P(t
k
) = x
2
k
. The
parameters define the whole matrix
ˆ
Q, thanks to its
structure.
The final step is the estimation of the stationary
covariance R, which can be obtained by least squares
fitting of R ·
ˆ
K to the sample covariance matrix Eq. (2)
Effects of Age, BMI, Anxiety and Stress on the Parameters of a Stochastic Model for Heart Rate Variability Including Respiratory
Information
19

Figure 1: Respiratory signal (upper) and HRV signal (lower) from a subject participating in the study.
of the single realization HRV data divided by the pre-
viously estimated
ˆ
Q. This division does not create
stability issues since
ˆ
Q is a strictly positive matrix.
3.3 Stochastic Model for HRV Signals
Suitable choices for the families of the functions q
and r depend on the data to be modelled. In our ap-
plication, the family of functions for q should allow
the modelling of a typically decreasing instantaneous
power, but should also include the exceptions of a sta-
tionary or even slightly increasing power. Therefore
we choose q to be an exponential function with two
parameters a > 0 and b ∈ [−1, 1]
q
a,b
(η) = a · exp(b · η) with η =
t +s
2
(3)
Clearly, the scaling parameter a corresponds to the
power at time zero, with a larger value of a corre-
sponding to higher power, whereas the value of b de-
scribes the power decrease or increase.
Since the function r should define a stationary co-
variance function, we choose a Gaussian function for
its flexibility and desirable properties
r
c
(τ) = exp

−
c
8
· τ
2

with τ = t − s (4)
with parameter c > 0. Intuitively, the parameter c de-
scribes the local stationarity of the data, with larger
values of c corresponding to a faster decaying auto-
correlation. Conversely, a smaller value of c corre-
sponds to a larger standard deviation of the Gaussian
bell, meaning longer lasting auto-correlation.
In Figure 2 we exemplify how the different param-
eters relate to the HRV sequence. In the top panel, we
compare a sequence with an estimated large value of
a, Figure 2 (a), to a sequence with a smaller estimated
a, Figure 2 (b). In the second row, the effect of the
parameter b can be observed: typically the estimated
value of b is negative and corresponds to the decrease
in amplitude of the instantaneous power, Figure 2 (c);
however, in a few cases, a value close to 0 or even
slightly positive has been observed, Figure 2 (d). The
most difficult parameter to interpret is c, related to lo-
cal stationarity of the underlying stochastic process.
In the bottom row, a sequence with an estimated high
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
20

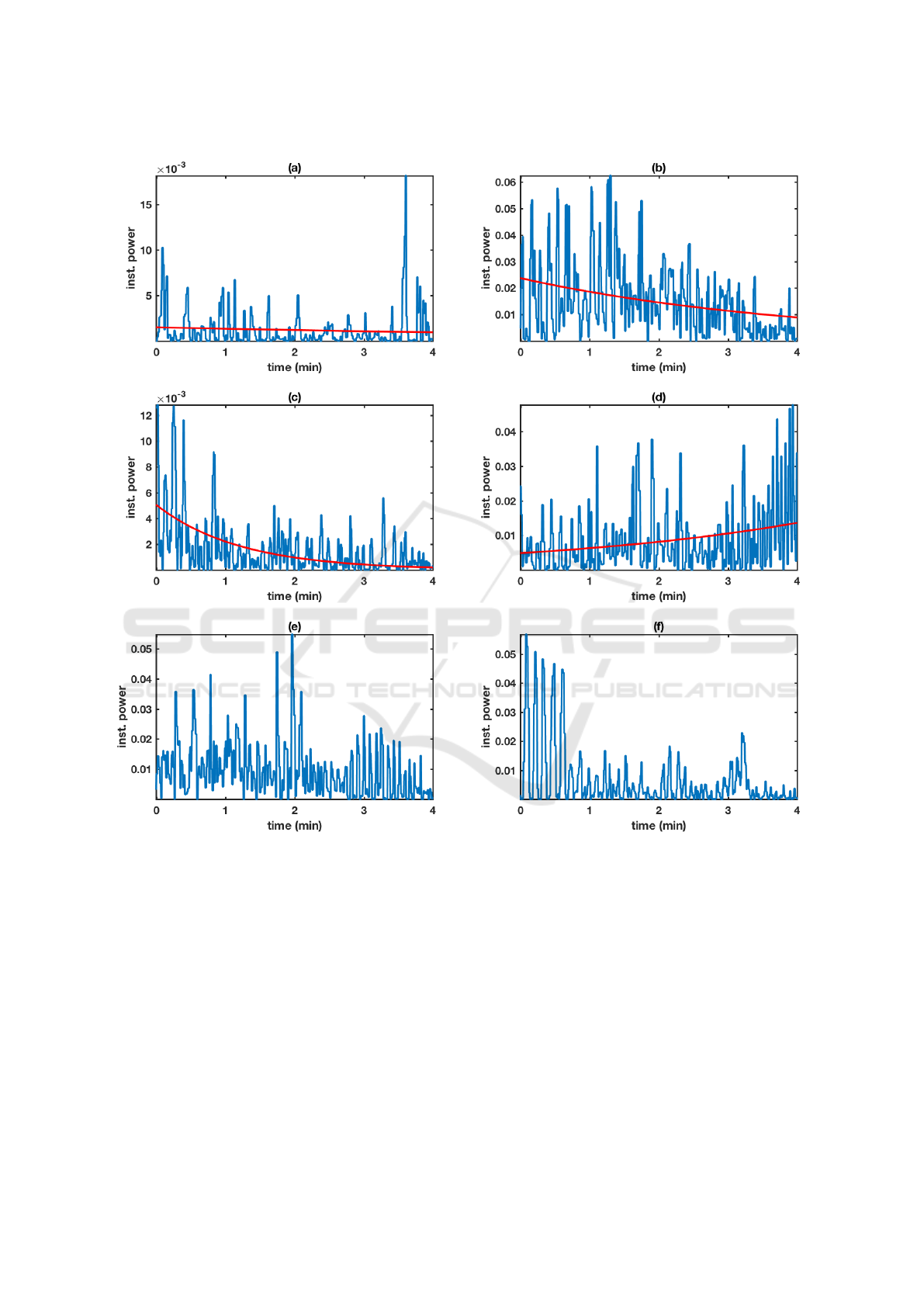
Figure 2: Examples of instantaneous power (blue) and fitted q function (red) for subjects with different estimated parameters:
a) a = 0.0015, b = −0.0019, c = 5.7744;
b) a = 0.0237, b = −0.0041, c = 0.0091;
c) a = 0.0051, b = −0.0138, c = 0.0064;
d) a = 0.0049, b = +0.0043, c = 0.0144;
e) a = 0.0152, b = −0.0040, c = 0.0109;
f) a = 0.0219, b = −0.0152, c = 4.3053.
value of c, Figure 2 (e), is compared to a sequence
with a smaller estimated c, Figure 2 (f).
3.4 Linear and Logistic Regression
Least squares regression analysis with each of the
LSCP model parameters (a, b, c) as response is per-
formed to explore the correlation of the parameters
with several factors of interest (Rawlings et al., 1998).
The considered factors are Age, Gender, Weight,
BMI, STAI (State Anxiety and Trait Anxiety) and
SMBQ. Median, mean and standard deviation for the
variables among the participants according to gender
are reported in table 1.
To isolate the effect of every factor, regression
models with a single explanatory variable (Simple
Effects of Age, BMI, Anxiety and Stress on the Parameters of a Stochastic Model for Heart Rate Variability Including Respiratory
Information
21

Table 1: Median, mean and standard deviation (sd) for the variables among the participants according to gender.
Women Men
(n=21) (n=26)
Median Mean sd Median Mean sd
Age 25 31.14 11.50 30.5 34.69 12.66
Weight 61 63.76 9.67 78.5 78.15 10
BMI 22 22.52 3.32 23.72 24.07 3.06
State Anxiety 35 33.09 6.70 29 30.15 7.70
Trait Anxiety 38 36.95 6.94 33 35.73 10.64
SMBQ 2.86 3.05 1.11 2.64 2.85 1.32
Table 2: Multivariate regression model for parameter a in-
cluding all observations.
coeff. est. S.E. p-value
Age -0.0748 0.0114 5.83·e
−08
***
State
Anxiety -0.0635 0.0231 0.0087 **
High Trait
Anxiety 0.7261 0.3189 0.0278 *
Table 3: Multivariate regression model for parameter a after
removal of influential observations.
coeff. est. S.E. p-value
Age -0.0873 0.0106 3.81·e
−10
***
State
Anxiety -0.0778 0.0203 0.000433 ***
High Trait
Anxiety 0.9471 0.2778 0.001498 **
Regression) has been tested first for each LSCP model
parameter and for each covariate.
Afterwards, multivariate models have been evalu-
ated based on statistical significance of the predictors,
coefficient of determination R
2
and the Akaike Infor-
mation Criterion (AIC). Levels of significance con-
sidered are 0.001, 0.01, 0.05, 0.1, denoted in the ta-
bles with significance codes ***,**,*, . respectively.
Regression diagnostics include residual analysis,
F-test for testing inclusion of variables, detection and
treatment of outliers and influential observations.
The analysis is performed with open source soft-
ware RStudio for programming language R (RStudio
Team, 2015; R Development Core Team, 2008).
4 RESULTS AND DISCUSSION
4.1 Parameter a
As a is a positive parameter representing the ampli-
tude multiplier that scales the exponential function, it
is natural to consider its logarithm transformation to
avoid positive skewness of the residuals.
Figure 3: Boxplots of log(a) divided in age groups.
When considering a single explanatory variable,
only the covariate Age is a significant predictor, while
other covariates become significant only in multivari-
ate models. The simple model with only Age as pre-
dictor achieves a coefficient of determination R
2
=
0.42. This result is expected, due to the high corre-
lation between HRV amplitude and age, reflected in
the scale parameter a, Figure 3.
Step-wise model selection based on AIC starting
from a model including all the covariates leads to a
multivariate model including Age as well as State and
Trait Anxiety. Age and State Anxiety are significant
predictors, with p < 0.001 and p < 0.05 respectively,
while Trait Anxiety has a p-value of 0.1013, which is
not significant at the usually considered levels.
However, the inclusion of Trait Anxiety in the
model improves the predictive power of State Anxi-
ety, which otherwise is not significant. This conflict
is solved by considering Trait Anxiety as a categorical
variable, distinguishing only between high and low
levels of Trait Anxiety, with the median of the popula-
tion (37) as threshold. Comparison through ANOVA
test with respect to the model with only Age and State
Anxiety leads to rejection of the null hypothesis at
level 0.05, i.e. the categorical variable for Trait Anx-
iety adds further explanation. Estimated coefficients
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
22

Table 4: Multivariate regression model for parameter b.
coeff. est. S.E. p-value
SMBQ -0.0387 0.0184 0.0413 *
Age -0.0023 0.0012 0.0641 .
Trait
Anxiety 0.0044 0.0024 0.0763 .
Table 5: Simple regression model for the value of b, re-
stricted to 43 subjects with b > 0.
coeff. est. S.E. p-value
Intercept -0.0028 0.0015 0.0662 .
SMBQ -0.0011 0.0005 0.0217 *
Table 6: Simple regression model for the value of b, re-
stricted to 43 subjects with b > 0.
coeff. est. S.E. p-value
Intercept -0.0047 0.0007 3.11e-07 ***
Stressed
Group -0.0025 0.0010 0.0169 *
Table 7: Logistic regression model for the sign of parameter
b.
coeff. est. S.E. p-value
Intercept -5.4757 1.9033 0.00402 **
Age 0.0806 0.0415 0.05203 .
with standard errors and corresponding p-values are
reported in Table 2. The model intercept does not sig-
nificantly differ from zero, therefore it is omitted. The
coefficient of determination is increased to R
2
= 0.51.
The fact that both Age and State Anxiety are sig-
nificant predictors of log(a) with a similar effect (neg-
ative slope and same scale) suggests an analogy be-
tween the effect on the HRV instantaneous power of
ageing and higher State Anxiety. The effect of an in-
creased anxiety as a temporary emotional state (State
Anxiety) is mitigated by the effect of a higher anxiety
as a consistent personality attribute (Trait Anxiety).
The removal of potentially influential observa-
tions according to Cook’s distance (3 out of 47) leads
to slightly different model coefficients with smaller
p-values and improved coefficient of determination
R
2
= 0.64, but similar overall conclusions, Table 3.
4.2 Parameter b
As mentioned in section 3, parameter b describes the
power decrease or increase. More precisely, a neg-
ative b with higher absolute value corresponds to a
faster power decrease, while a positive b with higher
absolute value corresponds to a faster power increase.
Since the increase in respiratory frequency due to the
chirp breathing task is usually related to a decrease in
power, in most cases the estimated value of b is nega-
tive; nevertheless, we have observed a positive b in 4
out of 47 subjects.
To investigate the relation of parameter b with the
available covariates, we first consider the estimated
value of b for all subjects. Step-wise model selection
based on AIC leads to the model presented in Table
4, where the SMBQ is the most significant predictor,
p < 0.05, followed by Age and Trait Anxiety, p <
0.1. The R
2
value for this model is only 0.14. None
of the factors are significant if considered as single
explanatory variable.
After outliers treatment (removal of 6 out of 47
subjects), the best model according to AIC includes
only the SMBQ, which is a significant predictor, p <
0.05, with a negative slope, i.e. higher value of the
SMBQ corresponds to a faster decrease of the instan-
taneous power of the HRV, Table 5. However, this
model achieves only an R
2
of 0.13, attesting that a
large portion of the variability between predictor and
response has not been accounted for.
Similar results are obtained when considering
the SMBQ as categorical variable, with threshold of
2.75 to distinguish between baseline category (control
group) and the stressed group, Table 6. SMBQ above
3.75 is considered as compatible with pre-Exhaustion
Disorder (J
¨
onsson et al., 2015); however there is no
statistical difference as predictors for the value of the
parameter b between the pre-Exhaustion Disorder cat-
egory (SMBQ above 3.75) and an additional category
defined through SMBQ in the range [2.75, 3.75].
Logistic regression to predict the sign of parame-
ter b leads to a single regression model with only Age
as covariate, Table 7. Unfortunately this result has
limited validity due to the small sample size, since the
estimated value of the parameter b is negative only for
4 subjects.
4.3 Parameter c
When considering a single explanatory variable for
the parameter c, the covariate Age is highly signif-
icant with p < 0.001, while BMI and Weight have
p < 0.01 and p < 0.05 respectively. Clearly Weight
and BMI are highly correlated covariates, and not sur-
prisingly Weight ceases to be significant once BMI is
included in the model. The step-wise selected model
according to AIC includes only Age and BMI, Ta-
ble 8. This model has a coefficient of determina-
tion R
2
= 0.5. We can observe that both covariates
have a positive slope, where an increase of one unit
in BMI has roughly the same effect of an increase of
two years of age.
If BMI is considered as a categorical variable with
levels underweight (BMI< 18), normal weight (18 ≤
Effects of Age, BMI, Anxiety and Stress on the Parameters of a Stochastic Model for Heart Rate Variability Including Respiratory
Information
23

Table 8: Regression model for parameter c.
coeff. est. S.E. p-value
Intercept -7.8773 1.9666 0.000235 ***
Age 0.1146 0.0228 9.04·e
−06
***
BMI 0.2416 0.0856 0.007143 **
Table 9: Regression model for parameter c with BMI as
categorical variable.
coeff. est. S.E. p-value
Intercept -2.4395 0.7507 0.002279
Age 0.1115 0.0214 5.21·e
−06
***
Obese 3.7010 0.9318 0.000274 ***
Table 10: Regression model for parameter c with BMI as
categorical variable.
coeff. est. S.E. p-value
Intercept -3.571 0.6885 6.14·e
−06
***
Age 0.1538 0.0210 5.83·e
−09
***
Obese 2.922 0.8821 0.00194 **
BMI < 25), overweight (25 ≤ BMI < 30) and obese
(BMI ≥ 30), only the category obese is significantly
different from the baseline category normal weight,
Table 9. This model achieves an R
2
value of 0.57.
However, it should be noted that only 4 people in this
study have a BMI above 30. Slightly different coeffi-
cients and R
2
= 0.65 are obtained when 3 outliers and
influential observations are removed from the popula-
tion, Table 10.
5 CONCLUSIONS
In this paper, we have considered a stochastic model
based on the definition of Locally Stationary Chirp
Processes, which enables the inclusion of the infor-
mation from the respiratory signal. Suitable families
of the functions with parameters defining the model
covariance have been selected to fit non-stationary
HRV data sequences. The HRV data from 47 subjects
is measured during breathing following a metronome
with increasing frequency. Respiratory information
has been included as a factor in the model covariance
matrix.
For each subject, the model parameters are esti-
mated with a novel inference method based on the
separability features possessed by the process covari-
ance function. Regression analysis with several avail-
able covariates is used to investigate the predictive
power with respect to the model parameters. Re-
sults show a statistically significant correlation of the
model parameters with age, BMI, State and Trait
Anxiety and SMBQ.
In particular, both Age and State Anxiety have
the effect of decreasing parameter a, which corre-
sponds to a decrease in the scale factor describing the
HRV power. This effect is mitigated by the effect of
a higher anxiety as a consistent personality attribute
(Trait Anxiety). For parameter b, related to the power
decrease or increase with the time-varying breathing
frequency, the SMBQ is the most significant predic-
tor, followed by Age and Trait Anxiety. After outliers
treatment, only SMBQ is significant. Both Age and
BMI are statistically highly significant predictors for
parameter c ruling the local behavior of the process,
with an increase of one unit in BMI, having roughly
the same effect of an increase of two years of age.
None of the model parameters has shown signifi-
cant differences related to gender. It is possible that
the demographic composition of the participants, with
women younger than men, could have masked possi-
ble correlation of the model parameters with gender.
Future research will investigate how the model pa-
rameters relate with other commonly used measures
for HRV, such as low frequency and high frequency
spectral components.
COMPLIANCE WITH ETHICAL
REQUIREMENTS
Data collection took place at the Department of Labo-
ratory Medicine, Division of Occupational and Envi-
ronmental Medicine, Lund University. The study was
approved by the central ethical review board at Lund
(Dnr 2013/754) and was conducted in correspondence
with the Helsinki declaration. All participants signed
an informed consent that clearly stated that participa-
tion was voluntary and could be discontinued at any
time.
CONFLICT OF INTEREST
The authors declare that they have no conflict of in-
terest.
REFERENCES
Anderson, R. and Sandsten, M. (2017). Stochastic mod-
elling and optimal spectral estimation of EEG sig-
nals. In EMBEC & NBC 2017: Joint Conference
of the European Medical and Biological Engineering
Conference (EMBEC) and the Nordic-Baltic Confer-
ence on Biomedical Engineering and Medical Physics
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
24

(NBC), Tampere, Finland, June 2017, pages 908–911.
Springer Singapore.
Billman, G. E. (2011). Heart rate variability - A historical
perspective. Frontiers in Physiology, 2.
Choi, J. and Gutierrez-Osuna, R. (2011). Removal of res-
piratory influences from heart rate variability in stress
monitoring. IEEE Sensors Journal, 11(11):2649.
Davari Dolatabadi, A., Khadem, S., and Asl, B. (2017). Au-
tomated diagnosis of coronary artery disease (CAD)
patients using optimized SVM. Computer Methods
and Programs in Biomedicine, 138:117–126.
Gates, K. M., Gatzke-Kopp, L. M., Sandsten, M., and Blan-
don, A. Y. (2015). Estimating time-varying RSA
to examine psychophysiological linkage of marital
dyads. Psychophysiology, 52(8):1059 – 1065.
Grossi, G., Perski, A., Eveng
˚
ard, B., Blomkvist, V., and
Orth-Gom
´
er, K. (2003). Physiological correlates of
burnout among women. Journal of Psychosomatic Re-
search, 55:309 – 316.
Hansen,
˚
A. M., Hogh, A., Persson, R., Karlson, B., Garde,
A. H., and Ørbæk, P. (2006). Original article: Bully-
ing at work, health outcomes, and physiological stress
response. Journal of Psychosomatic Research, 60:63
– 72.
Hansson-Sandsten, M. (2011). Optimal multitaper Wigner
spectrum estimation of a class of locally stationary
processes using Hermite functions. EURASIP Jour-
nal on Advances in Signal Processing, page 980805.
Hernando, A., Lazaro, J., Gil, E., Arza, A., Garzon, J.,
Lopez-Anton, R., De La Camara, C., Laguna, P.,
Aguilo, J., and Bailon, R. (2016). Inclusion of res-
piratory frequency information in heart rate variabil-
ity analysis for stress assessment. IEEE Journal
of Biomedical and Health Informatics, 20(4):1016 –
1025.
J
¨
onsson, P.,
¨
Osterberg, K., Wallerg
˚
ard, M., Hansen,
˚
A. M.,
Garde, A. H., Johansson, G., and Karlson, B. (2015).
Exhaustion-related changes in cardiovascular and cor-
tisol reactivity to acute psychosocial stress. Physiol-
ogy & Behavior, pages 327–337.
Khan, N. A., J
¨
onsson, P., and Sandsten, M. (2017). Per-
formance comparison of time-frequency distributions
for estimation of instantaneous frequency of heart rate
variability signals. Applied Sciences, 7(3).
Lennartsson, A., Jonsdottir, I., and Sj
¨
ors, A. (2016). Low
heart rate variability in patients with clinical burnout.
International Journal of Psychophysiology, 110:171–
178.
Lundgren-Nilsson,
˚
A., Jonsdottir, I. H., Pallant, J., and
Ahlborg, G. (2012). Internal construct validity of
the Shirom-Melamed burnout questionnaire (SMBQ).
BMC Public Health, 12(1).
Melamed, S., Kushnir, T., and Shirom, A. (1992). Burnout
and risk factors for cardiovascular diseases. Behav-
ioral Medicine, 18(2):53 – 60.
Melamed, S., Shirom, A., Toker, S., Berliner, S., and
Shapira, I. (2006). Burnout and risk of cardiovas-
cular disease: Evidence, possible causal paths, and
promising research directions. Psychological Bulletin,
132(3):327 – 353.
Persson, R. and Ørbæk, P. (2003). The influence of per-
sonality traits on neuropsychological test performance
and self-reported health and social context in women.
Personality and Individual Differences, 34:295 – 313.
Persson, R.,
¨
Osterberg, K., Karlson, B., and Ørbæk, P.
(2005). The meta-contrast technique: Relation-
ships with personality traits and cognitive abilities in
healthy women. Scandinavian Journal of Psychology,
46(2):169 – 177.
R Development Core Team (2008). R: A Language and
Environment for Statistical Computing. R Foundation
for Statistical Computing, Vienna, Austria. ISBN 3-
900051-07-0.
Rawlings, J. O., Pantula, S. G., and Dickey, D. A. (1998).
Applied Regression Analysis - A Research Tool. New
York:Springer-Verlag, London, 2nd edition.
RStudio Team (2015). RStudio: Integrated Development
Environment for R. RStudio, Inc., Boston, MA.
Shirom, A. (1989). Burnout in work organization. Interna-
tional Review of Industrial and Organizational Psy-
chology.
Shirom, A. (2003). Job-related burnout: A review. In Hand-
book of occupational health psychology, pages 245 –
264. American Psychological Association.
Silverman, R. (1957). Locally stationary random processes.
IRE Transactions on Information Theory, 3(3):182–
187.
Smith, S. (2005). Covariance, subspace, and intrinsic
Cram
´
er-Rao bounds. IEEE Transactions on Signal
Processing, 53(5):1610 – 1630.
Spielberger, C. D. and Gorsuch, R. L. (1983). Manual for
the state-trait anxiety inventory, STAI (form Y). Palo
Alto, CA, Consulting Psychologists Press.
Voss, A., Schroeder, R., Heitmann, A., Peters, A., and Perz,
S. (2015). Short-term heart rate variability - Influence
of gender and age in healthy subjects. PLoS ONE,
10(3):1 – 33.
Wahlberg, P. and Hansson, M. (2007). Kernels and multiple
windows for estimation of the Wigner-Ville spectrum
of Gaussian locally stationary processes. IEEE Trans-
actions on Signal Processing, 55(1):73 – 84.
Weippert, M., Behrens, K., Rieger, A., Kumar, M., and
Behrens, M. (2015). Effects of breathing patterns and
light exercise on linear and nonlinear heart rate vari-
ability. Applied Physiology Nutrition and Metabolism,
40(8):762 – 768.
Woo, J.-M. and Kim, T.-S. (2015). Gender plays signifi-
cant role in short-term heart rate variability. Applied
Psychophysiology & Biofeedback, 40(4):297 – 303.
Effects of Age, BMI, Anxiety and Stress on the Parameters of a Stochastic Model for Heart Rate Variability Including Respiratory
Information
25