Optimising Graphical Techniques Applied to Irreversible Tracers

Yasser Alzamil

1,2

,Yulia Hicks

, Xin Yang

and Christopher Marshall

Institute of Health, Technology and the Digital World, Cardiff University, School of Engineering,

Queen’s Buildings,The Parade, CF24 3AA, Cardiff, U.K.

Diagnostic Radiology Department, University of Hail, Applied Medical Sciences College,

P.O. Box 2440, Hail, Saudi Arabia

Wales Research & Diagnostic Positron Emission Tomography Imaging Centre PETIC, Cardiff University,

School of Medicine, UHWMainBuilding, HeathPark, CF14 4XN, Cardiff, U.K.

Keywords: PET, Patlak Graphical Analysis,

F-FDOPA Quantification, Image Analysis, Dpetstep Simulation.

Abstract: Graphical analysis techniques are often applied to positron emission tomography (PET) images to estimate

physiological parameters. Patlak analysis is primarily used to obtain the rate constant (K

) that indicates the

transfer of a tracer from plasma to the irreversible compartment and ultimately describes how the tracer binds

to the targeted tissue. One of the most common issues associated with Patlak analysis is the introduction of

statistical noise that affects the slope of the graphical plot and causes bias. In this study, several statistical

methods are proposed and applied to PET time activity curves (TACs) for both reversible and irreversible

regions that are involved in the equation. A dynamic PET imaging simulator for the Patlak model was used

to evaluate the statistical methods employed to reduce the bias introduced in the acquired data.

1 INTRODUCTION

This article describes the first experiment in the

optimisation process for 18F- FDOPA quantification

in Parkinson’s disease (PD) images. [18F]FDOPA

dynamic images of the brain are used and Patlak

graphical analysis will be applied first to the PET

data, then several statistical techniques will be

implemented to Patlak equations in terms of reducing

bias and noise as well as improving the accuracy of

the result. The calculation of goodness of fit of the

slope and the standard errors of the regression line

are the reference for the evaluation of result

improvement. Graphical techniques are considered

simple for the PET data analysis. Patlak equations for

irreversible tracers were used to establish another

graphical technique for reversible binding tracers.

These techniques are common and preferred due to

the independence from compartmental modelling,

which is harder compared to the graphical methods.

One issue usually generated with this type of analysis

is the bias introduced, which is caused by the

sensitivity to statistical noise (Logan 2003) that is

usually introduced by using the ordinary least

squares (OLS) method. This could be reduced by

selecting and applying several other methods that

include the feasible generalized linear least squares

(FGLS), total least square (TLS), robust fitting

regression (RFR).

In this article, these methods first will be applied on

simulated phantom PET data generated from

dPETSTEP simulation tool (Haggstrom et al. 2016)

to see how different statistical methods will affect the

image analysis result and how they behave with

different levels of noise. The equations, materials,

algorithms and tools used in the experiment will be

described and the result will be discussed and

evaluated in this article.

2 THEORY

The main thing that distinguishes between reversible

and irreversible tracers is the experiment length; in

other words, a tracer can be reversible over a long

period, but it could be irreversible during experiment

or scanning time (Logan 2000). For irreversible

tracers, the Patlak reference model is used to

calculate the [

F]FDOPA uptake in ROI, and it is the

same standard model using the blood data as an input

function except that the blood activity is replaced by

the activity of a reference TAC. The reference must

Alzamil, Y., Hicks, Y., Yang, X. and Marshall, C.

Optimising Graphical Techniques Applied to Irreversible Tracers .

DOI: 10.5220/0006513700170026

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 2: BIOIMAGING, pages 17-26

ISBN: 978-989-758-278-3

be devoid of targeted receptors (Patlak et al. 1983;

Patlak and Blasberg 1985). The Patlak method can

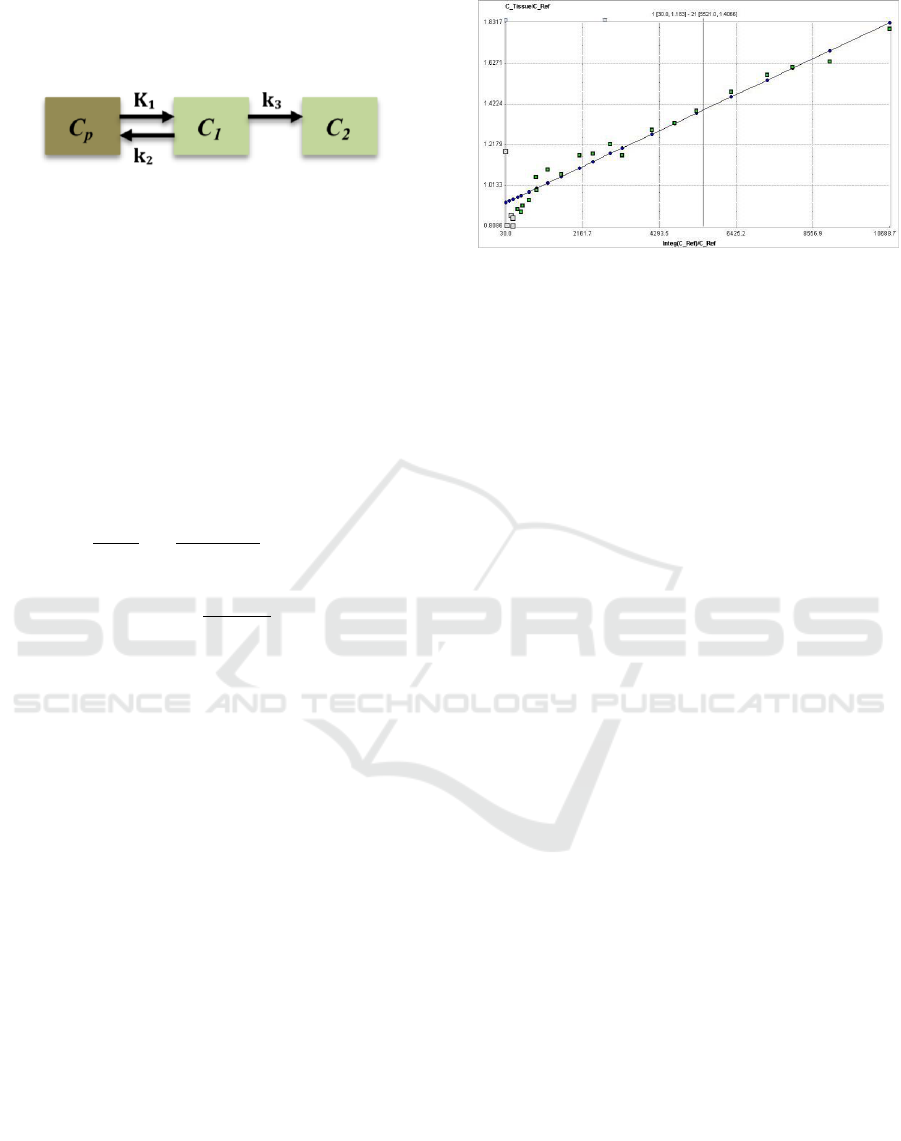
be modelled as two-tissue compartments (Figure 1).

Figure 1: Two-tissue compartmental model where Cp(t) is

the plasma tracer concentration at time (t). C1 is the free

tracer concentration in tissue and C2 is the trapped tracer

concentration. K1, k2 and k3 are unidirectional rate

constants of the tracer between plasma and tissues.

With FDOPA tracer, the regions used to generate

graphics include one reversible region (cerebellum)

and one irreversible region (striatum). TACs of

blood plasma usually calculated and used an input

function for Patlak analysis but a reference tissue

region replaces plasma measurement here. Patlak

plot equation with reference tissue as an input

function, which can be described by

T(t)

'(t)

=K







dτ

'(t)

+V

(1)

K=slope=

3

)

(2)

Where CT(t) is the TAC values of the ROI tissue

(striatum), CT’(t) is the reference tissue TAC

(cerebellum) at time t, K is the unidirectional net

uptake rate constant and V is the blood volume

fraction . The equation works for t > t*, t* is the

equilibration time where the radioactivity ratio

between reference and ROI tissue becomes

reasonably constant (Ikoma et al. 2008). K represents

the tracer net uptake calculated from the regression

slope, and V is the intercept, which is equal to the

volume fraction of blood in ROI tissue at time 0. This

means measured activity in ROI (striatum) is divided

by the reference tissue activity that represents (y-

axis), and plotted against the integral of the reference

TAC from the injection time divided by the reference

activity, which represents (x-axis). For

F-FDOPA

tracer that targets brain receptors in striatum, the

model plot will result in a straight line after t* (Patlak

and Blasberg 1985) as illustrated in (Figure 2).

Figure 2: PET activity measured from ROI is divided by

the reference tissue activity that represents (y-axis), and

plotted against the integral of the reference TAC from the

injection time divided by the reference activity, which

represents (x-axis). The model plot resulted in a straight

line after t* = 30 min in this analysis.

2.1 Ordinary Least Square

OLS is one of the simplest methods of linear

regression and it is frequently used to analyse both

experimental and observational data. It aims to

closely “fit” a function with the data by minimizing

the sum of squared differences between the observed

responses in the given dataset and those predicted by

a linear function. On a plotted graph, this is seen as

the sum of the squared vertical distances between

each data point in the set and the corresponding point

on the regression line (RL). The smaller the

differences, the better fitted the model of the data

(Hayashi 2000).

In the case of a model with p explanatory variables,

the OLS regression model is expressed as:

  



  











 

(3)

Where Y is the dependent variable, β

is the intercept

of the model, X

corresponds to the j

explanatory

variable of the model (j=1 to p), and ε is the random

error with expectation 0 and variance σ². With n

observations, the estimation of the predicted value of

the dependent variable Y for the i

observation is

given by:





 



  











(4)

In a model, this leads to the following estimators of

the parameters:

β = (X

DX)

-1

Dy σ² = 1/(W – p*)









- y

)

(5)

BIOIMAGING 2018 - 5th International Conference on Bioimaging

where β is the vector of the estimators of the βi

parameters, X is the matrix of the explanatory

variables preceded by a vector of 1s, y is the vector

of n observed values of the dependent variable, p* is

the number of explanatory variables to which we add

1 if the intercept is not fixed, w

is the weight of the

observation, W is the sum of the w

weights, and

D is a matrix with the w

weights on its diagonal. The

vector of the predicted values can be written as

follows (Freedman 2009):

y = X (X

DX)

-1

(6)

2.2 Generalized Linear Least Squares

Generalized linear least squares (GLLS) was applied

in different PET quantitative model equations

(Logan et al. 2001) to remove bias, and it was

developed originally by Feng et al. (1993). GLLS is

used for estimating the unknown parameters in

models based on a linear regression when calculated

data shows a certain degree of correlation in the

residuals. This method was applied to the data in two

parts: for times 0 to T1 and from T1 to the end time.

The parameters generated a curve used as input to the

linear regression analysis (Logan et al. 2001). The

two types of GLLS are called weighted least squares

(WLS) and feasible generalized least squares

(FGLS). WLS can be applied when all the off-

diagonal entries of the covariance error matrix (W)

are 0. In FGLS, the opposite occurs when the

covariance of errors are unknown (Strutz 2010).

With FGLS, the calculation progresses in two steps:

first, the residuals are obtained by using OLS to

establish the errors covariance matrix that shows a

consistency in estimation. Second is implementing

the idea of GLLS, which is to divide the data given

into two sides, and the part that has the low variance

is given more weight than the other sides to generate

a more accurate fitted line. With finite samples, an

estimator’s accuracy with FGLS can be improved by

an iteration process where residuals are used to

update the errors covariance estimator and

consequently FGLS estimation is updated (Long and

Trivedi 1992; Freedman 2008; Gujarati 2009). The

FGLS estimator may or may not be unbiased in small

samples but if (



) is a consistent estimator of (W),

then the FGLS estimator is asymptotically unbiased,

efficient, and consistent. Monte Carlo studies have

shown that the FGLS estimator generally yields

better estimates than the OLS estimator (Kennedy

2008).

The general linear regression model is defined by

the following set of assumptions:

• Linearity in parameters is the functional

form

y = X + 

(7)

• Error term has mean zero

E() = 0

(8)

• Errors are nonspherical

Cov() = E(T) = W

(9)

Where W is any nonsingular TxT

variance-

covariance matrix of disturbances.

• Error term has a normal distribution

 ~ N

• Error term is uncorrelated with each

independent variable.

Cov (,X) = 0

(10)

There are two types of nonspherical errors: First is

when an error term does not have constant variance,

and this is called heteroscedasticity. In this type of

error, the disturbances are drawn from probability

distributions that have different variances and the

error term has non-constant variance; the variance-

covariance matrix of disturbances is not given by a

constant multiplied by the identity matrix (i.e., W 



I). Second, the errors are correlated, which is

called autocorrelation or serial correlation where

disturbances are correlated with one another. It

occurs when using time-series data. When the

disturbances are correlated, the variance-covariance

matrix of disturbances is not given by a constant

multiplied by the identity matrix (i.e., W  

I). This

is because the elements off the principal diagonal of

W, which are the covariance of the disturbances, are

non-zero numbers (Granger 1994).

In a general linear regression model stated in matrix

format, the sample of T multivariate observations

, X

, …, X

) is generated by a process

explained below:

y = X + ,  ~ N(0, W)

(11)

y ~ N(X, W)

(12)

An FGLS estimator uses the sample of data to obtain

an estimate of W where the true W is replaced with

its estimate 



. The FGLS estimator is given by the

rule:





FGLS

= (X





-1





-1

(13)

Optimising Graphical Techniques Applied to Irreversible Tracers

The variance-covariance matrix of estimates for the

GLS estimator is

Cov(



) = (X





-1

(14)

The FGLS estimator is also a WLS estimator. The

WLS estimated is derived as follows. Find a TxT

transformation matrix P such that μ* = Pμ, where μ*

has variance-covariance matrix Cov(μ*) = E(μ*

μ*T) = σ

I. This transforms the original error term μ

that is nonspherical into a new error term that is

spherical. Use the matrix P to derive a transformed

model (Granger 1994; Kennedy 2008):

Py = PXβ + Pμ

(15)

= X

β + μ

(16)

Where y

= Py, X

= PX, and μ

= Pμ. The FGLS

estimator is the OLS estimator applied to the

transformed model, which is considered a

computational device only to obtain efficient

estimates of the parameters and standard errors of the

original model of interest.

2.3 Robust Fitting Regression

Robustness denotes the solidity of conclusions and

how their differences from assumptions are assigned

to a certain model. This means that small changes in

the data distribution do not cause large changes in the

variance of the estimates (Western 1995). RFR

provides an alternative to OLS when assumptions are

invalid within the model. RFR provides much

improved regression coefficient estimates when data

noise or outliers are existent. The influence of

outliers is down-weighted by making the outlying

residuals larger and simpler to detected, plus

performing an iterative procedure to identify outliers

and reduce the impact on the coefficient estimates.

Robust regression implements its own residual

analysis and reduces or completely removes

numerous data points, so a decision should be made

whether these observations are essential in the

analysis (Hintze 2001; Kutner et al. 2004). The most

common general method of robust regression is a

class of techniques called M-estimators that discount

the impact of outlying observations (Fox 2002),

introduced by Huber (1964). Consider the linear

model

= α + β

+ β

+ . . . + β

+ ε

= x’

β + ε

(17)

The fitted model for the ith of n observations is

= a + b

+ b

+ . . . + b

+ e

= x’

b + e

(18)

The general M-estimator minimizes the objective

function

ρ





i=1

ρy

-x'

b

i=1

(19)

The function ρ gives the contribution of each residual

to the objective function and should have the

following properties:

▪ ρ(e) ≥ 0

▪ ρ(0) = 0

▪ ρ(e) = ρ(−e)

▪ ρ(e

) ≥ ρ(e

i’

) for |e

| > |e

i’

For least-squares estimation, ρ(e

)=e

, let ψ=ρ’ be

the derivative of ρ, differentiating the objective

function while considering the coefficients b, and

assume the partial derivatives to be 0, which

enervates a system of k+1 estimating equations for

the coefficients:

ψy

-





bx'=0

i=1



(20)

Assume the weight function w(e) = ψ(e)/e , and let

= w(e

), then the estimating equations can be

written as

w

y

-





bx'=0

i=1

(21)

An iterative solution called iteratively reweighted

least-squares (IRLS) is required due to the

dependency between weights, residuals and the

estimated coefficients. The iteration is performed

following these steps:

1. Select initial estimates b(0); for example, the least-

squares estimates.

2. At each iteration t, calculate residuals e

(t-1)

and related weights w

(t-1)

=w[e

(t-1)

]

from the previous iteration.

3. Apply for new weighted-least-squares estimates





=[X'W

(t-1)

-1

X



(t-1)

y

(22)

BIOIMAGING 2018 - 5th International Conference on Bioimaging

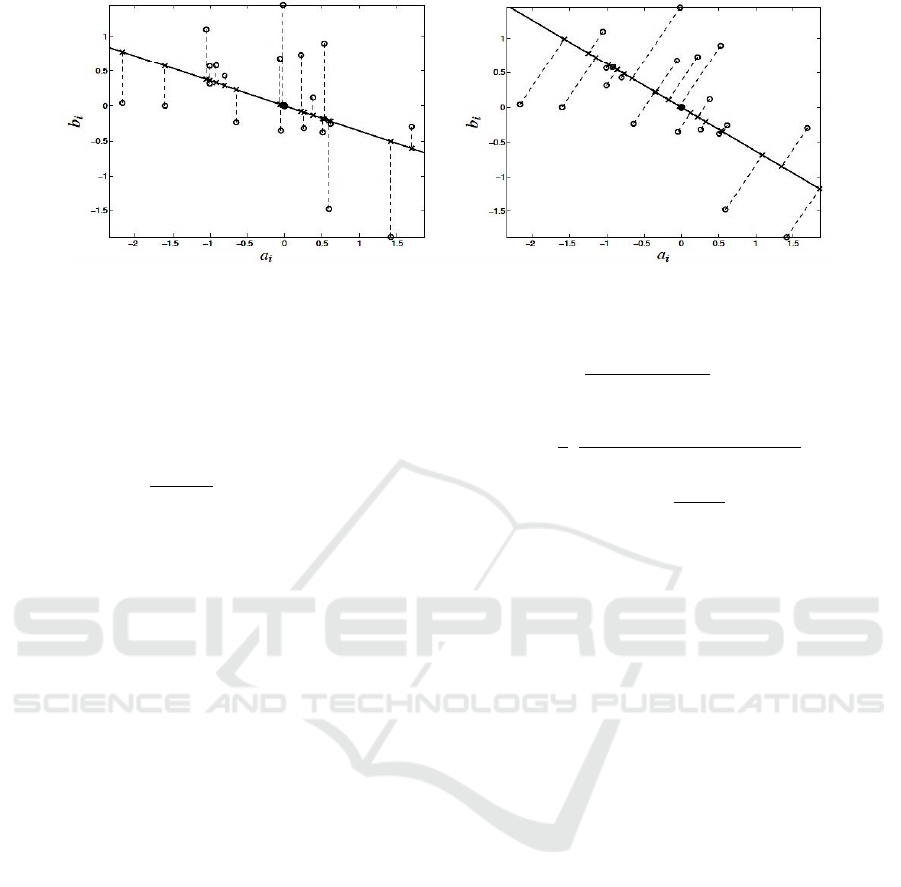
Figure 3: Ordinary least squares (Left) and total least squares (Right) fits of a set of

= 20 data points in the plane. (---)

data points, 







, x- approximations 









 , solid line (—) fitting model  



, dashed lines (---) approximation errors.

X is the model matrix, with 





as its i

row, and







 





is the current weight matrix.

These steps are repeated till the estimated coefficients

converge and covariance matrix of b is

Vb=

E(ψ

)

[E(ψ

)]

(X'X)

-1

(23)

Using



[ψ(e

)]

to estimate E(ψ

) and 



ψ '







to estimate



[Eψ']

 produces the estimated

covariance matrix V



(b).

2.4 Total Least Squares

The TLS method, known also as error-in-variables

method or orthogonal regression method, is a general

approach that can be used in n-dimensional space

(Petras and Podlubny 2010). Many areas of

application use the TLS method such as signal

processing, image processing and economics. The

orthogonal distance, distance between data point and

fitted line, is the main category of TLS and

mathematically can be expressed by the following

relation (Petráš and Bednárová 2010):

R= |d

i=1

(24)

d is the orthogonal distance and the target is to find a

minimum of R; the TLS approach minimizes the sum

of the squared d from the data points to the fitting line.

With the TLS method, well-known mathematical

tools are usually used.

For linear regression model of the expression:

y = bx + a

(25)

The coefficients a and b can be derived from the

following relations:

a=



i=1

-b



i=1

=y-bx

(26)

B=







i=1

-ny

-(



i=1

-nx

)

nxy-



i=1

(27)

b=-B±



+1

(28)

The OLS and TLS methods assess the fitting accuracy

in different ways: the OLS method minimizes the sum

of the squared vertical distances from the data points

to the fitting line, whereas the TLS method minimizes

the sum of the squared d from the data points to the

fitting line. Figure 3 shows OLS and TLS fitting lines

as well as the data approximation. In the least squares

case, the data approximation is obtained by correcting

the second coordinate only. In TLS, the data

approximation is obtained by correcting both

coordinates (Markovsky and Van Huffel 2007). This

method takes into account the noise in the

independent as well as dependent variables (Varga

and Szabo 2002).

3 MATERIALS AND METHODS

3.1 Scanner and Reconstruction

Parameters

The scanner available in the PET Imaging Centre at

the University Hospital of Wales is GE Discovery

690 PET/CT (General Electric Healthcare), and it is

made for clinical and research use. The reconstruction

method used with FDOPA imaging is a maximum

likelihood ordered subset estimation maximisation

(ML OSEM) with Vue Point FX algorithm with time

of flight (TOF) correction.

Optimising Graphical Techniques Applied to Irreversible Tracers

3.2 dPETSTEP and Simulation

Parameters

dPETSTEP is a dynamic PET simulator that can

generate PET brain images and allows full simulation

of kinetic modelling (Haggstrom et al. 2016).

Additionally, the dynamic PET data can then be

model-fitted to produce physiological parameter

estimates. dPETSTEP uses MATLAB as a platform

and works as an extension of another application

named PETSTEP, and they both share some

commands. Both applications are open source and

available on the GitHub© website. dPETSTEP is a

fast and simple tool and can be used as an alternative

to Monte Carlo (MC), as it is 8000 times faster than

MC. In terms of kinetic analysis, dPETSTEP is very

helpful for the evaluation of different processing

choices with dynamic and parametric images that

usually require a long time for image analysis where

each pixel is analysed. To run the simulation, at the

beginning, the settings of the simulation must be

adjusted to be consistent with the PET scanner

features that are targeted by the analysis or

evaluation. Table 1 shows all required simulation

settings to generate simulated dynamic PET data for

F-FDOPA images that are performed for a PD

patient. The simulated dynamic PET scan will be

acquired as 26 time frames over 94.5 min (1 × 30 sec,

4 × 1 min, 3 × 2 min, 3 × 3 min, and 15 × 5 min) with

a dose of 111 MBq. The cerebellum region from each

time frame will be used as the reference region tissue

(input function) for the quantitative analysis. The

output after running the simulator is a 4D matrix with

a reconstructed dynamic ordered subset expectation

maximization (OSEM) image with point spread

function (PSF) correction, which is similar in features

to the dynamic PET data produced by the real

scanner. The noise level of the 4D matrix is kept at a

minimum in its sinogram. The entire volume of

images is separated into single slices as 2D images

(Figure 4), and these are saved to a MATLAB version

4 MAT-file, which allows them to be loaded in any

MATLAB version with 2D double, character, sparse

arrays and without compression. This version allows

for each variable to have a maximum size of 100

million elements per array and 231 bytes per variable,

which allows all the data information to be kept

without losing any details. Scatter and decay

correction was applied during the reconstruction

process obtained from setting the parameters file

within the simulation codes. All slices introduced by

the 4D matrix are exported to PMOD 3.4 software to

perform further analysis in kinetic modelling with

specific ROI.

Figure 4: (Left) The entire volume of images is separated

into single slices as 2D images, which are saved to a

MATLAB version 4 MAT-file, which allows them to be

loaded to PMOD software (Right).

3.3 PMOD Software

PMOD software has been designed for researchers in

the molecular imaging field and provides suitable

tools for all quantitative data processing steps. This

will make researchers pay more attention to the

content and clinical data rather than programming

new tools from scratch. PMOD can process all type

of images such, as CT, MR and SPECT, in many

different imaging formats, from simple processing

tasks to sophisticated protocols and analysis all

packed into one graphical user interface application.

It is validated and refers to more than 1000 peer-

reviewed publication documents on kinetic modelling

and biomedical research (LLC 2017). In this

experiment, two applications are used for the

analysis, PBAS and PKIN, which allow import of the

simulated dynamic PET images and applying kinetic

analysis, respectively. PBAS is the main tool in

PMOD and can receive images in different proper

formats, one of which is v4 MAT-files, which should

be imported to PBAS as double SE data form. The

images imported must be in Bq/cc units, and the

orientation should be corrected if it looks different.

All corrections are already made by the simulator, and

PMOD should do nothing in terms of corrections. At

the beginning, all slices are merged into frames again,

and the times for each frame are consistent with the

protocol used with the simulator. After that, all

frames are saved as DICOM format, the Digital

Imaging and Communications in Medicine standard.

This format is data rich, and the header information

includes attenuation, scatter and decay correction,

normalisation, frame timing and reconstruction

parameters as well as the standard, required details of

matrix dimensions and pixel size. The computer

which was used for reconstruction of the images was

an Intel® Core™ I7-6700K processor 8MB Cache

4.00 GHz 4 Cores 8, with Windows 7 Enterprise 64-

bit OS and 32 GB RAM.

BIOIMAGING 2018 - 5th International Conference on Bioimaging

PBAS was used to draw and analyse the ROI (left

striatum) and reference tissue (cerebellum), the

reason for choosing the left striatum is that it is

assumed that in simulated images both the left and

right side will have the same amount of radioactivity.

The net influx rate constant (Ki) is usually calculated

over a range of 30-90 min for dynamic images, so all

frames between 30 and 90 minutes are averaged into

slices, and then the ROIs are drawn on all slices to

show them. Two volumes of interest (VOIs) at

minimum must be created; one VOI for the

cerebellum represents the reversible region, and

another one for the left striatum represents the

irreversible region. For regional analysis, the ROI is

drawn as one complete contour; ROI objects were

drawn freehand (Figure 5).

Figure 5: For regional analysis, the ROI is drawn as one

complete contour; ROI objects were drawn freehand;

simulated striatum (Left) and part of simulated cerebellum

(Right).

Each VOI includes contours that are drawn over the

simulated anatomical region required for the analysis,

and all VOIs are saved in a single file to be used again

as a template. In fact, even the ROIs’ contours are

drawn on the averaged dynamic frames; however, the

TACs at the end will be obtained from the original

dynamic PET volume. So, the images are averaged to

help guiding the drawing on all slices that show ROIs.

Then, the time activity curves (TACs) are generated

from the contours of regions required for the analysis.

TACs for all regions must be checked, and the tracer

in the reversible curve should show a clear washout.

PMOD has an algorithm to determine the best time

for t*. In this experiment, the Patlak reference tissue

analysis is based on t* = 30 min, and this is important

for slope calculations (Ki value). For regional

analysis, the result will be (Ki) value (slope). For each

specific ROI made, the intercepts that represent (V),

standard errors (SE) and Chi-square are calculated

within the analysis. The maximum standard error

accepted for (Ki) is 10%.

The simulation of the FDOPA dynamic PET data is

repeated 10 times and simulates different (Ki) values

within the normal healthy subjects, which are

between 0.012 and 0.014 according to literature,

considering that the imaging protocol of FDOPA for

scanning patients is based on giving both carbidopa

and entacapone. After finishing the kinetic modelling

analysis, Gaussian noise with a zero mean was

applied in 10 levels (0.05 – 0.5) for both the reference

tissue and ROI. All the TACs where then exported to

be analysed by our statistical calculation methods,

FGLS, TLS and RFR, which were explained before.

Codes were written in MATLAB software to analyse

all TACs obtained from the simulated images

processed by PMOD, and the (Ki) results were saved

to Excel sheets. The following section illustrates the

results for the simulated data, including statistics,

which were calculated to evaluate how the methods

affected the estimate of the final (Ki) values.

4 RESULTS

TACs for reference tissue (cerebellum) and ROI (left

striatum) that were obtained from the first simulation

data without noise are plotted as an example in Figure

6. The curves show that activity in the cerebellum

starts to increase significantly, reaching 12000

Kbq/cc, and then decreases (washout) to around 4000

Kbq/cc and starts what is known as the equilibration

stage, which is the time point most preferable for

Patlak analysis. The activity washout confirms the

reversibility of the cerebellum region. In contrast, the

left striatum TAC increased until it reached a stable

level for the remainder of the scan, which confirms

the irreversibility. For OLS, FGLS, TLS and RFR

calculation, the results include noisy and non-noisy

data. After fitting the data in the statistical models,

two numerical methods used to evaluate the goodness

of fit for all linear regression analyses were included:

the sum of squares due to error (SSE) and the standard

error (SE), known as the root mean squared error

(RMSE) as well. The numerical measures are more

closely concentrated on a specific aspect of the data

and often try to compress that information into a

single number. SSE measures the total deviation of

the response values from the fit, where a value closer

to 0 indicates a smaller random error component

within the model selected, and the fit will be more

useful for prediction. It is also known as the summed

square of residuals.

Optimising Graphical Techniques Applied to Irreversible Tracers

SSE= (y

-y



i=1

)

(29)

Where y

is the i

value of the variable to be

predicted, 



 is the predicted value of y

. SE is an

estimate of the standard deviation of the random

components in the data and is similar to the SSE. An

SE value closer to 0 indicates a fit that is more useful

for estimation. SE is described as

SE=



MSE,MSE=

SSE

,v=n-m

(30)

Where MSE is the mean square error or the residual

mean square and v indicates the number of

independent pieces of information involving the n

data points that are required to calculate the sum of

squares, which is calculated as the number of

response values n minus the number of fitted

coefficients m estimated from the response values.

Figure 6: TACs for the reference tissue (cerebellum) and

ROI (left striatum) that were obtained from the first

simulation data without noise are plotted as an example.

A one-way repeated measured analysis of variance

(ANOVA) was conducted to evaluate the null

hypothesis that there is no change in the simulations’

Ki value when calculated with different statistical

regression models in all four groups (N = 10). The

results of the ANOVA indicated a significant effect,

Wilks’ Lambda = .001, F(3, 7) = 41.17, p < 0.01, η2

= .75. Thus, there is significant evidence to reject the

null hypothesis. Follow-up comparisons indicated

that each pairwise difference was significant, p <

0.01, except between OLS and TLS, where p = 0.09.

There was a significant difference between the

statistical models used, suggesting that using a

different linear regression model reveals a different

Ki value, which is the main parameter of diagnosis. A

repeated measures ANOVA is performed when the

samples are considered related (dependent) and more

than two groups. Table 2 illustrates te SE and SSE for

each method applied to simulation data. With the

OLS method, the min SE in all simulations including

noisy data was 0.05680 and the max was 1.01070; the

average SE was 0.23551. For SSE, the min was

0.00029, max 0.09286 and the average 0.00741. The

fold change range was between 0.00041 and 2.09565.

FGLS calculations with the data showed the SE min

was 0.0012377, max 0.0105768 and the average

0.0041978. The SSE min was 0.0000001, max

0.0000102 and the average 0.0000020, with a general

fold change range of 0.0032366-2.3815366. For TLS

analysis, the min SE was 0.05337, max 18.79341 and

the average SE in all data calculations was 2.86733.

The SSE min was 0.00026, max 32.10839 and

average 1.58100. The fold change range was

0.00506-2.09567. The min SE in the RFR analysis

was 0.07026, max 0.92162 and the average 0.37945.

The SSE min was 0.00045, max 0.07722 and the

average 0.01797 with a fold change range of 0.00755-

2.83829.

Table 1: A one-way repeated measured analysis of variance

(ANOVA) result.

Test

Wilks’

Lambda

F(3, 7)

p -value

ANOVA

(N=10)

.001

41.17

p < 0.01

pairwise

difference

OLS and

TLS, pairwise

p < 0.01

p = 0.09

.75

Table 2: SE and SSE values for each method applied to

simulation data.

Stat. Model

SSE

fold

change

OLS

Min

0.0568

0.0003

0.7927

Max

1.0107

0.0929

Avg.

0.2355

0.0074

FGLS

Min

0.0012

0.1 



0.0049

2.5119

Max

0.0106

10.2 



Avg.

0.0042

2.0 



TLS

Min

0.0697

0.0004

0.0107

2.0719

Max

1.3071

0.1553

Avg.

0.4505

0.0237

RFR

Min

0.0703

0.0005

0.0196

1.6780

Max

0.9216

0.0772

Avg.

0.3795

0.0180

5 DISCUSSION

For most of the Ki values, it increases in proportion

to the level of noise. SE and SSE also increase with

higher noise level. In simulations 1-5, the data

behaved quite similarly with the noise effect

compared to simulations 6-10, which had more

scattering, and this could have been caused by

BIOIMAGING 2018 - 5th International Conference on Bioimaging

increasing the Ki amount for the data without noise.

A one-way repeated measurements ANOVA test

indicated that there is significant evidence to reject

the null hypothesis and confirm that those statistical

models reveal different results for the final Ki value.

Each statistical regression model dealt with the

simulation data in a different way, and based on the

goodness of fit evaluations, the best fitted regression

model can be chosen. Follow-up comparisons

indicated that each pairwise difference was

significant except between OLS and TLS. The p-

value between OLS and TLS shows that null-

hypothesis about equality can not be rejected at

confidence level 0.05 that is used with this test. The

significant difference between the statistical models

used, suggesting that using a different linear

regression model reveals a different Ki value, which

is the main parameter of Parkinson’s disease

diagnosis. The min SE and SSE were found with

FGLS, and this suggests that FGLS is the best of these

models to fit the noisy data. FGLS also had the second

lowest fold change rate, which measures the change

difference from the Ki value without noise. OLS and

TLS showed the lowest fold change rate, and that

indicates more resistance to the noise effect than the

other methods. RFR had the highest fold change rate

compared to the data without noise, which indicates

sensitivity to noise.

In the first simulation, the OLS Ki data had similar

values at all levels of noise, unlike the other data for

the rest of the simulations. For the first two

simulations, all statistical regression models behaved

similarly at all noise levels; thus, the Ki data points

were close in value. This could happen in link to the

original Ki values without noise where considered the

lowest among the other simulations. Other

simulations with low Ki values below 0.012, which

represents the diseased levels, could reveal more

details about how statistical models will behave. In

addition, Ki values lower than 0.012 could clarify

whether the noise could lead to moving the Ki values

to be considered normal. The big difference within

the SE from one noise level to another indicates the

high sensitivity to noise in linear regression analysis,

which confirms the previous results in the published

literature review. The experiment has contributed to

the knowledge in the field by suggesting using FGLS

as a linear regression method for Patlak graphical

analysis. From the above results, using FGLS could

provide better data fitting with low SE and SEE,

indicating more accurate results than other

approaches. Including lower Ki values without noise

could give more details and better confirms the best

fitting model from regression methods. Repeating the

experiment with different equivalent time (t*) points

could reveal more details and alter the accuracy of

those methods. It would be useful to apply those

models on clinical data obtained from patient

dynamic images and compare the results to the

outcome of this experiment.

6 CONCLUSION

Graphical techniques in PET data analysis from

reference tissue are considered simple means of

analysis to obtain physiological parameters. One

issue usually generated with this type of analysis is

the bias introduced, which is caused by the sensitivity

to statistical noise. The study shows there is a

significant difference between the statistical models

used, suggesting that using a different linear

regression model reveals a different Ki value, which

is the main parameter of Parkinson’s disease

diagnosis. Analysing the PET data with different

statistical regression approaches and evaluating each

approach graphically and numerically could improve

the final result for more accurate diagnosis. FGLS

regression model could provide better data fitting in

Patlak analysis with low SE and SEE, indicating more

accurate results than other approaches. In the next

work, these methods will be applied to clinical PET

data obtained from a clinical trial to see how the final

result will be affected.

REFERENCES

Feng, D., Wang, Z. and Huang, S.-C. 1993. A study on

statistically reliable and computationally efficient

algorithms for generating local cerebral blood flow

parametric images with positron emission tomography.

Medical Imaging, IEEE Transactions on 12(2), pp. 182-

188.

Feng, D. et al. 1996. An unbiased parametric imaging

algorithm for nonuniformly sampled biomedical system

parameter estimation. Medical Imaging, IEEE

Transactions on 15(4), pp. 512-518.

Fox, J. 2002. Robust regression. An R and S-Plus

companion to applied regression.

Freedman, D. A. 2008. On regression adjustments to

experimental data. Advances in Applied Mathematics

40(2), pp. 180-193.

Freedman, D. 2009. Statistical models: theory and practice.

Cambridge: Cambridge University Press.

Granger, C. W. J. 1994. Learning and practicing

econometrics: Griffiths, We, Hill, Rc, Judge, Gc.

Journal of Economic Literature 32(1), pp. 115-122.

Gujarati, D. N. 2009. Basic econometrics. Location: Tata

McGraw-Hill Education.

Optimising Graphical Techniques Applied to Irreversible Tracers

Haggstrom, I., Beattie, B. J. and Schmidtlein, C. R. 2016.

Dynamic PET simulator via tomographic emission

projection for kinetic modeling and parametric image

studies. Med Phys 43(6), p. 3104.

Haggstrom, I. et al. 2016. A fast dynamic PET simulator for

improved kinetic modeling estimation. Journal of

Nuclear Medicine 57(supplement 2), pp. 477-477.

Hayashi, F. 2000. Econometrics. Princeton, New Jersey:

Princeton University Press.

Hintze, J. 2001. NCSS and Pass. Number Cruncher

Statistical Systems, Kaysville.

Huber, P. J. 1964. Robust estimation of a location

parameter. The Annals of Mathematical Statistics

35(1), pp. 73-101.

Ikoma, Y. et al. 2008. PET kinetic analysis: error

consideration of quantitative analysis in dynamic

studies. Annals of Nuclear Medicine 22(1), pp. 1-11.

Kennedy, P. 2008. A guide to econometrics. 6th ed.

Malden, Massachusetts: Blackwell Pub.

Kutner, M. H., Nachtsheim, C. and Neter, J. 2004. Applied

linear regression models. Location: McGraw-

Hill/Irwin.

LLC, P. T. 2017. PMOD Biomedical Image Quantification.

[Format type]. Available at:

http://www.pmod.com/web/?page_id=476 [Accessed:

date].

Logan, J. 2000. Graphical analysis of PET data applied to

reversible and irreversible tracers. Nuclear Medicine

and Biology 27(7), pp. 661-670.

Logan, J. 2003. A review of graphical methods for tracer

studies and strategies to reduce bias. Nuclear Medicine

and Biology 30(8), pp. 833-844.

Logan, J. et al. 2001. A strategy for removing the bias in the

graphical analysis method. J Cereb Blood Flow Metab

21(3), pp. 307-320.

Long, J. S. and Trivedi, P. K. 1992. Some specification tests

for the linear regression model. Sociological Methods

& Research 21(2), pp. 161-204.

Markovsky, I. and Van Huffel, S. 2007. Overview of total

least-squares methods. Signal Processing 87(10), pp.

2283-2302.

Patlak, C. S. and Blasberg, R. G. 1985. Graphical

evaluation of blood-to-brain transfer constants from

multiple-time uptake data: generalizations. J Cereb

Blood Flow Metab 5(4), pp. 584-590.

Patlak, C. S., Blasberg, R. G. and Fenstermacher, J. D.

1983. Graphical evaluation of blood-to-brain transfer

constants from multiple-time uptake data. J Cereb

Blood Flow Metab 3(1), pp. 1-7.

Petráš, I. and Bednárová, D. 2010. Total least squares

approach to modeling: a MATLAB toolbox. Acta

Montanistica Slovaca 15(2), p. 158.

Petras, I. and Podlubny, I. 2010. Least Squares or Least

Circles? A comparison of classical regression and

orthogonal regression. Chance 23(2), pp. 38-42.

Strutz, T. 2010. Data fitting and uncertainty: a practical

introduction to weighted least squares and beyond.

Location: Vieweg and Teubner.

Varga, J. and Szabo, Z. 2002. Modified regression model

for the Logan plot. Journal of Cerebral Blood Flow &

Metabolism 22(2), pp. 240-244.

Western, B. 1995. Concepts and suggestions for robust

regression analysis. American Journal of Political

Science 39(3), pp. 786-817.

BIOIMAGING 2018 - 5th International Conference on Bioimaging