Accelerated Simulation of Brittle Objects for Interactive Applications

Philippe Meseure

, Xavier Skapin

, Emmanuelle Darles

and Guilhem Delaitre

University of Poitiers, CNRS, XLIM Lab, UMR 7252, 86962 Futuroscope CEDEX, France

University of Limoges, CNRS, XLIM Lab, UMR 7252, 87000 Limoges, France

Keywords:

Physically-based Animation, Fractures, Connected-component Detection, Topological Models, Real-time

Simulation.

Abstract:

This article presents a model that aims at computing deformation and simulating fractures. To allow the use

of linear elasticity in small displacements for deformation of a brittle object while still enabling any rigid

motion, a rigid reference is computed using the Shape Matching method and all displacements are evaluated

with respect to this reference. Fractures are handled using a stress tensor computed at each vertex of the

object’s 3D mesh. Some accelerations are proposed, that allow a faster determination of fracture areas and a

fast processing of new connected components.

1 INTRODUCTION

For a long time, fracture simulation has been one

of the main concerns of physically-based animation

(Terzopoulos and Fleisher, 1988; Norton et al., 1991).

However, despite the amount of proposed solutions,

it remains a tedious process. As far as “rigid” brit-

tle objects are concerned, the fracture simulation con-

sists in computing the (inﬁnitesimal) deformation of

the object when subject to external constraints and

detecting where a local strain or stress exceeds some

threshold. Finite element models using linear elas-

ticity (Hooke’s constitutive law) has been proposed

in the pioneering work presented in (O’Brien and

Hodgins, 1999). However, such an approach and all

its derivatives require the (non-linearized) Green/St-

Venant deformation tensor which makes them more

computationally demanding. Real time ﬁnite element

methods usually assume that displacements are small

and use Cauchy’s inﬁnitesimal strain tensor (Cotin

et al., 1999; Cotin et al., 2000). Since, in rigid bod-

ies, fractures occur upon small deformations, this ten-

sor seems a good choice for the simulation of such

objects. Unfortunately, it does not allow the object

to rotate (it produces large deformation instead), and

rigid displacements cannot directly be taken into ac-

count. This limit is crippling for rigid object simula-

tion. In this article, we propose a model that allows

both rigid motion computation and strain computation

using Cauchy’s linear tensor, which makes it well-

adapted for interactive or real time environments.

In time-critical applications, the fracture process

appears as a heavy step of the simulation that should

beneﬁt from any solution that allows computation

time gains. We therefore highlight a method that

avoids the computation of a costly fracture criterion

by ignoring places where no fracture is likely to occur.

Moreover, since our method explicitly computes rigid

motion, it is necessary to handle each connected com-

ponent of the object separately. However, after a frac-

ture, a simulated object can split into multiple compo-

nents. Unfortunately, connected component detection

is a global topological property that requires a walk

through the whole mesh of the object. Ideally, this

walk should be proceeded only when new connected

component have actually appeared. We thus propose

the use of an oracle that avoids, as much as possible,

such a walk.

The paper is organized as follows: After the pre-

sentation of previous work in Section 2, the model

is detailed in Section 3. Section 4 presents how frac-

tures are handled and different process improvements.

Finally, Section 5 shows the obtained results before

concluding.

2 PREVIOUS WORK

Fracture simulation relies primarily on deformation

computation (Nealen et al., 2006), but many ap-

proaches exist (Muguercia et al., 2014). Indeed, when

a deformation is computed, different criteria can be

used to make cracks appear in the structure. Geomet-

ric criteria have been proposed, such as an elongation

Meseure, P., Skapin, X., Darles, E. and Delaitre, G.

Accelerated Simulation of Brittle Objects for Interactive Applications.

DOI: 10.5220/0006526400280039

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages

28-39

ISBN: 978-989-758-287-5

of springs beyond a given threshold (Norton et al.,

1991) or an excessive strain tensor value (Terzopou-

los and Fleisher, 1988). Force or stress thresholds can

be used as well. Thus, O’Brien and Hodgins proposed

a simulation of fracture based on linear elasticity and

the computation of a separation tensor at each mesh

vertex (O’Brien and Hodgins, 1999). The separation

tensor of a vertex is obtained from the stress tensor

of the surrounding elements. By considering posi-

tive and negative eigenvalues separately, each tensor

is separated into a tensile tensor and a compressive

one. Tensor components of volumes surrounding a

node are associated to create a new node tensor that

allows to take into account both tensile and compres-

sive stresses. This method has been extended in var-

ious approaches, for instance (Pfaff et al., 2014) to

simulate 2D tearing and (Koschier et al., 2014) for

adaptive resolution models. To handle fractures, it is

also possible to rely on modal analysis (Glondu et al.,

2012), but this is a global method that can be quite

costly, especially for high resolution meshes. Bound-

ary element method have also been used (Hahn and

Wojtan, 2015; Hahn and Wojtan, 2016). Fractures

can also be applied on meshless models (Pauly et al.,

2005).

Cracks may be applied wherever a fracture crite-

rion is veriﬁed. However, it is possible to focus only

on high stress areas, and control cracks to avoid a

shattering effect (Koschier et al., 2014). Local ge-

ometry is not necessarily adapted to the topological

modiﬁcations that the mesh should undergo. Some

methods propose to virtually cut volumes while keep-

ing well-shaped elements but the used mesh is no

longer manifold (Molino et al., 2004). XFEM ap-

proaches consider discontinuous element shape func-

tions to represent and simulate fractures (Koschier

et al., 2017). Some interactive methods tend to

use predeﬁned crack patterns that locally modify the

mesh (M

uller et al., 2013; Chen et al., 2014; Parker

and O’Brien, 2009), but cracks are not “physically-

managed” in such cases. The solution proposed in

(Schvartzman and Otaduy, 2014) appears as a com-

promise where the crack pattern is completely applied

at the time of impact (no crack propagation) but is

adapted to the deformation energy ﬁeld in the fractur-

ing body and can be user-controlled.

Different deformable models can be used to ﬁnd

fracture zones, but many approaches rely on continu-

ous mechanics, solved by a ﬁnite element method, as

in (O’Brien and Hodgins, 1999) and subsequent work.

Since an object can break due to small displacements,

using a linearized, more computationally-efﬁcient,

strain tensor is possible, but is not compatible with

rotations of the object. The corotational method con-

sists in computing local rotations at each node to ex-

tract rotation and focus on deformation only (M

uller

et al., 2002). This method has been used to simu-

late fractures (M

uller et al., 2004; Chen et al., 2014),

but is known to produce ghost forces. To avoid such

forces, a rotation can be computed, not for every node

but for every element. However, in such a case, the

fracture criterion should rely on the stress computed

for each element (M

uller and Gross, 2004) and not on

each node. Indeed, a node has several possibly differ-

ent displacements, one for each surrounding element.

Considering a node-based measure of stress can be

seen as non-consistent. Approaches based on node

stress criteria for corotational FEM models have been

used in some work (Busaryev et al., 2013) although

they lack theoretical backgrounds.

To conciliate computationally-efﬁcient deforma-

tion measures and rigid motions, some methods con-

sider that a brittle object deforms and eventually

breaks only for given situations. They propose to sim-

ulate this object as a perfectly rigid one, but switch to

a static computation of (linear) deformation in case of

collisions (M

uller et al., 2001; Bao et al., 2007; Liu

et al., 2011). It is also the case in (Zhu et al., 2015)

by relying only on a surface mesh to compute both

deformation and crack path. Such approaches sup-

pose that only an instantaneous impact can produce

fractures. Nevertheless, to simulate a fracture result-

ing from a progressive deformation (see Figure 7), a

dynamic approach should be preferred (Glondu et al.,

2012; Koschier et al., 2014). Anyway, the simula-

tion of a rigid body simulation (with only 6 degrees of

freedom) is several orders of magnitude faster to com-

pute than a ﬁnite element mesh. In time-critical ap-

plications, the computation time of a simulation step

should be kept as constant as possible. It cannot be

envisaged to switch from a rigid body to a ﬁnite ele-

ment model without expecting a high variation of the

latency of the simulation system. Instead, for such ap-

plications, we think that simulating a breakable rigid

body, at every time step and not only time step with

collisions, using a low-deformable model is accept-

able.

Indeed, ﬁnite element methods for small displace-

ments appear to be fast enough to allow real-time in-

teractions (Cotin et al., 2000; M

uller et al., 2002). To

deal with rotations, rigid motions should be computed

by an additional, coupled, model. The pioneering

work in (Terzopoulos and Witkin, 1988) has shown

how to combine rigid body laws of motion with lin-

ear deformations. Unfortunately, the equations of

rigid motion and deformation are coupled and there-

fore hard to solve in real time. The Shape Matching

method aims at ﬁnding the minimum deformation be-

Accelerated Simulation of Brittle Objects for Interactive Applications

tween a given shape and a modiﬁcation of this shape.

This method has been used in Computer Graphics

to simulate the deformation of a body by comparing

the position of each node to its corresponding refer-

ence node in the undeformed body and adding a force

which tends to minimize the difference (M

uller et al.,

2005). In practice, this approach consists in inserting

a spring between these two positions. The resulting

simulation is fast and allows some special animation

effects, but is usually not realistic. Note that, while

observing a moving deformable object, the separa-

tion between the rigid motion and the deformation of

the body is quite arbitrary. Shape Matching appears

as a way to deﬁne, by minimizing deformation, the

rigid reference component. This can appear as a non-

physical approach, since the motion of this rigid com-

ponent is not guaranteed to be continuous (motion is

not taken into account in the computation, only po-

sitions are relevant with this method). However, it is

possible to smooth the motion of the rigid component

to make it look like continuous. Shape Matching must

be applied separately for each connected component

of the object. More generally, any method that com-

putes rigid motions explicitly, should precisely detect

each new detected component after a fracture (M

uller

et al., 2001).

To overcome the above-mentioned limitations,

this paper presents an approach that:

• Relies on linear elasticity to compute the deforma-

tion of a brittle object. Displacements are guar-

anteed to be small by optimizing the position of

a rigid reference from which displacements are

computed.

• Uses an accelerating technique based on Ger-

schgorin’s theorem to ﬁnd fracture locations

rapidly.

• Uses an oracle based on “vertex splitting” to de-

tect the appearance of any new connected compo-

nent and update the computation of the rigid ref-

erence of each connected component.

3 AN ALMOST-RIGID

DEFORMABLE MODEL

In our model, the deformation is considered to be as

small as possible (remember that most brittle objects

appear to be rigid at the macroscopic scale). In other

words, most energy of the system should be spent

for rigid motion, while the remaining energy should

be used for deformation. At each time step, position

and orientation corresponding to the rigid motion are

both determined using the Shape Matching method

and allow to deﬁne a, so-called, “rigid reference”. In

uller et al., 2005), the Shape Matching method was

mainly used to avoid the use of a mesh, by supplying

a mass/spring model with a fast way to handle its vol-

umetric behavior. On the contrary, in our approach,

the Shape Matching aims at computing the position

and orientation of a rigid reference to compute a min-

imum deformation and maintaining, as long as pos-

sible, the hypothesis of small displacements required

by the linear elasticity continuous model.

Figure 1 shows, for a block supported by immov-

able obstacles placed at its ends, both its deformed

state and rigid reference.

Figure 1: Model/reference coupling: A deformable model

(wireframe) is computed using dynamics laws and a rigid

reference (ﬁlled faces) is computed using Shape Matching.

3.1 Principles

Our model is a tetrahedral mesh where each vertex

i is characterized by a current position x

and a rest

position x

(deﬁned in an undeformed and centered

conﬁguration). At each time step, the process consists

in:

1. Applying Shape Matching with the current and

rest positions of the mesh vertices to obtain both

position (a translation vector τ) and orientation (a

rotation matrix R) of the rigid reference,

2. For each vertex, computing the reference position

ref

= Rx

+ τ and its displacements as d

= x

−

ref

3. Calculating the forces applied to each vertex by

each tetrahedron, using an explicit ﬁnite element

approach,

4. Summing all the forces applied to vertices, in-

ferring their accelerations and integrating them

twice,

5. Handling fractures.

An explicit ﬁnite element method is used (M

uller

et al., 2001) to solve the equations of linear elastic-

ity based on Cauchy’s inﬁnitesimal strain tensor. Let

C be the 6 × 6 stress-strain matrix based on Young

modulus and Poisson coefﬁcient. For each tetrahe-

dron (e), both 6 × 12 strain-displacement matrix B

(e)

and 12 × 12 rigidity matrix K

(e)

are computed during

a pre-processing phase:

(e)

= B

(e)

(1)

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

At each time step and for each tetrahedron (e), the

forces exerted on its vertices are computed as:

(e)

= K

(e)

(2)

where d

(e)

is a vector that gathers the displace-

ments of the four vertices, and f

(e)

gathers the forces

resulting from the deformation of the tetrahedron and

applied on the vertices.

The use of explicit or semi-implicit integration

schemes is theoretically possible, but in the case

of fractures, very small time step (microseconds or

tenths of microseconds) should be chosen. Indeed, to

simulate fracture and avoid large deformation, a high

stiffness (i.e. Young modulus) is required which di-

rectly impacts stability. Such small time steps are not

compatible with interactivity time constraints. The

implicit Euler method combined with the Newton-

Raphson method to solve non linear systems (Baraff

and Witkin, 1998) allows large time steps but can re-

sult in a highly-damped behavior for stiff systems.

Recently, exponential methods have been proposed

(Michels et al., 2017). These approaches allow the

resolution of stiff equations in a fast and robust way

while not loosing as much mechanical energy as im-

plicit methods. In our case, the implicit Euler system

is solved as proposed in (Hilde et al., 2001). This

method is mainly dedicated to small time steps and

does not require the computation of the Jacobian ma-

trix of the system while still allowing a good control

of the convergence of the system resolution. Other

integration methods such as implicit or exponential

ones could be used, for more efﬁcient computation

times for instance, but not with the intent of reducing

the time step.

Fractures are handled as in (Koschier et al., 2014).

Note that after one or more fractures, multiple con-

nected components may appear. Shape Matching

must therefore be applied on each connected compo-

nent (R and τ are computed for each one), so a pre-

cise detection of any new component is mandatory. In

our implementation, all the vertices that belong to hte

same connected component share the same id. The

various simulation steps that depend on connected

components (for instance, the deformation computa-

tion) are slightly modiﬁed, to take into account the

data related to the concerned connected component,

using the id stored in vertices.

The overall algorithm for computing the behavior

of a body is given in algorithm 1.

3.2 Using Shape Matching

As explained in (M

uller et al., 2005), for a given con-

nected component, the position of its rigid reference

Algorithm 1: computeDeformationForces().

Data: cc[] is a table containing the attributes of

each connected component

// Compute position and orientation

// of each connected component

computeCCState();

// Compute displacement of each vertex

foreach Vertex v do

Vec3 p = v.pos −cc[v.idCC].pos ;

Vec3 p0 = cc[v.idCC].orientation

× p ;

v.displacement = p0 − v.pos0 ;

end

// Compute deformation forces of each

// tetrahedron and distribute them

foreach Tetrahedron t do

Vec12 d = getVertexDisplacements(t) ;

Vec12 f = t.matK × d ;

foreach Vertex v of t do

v.force+ =

cc[v.idCC].orientation × f[v] ;

end

is deﬁned as the position of the center of mass G of

its point cloud:

∑

i=1

∑

i=1

(3)

where N is the number of vertices in the mesh, m

the mass of each of them and x

their position. The

rotation is extracted from the following matrix:

A =

∑

i=1

(4)

where p

is the relative position of the i

vertex

with respect to the center of mass, that is p

= x

−x

The computation is shown in algorithm 2. Note that

there is no loop such as “for each element of a con-

nected component”, which could cause computation

time overheads due to dedicated walk through the

topological structure of the simulated body.

This method is basically an approach that com-

putes a position that minimizes the length of all p

(grouped in a single energy function). Unfortunately,

the method ignores the history of motion. Therefore,

the temporal continuity of the rigid reference’s ori-

entation cannot be ensured. In practice, when the

number of vertices is high enough, no discontinuity

is observed. Indeed, the global minimum of the en-

ergy function varies slightly. Nevertheless, orienta-

tion discontinuities may appear with regards to con-

nected components with a small number of vertices.

Accelerated Simulation of Brittle Objects for Interactive Applications

Algorithm 2: computeCCState().

foreach Vertex v do

// Accumulate position and mass

// into v’s connected component

cc[v.idCC].pos+ = v.pos ;

cc[v.idCC].mass+ = v.mass ;

end

// Compute positions

foreach Connected Component idCC do

cc[idCC].pos/ = cc[idCC ].mass ;

// Compute matrix of equation (4)

foreach Vertex v do

p = v.pos − cc[v.idCC].pos ;

cc[idCC].matA+ = p × v.pos0

;

end

// Compute orientations

foreach Connected Component idCC do

cc[idCC].orientation =

extractRotation(cc[idCC].matA) ;

In this case, several local minima exist, and the global

one rapidly changes among these.

It turns out that only isolated tetrahedra (in other

words, connected components with only four ver-

tices), exhibit such a discontinuous behavior. We have

investigated a ﬁrst solution that considers isolated

tetrahedra as rigid, since they are atomic elements of

the initial mesh. This can be done in our algorithm

using only a slight modiﬁcation, by considering that

rigid bodies can be simulated using a constrained de-

formable model (van Overveld and Barenbrug, 1995).

More precisely, the vertices are ﬁrst moved according

to external forces, then Shape Matching is computed

for the tetrahedron, as done for any connected com-

ponent of the model. After that step, current vertex

positions x

in isolated tetrahedra are projected onto

their corresponding reference position (x

ref

). Veloc-

ity is adapted accordingly. This solution has a draw-

back: Isolated pseudo-rigid tetrahedra tend to stop ro-

tating quite quickly. Indeed, angular momenta are not

explicitly maintained by this approach, rotations re-

sult from the difference of velocities of the vertices

of the tetrahedra. Since vertices are forced to keep

their tetrahedron undeformed, they tend to loose ve-

locity and therefore, the orientation of their tetrahe-

dron steadies rapidly.

We have investigated another solution to compute

rotation of isolated tetrahedra, by using a QR decom-

position as proposed in (Nesme et al., 2005). This

method provides better stability for tetrahedra (i.e. ro-

tation matrix continuity), provided that the QR de-

composition is handled with the same vertex order be-

tween two steps.

3.3 Display

Even if a high Young modulus is applied, the object

can still exhibit visible deformations due to the com-

putation time step which is too large for fractures (see

Figure 1). To guarantee an accurate display of the ob-

ject, the rigid reference can be displayed instead of

the deformable body itself. This approach works well

in practice, but has an impact on the collision process

of the simulation, if overlaps must be avoided. For-

tunately, since the reference body is not physically

simulated, any modiﬁcation of position and orienta-

tion can be applied arbitrarily, for display only. Any

correction method that controls the position and ori-

entation of a rigid body, such as an optimization algo-

rithm to minimize overlap, can therefore be applied.

In our simulation, no correction was however neces-

sary, since overlaps were low enough in practice.

Shape Matching is applied independently on each

connected component. Should a new connected com-

ponent appear after a fracture, it is unlikely that its

newly-computed position and orientation are contin-

uous with respect to the position and orientation it

had previously, when it was still connected. Fig-

ure 2 illustrates this discontinuity problem. To avoid

the discontinuity of display, an interpolation between

its previous state and its newly-computed one is ap-

plied. More precisely, a current state is ﬁrst com-

puted, based on its original connected component.

This can be easily made by applying Shape Matching



ref



positions. Next, a target state is computed

by applying Shape Matching on

{

}

positions. Af-

ter a fracture, current and target states differ. Target

state should be used for the display of its correspond-

ing connected component, but its position may be too

far from the position where it was previously located.

Current state corresponds to the location of the con-

nected component at the fracture time. During the

following time steps, we choose to modify the posi-

tion and orientation of the current state so that it tends

to reach the target state. Although a proportional-

derivative controller could be used for this purpose,

only a simple proportional controller has been used

in our implementation and gives satisfying results in

practice. Let τ

cur

and τ

target

be the current and the

target translations respectively. Then τ

cur

is updated

to τ

cur

+ α(τ

target

− τ

cur

), where α is a small value

(typically 0.1 or less). A similar approach is used

for rotation, based on quaternions, since they offer

a convenient way to interpolate rotations (Shoemake,

1985). If q is a quaternion representing the rotation

that transforms the current orientation into the target

orientation of a connected component, the quaternion

q + 1 represents (after renormalization) half this rota-

tion. By repeating this simple formula several times,

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

we can quickly divide the angle of rotation between

current and target orientation by any power of 2. Ac-

cordingly, the α value used for translation is chosen

as the corresponding negative power of 2.

Note that the target state is also updated at each

time step, since all x

positions change. A more gen-

eral approach, where a rigid reference is simulated as

a perfect rigid body, linked by two springs, one linear

and the other one angular, to the deformed conﬁgu-

ration, and subject to collisions constraints is another

way to compute the current state at each time step.

This approach is physically-based but results in a 2

order control of the current state used for display, so

possibly an undesirable latency.

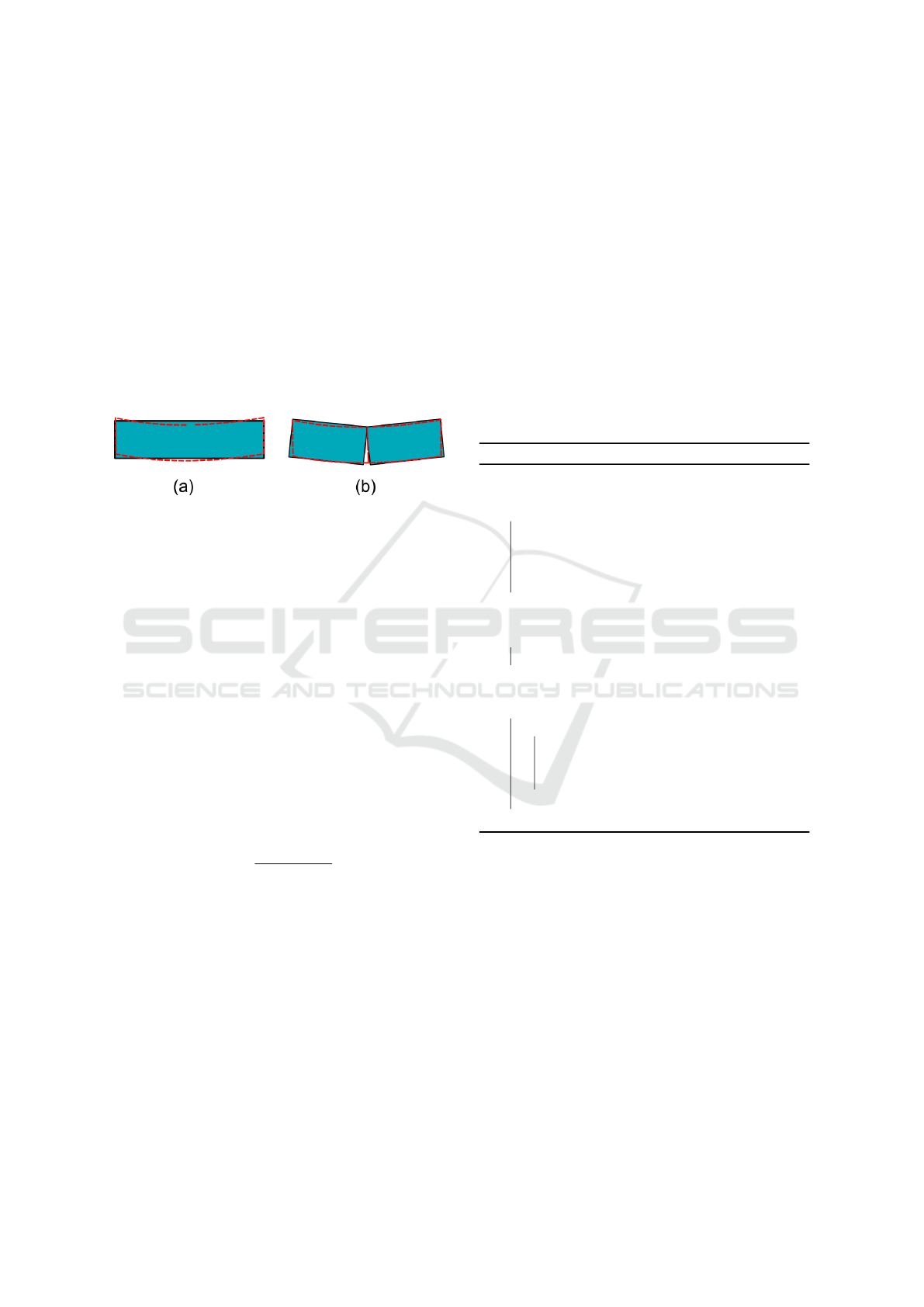
Figure 2: Discontinuity issue with Shape Matching. (a) A

red block is deformed (red dotted line) and Shape Matching

provides a position of the rigid reference (solid line). (b)

A fracture occurs and the object is split. Shape Matching

is separately applied on both connected components and re-

sults in a discontinuous state with respect to their positions

in (a).

4 FRACTURE PROCESS

Due to the linear interpolation functions used by the

ﬁnite element method, the stress tensor is constant all

over each tetrahedron and can be computed as:

(e)

= CB

(e)

(5)

As proposed in (Koschier et al., 2014), a node

stress tensor can be computed for each vertex as:

σ =

∑

(e)

∑

(e)

(6)

where m

(e)

is the mass of the element (e). Here,

the expression has been slightly modiﬁed compared

to the original article, but the result is the same. Our

notation only aims at showing that it is basically a

weighted average value of surrounding element stress

tensors. Note that, if each tetrahedron provides each

of its vertices with a quarter of its mass (mass lump-

ing technique), the denominator of equation 6 corre-

sponds to the mass of the concerned node multiplied

by 4. A fracture is applied on some vertex when

at least one eigenvalue of its stress tensor exceeds a

given threshold ξ. A fracture plane is built using the

related eigenvector as its normal. Each surrounding

tetrahedron is marked as “positive” or “negative” de-

pending on the side of the plane where its center is po-

sitioned. Any face that is adjacent to a pair of tetrahe-

dra with different signs is split to separate them. The

whole process aims at splitting a fan of faces around

the “fracture vertex” to make it split. If a fracture gen-

erates new connected components, these components

must be identiﬁed to allow distinct Shape Matching

applications when needed. This represents the last

step of the fracture process.

To accelerate this process, two lines of approach

have been considered: a fast location of fracture zones

and a fast identiﬁcation of new connected compo-

nents. The algorithm 3 give an overview of the frac-

ture process.

Algorithm 3: ﬁndFractures().

// Compute each tetrahedron stress tensor

and report it to its vertices

foreach Tetrahedron t do

Vec12 d = getVertexDisplacements(t) ;

t.σ = matC ×t.matB × d ;

foreach Vertex v of t do

v.σ+ = t.mass ×t.σ ;

end

// Average each vertex stress tensor

foreach Vertex v do

v.σ/ = (4 × v.mass) ;

end

// Check where a fracture occurs

foreach Vertex v do

if gerschgorinTest(v.σ,ξ) then

Vec3 eigenval = eigenValues(v.σ) ;

if max(eigenval) ≥ ξ then

split(v,eigenvec(max(eigenval)) ;

end

4.1 Finding Fracture Location

One important time loss during fracture location

comes from the necessity to compute eigenvalues of

stress tensors, merely to determine if one of them may

exceed some threshold ξ. In mechanical engineering,

this step is often sped up using the Gerschgorin’s the-

orem which, to our knowledge, has never been pro-

posed to the Computer Graphics community. This

theorem states that an upper bound of the eigenvalues

of a square matrix M can be computed considering

the sum of absolute values of some of its terms. In our

case, M is a symmetric matrix, so the upper bound can

be found by computing the maximum value of three

Accelerated Simulation of Brittle Objects for Interactive Applications

terms b

, one for each column i:

= M

∑

j6=i



(7)

After calculating the stress tensor of a vertex, the

associated b

values are computed. If all of them re-

main below the fracture threshold, no fracture appears

at this vertex and the eigenvalues computation can be

avoided. On the contrary, if the test fails, the eigenval-

ues must be computed since, if at least one of them is

greater than the given threshold, its associated eigen-

vector must be known for the following steps. Note

that the overall complexity is small, since only 6 ﬂoat-

ing point additions, 6 absolute values and 3 compar-

isons are necessary to complete Gerschgorin’s test at

a vertex.

4.2 Connected Component

Determination

Each connected component of the body is character-

ized by a rigid reference, deﬁned as a current state

(position and orientation) and a target state. When

a fracture occurs, one or more new connected com-

ponents might appear, which should be clearly iden-

tiﬁed to update their states. Connected components

identiﬁcation requires to scan all the elements (for in-

stance vertices) of the current connected component

and mark them (more precisely, in our implementa-

tion, “marking vertices” means providing them with

the id of their connected component). If some ele-

ments are not marked (i.e. these elements still store

the id of their connected component before fracture),

that means that another connected component must

be identiﬁed. Reversely, if all elements are marked,

that means that no other connected component exists.

This is a time-consuming process (linear with respect

to the number of elements to be marked, i.e. vertices

or volumes) that should be avoided when no new con-

nected component is created (in other words, when a

ﬁrst walk would uselessly mark every element).

We propose to use an oracle that can test this case,

in order to speed up the overall component identiﬁca-

tion. Of course, it must be efﬁcient enough to avoid

false positive cases as much as possible (that is, cases

where the oracle announces new connected compo-

nents whereas no such component has appeared ac-

tually). Moreover, the oracle should be fast enough:

If its computation algorithm is too complex, it will

not be able to compete with a complete walk through

the structure. We found an efﬁcient oracle by con-

sidering how many vertices split after each face split.

Indeed, when two adjacent tetrahedra are separated,

the support edges and vertices of the face must nec-

essarily split to allow the creation of a new connected

component. In Figure 3, it is shown that the three ver-

tices and three edges of a triangular face actually split

when a new connected component appears. Note that

if three vertices split, then the three edges necessar-

ily split. Therefore, after a face split, the vertices and

only the vertices of the face are checked for a split.

If, at least, one of these does not split, it is ensured

that no new connected component has been created.

On the contrary, if the three vertices split, then a new

connected component may appear, and this should be

checked further. Note that the vertex split criterion

must be checked after the split of each face of a fan

and not once the overall split is over. An appropriate

topological model should be used to ensure that the

vertex split is tested effectively (Lienhardt, 1994).

Figure 3: Oracle to detect if one new connected component

appears after a face split. In (a), only one vertex and two

edges split, so there is no new connected component. In (b),

three vertices and three edges split, so one new connected

component may appear.

Note that both criteria are local whereas the con-

nected property is global. It cannot be expected that

our oracle produces only right predictions, false pos-

itives are still possible: For instance, such a phe-

nomenon appears when two parts of an object are lo-

cally separated, but are still joined if the entire struc-

ture is considered, as shown in Figure 4. When using

the vertex split oracle, face ordering may sometimes

inﬂuence the ﬁnal result and produce false positive

cases,as shown in Figure 5. For each subﬁgure, the

red arrow shows the last face that is split. In (a), only

two vertices (green and yellow) split and in (b), only

one vertex (yellow) splits. In such cases, the oracle is

right and states that there cannot be a new connected

component (which is the case: the surrounding parts

remain adjacent, for instance around the black ver-

tices, since these vertices do not split). In (c), how-

ever, the last face makes three vertices split (red, green

and yellow ones). In this case, the oracle is false,

since it concludes that a new connected component

has appeared. Note that, if only one other face re-

mained to be split at that time, the central vertex of

the fan would not split (it splits only when the last

face is split) and the oracle would not conclude that

a new connected component appears. As a conse-

quence, faces of fans with an edge at the surface of

the object (as it is the case in the ﬁgure) should be

checked ﬁrst if possible, because these faces produces

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

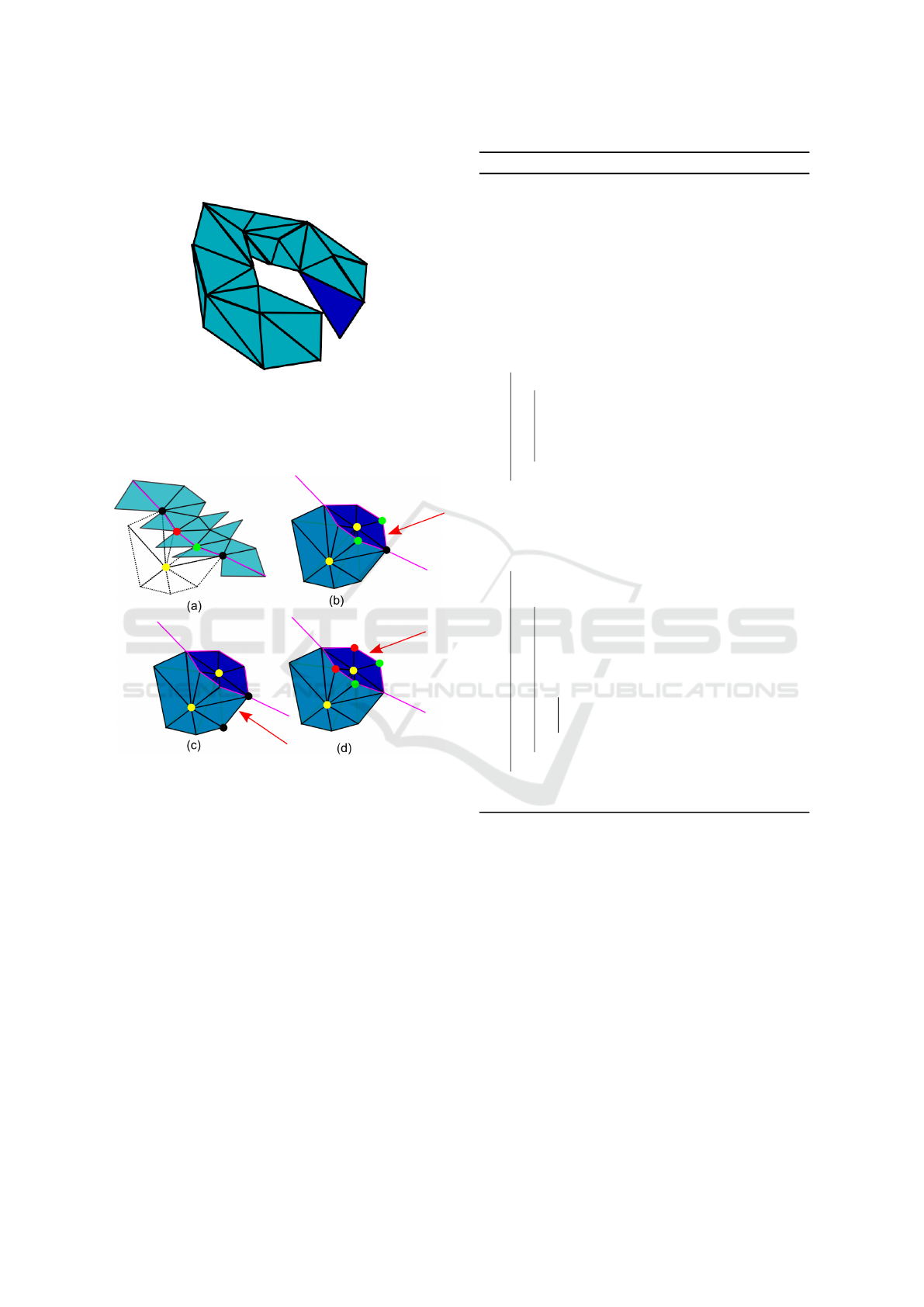
false positive if split at the end of the process. The al-

gorithm 4 show the complete split process.

Figure 4: False positive of any local oracle. A local sep-

aration has occured, so any local oracle predicts a new

connected component, but the separated faces still belong

to the same connected component (initially topologically-

equivalent to a torus).

Figure 5: False positive of split vertex oracle. (a) represents

a series of adjacent edges (in magenta) at the mesh surface

(in blue). A fan (dotted lines) is deﬁned around a vertex (in

yellow), inside the mesh, just below the surface faces. In

(b) and (c), if the pointed face is the last face to be split, at

least one of its vertex (in black) does not split. In (d), if the

pointed face is the last face to be split, the oracle predicts a

new connected component as its three vertices (red, yellow

and green) split. This face, with an edge at the surface of

the mesh, should be split when at least one other face of the

fan has not been split yet.

5 RESULTS

Several examples have been simulated and are repre-

sented in Figures 6 and 7. In both cases, the simu-

lated object is the same. The ﬁrst one (Figure 6) cor-

responds to a classical fracture scenario where rigid

objects are shot toward a breakable one. This example

shows the shattering effect obtained when a fracture

Algorithm 4: split(v,u).

Data: v is a vertex

Data: u is the normal of the fracture plane

curidCC = v.iddCC ;

// Get the signs of tetrahedra around v

relatively to fracture plane

foreach Tetrahedron t around v do

t.sign = getSign(center(t), plane(v,u)) ;

// Search for faces adjacent to

// positive and negative tetrahedra

Bool newCC = f alse ;

foreach Face f around v do

if tetrahedra( f ) have different signs then

splitFace(f) ;

// Check for oracle

if all vertices( f ) have split then

newCC = true ;

end

// If oracle predicts new connected

components, identify them

if not newCC then return;

foreach Split Face f do

Vertex v1 =one of f ’s vertices ;

if v1.idCC == curidCC then

newidCC = getNewIdCC() ;

// Only loop over

// a connected component

foreach Vertex v2 in

connectedcomp(v1) do

v2.idCC = newidCC ;

cc[newidCC]+ = v2.mass ;

end

releaseIdCC (curidCC) ;

is applied wherever the fracture criterion is true. The

second case study (Figure 7) corresponds to a tension

that progressively deforms an object so that it eventu-

ally breaks. First, this example shows that fractures

may appear well after a collision has occurred, so the

dynamic approach of fracture is mandatory. Second,

it illustrates that the display of the rigid reference is

very useful. Indeed, in practice, the deformable mesh

undergoes visible deformations before fracturing (this

is the reason why the object does not break imme-

diately). The display of the deformable mesh would

not have produced the same visual effect. Another

case study aims at simulating a more complex object,

namely the Stanford Bunny (Figure 8). The mesh pa-

rameters used by the simulation are given in table 1.

In these scenarios, collision and self-collision de-

Accelerated Simulation of Brittle Objects for Interactive Applications

Table 1: Different test scenarios and their characteristics.

Scenarios #Tetras #Vertices

Struck monolith 413 174

Strained block 413 174

Falling bunny 6142 1363

tection has been handled using an approximative but

fast approach. They were mainly based on a penalty

method: Any environment obstacle is approximated

by a force ﬁeld (for instance, ground or rigid bodies).

Every tetrahedron of the breakable body is bounded

by a sphere that also produces a repulsive force ﬁeld

for points located inside it. Each vertex is checked

against all the force ﬁelds (a regular grid is used for

speeding up this step). Collision between vertices and

tetrahedron force ﬁelds are taken into account only if

they do not belong to the same connected component

(this is quickly determined as each vertices knows

the id of its connected component). A more precise

but efﬁcient collision detection and response could be

used (Glondu et al., 2014), but requires to be adapted

to deformable bodies if used in our approach.

Note that the Broyden method to solve the implicit

integration equations does not converge as quickly

as a Newton-Raphson resolution. Note also that

no parallelization (CPU multithreading or GPU) has

been applied on the algorithms, except the use of

SIMD processor instructions for FEM computations.

We are completely aware that these times could be

largely improved as most similar approaches are usu-

ally based on GPU programming. However, the frac-

ture process is hard to parallelize in practice (because

of conﬂict access to the topological structures of the

object). This is why we did not worry on paralleliz-

ing the simulation itself to get a better performance

and chose to focus on fracture only.

The average and maximum simulation times are

shown in Table 2 for both corotational and our shape-

matching-based method. These times correspond to

a complete time step, including collision and self-

collision detection. The same object with the same

physical properties are simulated in both methods. As

shown, the corotational method is always slower than

ours. This mainly shows that the rotations for each

volume element always require more time to com-

pute than a shape-matching on the connected com-

ponents. Applying fractures on a simulated model

usually implies a computation time overhead, about

20% for simple models but that can be up to 50%

for the stanford bunny (which involves a lot of mul-

tiple synchroneous fractures). The maximum compu-

tation time when applying fractures is also mentioned

in the table, although we do ﬁnd this time very sig-

niﬁcant. Indeed, we have noticed that this maximum

time usually occurs once, at the beginning of a frac-

turing phase, and is not reached anymore during the

subsequent fractures.

Table 2: Average and maximum simulation times ob-

tained for our different scenarios using corotational and our

method without fracture (i.e. with an unreachable fracture

threshold). For our method, the average and maximum

computation times with fractures is also given. All these

times include collision and self-collision detection.

Scenarios Corotational Our method With fractures

av. max. av. max. av. max.

Struck monolith 34 60 28 44 34 84

Strained block 27 53 17 26 20 70

Falling bunny 291 408 218 380 340 1320

Figure 6: Two balls striking a monolith.

Figure 7: A brittle block collapses under its own weight.

The effect of the different accelerations have been

evaluated. First, the impact of Gerschgorin’s test

has been measured. This test is, in average, 3 times

faster than an immediate computation of the eigen-

values. Table 3 shows the effectiveness of this test,

since about 80% or more successful tests actually cor-

respond to a large eigenvalue that implies a fracture.

The split vertex oracle for new connected compo-

nents has also been tested. In table 3, the efﬁciency,

that is the ratio of true positives, for the split-vertex

oracle has been measured, in our different test cases.

It can be seen that, for over 90% of cases, the oracle

is right. So the oracle is a satisfactory way to detect

if some new component has appeared. Note also that,

in all our experiments, the oracle has never produced

any false negative.

Table 4 shows the computation times dedicated to

the fracture process. Several comments can be made.

First, the worst case for the basic rupture process, that,

by default, searches for new connected components,

occurs when no new connected component is created.

Indeed, all the structure must be (uselessly) walked

through to ﬁnd this result. This proves that an ora-

cle that speeds up the new connected component de-

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

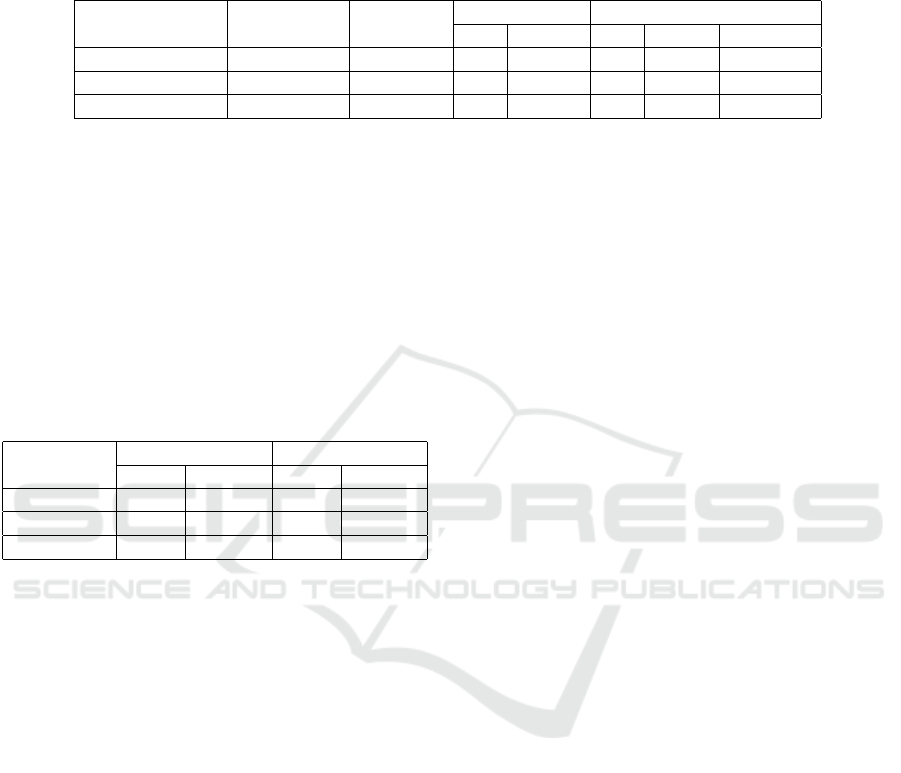
Table 3: Efﬁciency of Gerschgorin’s test and split-vertex oracle for different scenarios. The third column represents the

number of fan splits. The fourth column represents the number of fractures that actually result in the creation of new connected

components (CC) and the corresponding ratio. The ﬁfth column represents the number of cases where the split-vertex oracle

predicts new connected components, the corresponding ratio, as well as the efﬁciency calculated by checking if new connected

components actually appeared.

Gerschgorin #fractures #CC creations #new CC predictions

Scenarios efﬁciency # ratio # ratio efﬁciency

Struck monolith 85% 198 112 56.6% 119 61.1% 94.1%

Strained block 92% 190 104 54.7% 111 58.4% 93.7%

Falling bunny 78% 1639 759 46.3% 833 50.8% 91.1%

tection is really of interest. Next, the additional cost

of using split-vertex oracle is measured by compar-

ing the computations times in case of new connected

component creation using the oracle or not. This cost

represents of at most 2% of computation time. But,

this cost is clearly justiﬁed, because, when no new

component appears, the rupture time can be reduced

by, at least, 55%, and the global reduction can reach

67%.

Table 4: Computation times for the rupture process in dif-

ferent scenarios with and without split-vertex oracle, for

ruptures that create new connected components (CC) or not.

Without Oracle (ms) With Oracle (ms)

Scenarios new CC no new CC new CC no new CC

Struck monolith 0.97 1.2 0.99 0.5

Strained block 0.96 1.06 0.98 0.48

Falling bunny 30.73 32.3 31.2 10.66

To provide a meaningful comparison, we have im-

plemented the same node tensor fracture criterion on

a corotational FEM (even if, in previous work sec-

tion, we pointed out that this approach was lacking

a theoretical background). This implementation also

uses the Gerschgorin’s theorem to speed up the broad-

phase that seeks for fracture nodes. We found that

corotational FEM tends to produce lower node stress

tensors (which is quite expected: Node displacements

are lower since element rotations are cancelled). As

a consequence, the shattering effect is reduced and

the ﬁnal animation is quite different from the one ob-

tained with our method based on Shape Matching.

6 LIMITATIONS

The obtained fracture results heavily depend on

the initial tetrahedral mesh of the simulated object.

Remeshing techniques could be used to adapt the

mesh in the fracture zone, as several approaches have

already proposed (Su et al., 2009; M

uller et al., 2013).

These techniques are compatible with our method,

provided that the rest positions and mass of the new

vertices that appear after a remeshing are determined

and the mechanical data of elements (stiffness and

strain/deformation matrices) are updated accordingly,

which can be done at the price of a little computation

time. These techniques apply on a given connected

component, so no side-effect on existing connected

components are expected during the remeshing.

We actually investigated a local remeshing solu-

tion based on tetrahedron subdivisions based on Loop

scheme as proposed in (Meseure et al., 2015). This

kind of remeshing is adapted to physical simulation

since the shape of most elements is preserved, al-

though scaled by a factor 1/2. This solution works

well in practice for deformable body simulation, how-

ever, it is not adapted to fracture. Indeed, after a sub-

division, the strain-displacement matrix B

(e)

of each

new elements is scaled by a factor 2 and its volume,

and consequently its mass, by a factor 1/8. The node

stress tensor (Equation 6) is directly impacted by such

modiﬁcations and the choice of mass as a weighting

coefﬁcient is no longer adapted if the resolution of the

mesh is not uniform. Without a meaningful computa-

tion of node stress tensors, the criterion used to detect

fracture (a high eigenvalue) is no longer relevant. As

proposed in(Pfaff et al., 2014) in 2D, a more appro-

priate tensor, that is, independent on mesh resolution,

should be computed. More investigations are needed.

7 CONCLUSION AND FUTURE

WORK

This paper has presented a model that allows the

computation of small deformations of a brittle ob-

ject while still allowing rigid motions. To speed up

fracture management, the Gerschgorin’s test has been

proposed to easily locate fracture zones. A simple

oracle is also used to prevent the execution of heavy

algorithms needed in case of new connected compo-

nents. These improvements provide interesting com-

putation times, although no parallelization has been

exploited to compute deformations. It is deﬁnitely

one of our major goals, although the fracture pro-

Accelerated Simulation of Brittle Objects for Interactive Applications

cess itself is not really parallelizable. We also want

to improve visualization, by displaying more complex

fracture surfaces as done in (Koschier et al., 2014) (it

would only be a visual artifact, with no cost on the

fracture process itself). Furthermore, one remaining

problem concerns the number of cracks (that is fan

splitting) that can be handled in one step. Indeed,

if only one crack is allowed per simulation step, no

shattering effect occurs in general. The number of

handled cracks should however be bounded.

ACKNOWLEDGMENTS

We would like to thank the anonymous reviewers for

their comments that helped us to improve this paper.

This work has beneﬁted from the ﬁnancial support of

a M.Sc internship from the MIRES federation.

Figure 8: Shattering fracture of Stanford Bunny. The bot-

tom picture aims at highlighting the fracture surface and the

different connected components.

REFERENCES

Bao, Z., Hong, J.-M., Teran, J., and Fedkiw, R. (2007).

Fracturing rigid materials. IEEE Transactions on Vi-

sualization and Computer Graphics, 13(2):370–378.

Baraff, D. and Witkin, A. (1998). Large steps in cloth simu-

lation. In Proceedings of ACM SIGGRAPH 98, Com-

puter Graphics annual conference series, pages 43–54,

Orlando.

Busaryev, O., Dey, T. K., and Wang, H. (2013). Adaptive

fracture simulation of multi-layered thin plates. ACM

Transactions on Graphics (Proceedings of ACM SIG-

GRAPH 2013), 32(4).

Chen, Z., Yao, M., Feng, R., and Wang, H. (2014). Physics-

inspired adaptive fracture reﬁnement. ACM Transac-

tions on Graphics (Proceedings of ACM SIGGRAPH

2014), 33(4).

Cotin, S., Delingette, H., and Ayache, N. (1999). Real-time

elastic deformations of soft tissues for surgery simu-

lation. IEEE Transactions on Visualization and Com-

puter Graphics, 5(1):62–73.

Cotin, S., Delingette, H., and Ayache, N. (2000). A hybrid

elastic model allowing real-time cutting, deformation

and force-feedback for surgery training and simula-

tion. The Visual Computer, 16(8):437–452.

Glondu, L., Marchal, M., and Dumont, G. (2012). Real-

time simulation of brittle fracture using modal anal-

ysis. IEEE Transactions on Visualization and Com-

puter Graphics, 19(2):201–209.

Glondu, L., Schvartzman, S. C., Marchal, M., Dumont, G.,

and Otaduy, M. A. (2014). Fast collision detection for

fracturing rigid bodies. IEEE Transactions on Visual-

ization and Computer Graphics, 20(1):30–41.

Hahn, D. and Wojtan, C. (2015). High-resolution brittle

fracture simulation with boundary elements. ACM

Transactions on Graphics (Proceedings of ACM SIG-

GRAPH 2015), 34(4).

Hahn, D. and Wojtan, C. (2016). Fast approximations for

boundary element based brittle fracture simulation.

ACM Transactions on Graphics (Proceedings of ACM

SIGGRAPH 2016), 35(4).

Hilde, L., Meseure, P., and Chaillou, C. (2001). A fast im-

plicit integration method for solving dynamic equa-

tions of movement. In Proceedings of the ACM Con-

ference on Virtual Reality Software and Technology,

pages 71–76, Banff.

Koschier, D., Bender, J., and Thuerey, N. (2017). Robust

extended ﬁnite elements for complex cutting of de-

formables. ACM Transactions on Graphics (Proceed-

ings of ACM SIGGRAPH 2017), 36(4).

Koschier, D., Lipponer, S., and Bender, J. (2014). Adap-

tive tetrahedral meshes for brittle fracture simulation.

In Proceedings of the ACM SIGGRAPH/Eurographics

Symposium on Computer Animation, pages 57–66,

Copenhagen.

Lienhardt, P. (1994). N-dimensional generalized combi-

natorial maps and cellular quasimanifolds. Int. J. of

Computational Geometry and Applications, 4(3):275–

324.

Liu, N., He, X., Li, S., and Wang, G. (2011). Meshless sim-

ulation of brittle fracture. Computer Animation and

Virtual Worlds, 22(2–3):115–124.

Meseure, P., Darles, E., Skapin, X., and Touileb, Y. (2015).

Adaptive resolution for topology modiﬁcations in

physically-based animation. Technical report, XLIM

lab.

Michels, D. L., Luan, V. T., and Tokman, M. (2017). A

stifﬂy accurate integrator for elastodynamic problems.

ACM Transactions on Graphics (Proceedings of ACM

SIGGRAPH 2017), 36(4).

Molino, N., Bao, Z., and Fedkiw, R. (2004). A virtual node

algorithm for changing mesh topology during simula-

tion. ACM Transactions on Graphics (Proceedings of

ACM SIGGRAPH 2004), 23(3):385–392.

Muguercia, L., Bosch, C., and Patown, G. (2014). Frac-

ture modeling in computer graphics. Computers and

Graphics, 45(C):86–100.

uller, M., Chentanez, N., and Kim, T.-Y. (2013).

Real time dynamic fracture with volumetric approxi-

mate convex decompositions. ACM Transactions on

Graphics (Proceedings of ACM SIGGRAPH 2013),

32(4).

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

uller, M., Dorsey, J., McMillan, L., Jagnow, R., and Cut-

ler, B. (2002). Stable real-time deformations. In Pro-

ceedings of the ACM SIGGRAPH/Eurographics Sym-

posium on Computer Animation, pages 49–54, San

Antonio.

uller, M. and Gross, M. (2004). Interactive virtual mate-

rials. In Graphics Interface, pages 239–246, London

(Canada).

uller, M., Heidelberger, B., Teschner, M., and Gross, M.

(2005). Meshless deformations based on shape match-

ing. ACM Transactions on Graphics (Proceedings of

ACM SIGGRAPH 2005), 24(3):471–478.

uller, M., McMillan, L., Dorsey, J., and Jagnow, R.

(2001). Real-time simulation of deformation and frac-

ture of stiff materials. In Proceedings of the Eu-

rographics workshop on Computer Animation and

Simulation, pages 113–124, New York, NY, USA.

Springer-Verlag New York, Inc.

uller, M., Teschner, M., and Gross, M. (2004). Physically-

based simulation of objects represented by surface

meshes. In Proceedings of Computer Graphics Inter-

national, pages 26–33, Crete.

Nealen, A., M

uller, M., Keiser, R., Boxerman, E., and Carl-

son, M. (2006). Physically based deformable models

in computer graphics. Computer Graphics Forum (Eu-

rographics 2005 State of the Art Report), 25:809–836.

Nesme, M., Payan, Y., and Faure, F. (2005). Efﬁcient,

physically plausible ﬁnite elements. In Eurographics,

Dublin, Ireland.

Norton, A., Turk, G., Bacon, B., Gerth, J., and Sweeney, P.

(1991). Animation of fracture by physical modeling.

The Visual Computer, 7:210–219.

O’Brien, J. and Hodgins, J. (1999). Graphical modeling

and animation of brittle fracture. In Proceedings of

SIGGRAPH 99 Conference, Computer Graphics an-

nual conference series, pages 137–146, Los Angeles.

Parker, E. G. and O’Brien, J. F. (2009). Real-time defor-

mation and fracture in a game environment. In Pro-

ceedings of the ACM SIGGRAPH/Eurographics Sym-

posium on Computer Animation, pages 165–175, New

Orleans.

Pauly, M., Keiser, R., Adams, B., Dutr

e, P., Gross, M., and

Guibas, L. J. (2005). Meshless animation of fracturing

solids. ACM Transactions on Graphics (Proceedings

of ACM SIGGRAPH 2005), 24(3):957–964.

Pfaff, T., Narain, R., Miguel de Joya, J., and O’Brien, J. F.

(2014). Adaptive tearing and cracking of thin sheets.

ACM Transactions on Graphics (Proceedings of ACM

SIGGRAPH 2014), 33(4).

Schvartzman, S. C. and Otaduy, M. A. (2014). Fracture an-

imation based on high-dimensional voronoi diagrams.

In Proceedings of the ACM SIGGRAPH Symposium

on Interactive 3D Graphics and Games, pages 15–22.

Shoemake, K. (1985). Animating rotation with quaternion

curves. Computer Graphics (Proceedings of ACM

SIGGRAPH 85), 19(3):245–254.

Su, J., Schroeder, C., and Fedkiw, R. (2009). Energy stabil-

ity and fracture for frame rate rigid body simulations.

In Proceedings of the ACM SIGGRAPH/Eurographics

Symposium on Computer Animation, pages 155–164.

Terzopoulos, D. and Fleisher, K. (1988). Modeling in-

elastic deformation : Viscoelasticity, plasticity, frac-

ture. Computer Graphics (Proceedings of ACM SIG-

GRAPH 88), 22(4):269–278.

Terzopoulos, D. and Witkin, A. (1988). Physically based

models with rigid and deformable components. IEEE

Computer Graphics and Application, 8(6):41–51.

van Overveld, K. and Barenbrug, B. (1995). All you need

is force: a constraint-based approach for rigid body

dynamics in computer animation. In Proceedings of

the Eurographics workshop on Computer Animation

and Simulation, pages 80–94, Maastricht.

Zhu, Y., Bridson, R., and Greif, C. (2015). Simulating rigid

body fracture with surface meshes. ACM Transactions

on Graphics (Proceedings of ACM SIGGRAPH 2015),

34(4).

Accelerated Simulation of Brittle Objects for Interactive Applications