
Parameter Learning for Spiking Neural Networks
Modelled as Timed Automata
Elisabetta De Maria and Cinzia Di Giusto
Universit
´
e C
ˆ
ote d’Azur, CNRS, I3S, France
Keywords:
Neural Networks, Parameter Learning, Timed Automata, Temporal Logic, Model Checking.
Abstract:
In this paper we present a novel approach to automatically infer parameters of spiking neural networks. Neu-
rons are modelled as timed automata waiting for inputs on a number of different channels (synapses), for
a given amount of time (the accumulation period). When this period is over, the current potential value is
computed considering current and past inputs. If this potential overcomes a given threshold, the automaton
emits a broadcast signal over its output channel, otherwise it restarts another accumulation period. After each
emission, the automaton remains inactive for a fixed refractory period. Spiking neural networks are formalised
as sets of automata, one for each neuron, running in parallel and sharing channels according to the network
structure. This encoding is exploited to find an assignment for the synaptical weights of neural networks such
that they can reproduce a given behaviour. The core of this approach consists in identifying some correcting
actions adjusting synaptical weights and back-propagating them until the expected behaviour is displayed. A
concrete case study is discussed.
1 INTRODUCTION
The brain behaviour is the object of thorough studies:
researchers are interested not only in the inner func-
tioning of neurons (which are its elementary compo-
nents), their interactions and the way these aspects
participate to the ability to move, learn or remember,
typical of living beings; but also in reproducing such
capabilities (emulating nature), e.g., within robot con-
trollers, speech/text/face recognition applications, etc.
In order to achieve a detailed understanding of the
brain functioning, both neurons behaviour and their
interactions must be studied. Several models of the
neuron behaviour have been proposed: some of them
make neurons behave as binary threshold gates, other
ones exploit a sigmoidal transfer function, while, in
many cases, differential equations are employed. Ac-
cording to (Paugam-Moisy and Bohte, 2012; Maass,
1997), three different and progressive generations of
neural networks can be recognised: (i) first genera-
tion models handle discrete inputs and outputs and
their computational units are threshold-based transfer
functions; they include McCulloch and Pitt’s thresh-
old gate model (McCulloch and Pitts, 1943), the per-
ceptron model(Freund and Schapire, 1999), Hopfield
networks (Hopfield, 1988), and Boltzmann machines
(Ackley et al., 1988); (ii) second generation models
exploit real valued activation functions, e.g., the sig-
moid function, accepting and producing real values:
a well known example is the multi-layer perceptron
(Cybenko, 1989; Rumelhart et al., 1988); (iii) third
generation networks are known as spiking neural net-
works. They extend second generation models treat-
ing time-dependent and real valued signals often com-
posed by spike trains. Neurons may fire output spikes
according to threshold-based rules which take into ac-
count input spike magnitudes and occurrence times
(Paugam-Moisy and Bohte, 2012).
The core of our analysis are spiking neural net-
works (Gerstner and Kistler, 2002). Because of the
introduction of timing aspects they are considered
closer to the actual brain functioning than other gen-
erations models. Spiking neurons emit spikes taking
into account input impulses strength and their occur-
rence instants. Models of this sort are of great inter-
est, not only because they are closer to natural neural
networks behaviour, but also because the temporal di-
mension allows to represent information according to
various coding schemes (Recce, 1999; Paugam-Moisy
and Bohte, 2012): e.g., the amount of spikes occurred
within a given time window (rate coding), the recep-
tion/absence of spikes over different synapses (binary
coding), the relative order of spikes occurrences (rate
rank coding), or the precise time difference between
any two successive spikes (timing coding). Several
spiking neuron models have been proposed in the lit-
Maria, E. and Giusto, C.
Parameter Learning for Spiking Neural Networks Modelled as Timed Automata.
DOI: 10.5220/0006530300170028
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 3: BIOINFORMATICS, pages 17-28
ISBN: 978-989-758-280-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17

erature, having different complexities and capabili-
ties. Our aim is to produce a neuron model be-
ing meaningful from a biological point of view but
also amenable to formal analysis and verification, that
could be therefore used to detect non-active portions
within some network (i.e., the subset of neurons not
contributing to the network outcome), to test whether
a particular output sequence can be produced or not,
to prove that a network may never be able to emit, to
assess if a change to the network structure can alter its
behaviour, or to investigate (new) learning algorithms
which take time into account.
In this paper we focus on the leaky integrate &
fire (LI&F) model originally proposed in (Lapicque,
1907). It is a computationally efficient approximation
of single-compartment model (Izhikevich, 2004) and
is abstracted enough to be able to apply formal veri-
fication techniques such as model-checking. Here we
work on an extended version of the discretised formu-
lation proposed in (De Maria et al., 2016), which re-
lies on the notion of logical time. Time is considered
as a sequence of logical discrete instants, and an in-
stant is a point in time where external input events can
be observed, computations can be done, and outputs
can be emitted. The variant we introduce here takes
into account some new time-related aspects, such as a
lapse of time in which the neuron is not active, i.e., it
cannot receive and emit. We encode LI&F networks
into timed automata: we show how to define the be-
haviour of a single neuron and how to build a network
of neurons. Timed automata (Alur and Dill, 1994) are
finite state automata extended with timed behaviours:
constraints are allowed to limit the amount of time
an automaton can remain within a particular state, or
the time interval during which a particular transition
may be enabled. Timed automata networks are sets of
automata that can synchronise over channel commu-
nications.
Our modelling of spiking neural networks consists
of timed automata networks where each neuron is an
automaton. Its behaviour consists in accumulating the
weighted sum of inputs, provided by a number of in-
going weighted synapses, for a given amount of time.
Then, if the potential accumulated during the last
and previous accumulation periods overcomes a given
threshold, the neuron fires an output over the outgo-
ing synapse. Synapses are channels shared between
the timed automata representing neurons, while spike
emissions are represented by broadcast synchronisa-
tions occurring over such channels. Timed automata
are also exploited to produce or recognise precisely
defined spike sequences.
The closest related work is (Aman and Ciobanu,
2016). The authors provide a mapping of spiking neu-
ral P systems into timed automata. The underlying
model is considerably different from ours: refractory
period is considered in terms of number of applica-
tion of rules instead of durations and inhibitions are
represented as forgetting rules while we use negative
weights. Unlike our approach, where the dynamics is
compositional and implicit in the structure of the net-
work, in (Aman and Ciobanu, 2016) the semantics is
the result of the encoding of rules and neurons.
As a main contribution, we exploit our automata-
based modelling to propose a new methodology for
parameter inference in spiking neural networks. In
particular, our approach allows to find an assignment
for the synaptical weights of a given neural network
such that it can reproduce a given behaviour. We bor-
row inspiration from the SpikeProp rule (Bohte et al.,
2002), a variant of the well known back-propagation
algorithm (Rumelhart et al., 1988) used for supervised
learning in second generation learning. The Spike-
Prop rule deals with multi-layered cycle-free spiking
neural networks and aims at training networks to pro-
duce a given output sequence for each class of input
sequences. The main difference with respect to our
approach is that we are considering here a discrete
model and our networks are not multi-layered. We
also rest on Hebb’s learning rule (Hebb, 1949) and
its time-dependent generalisation rule, the spike tim-
ing dependent plasticity (STDP) rule (Sj
¨
ostr
¨
om and
Gerstner, 2010): they both act locally, with respect to
each neuron, i.e., no prior assumption on the network
topology is required in order to compute the weight
variations for some neuron input synapses. Differ-
ently from STDP, our approach takes into account
not only recent spikes but also some external feed-
back (advices) in order to determine which weights
should be modified and whether they must increase
or decrease. Moreover, we do not prevent excitatory
synapses from becoming inhibitory (or vice versa),
which is usually a constraint for STDP implementa-
tions. A general overview on spiking neural network
learning approaches and open problems in this con-
text can be found in (Gr
¨
uning and Bohte, 2014).
We apply the proposed approach to find suitable
parameters in mutual inhibition networks, a well stud-
ied class of networks in which the constituent neurons
inhibit each other neuron’s activity (Matsuoka, 1987).
The rest of the paper is organised as follows: in
Section 2 we describe our reference model, the leaky
integrate & fire one, in Section 3 we recall definitions
of timed automata networks and temporal logics, and
in Section 4 we show how spiking neural networks
can be encoded into timed automata networks and
how inputs and outputs are handled by automata. In
Section 5 we develop the novel parameter learning ap-
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
18

proach and we introduce a case study. Finally, Section
6 summarises our contribution and presents some fu-
ture research directions. An Appendix with additional
material is added for the reader convenience.
2 LEAKY INTEGRATE AND FIRE
MODEL
Spiking neural networks (Maass, 1997) are modelled
as directed weighted graphs where vertices are com-
putational units and edges represent synapses. The
signals propagating over synapses are trains of im-
pulses: spikes. Synapses may modulate these signals
according to their weight: excitatory if positive, or in-
hibitory if negative.
The dynamics of neurons is governed by their
membrane potential (or, simply, potential), represent-
ing the difference of electrical potential across the
cell membrane. The membrane potential of each neu-
ron depends on the spikes received over the ingoing
synapses. Both current and past spikes are taken into
account, even if old spikes contribution is lower. In
particular, the leak factor is a measure of the neu-
ron memory about past spikes. The neuron outcome
is controlled by the algebraic difference between its
membrane potential and its firing threshold: it is en-
abled to fire (i.e., emit an output impulse over all
outgoing synapses) only if such a difference is non-
negative. Spike propagation is assumed to be instan-
taneous. Immediately after each emission the neuron
membrane potential is reset and the neuron stays in a
refractory period for a given amount of time. During
this period it has no dynamics: it cannot increase its
potential as any received spike is lost and therefore it
cannot emit any spike.
Definition 1 (Spiking Integrate and Fire Neural Net-
work). A spiking integrate and fire neural network is
a tuple (V, A, w), where:
• V are spiking integrate and fire neurons,
• A ⊆ V ×V are synapses,
• w : A → Q ∩[−1,1] is the synapse weight function
associating to each synapse (u, v) a weight w
u,v
.
We distinguish three disjoint sets of neurons: V
i
(input
neurons), V
int
(intermediary neurons), and V
o
(output
neurons), with V = V
i
∪V
int
∪V
o
.
A spiking integrate and fire neuron v is characterized
by a parameter tuple (θ
v
,τ
v
,λ
v
, p
v
,y
v
), where:
• θ
v
∈ N is the firing threshold,
• τ
v
∈ N
+
is the refractory period,
• λ
v
∈ Q ∩ [0, 1] is the leak factor.
The dynamics of a spiking integrate and fire neuron v
is given by:
• p
v
: N → Q
+
0
is the [membrane] potential function
defined as
p
v
(t) =
∑
m
i=1
w
i
· x
i
(t), if p
v
(t − 1) > θ
v
∑
m
i=1
w
i
· x
i
(t)+ λ
v
· p
v
(t − 1), o/w.
with p
v
(0) = 0 and where x
i
(t) ∈ {0,1} is the sig-
nal received at the time t by the neuron through its
i
th
out of m input synapses (observe that the past
potential is multiplied by the leak factor while cur-
rent inputs are not weakened),
• y
v
: N → {0,1} is the neuron output function, de-
fined as
y
v
(t) =
(
1 if p
v
(t) > θ
v
0 otherwise.
As shown in the previous definition, the set of neu-
rons of a spiking integrate and fire neural network can
be classified into input, intermediary, and output ones.
Each input neuron can only receive as input external
signals (and not other neurons’ output). The output
of each output neuron is considered as an output for
the network. Output neurons are the only ones whose
output is not connected to other neurons.
3 PRELIMINARIES: TIMED
AUTOMATA AND TEMPORAL
LOGIC
This section is devoted to the introduction of the for-
mal tools we adopt in the rest of the paper, namely
timed automata and temporal logics.
Timed Automata. Timed automata (Alur and Dill,
1994) are a powerful theoretical formalism for mod-
elling and verifying real time systems. A timed
automaton is an annotated directed (and connected)
graph, with an initial node and provided with a fi-
nite set of non-negative real variables called clocks.
Nodes (called locations) are annotated with invariants
(predicates allowing to enter or stay in a location),
arcs with guards, communication labels, and possi-
bly with some variables upgrades and clock resets.
Guards are conjunctions of elementary predicates of
the form x op c, where op ∈ {>, ≥,=,<, ≤}, x is a
clock, and c a (possibly parameterised) positive inte-
ger constant. As usual, the empty conjunction is in-
terpreted as true. The set of all guards and invariant
predicates will be denoted by G.
Parameter Learning for Spiking Neural Networks Modelled as Timed Automata
19

Definition 2. A timed automaton TA is a tuple
(L,l
0
,X,Var, Σ,Arcs,Inv), where
• L is a set of locations with l
0
∈ L the initial one
• X is the set of clocks,
• Var is a set of integer variables,
• Σ is a set of communication labels,
• Arcs ⊆ L × (G ∪ Σ ∪ U) × L is a set of arcs be-
tween locations with a guard in G, a communica-
tion label in Σ ∪ {ε}, and a set of variable (linear
arithmetics) upgrades and clock resets;
• Inv : L → G assigns invariants to locations.
It is possible to define a synchronised product of
a set of timed automata that work and synchronise in
parallel. The automata are required to have disjoint
sets of locations, but may share clocks and communi-
cation labels which are used for synchronisation. We
restrict communications to be broadcast through la-
bels b!,b? ∈ Σ, meaning that a set of automata can
synchronise if one is emitting; notice that a process
can always emit (e.g., b!) and the receivers (b?) must
synchronise if they can.
Locations can be normal, urgent or committed.
Urgent locations force the time to freeze, committed
ones freeze time and the automaton must leave the
location as soon as possible, i.e., they have higher pri-
ority.
The synchronous product TA
1
k ... k TA
n
of
timed automata, where for each j ∈ [1,. .., n], TA
j
=
(L
j
,l
0
j
,X
j
,Var
j
Σ
j
,Arcs
j
,Inv
j
) and all L
j
are pairwise
disjoint sets of locations, is the timed automaton
TA = (L,l
0
,X,Var, Σ,Arcs,Inv)
such that:
• L = L
1
× .. . × L
n
and l
0
= (l
0
1
,.. .,l
0
n
),
• X =
S
n
j=1
X
j
,
• Var =
S
n
j=1
Var
j
,
• Σ =
S
n
j=1
Σ
j
,
• Arcs is the set of arcs (l
1
,.. .,l
n
)
g,a,u
−→ (l
0
1
,.. .,l
0
n
)
such that for all 1 ≤ j ≤ n then l
0
j
= l
j
.
• ∀l = (l
1
,.. .,l
n
) ∈ L : Inv(l) =
V
j
Inv
j
(l
j
),
The semantics of a synchronous product TA
1
k
... k TA
n
is the one of the underlying timed automaton
TA with the following notations. A location is a vec-
tor l = (l
1
,.. .,l
n
). We write l[l
0
j
/l
j
, j ∈ S] to denote
the location l in which the j
th
element l
j
is replaced
by l
0
j
, for all j in some set S. A valuation is a func-
tion ν from the set of clocks to the non-negative reals.
Let V be the set of all clock valuations, and ν
0
(x) = 0
for all x ∈ X. We shall denote by ν F the fact that
the valuation ν satisfies (makes true) the formula F.
If r ∈ U is a clock reset, we shall denote by ν[r] the
valuation obtained after applying the clock reset to ν;
and if d ∈ R
>0
is a delay, ν + d is the valuation such
that, for any clock x ∈ X, (ν + d)(x) = ν(x) + d. Fi-
nally, we use f to denote a valuation of variables in
Var, the set of all valuations is denoted F , f
0
(v) = 0
for all v ∈ Var and f [u] is the application of upgrades
in u to variables in Var.
The semantics of a synchronous product TA
1
k
... k TA
n
is defined as a timed transition system
(S,s
0
,→), where S = (L
1
×,.. . × L
n
) × V × F is the
set of states, s
0
= (l
0
,ν
0
, f
0
) is the initial state, and
→⊆ S × S is the transition relation defined by:
• (silent): (l, ν, f ) → (l
0
,ν
0
, f [u]) if there exists
l
i
g,ε,u
−→ l
0
i
, for some i, such that l
0
= l[l
0
i
/l
i
], ν g
and ν
0
= ν[r],
• (broadcast): (
¯
l,ν, f ) → (
¯
l
0
,ν
0
, f [u]) if there exists
an output arc l
j
g
j
,b!,u
j
−→ l
0
j
∈ Arcs
j
and a (possi-
bly empty) set of input arcs of the form l
k
g
k
,b?,u
k
−→
l
0
k
∈ Arcs
k
such that for all k ∈ K = {k
1
,.. .,k
m
} ⊆
{l
1
,.. .,l
n
} \ {l
j
}, the size of K is maximal, ν
V
k∈K∪{ j}
g
k
, l
0
= l[l
0
k
/l
k
,k ∈ K ∪ { j}] and ν
0
=
ν[r
k
,k ∈ K ∪ { j}];
• (timed): (l,ν, f ) → (l, ν + d, f ) if ν + d Inv(l).
The valuation function ν is extended to handle a
set of shared bounded integer variables: predicates
concerning such variables can be part of edges guards
or locations invariants, moreover variables can be up-
dated on edges firings but they cannot be assigned to
or from clocks.
In Appendix A we exemplify timed automata us-
age. Throughout our modelling, we have used the
specification and analysis tool Uppaal (Bengtsson
et al., 1995), which provides the possibility of design-
ing and simulating timed automata networks on top of
the ability of testing networks against temporal logic
formulae.
Temporal Logics and Model Checking. Model
checking is one of the most common approaches to
the verification of software and hardware (distributed)
systems (Clarke et al., 1999). It allows to automati-
cally prove whether a system verifies or not a given
specification. In order to apply such a technique, the
system at issue should be encoded as a finite transi-
tion system and the specification should be written
using propositional temporal logic. Formally, a tran-
sition system over a set AP of atomic propositions
is a tuple M = (Q, T,L), where Q is a finite set of
states, T ⊆ Q × Q is a total transition relation, and
L : Q → 2
AP
is a labelling function that maps every
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
20

state into the set of atomic propositions that hold at
that state.
Temporal logics are formalisms for describing
the dynamical evolution of a given system (Hughes
and Cresswell, 1968). The computation tree logic
CTL
∗
allows to describe properties of computation
trees. Its formulas are obtained by (repeatedly) apply-
ing Boolean connectives, path quantifiers, and state
quantifiers to atomic formulas. The path quantifier
A (resp., E) can be used to state that all the paths
(resp., some path) starting from a given state have
some property. The state quantifiers are X (next time),
which specifies that a property holds at the next state
of a path, F (sometimes in the future), which requires
a property to hold at some state on the path, G (always
in the future), which imposes that a property is true at
every state on the path, and U (until), which holds if
there is a state on the path where the second of its ar-
gument properties holds and, at every preceding state
on the path, the first of its two argument properties
holds.
The branching time logic CTL is a fragment of
CTL
∗
that allows quantification over the paths starting
from a given state. Unlike CTL
∗
, it constrains every
state quantifier to be immediately preceded by a path
quantifier.
Given a transition system M = (Q,T, L), a state
q ∈ Q, and a temporal logic formula ϕ expressing
some desirable property of the system, the model
checking problem consists of establishing whether ϕ
holds at q or not, namely, whether M,q |= ϕ.
4 SPIKING NEURAL NETWORKS
MODELLING
We present here our modelling of spiking integrate
and fire neural networks (in the following denoted as
neural networks) via timed automata networks. Let
S = (V,A, w) be a neural network, G be a set of input
generator neurons (these fictitious neurons are con-
nected to input neurons and generate input sequences
for the network), and O be a set of output consumer
neurons (these fictitious neurons are connected to the
broadcast channel of each output neuron and aim at
consuming their emitted spikes). The correspond-
ing timed automata network is obtained as the syn-
chronous product of the encoding of input generator
neurons, the neurons of the network (referred as stan-
dard neurons in the following), and output consumers
neurons. More formally:
JSK = ( k
n
g
∈G
Jn
g
K) k ( k
v
j
∈V
Jv
j
K) k ( k
n
c
∈O
Jn
c
K)
Input Generators. The behaviour of input genera-
tor neurons is part of the specification of the network.
Here we define two kinds of input behaviours: regu-
lar and non-deterministic ones. For each family, we
provide an encoding into timed automata.
Regular Input Sequences. Spike trains are “regu-
lar” sequences of spikes and pauses: spikes are instan-
taneous while pauses have a non-null duration. Se-
quences can be empty, finite or infinite. After each
spike there must be a pause, except when the spike is
the last event of a finite sequence. Infinite sequences
are composed by two parts: a finite and arbitrary pre-
fix and an infinite and periodic part composed by a fi-
nite sequence of spike–pause pairs which is repeated
infinitely often. More formally, such sequences are
given in terms of the following grammar:
B ::= Φ.(Φ)
ω
| P(d).Φ.(Φ)
ω
Φ ::= s.P(d).Φ | ε
with s representing a spike and P(d) a pause of dura-
tion d. The automaton generating input sequences is
given in Appendix B.1.
Non-deterministic Input Sequences. This kind of
input sequences is useful when no assumption is
available on neuron inputs. These are random se-
quences of spikes separated by at least T
min
time units.
Their precise encoding is given in Appendix B.2.
Standard Neurons. The neuron is a computational
unit behaving as follows: i) it accumulates potential
whenever it receives input spikes within a given ac-
cumulation period, ii) if the accumulated potential is
greater than the threshold, it emits an output spike, iii)
it waits during a refractory period, and restarts from
i). Observe that the accumulation period is not present
in the definition of neuron (Def. 1). It is indeed intro-
duced here to slice time and therefore discretise the
decrease of the potential value due to the leak factor.
We assume that two input spikes on the same synapse
cannot be received within the same accumulation pe-
riod (i.e., the accumulation period is shorter than the
minimum refractory period of the input neurons of the
network). Next, we give the encoding of neurons into
timed automata.
Definition 3. Given a neuron v = (θ,τ,λ, p,y) with
m input synapses, its encoding into timed automata is
N = (L, A,X,Var, Σ,Arcs,Inv) with:
• L = {A,W,D} with D committed,
• X = {t}
• Var = {p,a}
Parameter Learning for Spiking Neural Networks Modelled as Timed Automata
21

(a) Neuron model.
(b) Output consumer au-
tomaton.
Figure 1: Automata for standard neuron and output con-
sumer.
• Σ = {x
i
| i ∈ [1..m]} ∪ {y},
• Arcs = {(A,t ≤ T, x
i
?,{a := a + w
i
},A) |
i ∈ [1..m]} ∪ {(A,t = T, ,{p := a +
bλpc}, D),(D, p < θ, ,{a := 0},A), (D, p ≥
θ,y!, ,W),(W,t = τ, ,{a := 0,t := 0, p :=
0},A)} ;
• Inv(A) = t ≤ T, Inv(W) = t ≤ τ,Inv(D) = true.
The neuron behaviour, described by the automa-
ton in Figure 1(a), depends on the following channels,
variables and clocks:
• x
i
for i ∈ [1..m] are the m input channels,
• y is the broadcast channel used to emit the output
spike,
• p ∈ N is the current potential value, initially set to
zero,
• a ∈ N is the weighted sum of input spikes occurred
within the current accumulation period; it equals
zero at the beginning of each round.
The behaviour of the automaton modelling neuron
v can be summed up as follows:
• the neuron keeps waiting in state A (for Accumu-
lation) for input spikes while t 6 T and, whenever
it receives a spike on input x
i
, it updates a with
a := a + w
i
;
• when t = T , the neuron moves to state D (for De-
cision), resetting t and updating p according to the
potential function given in Definition 1:
p := a +
b
λ · p
c
Since state D is committed, it does not allow time
to progress, so, from this state, the neuron can
move back to state A resetting a if the potential
has not reached the threshold p < θ, or it can move
to state W, firing an output spike, otherwise;
• the neuron remains in state W (for Wait) for τ time
units (τ is the length of the refractory period) and
then it moves back to state A resetting a, p and t.
Output Consumers. In order to have a complete
modelling of a spiking neural network, for each out-
put neuron we build an output consumer automa-
ton O
y
. The automaton, whose formal definition is
straightforward, is shown in Figure 1(b). The con-
sumer waits in location W for the corresponding out-
put spikes on channel y and, as soon as it receives the
spike, it moves to location O. This location is only
needed to simplify model checking queries. Since it
is urgent, the consumer instantly moves back to loca-
tion W resetting s, the clock measuring the elapsed
time since last emission, and setting e to its negation,
with e being a boolean variable which differentiates
each emission from its successor.
We have a complete implementation of the spiking
neural network model proposed in the paper via the
tool Uppaal. It can be found on the web page (Ciatto
et al., ). We have validated our neuron model against
some characteristic properties studied in (Izhikevich,
2004) (tonic spiking, excitability, integrator, etc.).
These properties have been formalised in temporal
logics and checked via model-checking tools. All ex-
periments and results can be found in (Ciatto et al.,
2017).
Observe that, since we rely on a discrete time, we
could have used tick automata (Gruber et al., 2005), a
variant of B
¨
uchi automata where a special clock mod-
els the discrete flow of time. However, to the best of
our knowledge, no existing tool allows to implement
such automata. We decided to opt for timed automata
in order to have an effective implementation of our
networks to be exploited in parameter learning algo-
rithms.
5 PARAMETER INFERENCE
In this section we examine the Learning Problem: i.e.,
how to determine a parameter assignment for a net-
work with a fixed topology and a given input such
that a desired output behaviour is displayed. Here we
only focus on the estimation of synaptic weights in
a given spiking neural network; the generalisation of
our methodology to other parameters is left for future
work.
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
22
Our analysis takes inspiration from the SpikeProp
algorithm (Bohte et al., 2002); in a similar way, here,
the learning process is led by supervisors. Differ-
ently from the previous section, each output neuron
is linked to a supervisor instead of an output con-
sumer. Supervisors compare the expected output be-
haviour with the one of the output neuron they are
connected to. Thus either the output neuron behaved
consistently or not. In the second case and in order to
instruct the network, the supervisor back-propagates
advices to the output neuron depending on two pos-
sible scenarios: i) the neuron fires a spike, but it was
supposed to be quiescent, ii) the neuron remains qui-
escent, but it was supposed to fire a spike. In the
first case the supervisor addresses a should not have
fired message (SNHF) and in the second one a should
have fired (SHF). Then each output neuron modifies
its ingoing synaptic weights and in turn behaves as
a supervisor with respect to its predecessors, back-
propagating the proper advice.
The advice back-propagation (ABP) algorithm ba-
sically lies on a depth-first visit of the graph topology
of the network. Let N
i
be the i-th predecessor of an
automaton N , then we say that N
i
fired recently, with
respect to N , if N
i
fired during the current or pre-
vious accumulate-fire-wait cycle of N . Thus, upon
reception of a SHF message, N has to strengthen
the weight of each ingoing excitatory synapse corre-
sponding to a neuron which fired recently and weaken
the weight of each ingoing inhibitory synapse cor-
responding to a neuron which did not fire recently.
Then, it propagates a SHF advice to each ingoing ex-
citatory synapse corresponding to a neuron which did
not fire recently, and symmetrically a SNHF advice
to each ingoing inhibitory synapse corresponding to
a neuron which fired recently (see Algorithm 1 for
SHF, Algorithm 2 for the dual case of SNHF in given
in Appendix C; in both algorithms, ∆ is a constant
factor used to manage increments).
When the graph visit reaches an input generator, it
will simply ignore any received advice (because input
sequences should not be affected by the learning pro-
cess). The learning process ends when all supervisors
do not detect any more errors.
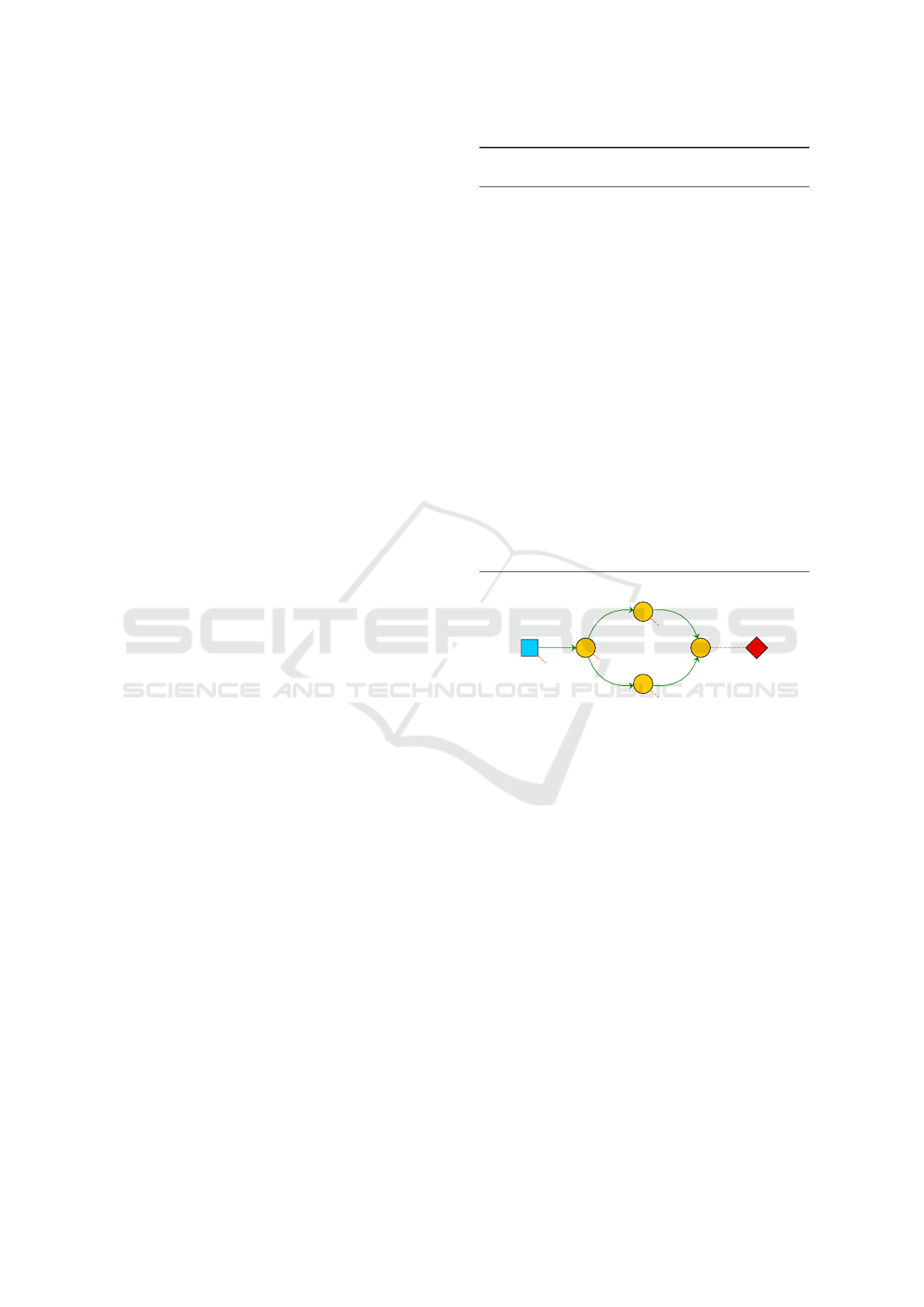
Example 1 (Turning on and off a diamond structure
of neurons.). This example shows how the ABP al-
gorithm can be used to make a neuron emit at least
once in a spiking neural network having the diamond
structure shown in Figure 2. We assume that N
1
is
fed by an input generator I that continuously emits
spikes. No neuron in the network is able to emit be-
cause all the weights of their input synapses are equal
to zero and their thresholds are higher than zero. We
want the network to learn a weight assignment so that
Algorithm 1 : Abstract ABP: Should Have Fired advice
pseudo-code.
1: procedure SHOULD-HAVE-FIRED(neuron)
2: if IS-VISITED(neuron) then
3: return
4: SET-VISITED(neuron, True)
5: for i ← 1 ... COUNT-
PREDECESSORS(neuron) do
6: weight
i
← GET-WEIGHT(neuron, i)
7: f ired
i
← FIRED-RECENTLY(neuron, i)
8: neuron
i
← GET-PREDECESSOR(neuron,
i)
9: INCREASE-WEIGHT(neuron, i, ∆)
10: if weight
i
≥ 0 then
11: if ¬ f ired
i
then
12: SHOULD-HAVE-FIRED(neuron
i
)
13: else
14: if f ired
i
then
15: SHOULD-NOT-HAVE-
FIRED(neuron
i
)
N
1
N
2
N
3
S
4
N
4
w
I,1
w
1,2
w
1,3
w
3,4
w
2,4
x
y
1
y
3
y
2
y
4
I
Figure 2: A neural network with a diamond structure.
N
4
is able to emit, that is, to produce a spike after an
initial pause.
At the beginning we expect no activity from neu-
ron N
4
. As soon as the initial pause is elapsed, we
require a spike but, as all weights are equal to zero,
no emission can happen. Thus a SHF advice is back-
propagated to neurons N
2
and N
3
and consequently
to N
1
. The process is then repeated until all weights
stabilise and neuron N
4
is able to fire.
There are several possibilities on how to realise
supervisors and the ABP algorithm. The approach we
choose is a model checking oriented one, where su-
pervisors are represented by temporal logic formulae.
Model-checking-oriented Advice Back-
Propagation. In the following we propose a
model checking-driven approach to parameter
learning. Such a technique consists in iterating
the learning process until a desired CTL property
concerning the output of the network is verified.
Parameter Learning for Spiking Neural Networks Modelled as Timed Automata
23
The hypothesis we introduce are the following
ones: (i) input generators, standard neurons, and out-
put consumers share a global clock which is never re-
set and (ii) for each output consumer, there exists a
clock measuring the elapsed time since the last re-
ceived spike. The CTL formula specifying the ex-
pected output of the network can only contain pred-
icates relative to the output consumers and the global
clock. At each step of the algorithm, we make an ex-
ternal call to the model checker to test whether the
network satisfies the formula or not. If the formula
is verified, the learning process ends; otherwise, the
model checker provides a trace as a counterexample.
Such a trace is exploited to derive the proper correc-
tive action to be applied to each output neuron, that
is, the invocation of either the SHF procedure, or the
SNHF procedure previously described (or no proce-
dure).
More in detail, given a timed automata network
representing some spiking neural network, we extend
it with a global clock t
g
which is never reset and, for
each output consumer O
K
relative to the output neu-
ron N
k
, we add a clock s
k
measuring the time elapsed
since the last spike consumed by O
k
. Furthermore,
let state
O
k
(O) be an atomic proposition evaluating to
true if the output consumer O
K
is in its O location, and
let eval
O
k
(s
k
) be an atomic proposition indicating the
value of the clock s
k
in O
K
. In order to make it possi-
ble to deduce the proper corrective action, we impose
the CTL formula describing the expected outcome of
the network to be composed by the conjunction of
sub-formulae respecting any of the patterns presented
in the following.
Precise Firing. The output neuron N
k
fires at time t:
AF
t
g
= t ∧ state
O
k
(O)
.
The violation of such a formula requires the invo-
cation of the SHF procedure.
Weak Quiescence. The output neuron N
k
is quies-
cent at time t:
AG
t
g
= t =⇒ ¬state
O
k
(O)
.
The SNHF procedure is called in case this formula
is not satisfied.
Relaxed Firing. The output neuron N
k
fires at least
once within the time window [t
1
, t
2
]:
AF
t
1
≤ t
g
≤ t
2
∧ state
O
k
(O)
.
The violation of such a formula leads to the invo-
cation of the SHF procedure.
Strong Quiescence. The output neuron N
k
is quies-
cent for the whole duration of the time window
[t
1
, t
2
]:
AG
t
1
≤ t
g
≤ t
2
=⇒ ¬state
O
k
(O)
.
The SNHF procedure is needed in this case.
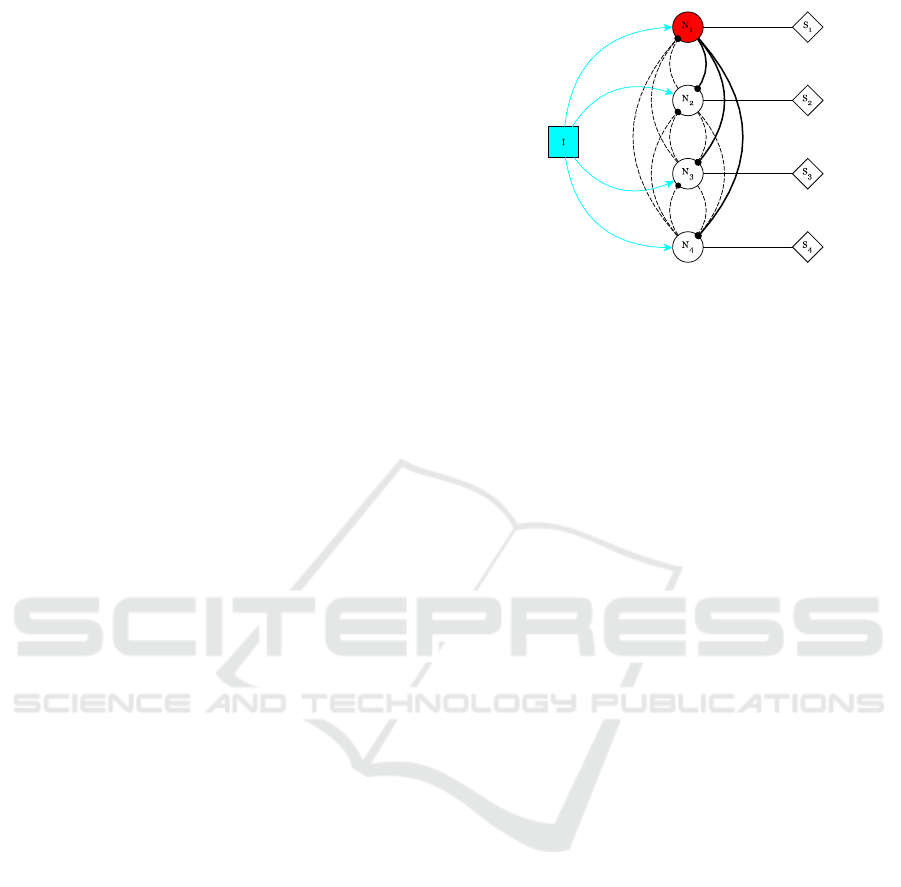
Figure 3: We denote neurons by N
i
. The network is fed by
an input generator I and the learning process is led by the
supervisors S
i
. Dotted (resp. continuous) edges stand for
inhibitions (resp. activations).
Precise Periodicity. The output neuron N
k
eventu-
ally starts to periodically fire a spike with exact
period P:
AF(AG( eval
O
k
(s
k
) 6= P =⇒ ¬state
O
k
(O))
∧ AG(state
O
k
(O) =⇒ eval
O
k
(s
k
) = P)).
If N
k
fires a spike while the s
k
clock is different
than P or it does not fire a spike while the s
k
clock
equals P, the formula is not satisfied. In the for-
mer (resp. latter) case, we deduce that the SNHF
(resp. SHF) procedure is required.
Relaxed Periodicity. The output neuron N
k
eventu-
ally begins to periodically fire a spike with a pe-
riod that may vary in [P
min
, P
max
]:
AF(AG( eval
O
k
(s
k
) /∈ [P
min
, P
max
] =⇒
¬state
O
k
(O))
∧ AF(state
O
k
(O) =⇒ P
min
≤ eval
O
k
(s
k
) ≤
P
max
)).
For the corrective actions, see the previous case.
As for future work, we intend to extend this set
of CTL formulae with new formulae concerning the
comparison of the output of two or more given neu-
rons. Please notice that the Uppaal model-checker
only supports a fragment of CTL where the use
of nested path quantifiers is not allowed. Another
model-checker should be called in order to fully ex-
ploit the expressive power of CTL.
Next we give an example of mutually inhibiting
networks.
Example 2 (Mutual inhibition networks.). In this ex-
ample we focus on mutual inhibition networks, where
the constituent neurons inhibit each other neuron’s
activity. These networks belong to the set of Control
Path Generators (CPGs), which are known for their
capability to produce rhythmic patterns of neural
activity without receiving rhythmic inputs (Ijspeert,
2008). CPGs underlie many fundamental rhythmic
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
24

activities such as digesting, breathing, and chewing.
They are also crucial building blocks for the locomo-
tor neural circuits both in invertebrate and vertebrate
animals. It has been observed that, for suitable pa-
rameter values, mutual inhibition networks present a
behaviour of the kind ”winner takes all”, that is, at
a certain time one neuron becomes (and stays) ac-
tivated and the other ones are inhibited (De Maria
et al., 2016).
We consider a mutual inhibition network of four
neurons, as shown in Fig. 3. This example, although
being small, it is not trivial as it features inhibitor
and excitatory edges as well as cycles. We look for
synaptical weights such that the ”winner takes all”
behaviour is displayed. We assume each neuron to be
fed by an input generator I that continuously emits
spikes. At the beginning, all the neurons have the
same parameters (that is, firing threshold, remaining
coefficient, accumulation period, and refractory pe-
riod), and the weight of excitatory (resp. inhibitory)
edges is set to 1 (resp. -1). We use the ABP algorithm
to learn a weight assignment so that the first neuron is
the winner. More precisely, we find a weight assign-
ment so that, whatever the chosen path in the corre-
sponding automata network is, the network stabilises
when the global clock t
g
equals 112.
6 CONCLUSION AND FUTURE
WORKS
In this paper we have introduced a novel methodology
for automatically inferring the synaptical weights of
spiking neural networks modelled as timed automata
networks. In these networks information process-
ing is based on the precise timing of spike emissions
rather than the average numbers of spikes in a given
time window. Timed automata turned out to be very
suited to model these networks, allowing us to take
into account time-related aspects, such as the exact
spike occurrence times and the refractory period, a
lapse of time immediately following each spike emis-
sion, when the neuron is not enabled to fire.
As for future work, we consider this work as the
starting point for a number of research directions:
we plan to study whether our model cannot repro-
duce behaviours requiring bursts emission capability,
as stated in (Izhikevich, 2004) (e.g., tonic or pha-
sic bursting), or some notion of memory (e.g., phasic
spiking, or bistability). Furthermore, it may be in-
teresting to enrich our formalisations to include mod-
elling of propagation delays.
As a main contribution, we combined learning
algorithms with formal analysis, proposing a novel
technique to infer synaptical weight variations. Tak-
ing inspiration from the back propagation algorithms
used in artificial intelligence, we have proposed a
methodology for parameter learning that exploits
model checking tools. We have focussed on a simpli-
fied type of supervisors: each supervisor describes the
output of a single neuron in isolation from the other
ones. Nonetheless, notice that the back-propagation
algorithm is still valid for more complex scenarios
that specify and compare the behaviour of groups of
neurons. As for future work, we intend to formalise
more sophisticated supervisors, allowing to compare
the output of several neurons. Moreover, to refine our
learning algorithm, we could exploit results coming
from the gene regulatory network domain, where a
link between the topology of the network and its dy-
namical behaviour is established (Richard, 2010).
We are currently working on a second type of
approach, where the parameters are modified during
the simulation of the network. Differently from the
model checking approach, supervisors are defined as
timed automata as well and they are connected to out-
put neurons instead of output consumers. The defi-
nition of supervisors is reminiscent of the one of in-
put generators and is basically a sequence of pauses
and spike actions. The simulation oriented ABP ap-
proach works in the following way: the simulation
starts and the supervisors expect a certain behaviour
from the connected supervisor (pause or spike). If
the behaviour matches, then the simulation proceeds
with the following action; otherwise a proper advice
is back propagated into the timed automata network.
As soon as the advice reaches the input neurons, the
simulation is restarted from the beginning with the
modified weight values. Whenever a supervisor de-
tects that the neurons actually learned to reproduce
the proper outcome, it will move to an acceptation lo-
cation where no more advices are back-propagated.
The learning process terminates when all the super-
visor automata are in the acceptation location. In this
case the values of all synaptic weights (of the last state
of the simulation) represent the result of the learning
process.
As a last step, we plan to generalise our technique
in order to be able to infer not only synaptical weights
but also other parameters, such as the leak factor or
the firing threshold.
ACKNOWLEDGEMENTS
We would like to thank Giovanni Ciatto for his imple-
mentation work and enthusiasm in collaborating with
us and all the anonymous reviewers for their careful
and rich suggestions on how to improve the paper.
Parameter Learning for Spiking Neural Networks Modelled as Timed Automata
25

REFERENCES
Ackley, D. H., Hinton, G. E., and Sejnowski, T. J. (1988). A
learning algorithm for boltzmann machines. In Waltz,
D. and Feldman, J. A., editors, Connectionist Models
and Their Implications: Readings from Cognitive Sci-
ence, pages 285–307. Ablex Publishing Corp., Nor-
wood, NJ, USA.
Alur, R. and Dill, D. L. (1994). A theory of timed automata.
Theor. Comput. Sci., 126(2):183–235.
Aman, B. and Ciobanu, G. (2016). Modelling and verifica-
tion of weighted spiking neural systems. Theoretical
Computer Science, 623:92 – 102.
Bengtsson, J., Larsen, K. G., Larsson, F., Pettersson, P., and
Yi, W. (1995). UPPAAL — a Tool Suite for Automatic
Verification of Real–Time Systems. In Proceedings of
Workshop on Verification and Control of Hybrid Sys-
tems III, number 1066 in Lecture Notes in Computer
Science, pages 232–243. Springer–Verlag.
Bohte, S. M., Poutr
´
e, H. A. L., Kok, J. N., La, H. A., Joost,
P., and Kok, N. (2002). Error-backpropagation in tem-
porally encoded networks of spiking neurons. Neuro-
computing, 48:17–37.
Ciatto, G., De Maria, E., and Di Giusto, C. Additional ma-
terial. https://github.com/gciatto/snn as ta.
Ciatto, G., De Maria, E., and Di Giusto, C. (2017). Model-
ing Third Generation Neural Networks as Timed Au-
tomata and verifying their behavior through Tempo-
ral Logic. Research report, Universit
´
e C
ˆ
ote d’Azur,
CNRS, I3S, France.
Clarke, Jr., E. M., Grumberg, O., and Peled, D. A. (1999).
Model checking. MIT Press, Cambridge, MA, USA.
Cybenko, G. (1989). Approximation by superpositions of a
sigmoidal function. Mathematics of Control, Signals
and Systems, 2(4):303–314.
De Maria, E., Muzy, A., Gaff
´
e, D., Ressouche, A., and
Grammont, F. (2016). Verification of Temporal Prop-
erties of Neuronal Archetypes Using Synchronous
Models. In Fifth International Workshop on Hybrid
Systems Biology, Grenoble, France.
Freund, Y. and Schapire, R. E. (1999). Large margin clas-
sification using the perceptron algorithm. Machine
Learning, 37(3):277–296.
Gerstner, W. and Kistler, W. (2002). Spiking Neuron Mod-
els: An Introduction. Cambridge University Press,
New York, NY, USA.
Gruber, H., Holzer, M., Kiehn, A., and K
¨
onig, B. (2005).
On timed automata with discrete time - structural and
language theoretical characterization. In Develop-
ments in Language Theory, 9th International Confer-
ence, DLT 2005, Palermo, Italy, July 4-8, 2005, Pro-
ceedings, pages 272–283.
Gr
¨
uning, A. and Bohte, S. (2014). Spiking neural networks:
Principles and challenges.
Hebb, D. O. (1949). The Organization of Behavior. John
Wiley.
Hopfield, J. J. (1988). Neural networks and physical sys-
tems with emergent collective computational abilities.
In Anderson, J. A. and Rosenfeld, E., editors, Neuro-
computing: Foundations of Research, pages 457–464.
MIT Press, Cambridge, MA, USA.
Hughes, G. E. and Cresswell, M. J. (1968). An Introduction
to Modal Logic. Methuen.
Ijspeert, A. J. (2008). Central pattern generators for loco-
motion control in animals and robots: A review. Neu-
ral Networks, 21(4):642–653.
Izhikevich, E. M. (2004). Which model to use for cortical
spiking neurons? IEEE Transactions on Neural Net-
works, 15(5):1063–1070.
Lapicque, L. (1907). Recherches quantitatives sur
l’excitation electrique des nerfs traitee comme une po-
larization. J Physiol Pathol Gen, 9:620–635.
Maass, W. (1997). Networks of spiking neurons: The third
generation of neural network models. Neural Net-
works, 10(9):1659 – 1671.
Matsuoka, K. (1987). Mechanisms of frequency and pattern
control in the neural rhythm generators. Biological
cybernetics, 56(5-6):345–353.
McCulloch, W. S. and Pitts, W. (1943). A logical calculus
of the ideas immanent in nervous activity. The bulletin
of mathematical biophysics, 5(4):115–133.
Paugam-Moisy, H. and Bohte, S. (2012). Computing with
Spiking Neuron Networks, pages 335–376. Springer
Berlin Heidelberg, Berlin, Heidelberg.
Recce, M. (1999). Encoding information in neuronal activ-
ity. In Maass, W. and Bishop, C. M., editors, Pulsed
Neural Networks, pages 111–131. MIT Press, Cam-
bridge, MA, USA.
Richard, A. (2010). Negative circuits and sustained oscilla-
tions in asynchronous automata networks. Advances
in Applied Mathematics, 44(4):378–392.
Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1988).
Learning representations by back-propagating errors.
In Anderson, J. A. and Rosenfeld, E., editors, Neuro-
computing: Foundations of Research, pages 696–699.
MIT Press, Cambridge, MA, USA.
Sj
¨
ostr
¨
om, J. and Gerstner, W. (2010). Spike-timing depen-
dent plasticity. Scholarpedia, 5(2).
APPENDIX
A Timed Automata Example
In Figure 4 we consider the network of timed au-
tomata TA
1
and TA
2
with broadcast communications,
and we give a possible run. TA
1
and TA
2
start in the
l
1
and l
3
locations, respectively, so the initial state is
[(l
1
, l
3
); x = 0]. A timed transition produces a de-
lay of 1 time unit, making the system move to state
[(l
1
, l
3
); x = 1]. A broadcast transition is now en-
abled, making the system move to state [(l
2
, l
3
); x =
0], broadcasting over channel a and resetting the x
clock. Two successive timed transitions (0.5 time
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
26

l
1
l
2
G:
x = 1
S:
a
!
U:
x := 0
x < 2
x < 2
G:
x > 0
S:
b
!
U:
-
G:
true
S:
a
?
U:
x := 0
G:
x = 1
S:
-
U:
-
l
3
l
4
TA
1
TA
2
(a) The timed automata network TA
1
k TA
2
.
[(l
1
, l
3
); x = 0]
↓
[(l
1
, l
3
); x = 1]
↓
[(l
2
, l
3
); x = 0]
↓
[(l
2
, l
3
); x = 0.5]
↓
[(l
2
, l
3
); x = 1]
↓
[(l
2
, l
4
); x = 1]
(b) A possible run.
Figure 4: A network of timed automata with a possible run.
units) followed by a broadcast one will eventually
lead the system to state [(l
2
, l
4
); x = 1].
B Additional Material for the
Spiking Neural Network Modeling
B.1 Input Sequence Generators
Regular input sequences are given in terms of the fol-
lowing grammar:
IS ::= Φ.(Φ)
ω
| P(d).Φ.(Φ)
ω
Φ ::= s.P(d).Φ | ε
with s representing a spike and P(d) a pause of dura-
tion d. It is possible to generate an emitter automaton
for any regular input sequence:
Definition 4 (Input generator). Let I ∈ L(IS)
be a word over the language generated by IS,
then its encoding into timed automata is JIK =
(L(I), f irst(I), {t}, {y}, Arcs(I), Inv(I)). It is induc-
tively defined as follows:
• if I := Φ
1
.(Φ
2
)
ω
– L(I) = L(Φ
1
)∪L(Φ
2
), where last(Φ
2
) is urgent
– f irst(I) = f irst(Φ
1
)
– Arcs(I) = Arcs(Φ
1
) ∪ Arcs(Φ
2
) ∪
{(last(Φ
1
),true,ε,
/
0, f irst(Φ
2
)),
(last(Φ
1
),true,ε,
/
0, f irst(Φ
2
))}
– Inv(I) = Inv(Φ
1
) ∪ Inv(Φ
2
)
(a) JΦ
1
.(Φ
2
)
ω
K
(b) JP(d).Φ
1
.(Φ
2
)
ω
K
(c) JεK (d) Js.P(d).Φ
0
K
Figure 5: Representation of the encoding of an input se-
quence.
• if I := P(d).Φ
1
.(Φ
2
)
ω
– L(I) = {P
0
} ∪ L(Φ
1
) ∪ L(Φ
2
), where last(Φ
2
)
is urgent
– f irst(I) = P
0
– Arcs(I) = Arcs(Φ
1
) ∪ Arcs(Φ
2
) ∪
{(P
0
,t ≤ d, ,{t := 0}, f irst(Φ
1
)),
(last(Φ
1
),true,ε,
/
0, f irst(Φ
2
)),
(last(Φ
1
),true,ε,
/
0, f irst(Φ
2
))}
– Inv(I) = {P
0
7→ t ≤ d} ∪ Inv(Φ
1
) ∪ Inv(Φ
2
)
• if Φ := ε
– L(Φ) = {E}
– f irst(Φ) = last(Φ) = E
– Arcs(Φ) =
/
0
– Inv(Φ) =
/
0
• if Φ := s.P(d).Φ
0
– L(Φ) = {S,P} ∪ L(Φ
0
)
– f irst(Φ) = S, last(Φ) = last(Φ
0
)
– Arcs(Φ) = Arcs(Φ
0
) ∪ {(S, true,y!,
/
0,P),
(P,t = d,ε,{t := 0}, f irst(Φ
0
))}
– Inv(Φ) = {P 7→ t ≤ d}∪ Inv(Φ
0
)
Figure 5 depicts the shape of input generators.
Figure 5(a) shows the generator JIK, obtained from
I := Φ
1
.(Φ
2
)
ω
. The edge connecting the last state
of JΦ
2
K to the first one allows Φ
2
to be repeated in-
finitely often. Figure 5(b) shows the case of an input
sequence I := P(d).Φ
1
.(Φ
2
)
ω
beginning with a pause
P(d): in this case, the initial location of JIK is P
0
,
which imposes a delay of d time units. The remain-
der of the input sequence is encoded as for the pre-
vious case. Figure 5(c) shows the induction basis for
encoding a sequence Φ, i.e., the case Φ := ε. It is en-
coded as a location E having no edge. Finally, Figure
5(d) shows the case of a non-empty spike–pause pair
sequence Φ := s.P(d).Φ
0
. It consists of an urgent lo-
cation S: when the automaton moves from S, a spike
Parameter Learning for Spiking Neural Networks Modelled as Timed Automata
27

Figure 6: Non-deterministic input sequence automaton.
is fired over channel y and the automaton moves to lo-
cation P, representing a silent period. After that, the
automaton proceeds with the encoding of Φ
0
.
B.2 Non-deterministic Input Sequences
Non-deterministic input sequences are valid input se-
quences where the occurrence times of spikes is ran-
dom but the minimum inter-spike quiescence duration
is T
min
. Such sequences can be generated by an au-
tomaton defined as follows:
Definition 5 (Non-deterministic input generator).
A non-deterministic input generator I
nd
is a tuple
(L,B,X , Σ,Arcs,Inv), with:
• L = {B, S, W}, with S urgent,
• X = {t}
• Σ = x
• Arcs = {(B,t = D,x!,
/
0,S), (S,true, ε,{t :=
0},W), (W,t > T
min
,x!,
/
0,S)}
• Inv(B) = (t ≤ D)
where D is the initial delay.
The behavior of such a generator depends on clock
t and broadcast channel x, and can be summarized as
follows: it waits in location B an arbitrary amount of
time before moving to location S, firing its first spike
over channel x. Since location S is urgent, the au-
tomaton instantaneously moves to location W, reset-
ting clock t. Finally, from location W, after an arbi-
trary amount of time t, it moves to location S, firing
a spike. Notice that an initial delay D may be intro-
duced by adding the invariant t ≤ D to the location B
and the guard t = D on the edge (B → S).
C Additional Material for the
Advice Back-Propagation
Algorithm
Here we provide more details on the ABP algorithm:
the pseudo-code handling the update of the synaptic
weights and the propagation of advices is given in Al-
gorithms 1 and 2. In both algorithms, ∆ is a constant
factor used to manage increments and decrements.
Algorithm 2: Abstract ABP: Should Not Have Fired ad-
vice pseudo-code.
1: procedure SHOULD-NOT-HAVE-
FIRED(neuron)
2: if IS-VISITED(neuron) then
3: return
4: SET-VISITED(neuron, True)
5: for i ← 1 ... COUNT-
PREDECESSORS(neuron) do
6: weight
i
← GET-WEIGHT(neuron, i)
7: f ired
i
← FIRED-RECENTLY(neuron, i)
8: neuron
i
← GET-PREDECESSOR(neuron,
i)
9: DECREASE-WEIGHT(neuron, i, ∆)
10: if weight
i
≥ 0 then
11: if f ired
i
then
12: SHOULD-NOT-HAVE-
FIRED(neuron
i
)
13: else
14: if ¬ f ired
i
then
15: SHOULD-HAVE-FIRED(neuron
i
)
Advice propagation
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
28
