
A Robust and Adaptive Algorithm for Real-time Muscle Activity Interval
Detection using EMG Signals
Rabya Bahadur
1,2
and Saeed ur Rehman
1
1
Department of Electrical & Computer Engineering, Center for Advanced Studies in Engineering, Islamabad, Pakistan
2
Department of Electrical Engineering, COMSATS Institute of Information Technology, Abbottabad, Pakistan
Keywords:
Electromyogram, Action Potentials, Muscle Activation Interval, Onset/Offset Detection.
Abstract:
Detection of Muscle Activity Interval plays a pivotal role in the design and implementation of real-time My-
oelectric controlled devices and their applications. This paper presents an algorithm for real-time detection
of onset/offset points in the muscles activity by employing adaptive threshold technique on the Correlation
Coefficient of Taeger Kaiser Energy Operator using low cost hardware. Performance of the algorithm has also
been evaluated through real-time tests carried out under various constrained scenarios and different signal to
noise ratios, revealing very promising results with a maximum accuracy of 99.9% using medium or no external
forces.
1 INTRODUCTION
In Neuro-rehabilitation, body signals are used as a
mean of controlling the assistive devices. The most
commonly used body signals for this purpose are ob-
tained through surface Electromyogram (sEMG). In
this technique, EMG signals are retrieved from the
skin surface using electrodes on the desired muscles
(non-invasively), which represent a convolution of the
electrical activity of the muscle fibers known as Motor
Unit Action Potential (MUAP) (Farina et al., 2014)
and are described using eqn. 1.
emg(t) =
N
∑
i=1
∞
∑
j=−∞
ψ
i
(t)δ(t − t
i j
) (1)
Where N is the number of active muscle fiber sig-
nals known as Active Motor Neurons, ψ
i
(t) represents
the waveform of the i
th
motor unit, δ(t) is the impulse
function and t
i j
is the time delay of the i
th
motor unit.
These signals are generally used to control the speed
of a motor or position of an actuator in prosthesis.
Therefore, the accurate detection of the points where
muscles initiate to move from their relaxed states is of
great significance in implementing real-time control
of prosthesis. The triggering of the muscular contrac-
tion is known as the onset point, while the end point of
the contraction is referred to as an offset point. These
onset/offset represents the duration of a muscle activ-
ity.
For neuro-rehabilitation active control of an external
device with maximum precision and minimum pro-
cessing time is a major requirement. Currently avail-
able myo-controlled prosthesis such as i-limb and Ot-
tobock utilize state machine based controller for se-
lection of movements (Farina et al., 2014). In such
systems real-time detection of these onsets/offsets
play a vital role. A great deal of work has been carried
out in this regard during the past two decades. (Merlo
et al., 2003) used amplitude threshold on continuous
time wavelet transform for the detection of presence
of MUAP . The method proposed is unsuitable for real
time activity detection because its accuracy depends
upon the shape of window selected which may vary
for different movements; in addition, the proposed
method is computationally intensive. (Solnik et al.,
2010) refer to the use of Teager-Kaiser Energy Op-
erator (TKEO) for the use of EMG detection, which
seems to be a very promising parameter . However,
they have used a threshold of 3 standard deviations
for 25 consecutive samples which makes the over-
all algorithm non-adaptable especially for scenarios
where signal variations due to changes in environ-
mental/physical conditions are experienced; this as-
pect is further discussed in section (6). The two stage
methodology proposed by (Drapala et al., 2010) is
based on initial estimation from the entire EMG fol-
lowed by local estimation. The first stage proposes
energy estimation of sEMG signal using the TKEO
algorithm. The estimated energy signal acts as input
Bahadur, R. and Rehman, S.
A Robust and Adaptive Algorithm for Real-time Muscle Activity Interval Detection using EMG Signals.
DOI: 10.5220/0006536200890096
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 4: BIOSIGNALS, pages 89-96
ISBN: 978-989-758-279-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
89

to Expectation Maximization (EM) clustering method
for the classification of EMG activity region vs. non
activity region . Once the active and non-active re-
gions are vividly separated they are further enhanced
using a single threshold algorithm. As the algorithm
needs complete signal for analysis and comparison,
therefore, their work is presented for offline analy-
sis, focusing more on precision as compared to com-
putational complexity. (Xu et al., 2013) present an
adaptive approach for onset/offset detection . Their
work merges Maximum Likelihood (ML) algorithm
with a look-up table, comprising of a set of thresh-
old values based on different Signal to Noise ratios
(SNR). The algorithm is not computationally inten-
sive and, therefore, can be adopted for real time signal
characterization but the major drawback is the use of
simulated data combined with Additive White Gaus-
sian Noise (AWGN) at different SNRs (a mean for
generating the look-up table) which cannot be mod-
eled for a real time EMG signal. Further investiga-
tions for onset/offset detection have also been carried
out using machine learning algorithms such as the
use of Gaussian Mixture Model and Hidden Markov
Model by (Liu et al., 2015a; Liu et al., 2015b; Naseem
et al., 2016). However, all such attempts are lim-
ited to offline sEMG and cannot be adopted for real
time analysis due to their computational complexity.
In this paper, the onset/offset points resulting in the
subsequent Muscle Activity Interval (MAI) are deter-
mined using temporal and statistical features for the
real time sEMG signals. The run-time performance of
the proposed algorithm has been evaluated using real-
time EMG signals under various constrained scenar-
ios. The algorithm was tested on signals from seven
healthy subjects using same experimental procedure
as discussed in section (2).
2 EXPERIMENTAL PROCEDURE
2.1 Testing Protocol
Seven healthy subjects volunteered in this study in-
volving three females and four males. All experi-
ments were approved by campus bioethics commit-
tee and written consent was also taken from each par-
ticipant. During these experiments, the elbow joint
was fixed while wrist flexion and extension were per-
formed with 0
◦
rest position. In order to check the
robustness of the proposed algorithm, three kinds of
exercises were performed by each participant.
i. Wrist flexion and extension in the absence of any
external force acting on the wrist.
ii. Wrist flexion and extension in the presence of an
opposing force acting on the wrist .
iii. Wrist flexion and extension while holding 1 kg, 2
kg, and, 5 kg weights, respectively.
In order to further investigate the accuracy of
the proposed algorithm, AWGN was added to the
recorded signals to generate different SNRs of 1.25, 3,
6, and 9 dBs. All offline simulations were performed
using MATLAB 2015a while all online results were
obtained using NI LabVIEW 2015.
2.2 Experimental Setup
Bipolar pre-gelled Ag/AgCl disposable surface elec-
trodes were placed on the left arm at flexer carpi
ulnaris and radialis muscles, as shown in Fig. 1,
following the recommendations of Surface Elec-
tromyography for Non-Invasive Assessment of Mus-
cles(SENIAM) (Hermens et al., 2000). The refer-
ence electrode was in particular placed on medial epi-
condyle of elbow joint which was kept at rest dur-
ing the entire experimentation process. This paper
presents results of a pilot study initiated at CASE,
Pakistan, to investigate the use of a low-cost hard-
ware for online detection of MAI. For this purpose, a
2 channel Olimex EKG/EMG bio-feedback shield was
used with Arduino Uno R3, despite its lower acqui-
sition signal bandwidth of 0.16Hz to 40Hz which is
much less than the required 500 Hz, for sEMG signal.
The main idea in this pilot study was to explore the
viability / suitability of information contents present
in lower frequency components of sEMG signals, for
estimation of MAI. sEMG signals were sampled at
frequency of 340Hz with 8-bit precision, and the ex-
perimental setup was interfaced with LabVIEW using
a baudrate of 57,600 bps. The EMG signals were dis-
played on a real time monitor for visual inspection to
ensure quality acquisition.
Figure 1: Electrode placement on upper limb for EMG ac-
quisition.
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
90

Figure 2: sEMG signal with energy operator (a) sEMG (b)
the Energy estimated using TKEO from eqn.2.
3 FEATURES
In order to estimate the onset/offset points following
aspects of the sampled sEMG signal have been uti-
lized in the proposed algorithm (discussed in detail in
section 4).
3.1 Teager-Kaiser Energy Operator
TKEO is a simple algorithm with two multiplication
and a single addition to determine the temporal energy
level of a signal at any instant of time as depicted in
eqn. 2. It has been used by different researchers for
EMG activity analysis with a fixed threshold (Micera
et al., 2001) (Xu and Adler, 2004). Fig. 2 presents the
Energy calculated using TKEO operator for a sEMG
signal.
τ(n) = x(n)
2
− x(n − 1)x(n + 1) (2)
Where, τ(n) is presents TKEO energy estimator and
x(n) is the input EMG signal.
3.2 Correlation Coefficient
The correlation coefficient is utilized in order to es-
timate the change in current state of activity. Cor-
relation between consecutive w samples is calculated
if the correlation coefficient of two consecutive win-
dows is approximately 0, it means the behavior in the
two windows is changing, referring to a change in cur-
rent state of the muscles. Thus, the transition points
of the correlation coefficient denoted by ZC{r(n)}
are the candidate onset/offset points termed as fidu-
cial points, as referred in eqn. 3 below.
r(n) =
cov(x(n − w : n − 1), x(n : n + w))
std(x(n − w : n − 1))std(x(n : n + w))
ZC{r(n)} =
0; |r(n)| < ε
1; Otherwise
(3)
Where r(n), is the correlation coefficient, x(n) is the
current n
th
sample of input signal, w is the size of
Figure 3: Black solid line presents sEMG signal while grey
dotted line show activity region where the small width ac-
tive regions are false alarms.
samples selected for correlation evaluation, which in
our case is 30, cov is the covariance function and std
represents the standard deviation; ε is zero crossing
threshold and ZC{r(n)} refers to potential candidate
points for onset/offset reference.
3.3 Minimum Activity Length
In order to complete a simple activity such as wrist
flexion or extension, it is expected that some definite
minimum time duration would be required. In our
case, we have assumed it to be around one half of a
second, i.e. if Fs is the total number of samples per
second then an activity interval must be at least Fs/2
samples long. Therefore, a second threshold based on
activity length is incorporated in the proposed algo-
rithm. If the length of the activity region identified
is found to be less than Fs/2, than the candidate ac-
tivity region is considered as no activity region and is
simply rejected. An example of such false alarms and
true activity regions is presented in Fig. 3.
4 ALGORITHM
During all the experiments performed, the hand was
initially kept at rest position. For this reason, the al-
gorithm was initialized with “no activity in progress”.
In order to estimate the onset/offset points, the TKEO
parameter for sEMG signal is calculated at every in-
stant, referred to as, τ(n), followed by correlation co-
efficient estimation of w consecutive samples. If the
correlation coefficient attains a value less than ε, it
denotes a change in current state of wrist position, re-
ferred as ZC{r(n)}. Once an initial onset point is iden-
tified, a record of energy between the current onset
points till the next fiducial point is tracked and time
interval for maximum energy is estimated. If the en-
ergy in current time interval is maximum so far, pre-
vious interval is cross examined. If the energy level in
the previous interval was at least half of the energy in
A Robust and Adaptive Algorithm for Real-time Muscle Activity Interval Detection using EMG Signals
91

the current interval, the starting point of previous in-
terval is considered as an onset else the fiducial point
of current band is the marked onset. The process con-
tinues till an offset is encountered. Once an onset has
been found, search for the offset is activated among
the subsequent fiducial points. For this purpose, en-
ergy of the two consecutive intervals, defined by the
subsequent fiducial points, is observed. If the energy
level in any two successive intervals falls below a cer-
tain threshold, which in our case has been taken equal
to 5% of the energy of the onset interval (based on ra-
tio of maximum and minimum power observed), we
mark the ending fiducial point of the second interval
as the offset. As the level of threshold is not against
a hard constant value rather 5% of the energy interval
therefore this initial search for onset/offset is referred
as the first adaptive threshold.
The candidate MAI from the first adaptive thresh-
old is then evaluated for minimum activity length. It
has been observed as well as adopted in different liter-
ature that the minimum duration for any hand activity
requires at least half a second (Merlo et al., 2003).
Therefore, in case the number of samples of the can-
didate MAI exceeds Fs/2, the interval is marked as
a valid MAI otherwise rejected as a false alarm. A
detailed step-by-step description of the algorithm is
provided in Table1 in the form of a pseudo code.
5 RESULTS
This paper presents the implementation of double
threshold adaptive algorithm for real time sEMG ac-
tivity interval detection. The algorithm was tested on
real time sEMG signals with three different types of
external forces, as discussed in Section 2. All results
were tested for both wrist flexion as well as wrist ex-
tension and while computing the qualitative measures
an average for each scenario using 30 signals for both
flexion and extension by each patient were quantified.
Performance rating for all scenarios is conducted by
comparing the mean error µ, and its respective stan-
dard deviation σ. The mean error was evaluated by
comparing the estimated fiducial points with visually
inspected fiducial points.
5.1 sEMG without Any External Force
Two channel sEMG signals were acquired from upper
limb ulnaris and radialus carpi muscles using Olimex
EKG/EMG shield with a sampling frequency of 340
Hz. The elbow was placed on a wooden table with
wrist flexed from 0
◦
rest position and in a similar
manner extended from the same rest area. A sample
Figure 4: sEMG for wrist flexion and extension without any
external force applied.
of the flexion and extension signals acquired with-
out any external force acting on the hand / wrist, as
discussed in the above fashion are presented in Fig.
4. Due to negligible external force the MAI from
sEMG signal is accurately characterized by the al-
gorithm with an error rate of 0.01 ± 0.01msec and a
maximum accuracy of 99.9%.
5.2 sEMG with Applied Opposing Force
(i.e. Frictional Force)
Flexion and extension were performed with a force
in the opposite direction of movement of hand act-
ing as a frictional force. The attributes of the ac-
quired sEMG signal with and without external force
are same in terms of data variation and other statisti-
cal means. However, an evident increase in the time
duration of MAI as well as additional harmonics are
observed as shown in Fig. 5(a& c). These oscillations
appears due to the resistance of the opposing force,
Figure 5: sEMG signals with opposing force applied; (a)
wrist flexion and (b) wrist extension, with respective energy
signals.
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
92

Table 1: Proposed Algorithm.
Input: A matrix X ∈ ℜ
[N×2]
with N representing number of samples and 2 are the number of channels.
Output :s =
0;I f activityinProgress
1;Otherwise
(4)
1. Initial Values: k=1;l=1;w=30; mE=0; onset=0;
2. τ(n) = x(n)
2
− x(n − 1)x(n + 1); n=1,2,3,...,N-w //TKEO
3. r(n) = corr(|τ(n − w : n)|,|τ(n : n + w)|) //correlation of w consecutive elements, N is the
total current length of input samples acquired
4. if(|r (n)|=<0.01) //For any channel using or operator
on(k)=n;
if (k == 1) //For initializing onset
onset=on(k)
end
k++;
if (k > 2) //Estimating the correct onset point using
maximum Energy interval
initial.Energy =
on(k)
∑
u=on(k−1)
|τ(u)| current.Energy =
on(k+1)
∑
u=0n(k)
|τ(u)| (5)
end
5.if(max.Energy<initial.Energy)
max.Energy=initial.Energy //Maximum Energy
if(2 ×
on(k−1)
∑
u=on(k−2)
|τ(u)| < initial.Energy) (6)
onset=on(k-1);
ty=on(k+1);
else
onset=on(k);
ty=on(k-2);
end
s=1;
end
6. if(onset = 0) //If activity is initialized
if (current.Energy < initial.Energy && current.Energy > max.Energy*0.05)
offset= on(ii+1);
s=0;
end
else
off= ty;
end
7. if (s==1 && n-onset > Fs/2)
Activity In Progress
elseif (offset-onset >Fs/2)
x(onset : offset) is the detected Activity Region
mE=0;k=1;onset=0;
end //Repeat Step 1 to 5 till the process continues
A Robust and Adaptive Algorithm for Real-time Muscle Activity Interval Detection using EMG Signals
93
resulting in an increase in MAI as compared to nor-
mal time for the wrist to complete its 90
◦
flexion or
extension from rest position. In order to choose the
correct onset, it is required to analyze the energy level
in the signal continuously. Due to the oscillatory be-
havior the TKEO based correlation results in multiple
closely detected onset candidates as highlighted with
black dots in Fig. 5. However, the energy threshold
between every two consecutive fiducial points tracks
the point from where a consistent increase in energy
level is observed, till the maximum energy value is
achieved, resulting in the identification of the accu-
rate onset point. It further investigates the existence of
offset point and continuously compares the detected
MAI with the set sample threshold.
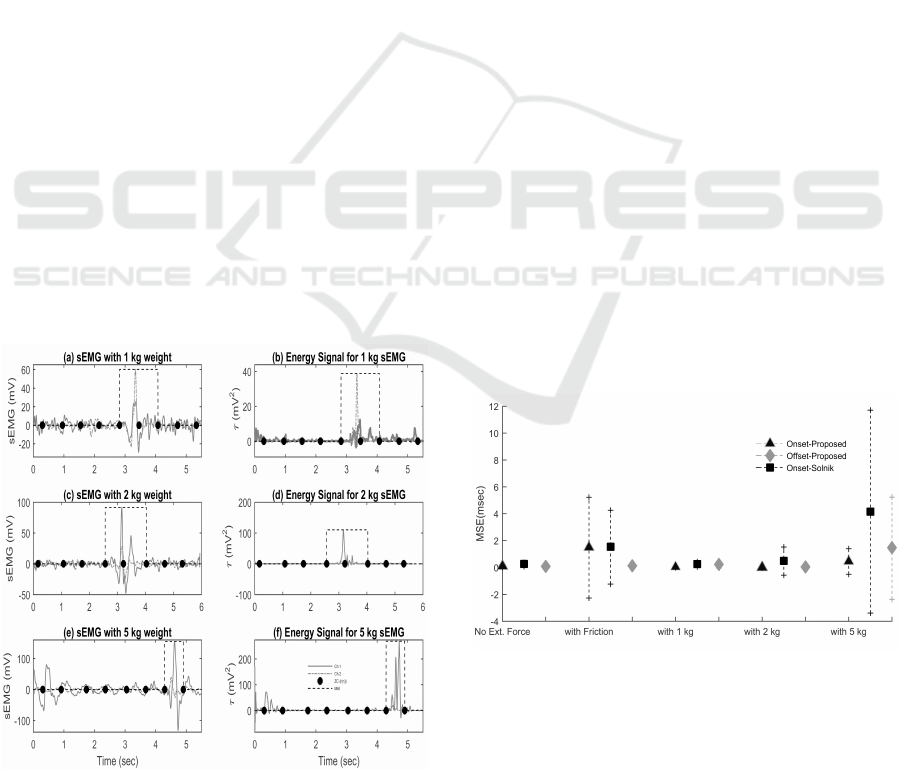
5.3 sEMG with Variable Weights
The same experiment of wrist flexion and extension
has been tested with multiple weights in order to in-
vestigate the robustness of the proposed algorithm.
Multiple alarms are activated in the form of ZC{r(n)}
which is an affirmation of presence of activity. How-
ever, the adaptive threshold is successful in identify-
ing the region of interest. With minimum weights
i.e. 1 kg and 2 kg the mean error observed is al-
most the same as no weight added (0.01 ± 0.01, &
0.01 ± 0.02msec, respectively). With the increase in
weight the energy level starts increasing as shown in
Fig. 6(b & d). At 5 kg as the weight becomes heavy,
there is a continuous pressure on the hand muscles re-
sulting in initial oscillations even when the wrist is at
Figure 6: Results of proposed algorithm for sEMG with its
corresponding TKEO graph for different weight lifted dur-
ing wrist extension (a, b) and flexion (c, d, e, & f).
rest position, as can be clearly observed in Fig. 6(f)
between 0.5 to 1 sec duration. As the proposed algo-
rithm is based on maximum energy as well as interval
length, it selects the second region as muscle activity
region and rejects the initial energy band as a false
alarm Fig. 6(e & f).
6 DISCUSSION
Muscle contraction or relaxation is responsible for the
accurate movement of any limb in human body. In or-
der to estimate muscle activity onset/offset point de-
tection, this paper proposes the use of adaptive thresh-
old based on correlation coefficient of TKEO energy
estimator. The proposed algorithm is tested for dif-
ferent scenarios such as free wrist i.e. no external
force applied, with an opposing force in the direction
of motion, and wrist movement with different weights
attached. The results for all above discussed scenarios
is presented in Fig. 7. The mean error in case of no
external force or 1 kg weight is near to zero, however,
when the weight is increased to 2 kg and 5 kg or in
case of opposing force, the error slightly increase with
a maximum error variation of 270 m sec and provides
lowest results with an acurracy of 98.3%. When the
hand muscle grasps a weight as heavy as 5 kg pressure
is exerted as a result of which additional harmonics
are observed in sEMG recorded even at rest position
of the wrist. Therefore, the results of MAI is not as
high as that in low weight sEMG signals. A compar-
ison with the onset MSE proposed by (Solnik et al.,
2010) is also presented in the Fig. 7. The onset de-
tection in no external force, lite weights and opposing
Figure 7: Performace comparison (on the basis of Mean
Square Error (MSE) and Standard Deviation values) of the
proposed algorithm with the algrithm presented by (Solnik
et al., 2010) under various loading scenarios. Bold sym-
bol shapes (i.e. Square, Diamond and Triangle) indicate
the Mean Error value while the vertical dotted lines repre-
sent the spread of error. Note that the proposed algorithm
detects both onset as well as offset points, whereas Solnik
algorithm detects onsets ONLY.
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
94

Table 2: Mean error and stand deviation comparison of algorithm results for sEMG Onset Detection with constrained and
unconstrained environment at different SNRs.
SNRs No Force Friction 1 kg 2 kg 5 kg
(dB) µ σ µ σ µ σ µ σ µ σ
x(t) 0.01 0.01 0.26 0.57 0.01 0.01 0.01 0.05 0.03 0.08
1.25 0.09 0.32 4.72 3.04 0.90 1.76 2.01 3.04 3.21 4.26
3 0.04 0.05 2.89 3.47 0.04 0.07 1.36 1.53 1.23 3.70
6 0.05 0.07 2.09 2.55 0.05 0.06 0.25 0.82 1.85 2.43
9 0.09 0.13 1.18 1.98 0.05 0.05 0.25 0.86 1.47 1.25
Table 3: Mean error and stand deviation comparison of algorithms results for sEMG Offset Detection with constrained and
unconstrained environment at different SNRs.
SNRs No Force Friction 1 kg 2 kg 5 kg
(dB) µ σ µ σ µ σ µ σ µ σ
x(t) 0.01 0.01 0.02 0.08 0.004 0.01 0.04 0.01 0.08 0.20
1.25 0.68 2.22 4.77 5.00 1.47 1.13 3.31 2.48 4.75 3.76
3 0.15 0.15 3.93 4.80 0.28 0.22 0.18 2.29 2.85 2.03
6 0.18 0.21 2.50 3.84 0.25 0.24 0.18 0.35 1.30 2.08
9 0.12 0.15 1.50 2.38 0.21 0.26 0.76 0.27 1.30 1.80
frictional force is comparable, where as in case of 5 kg
weight the proposed algorithm out performs the other
by an onset detection accuracy of 98.3% in compari-
son with 88.1% achieved by (Solnik et al., 2010).
In order to investigate the performance of algo-
rithm for external interference, AWGN with different
SNRs was added to the already acquired EMG sig-
nals. The algorithm was run offline on noise added
EMG signals to evaluate the performance for on-
set/offset detection accuracy. The results are summa-
rized in Table 2 & 3, respectively. For 3 and 9 dBs
SNR sEMG signals, with no external force, 1 kg, and
2 kg weights the mean error is below 280 msec. But
when the signal strength decreases as in case of 1.25
and 3 dB the algorithm has a slight increase in mean
error and standard deviation, especially in case of fric-
tional force and 5 kg weights applied. This is due to
the fact that when an external force is applied the mus-
cle tries to contract but the external force has a domi-
nant pressure on the muscle, resulting in muscle con-
traction noise. Further increase in SNR deteriorates
the strength of the signal thus an increase in error is
observed while estimating the MAI. sEMG acquired
in stressful scenarios have a higher frequency as com-
pare to sEMG acquired from wrist with no external
interference or lite weights such as 1 kg or 2 kg. The
results can be easily improved for such signals if the
window length w is increased. However, increase in
window length would make the algorithm less suit-
able for real time applications, therefore, an adaptive
window length selection needs to be catered in future.
All sEMG signals evaluated on sEMG focusing
easily available low cost equipment targeting lower
frequency band of 0.14 Hz-40 Hz. As the lower fre-
quencies provides information about the presence of
activity and higher frequencies tends to define the
particular movement, therefore, the use of lower fre-
quency range is sufficient for MAI detection. How-
ever, it may effect if the same low frequency sEMG
signals are used for movement identification.
7 CONCLUSION
The extraction of muscle activity interval can play
a vital role for real time Myo-electric controlled de-
vices and other clinical applications. The purpose
of the proposed work is to present an algorithm for
real time detection of muscle activity using affordable
hardware. Although the hardware selected focuses on
low frequency sEMG signal only, the detected MAI is
considerably accurate and therefore, low cost sEMG
acquisition devices such as Olimex EKG/EMG shield
can be utilized for control of automated prosthesis in
order to provide cheaper solutions.
While majority of the methods proposed in lit-
erature are limited to offline analysis and onset de-
tection; our proposed methodology is fast and easily
implementable for real-time systems as well as han-
dles both activity activation and deactivation regions.
The proposed algorithm not only detects the complete
muscle activity interval but also provides consider-
ably higher accuracy than other previously proposed
algorithms. The methodology presented adopts a dou-
A Robust and Adaptive Algorithm for Real-time Muscle Activity Interval Detection using EMG Signals
95

ble threshold adaptive algorithm for MAI detection.
The initial threshold is based on correlation coeffi-
cient and percentage of maximum energy providing
an adaptive behavior. The use of correlation coeffi-
cient provides better performance for different SNRs
while the percentage of maximum energy computed
over an interval selects the most optimum candidate
interval. The experimental results are achieved us-
ing real surface EMG signals in different scenarios as
well as cross checked with different levels of AWGN.
We have shown that the proposed algorithm is ro-
bust to estimate the closest correct onset and offset
point even with external interference. The proposed
algorithm performs best with lite or no external force,
achieving an accuracy of 99.9%, and improves perfor-
mance by 10.2% in worst case scenario in comparison
with previously proposed work.
REFERENCES
Drapala, J., Brzostowski, K., Szpala, A., and Kucharska,
A. (2010). Two stage emg onset detection method.
Archives of Control Science, 22:427–440.
Farina, D., Jiang, N., Rehbaum, H., Holobar, A., Grain-
mann, B., Dietl, H., and Aszmann, O. (2014). The
extraction of neural information from the surface emg
for the control of upper limb prosthesis: Emerging av-
enues and challenges. IEEE transaction on Neural
Systems and Rehabilitation Engineering, 22:797–809.
Hermens, H., Merlett, R., and Freriks, B. (2000). Surface
ElectroMyopGraphy for Non-Invasive Assessment of
Muscles(SENIAM).
Liu, J., Ying, D., and Rymer, W. (2015a). Emg burst pres-
ence probability: A joint time-frequency representa-
tion of muscle activity and its application to onset de-
tection. Journal of Biomechanics, 48.
Liu, J., Ying, D., Rymer, W. Z., and Zhou, P. (2015b). Ro-
bust muscle activity onset detection using an unsu-
pervised electromyogram learning framework. Plos
ONE, 10:1193–1197.
Merlo, A., Farina, D., and R., M. (2003). A fast and reliable
technique for muscle activity detection from surface
emg signals. IEEE transaction on Biomedical Engi-
neering, 50:316–323.
Micera, S., Vannozzi, G. andSabatini, A. M., and F., D.
(2001). Improving detection of muscle activation in-
tervals. IEEE Engineering in Medicine and Biology
Magazine, 20.
Naseem, A., Jabloun, M., Ravier, P., and Buttelli, O. (2016).
Muscular activation intervals detection using gaus-
sian mixture model gmm applied to semg signals.
In IEEE 18th International Conference on e-Health
Networking Applications and Services (Healthcom).
IEEE Xplore.
Solnik, S., Rider, P., Steinweg, K., DeVita, P., and Horto-
bagy, T. (2010). Taeger kaiser energy operator signal
conditioning improves emg onset detection. European
Journal of Applied Physiology, 110:489–498.
Xu, L. and Adler, A. (2004). An improved method for
muscle activation detection during gait. In Canadian
conference on Electrical and Computer Engineering.
IEEE Xplore.
Xu, Q., Quan, Y., Yang, L., and He, J. (2013). An adaptive
algorithm for the determination of the onset and offset
of muscle contraction by emg signal processing. IEEE
transaction on Neural Systems and Rehabilitation En-
gineering, 21:65–73.
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
96
