SmoothIsoPoints: Making PDE-based Surface Extraction

from Point-based Volume Data Fast

Paul Rosenthal

, Vladimir Molchanov

and Lars Linsen

2,3

University of Rostock, Rostock, Germany

Jacobs University, Bremen, Germany

Westf¨alische Wilhelms-Universit¨at M¨unster, M¨unster, Germany

Keywords:

Surface Extraction, Isosurfaces, Level Sets, Unstructured Point-based Volume Data.

Abstract:

PDE-based methods like level-set methods are a valuable and well-established approach in visualization to

extract surfaces from volume data. We propose a novel method for the efﬁcient computation of a signed-

distance function to a surface in point-cloud representation and embed this method into a framework for PDE-

based surface extraction from point-based volume data. This enables us to develop a fast level-set approach

for extracting smooth isosurfaces from data with highly varying point density. The level-set method operates

just locally in a narrow band around the zero-level set. It relies on the explicit representation of the zero-level

set and the fast generation of a signed-distance function to it. A level-set step is executed in the narrow band

utilizing the properties and derivatives of the signed-distance function. The zero-level set is extracted after

each level-set step using direct isosurface extraction from point-based volume data. In contrast to existing

methods for unstructured data which operate on implicit representations, our approach can use any starting

surface for the level-set approach. Since for most applications a rough estimate of the desired surface can

be obtained quickly, the overall level-set process can be shortened signiﬁcantly. Additionally, we avoid the

computational overhead and numerical difﬁculties of PDE-based reinitialization. Still, our approach achieves

equivalent quality, ﬂexibility, and robustness as existing methods for point-based volume data.

1 INTRODUCTION

Many modern simulation methods generate unstruc-

tured point-based volume data, i. e., scalar ﬁelds

where the data points may have an arbitrary distribu-

tion in a 3D space and do not exhibit any connectivity.

A major group of such data stems from Lagrangian

numerical simulations of natural phenomena such as

ﬂuid dynamics. They allow for the reproduction of

complex natural phenomena by not only simulating

the evolution of data at the sample points but also sim-

ulating the ﬂow of the sample points under respective

forces. Hence, data points move over time, change

their neighborhoods, and are distributed with a highly

varying density. Such simulations are typically car-

ried out with millions of particles.

Level-set methods have a large variety of applica-

tions. In scientiﬁc visualization, they are used to ex-

tract boundary surfaces of features from volume data.

Typically, the algorithms operate on rectilinear cells

and a given initial level-set function is modiﬁed to ex-

plicitly or implicitly minimize a given energy func-

tional.

An approach generalizing the basic idea of level

sets to work directly on unstructured point-based vol-

ume data was presented in (Rosenthal and Linsen,

2008b). They do not resample the data over a struc-

tured grid using scattered data interpolation, which

inevitably introduces resampling errors, which can

grow enormously for data sets with highly varying

point density, unless the sampling points are chosen

very densely which lets the data size explode. un-

structured points avoids this source of error.

The level-set approach models the evolution of a

surface by applying forces in normal direction. To

allow for easy change of the topology of the sur-

face, it is implicitly represented as the zero-level set

of a level-set function. The evolution is carried out

by transforming the level-set function using an itera-

tive numerical integration scheme, which implicitly

transforms the surface. The approach typically in-

duces complex calculations and the evaluation of par-

tial differential equations at each sample location and

each iteration step. When dealing with large data

sets and small time-integration steps, this can lead to

enormous computation times until convergenceof the

level-set process. The calculations for unstructured

point-based data are even more complex than those in

the gridded case which was the major drawback of the

method by Rosenthal and Linsen. Later, the approach

was modiﬁed to utilize a narrow-band technique and

signiﬁcantly speed up the computations (Rosenthal

Rosenthal, P., Molchanov, V. and Linsen, L.

SmoothIsoPoints: Making PDE-based Surface Extraction from Point-based Volume Data Fast.

DOI: 10.5220/0006537200170028

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages 17-28

ISBN: 978-989-758-289-9

(a) (b) (c) (d)

Figure 1: Illustration of our proposed level-set method for extracting smooth isosurfaces from an artiﬁcial 2D data set. a) As

input data we assume a volumetric scalar data set with unstructured sample positions and no connectivity. Colors indicate

function values at the data points. b) Directly extracting isosurfaces from the data may produce bumpy surfaces in regions with

highly varying point density. Black dots indicate the isosurface in point-cloud representation. Nevertheless, the isosurface

can be used by our method as a good initial guess for the PDE-based extraction of a smooth isosurface. In fact, every closed

surface (in point-cloud representation) can be used as initial zero-level set. c) In each step of the level-set iteration a narrow

band around the current zero-level set is generated and all data points within the narrow band are reinitialized with an efﬁcient

approximation of the signed-distance function to the zero-level set. Colors indicate the signed distance to the zero-level set.

d) After reaching a steady state, the zero-level set represents the smooth isosurface.

et al., 2010). However, due to the restriction to start

with a predeﬁned signed-distance function as level-

set function and the need for a time-consuming nu-

merical reinitialization, the approach is still not able

to process data sets with several million data points in

a reasonable amount of time.

We propose a level-set method which makes the

extraction of smooth isosurfaces from unstructured

point-based data sets with several million sample

points much faster:

• Similar to previous work, we achieve high accu-

racy and ﬂexibility by operating only on the un-

structured data points. We do not require any

scalar ﬁeld at positions other than the sample

points.

• We replace the time-consuming numerical reini-

tialization of previous work by a level-set func-

tion computation on basis of the approximation of

a signed-distance function to the respective zero-

level set. This procedure increases the accuracy

of the whole process, since every level-set step

is carried out with a level-set function very close

to a signed-distance function. Furthermore, the

computation of the approximation is so fast, that

the overall computation time of the level-set pro-

cess drops even if this computation is done in each

level-set step.

• We maintain the efﬁciency of restricting compu-

tations to a narrow band around the current zero-

level set. In each level-set step, only a small por-

tion of the data points around the current zero-

level set is marked to be active.

• We update the narrow band efﬁciently. The

bottleneck of narrow-band methods is often the

update of the narrow band, which includes the

computation of the level-set function values at

those points that are newly inserted into the nar-

row band. These points typically have no de-

ﬁned level-set function value. Using our efﬁcient

signed-distance function computation for estab-

lishing the level-set function, we can quickly de-

termine the required function values.

• We permit any point cloud as initial surface for the

level-set process. To initialize the whole level-set

process, only a point cloud with surface normals,

acting as initial zero-level set, has to be given.

The level-set function is computed as approxima-

tive signed-distance function to the zero-level set

allowing for the computation of the ﬁrst level-set

step. In particular, the initial surface can be an iso-

surface in point-cloud representation as computed

in (Rosenthal and Linsen, 2006). The normals at

the points are computed as gradients of the given

scalar ﬁeld.

The main approach of our local level-set method

and the structure of the visualization pipeline are ex-

plained in Section 3 and depicted in Figure 1: Given

a scalar ﬁeld in the form of point-based volume data

(a), one can extract an isosurface in point-cloud rep-

resentation. When dealing with highly varying point

densities, the isosurface may exhibit noise (b). We

want to remove the noise using a level set approach

that adds a smoothing term to the isosurface extrac-

tion functional. One main contribution of this paper is

to present a novel and efﬁcient signed distance func-

tion computation, which enables us to use the noisy

isosurface (b) as an initial surface for the level-set pro-

cess. All computations are only carried out within a

narrow band surrounding the zero-level set (c). Con-

sequently, the level-set process converges after a few

fast steps and produces a smooth isosurface (d).

To efﬁciently store the sample points and allow for

fast neighbor queries, we use a spatial decomposition

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

based on a three-dimensional kd-tree as described in

Section 4. In Section 5, the fast extraction of the zero-

level set and the determination of the narrow-band

points are described. The calculation of the level-set

function as approximated signed-distance function to

the zero-level set including the calculation of deriva-

tives is explained in Section 6. The actual level-set

process applied to the points of the narrow band and

considerations about time step restrictions are pre-

sented in Section 7. Finally, results and their discus-

sion, including the analysis of computation times and

detailed comparisons, are provided in Section 8.

2 RELATED WORK

Visualizing large unstructured point-based volume

data sets is challenging, especially when dealing with

highly varying sample point densities. The gener-

ation of a polyhedrization (Edelsbrunner and Shah,

1992) of the unstructured data points can be very slow

and is generally seen as impractical. The most com-

mon and well-established way of dealing with un-

structured point-based volume data is to resample to a

structured grid using scattered data interpolation tech-

niques (Franke and Nielson, 1991; Park et al., 2006;

Vuc¸ini et al., 2009). After this preprocessing step, a

variety of well-known visualization methods like iso-

surface extraction or level-set segmentation can be ap-

plied to the gridded data to generate the desired visu-

alizations.

In the majority of cases, level-set methods are ex-

ecuted on regular hexahedral grids that allow for fast

discrete derivative computations. Unfortunately, the

resampling to a regular grid always introduces inac-

curacies, which heavily depend on the resolution of

the grid and the point density of the data set. This

can lead to enormous interpolation errors when deal-

ing with data sets of highly varying point density and

assuming regular grids that ﬁt today’s hardware mem-

ory constraints. Using adaptive grids can reduce the

error, but the more adaptive it gets, the more compli-

cated the processing becomes. This observation raises

the desire to directly operate on unstructured point-

based volume data.

The original idea of level sets goes back to Sethian

and Osher (Osher and Sethian, 1988; Osher and Fed-

kiw, 2003), who ﬁrst describe the evolution of a sur-

face by representing the surface implicitly as the so-

lution of an equation with respect to an underlying

scalar ﬁeld. The solution is found by iterativelyapply-

ing partial differential equations (PDEs) to the scalar

ﬁeld. Many different approaches exist and the range

of application areas is wide. A general framework

for level-set segmentation of a large variety of regular

data sets is presented in (Breen et al., 2005). Enright

et al. apply a level-set approach to an octree-based

adaptive mesh (Enright et al., 2004).

Level-set methods on gridded data nowadays typ-

ically operate locally. The introduction of local

level-set methods goes back to (Adalsteinsson and

Sethian, 1995). Local level-set methods, also call-

ed narrow-band methods, have developed rapidly in

recent years (van der Laan et al., 2011; Nielsen

and Museth, 2006), and have also been remodeled

to work on today’s fast and parallel graphics hard-

ware (Lefohn et al., 2004). However, the latter meth-

ods highly utilize the structure of regular grids and are

not usable for unstructured data.

The only narrow-band approach, directly process-

ing level sets on unstructured point-based volume

data without any grid calculation or reconstruction

of the scalar ﬁeld was presented in (Rosenthal et al.,

2010). The level-setfunction is initialized as a signed-

distance function at the sample positions in a narrow

band around a simple starting surface. The whole

level-set evolution including the reinitialization of

the narrow-band and level-set function is only based

on these locations. Needed derivatives of the level-

set function are approximated by a least-squares ap-

proach. The required update of the narrow band is

done using an approximate signed-distance function

and a numerical reinitialization step keeps the level-

set function close to a signed-distance function. The

approach represents the zero-level set implicitly and

the level-set function must be initialized with a rather

simple and inﬂexible signed-distance function.

In contrast to common local level-set methods,

we further expand the idea of localization. After

each level-set step and subsequent extraction of the

zero-level set, the level-set function has to be set to

a signed-distance function to ensure good numerical

behavior (Peng et al., 1999). The common way of

achieving this would be the numerical reinitialization

of the level-set function to a signed-distance func-

tion (Schwartz and Colella, 2008), which is known

to be rather time consuming. The direct construc-

tion of a signed-distance function can be achieved

by the well-known fast-marching methods (Sethian,

1999; Tsai, 2002) which, however, always need an

underlying grid or tessellation. Several papers pro-

pose the construction of a signed-distance function

based on a moving least-squares ﬁtting (Adamson and

Alexa, 2003; Kolluri, 2008; Molchanov et al., 2010).

These approaches can also be applied to unstructured

point-based data. However, it is stated that they re-

quire a certain regular sampling density, which is also

demonstrated in Section 8, where we compare our

SmoothIsoPoints: Making PDE-based Surface Extraction from Point-based Volume Data Fast

signed-distance function approximation to those ap-

proaches.

To our knowledge, there exists no approach for

smooth isosurface extraction which combines the ac-

curacy of directly applying a narrow-band level-set

method to unstructured data and explicit construction

of the signed-distance function to the zero-level set.

We propose such an approach that directly operates

on unstructured point-based data. It does not need to

reconstruct any scalar ﬁeld at positions other than the

sample points. Furthermore, the proposed method for

approximating the signed-distance function is fast and

robust against highly varying point densities.

3 GENERAL APPROACH

Let D ⊂ R

be a bounded domain and M ⊂ D a set of

unstructured sample points x

∈ M. Furthermore, let

∈ R be the data values at the positions x

resulting

in an unstructured point-based data set representing

a scalar ﬁeld f : D → R. Our goal is to extract an

isosurface from this volumetric scalar data set with

respect to a given isovalue f

iso

∈ R. Moreover, the

smoothness of the extracted isosurface, i.e. the mean

curvature, should be controllable.

We use a level-set approach to manage the trade-

off between both goals with the level-set equation

∂ϕ

∂t



(1− λ)( f − f

iso

− ϕ) + λκ



k∇ϕk . (1)

Here ϕ : R

× R

→ R denotes the level-set function,

the mean curvature of the respective level set, and

λ ∈ [0, 1] the smoothness parameter. This level-set

equation models smooth isosurface extraction from

the given scalar ﬁeld f with respect to isovalue f

iso

and smoothness λ.

For extracting the smooth isosurface, we dynami-

cally modify a given initial surface Γ ⊂ R

, the zero-

level set, with respect to the level-set problem until

it reaches a steady state. To facilitate as much ﬂex-

ibility as possible, we assume the initial surface Γ

to be a closed surface represented as a point cloud

P ⊂ R

× S

, where S

denotes the two-dimensional

sphere in R

. Here, the pairs (p

, n

) ∈ P consist

of points p

∈ R

with associated surface normals

∈ S

. This surface representation is used, as it is

the output of the direct isosurface extraction process

from point-based volume data (Rosenthal and Linsen,

2006). This is how we typically generate the initial

surface. Any other surface representation (e. g., an

implicit surface representation or triangular meshes)

can be easily converted to the described point-cloud

representation.

Figure 2: Illustration of the proposed level-set pipeline.

The zero-level set is implicitly represented as ϕ =

0 with respect to the level-set function ϕ which is

modiﬁed following the level-set equation (1). This

task is carried out utilizing a narrow-band level-set

approach which only operates on the set of sample

points M. The pipeline of this level-set method con-

sists of three main phases: the initialization, the level-

set evolution, and the rendering. Its ﬂow chart is de-

picted in Figure 2.

In the initialization phase, the initial zero-level set

is generated by a direct isosurface extraction tech-

nique. When applying this approach to other tasks

(apart from smooth isosurface extraction), one can

start with other appropriate surfaces. Alternatively,

one can always start with a sphere lying in the bound-

ing box of the data set. Note, that, when not start-

ing with an initial surface close to the isosurface the

ﬁnal zero-level set can lack surface components of

the global solution, similar to most narrow-band ap-

proaches. However, such misses can only occur in

cases where the narrow band does not catch any part

of the respective surface component during the whole

level-set process. Moreover, this behavior can be used

to extract speciﬁc components of a surface.

Furthermore, we build data structures to store

and handle neighborhood information for the sample

points. The data structures are used to extract points

on the zero-level set efﬁciently, to generate the nar-

row band around the points of the zero-level set, and

to compute the signed-distance function. The data

structures we used are efﬁcient implementations of a

three-dimensional kd-tree.

In the iterative processing phase, ﬁrst a narrow

band of sample points is generated around the zero-

level set. The narrow band consists of all sample

points, which have a distance to the isosurface that

is smaller than a given width of the narrow band. For

all the sample points in the narrow band, the level-set

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

function ϕ is computed as signed-distance function

to the zero-level set using an approximating scheme.

The approximation results in an analytic representa-

tion of the signed-distance function, which allows for

the direct computation of derivatives using analytic

methods.

Subsequently, the actual level-set step following

the level-set equation (1) is performed at all sam-

ple points in the narrow band. Since an explicit Eu-

ler time discretization is used for updating the level-

set function at the sample points, the time steps are

bounded by the Courant-Friedrichs-Lewy(CFL) con-

dition (Courant et al., 1967) to permit numerical sta-

bility. In particular, this condition also guarantees that

the zero-level set cannot leave the narrow band in a

single iteration. In fact, we restrict the level-set step

so that the zero-level set does not move more than half

of the width of the narrow band.

The zero-level set to the processed level-set

function is extracted using direct isosurface extrac-

tion (Rosenthal and Linsen, 2006) and the surface

normals required are obtained by normalizing the

level-set function gradients. The approach compu-

tes points on the zero-level set (leading to a point-

based surface representation) by linear interpolation

between suitable neighbors of data points. This com-

pletes one iteration step.

The iterative process is executed until the level-set

function reaches a steady state. Note, that apart from

the local nature of the approach the resulting smooth

isosurface is independent of the starting surface and

does only depend on the convergence threshold and

the smoothness parameter λ. After convergence, the

zero-level set is rendered using point-based rendering

techniques (Gross and Pﬁster, 2007; Rosenthal and

Linsen, 2008a).

4 DATA MANAGEMENT

For efﬁcient calculations of neighborhood informa-

tion and access to the sample and zero-levelset points,

auxiliary data structures are needed. First, a structure

that allows for the efﬁcient extraction of the points of

the zero-level set from the sample points and the fast

generation of the narrow band is desired. Since the

positions of the sample points do not change during

the iterative phase, this can be static and, thus, created

in a preprocessing step. The unstructured data points

are stored using an efﬁcient three-dimensional kd-tree

implementation. From this kd-tree the neighborhood

information for extracting the zero-level set is derived

in the same way as it was proposed in (Rosenthal

and Linsen, 2008b). The determination of all sample

points lying in the narrow band is achieved by utiliz-

ing maximum distance queries from the zero-level set

points on the kd-tree of the sample points.

A second data structure is needed for speeding up

the approximation of the signed-distance function to

the zero-level set. Note that the ﬁrst kd-tree (contain-

ing the sample points) could also have been used for

this purpose. However, since distribution and quantity

of sample points and points of the zero-level set can

differ substantially, it is more efﬁcient to generate in

each iteration a new kd-tree for the points of the new

zero-level set.

5 ZERO-LEVEL SET

EXTRACTION AND CREATION

OF NARROW BAND

After each level-set step, the zero-level set is ex-

tracted in an explicit form, more precisely as a point-

cloud surface. This step is equivalent to extracting

the isosurface with isovalue 0 from the updated level-

set function. For extracting smooth isosurfaces from

scalar ﬁelds, a good initial guess of the smooth iso-

surface can be obtained by extracting the respective

isosurface from the given scalar ﬁeld.

Both tasks are done using the direct isosurface

extraction approach for unstructured point-based vol-

ume data presented in (Rosenthal and Linsen, 2006).

This approach utilizes the ﬁrst kd-tree that stores the

data samples. An appropriate neighborhood approxi-

mating the natural neighborhoodis generated for each

sample point utilizing an efﬁcient indexing scheme.

Points of the zero-level set are directly extracted by

linearly interpolating between neighboring samples

with different signs of the level-set function. This re-

sults in a zero-level set in point-cloud representation

with local point density proportional to the local point

density of the data set. Surface normals at the zero-

level set points are obtained as the normalized approx-

imated gradient of the underlying scalar ﬁeld using

a four-dimensional least-squares approach (Rosenthal

and Linsen, 2008b).

Each level-set step is bounded by the CFL-

condition, allowing for stability of the whole level-

set process. Thus, the movement of the zero-level set

is also bounded for each level-set iteration and it is

possible to restrict the level-set process to a narrow

band around the zero-level set without losing ﬂexi-

bility or distorting the result. For generating the nar-

row band, all sample points having a smaller distance

to the zero-level set than the width of the band are

marked as belonging to the band. As the zero-level set

SmoothIsoPoints: Making PDE-based Surface Extraction from Point-based Volume Data Fast

is extracted in a point cloud representation, we deﬁne

the distance of a sample point to the zero-level set as

the distance to the nearest point of the zero-level set.

For each zero-level set point all sample points with

distance smaller than the band’s width are efﬁciently

obtained by a nearest-neighbor query to the kd-tree

storing the sample points.

The width of this narrow band depends on the

distribution of the sample points, i.e., it is data-

dependent. To capture the entire area surrounding the

zero-level set, the width of the narrow band has to

be greater than the maximum distance of neighboring

zero-level set points. In fact, we use twice that dis-

tance to ensure that the zero-level set is kept in the

narrow band. In all our experiments, it was sufﬁcient

to choose one global value for the band’s width for the

whole local level-set process, even for data sets with

highly varying point densities. Nevertheless, the per-

formance of the approach can be tuned further by dy-

namically adjusting the band’s width with respect to

the CFL-condition. This condition restricts the time

step of each level-set step and thus the movement of

the zero-level set. Choosing the width of the narrow

band to the double of the maximum distance zero-

level set points move is more than sufﬁcient. In par-

ticular, when the level-set process is close to conver-

gence, the zero-levelset moves only slowly and a very

small narrow band can be chosen.

6 SIGNED-DISTANCE FUNCTION

COMPUTATION

Let P ⊂ R

× S

be a set of pairs (p

, n

), where

∈ R

is a point on a two-dimensional surface in

space and n

∈ S

is the associated surface normal.

Our goal is to approximate the signed-distance func-

tion to the surface represented by P. More precisely,

we want to construct a smooth scalar ﬁeld ϕ : R

→ R

with ϕ(p

) = 0 for all points p

on the surface and

k∇ϕ(x)k ≈ 1 for all points x ∈ R

Following the lines of the whole level-set method,

the approximation should not depend on an underly-

ing scalar ﬁeld and should be robust against highly

varying point density of the point cloud. The main

idea comes from the observation that the signed-

distance function can be approximated accurately on

the line γ

(t) = p

+ t · n

near each surface point by

setting ϕ(γ

(t)) = t. In a small neighborhood around

a line this measurement is still accurate and we can

approximate

ϕ(x) ≈ f

(x) := hx− p

, n

i , (2)

i. e., we use the signed distance between the projec-

tion of x to γ

and the point p

. Here h., .i denotes the

scalar product.

Figure 3: For the points of the surface the hypothetical two-

dimensional Voronoi diagram, depicted by the solid lines,

induces truncated cones in space, depicted by the dashed

lines. The blue line indicates the curve on the surface where

the third-nearest point and the fourth-nearest point, i. e., the

red and the green point, respectively, are equally distant.

This approximationshould be done for all points x

for which p

is the nearest neighbor,i. e., for all points

lying in the truncated cones induced by a hypotheti-

cal two-dimensional Voronoi diagram on the surface,

as illustrated by Figure 3. Just applying this approxi-

mation in the respective cones would result in discon-

tinuities in the resulting scalar ﬁeld at the borders of

the truncated cones. Hence, the respective functions

should be blended to produce a smooth scalar ﬁeld.

Although theoretically a large number of Voronoi

cells can meet at a vertex, in practice - when using

ﬂoating point representations of ﬁnite precision - one

can assume that at most three cells meet exactly at the

vertices of a 2D Voronoi diagram. These vertices re-

sult in edges between the associated truncated cones,

as illustrated in Figure 3. Consequently, the blending

between different cells has to handle the transition be-

tween the three nearest neighbors to a particular point

x, i. e., the signed-distance approximation has to be

symmetric in the three nearest neighbors of x.

Additional care to avoid discontinuities has to be

taken at the positions where the third-nearest neigh-

bor to x changes to a point which was not considered

before, as depicted by the blue line in Figure 3. More

precisely, the contribution of the third-nearest point to

ϕ should vanish when the distances of x to the third-

and fourth-nearest points are equal.

We implement these considerations by deﬁning an

approximation to the signed-distance function as fol-

lows: Let x ∈ R

and p

be the ith-nearest point of P

to x. We deﬁne the signed-distance function at x to P

ϕ =

· f

+ λ

· f

+ λ

· f

+ λ

, (3)

i. e., ϕ is the convex combination of the local signed-

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

distance functions

= f

(x) := hx− p

, n

i (4)

with weight functions deﬁned by

= d

(x) := kx− (p

+ f

(x) · n

)k (5)

= λ

(x) := l

(x) − l

(x) (6)

= l

(x) := kx − p

k . (7)

The continuous change of the signed-distance

function between the three nearest surface points is

accomplished by the functions d

(x), which calculate

the orthogonal distance of the point x to the line in-

duced by the ith-nearest surface point and its surface

normal. The functions λ

(x) represent the differences

of the distances from the point x to the fourth-nearest

surface point and from the point x to the ith-nearest

surface point. These functions λ

(x) assure a con-

tinuous behavior of the signed-distance function if

the third- and fourth-nearest neighbor of x are hav-

ing similar distances to x. In this region, indicated by

the blue line in Figure 3, the order of the third- and

fourth-nearest neighbor might switch. An illustration

of the functions is given in Figure 4.

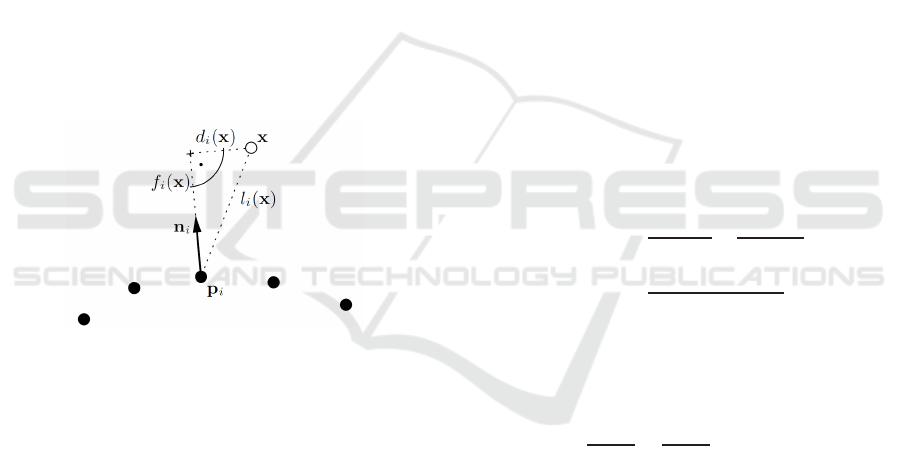
Figure 4: Illustration of the functions used to approximate

the signed-distance function. For a point x and each point

, f

(x) denotes the distance between p

and the base point

of x on γ

, d

(x) denotes the distance of the same base point

to x, and l

(x) is the distance between x and p

If the unlikelycase appears that more than three of

the nearest neighbors have very similar distances to x,

the λ

nearly vanish and the signed-distance function

would get very unstable. In our implementation, we

detect such cases with a threshold. For (λ

> 0.0001)

the standard procedure for computing ϕ is used. For

(λ

< 0.00001) we compute ϕ by setting λ

= 1. In

between we use a linear interpolation between the two

approaches.

To achieve a signed-distance function which is

differentiable everywhere, the weight functions d

and

can be smoothed with any standard kernel function.

In our implementation, we applied

p : [0, 1] → [0, 1] , p(t) := 6t

− 15t

+ 10t

(8)

which is the lowest-order polynomial with vanish-

ing ﬁrst- and second-order derivatives at 0 and 1.

The blending with this polynomial produces C

continuous transitions. The approximated signed-

distance function has the following properties:

1. ϕ(x) = f

(x) for all points x ∈ γ

with nearest

neighbor p

2. The change between cells of the Voronoi diagram

leads to a continuous change in ϕ, since ϕ is sym-

metric.

3. Changing third- and fourth-nearest neighbor leads

to a continuous change in ϕ, since λ

= 0.

In contrast to several related approaches, the pro-

posed signed-distance approximation is very robust

against non-uniformly sampled point clouds. This re-

sults in the minimization of artifacts even when deal-

ing with data sets of highly varying point density. We

demonstrate this property with the help of artiﬁcial

and real-world data sets in Section 8.

Derivatives Calculation

During the level-set process, not only the constructed

signed-distance function but typically also derivatives

of the function are used. Since the signed-distance

function is described analytically, all desired deriva-

tives can be computed. We list the ﬁrst derivatives of

the functions used:

∇λ

(x) =

(x− p

)

(x)

−

(x− p

)

(x)

(9)

∇d

(x) =

x− p

− f

(x) · n

(x)

(10)

∇f

(x) = n

(11)

Also higher-order derivatives can be easily derived.

In particular the curvature of a level set is given by

= ∇ ·

∇ϕ

k∇ϕk

(∇· ∇ϕ− 1) , (12)

which can be explicitly computed from the level-set

function, i. e., from the signed-distance function ap-

proximation.

To compute the signed-distance function values

and derivatives efﬁciently, a three-dimensional kd-

tree is built for the zero-level set points of each time

step. Utilizing this spatial space partitioning, the four

nearest zero-level set points are computed for each

sample point in the current narrow band.

7 LEVEL-SET PROPAGATION

The propagation of the level-set function is performed

following the level-set equation (1), which models the

SmoothIsoPoints: Making PDE-based Surface Extraction from Point-based Volume Data Fast

smooth isosurface extraction as combination of hy-

perbolic advection to the data scalar ﬁeld and mean

curvature ﬂow. This is done using an explicit time

discretization scheme of order one. For this level-set

process only the level-set function values and deriva-

tives obtained at the sample points are used. Further-

more, no information about the scalar ﬁeld other than

at the sample points in the narrow band is needed.

Since the level-set function is explicitly reset to

a signed-distance function in each level-set step, the

level-set propagation does not have to maintain this

property to produce high-quality results. However,

the used time step ∆t has to be chosen carefully to

keep the zero-level set always in the narrow band

and fulﬁll the CFL-condition. In fact, meeting the

CFL-condition described in (Rosenthal and Linsen,

2008b), i.e.

∆t



(1− λ)| f − f

iso

− ϕ|

min

k∇ϕk

kdivϕk +

6λ

min



< 1 (13)

with

kdivϕk :=





∂ϕ

∂x



∂ϕ

∂x



∂ϕ

∂x





(14)

and d

min

denoting the distance to the nearest neighbor,

is also sufﬁcient to keep the zero-level set within the

narrow band during computations. This was already

observed in (Peng et al., 1999).

8 RESULTS AND DISCUSSION

The presented approach was applied to a variety of

data sets to verify our method and evaluate it in terms

of accuracy and speed. All computation times were

measured on a single 2.66GHz XEON processor.

First we have tested our proposed signed-distance

function approximation approach in terms of accu-

racy, since this is a crucial part of our level-set

pipeline. We compared our approach with two very

related and recently presented methods (Adamson

and Alexa, 2003; Molchanov et al., 2010). For this

purpose, we have applied all three methods to an arti-

ﬁcial two-dimensional point cloud, which represents

the curve of a limac¸on of Pascal (Lawrence, 1972)

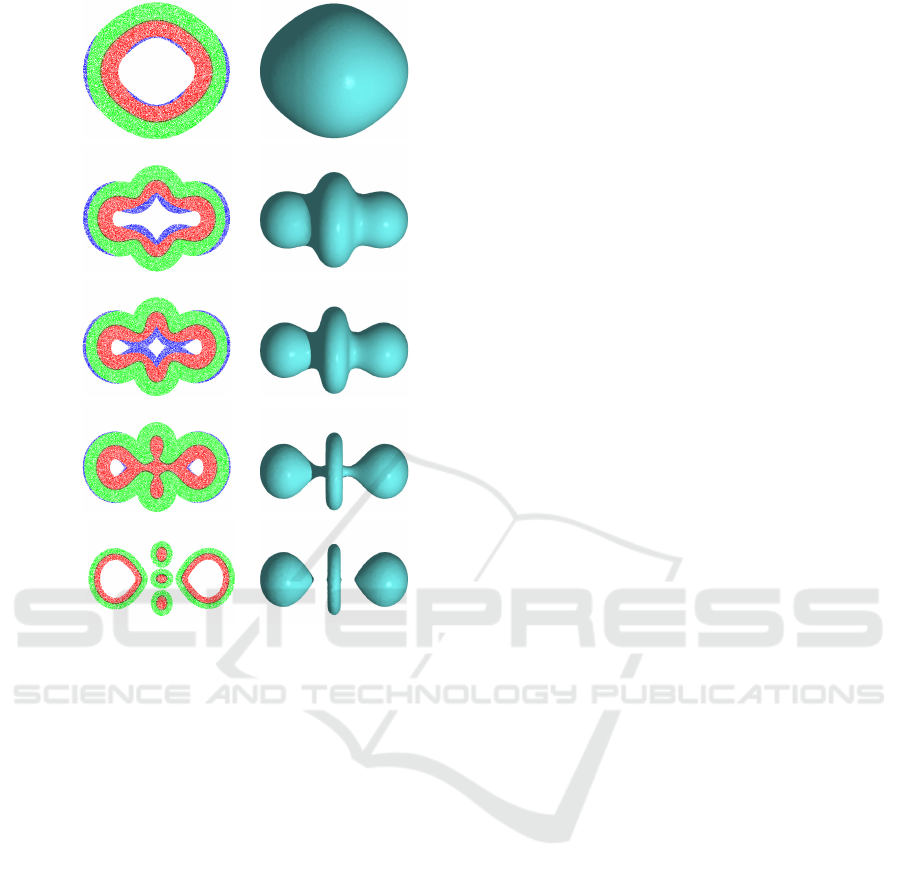
sampled at 1,000 random positions. Visualizations

of the respective isolines of the signed-distance func-

tion approximationsare shown in Figure 5. Following

suggestions of the respective papers, both competing

methods are applied with 15 neighbors for interpola-

tion. They require a relatively uniform sampled point

cloud and result in enormous errors in the approxima-

tion causing deformed isolines. Our method is robust

against highly varying point densities and does not ex-

hibit such artifacts. Still, computations of our method

are faster since only a ﬁxed number of four neigh-

bors is used. For a surface with 100,000 points and

240,000 distance computations the method of Adam-

son and Alexa and the method of Molchanov et al.

both need 112 seconds, in comparison to 103 seconds

with our method.

In addition, we compared the approximated and

exact signed-distance function values for our method

numerically. For this purpose, we sampled the curve

with different numbers of points and approximated

the signed-distance function at one million randomly

distributed sample points in a band around the curve.

At the same sample points of the band, we computed

the exact signed-distance function values using the

analytic expression of a limac¸on. The obtained nu-

merical differences are shown in Table 1. The relative

error of our approach is reciprocal to the number of

sample points on the curve. For the number of sur-

face points we encountered in our real-world exam-

ples (about 10

), we have a maximum error of 0.23%

and a relative error of 0.053%. All our experiments

showed, that this is sufﬁciently low to allow for accu-

rate level-set computations.

Table 1: Error analysis for signed-distance function approx-

imation to the limac¸on of Pascal. For different number of

random sample points on the curve, the relative average er-

ror and the relative maximum error is given when compar-

ing the approximated with the exact signed-distance func-

tion values at one million points in a band around the curve.

# points

rel. average error rel. maximum error

5.30· 10

−3

2.21· 10

−2

5.34· 10

−4

2.30· 10

−3

5.47· 10

−5

3.18· 10

−4

5.56· 10

−6

3.54· 10

−5

5.48· 10

−7

4.66· 10

−6

For the analysis of performance of our level-set

pipeline, we applied it to an unstructured point-based

volume data set with 16 million randomly distributed

sample points. The data set was generated by re-

sampling the regular Hydrogen data set (courtesy of

SFB 382 University T¨ubingen) of size 128 × 128 ×

128 to the random positions. (For all data sets that are

resampled from regular data to a random distribution,

we never make use of the original regular structure.)

An illustration of the evolution process for this data

set and a sphere as initial surface is shown in Fig-

ure 6. The whole level-set process for extracting a

smooth isosurface was performed in 18 minutes, in-

cluding preprocessing. In comparison, we achieved

a computation time of 36 minutes with the method

from (Rosenthal et al., 2010). When starting with

the (non-smooth) isosurface as a ﬁrst guess our com-

putation time drops to 22 seconds and we obtain a

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

Method of Adamson and Alexa Method of Molchanov et al. Our method

Figure 5: Qualitative comparison of our method with two competing methods for computing the signed-distance ﬁeld of a

limac¸on of Pascal, non-uniformly sampled at 1,000 positions. In the upper row, the points on the limac¸on are colored black.

Additionally, isolines to the respective signed-distance approximation are drawn, color-coded with respect to the isovalue.

The close-up views in the lower row show errors for the competing methods at the region of highly varying point density.

speed-up of two orders of magnitude. Starting with

the isosurface is not possible when using the approach

from (Rosenthal et al., 2010).

Table 2: Computation times for the iterative level-set phase

of a data set with 16 million sample points and 50,000 zero-

level set points. For different sizes of the narrow band (nb),

we list the number of sample points in the narrow band, the

computation time for determining the points in the narrow

band, and the computation time for the level-set (ls) step.

# points in nb

nb comp. ls step

200k 0.4 s 3.0 s

400k

2.0 s 5.1 s

800k

16.3 s 17.1 s

1,600k 67.5 s 70.6 s

We analyzed the computation time for the itera-

tive phase with respect to different widths of the nar-

row band, i. e., for different numbers of narrow-band

points. For the Hydrogen data with 16 million sample

points the times are given in Table 2. Here, the com-

putation time for the narrow-band creation includes

creation of a kd-tree for the zero-level set points, the

marking of all data points closer to the zero-level set

points than the width of the band, and the calculation

of the signed-distance function values and derivatives

at data points in the narrow band. The times for the

level-set step include the update of the level-set func-

tion values following the level-set equation, the ex-

traction of the new zero-level set, as well as the calcu-

lation of surface normals for the zero-level set points.

It is favorable to choose the width of the band with

respect to the CFL-condition to achieve an optimal

balance between large time step and small number of

processed sample points.

Finally, we applied our local level-set method to

real-world unstructured point-based volume data sets

with point densities varying in two orders of mag-

nitude. These highly varying point densities would

lead to enormous interpolation errors, when not oper-

ating directly on the sample point locations. The ﬁrst

data set stems from an astrophysical particle simula-

tion using smoothed particle hydrodynamics. In the

simulation, two stars orbiting each other are repre-

sented by a set of particles. During the simulation,

the stars exchange gas through a jet between them

and get distorted by the jet and gravity forces. In

Figure 7(a), we visualize a snapshot of the simula-

tion at a late point in time, when one star (the one

in the upper left) is already distorted, while the other

star (the one in the lower right) was not yet affected

signiﬁcantly. We compare our approach with direct

isosurface extraction on this data set with 2,600,000

sample points and extract surfaces with respect to gas

density. The whole computation time for 10 level-set

steps was 42 seconds. In contrast to direct isosurface

extraction, the smooth surface generated by our level-

set approach does not exhibit any outliers.

The direct isosurface extraction suffers from se-

vere incorrect outliers, caused by the very different

gradient magnitudes in the data set. This is also the

reason why we did not choose the isosurface as initial

zero-level set for our local level-set method. The er-

rors in the position of the isopoints can cause severe

errors in the surface normal approximationand lead to

SmoothIsoPoints: Making PDE-based Surface Extraction from Point-based Volume Data Fast

Step 1

Step 4

Step 5

Step 7

Step 11

Figure 6: Evolution of the zero-level set for normal advec-

tion to the Hydrogen data set with 16 million sample points.

For each time step, a splat-based ray tracing of the zero-

level set is shown on the right-hand side. On the left-hand

side, a point rendering of a slab of the data set is shown il-

lustrating the narrow band. The surface points extracted are

colored black, points with negative level-set function value

are colored red, and points with positive level-set function

value are colored green. Points which newly entered the

narrow band are colored blue. All data points not belonging

to the narrow band are not rendered. Note the easy change

of topology of the zero-level set and dynamic adjustment of

the narrow band. If the iterative process is close to steady

state, a much smaller width of the narrow band can be used.

an unusable signed-distance function approximation.

Instead, there are two different options for initializ-

ing such tricky cases. If the approximate shape of the

ﬁnal surface is known the zero-level set can be initial-

ized as an approximation to the ﬁnal surface, as in the

presented case, where the zero-level set was initial-

ized as two spheres centered at the stars’ barycenters.

Alternatively, one can extract the zero-level set as iso-

surface from a smoothed version of the original data

set. In most cases, the band around this initial surface

will still catch all parts of the ﬁnal smooth isosurface

and ensure a correct level-set propagation, which is

then carried out again with the original data.

The second data set is the White Dwarf data set

with 500,000 sample points already used by Rosen-

thal et al. It models a small star that is torn apart by

the strong gravity forces of a black hole. We used

the same parameters and initial surface as for their

method and achieved an overall computation time of

182 seconds, which still is two times faster compared

to 366 seconds of the competing method (Rosenthal

et al., 2010). In terms of quality, the results are com-

parable. A rendering of the extracted zero-level set

and a slab of the narrow band is shown in Figure 7(b).

The maximum distance between the points of the two

resulting surfaces was of the same order as the stop-

ping criterion used for both level-set processes.

All experiments have shown, that the proposed

method for approximating the signed-distance func-

tion produces results of high quality. The local level-

set method using explicit zero-level set representation

is signiﬁcantly faster than competing methods. Com-

pared to the previous local level-set approach (Rosen-

thal et al., 2010) the proposed method speeds up

each level-set step by reducing the number of needed

neighbors per point and omitting the numerical reini-

tialization. Additionally, it facilitates the usage of any

initial zero-level set, signiﬁcantly reducing compu-

tation times further. A comprehensive performance

overview of our approach for the various data sets in-

cluding comparisons to the prior narrow-band tech-

nique is given in Table 3. Note the remarkable speed

up when using the proposed method with a good ini-

tial guess as starting surface, compared to initializa-

tion with a sphere required by competing methods

with implicit zero-level set representation.

Still, experiments have shown that the proposed

method is, in terms of quality, equivalent to the previ-

ous global and local methods by Rosenthal et al. and

it has successfully been applied to real-world data.

Moreover and in contrast to the prior local level-set

approach (Rosenthal et al., 2010), it is able to extract

objects with complex topology very fast by using an

initial surface close to the expected ﬁnal result, such

as the (non-smooth) isosurface.

9 CONCLUSION

We have presented a local level-set method that com-

bines the accuracy of directly applying level sets to

unstructured data with the fast level-set computation

using narrow bands and an explicitly extracted zero-

level set. This option enables us to use any surface

as initial zero-level set and gives an additional speed-

up when using good initial guesses for the ﬁnal sur-

face. We directly operate on the unstructured data

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

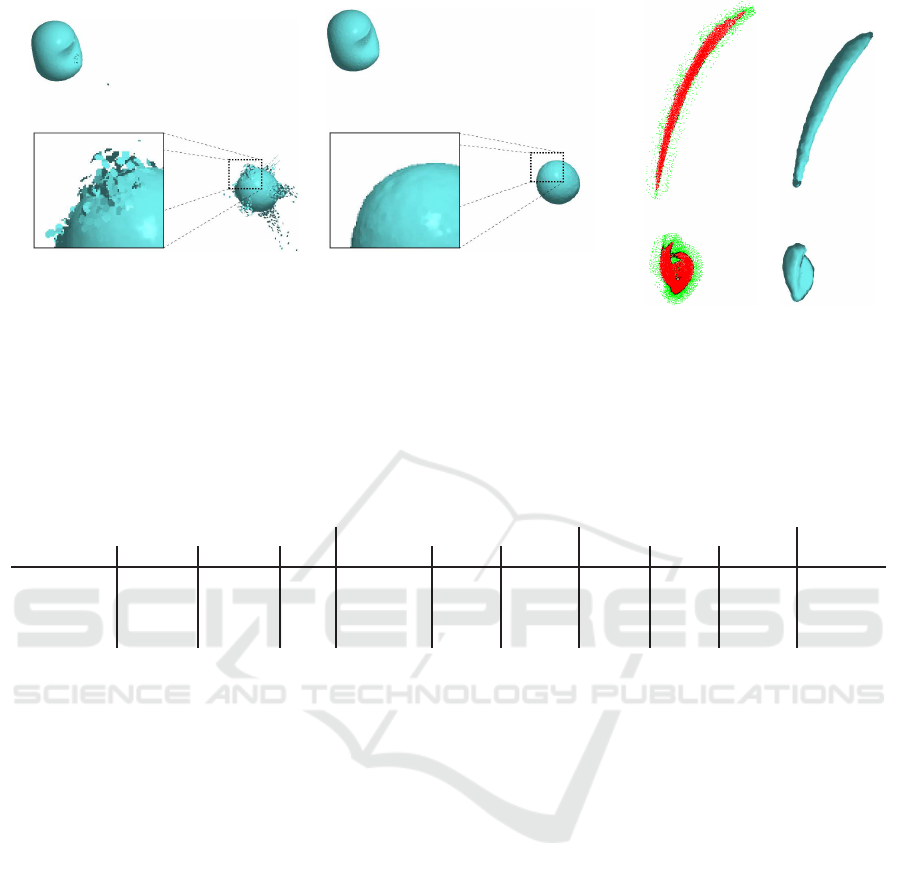
Direct Isosurface Extraction Smooth Isosurface Extraction

(a)

(b)

Figure 7: (a) Comparison between direct isosurface extraction on the left-hand side and smooth isosurface extraction on the

right-hand side for a stars simulation data set with 2.6 million sample points. Our level-set method effectively eliminates the

noise in the surface. (b) Illustration of the zero-level set for normal advection to the White Dwarf data set with 500,000 sample

points. On the left-hand side, a point rendering of a slab of the data set is shown illustrating the narrow band. A splat-based

ray tracing of the zero-level set after convergence of the level-set process is shown on the right-hand side.

Table 3: Performance comparison for the presented data sets. For each data set the number of points, the used isovalue, and

the used smoothness parameter is given. Additionally, the initial surface, the needed number of level-set steps, and the overall

computation time, including the generation of the initial zero-level set, is given for our approach and for the method proposed

by Rosenthal et al., followed by our achieved speed-up.

our method (Rosenthal et al., 2010)

data set # points f

iso

λ init. s. #steps time init. s. #steps time speed-up

Hydrogen 16.0M 30 0.05 isosurface 3 22 sec sphere 19 36 min 98.1

Engine

16.0M 70 0.10 isosurface 10 59 sec sphere 27 47 min 47.7

2 stars

2.6M 0.01 0.10 2 spheres 10 42 sec sphere – – –

Wh. Dwarf

0.5M 0.00006 0.10 sphere 37 182 sec sphere 39 366 sec 2.0

and do not need to process data at any position other

than the sample points. For each iteration, we build

a narrow band of sample points around the zero-level

set, compute the level-set function at these points as a

signed-distance function to the zero-level set, process

the level-set function in the narrow band with respect

to a given level-set equation, and extract the new zero-

level set. As we use a signed-distance function for the

level-set function, we avoid numerical reinitialization

steps, which further reduces computation times. Af-

ter convergence, the ﬁnal zero-level set is visualized

using point-based rendering techniques.

Similar to most narrow-band, thus local, tech-

niques our method is only able to extract surfaces

which are captured by the computation area during

the level-set process. However, this covering can be

guaranteed when using the directly extracted isosur-

face as starting surface for the level-set processing.

We have compared our results with the ones obtained

by Rosenthal et al. and achieved signiﬁcant speed-

ups. Still, the proposed method achieves the same

results in terms of quality. Our method is capable

of robustly processing data sets with several million

sample points and highly varying point density.

ACKNOWLEDGMENTS

This work was supported by the Deutsche

Forschungsgemeinschaft (DFG) under project

grant LI 1530/6-2.

REFERENCES

Adalsteinsson, D. and Sethian, J. A. (1995). A fast level set

method for propagating interfaces. Journal of Com-

putational Physics, 118(2):269–277.

Adamson, A. and Alexa, M. (2003). Approximating and

intersecting surfaces from points. In SGP ’03: Pro-

ceedings of the 2003 Eurographics/ACM SIGGRAPH

symposium on Geometry processing, pages 230–239,

Aire-la-Ville, Switzerland, Switzerland. Eurographics

Association.

Breen, D., Whitaker, R., Museth, K., and Zhukov, L. (2005).

Level set segmentation of biological volume datasets.

In Suri, J. S., Wilson, D. L., and Laxminarayan, S.,

editors, Handbook of Biomedical Image Analysis, Vol-

ume I: Segmentation Models, Part A, pages 415–478,

New York, NY, USA. Kluwer.

SmoothIsoPoints: Making PDE-based Surface Extraction from Point-based Volume Data Fast

Courant, R., Friedrichs, K. O., and Lewy, H. (1967).

On the partial difference equations of mathematical

physics. IBM Journal of Research and Development,

11(2):215–234.

Edelsbrunner, H. and Shah, N. R. (1992). Incremental topo-

logical ﬂipping works for regular triangulations. In

SCG ’92: Proceedings of the eighth annual sympo-

sium on Computational geometry, pages 43–52, New

York, NY, USA. ACM.

Enright, D., Losasso, F., and Fedkiw, R. (2004). A fast and

accurate semi-lagrangian particle level set method.

Computers and Structures, 83(6–7):479–490.

Franke, R. and Nielson, G. M. (1991). Scattered data in-

terpolation: A tutorial and survey. In Hagen, H.

and Roller, D., editors, Geometric Modeling: Meth-

ods and Applications, pages 131–160. Springer, New

York, NY, USA.

Gross, M. and Pﬁster, H. (2007). Point-Based Graph-

ics. Morgan Kaufmann Publishers Inc., San Fran-

cisco, CA, USA.

Kolluri, R. (2008). Provably good moving least squares.

ACM Trans. Algorithms, 4(2):1–25.

Lawrence, J. D. (1972). A Catalog of Special Plane Curves.

Dover Publications.

Lefohn, A. E., Kniss, J. M., Hansen, C. D., and Whitaker,

R. T. (2004). A streaming narrow-band algorithm: In-

teractive computation and visualization of level sets.

IEEE Transactions on Visualization and Computer

Graphics, 10(4):422–433.

Molchanov, V., Rosenthal, P., and Linsen, L. (2010). Non-

iterative second-order approximation of signed dis-

tance function for any isosurface representation. Com-

puter Graphics Forum, 29(3):1211–1220.

Nielsen, M. B. and Museth, K. (2006). Dynamic tubular

grid: An efﬁcient data structure and algorithms for

high resolution level sets. J. Sci. Comput., 26:261–

299.

Osher, S. and Fedkiw, R. (2003). Level set methods and

dynamic implicit surfaces. Springer, New York, NY,

USA.

Osher, S. and Sethian, J. A. (1988). Fronts propagating

with curvature-dependent speed: Algorithms based on

Hamilton-Jacobi formulations. Journal of Computa-

tional Physics, 79(1):12–49.

Park, S. W., Linsen, L., Kreylos, O., Owens, J. D., and

Hamann, B. (2006). Discrete Sibson interpolation.

IEEE Transactions on Visualization and Computer

Graphics, 12(2):243–253.

Peng, D., Merriman, B., Osher, S., Zhao, H., and Kang,

M. (1999). A PDE-based fast local level set method.

Journal of Computational Physics, 155(2):410–438.

Rosenthal, P. and Linsen, L. (2006). Direct isosurface ex-

traction from scattered volume data. In Santos, B. S.,

Ertl, T., and Joy, K. I., editors, EuroVis06: Proceed-

ings of the Eurographics/IEEE-VGTC Symposium on

Visualization, pages 99–106, Aire-la-Ville, Switzer-

land. Eurographics Association.

Rosenthal, P. and Linsen, L. (2008a). Image-space point

cloud rendering. In Proceedings of Computer Graph-

ics International, pages 136–143.

Rosenthal, P. and Linsen, L. (2008b). Smooth surface ex-

traction from unstructured point-based volume data

using PDEs. IEEE Transactions on Visualization and

Computer Graphics, 14(6):1531–1546.

Rosenthal, P., Molchanov, V., and Linsen, L. (2010). A nar-

row band level set method for surface extraction from

unstructured point-based volume data. In Skala, V.,

editor, Proceedings of WSCG, The 18th International

Conference on Computer Graphics, Visualization and

Computer Vision, pages 73–80, Plzen, Czech Repub-

lic. UNION Agency – Science Press.

Schwartz, P. and Colella, P. (2008). A second-order accurate

method for solving the eikonal equation. Proceedings

in Applied Mathematics and Mechanics, 7(1).

Sethian, J. A. (1999). Level Set Methods and Fast Marching

Methods. Cambridge University Press, Cambridge,

UK, 2nd edition.

Tsai, Y.-h. R. (2002). Rapid and accurate computation of

the distance function using grids. Journal of Compu-

tational Physics, 178(1):175–195.

van der Laan, W. J., Jalba, A. C., and Roerdink, J. B. T. M.

(2011). A memory and computation efﬁcient sparse

level-set method. Journal of Scientiﬁc Computing,

46(2):243–264.

Vuc¸ini, E., M¨oller, T., and Gr¨oller, M. E. (2009). On visu-

alization and reconstruction from non-uniform point

sets using b-splines. Computer Graphics Forum,

28(3):1007–1014.

IVAPP 2018 - International Conference on Information Visualization Theory and Applications