ECG-derived Blood Pressure Classiﬁcation using Complexity

Analysis-based Machine Learning

Monika Simjanoska

, Martin Gjoreski

, Ana Madevska Bogdanova

, Bojana Koteska

Matja

z Gams

and Jurij Tasi

Faculty of Computer Science and Engineering, Ss. Cyril and Methodius University,

Rugjer Boshkovikj 16, 1000 Skopje, Macedonia

Department of Intelligent Systems, Jozef Stefan Institute, International Postgraduate School,

Jamova cesta 39, 1000 Ljubljana, Slovenia

Faculty of Electrical Engineering, University of Ljubljana, Trzaska cesta 25, 1000 Ljubljana, Slovenia

Keywords:

Blood Pressure, ECG-derived, Complexity Analysis, Machine Learning, Stacking, Classiﬁcation.

Abstract:

The recent advancement on wearable physiological sensors supports the development of real-time diagnosis

in preventive medicine that demands various signal processing techniques to enable the extraction of the vital

signs (e.g., blood pressure). Blood pressure estimation from physiological sensors data is challenging task

that usually is solved by a combination of multiple signals. In this paper we present a novel complexity

analysis-based machine-learning perspective on the problem of blood pressure class estimation only from

ECG signals. We show that high classiﬁcation accuracy of 96.68% can be achieved by extracting information

via complexity analysis on the ECG signal followed by applying a stack of machine-learning classiﬁers. In

addition, the proposed stacking approach is compared to a traditional machine-learning approaches and feature

analysis is performed to determine the inﬂuence of the different features on the classiﬁcation accuracy. The

experimental data was gathered by daily monitoring of 20 subjects with two different ECG sensors.

1 INTRODUCTION

Real-time diagnosis in preventive medicine can sig-

niﬁcantly reduce the costs of expensive medical treat-

ments. The real-time preventive diagnosis and on-

time alarming in case of abnormal events (Lehocki

et al., 2014), demand various signal processing tech-

niques to enable continuous monitoring of vital signs

(heart rate, blood pressure, respiratory rate, oxygen

saturation), which usually are extracted from wear-

able sensors data (electrocardiogram - ECG, pho-

toplethysmogram - PPG, phonocardiogram - PCG,

breathing sensor, SPO2 sensor). The identiﬁcation of

morphologic characteristics and time intervals within

the physiological signals allow continuous monitor-

ing of vital signs and providing medical diagnosis

(Cosoli et al., 2015). Blood pressure (BP) is consid-

ered to be one of the most valuable vital sign, however

it still requires dedicated equipment for its estimation.

Moreover, the related research on BP estimation fo-

cuses on using several sources of data (e.g., ECG and

PPG) due to the complexity of the problem. In this

paper we present a method for BP classes estimation

by using only ECG as a single source of data.

The relationship between the BP and the morpho-

logical changes of the physiological signals is widely

discussed in the related work. A huge study encom-

passing more than 11,000 individuals has been con-

ducted by (Schroeder et al., 2003) where it has been

examined whether the hypertension leads to changes

in heart rate variability (HRV). The study reports re-

sults within 9 years period showing that even though

the subjects with hypertension had decreased HRV,

there was no signiﬁcant difference in the HRV be-

tween the groups with and without hypertension 9

years after one group was predicted to have a higher

risk of developing a hypertension. This conﬁrms

the complexity of the problem and suggests that new

methods for deriving BP should be considered. (Has-

san et al., 2008) investigate the relationship between

the heart rate (HR) and the systolic blood pressure

(SBP) at 10 healthy subjects. Even though the prelim-

inary results showed positive correlation, the physi-

cians do not completely agree that they proportionally

rise together, e.g., in an event of dangerous situation,

both the HR and BP might increase; however, the rise

of HR, does not automatically trigger the rise of BP

- appropriate example are the patients with coronary

282

Simjanoska, M., Gjoreski, M., Bogdanova, A., Koteska, B., Gams, M. and Tasi

c, J.

ECG-derived Blood Pressure Classiﬁcation using Complexity Analysis-based Machine Learning.

DOI: 10.5220/0006538202820292

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 5: HEALTHINF, pages 282-292

ISBN: 978-989-758-281-3

artery disease who have normal HR (Heart and Vas-

cular Team, 2016).

ECG alone has never been used for deriving BP,

instead most of the published literature refers to the

combination of both ECG and PPG. (Nye et al., 2015)

performed a deep survey categorizing the methods for

deriving BP into three major classes relying on: Pulse

Wave Velocity (PWV), Pulse Arrival Time (PAT) and

Pulse Transit Time (PTT). PWV is the rate at which

the pressure wave moves down the vessel and PTT

is the time at which the pressure wave propagates

through the arterial tree (Grenwis et al., 2012). PAT

is equal to the sum of PTT and the pre-ejection pe-

riod, however a study (Zhang et al., 2011) indicates

that PAT is not an adequate for PTT calculation since

it is unable to detect the challenging BP changes.

BP is measured in terms of systolic blood pres-

sure (SBP) and diastolic blood pressure (DBP), the

maximum and the minimum value of an arterial pres-

sure tracing, correspondingly. Assuming the PWV is

a reliable measure for estimation of the central BP,

(i Car

os, 2011) provides a comprehensive analysis of

the PWV-based techniques for continuous and non-

invasive monitoring of BP; even though it is claimed

that no clear information is provided on whether PWV

is related to SBP, DBP or mean BP. Alternative tech-

niques that do not rely on PWV are also discussed

such as those for multi-parametric processing of car-

diovascular variables, or those that consider parame-

ters within the heart sounds (PCG analysis). One ex-

ample is the analysis of R2 - the time interval from

a particular R peak in ECG, to the peak of the sec-

ond heart sound in PCG (Wong et al., 2006). Close

inverse correlation between the timing of the sec-

ond heart sound has been found by SBP(Zhang and

Zhang, 2006) . (Goli and T., 2014) used PTT derived

from ECG R-wave and the maximum ﬁrst derivative

PPG in correlation analysis at 11 healthy subjects.

The reported results show PTT to be strongly corre-

lated with SBP (0.734) and the DBP (0.731).

In another study, (Wong et al., 2009) perform a

half year study on the relationship between BP and

PTT, showing the PTT is highly correlated with SBP,

but not with DBP - probably due to the small varia-

tions of the DBP. Even though PPG signals are widely

used for the purpose of BP estimation and present

high prediction accuracy, there are also some experi-

ments that withstand those statements. (Nitzan, 2011)

compares multiple methods indicating that PPG is not

applicable for the estimation of DBP since no sub-

stantial change of blood ﬂow or PPG pulse is found

when the cuff pressure decreases. Similarly, (Payne

et al., 2006) proves that PTT extracted from ECG and

PPG is unreliable marker of beat-to-beat BP.

This research approaches the problem from a

completely different perspective of deriving BP from

ECG only. The rule presented by (Najarian and

Splinter, 2012) states that the healthy biomedical sys-

tems are of high complexity and once an abnormal-

ity occurs this complexity drops. The complexity de-

crease has been experimentally proven in the litera-

ture for problems related to brain activity in presence

of Alzheimers disease (G

omez et al., 2006); compar-

ative EEG study on pathological and healthy groups

(Bhattacharya et al., 2000); ECG analysis of ventric-

ular tachycardia and ﬁbrillation (Zhang et al., 2000);

complexity loss theory of aging and disease (Costa

et al., 2005); complexity analysis of respiratory sys-

tem (Raoufy et al., 2017), etc.

In order to explore the idea of using ECG com-

plexity analysis, 332 ECG signals were obtained dur-

ing normal physical activities from 20 subjects of dif-

ferent age groups. During the ECG acquisition, cuff-

based BP measurements at different timestamps were

manually performed, which later were used to label

the ECG signals with one of the BP classiﬁcation

groups reported by (Program et al., 2004): hypoten-

sion, normal, prehypertension, stage 1 hypertension,

stage 2 hypertension, isolated systolic hypertension

(ISH), and hypertensive crisis. Having extracted fea-

tures using the complexity analysis later discussed in

the Sect. 2, two types of Machine-Learning (ML) so-

lutions, a ﬂat (simple) design and a stacking design

were developed and compared.

The rest of the paper is organized as follows. Sect.

2 presents the methods and materials used in the ECG

signal processing system. Sect. 3 presents the ex-

periments and the obtained results. Sect. 4 and Sect.

5 present the discussion and the conclusions of the

study.

2 THE PROPOSED APPROACH

When developing the novel methodology we followed

the steps of a typical biomedical signal-processing

system (Najarian and Splinter, 2012) presented in Fig-

ure 1. The following subsections provide a detailed

explanation of the methods and techniques applied in

each step.

2.1 The Biological System

The ECG signal presents the electrical activity of the

heart. It is recorded by placing electrodes on the in-

dividual’s chest or limb. The heart system consists of

two atria for collecting the blood and two ventricles

for pumping the blood. There are two main phases, a

ECG-derived Blood Pressure Classiﬁcation using Complexity Analysis-based Machine Learning

283

The Biological

System (ECG + BP)

The Sensors

(ECG + BP)

ECG Signals

Preprocessing

Features Extraction

(Complexity Analysis)

Machine Learning

(Classification)

Figure 1: The ECG signal processing system.

ﬁlling (resting) phase called diastole, and a pumping

(contracting) phase called systole. The deoxygenated

blood is collected in the right atrium and therefrom is

passed to the right ventricle. While the ventricular is

in a systole phase, the deoxygenated blood is pumped

to the lungs where it will be oxygenated. The oxy-

genated blood is received by the left atrium and dur-

ing the atrial systole it is passed to the left ventricle.

The left ventricle is the largest and strongest chamber

since it has to pump the oxygenated blood to the rest

of the body. A normal HR during resting is about 70

bpm (beats per minute - measure for the rhythm of the

heart) (Rangayyan, 2015).

The pressure that is caused by the blood ﬂow

on the blood vessels walls is referred to as blood

pressure. BP is measured in millimeters of mercury

(mmHg), and depending on the different values of

the maximum pressure during one heart beat (SBP)

and the minimum pressure in between two heart beats

(DBP), there are seven categories published online

and in the literature (Program et al., 2004; AHA,

2016) presented in Tab. 1.

2.2 The ECG Sensors

The ECG signals used in this research were obtained

using two different ECG sensors and the reference BP

values were measured by using an electronic sphyg-

momanometer. Sixteen participants at age 16 - 72

were recorded by using ECG sensor as a part of

the Cooking hacks e-Health Sensor Platform (Cook-

ing Hacks, 2016). All the measurements were per-

formed in a sitting position in duration up to 60 sec-

onds at 125Hz sample rate, and a single measurement

of the SBP and DBP has been done for each ECG

signal. Additionally, 4 participants at age 25 - 27

were recorded using the 180°eMotion FAROS (Bit-

tium Biosignals, 2016) ECG sensor. In this case, the

sensor was attached to the participants for at least 4

hours, continuously capturing the electrical activity of

the heart at sampling rate of 1000Hz during the daily

activities. The participants were required to measure

the BP at particular times ranging from 30 minutes to

1 hour. All of the 20 participants had no history of

heart problems.

2.3 ECG Signals Preprocessing

A valid ECG information is considered to exist in

range of 0.05 - 100Hz (Rangayyan, 2015). The ap-

plication of the 180 eMotion FAROS sensor pro-

duced a high-resolution ECG sampled at frequency

of 1000Hz. Those ECG signals were ﬁltered by ap-

plying a low-pass Butterworth ﬁlter of 18th order and

cutoff frequency of 100Hz. The order of the ﬁlter was

optimally determined based on the ﬁlter design speci-

ﬁcations. All the signals were trimmed by taking only

the last 30 seconds before the BP measurement. Ex-

perimentally is observed that 30 seconds of ECG car-

ries the right information for BP class prediction. As

a result from the preprocessing, we created a database

that consists of 332 signals labeled with the appropri-

ate BP class as described in Tab. 1.

2.4 Feature Extraction from ECG -

Complexity Analysis

The ML approach in BP estimation from ECG signal

requires building distinguishing feature vectors that

will represent the created database. In this novel ap-

proach the feature extraction is based on complexity

analysis rather than on extraction of the morphologi-

cal characteristics, the conservative way of processing

the ECG signals as described in the literature (i Car

os,

2011; Wong et al., 2006; Zhang and Zhang, 2006;

Goli and T., 2014; Payne et al., 2006; Wong et al.,

2009; Nitzan, 2011).

As mentioned in the Introduction, a normal and

healthy biomedical system (the ECG signal) is con-

sidered to be a very complex one and once a dramatic

change occurs (as is the sudden change in BP), the

complexity drops (Najarian and Splinter, 2012). This

relationship is already proven in the literature pre-

sented (G

omez et al., 2006; Bhattacharya et al., 2000;

Zhang et al., 2000; Costa et al., 2005; Raoufy et al.,

2017). Considering the complexity features perfor-

mance presented in the related work (McBride et al.,

2014; Morabito et al., 2012; Eke et al., 2002; Cancio

et al., 2008), in this research the BP changes are mod-

eled by inspecting complexity measures of the ECG

signals to extract six features that deﬁne the feature

vectors:

HEALTHINF 2018 - 11th International Conference on Health Informatics

284

Table 1: Blood pressure categorization.

Category SBP (mmHg) Logical DBP (mmHg)

Hypotension ≤ 90 OR ≤ 60

Normal 90-119 AND 60-79

Prehypertension 120-139 OR 80-89

Stage 1 hypertension 140-159 OR 90-99

Stage 2 hypertension ≥ 160 OR ≥ 100

Isolated systolic hypertension ≥ 140 AND < 90

Hypertensive crisis ≥ 180 OR ≥ 110

2.4.1 Signal Mobility

Signal mobility represents the ﬁrst-order variations in

the signal. Let x

,i = 1,...,N be the ECG signal of

length N, and d

, j = 1,...,N − 1 be the ﬁrst-order

variation calculated as given in Eq. 1:

= x

j+1

− x

(1)

Then the ﬁrst-order factors S

and S

are obtained

as follows:

∑

i=1

(2)

∑

N−1

j=2

N − 1

(3)

Hereupon the signal mobility is simply calculated

as the ratio between the factors S

and S

Mobility =

, (4)

providing a quantitative measure of the level of varia-

tion along the signal.

2.4.2 Signal Complexity

Signal complexity represents the second-order vari-

ations in the signal. Given the ﬁrst-order variation

of the ECG signal d

, j = 1,...N − 1, the second-

order variation of the signal is presented by g

,k =

1,...,N − 2, or:

= d

k+1

− d

(5)

Consequently, the second-order factor is calcu-

lated as:

∑

N−2

k=3

N − 2

, (6)

and the signal complexity is calculated according to

the equation:

Complexity =

−

(7)

To compute both the signal mobility and com-

plexity, we used the Hjorth parameters method

(Kugiumtzis and Tsimpiris, 2010).

2.4.3 Fractal Dimension

Fractal dimension is a measure of self-similarity and

describes the fundamental patterns hidden in the sig-

nal. It works like a magniﬁer, zooming and compar-

ing different portions of the signal with the entire sig-

nal. Higuchi algorithm is one of the most efﬁcient

methods for calculating the fractal dimension and we

use it as implemented by (Alvarez, 2015). For choos-

ing the maximum number of subseries, k

max

, we fol-

lowed the advice by (Doyle et al., 2004). The Higuchi

algorithm forms a set of k subseries with different res-

olutions. For m = 1,...,k, the new time series X

are

formed as follows:

: x(m),x(m + k),x(m + 2k),...,x(m + b

N − m

ck)

(8)

Consequently, the length of the curve X

, l(k) is

calculated as:

l(k) =

(

∑

bN−m/kc

i=1

|x(m + ik) − x(m + (i − 1)k)|(N − 1))

N−m

c)k

(9)

For each k in range 1 to k

max

, the average length

is calculated as the mean of the k lengths l(k) for m =

1,...k. The fractal dimension is the estimation of the

slope of the plot ln(l(k)) vs. ln(1/k).

2.4.4 Entropy

Entropy measures the amount of information (the ran-

domness) in the signal. The reduction of entropy con-

sidering a signal as ECG is often associated with a

disease. The information can be represented through

the concept of probability. Assuming X is the ECG

signal and p

is the probability of each outcome x

within X for i = 1,...,N − 1. Then, by addressing all

the zero/inﬁnity problems, the equation for entropy

calculation gets the following form:

Entropy =

N−1

∑

i=0

log(

) (10)

ECG-derived Blood Pressure Classiﬁcation using Complexity Analysis-based Machine Learning

285

Low-pass filtering

Feature Extraction Class Labeling

DBP

SBP

Classifier

Feature Vector F = (f

,…,f

, label)

(F) P

(F)

. . .

. . . . . . . . .

EF = (P

(F), P

(F), …, P

(F), P

(F), …, P

(F), P

(F), …, P

(F), label)

Meta Classifier

BP Class Prediction

Preprocessing

Feature

Extraction

Stacking

Figure 2: Stacking Design.

2.4.5 Autocorrelation

Autocorrelation calculates the similarity of the signal

when it is compared to its shifted version - a similar-

ity will exhibit a peak which is captured and quanti-

tatively measured. Given τ is the amount of shift, the

autocorrelation function is calculated as follows:

(τ) =

+inf

−inf

x(t)x(t −τ)p

(x(t), x(t −τ))dt, (11)

where p

(x(t), x(t − τ)) presents the joint proba-

bility density function of x(t) and x(t − τ).

2.4.6 Age

A simple mathematical model that represents the

blood ﬂow in the arteries is made by (Labadin and Ah-

madi, 2006). It proves that the blood ﬂow is affected

by the size of the blood vessel. When the left ventri-

cle contracts to push the blood into the aorta (during

systole), a pressure wave is generated along the ar-

terial tree. Affected mostly by the age or some other

changes in the arterial wall, the vessels become stiffer,

meaning the pressure wave velocity increases. As a

result, the reﬂected pressure waves that move back to

the heart will also move faster, causing greater sys-

tolic pressure to handle the load. Having in mind that

the age affect the changes in the arterial wall, partic-

ipant’s age as one of the features is included in the

feature vectors.

2.5 The Machine Learning Approach

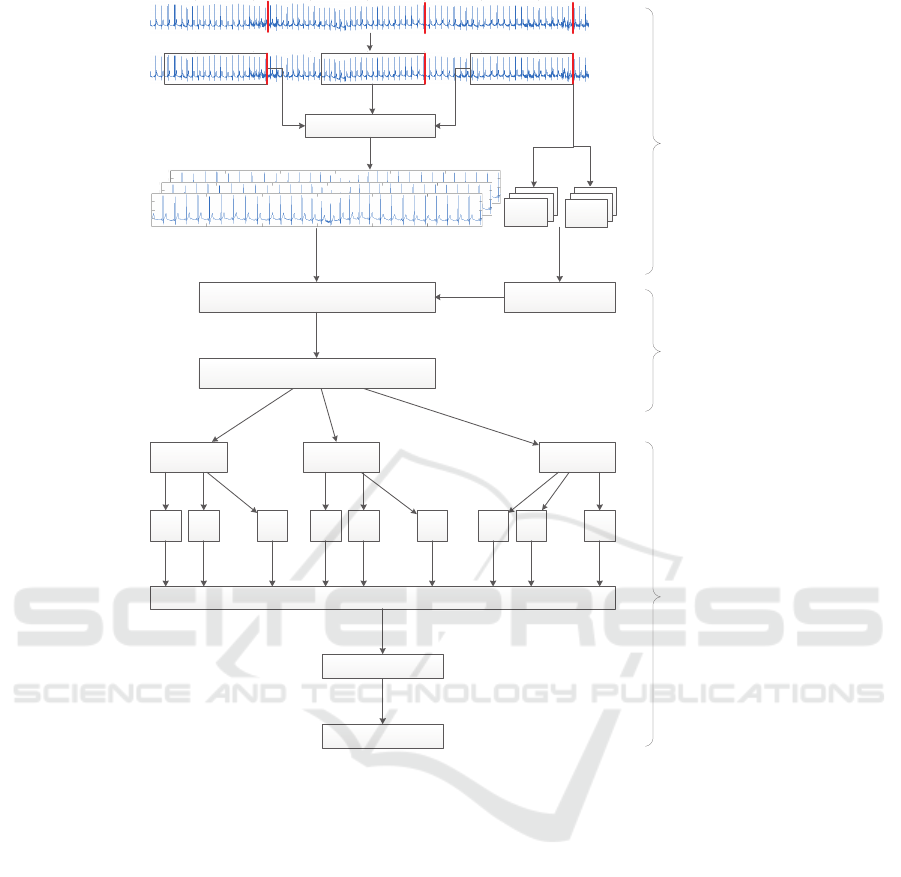
Fig. 2 presents a detailed scheme of the proposed

methodology by following the steps of a biomedi-

cal processing system as depicted in Fig. 1. On the

top of Fig. 2 an example of raw ECG signal is pre-

HEALTHINF 2018 - 11th International Conference on Health Informatics

286

sented with red marks (lines) that represent the mo-

ment when the subject’s BP has been measured. In the

next step, the raw ECG signals are segmented by tak-

ing windows of 30 seconds before each BP measure-

ment. Then, the low-pass ﬁltering is applied. Having

established the database of the ECG signals and the

corresponding SBP and DBP values, we proceed with

the feature extraction procedure that encompass both

the complexity analysis described in Sect. 2.4 and the

BP class labeling according to Tab. 1. Hereupon, two

ML approaches have been applied to train a model

that is able to predict the BP class for a given ECG

signal. The ﬁrst approach is a ﬂat ML design, includ-

ing the evaluation of seven different classiﬁcation al-

gorithms as described in Sect. 2.5.1. The second ap-

proach is stacking ML design, visually described in

Fig. 2 and comprehensively explained in Sect. 2.5.2.

2.5.1 The Flat Design

In the ﬂat design, ML models are trained by using

seven different classiﬁers, which model the data from

various aspects:

1. J48 - to rank the features according to the infor-

mation gain;

2. Naive Bayes (NB) - to consider strong indepen-

dence between the features;

3. KNN - to consider inter-instance similarity;

4. SVM - to recognize the most distinguishable fea-

ture vectors;

5. Random Forest (RF) - to combine multiple mod-

els built on varying features set in an ensemble;

6. Bagging (BGG) - to introduce dataset subsam-

pling as a way of reducing the variance of the de-

cision tree-based J48 algorithm, and

7. Boosting (BST) - to introduce instance weighting

in the dataset for addressing the mis-recognized

instances.

2.5.2 The Stacking Design

Assuming that different algorithms model different

structures in the data, we implemented a stacking

module presented in the third phase of Fig. 2. The im-

plementation mainly consists of tree phases. The ﬁrst

phase is the application of the seven different classi-

ﬁers described in the ﬂat design 2.5.1. Each of the

classiﬁers, K = 1, ...,7, is adapted to produce predic-

tion probabilities (Hall et al., 2009) for a given fea-

ture vector, F, to belong in each of the BP classes,

N = 1,...,6. The goal is to ensemble the probabilities,

(F),..., p

(F), produced by each of the applied

classiﬁers and create new feature vectors (the second)

Table 2: ECG instances categorization.

Category Instances Label

Hypotension 3 0

Normal 198 1

Prehypertension 110 2

Stage 1 hypertension 15 3

Stage 2 hypertension 2 4

Isolated systolic hypertension 4 5

Hypertensive crisis 0 6

phase. In the ﬁnal phase, a meta-classiﬁer (Random

Forest) is trained with the new feature vectors.

Leave-one-instance-out principle has been used

for both the creation of the probability vectors and

the meta-classiﬁer phase. The probability vector for

each instance was created when the instance is being

left out for testing. Having created the new proba-

bility vectors for all instances, the meta-classiﬁer has

also been evaluated by the same principle, leaving-

one-instance-out. Thus it means that in a particular

iteration, one instance is a test instance in both phases

at the same time, and the overﬁtting is avoided.

3 RESULTS

After the preprocessing phase, a database consisting

of 332 instances was created. The distribution of the

instances is provided in Tab. 2. The majority class

is the Normal class consisting of 198 ECG recordings

(59.6% of the signals). The more extreme the classes

are, the less instances are included since the partici-

pants involved in the measurements were random in-

dividuals with no diagnosis related to heart or blood

pressure problems. The most extreme class, Hyper-

tensive crisis, is completely empty and has been dis-

missed in the following analysis.

The experiments were performed by using a leave-

one-instance-out cross-validation, i.e., the ML models

are built by using all the instances except one that is

left out for testing. The procedure is repeated 332

times (the number of instances in the database) and

the results are averaged. We present three metrics: F-

measure as a balanced mean between precision and

recall, ROC area to measure the trade-off between the

recall and the false positive rate, and the overall ac-

curacy of each classiﬁer. In addition, we performed a

10-fold cross-validation and obtained similar results.

3.1 Flat ML Results

Tab. 3 presents the results for each of the seven

distinct classiﬁers used as part of the ﬂat ML ap-

ECG-derived Blood Pressure Classiﬁcation using Complexity Analysis-based Machine Learning

287

Table 3: Flat ML results. Leave-one-instance-out evaluation.

Metric Class J48 NB KNN SVM RF BGG BST

F-

Measure

0 0.00 0.00 0.00 0.00 0.00 0.00 0.00

1 0.86 0.74 0.85 0.78 0.85 0.88 0.80

2 0.76 0.12 0.71 0.34 0.71 0.75 0.43

3 0.58 0.00 0.34 0.00 0.37 0.53 0.00

4 0.00 0.00 0.00 0.00 0.00 0.00 0.00

5 0.85 0.14 0.25 0.00 0.66 0.00 0.00

ROC

Area

0 0.62 0.53 0.49 0.06 0.40 0.21 0.33

1 0.80 0.61 0.81 0.61 0.90 0.87 0.31

2 0.80 0.55 0.78 0.59 0.87 0.83 0.30

3 0.75 0.68 0.65 0.48 0.85 0.81 0.06

4 0.29 0.06 0.49 0.53 0.44 0.25 0.56

5 0.86 0.95 0.62 0.94 0.86 0.95 0.86

Accuracy (%) all 81.32 54.21 76.80 66.26 78.01 81.32 68.67

Accuracy 10-fold (%) all 79.81 55.12 76.50 66.26 80.42 78.31 68.67

Table 4: Stacking ML results. Leave-one-instance-out evaluation.

Metric/Class 0 1 2 3 4 5

Precision 1.00 0.97 0.94 1.00 0.00 1.00

Recall 0.33 0.99 0.99 0.73 0.00 0.75

F-measure 0.50 0.98 0.96 0.84 0.00 0.85

ROC Area 0.94 0.99 0.99 0.98 0.42 0.99

Accuracy (%) 96.68

Accuracy 10-fold (%) 96.68

Table 5: Confusion matrix. Leave-one-instance-out evalua-

tion.

Real/Predicted 0 1 2 3 4 5

0 1 2 0 0 0 0

1 0 197 1 0 0 0

2 0 1 109 0 0 0

3 0 1 3 11 0 0

4 0 1 1 0 0 0

5 0 0 1 0 0 3

Correctly classiﬁed 321

Incorrectly classiﬁed 11

proach. From the results it can be observed that the

least recognized classes are the ones with only a few

instances available. However, even for the sparse

class ”Isolated systolic hypertension (label 5)”, J48

has achieved an F-measure of 0.86, and Bagging (also

NB) has achieved ROC area over 0.85. For the classes

0 and 4 (”Hypotension” and ”Stage 2 hypertension”)

with the least number of instances, all of the mod-

els perform worse in comparison to the performance

for the rest of the classes. However, the ROC area

measure, even though in range between random and

poor prediction, provides promising results for Boost-

ing and J48, and we expect this results to be im-

proved when more instances will be provided. Class

3, ”Stage 1 hypertension”, is also considered to be

sparse class; however, Random Forest and J48 show

slightly better results compared to class 0 and class

4. The classes 1 and 2, ”Normal” and ”Prehyperten-

sion”, contain the majority (92.77%) of the all the in-

stances. Random Forest, J48 and Bagging provide the

best results, but also KNN and to some extent SVM

show promising performance. The results from the

overall accuracy ranks the classiﬁers as follows: J48,

Bagging, Random Forest, KNN, Boosting, SVM and

Naive Bayes.

3.2 Stacking ML Results

Since all the classiﬁers in the ML experiments per-

formed well at different cases, we chose to combine

their outputs for the purpose of improved classiﬁca-

tion performance. As meta-classiﬁer we used Ran-

dom Forest. The stacking design produced the results

presented in Tab. 4. It can be seen that this approach

improved the prediction even for the sparse classes.

The overall accuracy is 96.68%, which is for 15.36

percentage points better than the highest accuracy ob-

tained by the ﬂat ML design.

Tab. 5 presents the confusion matrix for the stack-

ing design. It is a good indicator showing the ten-

dency of the classiﬁer to classify the sparse classes

HEALTHINF 2018 - 11th International Conference on Health Informatics

288

Table 6: Classiﬁcation with ”Age” elimination.

Classiﬁer Accuracy (with ”Age”) (%) Accuracy (without ”Age”) (%)

J48 81.32 80.72

NB 54.21 54.82

KNN 76.80 73.49

SVM 66.26 65.96

RF 78.01 76.81

BGG 81.32 76.2

BST 68.67 68.67

Table 7: Feature’s information gain.

Feature Average merit

Age 0.54

Fractal dimension 0.28

Complexity 0.25

Entropy 0.15

Autocorrelation 0.13

Mobility 0.01

Table 8: Variable ECG length accuracy comparison from

10-fold cross-validation.

Accuracy (%) 10s 30s 50s

J48 79.81 79.81 70.27

NB 58.43 55.12 24.32

KNN 74.39 76.50 54.05

SVM 65.96 66.26 70.27

RF 79.21 80.42 62.16

BGG 77.71 78.31 70.27

BST 68.67 68.67 70.27

Mean 72.02 72.15 60.23

0.00 0.66 1.99 3.32

Number of participants

Variance

Class variance distribution

Figure 3: Distribution of the classes variance among the

participants.

into the classes 1 and 2 that encompass the majority

of the instances.

4 DISCUSSION

The premise of using 30 seconds ECG signals is ex-

perimentally proved by using the proposed method-

ology in the paper considering variable-length ECG

windows starting from 10 up to 50 seconds. The

ﬂat design produced the accuracy results presented in

Tab. 8. The results indicate that the feature extrac-

tion methodology is less informative for longer ECG

signals. The accuracies for 10 and 30 seconds ECG

signals provide nearly same average result; however,

the 30s length performs better for KNN, SVM, RF

and BGG, thus is considered to be used in the further

analysis.

Observing the experimental results in Sect. 3, it

can be seen that for the sparse class Isolated systolic

hypertension (label 5), J48 has achieved an F-measure

of 0.86, and both Bagging and NB have achieved

ROC area over 0.95. This results lead to a conclusion

that the class itself is easy to be recognized because of

its nature (characterized by high SBP and low DBP).

Additional analysis is done on the feature’s inﬂu-

ence by measuring the information gain (entropy) for

each feature with respect to the class labels. Con-

sidering the feature ranking presented in Tab. 7, age

is found to be the top feature, fractal dimension and

complexity is the second and the third most inﬂuen-

tial attribute, correspondingly. Then follows the en-

tropy, the autocorrelation and mobility at last. It is

interesting that the second-order variations (complex-

ity) are found to be more informative than the ﬁrst-

order variations (mobility). Obtaining the top most

in inﬂuential features does not mean they are enough

for highly accurate classiﬁcation, instead the experi-

ments show that the elimination of each of the fea-

tures ranked bottom-up degrades the accuracy.

Given the fact that the feature age has highest rank

in Tab. 7 and also the fact that we performed multiple

measurements for each subject, we suspected that age

might act as a kind of ”ID” and therefore to intrigue

person-speciﬁc overﬁtting. In order to eliminate this

possibility, we performed additional testings by ex-

ECG-derived Blood Pressure Classiﬁcation using Complexity Analysis-based Machine Learning

289

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

1.20 2.41 3.61 4.81 6.02

Entropy

Class 1 Class 2 Class 3

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

0.04 0.22 0.40 0.58 0.76 0.94 1.12 1.30

Mobility

Class 1 Class 2 Class 3

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

1.20 2.41 3.61 4.81 6.02

Complexity

Class 1 Class 2 Class 3

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

1.13 1.37 1.61 1.86 2.10

Fractal dimension

Class 1 Class 2 Class 3

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

0.14 0.28 0.42 0.56 0.69 0.83 0.97 1.11

Autocorrelation

Class 1 Class 2 Class 3

10%

20%

30%

40%

50%

60%

70%

80%

90%

100%

1.00 2.00 3.00 4.00

Age

Class 1 Class 2 Class 3

Figure 4: Features absolute values distributions over classes.

cluding the age from the feature vectors.

The results of the overall accuracy for each clas-

siﬁer are presented in Tab. 6 and are compared to the

old classiﬁcation accuracy with the age included in

the feature vectors. The results show that the elimina-

tion of the age feature degrades the classiﬁcation for

at most 5% at the Bagging classiﬁer and for all the

rest there is only minor degradation in the classiﬁers

performance. This eliminates the suspicion of overﬁt-

ting and actually conﬁrms the assumptions for the age

inﬂuence provided in Sect. 2.4.

Another suspicion is the person-speciﬁc overﬁt-

ting that might appear due to a small class vari-

ance. Fig. 3 presents the classes variance distribution

among the different participants. The ﬁgure shows

that for 14 out of 20 participants the class variance is

in range from 0.66 to 3.32, meaning they have suf-

fered variability in their BP measurements.

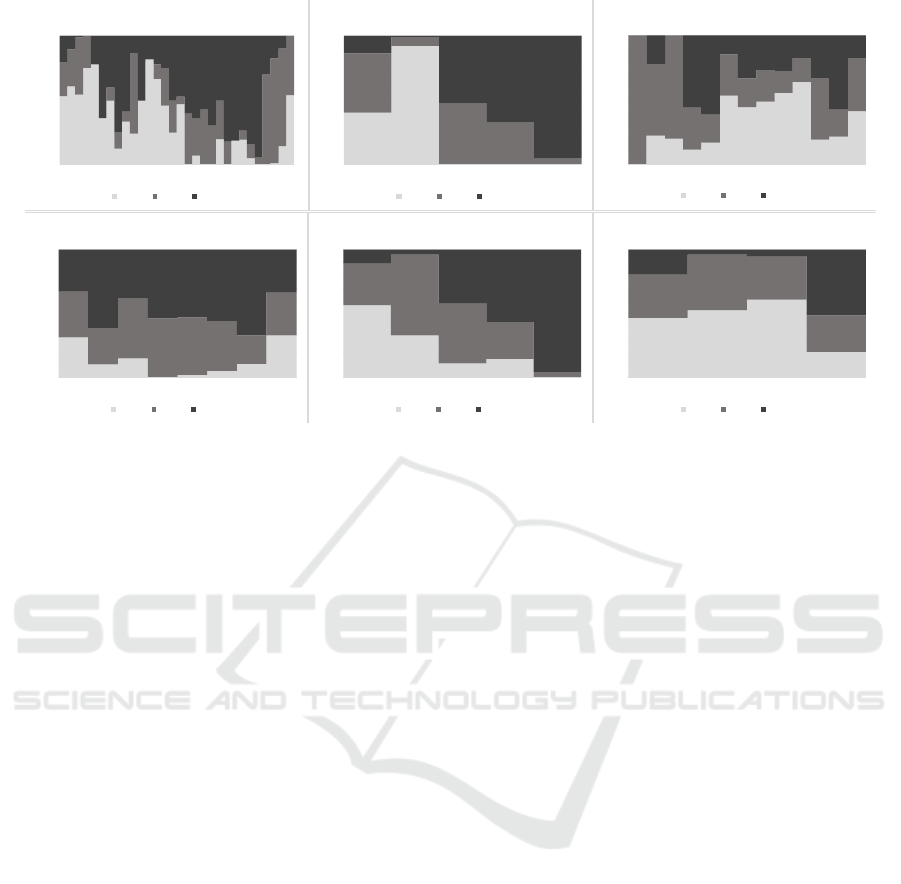
Fig. 4 presents the absolute values ranges of the

features in each of the BP classes. The ﬁgure shows

the amount of values (as % on the y-axis) correspond-

ing to the given range on the x-axis. Observing the en-

tropy as best visual representative, it can be seen that

most of the entropy absolute values obtained from the

instances in class 1 range from 1.20 up to 2.40; for

class 2 this range tends to be from 2.40 to 3.60, and in

class 3 most of the values are in range around 6. For

the autocorrelation, it can be concluded that the limits

are not so strict for the different classes, as well as for

the mobility feature. This is not surprising since both

of them have small average merit obtained from the

feature’s information gain results; however they still

inﬂuence the prediction results. For the complexity

and the fractal dimension feature, the ranges are more

clear as in the entropy case. The age feature distri-

bution over classes speaks that participants from all

the age groups (x-axis) can be found in each class.

However, observing the chart it can be concluded that

older population suffers from higher BP and belongs

to class 2 and 3. The age groups are created accord-

ing to the age ranges proposed in the literature (Arm-

strong, 2008).

5 CONCLUSION

The recent efforts on BP estimation mainly focus on

the morphological analysis of the physiological sig-

nals. The presented novel approach for BP classiﬁ-

cation takes into consideration complexity analysis of

the ECG signal for the feature vectors creation. The

experimental results from the ﬂat ML approach con-

ﬁrm that the features are suitable for BP classiﬁcation,

i.e., J48 and Bagging have achieved accuracy of 81%,

which is for 21 percentage points better than the ma-

jority class.

In addition, we proposed a stacking scheme by

combining the output of different ML algorithms. The

stacking scheme achieved an accuracy of 96.68%,

which is for 15.36% improvement when compared

to the best accuracy obtained by the ﬂat ML design,

or 36.36 percentage points improvement compared to

the majority class.

Compared to the newest related work, the pre-

sented results show signiﬁcant improvement in terms

of simplicity and accuracy, avoiding the complex pro-

cedures when multiple types of signals and devices

are involved for the BP estimation. We performed

HEALTHINF 2018 - 11th International Conference on Health Informatics

290

several analyses to explain the accuracy improve-

ments and our current hypothesis is that the complex-

ity analysis on the ECG signals provides enough in-

formation for accurate BP class estimation. If that is

indeed so, future BP measurements may be performed

using only an ECG sensor. However, to completely

conﬁrm this hypothesis, our method should be evalu-

ated on a bigger dataset with a leave-one-subject-out

evaluation technique, including the publicly available

physiological signals from the Physionet databases

(Goldberger et al., 2000).

Our future work is towards the collection of ECG

signals encompassing various ECG sensors and dif-

ferent target groups, since the research community is

missing this kind of data. The goal is to create a bal-

anced database, covering the critical BP classes (e.g.,

hypertensive crisis), and to develop sensor indepen-

dent methodology for BP estimation. Finally, we plan

to improve the methodology to be able to estimate the

real SBP and DBP values (e.g., using regression tech-

niques), and thus to contribute to the ”single-sensor

ﬁts all” paradigm of using as least equipment to de-

rive as much vital signs as possible.

ACKNOWLEDGEMENTS

This research is supported by SIARS, NATO multi-

year project NATO.EAP.SFPP 984753.

REFERENCES

AHA (2016). Understanding blood pressure readings.

Alvarez, J. M. (2015). Higuchi and katz fractal dimension

measures.

Armstrong, T. (2008). The Human Odyssey: Navigating the

Twelve Stages of Life. Sterling, New York.

Bhattacharya, J. et al. (2000). Complexity analysis of

spontaneous eeg. Acta neurobiologiae experimentalis,

60(4):495–502.

Bittium Biosignals (2016). emotion faros.

Cancio, L. C., Batchinsky, A. I., Salinas, J., Kuusela,

T., Convertino, V. A., Wade, C. E., and Holcomb,

J. B. (2008). Heart-rate complexity for prediction

of prehospital lifesaving interventions in trauma pa-

tients. Journal of Trauma and Acute Care Surgery,

65(4):813–819.

Cooking Hacks (2016). e-health sensor platform v2. 0 for

arduino and raspberry pi [biometric/medical applica-

tions].

Cosoli, G., Casacanditella, L., Pietroni, F., Calvaresi, A.,

Revel, G., and Scalise, L. (2015). A novel approach

for features extraction in physiological signals. In

Medical Measurements and Applications (MeMeA),

2015 IEEE International Symposium on, pages 380–

385. IEEE.

Costa, M., Goldberger, A. L., and Peng, C.-K. (2005). Mul-

tiscale entropy analysis of biological signals. Physical

review E, 71(2):021906.

Doyle, T. L., Dugan, E. L., Humphries, B., and Newton,

R. U. (2004). Discriminating between elderly and

young using a fractal dimension analysis of centre of

pressure. Int J Med Sci, 1(1):11–20.

Eke, A., Herman, P., Kocsis, L., and Kozak, L. (2002). Frac-

tal characterization of complexity in temporal physio-

logical signals. Physiological measurement, 23(1):R1.

Goldberger, A. L., Amaral, L. A., Glass, L., Hausdorff,

J. M., Ivanov, P. C., Mark, R. G., Mietus, J. E., Moody,

G. B., Peng, C.-K., and Stanley, H. E. (2000). Phys-

iobank, physiotoolkit, and physionet. Circulation,

101(23):e215–e220.

Goli, S. and T., J. (2014). Cuff less continuous non-invasive

blood pressure measurement using pulse transit time

measurement. International Journal of Recent Devel-

opment in Engineering and Technology, 2(1):86–91.

omez, C., Hornero, R., Ab

asolo, D., Fern

andez, A., and

opez, M. (2006). Complexity analysis of the magne-

toencephalogram background activity in alzheimer’s

disease patients. Medical engineering & physics,

28(9):851–859.

Grenwis, J., Bogie, H., and Main, B. (2012). A chronic

method for measuring real-time pulse wave veloc-

ity in conscious rodents. The FASEB Journal, 26(1

Supplement):870–10.

Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,

P., and Witten, I. H. (2009). The weka data min-

ing software: an update. ACM SIGKDD explorations

newsletter, 11(1):10–18.

Hassan, M. K. B. A., Mashor, M., Nasir, N. M., and Mo-

hamed, S. (2008). Measuring of systolic blood pres-

sure based on heart rate. In 4th Kuala Lumpur Interna-

tional Conference on Biomedical Engineering 2008,

pages 595–598. Springer.

Heart and Vascular Team (2016). Busting 6 myths about

blood pressure and heart rate.

i Car

os, J. M. S. (2011). Continuous non-invasive

blood pressure estimation. PhD thesis, Universitat

Polit

ecnica de Catalunya.

Kugiumtzis, D. and Tsimpiris, A. (2010). Measures of anal-

ysis of time series (mats): A matlab toolkit for compu-

tation of multiple measures on time series data bases.

arXiv preprint arXiv:1002.1940.

Labadin, J. and Ahmadi, A. (2006). Mathematical mod-

eling of the arterial blood ﬂow. In Proceedings

of the 2nd IMT-GT Regional Conference on Mathe-

matics, Statistics and Applications, Universiti Sains

Malaysia, Penang.

Lehocki, F., Kossaczky, I., Homola, M., Skalicky, D., My-

dliar, M., and Thurzo, A. (2014). Yet another hyper-

tension telehealth solution? the rules will tell you.

In Biomedical Engineering and Sciences (IECBES),

2014 IEEE Conference on, pages 510–515. IEEE.

McBride, J. C., Zhao, X., Munro, N. B., Smith, C. D.,

Jicha, G. A., Hively, L., Broster, L. S., Schmitt, F. A.,

ECG-derived Blood Pressure Classiﬁcation using Complexity Analysis-based Machine Learning

291

Kryscio, R. J., and Jiang, Y. (2014). Spectral and com-

plexity analysis of scalp eeg characteristics for mild

cognitive impairment and early alzheimer’s disease.

Computer methods and programs in biomedicine,

114(2):153–163.

Morabito, F. C., Labate, D., La Foresta, F., Bramanti, A.,

Morabito, G., and Palamara, I. (2012). Multivariate

multi-scale permutation entropy for complexity anal-

ysis of alzheimers disease eeg. Entropy, 14(7):1186–

1202.

Najarian, K. and Splinter, R. (2012). Biomedical Signal and

Image Processing. CRC Press.

Nitzan, M. (2011). Automatic noninvasive measurement

of arterial blood pressure. IEEE Instrumentation &

Measurement Magazine, 14(1):32–37.

Nye, R., Zhang, Z., and Fang, Q. (2015). Continuous

non-invasive blood pressure monitoring using pho-

toplethysmography: A review. In Bioelectronics

and Bioinformatics (ISBB), 2015 International Sym-

posium on, pages 176–179. IEEE.

Payne, R., Symeonides, C., Webb, D., and Maxwell, S.

(2006). Pulse transit time measured from the ecg:

an unreliable marker of beat-to-beat blood pressure.

Journal of Applied Physiology, 100(1):136–141.

Program, N. H. B. P. E. et al. (2004). The seventh report of

the joint national committee on prevention, detection,

evaluation, and treatment of high blood pressure.

Rangayyan, R. M. (2015). Biomedical signal analysis, vol-

ume 33. John Wiley & Sons.

Raoufy, M. R., Ghafari, T., and Mani, A. R. (2017). Com-

plexity analysis of respiratory dynamics. American

Journal of Respiratory And Critical Care Medicine,

(ja).

Schroeder, E. B., Liao, D., Chambless, L. E., Prineas, R. J.,

Evans, G. W., and Heiss, G. (2003). Hypertension,

blood pressure, and heart rate variability. Hyperten-

sion, 42(6):1106–1111.

Wong, M., Poon, C., and Zhang, Y. (2006). Can the timing-

characteristics of phonocardiographic signal be used

for cufﬂess systolic blood pressure estimation? In

Engineering in Medicine and Biology Society, 2006.

EMBS’06. 28th Annual International Conference of

the IEEE, pages 2878–2879. IEEE.

Wong, M. Y.-M., Poon, C. C.-Y., and Zhang, Y.-T. (2009).

An evaluation of the cufﬂess blood pressure estima-

tion based on pulse transit time technique: a half year

study on normotensive subjects. Cardiovascular En-

gineering, 9(1):32–38.

Zhang, G., Gao, M., Xu, D., Olivier, N. B., and Mukka-

mala, R. (2011). Pulse arrival time is not an adequate

surrogate for pulse transit time as a marker of blood

pressure. Journal of applied physiology, 111(6):1681–

1686.

Zhang, H. X., Zhu, Y. S., and Wang, Z. M. (2000).

Complexity measure and complexity rate information

based detection of ventricular tachycardia and ﬁbrilla-

tion. Medical and Biological Engineering and Com-

puting, 38(5):553–557.

Zhang, X.-Y. and Zhang, Y.-T. (2006). A model-based

study of relationship between timing of second heart

sound and systolic blood pressure. In Engineering in

Medicine and Biology Society, 2006. EMBS’06. 28th

Annual International Conference of the IEEE, pages

1387–1390. IEEE.

HEALTHINF 2018 - 11th International Conference on Health Informatics

292