A Simple and Robust Approach to Computation of Meshes Intersection

era Skorkovsk

, Ivana Kolingerov

and Bedrich Benes

Department of Computer Science and Engineering, University of West Bohemia,

Univerzitn

ı 8, 306 14, Plze

n, Czech Republic

Department of Computer Graphics Technology, Purdue University,

401. N. Grant Street, 47907-2021, West Lafayette, IN, U.S.A.

Keywords:

Triangular Mesh, Mesh Repair, Intersections, Neighbor Tracing.

Abstract:

Triangular meshes are important in many ﬁelds in both basic and applied research that rely on their correctness

and accuracy. Many operations with meshes can lead to undesirable situations and the resulting models can be

damaged and further unusable. Self-intersection and mesh-to-mesh intersection are types of operations that are

often present and can cause such problems. We propose an accurate geometry-based method for local repair

of intersecting meshes. The state-of-the-art methods either solve the problem inaccurately, or use methods

such as arbitrary precision arithmetic or virtual perturbation to deal with the troublesome boundary cases. Our

method represents a robust way to repair intersecting meshes accurately without the need to manipulate with

the input data or to employ arbitrary precision arithmetic. The correct solution is obtained through a careful

classiﬁcation of the cases that could result from a numerical imprecision of the ﬂoating point arithmetic.

1 INTRODUCTION

3D surface models are often used in various ﬁelds,

ranging from animation and gaming industry to archi-

tectural design and CAD. Applications dealing with

3D models usually require correct meshes. Depend-

ing on the correctness deﬁnition, many types of de-

fects can be found in polygon meshes that have to be

repaired before any further use of the model. For a

thorough survey on the defect types and their repair

we refer to (Attene et al., 2013; Botsch et al., 2007).

This paper addresses the problem of mesh-to-

mesh intersections and self-intersections. These in-

tersections are unacceptable in many applications, for

example when the mesh represents a boundary of a

solid volume. The existing algorithms addressing this

problem are usually designed to be either robust, ef-

ﬁcient, or accurate. To the best of our knowledge, no

method grants all the three desired properties. The

accuracy of the mesh-repair methods is probably the

most problematic and ignored topic, although it is the

main interest in applications such as CAD modeling

or exact physics simulations.

We propose a novel method for repair of intersect-

ing meshes. Our algorithm uses a neighbor tracing al-

gorithm (Lo and Wang, 2004; McLaurin et al., 2013),

works with ﬂoating point arithmetic, and has a high

accuracy achieved via a careful classiﬁcation of all

cases of intersections possibly caused by the numer-

ical imprecision. The method deals with both self-

intersections of a single mesh and intersections of two

meshes. The method does not use virtual perturba-

tion to avoid singular cases which makes it suitable

for applications where alterations of the input model

are undesirable. Our solution represents a robust way

of handling mesh (self-)intersections in applications

where accuracy of the solution is the main concern.

Our algorithm ﬁrst detects the intersection bound-

ary. In the second step the triangles containing the

boundary are cut along the boundary, dividing the tri-

angles into a valid part that is a part of the repaired

mesh, and an invalid part that needs to be removed.

The invalid parts are then discarded and the valid parts

are triangulated. Finally, the valid parts of the mesh

are stitched together. The correct identiﬁcation of the

intersection boundary in the ﬁrst step is essential for

the correct behavior of the rest of the algorithm and it

is the main contribution of this paper.

Figure 1 shows an example of a result generated

by our algorithm. The scene consists of six Stanford

dragons and six Stanford bunnies (Levoy et al., 2005)

placed at random positions with random rotation. 172

intersection boundaries were identiﬁed in the over-

lapped meshes by the ﬁrst step of our algorithm. The

detected intersections were repaired and the resulting

output mesh does not contain any intersections.

Skorkovská, V., Kolingerová, I. and Benes, B.

A Simple and Robust Approach to Computation of Meshes Intersection.

DOI: 10.5220/0006538401750182

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages

175-182

ISBN: 978-989-758-287-5

175

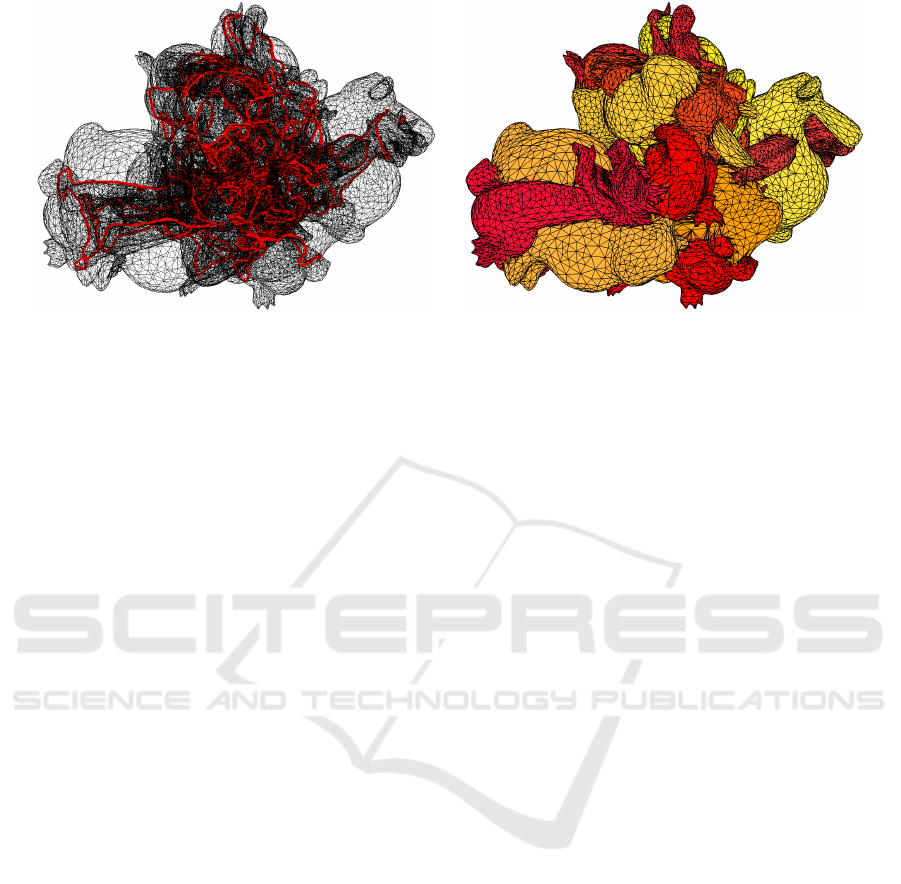
Figure 1: Six Stanford dragons and six Stanford bunnies (Levoy et al., 2005) intersect in 172 separate intersection boundaries

(left). The ﬁnal merged mesh (right) does not contain any intersections.

2 RELATED WORK

Many methods for repairing mesh intersections and

self-intersections have been proposed. The ap-

proaches can be divided into two main categories:

global (volumetric) and local (surface oriented) ap-

proaches (Attene et al., 2013).

Global approaches convert the polygonal mesh to

an intermediate representation which is then used to

generate a new valid mesh. Early methods utilize vol-

umetric representation (And

ujar et al., 2002; Noorud-

din and Turk, 2003). While being effective at repair-

ing the defects, this approach is sensitive to the res-

olution of the intermediate structure. Adaptive ap-

proaches exist that change the resolution of the in-

termediate structure according to the required detail

(Ju, 2004; Bischoff et al., 2005). Binary space par-

tition trees (Murali and Funkhouser, 1997), level set

methods (Osher and Fedkiw, 2002; Enright et al.,

2002) and deformable simplicial complexes (Misz-

tal and Bærentzen, 2012; Christiansen et al., 2014)

have been also used to solve this problem. The use of

global approaches is appropriate if the mesh is highly

inconsistent. It typically allows creating very robust

methods at the cost of lower accuracy and efﬁciency.

Local approaches work directly with the input

mesh and identify individual self-intersections which

are then repaired locally, usually one at a time, and

leave the rest of the mesh unchanged. These ap-

proaches change the input mesh as little as possible

which is desirable in applications where accuracy of

the solution is the main interest. Local approaches are

more suitable when the intersections are located only

at isolated parts of the mesh.

Some local approaches take a global method and

apply it only in the local scale (Bischoff and Kobbelt,

2005; Attene, 2010; Wojtan et al., 2009). These meth-

ods depend highly on the grid resolution and can also

lead to changes in the volume encompassed by the

mesh. Other group of methods does not rely on the

use of an intermediate data structure but works di-

rectly with the mesh. Zaharescu et al. (Zaharescu

et al., 2011) search the mesh for partially valid faces

and locally repair them. Others (Lo and Wang, 2004;

McLaurin et al., 2013) use neighbor tracing to speed

up the process of ﬁnding intersected faces and to

achieve reliable results. A similar approach is used to

simulate the interaction of dynamic meshes (Brochu

and Bridson, 2009) and to simulate interactions be-

tween solids and liquids (Clausen et al., 2013). These

geometric approaches often use exact arithmetic to

achieve numerical stability of the intersection calcu-

lations, while boundary cases are avoided by using

virtual perturbation method.

The above-mentioned methods usually concen-

trate on either being robust, accurate, or efﬁcient. To

the best of our knowledge, none of them satisfy all

the three properties. We focus on the accuracy of the

solution as it is very often overlooked.

The most accurate solutions can be found among

local geometric solutions. They usually use vertex

displacement or arbitrary precision arithmetic to im-

prove the robustness. However, the vertex displace-

ment changes the input mesh which can be unaccept-

able whereas the use of arbitrary precision arithmetic

leads to lower efﬁciency of the method. If the perfor-

mance of the algorithm is crucial, the use of ﬂoating

point arithmetic may be preferred.

Our goal is to propose an accurate method for

repairing (self-)intersections working with ﬂoating

point arithmetic. The proposed solution ranks among

local methods and extends the neighbor tracing algo-

rithm (Lo and Wang, 2004; McLaurin et al., 2013)

with the emphasis on the accuracy of the solution.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

176

intersection

boundary

mesh 1

mesh 2

invalid

parts

Figure 2: Left to right: intersection boundary detection, invalid parts elimination, polygon triangulation, and mesh stitching.

3 PROPOSED SOLUTION

Figure 2 shows an overview of our method. The input

are two triangle meshes (or two nonadjacent parts of

a single mesh) which are examined for intersection.

In the ﬁrst step we identify the intersection boundary,

then cut both parts of the mesh along the boundary,

triangulate the newly generated polygons, and then

we stitch the mesh together.

Our method for ﬁnding the intersection boundary

is based on the neighbor tracing algorithm (tracing the

neighbors of intersecting triangles - TNOIT) by Lo

and Wang (Lo and Wang, 2004) with further empha-

sis on the correct solution of singular cases of inter-

section.

The TNOIT algorithm (Lo and Wang, 2004)

repairs mesh intersections only if the intersection

segments of the boundary are calculated precisely

enough to be correctly classiﬁed. The TNOIT algo-

rithm fails when an intersection is not determined cor-

rectly. However, such cases are very common in real-

world situations.

The problem can be alleviated by increasing the

precision of the ﬂoating point arithmetic as shown

in (Karasick et al., 1991). However, this decreases the

algorithm performance and may limit time-critical ap-

plications such as real-time simulations. Moreover, it

only shifts the problems to higher frequencies. An-

other way of solving the problem is to use a vir-

tual perturbation method (e.g., Simulation of Simplic-

ity (Edelsbrunner and M

ucke, 1990)) to slightly dis-

place the vertices of the mesh, avoiding the boundary

cases altogether. However, the vertex displacement

can be unacceptable in applications where a precise

solution is needed.

We address this issue by a careful inspection of all

the cases which can occur due to the imprecise cal-

culation of the intersection, while using only ﬂoating

point arithmetic. Our solution represents a robust way

of handling mesh (self-)intersections in applications

where the accuracy of the solution is the main con-

Figure 3: Nonparallel planes intersecting at the line p.

cern.

3.1 Numerical Imprecision Problem

Let us open the description by an analysis of a case

where numerical imprecision could cause problems.

Let ρ

and ρ

be two nonparallel planes intersecting

at line p. Triangles T

and R

in these planes inter-

sect only if they intersect the line p and if the corre-

sponding intersection segments overlap. An example

in Figure 3 shows this case; triangle T

intersects the

line p in segment I

, triangle R

intersects p in seg-

ment I

. The line segments overlap, i.e., the line

segment I

is the intersection of T

and R

. To cor-

rectly determine the intersection of the triangles, we

need to identify the corresponding intersecting seg-

ments. Considering a triangle T located in the plane ρ

and a line p in the same plane, there are ﬁve ways the

triangle T can intersect the line p (see Figure 4):

1. Line p does not intersect the triangle T .

2. Line p intersects the triangle T at two of its edges.

3. Line p intersects the triangle T at a vertex.

4. Line p intersects the triangle T at a vertex and the

opposite edge.

5. Line p intersects the triangle T at two of its ver-

tices and the edge formed by these two vertices is

in the line p.

The cases 1-2 can be handled even in the context

of ﬂoating point arithmetic, but the situation is more

A Simple and Robust Approach to Computation of Meshes Intersection

177

(1)

(2)

(3)

(4)

(5)

Figure 4: Intersections of a triangle and a line. Left to right,

top to bottom: no intersection, intersection at two edges, at

a vertex, at a vertex and an edge, and at two vertices.

Figure 5: Intersections of line and triangle edges. Left: an

example situation, right: vertices rotated counterclockwise.

difﬁcult when we get closer to the boundary cases, be-

cause even a small error can cause an incorrect clas-

siﬁcation of the intersection cases.

We suggest a solution to this problem based on a

careful classiﬁcation of all the possible cases which

can be caused by the incorrect calculation of the in-

tersection. For each pair of triangles, we ﬁrst identify

the intersection line p (Figure 3). Then we calculate

the intersection segment for each triangle. The inter-

section line p is guaranteed to lie in the same plane as

the triangle, allowing us to compute the intersections

of the line p and all edges of the triangle. An exam-

ple of the situation is shown in Figure 5. Line p can

intersect the line containing an edge in three ways:

intersection lies outside the edge (I

), at a vertex, or

inside the edge (I

, I

Based on the position of the intersection points I

, I

, we classify the situation into one of the cases

depicted in Figure 4. The problem gets more com-

plicated when we take into consideration the fact that

some (or all) of the intersection points might not have

been determined correctly due to the numerical im-

precision of the ﬂoating point arithmetic. We intro-

duce the following substitute symbols for the relative

position of the intersection points:

• 0 - the intersection point lies outside the edge,

• 1 - the intersection point lies at a vertex, and

• 2 - the intersection point lies inside the edge.

The order of the points is not relevant for the clas-

siﬁcation and so we can sort the symbolic represen-

tation in the ascending order. Using this notation, we

can describe the situation from Figure 5 (left) as 022

- I

lies outside the edge e

, I

and I

lie inside the

edges e

and e

respectively. Let us consider a similar

situation where the vertices of the triangle are rotated

counterclockwise (Figure 5 (right)). The description

of the situation using the substitute symbols would be

220. As mentioned above, we can sort the symbolic

representation without the loss of generality, getting

the same representation (022) for both cases. This

simpliﬁcation leaves us with 10 cases to address:

• 000 - all intersections outside the edges → case 1,

• 001 - impossible case,

• 002 - impossible case,

• 011 - one intersection outside, two intersections at

vertices,

– two intersections at the same vertex → case 3,

– intersections at different vertices → case 5,

• 012 - impossible case,

• 022 - one intersection outside, two intersections

inside the edges → case 2,

• 111 - three intersections at vertices → case 5,

• 112 - one intersection inside, two intersections at

vertices,

– two intersections at the same vertex, one inter-

section at the opposite edge → case 4,

– intersections at two different vertices and on the

edge between them → case 5,

• 122 - impossible case, and

• 222 - impossible case.

The impossible cases cannot occur as a result of a

correct calculation. For these cases, no such straight

line exists that all the intersection points would lie

on it. An example of this situation is in Figure 6

where the line p intersects edges e

and e

close to

vertex V

. However, the incorrect calculation of the

intersection puts the point I

outside e

whereas the

point I

inside e

, causing a contradiction with the

original assumption that all the intersection points lie

on the line p (points I

, I

and I

are not collinear).

If the classiﬁcation of the intersection ends up as

one of the impossible cases, we know that the results

must have been caused by numeric imprecision. In

such a case we need to correct the results before the

neighbor tracing algorithm can continue.

Even if the result of the classiﬁcation is a valid op-

tion, some numeric error might have been introduced.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

178

≈

Figure 6: Impossible case of the intersection points as a

result of numeric imprecision during the calculations.

≈

I´

Figure 7: Incorrect intersection classiﬁcation. The com-

puted intersections I

and I

lie inside the edges while the

correct intersections I

and I

lie at the vertex V

The numeric errors during the calculation can cause

an incorrect classiﬁcation. Figure 7 shows an exam-

ple of such a situation. Line p intersects the edges e

and e

at the vertex V

but the computed intersection

points I

and I

are located inside the corresponding

edges. This error causes an incorrect classiﬁcation as

the case 022 instead of the correct case 011.

We cannot tell if the classiﬁcation is valid if any of

the intersection points lies close to a vertex. However,

if the mesh does not contain any nearly degenerate tri-

angles with edges shorter than the maximum error ε,

we can continue the neighbor tracing. In such a case

we can never stray away from the exact solution far-

ther than to the direct neighbor. Figure 8 shows an

example of such a situation where several incorrect

classiﬁcations took place in a row. The green dashed

line marks the exact intersection boundary while the

red dotted line represents the computed intersection

boundary affected by the computational error. The

exact intersection is close to a vertex. The numeri-

cal imprecision causes an incorrect classiﬁcation of

the intersection with triangle T

, leading the intersec-

tion boundary to T

instead of T

. In an unlikely sce-

nario it is possible for several incorrect classiﬁcations

to chain, e. g., as in Figure 8, where the intersection

is incorrectly classiﬁed for triangles T

, T

and T

Triangles T

, T

and T

should not be a part of the in-

tersection at all, but they are included as a result of

the numeric error of the calculation.

Subsequently, no intersection is found for triangle

. The failure to identify the intersection suggests

that the previous segment or segments of the intersec-

tion boundary were affected by the numerical impre-

cision. Yet thanks to the condition we put on the in-

I´

Figure 8: A chain of several incorrect classiﬁcations of the

intersection. The green dashed line represents the exact in-

tersection boundary, the red dotted line represents the com-

puted intersection boundary.

put triangle mesh (no nearly degenerate triangles), we

know the correct solution is going through a neigh-

boring triangle. In such a case we have to test other

possible classiﬁcation solutions to ﬁnd the right tri-

angle where the intersection boundary continues. We

start with the original case that we got as a result of the

classiﬁcation of the intersection of triangle T and look

for the next closest option until we ﬁnd the pair of

triangles where the intersection boundary of the two

meshes continues. The same approach is used if the

original classiﬁcation results in an impossible case.

3.2 Mesh Fixing

After the intersection boundary was found by the al-

gorithm from Section 3.1, we can ﬁx the mesh. We

propose a novel method for repairing the mesh by us-

ing the detected intersection boundary. For each in-

tersection segment found during the neighbor tracing,

we store the pair of triangles which formed the in-

tersection. This information is used during the repair

step to ﬁx the connectivity and topology of the mesh.

For each triangle participating in the intersection,

a new valid polygon is created by cutting the incon-

sistent parts off (see Figure 9). To create the polygon,

we ﬁrst need to identify all the polylines that inter-

sect it. We insert the polylines into an auxiliary data

structure which helps to correctly trace the polygon

as shown in Figure 10. We start with an empty list

and insert the vertices of the triangle. We then insert

the ﬁrst point of each intersecting polyline into the

list at the appropriate position corresponding to the

line segment where the point is located in the orig-

inal triangle. Finally, we connect the end points of

the polylines with the vertices that come after them in

the polygon boundary. Then we trace the boundary of

the polygon: starting with any polyline, we trace the

boundary following the pointers we set up in the aux-

iliary structure until we get back to the starting point.

The points we visited form the boundary of the new

polygon. If any polyline is left unvisited, the origi-

nal triangle needs to be cut into more pieces. We re-

peat this process until all the polygons are found (Fig-

A Simple and Robust Approach to Computation of Meshes Intersection

179

Figure 9: Polygon reconstruction. Intersecting polylines

(left) and newly created polygons (right).

B C

Figure 10: Left to right, top to bottom: list initiation; inser-

tion of polylines; linking end points; polygon tracing.

ure 9). The order of the processing does not affect the

outcome of the algorithm.

Then we use the ear cutting algorithm (Meisters,

1975) to triangulate the polygons created in the pre-

vious step. Finally, correct connectivity is restored

through the shared intersection boundary.

4 RESULTS AND DISCUSSION

We tested our algorithm in various scenarios to show

its robustness and correctness. Our implementation is

a single-threaded C++ code and it was tested on Intel

Core i7 clocked at 3.07 GHz with 8 GB RAM.

Our algorithm addresses the problem of numerical

inaccuracy of ﬂoating point calculations which can af-

fect the result of the neighbor tracing algorithm (Lo

and Wang, 2004) when operating near the boundary

cases. We created a simple scene to demonstrate the

problem. A cuboid with edge ratio 2:2:2 intersects

a cuboid with edge ratio 4:1:1 in Figure 11. The

cuboids are aligned so that the intersection bound-

ary is going exactly along the edges of the faces.

The cuboids are rotated one degree along the x axis

to magnify the inaccuracy problem. The position of

some vertices cannot be represented exactly in ﬂoat-

ing point arithmetic after the rotation, amplifying the

inaccuracy of the subsequent calculations.

The scene was set up in such a way so that we

know the exact result of the intersection and can com-

pare it with the results of our algorithm. The inter-

section boundary is aligned with the edges, so we can

Figure 11: Two cuboids (left) and their intersection (right).

Figure 12: Input (left) and repaired model (right).

assume that every triangle participating in the inter-

section will have one of its vertices or edges lying on

the intersection boundary. Using the notation intro-

duced in Section 3.1, the result for each segment of

the boundary should be 011, 111, or 112. However,

the measured results differ from these expected values

due to the numerical imprecision of the ﬂoating point

arithmetic. Table 1 summarizes the results measured

for the two cuboids with increasing resolution. For

the example in Figure 11 consisting of 3, 072 faces,

the calculation results in impossible cases in 57 out of

128 instances. Furthermore, not even the valid results

correspond to the expected outcome - none of the in-

tersections was correctly identiﬁed as the cases 011,

111 or 112. Using the proposed method, we were able

to repair the intersection despite the incorrect identiﬁ-

cation of the intersection cases. Existing methods (Lo

and Wang, 2004; McLaurin et al., 2013) fail on these

types of scenes unless exact arithmetic or virtual per-

turbation methods are used.

Our algorithm can also be used for other prob-

lems. It can detect and repair not only the inter-

section between separate objects, but also the self-

intersections of a single model. Figure 12 captures

such a self-intersecting object. The middle ring rep-

resents an inconsistent part of the mesh, where the

normals are reversed as a results of the mesh overlap -

the normals are pointing inwards instead of outwards.

We can detect the two intersection boundaries using

our algorithm and repair the mesh.

The algorithm can also easily be used to perform

boolean operations on triangle meshes. Having two

meshes A and B (Figure 13), we can perform boolean

operations on them by setting the orientation of the

normals of the mesh. As we cannot change the actual

normals, we use temporary normals to obtain the de-

sired behavior; these temporary normals are used dur-

ing the repair of the mesh to determine, which part of

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

180

Table 1: The number of occurrences of possible intersection cases for the scene captured in Figure 11, with increasing

resolution, using the notation introduced in Section 3.1.

faces 000 001 002 011 012 022 111 112 122 222 valid impossible

336 11 8 0 0 5 8 0 0 0 0 19 13

3 072 33 1 55 0 1 38 0 0 0 0 71 57

49 152 116 0 201 0 5 188 0 0 0 0 304 206

196 608 224 2 364 0 0 426 0 0 0 0 650 366

Figure 13: Boolean operation on cube A and sphere B. Left

to right, top to bottom: A ∪ B, A ∩ B, A \B, and B \ A.

Table 2: The resolution of the scenes.

faces vertices

Self-intersection (Fig. 12) 5 120 2 564

Boolean - union (Fig. 13) 13 568 6 790

Two cuboids (1) (Fig. 11) 49 152 24 582

Two cuboids (2) (Fig. 11) 196 608 98 310

Dragons & bunnies (Fig. 1) 76 716 38 372

the mesh should be discarded. To get the union A ∪ B,

the temporary normals are identical to the actual nor-

mals. On the contrary, the boolean operation intersec-

tion A ∩ B can be deﬁned by setting all the temporary

normals pointing inward the mesh. For the difference

A \ B, the temporary normals of A are pointing out-

wards, while the normals of B are pointing inwards.

Table 2 contains the number of faces and ver-

tices of the scenes presented in this paper. Table 3

shows the measured execution time. The measured

data demonstrate that we usually ﬁnd all the inter-

section boundaries long before we search the entire

mesh, e.g., in the Two cuboids (2) example (Fig-

ure 11). Nevertheless, we cannot stop the calculation

early, because we do not know if all the boundaries

Table 3: The execution time of steps of the algorithm (in

ms). Description of the scenes can be found in Table 2.

Find

intersection

boundaries

whole

mesh

Fix

mesh

Self-intersection 5 72 15

Boolean - union 24 221 43

Two cuboids (1) 63 394 33

Two cuboids (2) 24 1 454 76

Dragons & Bunnies 7 358 7 631 476

have been found until we ﬁnish searching the whole

mesh. The Dragons & bunnies example (Figure 1)

shows that for complex scenes with many separate in-

tersection boundaries we have to go through most of

the mesh to ﬁnd all the intersections.

We do not focus on the speed of the method. We

explore the capabilities of the method and its robust-

ness. The examples presented in this section demon-

strate the ability of the method to ﬁnd the intersection

boundary and repair the intersecting meshes even in

the non-trivial cases, such as a scene containing many

separate intersection loops (Figure 1) or a scene with

many boundary cases (Figure 11).

5 CONCLUSION

We have proposed an approach for the repair of in-

tersecting meshes based on the neighbor tracing al-

gorithm (Lo and Wang, 2004; McLaurin et al., 2013)

with the emphasis on the accuracy. Unlike the previ-

ous work, we do not use arbitrary precision arithmetic

to achieve the accuracy of the solution, nor do we use

virtual perturbation to avoid the undesirable boundary

cases, as the change of input data can be unacceptable

in some applications. Our method does not introduce

any alteration of the input, works with ﬂoating point

arithmetic and achieves accuracy through a careful

classiﬁcation of all sub-cases that could be caused by

numerical imprecision. The neighbor tracing can be

damaged by a numeric error near the boundary cases

but for a mesh without nearly degenerate triangles, the

intersection boundary can be correctly traced and re-

A Simple and Robust Approach to Computation of Meshes Intersection

181

paired thanks to the classiﬁcation of the intersection.

The method is designed for data in which we can

expect a lot of boundary cases participating in the in-

tersection boundary. We have tested the method on

an example of two intersecting edge-aligned cuboids,

where every segment of the intersection boundary

represents a boundary case. We have also tested the

method on a scene composed of several Stanford bun-

nies and Stanford dragons (Levoy et al., 2005) to

demonstrate the correct behavior of the method in

larger scene containing many intersection boundaries.

Our experiments proved that the method can ﬁnd the

correct solution even in these non-trivial situations.

The correct behavior of the method can be guaran-

teed only if the maximum error ε of the calculation is

smaller than the shortest edge of the mesh. For mod-

els that contain almost degenerate edges the algorithm

may not be working correctly because the calculation

error may corrupt the output of the method.

As the method works with single precision ﬂoat-

ing point arithmetic, it could be implemented on the

GPU, where the higher precision operations can be

very expensive. The transformation of the algorithm

to be able to run it on the GPU is one of the possible

avenues for this work.

ACKNOWLEDGEMENTS

This work has been supported by the project SGS-

2016-013 - Advanced Graphical and Computing Sys-

tems.

REFERENCES

And

ujar, C., Brunet, P., and Ayala, D. (2002). Topology-

reducing surface simpliﬁcation using a discrete solid

representation. ACM Trans. Graph., 21(2):88–105.

Attene, M. (2010). A lightweight approach to repair-

ing digitized polygon meshes. The Visual Computer,

26(11):1393–1406.

Attene, M., Campen, M., and Kobbelt, L. (2013). Poly-

gon mesh repairing: An application perspective. ACM

Comput. Surv., 45(2):15:1–15:33.

Bischoff, S. and Kobbelt, L. (2005). Structure preserv-

ing cad model repair. Computer Graphics Forum,

24(3):527–536.

Bischoff, S., Pavic, D., and Kobbelt, L. (2005). Automatic

restoration of polygon models. ACM Trans. Graph.,

24(4):1332–1352.

Botsch, M., Pauly, M., Kobbelt, L., Alliez, P., L

evy, B.,

Bischoff, S., and R

oossl, C. (2007). Geometric Mod-

eling Based on Polygonal Meshes. This document is

the support of a SIGGRAPH 2007 course.

Brochu, T. and Bridson, R. (2009). Robust topological op-

erations for dynamic explicit surfaces. SIAM Journal

on Scientiﬁc Computing, 31(4):2472–2493.

Christiansen, A. N., Nobel-Jørgensen, M., Aage, N., Sig-

mund, O., and Bærentzen, J. A. (2014). Topology op-

timization using an explicit interface representation.

Struct. Multidiscip. Optim., 49(3):387–399.

Clausen, P., Wicke, M., Shewchuk, J. R., and O’brien, J. F.

(2013). Simulating liquids and solid-liquid interac-

tions with lagrangian meshes. ACM Trans. Graph.,

32(2):17:1–17:15.

Edelsbrunner, H. and M

ucke, E. P. (1990). Simulation

of simplicity: A technique to cope with degenerate

cases in geometric algorithms. ACM Trans. Graph.,

9(1):66–104.

Enright, D., Fedkiw, R., Ferziger, J., and Mitchell, I. (2002).

A hybrid particle level set method for improved in-

terface capturing. Journal of Computational Physics,

183(1):83–116.

Ju, T. (2004). Robust repair of polygonal models. ACM

Trans. Graph., 23(3):888–895.

Karasick, M., Lieber, D., and Nackman, L. R. (1991). Efﬁ-

cient delaunay triangulation using rational arithmetic.

ACM Trans. Graph., 10(1):71–91.

Levoy, M., Gerth, J., Curless, B., and Pull, K. (2005).

The Stanford 3D Scanning Repository. http://

graphics.stanford.edu/data/3Dscanrep/.

Lo, S. and Wang, W. (2004). A fast robust algorithm for

the intersection of triangulated surfaces. Engineering

with Computers, 20(1):11–21.

McLaurin, D., Marcum, D., Remotigue, M., and Blades, E.

(2013). Repairing unstructured triangular mesh inter-

sections. International Journal for Numerical Meth-

ods in Engineering, 93(3):266–275.

Meisters, G. H. (1975). Polygons Have Ears. The American

Mathematical Monthly, 82(6):648–651.

Misztal, M. K. and Bærentzen, J. A. (2012). Topology-

adaptive interface tracking using the deformable sim-

plicial complex. ACM Trans. Graph., 31(3):24:1–

24:12.

Murali, T. M. and Funkhouser, T. A. (1997). Consis-

tent solid and boundary representations from arbitrary

polygonal data. In Proceedings of the 1997 Sympo-

sium on Interactive 3D Graphics, I3D ’97, pages 155–

ff., New York, NY, USA. ACM.

Nooruddin, F. S. and Turk, G. (2003). Simpliﬁcation and re-

pair of polygonal models using volumetric techniques.

IEEE Transactions on Visualization and Computer

Graphics, 9:191–205.

Osher, S. and Fedkiw, R. (2002). Level Set Methods and Dy-

namic Implicit Surfaces (Applied Mathematical Sci-

ences). Springer, 2003 edition.

Wojtan, C., Th

urey, N., Gross, M., and Turk, G. (2009).

Deforming meshes that split and merge. ACM Trans.

Graph., 28(3):76:1–76:10.

Zaharescu, A., Boyer, E., and Horaud, R. (2011). Topology-

adaptive mesh deformation for surface evolution, mor-

phing, and multiview reconstruction. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

33(4):823–837.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

182