Deep Parts Similarity Learning for Person Re-Identiﬁcation

Mar

ıa Jos

e G

omez-Silva, Jos

e Mar

ıa Armingol and Arturo de la Escalera

Intelligent Systems Lab (LSI) Research Group,

Universidad Carlos III de Madrid, Legan

es, Madrid, Spain

Keywords:

Deep Learning, Convolutional Neural Network, Mahalanobis Distance, Person Re-Identiﬁcation.

Abstract:

Measuring the appearance similarity in Person Re-Identiﬁcation is a challenging task which not only requires

the selection of discriminative visual descriptors but also their optimal combination. This paper presents a

uniﬁed learning framework composed by Deep Convolutional Neural Networks to simultaneously and auto-

matically learn the most salient features for each one of nine different body parts and their best weighting to

form a person descriptor. Moreover, to cope with the cross-view variations, these have been coded in a Ma-

halanobis Matrix, in an adaptive process, also integrated into the learning framework, which takes advantage

of the discriminative information given by the dataset labels to analyse the data structure. The effectiveness

of the proposed approach, named Deep Parts Similarity Learning (DPSL), has been evaluated and compared

with other state-of-the-art approaches over the challenging PRID2011 dataset.

1 INTRODUCTION

Person re-identiﬁcation (re-id) consists of recognizing

an individual through images from non-overlapping

camera views at different locations and time. Auto-

mating this task has become one of the major goals

in intelligent video-surveillance, since many other ap-

plications, like tracking or behaviour analysis, rely on

the person re-id performance. Usually, in real-world

surveillance scenarios, ﬁne biometric cues are unavai-

lable, so the research has been mainly focused on the

appearance-based approaches.

The literature presents two re-id strategies: sin-

gle shot recognition, (Munaro et al., 2014), where

only one image per person and per view is used, and

multi-shot recognition, (Khan and Br

emond, 2016)

and (Chan-Lang et al., 2016), where a tracklet of

every individual (i.e. small sequence of images) is

available for each camera view. This paper is focu-

sed on the single-shot case, where the aim of the re-id

task is to identify the person represented by an image

from one view (probe image) among all the images

from the other view (gallery images).

The single-shot re-identiﬁcation problem can be

treated as a pairwise binary classiﬁcation, consisting

of two steps: the features extraction for pairs of ima-

ges and the learning of their optimal combination to

discriminate similar and dissimilar pairs.

The selection of features based on visual appea-

rance becomes a remarkable challenge in unconstrai-

ned scenarios, because of the inter-class ambiguities

and the intra-class variations. The ﬁrst ones are pro-

duced by the similar appearances when different pe-

ople are wearing similar clothes or hairstyles, and the

second ones are due to the changes in resolution, il-

lumination, pose, perspective, background, etc. bet-

ween the two cameras views that cause extremely dif-

ferent representations of the same person.

In order to face this problem, two research streams

can be found: those which enhance the design of the

features, or the ones focused on improving the way

of combining them. The ﬁrst group tries to represent

the most discriminant aspects of an individuals appea-

rance, advancing in the direction of extracting seman-

tically meaningful attributes (Layne et al., 2014).

On the other hand, the learning of a distance to

optimally combine some visual features can boost

the re-identiﬁcation performance using quite simple

hand-crafted features, mainly based on colour or tex-

ture. Some methods address the distance learning

through evaluating the discriminative importance of

different types of features, as it is presented in (Liu

et al., 2014). Other methods are meant to learn a me-

tric that reﬂects the visual camera-to-camera transi-

tion, (Roth et al., 2014).

Most of these approaches optimize a linear

function to properly weight the absolute difference

between the images features of a pair, after that fe-

atures have been computed for a dataset, treating the

features selection and the distance learning as two in-

Gómez-Silva, M., Armingol, J. and Escalera, A.

Deep Parts Similarity Learning for Person Re-Identiﬁcation.

DOI: 10.5220/0006539604190428

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

419-428

ISBN: 978-989-758-290-5

419

dependent stages. On the contrary, this paper pre-

sents a training framework were the features and their

combination are jointly learnt in a uniﬁed architec-

ture formed by Deep Convolutional Neural Networks

(DCNN). This proposal, hereinafter called Deep Parts

Similarity Learning (DPSL), presents the following

highlights:

1. The feature learning has been divided according

to nine body parts, to get more robustness against

partial occlusions. The features corresponding to

each body part are parallelly learnt in the same

process, getting a representation which is more

invariant to the pose and eliminating a huge part

of the background dependency. A body parts ex-

traction stage has been designed using a Convo-

lutional Pose Machine (CPM), (Wei et al., 2016),

which has been integrated into the learning frame-

work, leading to a highly-layered architecture.

2. The proper weighting of the learnt features has

been also addressed by the deep learning strategy,

allowing the automatic search of the most discri-

minative person descriptor. This is achieved by a

fully connected layer, whose inputs are the extrac-

ted features for every body part.

3. The intra-class variations are coped with a discri-

minative analysis of the data structure, which has

been encompassed in a Mahalanobis Matrix. The

Mahalanobis Matrix is employed to code the vi-

sual camera-to-camera transitions, and its estima-

tion has been optimized by the adaptively learning

of the covariance matrices of two features spaces,

the similar and dissimilar ones.

4. All the stages, body parts extraction, feature and

weighting learning, and data structure analysis,

are integrated into a uniﬁed learning framework.

The re-id capacity of the proposed approach has

been evaluated over one of the most challenging and

commonly used re-id datasets: PRID2011

(Hirzer

et al., 2011), using the standard protocols. The ex-

perimental results have proved the improvements in

comparison with other state-of-the-art methods.

The rest of the paper is organized as follows.

Section 2 presents the existing related work. The

proposed re-id learning framework is described in

Section 3. Section 4 evaluates the learning process

evolution and presents the experimental results, and

some concluding remarks are given in Section 5.

The dataset is publicly available under http://lrs.icg.

tugraz.at/download.php

2 RELATED WORK

With the aim of solving the re-id problem, many

works have been dedicated to the design of featu-

res able to represent the most discriminant aspects

of an individual's appearance. RGB or HSV histo-

grams (Bazzani et al., 2013), Gabor ﬁlters (Zhang and

Li, 2011) and HOG-based signatures (Oreifej et al.,

2010), are examples of descriptors based on low-level

local features, such as colour, texture, and shape re-

spectively.

Traditionally, many algorithms have used Princi-

pal Component Analysis (PCA) method to reduce the

dimensionality of the computed features, like in (Roth

et al., 2014). An alternative to the dimensionality re-

duction is the integration of several types of features

into a global signature, such as Bag-of-words (BoW)

models. In (Ma et al., 2014), BoW model is improved

by means of using the Fisher Vector, (S

anchez et al.,

2013), which encodes higher order statics of local fe-

atures.

To make the features invariant to pose and robust

against partial occlusions, region-based approaches

decompose the human shape in different articulated

parts and extract features for each one, like (Bazzani

et al., 2014), where a symmetry-based silhouette par-

tition is used to detect salient body regions. In (Cheng

and Cristani, 2014), a pose estimation stage, based on

Pictorial Structures, (Felzenszwalb and Huttenlocher,

2005), is presented, from which traditional features

are subsequently computed. Instead of that, this pa-

per proposes the integration of a Convolutional Pose

Machine (CPM), (Wei et al., 2016), into the learning

framework. In that way, spatial information is also

integrated into the feature representation.

In order to get only one metric value to measure

the similarity between two images, the matching is

performed by computing a certain distance between

the descriptors. In (Hirzer et al., 2012) the Euclidean

distance is used. However, recently, a large amount

of research has been focused on searching for the op-

timal metric. In that way, the features selection pro-

blem is addressed not only improving the descriptors

design but also the selection mechanism.

In (Liu et al., 2014), a Prototype-Sensitive Fea-

ture Importance based method is proposed to adap-

tively weigh the features according to different clus-

ters of population, instead of using a Global Feature

Importance (GFI) measure. This last approach is wi-

dely extended and assumes a global weighting, i.e.

a vector of generic weights and invariant to the po-

pulation. Some examples are Boosting (Gray and

Tao, 2008), Ranking Support Vector Machines (Rank-

SVM), (Prosser et al., 2010), Probabilistic Relative

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

420

Figure 1: DPSL architecture.

Distance Comparison (PRDC), (Zheng et al., 2011),

or Metric Learning algorithms, such as Linear Discri-

minant Analysis (LDA) (Fisher, 1936) and Logistic

Discriminant Metric Learning (LDML) (Guillaumin

et al., 2009).

Rank-SVM (Prosser et al., 2010) is used to le-

arn an independent weight for each feature. Instead

of that, Mahalanobis metric learning optimizes a full

matrix that relates all the features between each ot-

her, exploiting the structure of the data, under the as-

sumption that the classes present the same distribu-

tion. Therefore, this is employed in this work to code

the view-to-view transitions, so that, the cross-view

variations are reduced.

The Mahalanobis matrix estimation has been

made through an adaptive data analysis process inte-

grated into the features and weighting learning, which

affects on the learning evolution, improving it.

The recent boost of deep learning algorithms has

made possible the automatic search of salient high-

level representations from the pixels of an image by

means of training DCNNs like it is proposed in this

work. Concretely for the re-id task, the learning has

been commonly performed by Siamese Networks (Yi

et al., 2014), consisting of two DCNNs sharing pa-

rameters and joined in the last layer, where the loss

function leads the whole network to discriminate bet-

ween pairs of similar or dissimilar images.

3 DEEP PART SIMILARITY

LEARNING, DPSL

In this section, the DPSL framework is presented. A

general view of the architecture is given in the ﬁrst

subsection. The rest of the subsections describe each

one of the stages, compounding it, in detail.

3.1 Architecture

To learn to identify the similarity between two per-

son images, a Siamese architecture is used. The Si-

amese network is formed by two branches (one per

person image) which are composed of a combination

of DCNN to learn the optimal person representation

for each person of a pair. The branches are joined in

the ﬁnal layers, where the similarity is measured, by

means of comparing the obtained features. The whole

architecture is presented in Figure 1, which is explai-

ned below.

The input of each branch is one of the images, I

of the pair to compare, where the index p indicates

each one of the two branches, a, or, b.

Moreover, each image has an identity number,

ID(I

), to identify the person to whom the image be-

longs. The labeller layer is in charge of checking if

the pair is a positive one, when the represented person

is the same in both images (same identity numbers),

or a negative one, otherwise. Its output, y, takes value

1 for positive pairs, and 0, for negative ones.

Firstly, from each person image, nine different

body parts images,

, are extracted. The index

bp indicates the query body part, taking the following

values: h, head; ula, upper left arm; lla, lower left

arm; ura, upper right arm; lra, lower right arm; ull,

upper left leg; lll, lower left leg; url, upper right left;

lrl, lower right leg.

Secondly, a DCNN computes a multi-dimensional

descriptor,

, for each one of the mentioned parts.

Subsequently, the descriptors are weighted to com-

pose a feature array, F

, to represent each person

image. These representations are analysed in every

iteration to get an estimation of the Mahalanobis Ma-

trix, M, in the Data Structure Analysis stage, where

the discriminative information given by the label y is

also considered.

Deep Parts Similarity Learning for Person Re-Identiﬁcation

421

Figure 2: DCNN used to learn the head feature matrix,

Then, in the connection layer, the Mahalanobis

distance is computed and its value is taken as a dis-

tance metric, dm, to measure the dissimilarity bet-

ween the feature arrays.

Finally, the loss function measures the deviation

of the distance value with respect to the established

objective values for positive and negative pairs. The

loss value determines the evolution of the whole lear-

ning process by means of the forward and back pro-

pagation method (Rumelhart et al., 1988).

3.2 Body Parts Extractor

The body parts extractor layer takes as input a person

image, I

, and returns nine body parts images,

whose sizes have been pre-established according to

the human shape proportions applied to a human re-

presentation with a height of 128-pixels, which is the

height value presented by the samples in most of the

re-identiﬁcation datasets. Eventually, the established

body part sizes are 45x45, for

, 30x40 for

ula

lla

ura

, and

lra

, and 30x60 for

ull

lll

url

and

lrl

This body parts extractor layer is mainly based on

the CPM presented in (Wei et al., 2016), whose out-

puts are a set of body joints locations.

For each body part a Region Of Interest, ROI,

which is deﬁned by a rotated rectangle, is extracted

from the input image. The orientation angle of the

rectangle is the one presented by the line resulting

of joining the extreme joints of the query body part.

The location of the upper joint is chosen as the upper

central pixel of the ROI and the location of the lower

joint, as its lower central pixel.

3.3 Deep Convolutional Neural

Network, DCNN

For each body part image,

, a DCNN is used to

learn the corresponding part feature,

, which is a

multi-dimensional descriptor. This can be understood

as a matrix whose elements are vectors with a length

value of 64. The resulting matrix dimensions are 8x8

for

, 7x4 for

ula

lla

ura

, and

lra

, and

12x4 for

ull

lll

url

, and

lrl

Even, the weights and dimensions of these nine

types of networks are different, they present an iden-

tical structure. As an example, Figure 2 presents the

DCNN corresponding to the head, essentially formed

by two types of layers: convolutional (in red) and

max-pooling (in yellow) layers, using a rectiﬁed li-

near unit (ReLU) as activation function. This neural

network architecture is based on the ﬁrst layers con-

ﬁguration of the mnistsiamese example, implemented

by the Caffe libraries (Jia et al., 2014), which presents

a traditional CNN architecture.

The nine DCNN have been duplicated sharing the

same weights, so the learnt descriptors are the same in

both branches, which is the base of a Siamese Neural

Network training.

3.4 Weighting

Once each part feature,

, has been computed, the

optimal weighting is learnt, using an inner product

layer, which is a fully connected layer, that weighs

and combines all the part features to create the ele-

ments of a general person descriptor, F

, whose size,

N(N = 100)has been experimentally ﬁxed.

However, the inputs of the inner product must be

the elements of a single matrix, so a ﬁrst stage of con-

catenation is needed to form it from the parts features

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

422

Figure 3: Creation of the Person Feature array, F

matrices, resulting in a 46x8 matrix as the Figure 3

describes.

3.5 Labeller

Throughout the learning process every input image, I,

is accompanied by an Identiﬁcation Number, ID(I).

With the aim of knowing if the computed features, F

and F

, represent a positive or a negative pair of ima-

ges, the labeller function, y(F

, F

), takes the values

1 or 0 according to (1).

y(F

, F

)



1 ID(I

) = ID(I

)

0 ID(I

) 6= ID(I

)

(1)

3.6 Connection Function

Once the person representation, F

, has been com-

puted for each one of the images of an input pair,

they must be compared by the connection function,

, F

), in order to get the distance metric, dm,

that measures the dissimilarity between the images.

The connection function, f

, F

), takes two

different formulations along the learning process, as

(2) shows, so the comparison of features is made by

the Euclidean distance, d

, until the number of le-

arning iterations, it, achieves a certain threshold, T

then, the comparison is made by the Mahalanobis dis-

tance, d

, instead.

The Euclidean distance between the descriptors,

, F

), is deﬁned by (3), where f

renders each

element of a person descriptor, F

The Mahalanobis distance, d

, F

), is deﬁned

by (4), where M is the Mahalanobis Matrix. This can

be understood as the inverse matrix of the covariance

matrix for the variable formed by the difference of our

feature arrays, F

− F

dm = f

, F

) =



, F

) it < T

, F

) it ≥ T

(2)

, F

) =

∑

n=1

( f

− f

) (3)

, F

) =

− F

)

M(F

− F

) (4)

Therefore, M allows us to consider the data struc-

ture for that new array, F

− F

, encoding the relati-

onship of each one of its elements with each other, as

it is described in Section 3.7.

However, a reliable estimation for the Mahalano-

bis Matrix is not achieved until executing an experi-

mentally observed number of learning iterations, T

For that reason the Euclidean distance is employed in

the ﬁrst stage of the learning process.

3.7 Discriminative Data Structure

Analysis

The objective of this module is to estimate the Ma-

halanobis matrix that the connection function needs

by means of analysing the probabilistic distribution

of the variable formed by the difference between the

computed features, F

− F

, and discriminating if

they belong to positive or negative samples, thanks

to the information given by the labeller function, y.

In every iteration of the DPSL, the input is not

only a single pair of images but a batch of them. The-

refore, the input of this module is a Batch of Pairs of

features BoP, deﬁned by (5), where B is the batch size

(B = 128).

BoP = {P

: P

= (F

, F

) ∀s ∈ [1, B]}. (5)

Subsequently, the BoP is divided into two subsets:

the similarity set, S, and the dissimilarity set, D, deﬁ-

ned by (6) and (7) respectively.

S = {|F

− F

| | y(F

, F

) = 1 ∧ s ∈ [1, B]}. (6)

D = {|F

− F

| | y(F

, F

) = 0 ∧ s ∈ [1, B]}. (7)

We call SQ to a FIFO (First In, First Out) queue of

size K(K = 1000) where the elements of the subset S,

are added in every iteration, and, in the same way, DQ

to a queue of size K that accumulates the elements of

the subset D.

Therefore, these queues are KxN matrices, since

N is the dimension of the features arrays and con-

sequently the dimension of their difference vector,

− F

. When the queues are full, the ﬁrstly added

elements are deleted to continue adding new ones in

Deep Parts Similarity Learning for Person Re-Identiﬁcation

423

order to consider the effects of the most recent trai-

ning samples on the Mahalanobis Matrix, M, learning

in every iteration.

SQ and DQ represent a subset of the difference

feature space for the situation of similarity (positive

pairs) or dissimilarity (negative pairs), so they are

used to computed the similarity covariance matrix,

, and the dissimilarity covariance matrix, Σ

, as it

is described by (8) and (9) respectively. µ

S,i

, is the ex-

pected value for the element i of the difference vector

for the similarity subspace, and it is computed as its

mean value with (10). In the same way, the expected

value, µ

D,i

, is deﬁned by (11).

S,i j

∑

k=1

(SQ

− µ

S,i

)(SQ

k j

− µ

S, j

)

(8)

D,i j

∑

k=1

(DQ

− µ

D,i

)(DQ

k j

− µ

D, j

)

(9)

S,i

∑

k=1

(10)

D,i

∑

k=1

(11)

Once both covariance matrices have been calcu-

lated, the Mahalanobis Matrix, M, is estimated using

the formulation presented in (Koestinger et al., 2012)

and shown by (12).

M = (Σ

−1

− Σ

−1

) (12)

The computed features are different in every le-

arning iteration, not only due to the different inputs

but also to the different computation of the descrip-

tors themselves since the DCNN weights are being

learned. For that reason, the estimation of the Ma-

halanobis Matrix, M, must be updated in every lear-

ning iteration, considering the new information, given

by the elements added to the two queues. The size,

K, of both queues takes a value (K = 1000), large

enough to comprise the contribution of several bat-

ches (B = 128) of samples.

3.8 Loss Function

The connection function returns a distance metric,

dm, which represents the degree of dissimilarity be-

tween two person images.

The learning process requires a loss function, f

to quantify the deviation of dm with respect ﬁxed ob-

jective values, for both positive (y = 1) and negative

samples (y = 0). The loss value is consequently used

by the back propagation method (Rumelhart et al.,

1988) to force the weights in both branches of the Si-

amese network to values which make the metric get

closer to the objective.

In this work, the function used to measure the loss

is the Normalised Double-Margin Contrastive Loss

function

, presented in (G

omez-Silva et al., 2017),

and deﬁned by (13). This is an improved version of

the traditional contrastive function commonly used to

train Siamese networks.

(ND,Y ) =

∑

s=1

· max(nd

− m

, 0)+

(1 − y

) · max(m

− nd

, 0)]

(13)

ND(nd

, . . . , nd

) is an array, where every ele-

ment, nd

, is the normalized distance metric for one

of the pairs of the treated batch in one learning itera-

tion. That means that, for every sample s of the batch,

the metric computed by the connection function, dm,

has been previously normalized with the function de-

ﬁned by (14). In the same way, Y is an array, where

every element, y

, is the value given by the labeller

function for the pair s.

nd = 2



1 + e

−dm

− 0.5



(14)

The function f

measures the half average of the

error computed for every pair, with respect m

and

, which are two constant parameters called mar-

gins. Therefore, a good training leads the nd to be lo-

wer than m

for positive samples and higher than m

for negative ones. Consequently, small values of the

metric, dm, must represent a high similarity between

the images, and vice versa.

4 EVALUATION

In this section, the dataset used to train and to test the

proposed approach is described. Moreover, the evo-

lution of the learning process is analysed. Then the

evaluation metric used to test the DPSL is explained.

Finally, the results of comparing the proposed ap-

proach with other state-of-the-art methods are presen-

ted and discussed.

The Normalised Double-Margin Contrastive Loss

function is implemented in a python layer, which is pu-

blicly available under http://github.com/magomezs/N2M-

Contrastive-Loss-Layer

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

424

4.1 Dataset

The proposed DPSL has been evaluated over the

PRID 2011 dataset (Hirzer et al., 2011). This is one

of the most widely used datasets for evaluating re-

identiﬁcation approaches since it is composed of per-

son images captured from two camera views with re-

markable differences in camera parameters, illumina-

tion, person pose, and background.

In the single-shot version, used in this work, ca-

mera view A contains 385 different images, and ca-

mera B, 749. 200 of the individuals are rendered in

both sets, and 100 of them have been randomly ex-

tracted to be used as training set.

For evaluation on the test set, the procedure des-

cribed in (Hirzer et al., 2011) is followed, i.e., the

images of view A for the 100 remaining individuals

have been used as probe set, and the gallery set has

been formed by 649 images belonging to camera view

B (all images of view B except the 100 corresponding

to the training individuals).

4.2 DPSL Process Evaluation

In this section, the evolution of the loss value throug-

hout a learning process is analysed. The learning pro-

cess has been conducted by the DPSL framework pre-

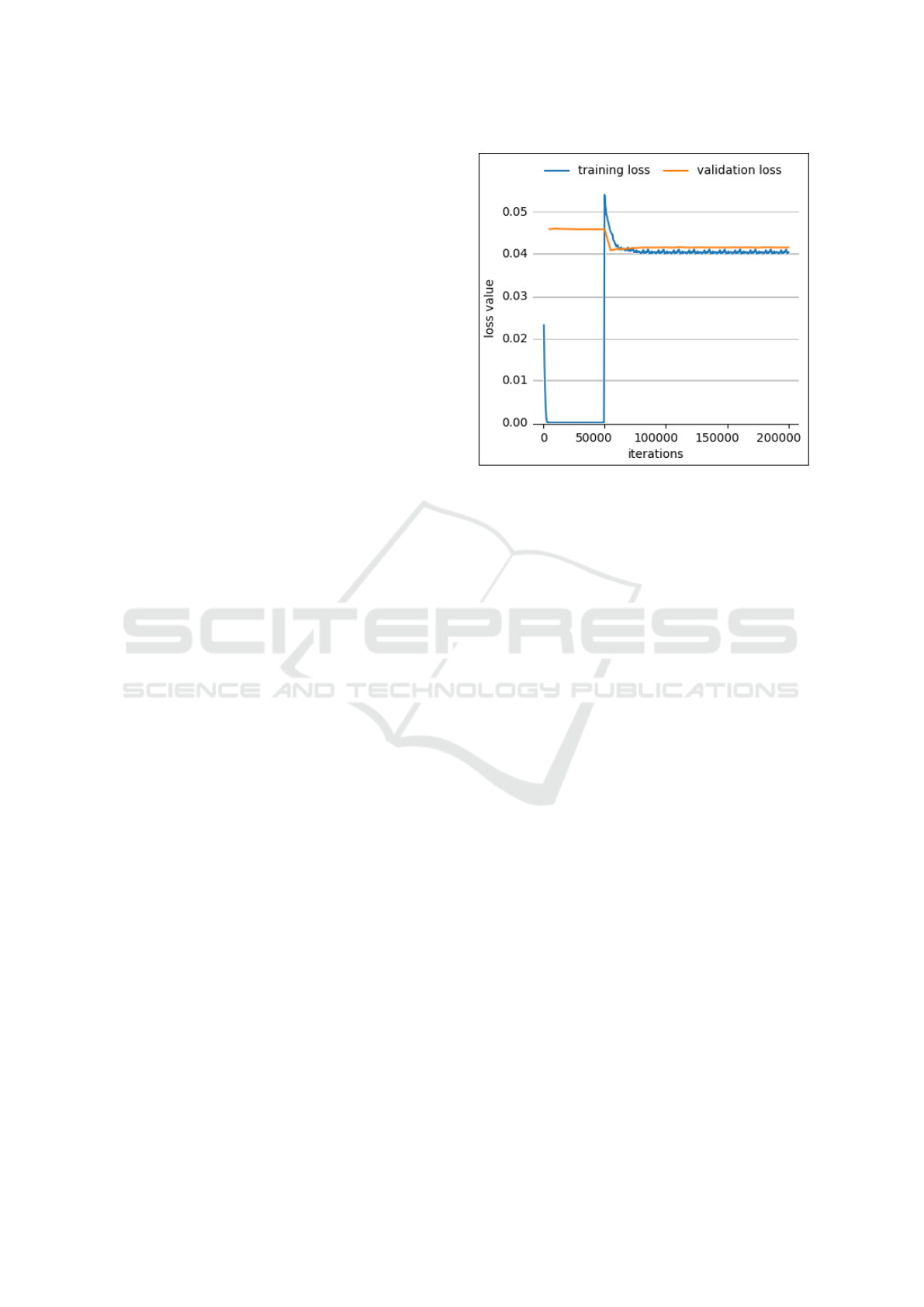
sented in Section 1. Figure 4 renders the learning

curve for that training process, that is the loss value

for different iteration numbers.

The 100 individuals selected for training (menti-

oned in subsection 4.1) have been coupled with each

other to form a huge number of positive and negative

pairs. This large set of samples has been divided into a

training and a cross-validation set in a 70%-30% pro-

portion.

Although the proposed algorithm has been trained

only using the training set, the loss value, for both the

training and the cross-validation sets, has been repre-

sented, in blue and orange respectively.

The training loss quickly decreases during the ﬁrst

iterations until it almost achieves the value zero. Ho-

wever, in the iteration 50000 the loss value is drasti-

cally increased. The reason is that 50000, is the value

of the iteration threshold, T

, taken by the connection

function, deﬁned by (2). From that iteration, the Ma-

halanobis distance is used as metric distance, dm, to

feed the loss function, (13), instead of the Euclidean

distance, previously used.

Even though the training loss is really low in

the ﬁrst iterations, that is not the case for the cross-

validation loss. That means the networks have been

over-ﬁtted and the algorithm does not generalises pro-

perly with new samples.

Figure 4: Learning Curve.

Therefore, the model learnt in further iterations,

for instance in the iteration 200,000, has been the one

chosen as deﬁnitive to do the experiments, because

both losses values achieve a certain balance at that

point since the validation loss is also reduced from

the iteration T

This means that the algorithm is able to give a ge-

neralised solution for unknown samples (the test sam-

ples). This fact is due to the proposed Discriminative

Data Structure Analysis, Subsection 3.7, to learn the

Mahalanobis matrix, which codes the view variations

from the two different cameras sets.

4.3 Evaluation Metric

To evaluate the proposed DPSL, a standard re-id

performance measurement has been calculated, the

Cumulative Matching Characteristic (CMC) curve

(Moon and Phillips, 2001).

To obtain the CMC curve, ﬁrst, every image from

the probe set is coupled with all the images from the

gallery set and the corresponding distance metrics,

dm, are computed. Both sets were deﬁned in Sub-

section 4.1.

Then the CMC curve renders the expectation of

ﬁnding the correct match within the top r matches,

for different values of r, called rank. The matches

presenting the lowest values for dm are considered as

the top matches.

4.4 Experimental Results

In order to analyse the effects of using the Mahala-

nobis distance to measure the similarity between two

Deep Parts Similarity Learning for Person Re-Identiﬁcation

425

person images, we have tested our, Deep Parts Simi-

larity Learning, DPSL, algorithm using both, the Ma-

halanobis and the Euclidean distance as distance me-

trics.

The resulting CMC scores are presented in Table 1

and their corresponding curves are rendered in Figure

5 to make easier a visual comparison.

The scores are generally better for the use of

the Mahalanobis distance, especially in the ﬁrsts

ranks which are the most critical ones for the re-

identiﬁcation task. The reason is that the Mahalanobis

matrix codes the visual camera-to-camera transitions

making the Mahalanobis distance able to cope with

the intra-class variations.

Moreover, with the aim of studying the advanta-

ges of using a deep learning approach to select the

proper features, the Table 1 and Figure 5 also show

the results given by the algorithm presented in (Hirzer

et al., 2012), since this uses low-level features (LLF)

based on colour and texture and they are compared

using also the Euclidean distance as distance metric.

Table 1: CMC scores(in [%]) for different feature extraction

approaches and distances.

Method r=1 10 20 50 100

DPSL+Mahalanobis 7 31 36 49 63

DPSL+Euclidean 4 24 31 48 69

LLF+Euclidean 3 10 14 28 45

Figure 5: CMC curves for different feature extraction ap-

proaches and distances.

The proposed DPSL framework produces better

results because it automatically ﬁnds the most salient

features, which causes a remarkable improvement

with respect to the use of low-level hand-crafted fe-

atures.

The main contributions of the proposed DPSL fra-

mework are the deeply learnt weighting, and the dis-

criminative data structure analysis to learn the Maha-

lanobis matrix. For that reason, two methods compa-

risons have been performed with other state-of-the-art

algorithms.

For the ﬁrst comparison, the following weighting

algorithms have been evaluated and compared with

the proposed DPSL: two Global Feature Importance

(GFI) based methods, the Ranking Support Vector

Machines (Rank-SVM), (Prosser et al., 2010), and

Probabilistic Relative Distance Comparison (PRDC),

(Zheng et al., 2011), and the fusion of both with the

Prototype-Sensitive Feature Importance based met-

hod presented in (Liu et al., 2014).

The obtained CMC scores, for the ﬁrst ranks, are

listed in Table 2 and the corresponding curves are ren-

dered in Figure 6 to provide a more intuitive compa-

rison representation.

Table 2: Comparison of CMC scores(in [%]) for different

weighting methods.

Method r=1 5 10 20 50

DPSL 7 17 31 36 49

PSFI+PRDC 3 9 16 24 39

PRDC 3 10 15 23 38

PSFI+RankSVM 4 9 13 20 32

RankSVM 4 9 13 19 32

Figure 6: Comparison of CMC curves for different weig-

hting methods.

The proposed DPSL method produces a consi-

derable improvement of the re-identiﬁcation perfor-

mance, as the CMC scores prove. This is due to the

fact of using a fully connected layer which automa-

tically ﬁnds the best weights for each one of the ex-

tracted body part features to combine them forming a

proper person descriptor.

For the second comparison, the Linear Discri-

minant Analysis (LDA) (Fisher, 1936) and Logistic

Discriminant Metric Learning (LDML) (Guillaumin

et al., 2009) algorithms have been tested, which fol-

low a probabilistic approach. The obtained CMC sco-

res are listed in Table 3 and the corresponding curves

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

426

Table 3: Comparison of CMC scores(in [%]) for different

discriminant distance learning methods.

Method r=1 10 20 50 100

DPSL 7 31 36 49 63

LDA 4 14 21 35 48

LDML 2 6 11 19 32

Figure 7: Comparison of CMC curves for different discri-

minant distance learning methods.

are shown in Figure 7.

The CMC scores have been enhanced with the

DPSL method thanks to the adaptive process of

data analysing, conducted in every learning iteration,

which considers the discriminative information given

by the samples labels to create two different features

spaces. One of the features spaces represents the si-

milarity class and the other the dissimilarity class, and

from both, the covariance matrices have been com-

puted and used to code the view-to-view transforma-

tions, related to changes in illumination, resolution,

point of view, etc. All this information is encompas-

sed in the Mahalanobis matrix, reducing the effect of

the intra-class variation and making easier the task re-

identiﬁcation, whose performance has been remarka-

bly improved by the proposed approach.

5 CONCLUSIONS

The goal of the presented work was to address the per-

son re-identiﬁcation problem through a Deep Parts Si-

milarity Learning (DPSL) framework, which uniﬁes

the feature and metric selections tasks.

The re-identiﬁcation of a person in two images be-

comes a important challenge when both representa-

tions are signiﬁcantly dissimilar, causing intra-class

variations. Some of such variations, like the presen-

ted in resolution, scale, illumination or point of view,

are due to the different location and speciﬁcations of

each one of the cameras. Those view-to-view tran-

sitions can be learnt and considered during the re-

identiﬁcation task to make it easier and improve its

performance.

In this paper, the Mahalanobis matrix has been

proposed to code such information, so the Mahalano-

bis distance has been used to compute the degree of

similarity between a pair of images. The estimation

of that matrix has been conducted with a Discrimi-

native Data Structure Analysis layer, which has been

integrated into the learning framework. In that way

the features and the Mahalanobis matrix learning take

advantage of each other, improving and accelerating

both learning processes simultaneously. This solution

has been compared with other Discriminant Distance

Learning methods, providing successful results.

In addition, the presented uniﬁed approach has al-

lowed solving the problem of over-ﬁtting in the fea-

tures learning process, as it has been proved with the

representation of its learning curve.

On the other hand, the variations caused by the

different backgrounds and poses in the images to

compare, have been minimised thanks to a ﬁrst layer,

which extracts several body parts, independently from

the images scale. This parts extraction layer is based

on a Convolutional Pose Machine (CPM), (Wei et al.,

2016), and it has been integrated into the feature lear-

ning framework, improving the selection of the most

salient features.

The extraction of features for each body part has

been also addressed with the training of deep con-

volutional neural networks, where the use of a fully

connected layer automatically weighs the descriptors

to get the optimal person representation. The evalua-

tion of this approach has resulted in a remarkable im-

provement of the re-identiﬁcation performance with

respect to other feature selection and weighting met-

hods.

In summary, all these contributions have been uni-

ﬁed in a Deep Part Similarity Learning algorithm,

which follows a Siamese Network architecture. The

proposed approach provides a novel method for me-

asuring the appearance similarity between two per-

son images, which successfully addresses the re-

identiﬁcation problem, as the experiments have pro-

ved with hopeful and prominent results.

ACKNOWLEDGEMENTS

This work was supported by the Spanish Government

through the CICYT project (TRA2013-48314-C3-1-

R), (TRA2015-63708-R) and Ministerio de Educa-

cin, Cultura y Deporte para la Formacin de Profeso-

rado Universitario (FPU14/02143), and Comunidad

Deep Parts Similarity Learning for Person Re-Identiﬁcation

427

de Madrid through SEGVAUTO-TRIES (S2013/MIT-

2713).

REFERENCES

Bazzani, L., Cristani, M., and Murino, V. (2013).

Symmetry-driven accumulation of local features for

human characterization and re-identiﬁcation. Compu-

ter Vision and Image Understanding, 117(2):130–144.

Bazzani, L., Cristani, M., and Murino, V. (2014). Sdalf:

modeling human appearance with symmetry-driven

accumulation of local features. In Person Re-

Identiﬁcation, pages 43–69. Springer.

Chan-Lang, S., Pham, Q. C., and Achard, C. (2016). Bidi-

rectional sparse representations for multi-shot person

re-identiﬁcation. In Advanced Video and Signal Ba-

sed Surveillance (AVSS), 2016 13th IEEE Internatio-

nal Conference on, pages 263–270. IEEE.

Cheng, D. S. and Cristani, M. (2014). Person re-

identiﬁcation by articulated appearance matching. In

Person Re-Identiﬁcation, pages 139–160. Springer.

Felzenszwalb, P. F. and Huttenlocher, D. P. (2005). Pic-

torial structures for object recognition. International

journal of computer vision, 61(1):55–79.

Fisher, R. A. (1936). The use of multiple measurements in

taxonomic problems. Annals of eugenics, 7(2):179–

188.

omez-Silva, M. J., Armingol, J. M., and de la Escalera,

A. (2017). Deep part features learning by a normali-

sed double-margin-based contrastive loss function for

person re-identiﬁcation. In VISIGRAPP (6: VISAPP),

pages 277–285.

Gray, D. and Tao, H. (2008). Viewpoint invariant pede-

strian recognition with an ensemble of localized fea-

tures. Computer Vision–ECCV 2008, pages 262–275.

Guillaumin, M., Verbeek, J., and Schmid, C. (2009). Is that

you? metric learning approaches for face identiﬁca-

tion. In Computer Vision, 2009 IEEE 12th internatio-

nal conference on, pages 498–505. IEEE.

Hirzer, M., Beleznai, C., Roth, P. M., and Bischof, H.

(2011). Person re-identiﬁcation by descriptive and

discriminative classiﬁcation. In Scandinavian confe-

rence on Image analysis, pages 91–102. Springer.

Hirzer, M., Roth, P., K

ostinger, M., and Bischof, H.

(2012). Relaxed pairwise learned metric for person

re-identiﬁcation. Computer Vision–ECCV 2012, pa-

ges 780–793.

Jia, Y., Shelhamer, E., Donahue, J., Karayev, S., Long, J.,

Girshick, R., Guadarrama, S., and Darrell, T. (2014).

Caffe: Convolutional architecture for fast feature em-

bedding. In Proceedings of the 22nd ACM internatio-

nal conference on Multimedia, pages 675–678. ACM.

Khan, F. M. and Br

emond, F. (2016). Unsupervised data

association for metric learning in the context of multi-

shot person re-identiﬁcation. In Advanced Video and

Signal Based Surveillance (AVSS), 2016 13th IEEE In-

ternational Conference on, pages 256–262. IEEE.

Koestinger, M., Hirzer, M., Wohlhart, P., Roth, P. M., and

Bischof, H. (2012). Large scale metric learning from

equivalence constraints. In Computer Vision and Pat-

tern Recognition (CVPR), 2012 IEEE Conference on,

pages 2288–2295. IEEE.

Layne, R., Hospedales, T. M., and Gong, S. (2014).

Attributes-based re-identiﬁcation. In Person Re-

Identiﬁcation, pages 93–117. Springer.

Liu, C., Gong, S., Loy, C. C., and Lin, X. (2014). Evaluating

feature importance for re-identiﬁcation. In Person Re-

Identiﬁcation, pages 203–228. Springer.

Ma, B., Su, Y., and Jurie, F. (2014). Discriminative image

descriptors for person re-identiﬁcation. In Person Re-

Identiﬁcation, pages 23–42. Springer.

Moon, H. and Phillips, P. J. (2001). Computational and

performance aspects of pca-based face-recognition al-

gorithms. Perception, 30(3):303–321.

Munaro, M., Fossati, A., Basso, A., Menegatti, E.,

and Van Gool, L. (2014). One-shot person re-

identiﬁcation with a consumer depth camera. In Per-

son Re-Identiﬁcation, pages 161–181. Springer.

Oreifej, O., Mehran, R., and Shah, M. (2010). Human iden-

tity recognition in aerial images. In Computer Vision

and Pattern Recognition (CVPR), 2010 IEEE Confe-

rence on, pages 709–716. IEEE.

Prosser, B., Zheng, W.-S., Gong, S., Xiang, T., and Mary,

Q. (2010). Person re-identiﬁcation by support vector

ranking. In BMVC, volume 2, page 6.

Roth, P. M., Hirzer, M., K

ostinger, M., Beleznai, C., and

Bischof, H. (2014). Mahalanobis distance learning for

person re-identiﬁcation. In Person Re-Identiﬁcation,

pages 247–267. Springer.

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1988).

Learning representations by back-propagating errors.

Cognitive modeling, 5(3):1.

anchez, J., Perronnin, F., Mensink, T., and Verbeek, J.

(2013). Image classiﬁcation with the ﬁsher vector:

Theory and practice. International journal of com-

puter vision, 105(3):222–245.

Wei, S.-E., Ramakrishna, V., Kanade, T., and Sheikh, Y.

(2016). Convolutional pose machines. In Proceedings

of the IEEE Conference on Computer Vision and Pat-

tern Recognition, pages 4724–4732.

Yi, D., Lei, Z., Liao, S., and Li, S. Z. (2014). Deep me-

tric learning for person re-identiﬁcation. In Pattern

Recognition (ICPR), 2014 22nd International Confe-

rence on, pages 34–39. IEEE.

Zhang, Y. and Li, S. (2011). Gabor-lbp based region covari-

ance descriptor for person re-identiﬁcation. In Image

and Graphics (ICIG), 2011 Sixth International Confe-

rence on, pages 368–371. IEEE.

Zheng, W.-S., Gong, S., and Xiang, T. (2011). Person re-

identiﬁcation by probabilistic relative distance com-

parison. In Computer vision and pattern recognition

(CVPR), 2011 IEEE conference on, pages 649–656.

IEEE.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

428