
Overcoming the Curse of Dimensionality
When Clustering Multivariate Volume Data
Vladimir Molchanov
1
and Lars Linsen
1,2
1
Jacobs University, Bremen, Germany
2
Westf
¨
alische Wilhelms-Universit
¨
at M
¨
unster, M
¨
unster, Germany
Keywords:
Multi-dimensional Data Visualization, Multi-field Data, Clustering.
Abstract:
Visual analytics of multidimensional data suffer from the curse of dimensionality, i.e., that even large numbers
of data points will be scattered in a high-dimensional space. The curse of dimensionality prohibits the proper
use of clustering algorithms in the high-dimensional space. Projecting the space before clustering imposes a
loss of information and possible mixing of separated clusters. We present an approach where we overcome
the curse of dimensionality for a particular type of multidimensional data, namely for attribute spaces of
multivariate volume data. For multivariate volume data, it is possible to interpolate between the data points in
the high-dimensional attribute space based on their spatial relationship in the volumetric domain (or physical
space). We apply this idea to a histogram-based clustering algorithm. We create a uniform partition of the
attribute space in multidimensional bins and compute a histogram indicating the number of data samples
belonging to each bin. Only non-empty bins are stored for efficiency. Without interpolation, the analysis is
highly sensitive to the cell sizes yielding inaccurate clustering for improper choices: Large cells result in no
cluster separation, while clusters fall apart for small cells. Using tri-linear interpolation in physical space,
we can refine the data by generating additional samples. The refinement scheme can adapt to the data point
distribution in attribute space and the histogram’s bin size. As a consequence, we can generate a density
computation, where clusters stay connected even when using very small cell sizes. We exploit this result to
create a robust hierarchical cluster tree. It can be visually explored using coordinated views to physical space
visualizations and to parallel coordinates plots. We apply our technique to several datasets and compare the
results against results without interpolation.
1 INTRODUCTION
Visualization of multivariate volume data has become
a common, yet still challenging task in scientific vi-
sualization. Data sets come from traditional scien-
tific visualization applications such as numerical sim-
ulations, see VisContest 2008 (Whalen and Norman,
2008), or medical imaging, see VisContest 2010 (Vis,
2010). While looking into individual attributes can
be of high interest, the full phenomena are often only
captured when looking into all attributes simultane-
ously. Consequently, visualization methods shall al-
low for the investigation and analysis of the multidi-
mensional attribute space. The attribute space may
consist of measured and/or simulated attributes as
well as derived attributes including statistical proper-
ties (e.g., means, variances) or vector and tensor field
properties (e.g., divergence, finite time Lyupanov ex-
ponent, diffusion tensor eigenvalues). Hence, we are
facing a multidimensional data analysis task, where
dimension here refers to the dimensionality of the at-
tribute space.
Multidimensional data analysis typically requires
some automatic components that need to be used
to produce a visual encoding. Typical components
are clustering approaches or projections from higher-
dimensional spaces into 2D or 3D visual spaces. Of-
ten, clustering and projections are combined to pro-
duce a visualization of a clustering result. The clus-
tering approach shall be applied first to produce high-
dimensional clusters, which can be used as an input
for an improved projection. Unfortunately, clustering
in a high-dimensional space faces the problem that
points belonging to the same cluster can be rather
far apart in the high-dimensional space. This obser-
vation is due to the curse of dimensionality, a term
coined by Bellman (Bellman, 1957). It refers to the
fact that there is an exponential increase of volume
when adding additional dimensions.
The impact of the curse of dimensionality on prac-
Molchanov, V. and Linsen, L.
Overcoming the Curse of Dimensionality When Clustering Multivariate Volume Data.
DOI: 10.5220/0006541900290039
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages 29-39
ISBN: 978-989-758-289-9
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
29

tical issues when clustering high-dimensional data is
as follows: Clustering approaches can be categorized
as being based on distances between data points or
being based on density estimates. However, only
distance-based clustering algorithms can effectively
detect clusters of arbitrary shape. Distance-based
clustering approaches require local density estimates,
which are typically based on space partitioning (e.g.,
over a regular or an adaptive grid) or on a kernel func-
tion. Both grid-based and kernel-based approaches
require the choice of an appropriate size of locality
for density estimation, namely, the grid cell size or
the kernel size, respectively. Using a too large size
leads to not properly resolving the clusters such that
clusters may not be separated. Hence, a small size is
required. However, due to the curse of dimensional-
ity, clusters fall apart when using a too small size and
one ends up with individual data points rather than
clusters thereof.
Attribute spaces of multivariate volume data are
a specific case of multidimensional data, as the un-
structured data points in attribute space do have a
structure when looking into the corresponding phys-
ical space. We propose to make use of this struc-
ture by applying interpolation between attribute-space
data points whose corresponding representations in
physical space exhibit a neighbor relationship.
The overall approach presented in this paper takes
as input a multivariate volume data set. First, it
applies an interpolation scheme to upsample the at-
tribute space, see Section 4 for the main idea, Sec-
tion 5 for an improved computation scheme, and Sec-
tion 6 for an amendment to handle sharp material
boundaries. The upsampled attribute space is, then,
clustered using a hierarchical density-based cluster-
ing approach, see Section 3. Based on the clustering
result, Section 7 describes how a combined visual ex-
ploration of physical and attribute space using coor-
dinated views can be employed. The results of the
approach are presented in Section 8 and its proper-
ties are discussed in Section 9. It is shown that our
approach manages to produce high-quality clustering
results without the necessity of tweaking the grid cell
size or similar. We also document that comparable re-
sults cannot be obtained when clustering without the
proposed interpolation step. The linked volume vi-
sualization, therefore, reflects the phenomena in the
multivariate volume data more reliably.
2 RELATED WORK
2.1 Multivariate Volume Data
Visualization
Traditionally, spatial data visualization focuses on
one attribute, which may be scalar, vector, or tensor-
valued. In the last decade, there was an increase on
attempts to generalize the visualization methods to
multivariate volume data that allow for the visual ex-
traction of multivariate features. Sauber et al. (Sauber
et al., 2006) suggested to use multigraphs to gener-
ate combinations of multiple scalar fields, where the
number of nodes in the graph increase exponentially
with the number of dimensions. Similarly, Woodring
and Chen (Woodring and Shen, 2006) allowed for
boolean set operations of scalar field visualization. In
this context, Akiba and Ma (Akiba and Ma, 2007) and
Blaas et al. (Blaas et al., 2007) were the first who
used sophisticated visualization methods and inter-
action in the multi-dimensional attribute space. Ak-
iba and Ma (Akiba and Ma, 2007) suggested a tri-
space visualization that couples parallel coordinates
in attribute space with volume rendering in physi-
cal space in addition to one-dimensional plots over
time. Blaas et al. (Blaas et al., 2007) use scatter
plots in attribute space, where the multi-dimensional
data is projected into arbitrary planes. Daniels II et
al. (Daniels II et al., 2010) presented an approach for
interactive vector field exploration by brushing on a
scatterplot of derived scalar properties of the vector
field, i.e., a derived multivariate attribute space. How-
ever, their interactive attribute space exploration ap-
proach does not scale to higher-dimensional attribute
spaces. Other approaches are based on statistics rather
than interactive visual feature extraction: J
¨
anicke et
al. (J
¨
anicke et al., 2007) use statistical measures to de-
tect regions of a certain behavior in multi-dimensional
volume data, while Oeltze et al. (Oeltze et al., 2007)
use correlation and principal component analysis to
visualize medical perfusion data.
Recently, there has been the approach to couple
attribute space clustering with visual interactive ex-
ploration of multivariate volume data. Maciejewski
et al. (Maciejewski et al., 2009) developed multi-
dimensional transfer functions for direct volume ren-
dering using 2D and 3D histograms and density-based
clustering within these histograms. Since interactions
with the histograms are necessary for visual anal-
ysis of the data, their approach is restricted to at-
tribute spaces of, at most, three dimensions. Linsen et
al. (Linsen et al., 2008; Linsen et al., 2009) proposed
an approach that can operate on multivariate volume
data with higher-dimensional attribute spaces. The at-
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
30

tribute space is clustered using a hierarchical density-
based approach and linked to physical-space visual-
ization based on surface extraction. Recently, the ap-
proach was extended by Dobrev et al. (Dobrev et al.,
2011) to an interactive analysis tool incorporating di-
rect volume rendering. Dobrev et al. show that the
generated clustering result is often not as desired and
propose interactive means to fix the clustering result.
In this paper, we make use of the same clustering ap-
proach, see Section 3, and show how we can improve
the results with the methods proposed here.
2.2 Clustering
Cluster analysis divides data into meaningful or use-
ful groups (clusters). Clustering algorithms can be
categorized with respect to their properties of being
based on partitioning, hierarchical, based on density,
or based on grids (Jain and Dubes, 1988; Han and
Kamber, 2006). In partitioning methods, data sets are
divided into k clusters and each object must belong to
exactly one cluster. In hierarchical methods, data sets
are represented using similarity trees and clusters are
extracted from this hierarchical tree. In density-based
methods, clusters are a dense region of points sepa-
rated by low-density regions. In grid-based methods,
the data space is divided into a finite number of cells
that form a grid structure and all of the clustering op-
erations are performed on the cells.
Hartigan (Hartigan, 1975; Hartigan, 1985) first
proposed to identify clusters as high density clusters
in data space. Wong and Lane (Wong and Lane, 1983)
define neighbors for each data point in data space
and use the kth nearest neighbors to estimate density.
After defining dissimilarity between neighboring pat-
terns, a hierarchical cluster tree is generated by ap-
plying a single-linkage algorithm. In their paper, they
show that the high density clusters are strongly con-
sistent. However, they do not examine modes of the
density function.
Ester et al. (Ester et al., 1996) introduced the DB-
SCAN algorithm. The first step of the DBSCAN
algorithm is to estimate the density using an E ps-
neighborhood (like a spherical density estimate). Sec-
ond, DBSCAN selects a threshold level set MinPts
and eliminates all points with density values less than
MinPts. Third, a graph is constructed based on the
two parameters E ps and MinPts. Finally, high den-
sity clusters are generated by connected components
of the graph. The drawback is the need to define
appropriate parameters. Hinneburg and Keim in-
troduced the DENCLUE approach (Hinneburg and
Keim, 1998), where high density clusters are identi-
fied by determining density attraction. Hinneburg et
al. further introduced the HD-Eye system (Hinneburg
et al., 1999) that uses visualization to find the best
contracting projection into a one- or two-dimensional
space. The data are divided based on a sequence of
the best projections determined by the high density
clusters. The advantage of this method is that it does
not divide regions of high density.
Ankerst et al. (Ankerst et al., 1999) introduced the
OPTICS algorithm, which computes a complex hi-
erarchical cluster structure and arranges it in a lin-
ear order that is visualized in the reachability plot.
Stuetzle (Stuetzle, 2003) also used a nearest neighbor
density estimate. A high density cluster is generated
by cutting off all minimum spanning tree edges with
length greater than a specific parameter (depending
on the level-set value of the density function). Stuet-
zle and Nugent (Stuetzle and Nugent, 2007) proposed
to construct a graph whose vertices are patterns and
whose edges are weighted by the minimum value of
the density estimates along the line segment connect-
ing the two vertices. The disadvantage of this hierar-
chical density-based approach is that the hierarchical
cluster tree depends on a threshold parameter (level-
set value) that is difficult to determine.
We use a hierarchical density-based approach that
computes densities over a grid. The main advantage
of our approach is the direct identification of clusters
without any threshold parameter of density level sets.
Moreover, it is quite efficient and scales well. The
main idea of the approach is described in Section 3.
For a detailed analysis and comparison to other clus-
tering approaches, which is beyond the scope of this
paper, we refer to the literature (Long, 2009).
2.3 Interpolation in Attribute Space
Our main idea is based on interpolation in attribute
space, which is possible due to a meaningful neigh-
borhood structure in physical space that can be im-
posed onto the attribute space. Similar observations
have been used in the concept of continuous scatter-
plots (Bachthaler and Weiskopf, 2008; Bachthaler and
Weiskopf, 2009; Heinrich et al., 2011; Lehmann and
Theisel, 2010; Lehmann and Theisel, 2011). Con-
tinuous scatterplots generalize the concept of scatter-
plots to the visualization of spatially continuous in-
put data by a continuous and dense plot. The high-
dimensional histograms we create can be regarded
as a generalization of the 2D continuous histograms
created by Bachthaler and Weiskopf (Bachthaler
and Weiskopf, 2008). It is a more difficult prob-
lem to compute continuous histograms in higher-
dimensional spaces. However, in the end, we only
need a discrete sampling of the continuous histogram.
Overcoming the Curse of Dimensionality When Clustering Multivariate Volume Data
31

Hence, our computations do not aim at computing
continuous histograms, but rather stick to operating
on a discrete setting.
3 CLUSTERING
We present a hierarchical density cluster construction
based on nonparametric density estimation using mul-
tivariate histograms. Clusters can be identified with-
out any threshold parameter of density level sets. Let
the domain of the attribute space be given in form
of a d-dimensional hypercube, i.e., a d-dimensional
bounding box. To derive the density function, we spa-
tially subdivide the domain of the data set into cells
(or bins) of equal shape and size. Thus, the spa-
tial subdivision is given in form of a d-dimensional
regular structured grid with equidistant d-dimensional
grid points, i.e., a d-dimensional histogram. For each
bin of the histogram, we count the number of sample
points lying inside. The multivariate density function
is estimated by the formula
f (x) =
n
bin
n ·A
bin
for any x within the cell, where n is the overall number
of data points, n
bin
is the number of data points inside
the bin, and A
bin
is the area of the d-dimensional bin.
As the area A
bin
is equal for all bins, the density of
each bin is proportional to the number n
bin
of data
points lying inside the bin. Hence, it suffices to just
operate with those numbers n
bin
.
To estimate all non-empty bins, we use a parti-
tioning algorithm that iterates through all dimensions.
Figure 1 illustrates the partition process for a two-
dimensional data set: The first dimension is divided
into 5 equally-sized intervals on the left-hand side of
Figure 1. Only four non-empty intervals are obtained.
These intervals are subsequently divided in the sec-
ond dimension, as shown on the right-hand side of
Figure 1. The time complexity for partitioning the
data space is O(nd), i.e., it can handle both data sets
with large number of samples n and data sets with
high dimensionality d.
Given the d-dimensional histogram, clusters are
defined as largest sets of neighboring non-empty bins,
where neighboring refers to sharing a common vertex.
To detect higher-density clusters within each cluster,
we remove all cells containing the minimum number
of points in this cluster and detect among the remain-
ing cells, again, largest sets of neighboring cells. This
step may lead to splitting of a cluster into multiple
higher-density clusters. This process is iterated until
no more clusters split. Recording the splitting infor-
mation, we obtain a cluster hierarchy. Those clusters
Figure 1: Grid partition of two-dimensional data set: The
space is divided into equally-sized bins in the first dimen-
sion (left) and the non-empty bins are further subdivided in
the second dimensions (right).
that do not split anymore represent local maxima and
are referred to as mode clusters. Figure 2 (left) shows
a set of non-empty cells with six different density lev-
els in a two-dimensional space. First, we find the two
low-density clusters as connected components of non-
empty cells. They are represented in the cluster tree
as immediate children nodes of the root node (cyan
and yellow), see Figure 2 (right). From the cluster
colored cyan, we remove all minimum density level
cells (cyan). The cluster remains connected. Then,
we again remove the cells with minimum density level
(green). The cluster splits into three higher-density
clusters (red, magenta, and blue). They appear as chil-
dren nodes of the cyan node in the cluster tree. As
densities are given in form of counts of data points,
they are always natural numbers. Consequently, we
cannot miss any split of a density cluster when iterat-
ing over the natural numbers (from zero to the maxi-
mum density). The time complexity to create a hier-
archical density cluster tree is O(m
2
), where m is the
number of non-empty cells.
Figure 2: Left: Grid partition of two-dimensional data set
with six different density levels. Right: Respective density
cluster tree with four modes shown as leaves of the tree.
Figure 3 shows that the clustering approach is ca-
pable of handling clusters of any shape and that it
is robust against changing cluster density and noise.
Noise has been handled by removing all cells with a
number of sample points smaller than a noise thresh-
old. The data set is a synthetic one (Karypis et al.,
1999). Figure 4 shows the visualization of a cluster
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
32
hierarchy for the “out5d” data set with 16,384 data
points and five attributes, namely, spot (SPO), mag-
netics (MAG), potassium (POS), thorium (THO), and
uranium (URA), using a projection in optimized 2D
star coordinates (Long, 2009). The result seems fea-
sible and all clusters were found without defining any
density thresholds, but the choice of the bin size had
to be determined empirically in an interactive visual
analysis using coordinated views as described in this
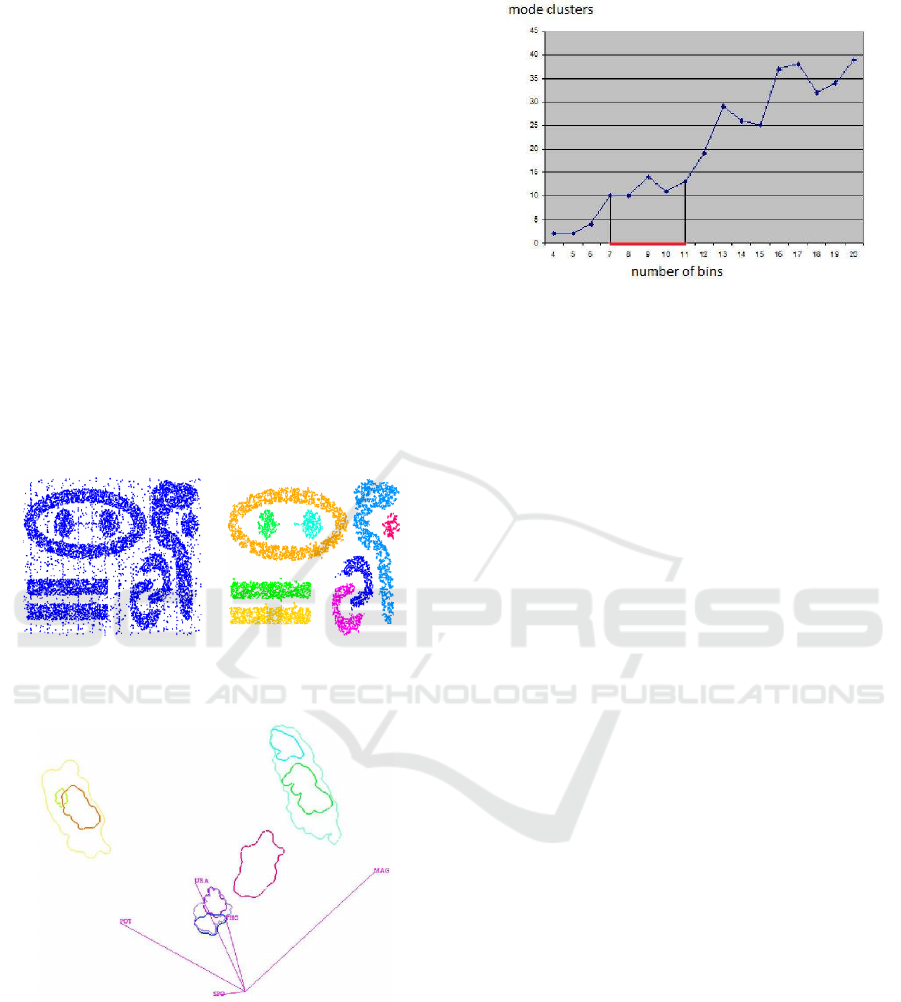
paper. Figure 5 shows how sensitive the result is to the
bin size: Using smaller bin sizes merges some clus-
ters, while using larger sizes makes clusters fall apart.
The result in Figure 4 was obtained using the heuris-
tic that cluster numbers only vary slowly close to the
optimal bin size value (area marked red in Figure 4).
However, in practice one would not generate results
for the entire range of possible bin sizes for being able
to apply this heuristic. Instead, one would rather use
a trial-and-error approach, not knowing how reliable
the result is.
Figure 3: Clustering of arbitrarily shaped clusters. Left:
Original data set. Right: Histogram-based clustering result.
Figure 4: Visualization of cluster hierarchy in optimized 2D
star coordinates.
4 INTERPOLATION
Let the attribute values of the multivariate volume
data be given at points p
i
, i = 1,...,n, in physical
space. Moreover, let a
j
(p
i
), j = 1,...,d, be the at-
tribute values at p
i
. Then, the points p
i
exhibit some
Figure 5: Sensitivity of clustering results with respect to the
bin size. The graph plots the number of mode clusters over
the number of bins per dimension.
neighborhood relationship in physical space. Typi-
cally, this neighborhood information is given in form
of grid connectivity, but even if no connectivity is
given, meaningful neighborhood information can be
derived in physical space by looking at distances (e.g.,
nearest neighbors or natural neighbors). Based on
this neighborhood information, we can perform an
interpolation to reconstruct a continuous multivari-
ate field over the volumetric domain. In the follow-
ing, we assume that the points p
i
are given in struc-
tured form over a regular (i.e., rectangular) hexahe-
dral grid. Thus, the reconstruction of a continuous
multivariate field can be obtained by simple trilinear
interpolation within each cuboid cell of the underly-
ing grid. More precisely: Let q be a point inside a
grid cell with corner points p
uvw
, u,v,w ∈ {0,1}, and
let (q
x
,q
y
,q
z
) ∈ [0,1]
3
be the local Cartesian coordi-
nates of q within the cell. Then, we can compute the
attribute values at q by
a
j
(q) =
1
∑
u=0
1
∑
v=0
1
∑
w=0
q
u
x
q
v
y
q
w
z
(1 −q
x
)
1−u
(1 −q
y
)
1−v
(1 −q
z
)
1−w
a
j
(p
uvw
)
for all attributes ( j = 1,...,d). In attribute
space, we obtain the point (a
1
(q),...,a
d
(q)), which
lies within the convex hull of the set of points
(a
1
(p
uvw
),...,a
d
(p
uvw
)), u,v,w ∈ {0,1}.
Now, we want to use the interpolation scheme to
overcome the curse of dimensionality when creating
the d-dimensional density histogram. Using the tri-
linear interpolation scheme, we reconstruct the mul-
tivariate field within each single cell, which corre-
sponds to a reconstructed area in attribute space. The
portion r ∈ [0, 1] by which the reconstructed area in
attribute space falls into a bin of the d-dimensional
density histogram defines the amount of density that
should be added to the respective bin of the histogram.
Overcoming the Curse of Dimensionality When Clustering Multivariate Volume Data
33

Under the assumption that each grid cell has volume
1
c
, where c is the overall number of grid cells, one
should add the density r ·
1
c
to the respective bin of
the histogram. However, we propose to not com-
pute r exactly for two reasons: First, the computa-
tion of the intersection of a transformed cuboid with
a d-dimensional cell in a d-dimensional space can be
rather cumbersome and expensive. Second, the re-
sulting densities that are stored in the bins of the his-
togram would no longer be natural numbers. The
second property would require us to choose density
thresholds for the hierarchy generation. How to do
this without missing cluster splits is an open question.
Our approach is to approximate the reconstructed
multivariate field by upsampling the given data set.
This discrete approach is reasonable, as the output
of the reconstruction/upsampling is, again, a discrete
structure, namely a histogram. We just need to as-
sure that the rate for upsampling is high enough such
that the histogram of an individual grid cell has all
non-empty bins connected. Thus, the upsampling rate
depends on the size of the histogram’s bins. More-
over, if we use the same upsampling rate for all grid
cells, density can still be measured in form of number
of (upsampled) data points per bin. Hence, the gen-
eration of the density-based cluster hierarchy is still
working as before.
Figure 6 shows the impact of upsampling in the
case of a 2D physical space and a 2D attribute space,
i.e., for a transformed 2D cell with corners a
uv
=
(a
1
(p
uv
),...,a
d
(p
uv
)), u, v ∈ {0,1}, and a histogram
with d = 2 dimensions. Without the upsampling, the
non-empty bins of the histogram are not connected.
After upsampling, the bins between the original non-
empty bins have also been filled and the 2D cell rep-
resents a continuous region in the 2D attribute space.
00
10
a
a
a
11
01
a
00
10
a
a
a
11
01
a
Figure 6: Upsampling for a 2D physical space and a 2D
attribute space. Left: The corner points of the 2D cell corre-
spond to bins of the histogram that are not connected. Right:
After upsampling, the filled bins of the histogram are con-
nected.
When performing the upsampling for all cells of
the volumetric grid, we end up with a histogram,
where all non-empty cells are connected. Hence, we
have overcome the curse of dimensionality. On such a
histogram, we can generate the density-based cluster
hierarchy without the effect of clusters falling apart.
5 ADAPTIVE SCHEME
In order to assure connectivity of non-empty his-
togram bins, we have to upsample in some regions
more than in other regions. As we want to have a
global upsampling rate, some regions may be over-
sampled. Such an oversampling is not a problem in
terms of correctness, but a waste of computation time.
To reduce computation time, we propose to use an
adaptive scheme for upsampling. Since we are deal-
ing with cuboid grid cells, we can adopt an octree
scheme: Starting with an original grid cell, we up-
sample with a factor of two in each dimension. The
original grid cell is partitioned into eight subcells of
equal size. If the corners of a subcell S all corre-
spond to one and the same histogram bin B, i.e., if
(a
1
(p
uvw
),...,a
d
(p
uvw
)) fall into the same bin B for
all corners p
uvw
, then we can stop the partitioning S.
If the depth of the octree is d
max
and we stop parti-
tioning S at depth d
stop
, we increase the bin count (or
density, respectively) of bin B by 8
d
max
−d
stop
. If the
corners of a subcell S do not correspond to the same
histogram bin, we continue with the octree splitting
of S until we reach the maximum octree depth d
max
.
Memory consumption is another aspect that we
need to take into account, since multivariate volume
data per se are already quite big and we further in-
crease the data volume by applying an upsampling.
However, we can march through each original cell,
perform the upsampling for that cell individually, and
immediately add data point counts to the histogram.
Hence, we never need to store the upsampled version
of the full data. However, we need to store the his-
togram, which can also be substantial as bin sizes are
supposed to be small. We handle the histogram by
storing only non-empty bins in a dynamic data struc-
ture.
6 SHARP MATERIAL
BOUNDARIES
Some data like the ones stemming from medi-
cal imaging techniques may exhibit sharp material
boundaries. It is inappropriate to interpolate across
those boundaries. In practice, such abrupt changes
in attribute values may require our algorithm to exe-
cute many interpolation steps. To avoid interpolation
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
34

across sharp feature boundaries, we introduce a user-
specified parameter that defines sharp boundaries. As
this is directly related to the number of interpolation
steps, the user just decides on the respective maximal
number of interpolation steps d
max
. If two neighbor-
ing points in physical space have attribute values that
lie in histogram cells that would not get connected af-
ter d
max
interpolation steps, we do not perform any in-
terpolation between those points. This is important, as
performing some few interpolation steps across sharp
material boundary may introduce noise artifacts lead-
ing to artificial new clusters.
7 INTERACTIVE VISUAL
EXPLORATION
After having produced a clustering result of the at-
tribute space that does not suffer from the curse of
dimensionality, it is, of course, of interest to also in-
vestigate the clusters visually in physical and attribute
space. Hence, we want to visualize, which regions in
physical space belong to which attribute space cluster
and what are the values of the respective attributes.
For visualizing the attribute space clusters we
make use of the cluster tree, see Figure 2 (right), and
visualize it in a radial layout, see Figure 8 (lower
row). The cluster tree functions as an interaction wid-
get to select any cluster or any set of clusters. The
properties of the selected clusters can be analyzed us-
ing a linked parallel coordinates plot that shows the
function values in attribute space, see Figure 10 (mid-
dle row).
The distribution of the selected clusters in volume
space can be shown in a respective visualization of
the physical space. We support both a direct volume
rendering approach and a surface rendering approach.
The 3D texture-based direct volume renderer takes
as input only the density values stemming from the
clustering step and the cluster indices, see (Dobrev
et al., 2011). Similarly, we extract boundary surfaces
of the clusters using a standard isosurface extraction
method, see Figure 10 (bottom). We illuminate our
renderings using normals that have been derived as
gradients from the density field that stems from the
clustering approach.
8 RESULTS
First, we demonstrate on a simple scalar field example
how our approach works and show that the discrete
histogram of interpolated data approaches the contin-
uous analogon as the interpolation depth increases.
Let scalar field f (r) be defined as follows:
f (r) =
br
2
for r ≥ 0.8,
1 else,
b = 0.85/0.8
2
,
where r stands for the Euclidean distance to the center
of domain [−1,1)
3
, see Figure 7 (left). The continu-
ous histogram h(x) can be computed using the rela-
tion
r
Z
0
h(x)dx =
4π
3
f
−1
(r)
3
, 0 ≤ r ≤ 0.8,
which leads to
h(r) =
4π
a
3/2
√
r, 0 ≤ r ≤ 0.8.
The continuous histogram is plotted in Fig-
ure 7 (right). The continuous data are clearly
separated into two clusters, which represent the
interior of a sphere and the background in physical
space. However, when sampling the field at 30
3
regular samples in the physical domain. the use of
100 bins in the attribute space leads to the effect
that the sphere cluster breaks into many small parts.
In Figure 8, we demonstrate how our interpolation
approach corrects the histogram (upper row) and the
respective cluster tree (lower row). The resulting
discrete histograms approach the shape of the contin-
uous one as upsampling depth grows. Depth d
max
= 7
is needed to converge to the correct result of the two
clusters.
0.0
0.2
0.4
0.6
0.8
1.0
r
0.2
0.4
0.6
0.8
1.0
Scalar field
0.0
0.2
0.4
0.6
0.8
1.0
x
1
2
3
4
Histogram
Figure 7: Scalar field distribution (left) and continuous his-
togram (right) for artificial data. Bold vertical line denotes
the scaled Dirac function in the histogram.
Second, we design a volumetric multi-attribute
data set, for which the ground truth is known, show
how the size of bins affects the result of the clustering
procedure and demonstrate that interpolation helps to
resolve the issue. Given physical domain [−1; 1)
3
, we
use the following algebraic surfaces
F
1
(x,y,z) = x
2
−y
2
−5z = 0, (1)
F
2
(x,y,z) = x
2
+ y
2
+ (z −1)z
2
= 0, (2)
see Figure 9 (left). We construct the distributions of
two attributes as functions of algebraic distances to
the surfaces above, i.e.,
f
i
= f
i
(F
i
(x,y,z)), i = 1, . ..,2.
Overcoming the Curse of Dimensionality When Clustering Multivariate Volume Data
35

Figure 8: Discrete histograms with 100 bins each and cluster trees at different interpolation depth for data in Figure 7. Red
bins are local minima corresponding to branching in trees. Interpolation makes histograms approach the form of continuous
distribution and corrects cluster tree.
Functions f
i
are chosen to have a discontinuity or a
large derivative at the origin, respectively, see Fig-
ure 9 (middle). Thus, the surfaces F
i
are cluster
boundaries in the physical space. The distribution
of the attribute values f
i
is shown in a 2D scatter-
plot in Figure 9 (right) when sampling over a regular
grid with 50
3
nodes. The data represent four clus-
ters. Using 10 bins for each attribute to generate the
histogram is not enough to separate all clusters result-
ing in a cluster tree with only 2 clusters as shown in
Figure 10 (upper row). A larger number of bins is
necessary. When increasing the number of bins to 30
for each attribute clusters fall apart due to the curse
of dimensionality, which leads to a noisy result with
too many clusters, see Figure 10 (middle row). How-
ever, applying four interpolation steps fixes the his-
togram. Then, the cluster tree has the desired four
leaves and the boundary for all four clusters are cor-
rectly detected in physical space, see Figure 10 (lower
row).
f
1
f
2
- 1
1
- 1
1
f
1
f
Figure 9: Designing a synthetic dataset: Algebraic surfaces
separate clusters in physical space (left). Functions of al-
gebraic distance to the surfaces (middle) define distribution
of two attributes. The resulting distribution in the attribute
space in form of a 2D scatterplot (right).
Figure 10: Effect of bin size choice and interpolation pro-
cedure on synthetic data with known ground truth. 10
2
bins
are not enough to separate all clusters resulting in a degen-
erate tree (upper row). 30
2
bins are too many to keep clus-
ters together (middle row). Interpolation of data with the
same number of bins corrects the tree (lower row). Cluster
trees, parallel coordinates, and clusters in physical space are
shown in the left, mid, and right columns, correspondingly.
Matching colors are used in the coordinated views to allow
for analyzing correspondences.
Next, we apply our methods to the simulation-
based dataset provided in the 2008 IEEE Visualiza-
tion Design Contest (Whalen and Norman, 2008) and
quantify the gain of (modified) adaptive upsampling.
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
36

We picked time slice 75 of this ionization front in-
stability simulation. We considered the 10 scalar
fields (mass density, temperature, and mass fractions
of various chemical elements). What is of interest
in this dataset are the different regions of the transi-
tion phases between atoms and ions of hydrogen (H)
and helium (He). To reduce computational efforts,
we made use of the symmetry of the data with re-
spect to the y = 124 and the z = 124 planes and re-
stricted consideration to data between x = 275 and
x = 500 localizing the front. When applying the clus-
tering approach to the original attribute space using
a 10-dimensional histogram with 10 bins in each di-
mension, we obtain a cluster tree with 15 mode clus-
ters. The cluster tree and the corresponding paral-
lel coordinates plot are shown in Figure 11(a). Not
all of the clusters are meaningful and some of them
should have been merged to a single cluster. These
mode clusters are not clearly separated when observ-
ing the parallel coordinates plot. After applying our
approach with d
max
= 5, such clusters were merged
leading to 12 modes and a simplified cluster tree. Re-
sults are shown in Figure 11(b). The timings of adap-
tive and non-adaptive upsampling for different inter-
polation depths are given in Table 1. “Modified adap-
tive” upsampling refers to the approach with no up-
sampling across sharp material boundaries, see Sec-
tion sec:sharp. The adaptive schemes lead to a signif-
icant speed up (up to one order of magnitude). All nu-
merical tests presented in this section were performed
on a PC with an Intel Xeon 3.20GHz processor.
Table 1: Computation times for non-adaptive vs. adaptive
upsampling scheme at different upsampling depths (2008
IEEE Visualization Design Contest dataset).
d
max
0 1 2 3 4
Non-adaptive 7.57s 59.84s 488.18s 3929s 27360s
Adaptive 5.99s 27.5s 136.56s 717.04s 3646s
Non-empty bins 1984 3949 6400 9411 12861
Modified adaptive 14.3s 26.0s 80.91s 437.76s 2737s
Non-empty bins 1984 2075 2451 3635 5945
Finally, we demonstrate that scatterplots of up-
sampled data approach the quality of continu-
ous scatterplots as presented by Bachthaler and
Weiskopf (Bachthaler and Weiskopf, 2008) and the
follow-up papers. The “tornado” dataset was sam-
pled on a uniform grid of resolution 128
3
. Similar
to (Bachthaler and Weiskopf, 2008), the magnitude of
the velocity and the velocity in z-direction were taken
as two data dimensions. In Figure 12, we show scat-
terplots of the original data and of the adaptively up-
sampled data with interpolation depth 5. The number
of bins is 300 for each attribute. The quality of the up-
sampled scatterplot is similar to the continuous scat-
terplot presented in (Bachthaler and Weiskopf, 2008).
We would like to note that rigorously speeking, eval-
(a) d
max
= 0, modes: 15 (b) d
max
= 5, modes: 12
Figure 11: Cluster tree (upper row), parallel coordinates
plot (middle row), and physical space visualization (lower
row) for the 2008 IEEE Visualization Design Contest data
set, time slice 75, for original attribute space using a 10-
dimensional histogram (a) before and (b) after interpolation.
Several mode clusters are merged when applying our ap-
proach, which leads to a simplification of the tree and better
cluster separation. Matching colors are used in the coordi-
nated views to allow for analyzing correspondences.
uation of vector magnitude and interpolation are not
commutative operations. Thus, the upsampling with
respect to the first chosen parameter could have sig-
nificant errors in both the continuous and the discrete
setting. However, we intentionally followed this way
to be able to compare our results with results pre-
sented in (Bachthaler and Weiskopf, 2008).
Figure 12: Scatterplots of the “tornado” dataset initially
sampled on 128
3
regular grid. Original data (left) and result
of adaptive upsampling with interpolation depth 5 (right)
are shown.
Overcoming the Curse of Dimensionality When Clustering Multivariate Volume Data
37

9 DISCUSSION
Histogram Bin Size. The size of the bins of the his-
togram can be chosen arbitrarily. Of course, smaller
bin sizes produce better results, as they can resolve
better the shape of the clusters. Too large bin sizes
lead to an improper merging of clusters. In terms of
clustering quality, bin sizes can be chosen arbitrar-
ily small, as very small bin sizes do not affect the
clustering result negatively. However, storing a high-
dimensional histogram with small bin sizes can be-
come an issue. Our current implementation stores the
histogram in main memory, which limits the bin sizes
we can currently handle. This in-core solution allows
us to produce decent results, as we are only storing
non-empty bins. Nevertheless, for future work, it may
still be desirable to implement an out-of-core version
of the histogram generation. This can be achieved
by splitting the histogram into parts and only storing
those parts. However, an out-of-core solution would
negatively affect the computation times. Also, the
smaller the bin sizes, the more upsampling is neces-
sary.
Upsampling Rate. The upsampling rate is influ-
enced by the local variation in the values of the multi-
variate field and the bin size of the histogram. Let s
bin
be the bin size of the histogram. Then, an upsampling
may be necessary, if two data points in attribute space
are more than distance s
bin
apart. As the upsampling
rate is defined globally, it is determined by the largest
variation within a grid cell. Let s
data
is the maximum
distance in attribute space between two data points,
whose corresponding points in physical space belong
to one grid cell. Then, the upsampling rate shall be
larger than
s
data
s
bin
. This ratio refers to the upsampling
rate per physical dimension.
When using the adaptive scheme presented in Sec-
tion 5, the upsampling rate per dimension is always
a power of two. When a sufficiently high upsam-
pling rate has been chosen, the additional computa-
tions when upsampling with the next-higher power of
two in the adaptive scheme are modest, as computa-
tions for most branches of the octree have already ter-
minated.
10 CONCLUSION
We presented an approach for multivariate volume
data visualization that is based on clustering the
multi-dimensional attribute space. We overcome the
curse of dimensionality by upsampling the attribute
space according to the neighborhood relationship in
physical space. Trilinear interpolation is applied
to the attribute vectors to generate multidimensional
histograms, where the support, i.e., all non-empty
bins, is a connected component. Consequently, the
histogram-based clustering does not suffer from clus-
ters falling apart when using small bin sizes. We ap-
ply a hierarchical clustering method that generates a
cluster tree without having to pick density thresholds
manually or heuristically. In addition to a cluster tree
rendering, the clustering results are visualized using
coordinated views to parallel coordinates for an at-
tribute space rendering and to physical space render-
ing. The coordinated views allows for a comprehen-
sive analysis of the clustering result.
ACKNOWLEDGMENTS
This work was supported by the Deutsche
Forschungsgemeinschaft (DFG) under project
grant LI 1530/6-2.
REFERENCES
(2010). Competition data set and description.
2010 IEEE Visualization Design Contest,
http://viscontest.sdsc.edu/2010/.
Akiba, H. and Ma, K.-L. (2007). A tri-space visualization
interface for analyzing time-varying multivariate vol-
ume data. In In Proceedings of Eurographics/IEEE
VGTC Symposium on Visualization, pages 115–122.
Ankerst, M., Breunig, M. M., Kriegel, H.-P., and Sander, J.
(1999). Optics: ordering points to identify the clus-
tering structure. In Proceedings of the 1999 ACM
SIGMOD international conference on Management of
data, pages 49 – 60.
Bachthaler, S. and Weiskopf, D. (2008). Continuous scatter-
plots. IEEE Transactions on Visualization and Com-
puter Graphics (Proceedings Visualization / Informa-
tion Visualization 2008), 14(6):1428–1435.
Bachthaler, S. and Weiskopf, D. (2009). Efficient and adap-
tive rendering of 2-d continuous scatterplots. Com-
puter Graphics Forum (Proc. Eurovis 09), 28(3):743
– 750.
Bellman, R. E. (1957). Dynamic programming. Princeton
University Press.
Blaas, J., Botha, C. P., and Post, F. H. (2007). Interactive
visualization of multi-field medical data using linked
physical and feature-space views. In EuroVis, pages
123–130.
Daniels II, J., Anderson, E. W., Nonato, L. G., and Silva,
C. T. (2010). Interactive vector field feature identifi-
cation. IEEE Transactions on Visualization and Com-
puter Graphics, 16:1560–1568.
IVAPP 2018 - International Conference on Information Visualization Theory and Applications
38

Dobrev, P., Long, T. V., and Linsen, L. (2011). A cluster
hierarchy-based volume rendering approach for inter-
active visual exploration of multi-variate volume data.
In Proceedings of 16th International Workshop on Vi-
sion, Modeling and Visualization (VMV 2011), pages
137–144. Eurographics Association.
Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996).
A density-based algorithm for discovering clusters in
large spatial databases with noise. In Proceedings of
the second international conference on knowledge dis-
covery and data mining, page 226231.
Han, J. and Kamber, M. (2006). Data Mining: Concepts
and Techniques. Morgan Kaufmann Publishers.
Hartigan, J. A. (1975). Clustering Algorithms. Wiley.
Hartigan, J. A. (1985). Statistical theory in clustering. Jour-
nal of Classification, 2:62–76.
Heinrich, J., Bachthaler, S., and Weiskopf, D. (2011). Pro-
gressive splatting of continuous scatterplots and par-
allel coordinates. Comput. Graph. Forum, 30(3):653–
662.
Hinneburg, A. and Keim, D. (1998). An efficient approach
to clustering in large multimedia databases with noise.
In Proceedings of the fourth international conference
on knowledge discovery and data mining, page 5865.
Hinneburg, A., Keim, D. A., and Wawryniuk, M. (1999).
Hd-eye: Visual mining of high-dimensional data.
IEEE Computer Graphics and Applications, pages
22–31.
Jain, A. K. and Dubes, R. C. (1988). Algorithms for Clus-
tering Data. Prentice Hall.
J
¨
anicke, H., Wiebel, A., Scheuermann, G., and Kollmann,
W. (2007). Multifield visualization using local statis-
tical complexity. IEEE Transaction on Visualization
and Computer Graphics, 13(6):1384–1391.
Karypis, G., Han, E. H., and Kumar, V. (1999). Chameleon:
Hierarchical clustering using dynamic modeling.
Computer, 32(8):68–75.
Lehmann, D. J. and Theisel, H. (2010). Discontinuities in
continuous scatter plots. IEEE Transactions on Visu-
alization and Computer Graphics, 16:1291–1300.
Lehmann, D. J. and Theisel, H. (2011). Features in continu-
ous parallel coordinates. Visualization and Computer
Graphics, IEEE Transactions on, 17(12):1912 –1921.
Linsen, L., Long, T. V., and Rosenthal, P. (2009). Link-
ing multi-dimensional feature space cluster visual-
ization to surface extraction from multi-field volume
data. IEEE Computer Graphics and Applications,
29(3):85–89. linsenlongrosenthalvcgl.
Linsen, L., Long, T. V., Rosenthal, P., and Rosswog, S.
(2008). Surface extraction from multi-field particle
volume data using multi-dimensional cluster visual-
ization. IEEE Transactions on Visualization and Com-
puter Graphics, 14(6):1483–1490. linsenlongrosen-
thalrosswogvcglsmoothvis.
Long, T. V. (2009). Visualizing High-density Clusters in
Multidimensional Data. PhD thesis, School of Engi-
neering and Science, Jacobs University, Bremen, Ger-
many.
Maciejewski, R., Woo, I., Chen, W., and Ebert, D. (2009).
Structuring feature space: A non-parametric method
for volumetric transfer function generation. IEEE
Transactions on Visualization and Computer Graph-
ics, 15:1473–1480.
Oeltze, S., Doleisch, H., Hauser, H., Muigg, P., and Preim,
B. (2007). Interactive visual analysis of perfusion
data. IEEE Transaction on Visualization and Com-
puter Graphics, 13(6):1392–1399.
Sauber, N., Theisel, H., and Seidel, H.-P. (2006). Multifield-
graphs: An approach to visualizing correlations in
multifield scalar data. IEEE Transactions on Visual-
ization and Computer Graphics, 12(5):917–924.
Stuetzle, W. (2003). Estimating the cluster tree of a density
by analyzing the minimal spanning tree of a sample.
Journal of Classification, 20:25–47.
Stuetzle, W. and Nugent, R. (2007). A generalized single
linkage method for estimating the cluster tree of a den-
sity. Technical Report.
Whalen, D. and Norman, M. L. (2008). Com-
petition data set and description. 2008
IEEE Visualization Design Contest,
http://vis.computer.org/VisWeek2008/vis/contests.html.
Wong, A. and Lane, T. (1983). A kth nearest neighbor clus-
tering procedure. Journal of the Royal Statistical So-
ciety, Series B, 45:362–368.
Woodring, J. and Shen, H.-W. (2006). Multi-variate, time
varying, and comparative visualization with contex-
tual cues. IEEE Transactions on Visualization and
Computer Graphics, 12(5):909–916.
Overcoming the Curse of Dimensionality When Clustering Multivariate Volume Data
39
