
The Discriminative Generalized Hough Transform as a Proposal
Generator for a Deep Network in Automatic Pedestrian Localization
Eric Gabriel
1,2
, Hauke Schramm
1,2
and Carsten Meyer
1,2
1
Institute of Applied Computer Science, Kiel University of Applied Sciences, Kiel, Germany
2
Department of Computer Science, Kiel University (CAU), Kiel, Germany
Keywords:
Object Detection, Pedestrian Detection, Hough Transform, Proposal Generation, Patch Classification,
Convolutional Neural Network.
Abstract:
Pedestrian detection is one of the most essential and still challenging tasks in computer vision. Among traditi-
onal feature- or model-based techniques (e.g., histograms of oriented gradients, deformable part models etc.),
deep convolutional networks have recently been applied and significantly advanced the state-of-the-art. While
earlier versions (e.g., Fast-RCNN) rely on an explicit proposal generation step, this has been integrated into
the deep network pipeline in recent approaches. It is, however, not fully clear if this yields the most efficient
way to handle large ranges of object variability (e.g., object size), especially if the amount of training data
covering the variability range is limited. We propose an efficient pedestrian detection framework consisting
of a proposal generation step based on the Discriminative Generalized Hough Transform and a rejection step
based on a deep convolutional network. With a few hundred proposals per (2D) image, our framework achie-
ves state-of-the-art performance compared to traditional approaches on several investigated databases. In this
work, we analyze in detail the impact of different components of our framework.
1 INTRODUCTION
Pedestrian detection gained a lot of attention and yet
remains an important and challenging task in com-
puter vision (Benenson et al., 2014; Dollar et al.,
2012). Traditionally, feature- or model-based techni-
ques (e.g., Viola-Jones (Viola et al., 2005), histo-
grams of oriented gradients (HOG) (Dalal and Triggs,
2005) and deformable part models (DPM) (Felzensz-
walb et al., 2008) or Roerei (Benenson et al., 2013),
respectively) have been employed. There also ex-
ist Random Forest-based approaches such as (Marin
et al., 2013). Since the success of deep convolutional
networks (CNN) in image classification tasks (Kriz-
hevsky et al., 2012; Zeiler and Fergus, 2014; Simo-
nyan and Zisserman, 2015), such networks have also
been applied to object detection in general (Ren and
others., 2015; Redmon et al., 2016a; Wei et al., 2016)
and pedestrian detection in particular (e.g., (Angelova
et al., 2015)). First attempts involved a proposal ge-
neration mechanism (Girshick et al., 2014; Girshick,
2015), where in the first step regions of interest have
been extracted, e.g., based on low-level hierarchical
segmentations (Arbelaez et al., 2014) or several fe-
ature types using a bag-of-visual-words approach as
in (Uijlings et al., 2012). Recent approaches aim at
integrating the proposal generation step into the deep
network (Ren and others., 2015). (Lenc and Vedaldi,
2015) even show that a separate proposal generation
step is not necessary and a plain CNN can accomplish
the complete object detection task. However, it is
known that CNNs usually need significant amounts of
training data, which have to cover the expected object
variability. Thus, one can argue that proposal genera-
tion may still be a useful component either to handle
a larger range of object variability or to increase ef-
ficiency or both. Besides, (groups of) small objects
still remain a problem for CNNs (Lenc and Vedaldi,
2015; Redmon et al., 2016a), which might be over-
come with accurate region proposals. Thus, we pro-
pose an object detection framework which relies on a
proposal generation step based on the Discriminative
Generalized Hough Transform (DGHT) generating a
number of quite accurate proposals, which are then
accepted or rejected based on a deep network. In a
previous manuscript, we have shown the general fe-
asibility of such a framework (Gabriel et al., 2017).
The contributions of the present paper are:
• We propose an efficient model scaling approach
to handle variable object sizes, replacing the often
Gabriel, E., Schramm, H. and Meyer, C.
The Discriminative Generalized Hough Transform as a Proposal Generator for a Deep Network in Automatic Pedestrian Localization.
DOI: 10.5220/0006542401690176
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theor y and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages
169-176
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
169

used image scaling approach. The image scaling
approach requires a separate feature extraction for
each scale as applied in (Gabriel et al., 2017).
• We analyze the contribution of an additional pro-
posal rejection operating in the Hough space, the
so-called shape consistency measure (SCM), and
demonstrate its role in reducing the number of ge-
nerated proposals.
• We investigate the role of the edge detector for
the DGHT, i.e., comparing a sophisticated Struc-
tured Edge Detector (Dollar and Zitnick, 2015) to
Canny edge detection.
• We address the impact of the amount of training
data for the DGHT pedestrian model on the de-
tection performance.
Overall, we demonstrate that the advantage of the
DGHT-based proposal generation is the relatively low
number of misses (false negatives) at a moderate num-
ber of generated candidates (a few hundred per 2D
image) along with the efficiency of a Hough-based
approach. We achieve state-of-the-art performance on
several databases compared to traditional approaches.
2 METHODS
In this Section, we provide a general algorithmic over-
view of our approach. Since the DGHT – as well
as other Hough-based approaches – operates on edge
images, the first step is an efficient edge detection. In
this work, we compare the effect of two edge detec-
tors (Canny versus Structured Edge Detection) on the
performance of our pedestrian detection pipeline.
2.1 Canny Edge Detection
A well-known, general and robust approach for edge
detection in digital images was introduced in (Canny,
1986). The values of the first derivatives in horizontal
and vertical direction are obtained by applying the So-
bel operator to the smoothed input image I : Ω → R.
Using these values, the gradient magnitude and the
edge direction can be calculated. The resulting edges
are thinned using non-maximum suppression (NMS).
Subsequently, the remaining edge pixels are classified
using a high and a low threshold. Edges above the
high threshold are kept, edges below the low thres-
hold are discarded. Edges between the low and the
high threshold are only kept if there is an edge pixel
within the respective 8-connected neighborhood. See
Fig. 1 (b) for an example edge image I
E
: Ω → {0,1}.
2.2 Structured Edge Detection (SED)
A more sophisticated, yet still real-time edge de-
tection framework incorporating information of the
objects of interest has been proposed by (Dollar and
Zitnick, 2015). Here, a Random Forest (Breiman,
2001) maps patches of the input image I to output
edge image patches using pixel-lookups and pairwise-
difference features of 13 (3 color, 2 magnitude and
8 orientation) channels. While testing, densely sam-
pled, overlapping image patches are fed into the trai-
ned detector. The edge patch outputs which refer to
the same pixel are locally averaged. The resulting in-
tensity value can be seen as a confidence measure for
the current pixel belonging to an edge. Subsequently,
a NMS can be applied in order to sharpen the edges
and reduce diffusion. For further details see (Dollar
and Zitnick, 2015). An example of an edge image
I
E
: Ω → [0,1] is shown in Fig. 1 (c).
2.3 Discriminative Generalized Hough
Transform
The Generalized Hough Transform (GHT) (Ballard,
1981) is well-known as a general model-based appro-
ach for object localization. It is based on a shape mo-
del M = {m
j
| j = 1,... ,M} consisting of M model
points m
j
. Each m
j
is represented by its coordinates
x
j
in a local coordinate system with respect to some
chosen reference point (e.g., object center of gravity),
and its direction ϕ
j
: M = {(x
j
,ϕ
j
)| j = 1, .. ., M} ⊂
R
2
× [0, 2π[. In most cases, the direction ϕ
j
of a mo-
del point m
j
is defined as the expected gradient of the
object (edge) at location m
j
in the local coordinate sy-
stem. Using the shape model M , the GHT transforms
an edge image I
E
(Sect. 2.2) – where for each point
e ∈ I
E
the edge gradient direction γ(e) is computed
(in the original image) – into a parameter space H
M
,
called Hough space, by a voting procedure. Specifi-
cally, if the actual edge gradient γ(e) for an edge pixel
e matches the expected gradient ϕ
j
of model point j
(up to some tolerance ∆φ), a vote I
E
(e) is generated in
a Hough cell c ∈ Ω matching the position c = e − x
j
of the object’s reference point in the global coordinate
system (up to a quantization factor ρ = 2):
f
j
(c,I
E
) =
∑
(e,γ(e))∈I
E
I
E
(e), if c = b(e − x
j
)/ρc
and |γ(e) − ϕ
j
| < ∆φ
0, otherwise.
(1)
The contributions of all model points are then sum-
med to generate the Hough space (see Eq. 2 with λ
j
= 1). The Discriminative GHT (DGHT) (Ruppertsho-
fen, 2013) extends the GHT by assigning individual
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
170

Figure 1: (a) input image (b) Canny edges (c) Structured edges (d) DGHT model (e) Canny results (f) Structured edges results;
green: ground truth, yellow: detection, blue: false positive, red: false negative.
model point weights λ
j
∈ R:
H
M
(c,I
E
) =
∑
j∈M
λ
j
f
j
(c,I
E
) (2)
For ensuring good localization quality, the model
should yield a large number of votes at true object
locations and only a small number of votes at locati-
ons of confusable objects. The DGHT achieves this
by an iterative, discriminative training procedure star-
ting with an initial model of superimposed annotated
edge images at the reference point. In each iteration,
the model point weights λ
j
are optimized using a Mi-
nimum Classification Error (MCE) approach and, af-
terwards, the model is extended by target structures
from training images which still have a high locali-
zation error. To reduce model size, all model points
with a low (absolute) weight are eliminated. This pro-
cedure is repeated until all training images are used or
have a low localization error. Thus, the training pro-
cess allows to automatically generate the model set
M . Further details on this technique can be found in
(Ruppertshofen, 2013).
Image Scaling: Traditionally, image scaling has
been proposed to handle object size variability in new
test images (Dollar et al., 2010). Here, an image py-
ramid is defined by a fixed set of scaling factors to
cover the expected object size range. The edge ima-
ges have to be recomputed for each scaling factor.
Then, the DGHT model M is (independently) app-
lied to each scaled edge image, thus generating a set
of Hough spaces (one for each scaling factor).
Model Scaling: In this work, we suggest an al-
ternative approach to handle the variability of object
sizes by adopting the template pyramid as in (Dol-
lar et al., 2010; Ohn-Bar and Trivedi, 2015) to our
DGHT framework. Central idea is to handle object
variability by applying a set of transformations (co-
vering the expected object variability) to the DGHT
model M . Since we focus on different object sizes,
we use a set of simple scaling operations applied to
the set of model points m
j
, i.e., to the (local) coor-
dinates x
j
. For simplicity, we use the same scaling
factor for both the x- and the y-axis. In this model
scaling scheme, the edge image has to be computed
only once. Afterwards, the model pyramid is applied
(in parallel) to the single input edge image, again ge-
nerating a set of Hough spaces (one for each model
scale). A limitation of this approach is that at very
small or large scales model points could intersect or
get too coarse which might lead to mislocalizations.
Finally, in each resulting Hough space H local
maxima C = {
ˆ
c
i
} are identified using a NMS with
a minimum distance of 1/3 of the respective model
width. An ordered list C = (
ˆ
c
1
,. .. ,
ˆ
c
n
) of most proba-
ble object positions
ˆ
c
i
is derived, which are then used
as proposals in our object detection pipeline.
2.4 Rejection of Proposals
2.4.1 Shape Consistency Measure (SCM)
Using the iterative training procedure described in
Sect. 2.3, a DGHT model may cover medium object
The Discriminative Generalized Hough Transform as a Proposal Generator for a Deep Network in Automatic Pedestrian Localization
171

variability
1
by containing model points that represent
the most important modes of variation observed in the
training data. Due to the independent voting proce-
dure (see Eq. 2), a Hough cell might get a large num-
ber of votes from different variability modes which
may lead to a mislocalization.
To this end, (Hahmann et al., 2015) suggested to
analyze the model point pattern voting for a particu-
lar Hough cell
ˆ
c
i
. More specifically, a Random Forest
(Breiman, 2001) is applied to classify the voting mo-
del point pattern into a class “regular shape” σ
r
(re-
presenting e.g., a frontal or a side view of a person)
and a class “irregular shape” σ
i
.
To train the Random Forest Classifier, the DGHT
is applied to each training image. Afterwards, the
class labels σ
r
and σ
i
are assigned to the individual
Hough cells of the training images: Cells with a loca-
lization error < ε
1
are labeled as class σ
r
while those
with an error > ε
2
are assigned to class σ
i
.
For a test edge image I
E
, a DGHT model is ap-
plied to generate a Hough space H. For each lo-
cal maximum
ˆ
c
i
in H, the Random Forest Classi-
fier is used to calculate the probability p
ˆ
c
i
(σ
r
) that
the set of model points voting for
ˆ
c
i
has a regular
shape. The obtained probability is used as an additi-
onal weighting factor for the Hough space votes, i.e.,
S(
ˆ
c
i
,I
E
) = H(
ˆ
c
i
,I
E
) · p
ˆ
c
i
(σ
r
). The local maxima in
H are now sorted according to decreasing S(
ˆ
c
i
,I
E
) to
provide an ordered list C = (
ˆ
c
1
,. .. ,
ˆ
c
n
) of most pro-
bable object positions
ˆ
c
i
.
2.4.2 Deep Convolutional Neural Networks
In this work, we use a deep CNN to individually
accept or reject each proposal
ˆ
c
i
out of the list C
generated by the DGHT or DGHT+SCM. Specifi-
cally, each candidate position
ˆ
c
i
∈ C is transferred
from Hough space to image space (scaled when using
image scaling). Then, a bounding box corresponding
to the mean object size is centered around that posi-
tion. Note that in case of model scaling, the mean
object size (and thus the bounding box) is scaled in
the same way as the model. The image patch corre-
sponding to the bounding box is rescaled to a fixed
input size. The patch pixel intensities of all three co-
lor channels are normalized to [0,1], and then used as
input to a deep CNN. The output of the CNN is a soft-
max layer with 2 classes, pedestrian and background.
We use the probability p
ˆ
c
i
(pedestrian) for the pede-
strian class, generated for the image patch correspon-
ding to Hough cell
ˆ
c
i
, for candidate rejection. With an
1
The DGHT model is generated from a restricted object
size range (see Sect. 3.2); the training data, however, con-
tains other modes of variation (e.g., frontal / side views).
appropriate rejection threshold θ, any candidate
ˆ
c
i
is
rejected if p
ˆ
c
i
(pedestrian) < θ. The remaining candi-
dates are grouped using the mutual overlap. A NMS
using p
ˆ
c
i
(pedestrian) is then applied to each group.
3 EXPERIMENTAL SETUP
3.1 Databases
IAIR-CarPed. We perform most experiments on the
IAIR-CarPed (Wu et al., 2012) database, because it
has a reasonable amount of independent 2D images
and additionally offers difficulty labels (e.g., occlu-
sion, low contrast) for each annotation. As suggested
in (Wu et al., 2012), we train on a random 50%-split
of the available pedestrian images, i.e., in total 1046
images containing 2341 pedestrians with an object
height range from 45 to 383px (mean height: 160px).
The remaining 1046 images (2367 pedestrians with a
similar object height range and mean height) are used
for evaluation. Training and test corpus each contain
all types of difficulties.
INRIA Person. We also evaluate our approach
on the well-known INRIA Person database (Dalal and
Triggs, 2005). The test set contains 288 images which
contain 561 annotated persons with a height range
from 100 - 788px (mean height: 299px).
TUD Pedestrians. Moreover, we report error ra-
tes on the TUD Pedestrians data set (Andriluka et al.,
2008). The test set consists of 250 images containing
311 annotated pedestrians with a height range from
71 to 366px (mean height: 213px).
3.2 Experimental Setup and System
Parameters
We detect pedestrians in a 2D RGB image as follows
(see also Fig. 2):
Edge Detection: As input images for training
and testing, we use the output of either the Canny or
the Structured Edge Detector (see Sect.2.1 and 2.2).
We train the latter specifically for pedestrians on the
PennFudan database (Wang et al., 2007). Compared
to Canny edge detection, the Structured Edge Detec-
tor suppresses most of the background edges and thus
significantly reduces background variability (Gabriel
et al., 2016) (see Fig. 1).
DGHT Model and SCM Training: For both
image and model scaling, we train a DGHT pede-
strian model comprising a limited amount of size va-
riability. Specifically, we allow a size range of 144 -
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
172
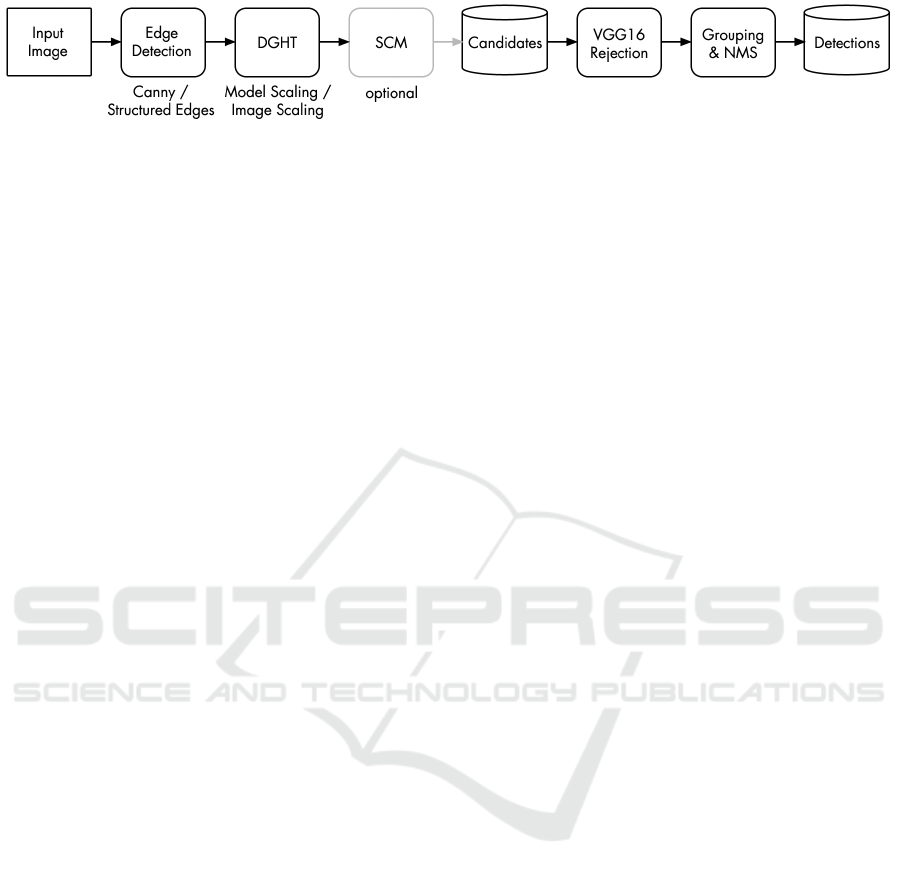
Figure 2: Components of the detection pipeline.
176px (mean object height ±10%). All training ima-
ges with pedestrians not in this size range are scaled
to a person size selected randomly from the allowed
range (uniform distribution), separately for each pe-
destrian in an image. To train our DGHT shape mo-
del (see Sect. 2.3), we only use those training images
containing “simple” pedestrians (IAIR difficulty type
“S”, 1406 pedestrians / 775 images). With the trained
DGHT model, we additionally train the SCM on the
full IAIR training set comprising all difficulty types
and all pedestrians scaled to the range 144–176px as
described above (see also Sect. 2.4.1). We set ε
1
for
class σ
r
to 5 and ε
2
for class σ
i
to 15 Hough cells.
Proposal Generation: To handle the large range
of object sizes contained in the test images, we either
use model or image scaling as described in Sect. 2.3.
When using image scaling, we scale each test image
by the following heuristic set of 10 scaling factors
such that each pedestrian should roughly fit into the
expected object range (mean object height ±10%):
50%, 62.5%, 75%, 100%, 150%, 200%, 225%,
250%, 275%, 300%.
The trained DGHT model is applied indepen-
dently to each scaled image, i.e., a set of Hough spa-
ces is generated (one for each scaling factor).
When using model scaling, we partition the ob-
ject range into 10 adjacent, non-overlapping intervals
such that their range corresponds to 2 · 10% of their
center: 37%, 45%, 55%, 67%, 82%, 100%, 122%,
149%, 182%, 222%
The scaled models are independently applied to
the edge image of each input image, thus again ge-
nerating a set of Hough spaces (one for each model
scaling factor). Note that in contrast to image scaling,
the edge image is only computed once.
Optionally, each Hough space of either model or
image scaling is then weighted by the SCM (Sect.
2.4.1). Finally, local maxima C = {
ˆ
c
i
} are identi-
fied using a NMS with a minimum distance of 1/3
of the model width. To reduce the amount of candi-
dates, we discard those candidates
ˆ
c
i
with S(
ˆ
c
i
,I
E
) <
maxS(I
E
) · 0.2, when having applied the SCM, or
H(
ˆ
c
i
,I
E
) < maxH(I
E
) · 0.2 otherwise.
CNN Rejection: Any candidate position
ˆ
c
i
is
transferred to image space (scaled in case of image
scaling) yielding a location and a bounding box cor-
responding to the mean model size (scaled in case of
model scaling) centered around the corresponding po-
sition in image space. A deep CNN is then used to re-
ject
ˆ
c
i
if p
ˆ
c
i
(pedestrian) < θ (see Sect. 2.4.2). We use
the standard Keras VGG16 model, which is initialized
on ImageNet. We fine-tune this model on our IAIR
training corpus, using the annotated pedestrian boun-
ding boxes scaled to (64 ×64 ×3) as positive samples
and the same candidates as for class σ
i
in the SCM
training as negative samples, i.e., high scoring peaks
with a minimum error of 15 Hough cells. For fine-
tuning we use the Adam optimizer (Kingma and Ba,
2015) with categorical cross-entropy loss, a learning
rate η of 0.001, which is reduced on plateaus, and an
input dimension of (64 × 64 × 3).
Combining Scales and Post-processing: Subse-
quent to the rejection step, the remaining candidate
bounding boxes are greedily grouped based on the
mutual overlap (set to 30%) and finally a NMS is ap-
plied to each group using p
ˆ
c
i
(pedestrian) as criterion
in order to avoid double detections.
3.3 Comparison to State-of-the-art
Approaches
We compare our approach against several state-of-
the-art algorithms. For our IAIR-CarPed test corpus,
we compare against the latest DPM release (DPMv5)
(Girshick et al., 2013) trained on PASCAL, the pre-
trained YOLOv1 (Redmon et al., 2016a) full model
as well as the pre-trained YOLOv2 (Redmon et al.,
2016b) full model (both pre-trained on ImageNet and
fine-tuned on PASCAL), as the latter is currently the
best performing algorithm on PASCAL VOC. Add-
titionally, we used the pre-trained YOLOv1 full mo-
del and fine-tuned it on our IAIR-CarPed training set.
The details of these state-of-the-art approaches can be
found in the respective references. For the other da-
tabases, we use the benchmark results from (Caltech,
2017) and (Yao et al., 2014), respectively.
3.4 Evaluation Metrics
As suggested by (Dollar et al., 2012) for single
frame evaluation, we compute Detection Error Tra-
deoff (DET) curves plotting the miss rate against the
The Discriminative Generalized Hough Transform as a Proposal Generator for a Deep Network in Automatic Pedestrian Localization
173
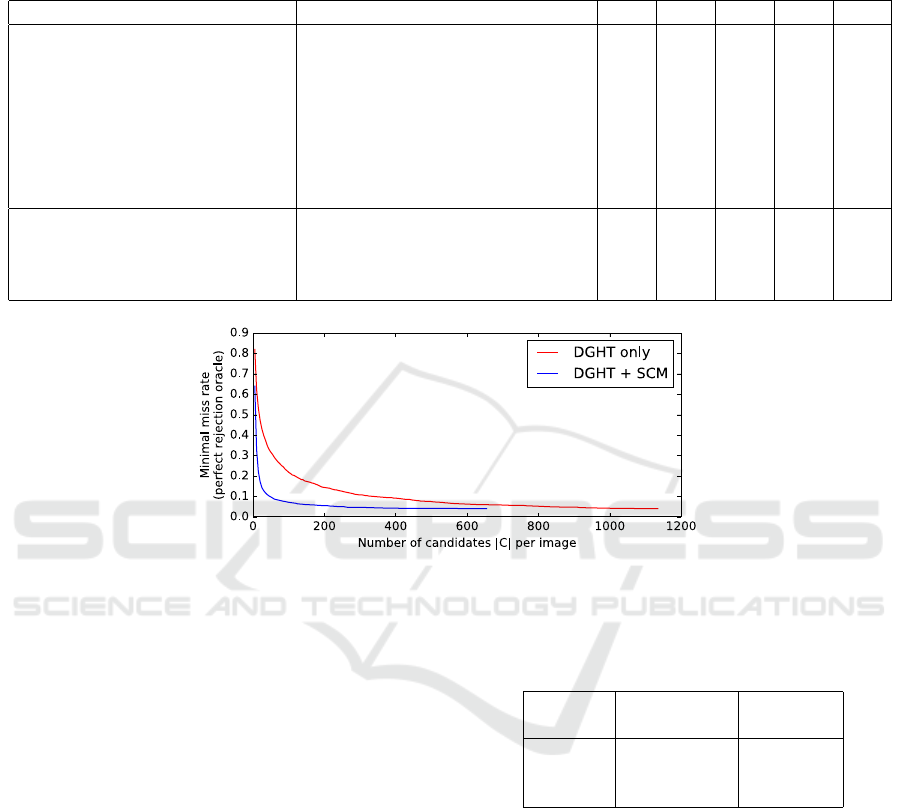
Table 1: Performance comparison (miss rates at 0.3 FPPI) of different configurations of our DGHT+VGG16 pipeline on the
IAIR-CarPed test corpus: Canny or Structured Edge Detection (SED), model or image scaling, with/without SCM. We also
show results for the DPMv5 and YOLOv1/2 detections. Note, however, that the training data used for the other algorithms
differ as indicated. S: Simple, D1: Occlusion, D2: Low Contrast, D3: Infrequent Shape.
Approach Setup S D1 D2 D3 All
DGHT+VGG16 Model Scaling, Canny 0.29 0.40 0.48 0.48 0.36
DGHT+VGG16 Model Scaling, Canny, SCM 0.20 0.36 0.44 0.45 0.29
DGHT+VGG16 Model Scaling, SED 0.13 0.27 0.43 0.33 0.23
DGHT+VGG16 Model Scaling, SED, SCM 0.12 0.30 0.47 0.33 0.23
DGHT+VGG16 Image Scaling, Canny 0.16 0.37 0.41 0.36 0.26
DGHT+VGG16 Image Scaling, Canny, SCM 0.14 0.37 0.42 0.31 0.25
DGHT+VGG16 Image Scaling, SED 0.12 0.31 0.46 0.25 0.22
DGHT+VGG16 Image Scaling, SED, SCM 0.11 0.35 0.44 0.26 0.23
DPMv5 (Girshick et al., 2013) Pre-trained on PASCAL 0.20 0.40 0.51 0.48 0.32
YOLOv1 (Redmon et al., 2016a) Pre-trained on ImageNet/PASCAL 0.42 0.51 0.89 0.50 0.53
YOLOv1 (Redmon et al., 2016a) Fine-tuned on Im.Net/PASC./IAIR 0.06 0.19 0.24 0.20 0.14
YOLOv2 (Redmon et al., 2016b) Pre-trained on ImageNet/PASCAL 0.15 0.30 0.36 0.24 0.23
Figure 3: Minimal miss rate on the IAIR test corpus based on an ordered list C of proposals provided by the DGHT /
DGHT+SCM, as function of the length |C| of the list (image scaling, SED).
false positives per image (FPPI) on a log-log scale by
modifying the rejection threshold θ. For comparison,
the miss rates at 0.3 FPPI are shown as this is the
highest miss rate achieved by our approach (all other
false positive candidates are rejected by the VGG16
classifier). For the TUD Pedestrians database, we use
the recall at equal error rate (EER), as other groups
have frequently used this measure. For measuring
the candidate quality, we use the Average Best Over-
lap (ABO) score from (Uijlings et al., 2012). Here,
the best overlap between each ground truth annota-
tion and the candidate list C is computed and averaged
over all annotations in all test images.
4 RESULTS
In this section, we analyze in detail the influence
of different components of our detection pipeline
(“DGHT + VGG16”), namely Canny versus structu-
red edge detection (Sect. 2.1 and 2.2), image versus
model scaling to handle object size variability (Sect.
2.3) and including the SCM (in addition to the deep
Table 2: Detection results (IAIR test corpus) using fracti-
ons of the IAIR training corpus for DGHT/VGG16. Setup:
image scaling, SED and SCM.
Training Miss Rate at Minimal
Data 0.3 FPPI Miss Rate
100% 0.23 0.04
50% 0.23 0.02
25% 0.26 0.02
network) as rejection mechanism or not (Sect. 2.4.1).
The detection results (miss rate at 0.3 FPPI) for all
different configurations are shown in Tab. 1, toget-
her with results for other state-of-the-art algorithms.
All configurations of our algorithm outperform previ-
ously published results (Wu et al., 2012). Using struc-
tured edge detection, the different DGHT + VGG16
configurations (i.e., including the SCM or not, model
versus image scaling) perform similarly. With Canny
edge detection, miss rates are larger, especially with
model scaling. On the other hand, model scaling is
more efficient (40% less voting time, only one edge
image) and performs well with structured edges. Note
that the DGHT is not yet implemented on a GPU for
parallel processing. However, due to the independent
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
174

Table 3: Recall at EER on TUD Pedestrians without retraining.Setup 1: image scaling, SED, SCM; Setup 2: model scaling,
SED, no SCM.
Approach Training Data Recall at EER
Setup 1 IAIR 0.88
Setup 2 IAIR 0.85
PartISM (Andriluka et al., 2008) TUD/INRIA 0.84
HoughForests (Gall and Lempitsky, 2009) TUD/INRIA 0.87
Yao et al. (Yao et al., 2014) TUD/INRIA 0.92
Table 4: Miss Rate at 1 FPPI on INRIA Person without retraining. Setup 1: image scaling, SED, SCM; Setup 2: model
scaling, SED, no SCM.
Approach Training Data Miss Rate
Setup 1 IAIR 0.14
Setup 2 IAIR 0.15
ICF (Dollar et al., ) INRIA 0.14
Yao (Yao et al., 2014) INRIA 0.12
FPDW (Dollar et al., 2010) INRIA 0.09
VeryFast (Benenson et al., 2012) INRIA 0.07
Spat.Pool. (Paisitkriangkrai et al., 2014) INRIA/Caltech 0.04
voting of model points, the DGHT (especially using
model scaling) exhibits a high potential for paralleli-
zation. In future, we plan to analyze the runtime of
the different components.
Assuming a perfect rejection oracle – which se-
lects for each ground truth annotation the best mat-
ching candidate out of the list C generated by either
the DGHT or the DGHT+SCM and rejects all other
candidates – we also quantify the minimal miss rates
in case of perfect proposal rejection. For all inves-
tigated setups, the minimal miss rate is in the range
of 0.03 - 0.05 showing that there is still potential for
improvement of the VGG16 rejection. In particular,
we analyze the minimal miss rate as a function of the
number |C| of proposals per image with and without
the SCM (Fig. 3). With the SCM, the number of pro-
posals per image (controlled by the threshold θ) can
be significantly smaller than without the SCM at no
performance loss, since the SCM effectively removes
many wrong proposals from the list. This also holds
for the other DGHT configurations.
An advantage of the DGHT is the relatively low
amount of training material needed (as compared to
deep networks). To demonstrate this, we reduce the
amount of training data by randomly selecting 25%
and 50% from our IAIR training corpus and use this
restricted set to train the DGHT, the SCM and to fine-
tune the VGG16 classifier; the detection results on the
IAIR test corpus (using image scaling, SED and inclu-
ding the SCM) are shown in Tab. 2.
Tab. 3 and 4 show the evaluation results of our
pedestrian detection pipeline (trained on IAIR) on
the TUD Pedestrians and INRIA Person test sets, re-
spectively, using image scaling, structured edges and
the SCM vs. model scaling and Canny edges without
the SCM. Note that in these experiments no com-
ponent of our system has been retrained on the re-
spective database. When using the SCM for candi-
date reduction, we obtain minimal miss rates of 0.01
(75.8% ABO) at 55 candidates per image and 0.01
(76.8% ABO) at 102 candidates per image on TUD
Pedestrians and INRIA Person, respectively. Thus,
our approach has less candidates than Selective Se-
arch (Uijlings et al., 2012) (2,000 - 10,000 candida-
tes) or the region proposals of Faster R-CNN (Ren
and others., 2015) (300+ candidates). In future work,
we plan to compare against Faster R-CNN.
In first experiments on a car detection task (trai-
ning on UIUC (single scale) training corpus, test on
UIUC multi-scale test corpus (Agarwal et al., 2004))
we obtained a miss rate of 0.03 (0.06) at 0.5 FPPI
at 16 (58) average candidates per image for image
scaling with SCM (model scaling without SCM), re-
spectively, using structured edge detection. This is
a first indication that our detection pipeline can be
successfully applied to other object categories as well.
5 CONCLUSIONS
In this work, we investigated a pedestrian detection
framework based on proposal generation using the
Discriminative Generalized Hough Transform, follo-
wed by a proposal rejection step (in image space) ba-
sed on a deep convolutional neural network. In par-
ticular, we suggested an efficient approach to handle
object size variability, namely scaling of the DGHT
The Discriminative Generalized Hough Transform as a Proposal Generator for a Deep Network in Automatic Pedestrian Localization
175

model. Using Structured Edge Detection as input to
the DGHT, this model scaling approach showed si-
milar performance to traditional image scaling at re-
duced runtime, even on different pedestrian databa-
ses (TUD Pedestrians, INRIA) than used in training
(IAIR). We also showed that an additional proposal
rejection step operating in the Hough space, the shape
consistency measure (SCM), can be used to signifi-
cantly reduce the number of proposals per image wit-
hout performance loss. Our framework generates be-
tween 50 and 350 proposals per image, depending on
the database, which is much less than current propo-
sal generation approaches. Furthermore, when using
only 25% of the (IAIR) training images (352 pedestri-
ans) for DGHT and SCM training, we obtained only
a moderate degradation in detection accuracy. Cur-
rently, we do not perform any bounding box refine-
ment which would further improve the detection accu-
racy. Still, our detection results compare well to other
state-of-the-art approaches (taking into account diffe-
rent training sets). First results in a car detection task
suggest that our detection framework can be success-
fully applied to other object detection tasks as well.
Thus, our framework could be useful especially for
detecting specific object categories with limited avai-
lable training material.
REFERENCES
Agarwal, S. et al. (2004). Learning to detect objects in ima-
ges via a sparse, part-based representation. In PAMI.
Andriluka, M. et al. (2008). People-Tracking-by-Detection
and People-Detection-by-Tracking. In CVPR.
Angelova, A. et al. (2015). Real-Time Pedestrian Detection
with Deep Network Cascades. In BMVC.
Arbelaez, P. et al. (2014). Multiscale Combinatorial Grou-
ping. In CVPR.
Ballard, D. (1981). Generalizing the Hough Transform to
Detect Arbitrary Shapes. In Pattern Recognition.
Benenson, R. et al. (2012). Pedestrian Detection at 100 FPS.
In CVPR.
Benenson, R. et al. (2013). Seeking the Strongest Rigid
Detector. In CVPR.
Benenson, R. et al. (2014). Ten Years of Pedestrian De-
tection, What Have We Learned? In ECCV.
Breiman, L. (2001). Random Forests. In Machine Learning.
Caltech (2017). Caltech Pedestrian Detection Bench-
mark. http://www.vision.caltech.edu/Image
Datasets/
CaltechPedestrians. [Online; accessed 28-July-2017].
Canny, J. (1986). A Computational Approach to Edge De-
tection. In PAMI.
Dalal, N. and Triggs, B. (2005). Histograms of Oriented
Gradients for Human Detection. In CVPR.
Dollar, P. et al. Integral channel features.
Dollar, P. et al. (2010). The Fastest Pedestrian Detector in
the West. In BMVC.
Dollar, P. et al. (2012). Pedestrian Detection: An Evaluation
of the State of the Art. In PAMI.
Dollar, P. and Zitnick, C. (2015). Fast Edge Detection Using
Structured Forests. In PAMI.
Felzenszwalb, P. et al. (2008). A Discriminatively Trained,
Multiscale, Deformable Part Model. In CVPR.
Gabriel, E. et al. (2016). Structured Edge Detection for Im-
proved Object Localization Using the Discriminative
Generalized Hough Transform. In VISAPP.
Gabriel, E. et al. (2017). Analysis of the Discriminative Ge-
neralized Hough Transform for Pedestrian Detection.
In ICIAP.
Gall, J. and Lempitsky, V. (2009). Class-specific Hough
Forests for Object Detection. In CVPR.
Girshick, R. (2015). Fast R-CNN. In ICCV.
Girshick, R. et al. (2013). Discriminatively Trained Defor-
mable Part Models.
Girshick, R. et al. (2014). Rich Feature Hierarchies for
Accurate Object Detection and Semantic Segmenta-
tion. In CVPR.
Hahmann, F. et al. (2015). A Shape Consistency Measure
for Improving the GHT. In VISAPP.
Kingma, D. and Ba, J. (2015). Adam: A Method for Stoch.
Optimization. In ICLR.
Krizhevsky, A. et al. (2012). ImageNet Classification with
Deep CNNs. In NIPS.
Lenc, K. and Vedaldi, A. (2015). R-cnn minus r. In BMVC.
Marin, J. et al. (2013). Random Forests of Local Experts
for Pededestrian Detection. In ICCV.
Ohn-Bar, E. and Trivedi, M. (2015). Looking outside of the
Box: Object Detection and Localization with Multi-
scale Patterns. In arXiv:1505.03597.
Paisitkriangkrai, S. et al. (2014). Strengthening the Effecti-
veness of Pedestrian Detection. In ECCV.
Redmon, J. et al. (2016a). YOLO: Unified, Real-time Ob-
ject Detection. In CVPR.
Redmon, J. et al. (2016b). YOLO9000: Better, Faster,
Stronger. In arXiv:1612.08242.
Ren, S. and others. (2015). Faster R-CNN: Towards Real-
Time Object Detection with RPNs. In NIPS.
Ruppertshofen, H. (2013). Automatic Modeling of Anato-
mical Variability for Object Localization in Medical
Images. In BoD–Books on Demand.
Simonyan, K. and Zisserman, A. (2015). Very Deep Con-
vNets for Large-Scale Image Recognition. In ICLR.
Uijlings, J. et al. (2012). Selective Search for Object Re-
cognition. In IJCV.
Viola, P. et al. (2005). Det. Pedestrians Using Patterns of
Motion and Appearance. In IJCV.
Wang, L. et al. (2007). Object Detection Combining Recog-
nition and Segmentation. In ACCV.
Wei, L. et al. (2016). SSD: Single Shot Multibox Detector.
In ECCV.
Wu, Y. et al. (2012). Iair-carped: A psychophys. annotated
dataset with fine-grained and layered semantic labels
for object recognition. In Pattern Recognition Letters.
Yao, C. et al. (2014). Human Detection Using Learned Part
Alphabet and Pose Dictionary. In ECCV.
Zeiler, M. and Fergus, R. (2014). Visualizing and Under-
standing ConvNets. In ECCV.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
176
