
Learning Rigid Image Registration
Utilizing Convolutional Neural Networks for Medical Image Registration
J. M. Sloan
1,2
, K. A. Goatman
1
and J. P. Siebert
2
1
Toshiba Medical Visualisation Services, Europe Ltd., 2 Anderson Place, EH6 5NP, Edinburgh, U.K.
2
Department of Computing, Glasgow University, 18 Lilybank Gardens, Glasgow G12 8RZ, Glasgow, U.K.
Keywords:
Rigid Registration, Deep Learning, Mono-modality, Multi-modality, Magnetic Resonance Imaging, Inverse
Consistency.
Abstract:
Many traditional computer vision tasks, such as segmentation, have seen large step-changes in accuracy and/or
speed with the application of Convolutional Neural Networks (CNNs). Image registration, the alignment of
two or more images to a common space, is a fundamental step in many medical imaging workflows. In this
paper we investigate whether these techniques can also bring tangible benefits to the registration task. We
describe and evaluate the use of convolutional neural networks (CNNs) for both mono- and multi- modality
registration and compare their performance to more traditional schemes, namely multi-scale, iterative regis-
tration.
This paper also investigates incorporating inverse consistency of the learned spatial transformations to impose
additional constraints on the network during training and investigate any benefit in accuracy during detection.
The approaches are validated with a series of artificial mono-modal registration tasks utilizing T1-weighted
MR brain images from the Open Access Series of Imaging Studies (OASIS) study and IXI brain development
dataset and a series of real multi-modality registration tasks using T1-weighted and T2-weighted MR brain
images from the 2015 Ischemia Stroke Lesion segmentation (ISLES) challenge.
The results demonstrate that CNNs give excellent performance for both mono- and multi- modality head and
neck registration compared to the baseline method with significantly fewer outliers and lower mean errors.
1 INTRODUCTION
Medical image registration is concerned with the au-
tomatic alignment of multiple datasets to a common
space. It is an essential component in a diverse array
of applications, including diagnosis, treatment plan-
ning, atlas construction and augmented reality.
This paper focusses on directly learning the trans-
formation parameters in a single pass, given two im-
ages as opposed to learning a similarity metric (Si-
monovsky et al., 2016; Lee et al., 2009). By di-
rectly learning the transformation parameters in a sin-
gle pass, we avoid the common pitfalls of traditional
iterative approaches of non-convex optimisation and
poor convergence due to sharply peaked optima.
We also investigate whether imposing inverse con-
sistency constraints (Song and Tustison, 2010) upon
transformations from a reference to template and tem-
plate to reference can benefit the proposed learned
registration. Inverse consistency has proved valu-
able in classic registration algorithms before, most
notably with Song et al (Song and Tustison, 2010)
EMPIRE10 winning solution.
1.1 Previous Work
Much work has been done in utilising deep learn-
ing for medical image registration. A particular fo-
cus has been on patch-based schemes, where the reg-
istration is cast as a classification problem to learn
whether two patches are aligned (positive) or mis-
aligned (negative). These classifications are used to
construct cost fields across the images from which the
patches have been extracted. These cost spaces are
then used to construct dense displacement fields (Si-
monovsky et al., 2016; Lee et al., 2009; Jiang et al.,
2008). Other patch-based schemes include computing
compact representations using stacked autoencoders
and using correlating features to compute a displace-
ment field (Wu et al., 2016).
There has been specific work focussed on rigid
registration, including 2D/3D registration of binary
Sloan, J., Goatman, K. and Siebert, J.
Learning Rigid Image Registration - Utilizing Convolutional Neural Networks for Medical Image Registration.
DOI: 10.5220/0006543700890099
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 2: BIOIMAGING, pages 89-99
ISBN: 978-989-758-278-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
89

masks of wrist implants to wrist images collected by
X-ray by Miao et al (Miao et al., 2016) where they
partition the transformation space and train regressors
for each partitioned zone. Becker et al (Gutierrez-
Becker et al., 2017) use regression forests to itera-
tively compute the transformation parameter for both
mono- and multi-modal experiments.
Simonovsky et al (Simonovsky et al., 2016) uses
a CNN to classify whether two given patches are sim-
ilar with binary predictions, sum the predictions for
each voxel belonging to a given overlapping patch
then use the first-order gradient of the constructed
cost field to compute transformation updates.
Lee et al (Lee et al., 2009) use a max-margin
structured output learning algorithm to learn a bi-
nary predictor of similarity for two given multi-modal
patches, whose responses are used within a classical
registration framework.
Gutierrez-Becker et al (Gutierrez-Becker et al.,
2017) train a regression forest to predict the displace-
ments between two given patches. The regression
forests are given randomly sampled long-range con-
text Haar wavelet features computed around a point x
from the reference and template images. To train the
forest, a series of decision trees are trained upon the
described features to predict the local translation to
align the two points the long-range Haar wavelet fea-
tures have been constructed. After training, the forest
is culled to a small subset of trees with the tree se-
lection criterion being that the the trees which predict
the best estimate of the displacement with lowest co-
variance at the leaf node. Finally, at test time the pre-
dicted displacement for a given point by the forest is
the average over the predictions made by the reduced
forest.
The closest previous work to the presented work
is by Miao et al (Miao et al., 2016) where they train
multiple hierarchial CNN regressors for a partitioned
affine transformation space to align a binary wrist im-
plant image with X-ray wrist image, given the resid-
ual/difference image between the implant and X-ray
images.
1.2 Motivation
The motivation of this work is to investigate the abil-
ity of convolutional neural networks to accurately
regress rigid transformation parameters with a range
of architectures and classic registration constraints.
We explore the viability of these methods for both
mono- and multi-modality registration experiments
with a series of synthetic and real registration tasks.
We initially present a series of synthetic mono-
modality experiments where the reference and tem-
plate images are identical up to a noise term and a
synthetic rigid distortion applied to the template. The
neural networks, given the reference and template im-
age regress the transformation parameters to bring the
reference and template back into alignment.
We also present a series of real-world multi-
modality experiments to align MR T1- and T2-
weighted images using a variety of neural networks
which incorporate user-knowledge of the task.
Throughout the series of learned registration ex-
periments, the neural network predicts the transfor-
mation parameters in a single pass. This allows fast,
real-time registration while avoiding the traditional
pitfalls of iterative optimisation schemes, namely
non-convex and sharply peaked optimisation surfaces
which are anathema to gradient based schemes.
We compare the registration results to results ob-
tained by using multi-scale, iterative registration us-
ing Mattes mutual information (Mattes et al., 2001;
Smriti et al., 2005). We use the Python bindings to
the well-known Insight Segmentation and Registra-
tion Toolkit SimpleITK
1
.
1.3 Data
The Open Access Series of Imaging Studies (OASIS)
(Marcus et al., 2007) was a project aimed at making
MRI datasets freely available to the scientific com-
munity, and has seen use in a number of registra-
tion papers over the past years. We use the OASIS
cross-sectional dataset which consists of 416 subjects
ranging in age from 18 to 96. Each subject has been
scanned multiple times within a single session, with
100 of the subjects being clinically diagnosed with
very mild to moderate Alzheimer’s disease. We use
a single scan from each subject to avoid training and
testing on the same subjects. Each of the volumes has
dimensions of 256×256×128 and voxel resolution of
1mm×1mm×1.25mm orientated saggitally.
The Information eXtraction from Images (IXI)
(Imperial College London, 2010) dataset consists of
600 T1-, T2- weighted MRI, MRA and Diffusion-
weighted scans from healthy and normal subjects
which were collected across 3 hospitals in London.
The ISLES 2015 (ISL, 2015) datasets consists
of 28 subjects, each of which has a MR-T1, MR-
T2 weighted, FLAIR and Diffusion-weighted MR
head volume collected. Each subject’s volumes have
been resampled to isotropic 1 mm
3
, skull-stripped and
manually co-registered, which affords us a rare op-
portunity of possessing multiple co-registered multi-
modal volumes of the same subject. To this end, we
1
http://www.simpleitk.org/SimpleITK/resources/softwa
re.html
BIOIMAGING 2018 - 5th International Conference on Bioimaging
90

will attempt to learn the transformation to rigidly reg-
ister MR-T1 → MR-T2 2D images. We will compare
the results to those obtained by multi-scale, iterative
registration using mutual information.
2 METHODOLOGY
In this section are descriptions of the mono- and
multi-modality experiments performed to investigate
the proposed method and the baseline methods used
for comparisons.
2.1 Mono-modality Experiments
To construct the training and testing data, we ran-
domly selected a volume from the respective cohort
of data and then selected a sagittal 256 × 256 slice
randomly from that volume (excluding any slices con-
taining solely air). The intensities were normalised
to lie within [0, 1] for a reference image. Given the
reference, a random x- and y-translation drawn inde-
pendently from U(−30, 30) pixels, and a random ro-
tation from U(−15, 15) degrees was applied to con-
struct a template image. Finally, Gaussian random
noise, N(µ = 0, σ
2
= 0.01), was added to the image
intensity values of both the reference and template im-
age.
The first monomodal experiment implements two
archetypes of convolutional neural network (CNN) to
regress the transformation parameters. One model is
a typical structure of convolutional layers fed into a
series of dense, fully connected layers and the other
model is a fully convolutional neural network (FCN)
which utilises strided convolutions to learn the trans-
formation. Both models are described in full directly
below.
The CNN consists of two inputs, one for the ref-
erence image and the other for the template image.
Each input has a series of shared 3 × 3 convolutional
weights with linear rectifier unit activation. A skip
connection (Drozdzal et al., 2016) is present after the
first convolution to provide a richer set of features.
The filter responses from the reference and template
image are concatenated along the channel axis and
flattened into a single 1D array. The concatenated,
flattened filter responses are then fed into 3 stacked
dense layers, where the final layer produces the re-
gressed transformation parameters. A graphic of the
described convolutional neural network is displayed
in figure 1.
In an attempt to regularise the massive number
of weights between the concatenated output of the
shared vision towers and the first dense layer, we used
dropout (Srivastava et al., 2014) and set the fraction
of neurons in the first dense layer to be dropped out at
0.5.
The fully convolutional neural network (FCN)
consists of two inputs, one for the reference image
and the other for the template image. Each input has a
series of shared 5 × 5 convolutional weights with lin-
ear rectifier unit activations. A skip connection is also
present to concatenate the activations of the convolu-
tional layers along the channel axis. The concatenated
responses from the shared vision towers are then fed
into a series of strided convolutions until the output of
the final layer has the correct dimensions of 3 scalars
ie. the transformation parameters. Each of the strided
convolutional layer (except the final layer) has 7 ker-
nels with each kernel possessing dimensions of 5×5
with leaky rectifier unit activations and strides of 2
along the x- and y-dimensions of the feature maps.
The final layer has 3 kernels with each kernel having
dimensions of 3×3 with a linear activation to allow
the model to regress negative values.
A key decision we have made in designing the
described convolutional neural networks is not using
max pooling (Scherer et al., 2010) anywhere within
the model. This is because max pooling has the well-
known property of providing local shift invariance to
input feature maps ie. the output feature maps do not
change if the input feature maps are shifted by a small
amount. The purpose of our networks is to regress
these small shifts as accurately as possible so the in-
clusion of max pooling would most likely lead to a
degradation of results.
Both the described models were trained on 30000
registration instances constructed from the OASIS
data, using an Adadelta optimizer (learning rate = 1,
ρ=0.95) for 30 epochs. We used the mean squared
error (MSE) function between the true transforma-
tion parameters T
true
and the predicted transformation
parameters T
pred
to train the described CNN over a
batchsize M:
MSE(T
true
, T
pred
) =
1
M
M
∑
i=1
(T
true
i
− T
pred
i
)
2
(1)
We tested on 500 registration instances con-
structed from subjects from the OASIS dataset not
previously used to construct training data. This al-
lows us to test how well the model generalises to un-
seen subjects collected on the same scanners as the
subjects used to construct the training data.
In addition to this, both models were tested on
500 registration instances constructed from the IXI
brain development dataset (Imperial College London,
2010) to investigate how well the model generalises
Learning Rigid Image Registration - Utilizing Convolutional Neural Networks for Medical Image Registration
91
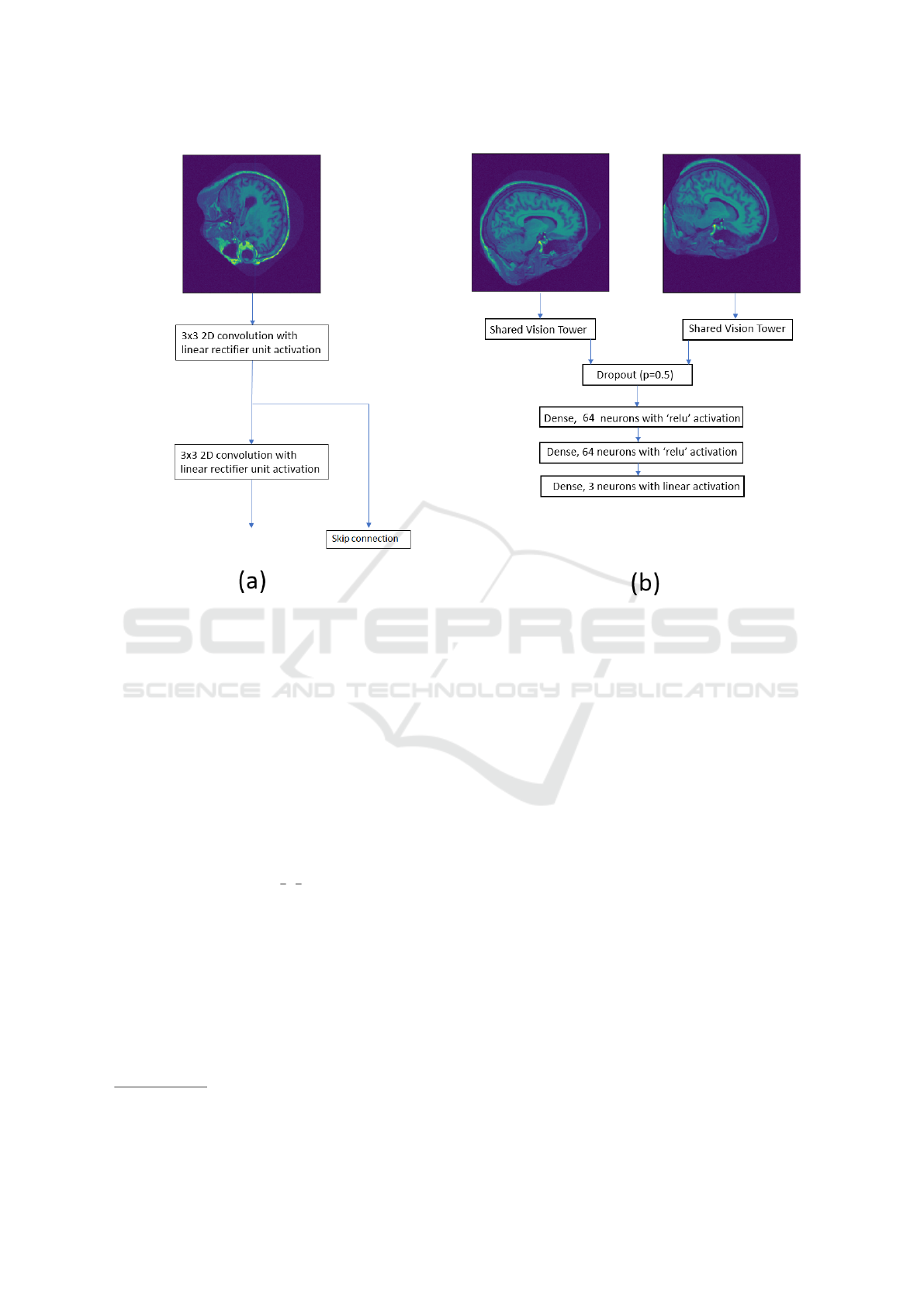
Figure 1: (a) The vision tower used for feature extraction from the input image. (b) The CNN model used for registration,
where the final layer is the regressed transformation parameters ie. x- and y-translation and the rotation around the centre.
The shared vision tower is the model displayed in (a).
to other datasets. Coronal slices from the IXI dataset
were used to construct testing data in an identical
manner to how the training instances from the training
subjects of the OASIS dataset were constructed.
We compare the registration results to results ob-
tained by using multi-scale, iterative registration us-
ing Mattes mutual information (Mattes et al., 2001).
We use the Python bindings to the well-known Insight
Segmentation and Registration Toolkit SimpleITK
2
.
We used the mutual information between the refer-
ence and template image as a similarity metric, and
used a scale pyramid of {
1
4
,
1
2
, 1}, with a smoothing
sigma of {2, 1, 0} at each respective scale. The joint
histogram used to compute the mutual information
was 60 × 60 bins, and the maximum number of itera-
tions was set to 100.
2.2 Multi-modality Experiments
We used the first 22 subjects from ISLES 2015 to gen-
erate training data, and the remaining 6 subjects to
generate the testing data. We used the same process as
2
http://www.simpleitk.org/SimpleITK/resources/softwa
re.html
described in subsection 2.1 to construct training and
testing instances, but we apply the randomly sampled
transformation to the corresponding T2 axial slice of
the randomly selected T1 axial slice.
The content of the multi-modal experiments is
very similar to that of the mono-modal experiments
described in section 2.1, but we are trying to regress
transformation parameters to register MR-T2 → MR-
T1. The transformation parameters being regressed
are in the same range as the mono-modal experiments,
with x and y- translation sampled from U (−30, 30)
pixels and the rotations around the centre of the im-
age sampled from U(−15
◦
, 15
◦
). Examples slices of
ISLES data can be found in figure 2.
For the first multi-modal experiment, we attempt
to use a CNN to regress the transformation param-
eters. The CNN used for the mono-modal registra-
tion experiments, as described in section 2.1, is al-
most identical in structure to the CNN used in this
experiment. As the reference and template images
are different modalities with visibly different spatial
resolution (see figure 2), it is not necessarily opti-
mal to have shared convolutional weights so the con-
volutional weights applied to the T1 and T2 image
were not shared. This adds 18 additional free weights
BIOIMAGING 2018 - 5th International Conference on Bioimaging
92

Figure 2: The left image is an example slice of a T1-
weighted MR slice from the ISLES dataset and the right
image is the corresponding T2-weighted MR slice. Note
the different spatial resolutions of the images.
to optimise when compared to the CNN used in the
monomodal experiments, which is very small when
compared to the total number of weights to optimise
in the entire model. We tested the model on 500 test
instances generated from the remaining 6 subjects of
the ISLES dataset.
The second multi-modal experiment consists of
repeating the first CNN multi-modality experiment
with 30000 training instances generated from the first
10 subjects of the ISLES data. This was done to test
how well the CNN generalises with only a small num-
ber of unique subjects to train on. The 500 testing in-
stances were constructed from the remaining 18 sub-
jects.
The third and fourth multi-modality experiments
are training two FCNs, one of which possess shared
weights within the vision towers (as displayed in fig-
ure 3 and the other possessing separate weights within
the vision towers applied to the reference and tem-
plate image. This was to test whether learning sepa-
rate image features within the vision towers for differ-
ent modalities was beneficial or detrimental.
The fifth multi-modal experiment consists of us-
ing SimpleITK to register the same test instances as
the first multi-modality experiment. We used the mu-
tual information between the reference and template
image as the similarity metric, and used a scale pyra-
mid of {
1
4
,
1
2
, 1}, with a smoothing sigma of {2, 1, 0}
at each respective scale. The joint histogram used
to compute the mutual information was 60 × 60 bins,
and the maximum number of iterations was set to 100.
2.3 Introducing Inverse Consistency
Errors
Inverse consistency error (ICE) is a classic vision
problem which measures the difference between map-
pings T
1
and T
2
computed by some algorithm that map
the space X to another space Y and from Y to X re-
spectively. If the algorithm correctly computes T
1
and
T
2
, then T
1
= T
−1
2
(with the assumption of bijective
mappings between the spaces). This constraint has
been imposed on a number of problems such as style
transfer by (Zhu et al., 2017) and most notably within
the registration community by Song et al (Song and
Tustison, 2010) which lead to the EMPIRE (Murphy
et al., 2011) challenge winning solution.
We will perform two experiments to incorpo-
rate inverse consistency to our learned registration
paradigm. Firstly, we attempt to implicitly use ICE
during training time by giving the model the refer-
ence as the reference and the template as the template
and fit the model to the true transformation parame-
ters. Simultaneously, we pass the model the template
as the reference and the reference as the template and
fit the model to the inverse transformation parameters.
To update the weights within the model, the gradients
from both operations are summed and the model op-
timised accordingly. This acts as a data augmentation
technique but additionally becomes a soft constraint
for ICE. To test this, we rerun the mono-modality ex-
periments involving the FCN as described in subsec-
tion 2.1 but with the described simultaneous training
method incorporating inverse transformations. This
experiment is denoted as ICE implicit.
The second experiment to incorporate ICE is us-
ing a transformation regressor during detection time
to regress the transformation T
1
from reference to
template and additionally regress the transforma-
tion T
2
from template to reference. For the final
transformation T
f inal
from reference to template, we
use ’half’ of T
1
= {θ
1
, t
x
1
, t
y
1
} and ’half’ of T
−1
2
=
{θ
2
, t
x
2
, t
y
2
} such that the transformation matrix
ˆ
T
f inal
of T
f inal
is of the form:
ˆ
T
f inal
=
cos(
θ
1
+θ
2
2
) − sin(
θ
1
+θ
2
2
)
t
x
1
+t
x
2
2
sin(
θ
1
+θ
2
2
) cos(
θ
1
+θ
2
2
)
t
y
1
+t
y
2
2
0 0 1
(2)
This experiment is denoted as ICE explicit.
3 EVALUATION
Displayed in table 1 are the results from the experi-
ments as described in the previous section.
Also displayed are scatter plots of predicted trans-
formation parameter vs. known transformation pa-
rameter for a choice set of experiments described in
sections 2.1 & 2.2. Figure 4 displays the results of
the FCN trained on the first 100 OASIS subjects and
then tested on the registration instances constructed
from the remaining subjects. Figure 5 displays the re-
sults of the same FCN tested on unseen IXI subjects.
Learning Rigid Image Registration - Utilizing Convolutional Neural Networks for Medical Image Registration
93
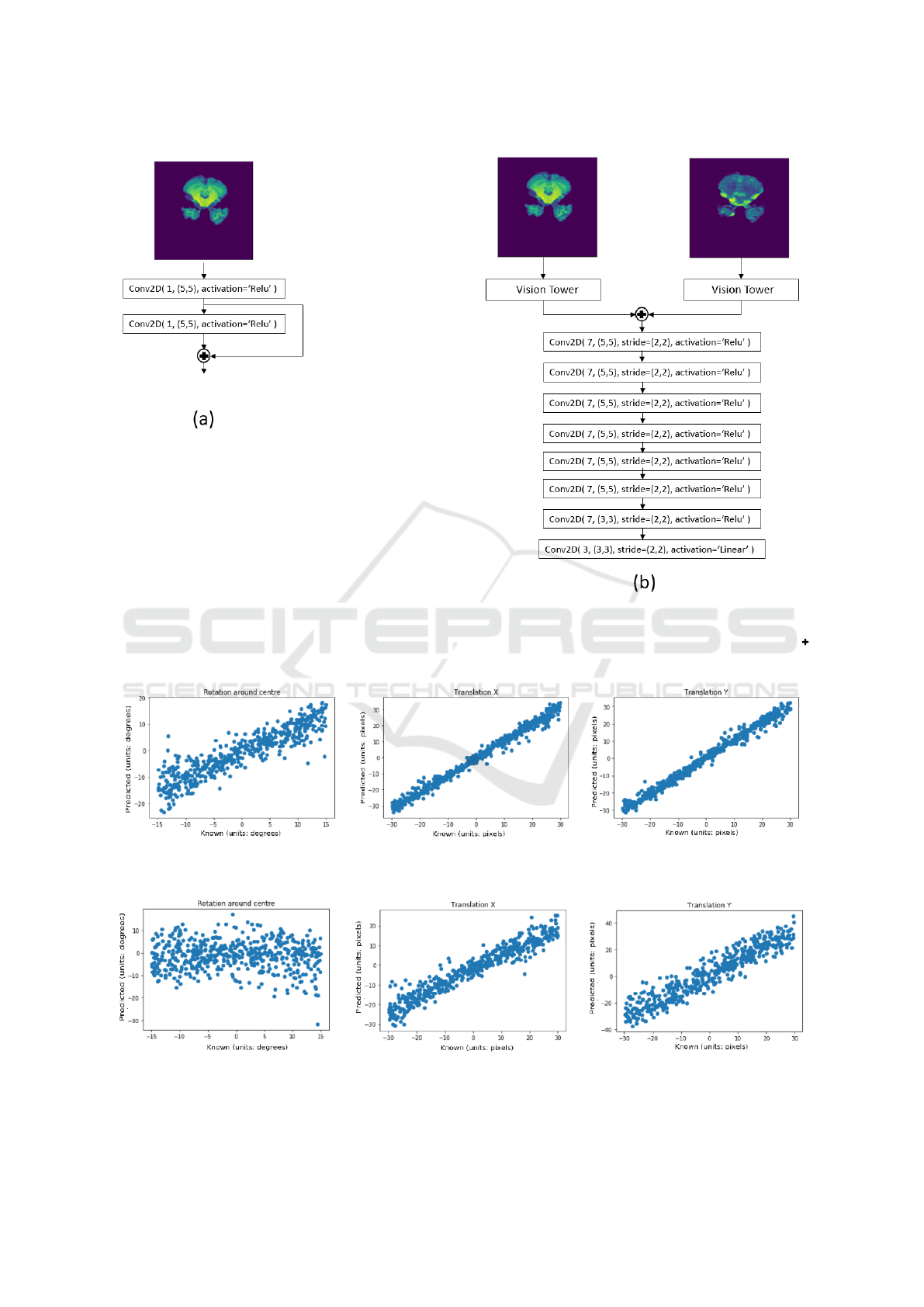
Figure 3: Fully convolutional neural network (FCN) used for the multi-modality experiments. Model (a) is the vision tower
used to extract features from the input images. Model (b) is the FCN which regress the transformation between a given
reference and template image with Model (a) possessing either shared or separate weights, depending on the experiment.
indicates the two inputs are merged via concatenation along the channel axis of the input tensors and outputted.
Figure 4: Scatter plot of predicted vs. known transformation parameters for the mono-modality experiment and testing on
unseen OASIS data, using the FCN with shared vision towers as the transformation regressor.
Figure 5: Scatter plot of predicted vs. known transformation parameters for the mono-modality experiment and testing on
unseen IXI data, using the FCN with shared vision towers as the transformation regressor.
BIOIMAGING 2018 - 5th International Conference on Bioimaging
94
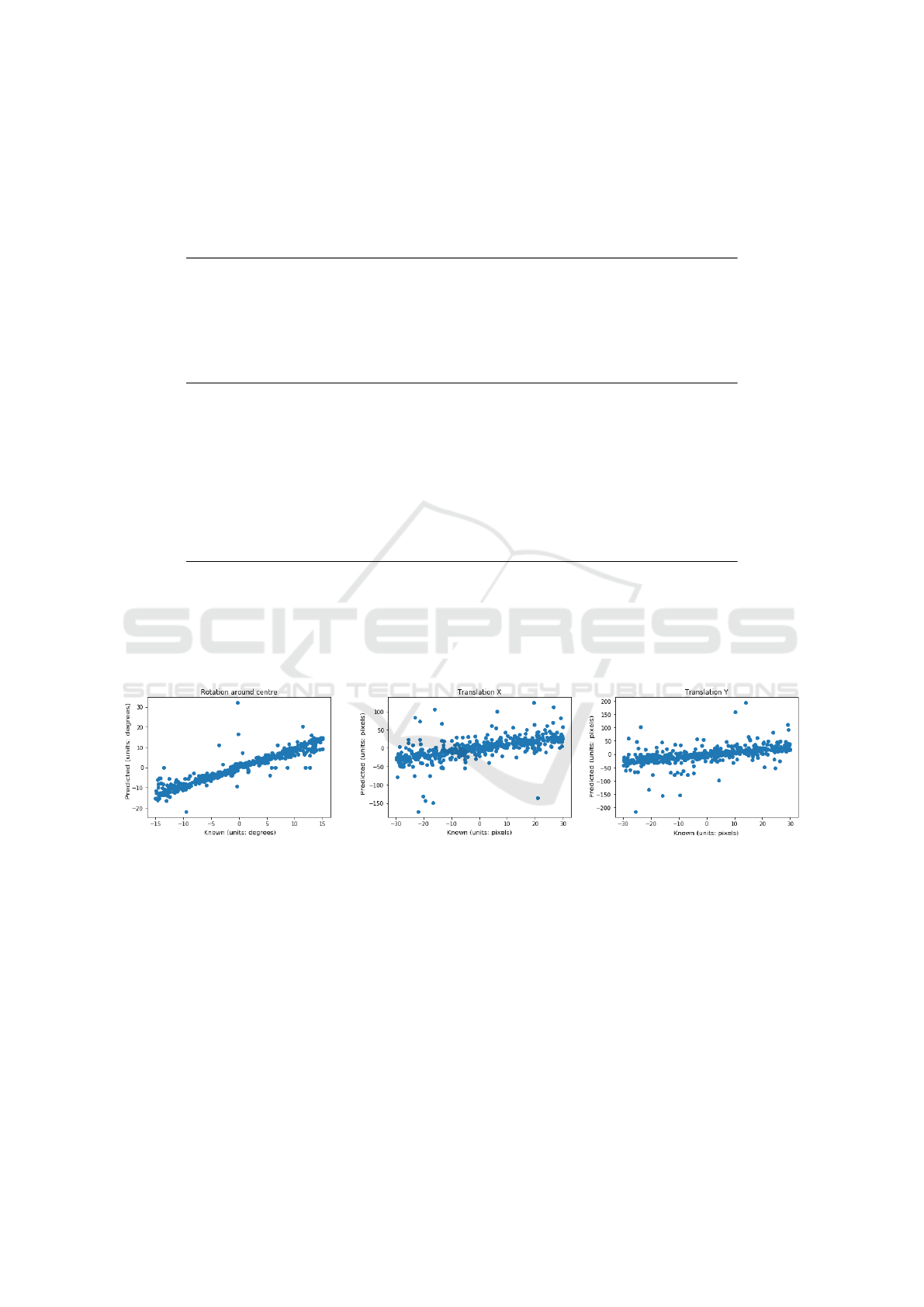
Table 1: Mono-modal and multi-modal results from experiments described in section 2. Mean absolute error and standard
deviation between the measured and known transform parameters for the multi-scale iterative registration and the CNN re-
gression methods. Rotation error is measured in degrees and translation errors are measured in pixels.
Mono-modality results
OASIS experiments Rotation Translation X Translation Y
CNN 2.45 ± 2.78 1.66 ± 2.13 1.81 ± 2.78
FCN 1.71 ± 2.35 1.40 ± 1.74 1.44 ± 1.82
FCN (ICE implicit) 2.21 ± 3.06 1.58 ± 2.09 1.70 ± 2.17
FCN (ICE explicit) 2.90 ± 3.80 1.52 ± 2.12 1.65 ± 2.20
SimpleITK 3.02 ± 5.04 18.97 ± 31.2 17.75 ± 30.26
IXI experiments Rotation Translation X Translation Y
CNN 6.81 ± 7.85 4.22 ± 5.24 4.66 ± 6.81
FCN 9.22 ± 11.06 4.92 ± 6.08 4.67 ± 5.61
FCN (ICE implicit) 8.80 ± 10.86 5.80 ± 7.20 4.56 ± 5.71
FCN (ICE explicit) 8.94 ± 10.66 4.80 ± 6.25 4.26 ± 5.35
SimpleITK 1.59 ± 2.88 21.33 ± 34.78 23.90 ± 38.91
Multi-modality results
ISLES experiments Rotation Translation X Translation Y
CNN (trained on 22 subjects) 3.93 ± 4.60 2.38 ± 3.07 2.45 ± 3.15
CNN (trained on 10 subjects) 4.09 ± 5.40 3.14 ± 3.92 2.18 ± 2.84
FCN (separable vision) 3.24 ± 3.90 2.65 ± 3.25 2.11 ± 2.36
FCN (shared vision) 2.66 ± 3.68 1.64 ± 2.07 1.40 ± 1.99
SimpleITK 1.29 ± 2.24 2.92 ± 7.31 2.82 ± 4.07
Figure 6: Scatter plot of predicted vs. known transformation parameters for the mono-modality experiment, using the Sim-
pleITK implementation as described in sub-section 2.1.
Figure 7 displays the results of the FCN with shared
vision towers, trained on the first 18 subjects of the
ISLES dataset and tested on the remaining 6 subjects.
4 DISCUSSION
As can be seen from table 1, our method performs
well when compared with the SimpleITK implemen-
tation for the OASIS and IXI test datasets for the
mono-modal experiments. A major failing of our
method is the rotation regression on the IXI dataset
is very poor. Indeed, it’s predictions for rotation do
not appear to correlate with the known rotation at all
(see the left plot of figure 5). This suggests that our
method does not generalise well to subjects which
have been collected from another scanner or differ-
ent scanning protocol. This is known generally as the
problem of domain adaptation (Ganin et al., 2015;
Kamnitsas et al., 2017).
Domain adaptation is the problem of images that
at a high-level are similar but there is sufficient differ-
Learning Rigid Image Registration - Utilizing Convolutional Neural Networks for Medical Image Registration
95
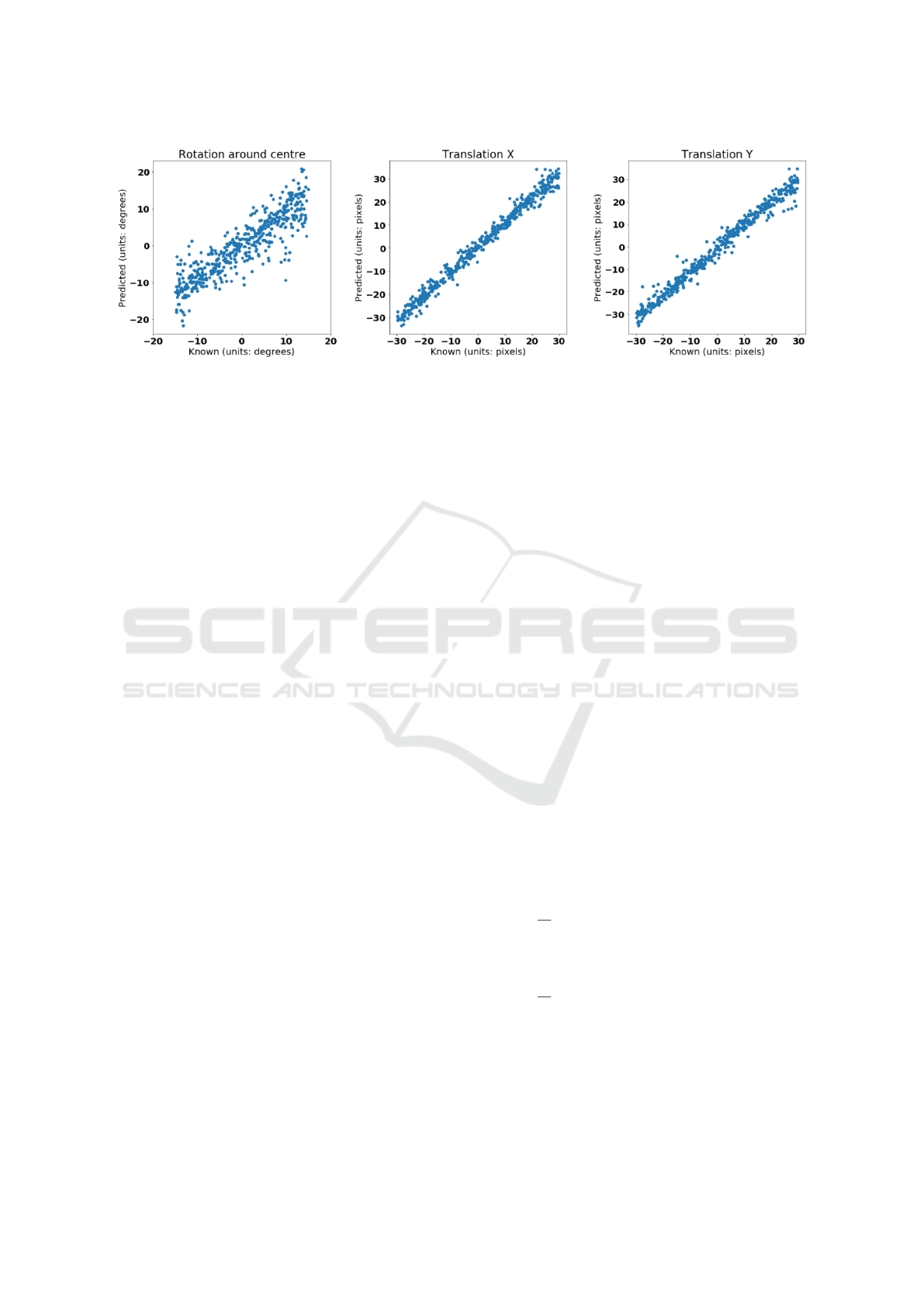
Figure 7: Scatter plot of predicted vs. known transformation parameters for the multi-modality experiment, using the FCN
with shared vision towers as the transformation regressor.
ences that a deep learning, or any machine learning al-
gorithm does not generalise to these unseen datasets.
The differences can be a number of low-level prop-
erties such as noise characteristics or image resolu-
tion and high-level properties such as scanning proto-
col or underlying anatomy being imaged. The OASIS
dataset is collected from a single scanner in a Wash-
ington hospital while the IXI dataset was collected
from 3 scanners from different hospitals across Lon-
don. There is sufficient differences between the two
datasets that a deep learning algorithm trained on a
subset of the OASIS subjects generalises well to un-
seen subjects from OASIS but performs poorly on un-
seen subjects from the IXI dataset.
To test our hypothesis of domain adaptation, we
trained a FCN on a subset of the IXI dataset to regress
the rigid transformation parameters as described in
previous experiments and tested on unseen subjects
from the IXI dataset and unseen subjects from the
OASIS subject. The results (as shown in table 2)
demonstrate that our method generalises well to sub-
sets of IXI subjects when trained on other subsets of
IXI datasets but performs poorly on OASIS subjects.
This suggests that the proposed method suffers
from the effect of domain adaptation as our method
gives excellent results on unseen subjects from IXI
when trained on another subset of IXI subjects but
generalises poorly to OASIS subjects.
Our method also performs well with the multi-
modality test datasets and is of comparable perfor-
mance with the SimpleITK implementation but our
method possesses fewer outliers (observe the standard
deviation of the results). The multi-modality experi-
ments may be considered a more powerful and real-
istic demonstration of the proposed method as there
will be a small amount of non-rigid deformation be-
tween the acquisition of the MR T1- and T2- weighted
images used to construct the reference and template,
unlike the mono-modality experiments where the un-
derlying anatomy of the reference and template are
identical up to the added noise term.
The CNN trained on only 10 subjects and testing
on the remaining 16 subjects shows the method gen-
eralises well even though there is a restricted number
of subjects to train on as the results between the CNN
trained on 22 and 10 subjects respectively are not sig-
nificantly different.
Throughout all of the learned registration models,
the rotation parameter consistently has larger mean
absolute error and standard deviation than the x- and
y- translation parameters (see tables 1 & 2). We hy-
pothesised that because the maximum and minimum
values of the rotation parameter and translation pa-
rameters are {−15
◦
, 15
◦
} and {−30 pixels, 30 pixels}
respectively, the mean squared error objective func-
tion (equation 1) used to train each of the models is
likely to change the weights to minimise the errors
due to translation errors as they contribute proportion-
ally more to the error function. To test this hypothe-
sis, we re-evaluated the multi-modality experiments
but used a weighted objective function to train the
networks to balance the loss contributions from the
translations and rotation:
MSE(T
true
, T
pred
)
=
1
M
M
∑
i=1
(x
true
i
− x
pred
i
)
2
+ (y
true
i
− y
pred
i
)
2
+ (2(θ
true
i
− θ
pred
i
)
2
)
=
1
M
M
∑
i=1
(x
true
i
− x
pred
i
)
2
+ (y
true
i
− y
pred
i
)
2
+ 4(θ
true
i
− θ
pred
i
)
2
(3)
After re-evaluating the multi-modality experi-
ments with the weighted loss objective function, we
still observed consistently higher errors for the rota-
tion parameter.
BIOIMAGING 2018 - 5th International Conference on Bioimaging
96

Table 2: Domain adaption experiments, where we train a FCN on a subset of the IXI dataset and test on unseen IXI subjects
and the OASIS dataset to regress rigid 2D transformation parameters. Mean absolute error and standard deviation between
the measured and known transform parameters for the multi-scale iterative registration and the CNN regression. Rotation
measured in degrees and translations measured in pixels.
Domain adaptation experiments Rotation Translation X Translation Y
Unseen IXI subjects 1.70 ± 2.26 1.43 ± 1.88 1.36 ± 1.64
Unseen OASIS subjects 8.43 ± 10.14 3.14 ± 4.70 3.74 ± 4.89
The FCN models with shared and separable
weights within the the vision towers for multi-
modality registration produce results which are not
statistically significant.
4.1 Inverse Consistency Discussion
Our inverse consistency experiments demonstrated
that inverse consistency does not improve the results,
regardless of whether it is imposed implicitly by up-
dating the weights of the network when training on
registration instances of the R → T and T → R simul-
taneously or using half of the forward transform from
R → T and half of the inverse transform from T → R
to compose a transform from R → T (see equation 2).
It is not surprising that composing half transforma-
tions to form a final transformation from R & T does
not improve the results as it is not obvious where any
additional benefit would come from. Within the work
of Song et al (Song and Tustison, 2010), imposing in-
verse consistency using half-transformations provides
the benefit of making the displacement field diffeo-
morphic but for our experiments of rigid transforma-
tions there is no such benefit.
It is perhaps more surprising that the explicit in-
verse consistency experiments of passing the network
the reference and template images and training on reg-
istration instances of the R → T and T → R simulta-
neously did not improve the results. We might have
expected the results to have improved solely because
though we passed the model 12000 training instances,
the number of training instances effectively doubles
as the model is fitted to R → T and T → R. By effec-
tively doubling the amount of training data, the model
would have been expected to improve but the results
indicate this is not the case.
4.2 Comparison to State-of-the-art
Methods
Displayed in figures 8 and 9 are the transformation
parameter updates for the methods presented by (Si-
monovsky et al., 2016) and (Gutierrez-Becker et al.,
2017) respectively. These plots are equivalent to our
plots presented in figures 4 and 7 where we display
the predicted transformation updates vs. the known
transformation using our described method. Note that
their plots are highly non-linear and thus could never
predict the transformation parameters in a single pass.
Indeed, it is the linearity of our plots that allow us to
do so in a single pass.
Simonovsky et al (Simonovsky et al., 2016)
plots look like classic transformation updates from a
sharply peaked metric at the optimal transformation
update. The steep gradient at either side of the opti-
mum results in large transformation updates a small
perturbation from the optimal transformation. This is
typified by the x- transformation update (green plot-
ted line in the left plot of figure 8 when perturbing
the image along the x-axis and the rotation around the
x-axis transformation update when perturbing around
the x-axis (green plotted line of the right plot in figure
8. Additionally, they compute the transformation up-
dates θ
update
as first-order gradients
∂M
∂θ
of the learned
metric M such that θ
update
= α
∂M
∂θ
where α is a user
set gain coefficient. If one wanted to design a met-
ric that provides linear transformation updates vs per-
turbation, the metric M, learned or otherwise, should
have a parabolic profile:
α.
∂M
∂θ
!
= θ
perturbation
, set α = 1
Z
∂M =
Z
θ
perturbation
.∂θ
M = θ
2
perturbation
+C
(4)
Becker et al (Gutierrez-Becker et al., 2017)
present more interesting transformation updates (top
row of figure 9) which look smoother and translation
updates which look like they monotonically decrease
(though this may be due to sparser sampling of per-
turbations). The smoothness of the predicted trans-
formation updates is most likely due the smooth solu-
tions generally computed by regression forests which
are conventionally the average of the predicted values
of each decision tree within the forest. Interestingly,
the translation updates resemble a Fermi-Dirac distri-
bution but the authors make no comment on this.
However neither of the plotted regressed transla-
tion and rotation parameter demonstrate linearity with
respect to the known transformation perturbation.
Learning Rigid Image Registration - Utilizing Convolutional Neural Networks for Medical Image Registration
97

Figure 8: Taken from Simonovsky et al (Simonovsky et al.,
2016). The plot on the left displays their learned deep multi-
modal metric value and it’s derivative w.r.t x, y and z as a
test image is perturbed along the x-axis with respect to the
corresponding multi-modal image. The plot on the right
displays the same metric and it’s derivatives w.r.t rotations
around the x, y and z axis as the test image is rotated around
the x-axis with respect to corresponding multi-modal im-
age.
Figure 9: Taken from Gutierrez-Becker et al (Gutierrez-
Becker et al., 2017). The top left plot displays the transfor-
mation parameter update predicted by their regression for-
est method, where each plotted line is the predicted trans-
formation update as the images are perturbed along that di-
mension and keeping the other transformation parameters
fixed at zero. The top right plot is similar to the top left
plot where the rotation around each axis is perturbed and
the transformation parameter computed by their method to
correct the perturbation. The bottom left and right plots are
the same experiment as the top row but the transformation
parameters are computed using Normalised Mutual Infor-
mation for comparison as a baseline.
5 CONCLUSIONS
We have presented a novel method of registering im-
ages by regressing the transformation parameters us-
ing a convolutional neural network and demonstrated
its efficacy for both mono- and multi-modal applica-
tions. We have demonstrated it is possible to accu-
rately register images in a single pass.
For our mono-modal experiments, we demon-
strated that the model generalises well to unseen sub-
jects from the same dataset. This is likely because
the training and testing subjects were collected from
the same scanner, and thus the image resolutions will
be similar and the scanning protocols the same. The
method did not generalise as well to subjects from the
IXI dataset and thus the method is subject to the prob-
lem of domain adaptation (Ganin et al., 2015) which
afflicts many medical imaging applications.
For our multi-modal experiments, we demon-
strated that our model produces comparable results to
that of the described multi-scale iterative scheme us-
ing mutual information. We also demonstrated that
the proposed CNN method generalises sufficiently
well with a small number of unique subjects, by train-
ing 2 convolutional networks which are identical in
structure with training data constructed from 22 and
10 unique subjects respectively and no significant de-
crease in accuracy was observed.
For mono-modality registration, we can build near
infinite sets of training datasets as any image can be
translated and rotated with respect to itself to produce
a training instance.
For multi-modality registration, we are restricted
by the availability of co-registered multi-modal data
such as CT and MR to construct training data. Build-
ing datasets of manually co-registered multi-modal
images requires additional effort, but can be well jus-
tified if traditional metrics are not sufficient.
REFERENCES
(2015). Ischemia Stroke Lesion Segmentation 2015 Chal-
lenge.
Drozdzal, M., Vorontsov, E., Chartrand, G., Kadoury, S.,
and Pal, C. (2016). The Importance of Skip Connec-
tions in Biomedical Image Segmentation. MICCAI
2016 DL workshop, 10008:197–205.
Ganin, Y., Ustinova, E., Ajakan, H., Germain, P.,
Larochelle, H., Laviolette, F., Marchand, M., Lempit-
sky, V., Dogan, U., Kloft, M., Orabona, F., and Tom-
masi, T. (2015). Domain-Adversarial Training of Neu-
ral Networks. Journal of Machine Learning Research,
17:1–35.
Gutierrez-Becker, B., Peter, L., Mateus, D., and Navab,
N. (2017). Learning Optimization Updates for Mul-
timodal Registration. In MICAAI 2017.
Imperial College London (2010). IXI brain development
homepage.
Jiang, J., Zheng, S., Toga, A., and Tu, Z. (2008). Learning
Based Coarse-to-fine Image Registration. Computer
Vision and pattern Recognition, 2008. CVPR 2008.
Kamnitsas, K., Baumgartner, C., Ledig, C., Newcombe, V.,
Simpson, J., Kane, A., Menon, D., Nori, A., Criminisi,
BIOIMAGING 2018 - 5th International Conference on Bioimaging
98

A., Rueckert, D., and Glocker, B. (2017). Unsuper-
vised domain adaptation in brain lesion segmentation
with adversarial networks. Lecture Notes in Computer
Science (including subseries Lecture Notes in Artifi-
cial Intelligence and Lecture Notes in Bioinformatics),
10265 LNCS:597–609.
Lee, D., Hofmann, M., Steinke, F., Altun, Y., Cahill,
N. D., and Sch
¨
olkopf, B. (2009). Learning sim-
ilarity measure for multi-modal 3D image registra-
tion. 2009 IEEE Computer Society Conference on
Computer Vision and Pattern Recognition Workshops,
CVPR Workshops 2009, pages 186–193.
Marcus, D. S., Wang, T. H., Parker, J., Csernansky, J. G.,
Morris, J. C., and Buckner, R. L. (2007). Open access
series of imaging studies (OASIS): Cross-sectional
MRI data in young, middle aged, nondemented, and
demented older adults. Journal of Cognitive Neuro-
science, 19:1498–1507.
Mattes, D., Haynor, D., Vesselle, H., Lewellen, T., and Eu-
bank, W. (2001). Non-rigid multimodality image reg-
istration. In Medical Imaging 2001: Image Process-
ing. SPIE Publications, pages 1609–1620.
Miao, S., Wang, Z. J., Zheng, Y., and Liao, R. (2016). Real-
time 2D/3D registration via CNN regression. Pro-
ceedings - International Symposium on Biomedical
Imaging, 2016-June:1430–1434.
Murphy, K., Ginneken, B. V., Reinhardt, J. M., Member,
S., Kabus, S., Ding, K., Deng, X., Cao, K., Du, K.,
Christensen, G. E., Garcia, V., Vercauteren, T., Ay-
ache, N., Commowick, O., Malandain, G., Glocker,
B., Paragios, N., Navab, N., Gorbunova, V., Sporring,
J., Bruijne, M. D., Han, X., Heinrich, M. P., Schn-
abel, J. A., Jenkinson, M., Lorenz, C., Modat, M.,
Mcclelland, J. R., Ourselin, S., Muenzing, S. E. A.,
Viergever, M. A., Nigris, D. D., Collins, D. L., Arbel,
T., Peroni, M., Li, R., Sharp, G. C., Schmidt-richberg,
A., Ehrhardt, J., Werner, R., Smeets, D., Loeckx, D.,
Song, G., Tustison, N., Avants, B., Gee, J. C., Star-
ing, M., Klein, S., Stoel, B. C., Urschler, M., Werl-
berger, M., Vandemeulebroucke, J., Rit, S., Sarrut, D.,
and Pluim, J. P. W. (2011). Evaluation of Registration
Methods on Thoracic CT : The EMPIRE10 Challenge.
IEEE transactions on medical imaging, 30(11):1901–
1920.
Scherer, D., Andreas, M., and Behnke, S. (2010). Evalua-
tion of Pooling Operations in Convolutional Architec-
tures for Object Recognition. In International Confer-
ence on Artifical Neural Networks, number September
2010.
Simonovsky, M., Guti
´
errez-Becker, B., Mateus, D., Navab,
N., and Komodakis, N. (2016). A Deep Metric for
Multimodal Registration. In Medical Image Com-
puting and Computer-assisted Intervention – MICCAI
2016, pages 1–10.
Smriti, R., Steredney, D., Schmalbrock, P., and Clymer,
B. D. (2005). Image Registration Using Rigid Reg-
istration and Maximisation of Mutual Information. In
13th Annual Medicine Meets Virtual Reality Confer-
ence, pages 26–29.
Song, G. and Tustison, N. J. (2010). Lung CT image reg-
istration using diffeomorphic transformation models.
Medical Image Analysis for the Clinic, pages 23–32.
Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. (2014). Dropout: A Simple
Way to Prevent Neural Networks from Overfitting.
Journal of Machine Learning Research, 15:1929–
1958.
Wu, G., Kim, M., Wang, Q., Brent, M., and Shen, D.
(2016). Scalable High Performance Image Registra-
tion Framework by Unsupervised Deep Feature Rep-
resentations Learning. IEEE Transactions on Biomed-
ical Engineering, 63(7):1505–1516.
Zhu, J.-Y., Park, T., Isola, P., and Efros, A. A. (2017).
Unpaired Image-to-Image Translation using Cycle-
Consistent Adversarial Networks.
Learning Rigid Image Registration - Utilizing Convolutional Neural Networks for Medical Image Registration
99
