
Efficient Projective Transformation and Lanczos Interpolation on ARM
Platform using SIMD Instructions
Konstantinos Papadopoulos and Kyriakos Vlachos
Computer Engineering and Informatics Department, University of Patras, Patras, Greece
Keywords:
NEON, SIMD, Image Processing, Projective Transformation.
Abstract:
This paper proposes a novel way of exploiting NEON SIMD instructions for accelerating projective transfor-
mation in ARM platforms. Instead of applying data parallelism to linear algorithms, we study the effectiveness
of SIMD intrinsics on this non-linear algorithm. For image resampling, Lanczos interpolation is used since
it is adequately accurate, despite its rather large complexity. Multithreading is also employed for optimal use
of system resources. Moreover, qualitative and quantitative results of NEON’s performance are presented and
analyzed.
1 INTRODUCTION
Projective transformation is used in a wide range of
computer vision applications. It provides a linear
mapping between arbitrary quadrilaterals which is
very useful for deforming images controlled by mesh
partitioning. Some of the most well-known applicati-
ons are the removal of perspective distortion, image
stabilization, panoramic mosaic creation and object
tracking. Moreover, Lanczos resampling is one of
the most accurate algorithms for image upscaling, ac-
cording to (Burger and Burge, 2009). However, it is
computationally intensive, which can result in a poor
performance. The demand of faster multimedia appli-
cations is high, therefore improving projective trans-
formation’s processing time is crucial.
SIMD units’ contribution in multimedia applica-
tion development has been significant over the past
years. It allows parallel execution of both data type
operations (arithmetic, logical, etc.) and load/store
operations. Theoretically, this unit is able to accele-
rate operations up to 16 times, but this applies only
to certain data types. Optimal use of SIMD is possi-
ble at the low assembly level. However, developers
have the option to use SIMD intrinsics in high-level
programming (C/C++), taking advantage of interope-
rability and improved control over data.
Work presented in (Welch et al., 2012) regards
the implementation 2D bilinear interpolation algo-
rithm using NEON SIMD instructions. This algo-
rithm is exclusively used for image scaling. The
speedup achieved compared to the baseline algorithm
was 1.97-2.06 times. Moreover, in (Mitra et al.,
2013), authors proposed SIMD vector operations to
accelerate code performance on both low-powered
ARM and Intel platforms. They implemented Float
to Short data type conversion, binary image threshol-
ding, Gaussian Blur filter, Sobel filter and edge de-
tection algorithms in various ARM devices and ma-
naged to achieve speed gains from 1.05 to 13.88 com-
pared to compiler auto-vectorization. In addition,
(Mazza et al., 2014) achieved a speed gain of 3.76-
3.86 in bilinear interpolation using multithreading (2
Cortex-A9 cores) and SIMD instructions. Additional
work in SIMD multimedia processing field includes
linear image processing using OpenCL’s SIMD capa-
bilities in (Antao and Sousa, 2010) and acceleration of
alpha blending algorithm in a Flash application using
the Intel x86-64 platform’s SIMD (SSE) instructions
in (Perera et al., 2011).
This paper proposes a way of accelerating pro-
jective transformation using NEON SIMD instructi-
ons. The chosen resampling method is Lanczos in-
terpolation which is demanding and computationally
heavy, but produces notably results in terms of accu-
racy. Multithreading is utilized too, offering efficient
use of CPUs’ resources. Overall performance evalu-
ation of the proposed implementation is based on the
speed gains. Qualitative evaluation is also provided
for the output frames.
Papadopoulos, K. and Vlachos, K.
Efficient Projective Transformation and Lanczos Interpolation on ARM Platform using SIMD Instructions.
DOI: 10.5220/0006547000950100
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages
95-100
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
95

2 SIMD IMPLEMENTATION
Our implementation is divided into two separate
parts: projective mapping function and resampling.
Each of these parts affects differently the way of data
parallelization.
2.1 SIMD Projective Mapping
Inverse mapping approach is used in this context.
This means that, for each discrete pixel position
(u,v) in output image, the corresponding continuous
point (x, y) is computed, using the inverse geometrical
transformation T
−1
. In this method, each pixel of the
target image I
0
is calculated and filled exactly once,
so that there are no empty spots or multiple fillings.
The calculation of coordinates x and y is shown in (1)
and (2), respectively:
x =
1
h
0
· (d
11
x
0
+ d
12
y
0
+ d
13
) =
d
11
x
0
+ d
12
y
0
+ d
13
d
31
x
0
+ d
32
y
0
+ 1
(1)
y =
1
h
0
· (d
21
x
0
+ d
22
y
0
+ d
23
) =
d
21
x
0
+ d
22
y
0
+ d
23
d
31
x
0
+ d
32
y
0
+ 1
(2)
where d
i j
is the corresponding A
ad j
element.
The parallelization of data processing is perfor-
med between iterations. Thus, inner loop is changed
so that four consecutive coordinate pairs are loaded
into a Q NEON register (128-bit).
Apparently, floating-point data type must be pre-
served for easier homogenization. On one hand, in
case of integers, homogenization could not be ef-
fective as it would require independent processing of
each point (there is no division instruction for inte-
gers). On the other hand, there is a floating-point
NEON SIMD intrinsic (vrecpsq
f32()) which finds
the reciprocal of a NEON register’s lanes using the
Newton-Raphson iteration. In our case, this operation
is performed twice for more accurate results. Algo-
rithm 1 demonstrates the projective mapping function
using SIMD instructions.
2.2 SIMD Lanczos Interpolation
The interpolation method used in this context is 2nd
order Lanczos because it maintains balance between
computational cost (in contrast to higher order Lan-
czos interpolation) and accuracy. Its 1D kernel is de-
fined in (3):
Algorithm 1: Projective mapping function using SIMD in-
structions.
1: D ← ad joint(A); A: 3x3 Transformation
Matrix
2: for x in image height do
3: y
0
temp
← vload 4(x · D
12
+ D
13
);
4: x
0
temp
← vload 4(x · D
22
+ D
23
);
5: h
temp
← vload 4(x · D
32
+ D
33
);
6: for y in image width step 4 do
7: vec
y
← vload 4([y : y + 3]);
8: temp
y
← vmac 4(y
0
temp
,vec
y
,D
11
);
9: temp
x
← vmac 4(x
0
temp
,vec
y
,D
21
);
10: temp
h
← vmac 4(h
temp
,vec
y
,D
31
);
11: vec
recip
← vreciprocal 4(temp
h
);
12: temp
y
← vmultiply 4(temp
y
,vec
recip
);
13: temp
x
← vmultiply 4(temp
x
,vec
recip
);
14: [y
0
: y
0
+ 3] ← vstore 4(temp
y
);
15: [x
0
: x
0
+ 3] ← vstore 4(temp
x
);
16: end for
17: end for
w
L
2
(x) =
1 , |x| = 0
2 ·
sin
π
x
2
· sin(πx)
π
2
x
2
, 0 < |x| < 2
0 , |x| ≥ 2
(3)
Due to its high complexity, a LookUp Table (LUT) of
10000 fixed-point kernel values is used. In addition,
this kernel is x/y − separable, therefore the 2D Lan-
czos interpolation can be expressed as in equation (4):
I
0
=
1
w
byc+2
∑
v=byc−1
w
L
2
(y−v)
bxc+2
∑
u=bxc−1
I(u, v)·w
L
2
(x−u)
(4)
where w =
byc+2
∑
v=byc−1
w
L
2
(y −v)
bxc+2
∑
u=bxc−1
w
L
2
(x −u)
In ARGB colorspace, four output subpixel values
will be processed in each iteration. Moreover, every
output pixel will have to be normalized in order to
avoid image artifacts. The proposed procedure for the
SIMD implementation of Lanczos 2 interpolation fol-
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
96
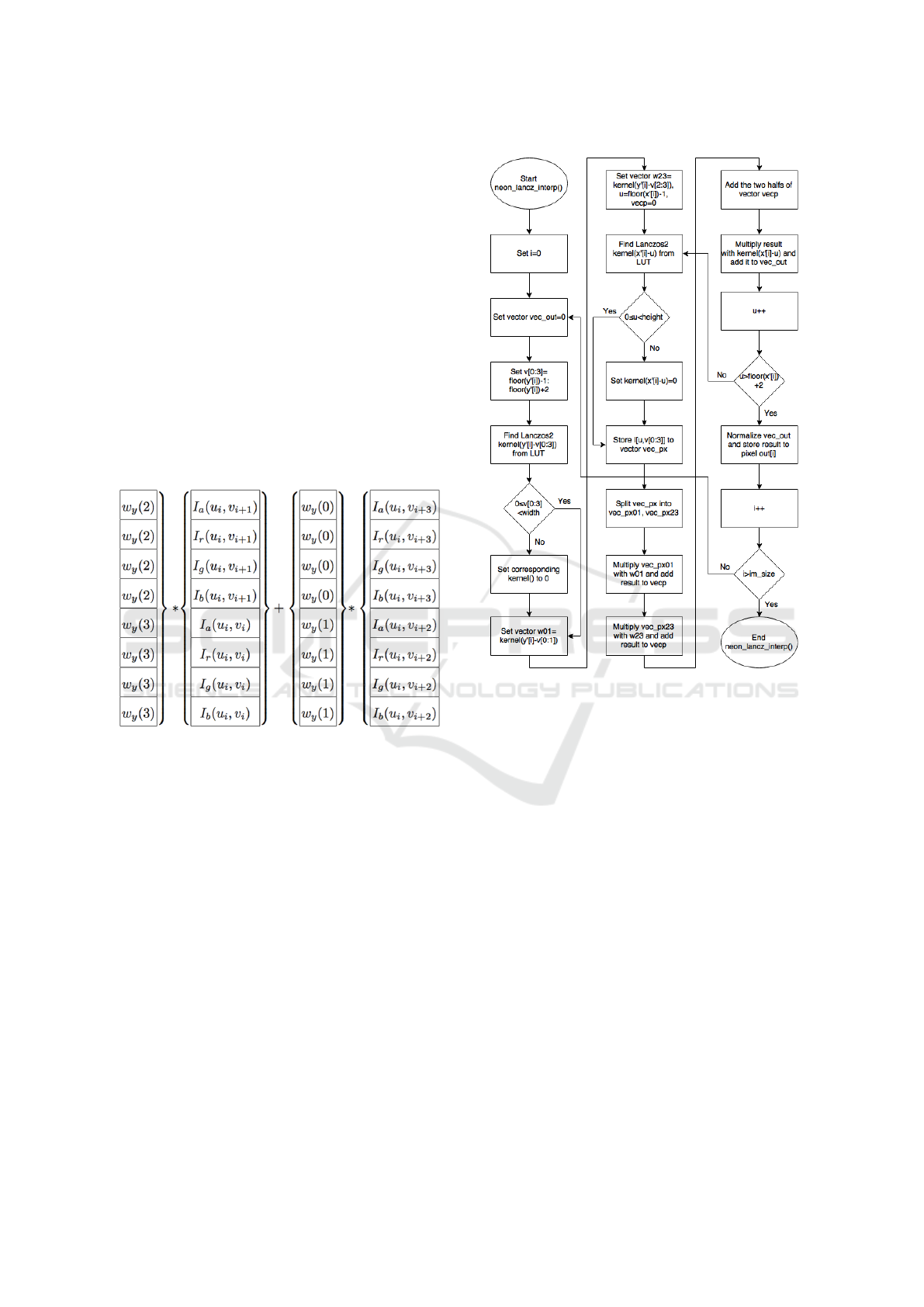
lows. Initially, out-of-frame image pixels are removed
using logical operations instead of if-clauses. This
operations’ results are used to mask both y-axis and
x-axis Lanczos kernel values (w
y
(i) = w
L
2
(y
0
− v
i
),
w
x
(i) = w
L
2
(x
0
− u
i
), i = 0 ...3) loaded from LUT.
Then, y-axis kernel values are loaded into two NEON
registers of 8 lanes each, where every w
y
(i) is put into
four consecutive lanes.
Following, four pixels
I(u
i
,v
j
), I(u
i
,v
j+1
),
I(u
i
,v
j+2
), I(u
i
,v
j+3
)
are loaded in one NEON re-
gister using 16 subpixels of 8 bits each. These values
are converted into 16-bit signed integers and are sto-
red in two NEON registers of 8×16 lanes. Thereaf-
ter, each subpixel is multiplied with its corresponding
Lanczos kernel value and these two vectors are added
together, as shown in Figure 1. After that, the upper
and the lower half of register are added pairwise and
multiplied with scalar w
x
(i), i = 0...3.
Figure 1: Vectorized convolution in y axis.
The above procedure is repeated four times for
each w
x
(i) during SIMD convolution. The implemen-
tation concludes with output pixel normalization. The
reciprocal of w is computed and then multiplied with
output subpixels, followed by the clamping of their
values in 0 − 255 range. Finally, each produced pixel
is stored as 32-bit unsigned integer in output image ar-
ray. The dataflow diagram of overall SIMD Lanczos
interpolation is presented in Figure 2.
3 RESULTS
In this section, qualitative and quantitative results are
presented. Performance of both baseline and SIMD
projective transformation is compared, for examining
the effectiveness of the NEON unit. For this pur-
pose we use two different CPUs: one Cortex-A9
Exynos 4412 Quad CPU, clocked at 1.6 GHz, which
Figure 2: SIMD Lanczos interpolation dataflow diagram.
NEON unit uses 64-bit long registers (128-bit Q re-
gisters) and one Qualcomm MSM8992 Snapdragon
808 which consists of two CPUs (quad-core 1.44 GHz
Cortex-A53 & dual-core 1.82 GHz Cortex-A57).
Input and output images are considered to have the
same size, since we keep only the input image map-
ping coordinates which correspond to the central part
of the output image. Subsequently, if output image is
larger than source image, then only the central part of
it (of same dimensions) will appear on display. Other-
wise, output image is supposed to appear in the center
of the screen.
Initially, our implementation’s qualitative re-
sults are examined. For this purpose, MATLAB
is used in order to produce algorithm’s original
output and our results are compared with them
using its built-in imshowpair() function. Figu-
res 3 and 4 display two of these comparisons.
In particular, Figures 3(a) and 4(a) display the
initial image, Figures 3(b) and 4(b) the results
for transformation matrix [−2,0.3,0; 0,−2,0; 0,0,1]
and [−2,0.3,0;0,−2,0;0,0,1] respectively and Fi-
gures 3(c) and 4(c) the results for transforma-
Efficient Projective Transformation and Lanczos Interpolation on ARM Platform using SIMD Instructions
97

Figure 3: Input image in subfigure (a) and two of our pro-
posed system’s results compared to MATLAB’s correspon-
ding results in subfigures (b) and (c), where gray area is
common for compared systems’ results.
tion matrix [1.7, 0.1, 0.0006; 0.3, 1.7, 0.0001; 0, 0, 1]
and [1.2,0.2,0.0002; 0.3,1.3,0.0001; 0,0,1] respecti-
vely (gray area is the common part of our proposed
system’s and MATLAB’s results).
In order to produce the performance results, three
different image sizes are used for each platform. Furt-
hermore, three different cases are examined, based
on the parallelization technique. The first case is the
baseline algorithm without any parallelization at all.
The second case is NEON algorithm and the third
Figure 4: Input image in subfigure (a) and our proposed
system’s results compared to MATLAB’s corresponding
results in subfigures (b) and (c) (source: http://car-from-
uk.com/carphotos/full/1359406159545035.jpg).
case is NEON+multithreading (NEON+mt) algorithm
in which all CPU cores are utilized. For each case,
three different examples of transformation matrices
are examined: a simple scale matrix, an affine matrix
and a projective matrix. The performance of baseline
and NEON cases is presented in Tables 1 and 2.
Using the projective matrices, the processing
times for Small, Medium and Large images are
247.188 ms, 495.519 ms and 1878.818 ms respecti-
vely for baseline implementation and 111.603 ms,
223.969 ms and 801.489 ms respectively for NEON
implementation. There is a small deviation in proces-
sing times for affine and scale matrices.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
98
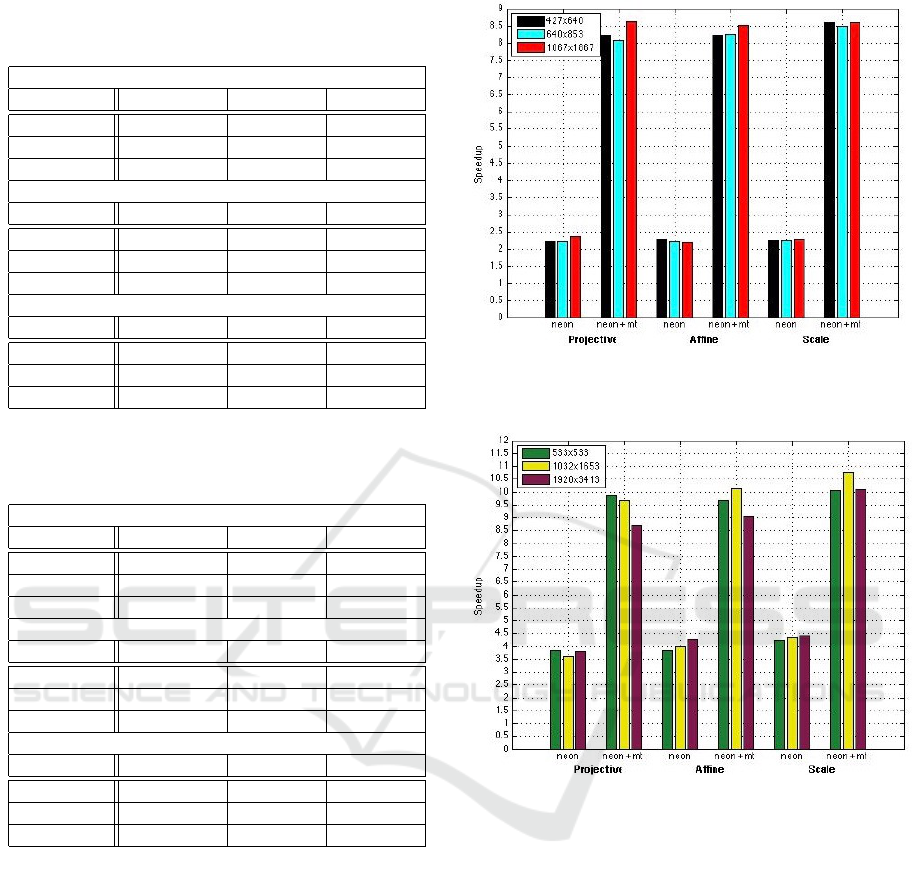
Table 1: Execution times for baseline, NEON and
NEON+multithreading cases for each image size and trans-
formation matrix (Cortex-A9).
Projective
image size baseline neon neon+mt
427x640 247.19 ms 111.6 ms 30.03 ms
640x853 495.52 ms 223.97 ms 61.44 ms
1067x1867 1878.82 ms 801.49 ms 217.73 ms
Affine
image size baseline neon neon+mt
427x640 246.88 ms 108.79 ms 29.97 ms
640x853 491.52 ms 222.15 ms 59.54 ms
1067x1867 1801.91 ms 818.83 ms 211.48 ms
Scale
image size baseline neon neon+mt
427x640 243.37 ms 107.99 ms 28.32 ms
640x853 486.24 ms 215.49 ms 57.33 ms
1067x1867 1779.05 ms 781.94 ms 207.17 ms
Table 2: Execution times for baseline, NEON and
NEON+multithreading cases for each image size and trans-
formation matrix (Cortex-A53 & Cortex-A57).
Projective
image size baseline neon neon+mt
533x533 168.95 ms 43.83 ms 17.09 ms
1032x1653 993.12 ms 277.55 ms 102.59 ms
1920x3413 3959.02 ms 1035.4 ms 455.32 ms
Affine
image size baseline neon neon+mt
533x533 161.17 ms 42.12 ms 16.71 ms
1032x1653 965.71 ms 242.37 ms 95.49 ms
1920x3413 3798.38 ms 888.65 ms 420.18 ms
Scale
image size baseline neon neon+mt
533x533 156.22 ms 36.86 ms 15.53 ms
1032x1653 952.38 ms 219.38 ms 88.57 ms
1920x3413 3639.23 ms 825.89 ms 361.18 ms
Figures 5 and 6 display the speed gain of NEON
implementation. The speedup factor achieved in Cor-
tex A9 CPUs ranges from 2.2 to 2.34 and, if all four
NEON units (included in CPU cores) are utilized, the
speedup factor increases to 8.06-8.63. In the mean-
time, the speed gain achieved in Cortex A53 + Cortex
A57 CPUs is significantly higher. In particular, it ran-
ges from 3.58 to 4.41 for simple NEON implementa-
tion and increases to 8.7-10.75 for NEON+mt case.
The contribution of SIMD Lanczos interpolation
in the above results is significant. On Cortex A9 CPU,
it offers an average speedup factor of 2.46, while
SIMD projective mapping is only 1.38 times faster
compared to baseline projective mapping. Moreo-
ver, on Cortex A53 + Cortex A57 CPU, respective
speedups are much larger. SIMD Lanczos interpo-
lation is 4.72 times faster than baseline Lanczos in-
Figure 5: Speed gain diagram of baseline, NEON and
NEON+ multithreading cases for each image size and trans-
formation matrix (Cortex-A9).
Figure 6: Speed gain diagram of baseline, NEON and
NEON+multithreading cases for each image size and trans-
formation matrix (LG G4).
terpolation, while SIMD projective mapping reaches
a speedup factor of 1.97.
Figure 7 shows the profiling of NEON+mt case on
Cortex-A9 CPU using ARM Streamline Community
Edition. According to the results, combining SIMD
and multithreading programming leads to optimal uti-
lization of system resources during the main proces-
sing.
4 CONCLUSIONS
In this paper, SIMD implementation of projective
transformation is presented. Despite its non-linearity,
a significant speedup is achieved, as a result of the ef-
fective use of SIMD instructions. Combining SIMD
Efficient Projective Transformation and Lanczos Interpolation on ARM Platform using SIMD Instructions
99

Figure 7: NEON+mt implementation profiling.
with multithreading programming offered the best
possible speed gain which, in many cases, exceeded
800%. Future work includes testing of modern ARM
architectures and further acceleration in order to re-
ach real-time performance for high definition video
applications.
ACKNOWLEDGEMENTS
This work was partially supported by a graduate grant
from IRIDA labs (http://www.iridalabs.gr/). The aut-
hors would like to thank Dr. Christos Theocharatos
and Dr. Nikos Fragoulis for their support and their
fruitful discussions.
REFERENCES
Antao, S. and Sousa, L. (2010). Exploiting simd extensions
for linear image processing with opencl. In Internati-
onal Conference on Computer Design (ICCD). IEEE.
Burger, W. and Burge, M. J. (2009). Principles of Digital
Image Processing, Core Algorithms. Springer.
Mazza, J., Patru, D., Saber, E., Roylance, G., and Larson, B.
(2014). A comparison of hardware/software techni-
ques in the speedup of color image processing algo-
rithms. In Image and Signal Processing Workshop
(WNYISPW). IEEE.
Mitra, G., Johnston, B., Rendell, A. P., McCreath, E.,
and Zhou, J. (2013). Use of simd vector operations
to accelerate application code performance on low-
powered arm and intel platforms. In 27th Internati-
onal Parallel and Distributed Processing Symposium
Workshops & PhD Forum (IPDPSW). IEEE.
Perera, C., Shapiro, D., Parri, J., Bolic, M., and Groza, V.
(2011). Accelerating image processing in flash using
simd standard operations. In The Third International
Conferences on Advances in Multimedia (MMEDIA).
Welch, E., Patru, D., Saber, E., and Bengtson, K. (2012).
A study of the use of simd instructions for two image
processing algorithms. In Image Processing Workshop
(WNYIPW).
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
100
