Learning Transformation Invariant Representations

with Weak Supervision

Benjamin Coors

1,2

, Alexandru Condurache

, Alfred Mertins

and Andreas Geiger

1,4

Autonomous Vision Group, MPI for Intelligent Systems, T

ubingen, Germany

Robert Bosch GmbH, Leonberg, Germany

Institute for Signal Processing, University of L

ubeck, Germany

Computer Vision and Geometry Group, ETH Z

urich, Switzerland

Keywords:

Deep Learning, Transformation Invariance, Weak Supervision, Object Recognition.

Abstract:

Deep convolutional neural networks are the current state-of-the-art solution to many computer vision tasks.

However, their ability to handle large global and local image transformations is limited. Consequently, exten-

sive data augmentation is often utilized to incorporate prior knowledge about desired invariances to geometric

transformations such as rotations or scale changes. In this work, we combine data augmentation with an unsu-

pervised loss which enforces similarity between the predictions of augmented copies of an input sample. Our

loss acts as an effective regularizer which facilitates the learning of transformation invariant representations.

We investigate the effectiveness of the proposed similarity loss on rotated MNIST and the German Trafﬁc

Sign Recognition Benchmark (GTSRB) in the context of different classiﬁcation models including ladder net-

works. Our experiments demonstrate improvements with respect to the standard data augmentation approach

for supervised and semi-supervised learning tasks, in particular in the presence of little annotated data. In

addition, we analyze the performance of the proposed approach with respect to its hyperparameters, including

the strength of the regularization as well as the layer where representation similarity is enforced.

1 INTRODUCTION

A central problem in computer vision is to train clas-

siﬁers which are robust to geometric transformations

of the input that are irrelevant to the problem at hand.

The most commonly used solution to ensure robus-

tness of a classiﬁer to geometric transformations is

data augmentation (Simard et al., 2003; Krizhevsky

et al., 2012; Laptev et al., 2016). Data augmentation

artiﬁcially enlarges the training set and acts as a re-

gularizer, which prevents a classiﬁer from overﬁtting

to the training set. As an alternative to data augmen-

tation, transformation invariances can be directly en-

coded into the convolutional ﬁlters of convolutional

neural networks (CNNs) (Cohen and Welling, 2016;

Worrall et al., 2017; Zhou et al., 2017). However,

these approaches are currently limited to simple ge-

ometric transformations such as rotations.

In this work, we propose to leverage an unsuper-

vised similarity loss for training deep neural networks

invariant to arbitrary transformations. The similarity

loss is computed with respect to transformed copies

of an input and presents a very simple and effective

regularizer, enforcing the desired transformation in-

variances. In contrast to na

ıve data augmentation, it

encourages smooth decision boundaries with respect

to transformations of the input and leads to higher per-

formance, in particular in the presence of little anno-

tated examples. Besides, our method allows for easy

incorporation of additional unlabeled examples, as the

similarity loss does not utilize label information and

is thus suitable for semi-supervised learning tasks. To

the best of our knowledge, this is the ﬁrst work to pro-

pose a similarity loss for training transformation inva-

riant CNNs with weak supervision. The contributions

of this paper are:

• We propose a similarity loss which acts as an ad-

ditional regularizer and utilizes unlabeled training

data for learning transformation invariance.

• We present a detailed investigation on the weig-

hting and placement of the loss.

• We show improved performance in supervised

and semi-supervised learning on rotated MNIST

and GTSRB when little labeled data is available.

Coors, B., Condurache, A., Mertins, A. and Geiger, A.

Learning Transformation Invariant Representations with Weak Supervision.

DOI: 10.5220/0006549000640072

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

64-72

ISBN: 978-989-758-290-5

2 RELATED WORK

As an alternative to data augmentation, knowledge

about geometric transformations can be directly en-

coded into the ﬁlters of a convolutional neural net-

work. Scattering convolution networks use predeﬁ-

ned wavelet ﬁlters to create networks that are invari-

ant to translations, rotations, scaling and deformati-

ons (Bruna and Mallat, 2013; Sifre and Mallat, 2013).

While scattering networks guarantee stability to ge-

ometric transformations, their parameters cannot be

trained and thus they are generally outperformed by

supervised deep convolutional networks (Oyallon and

Mallat, 2015).

Consequently, several recent works have sugge-

sted to combine the encoding of invariances with the

learning of the convolutional ﬁlters (Kivinen and Wil-

liams, 2011; Sohn and Lee, 2012; Cohen and Welling,

2016; Worrall et al., 2017; Zhou et al., 2017). Trans-

formation invariant or equivariant restricted Boltz-

mann machines infer the best matching ﬁlters by

transforming them using linear transformations (Ki-

vinen and Williams, 2011; Sohn and Lee, 2012). Si-

milarly, group equivariant CNNs apply learned base

ﬁlters under different transformations and pool their

responses to create invariant representations (Cohen

and Welling, 2016). Harmonic networks exhibit glo-

bal rotation equivariance (Worrall et al., 2017). While

these works have demonstrated state-of-the-art results

and shown promise in improving the data-efﬁciency

of deep convolutional networks, they are, unlike our

approach, typically restricted to simple transformati-

ons (e.g, rotations).

Another approach to transformation invariance in

CNNs is to resample the input space. An exam-

ple for this approach are spatial transformer networks

(STNs) (Jaderberg et al., 2015), which use a separate

network to learn the parameters of a spatial transfor-

mation of an input. Based on the predicted trans-

formation parameters a sampling grid is created and

applied to the input. A more lightweight alternative

to STNs are deformable convolutional networks (Dai

et al., 2017), which do not learn transformation pa-

rameters or warp the feature map but instead directly

learn offsets to the regular sampling grid of standard

convolutions. While these approaches increase the

ﬂexibility of neural networks in handling geometric

transformations, they assume that a canonical repre-

sentation can be easily deduced from the input.

Because of the shortcomings of the aforementi-

oned techniques, data augmentation remains one of

the most commonly used solutions for making deep

networks invariant to complex input transformati-

ons (Simard et al., 2003; Krizhevsky et al., 2012).

A recently proposed variant of data augmentation is

transformation-invariant pooling (TI-pooling) (Lap-

tev et al., 2016), which feeds multiple augmented

copies of an input into the network and pools their

responses. While this simple idea works well in

practice, test time complexity grows exponentially

with the dimension of the transformation, rendering

this approach infeasible for real-time applications. In

contrast, our loss encourages representation similarity

during training and does not affect test time perfor-

mance.

The proposed approach is also related to the to-

pic of self-supervised learning, where freely avai-

lable auxiliary labels are used to train algorithms

without human supervision. Recently proposed

proxy tasks for self-supervision include context pre-

diction (Doersch et al., 2015), solving jigsaw puzz-

les (Noroozi and Favaro, 2016) or predicting egomo-

tion signals (Agrawal et al., 2015). Compared to these

works on self-supervision, our work does not use an

auxiliary training loss but directly optimizes the desi-

red loss metric.

The idea of using an input sample more than once

in each training step has previously been proposed

in the context of protecting neural networks against

adversarial perturbations (Zheng et al., 2016; Miyato

et al., 2016). Similar to the idea of improving mo-

del generalization by injecting adversarial examples

during training, we aim to improve model generali-

zation w.r.t. transformations by enforcing similarity

between feature representations of transformed input

images.

Besides, state-of-the-art results in semi-

supervised learning have been recently presen-

ted using a similarity loss in combination with a

mutual-exclusivity loss (Sajjadi et al., 2016) or via an

imaginary walker that is tasked with forming ”associ-

ations” between embeddings (Haeusser et al., 2017).

In contrast to these works, here we investigate the uti-

lity of a similarity loss when learning representations

invariant to geometric transformations and present

a detailed analysis on the placement and weighing

of the loss. Our loss applies to the supervised and

semi-supervised setting and is particularly effective

in the presence of little labeled data.

3 METHOD

While the proposed similarity loss is applicable to

a variety of tasks, we use image classiﬁcation as a

test bench in this work. Let x ∈ R

w×h×c

denote an

image of dimensions w ×h with c channels and let f :

w×h×c

→ R

be a non-linear mapping represented

Learning Transformation Invariant Representations with Weak Supervision

by a neural network which takes an input image x and

produces a score for each of the C classes. Let further

∈ T denote two transformations from a set of

transformations T (e.g, rotation, afﬁne, perspective)

which take the input image x and produce transfor-

med versions t

(x) ∈ R

w×h×c

and t

(x) ∈ R

w×h×c

it. Finally, let f

(t(x)) denote the feature maps of the

neural network in layer l when passing t(x) as input.

For clarity, we will drop the dependency on the input

image x in the following.

In order to encourage a neural network to learn

transformation invariant representations, we propose

the use of a similarity loss L

sim

which penalizes large

distances between the predictions or feature embed-

dings of transformed copies of the input. The simila-

rity loss is computed using a siamese network archi-

tecture, where the transformed copies of the input are

simultaneously fed into separate streams of the net-

work that share their weights. By transforming both

inputs, convergence of the model is accelerated and

overﬁtting to small label sets is avoided. An abstract

network architecture, where the similarity loss is ap-

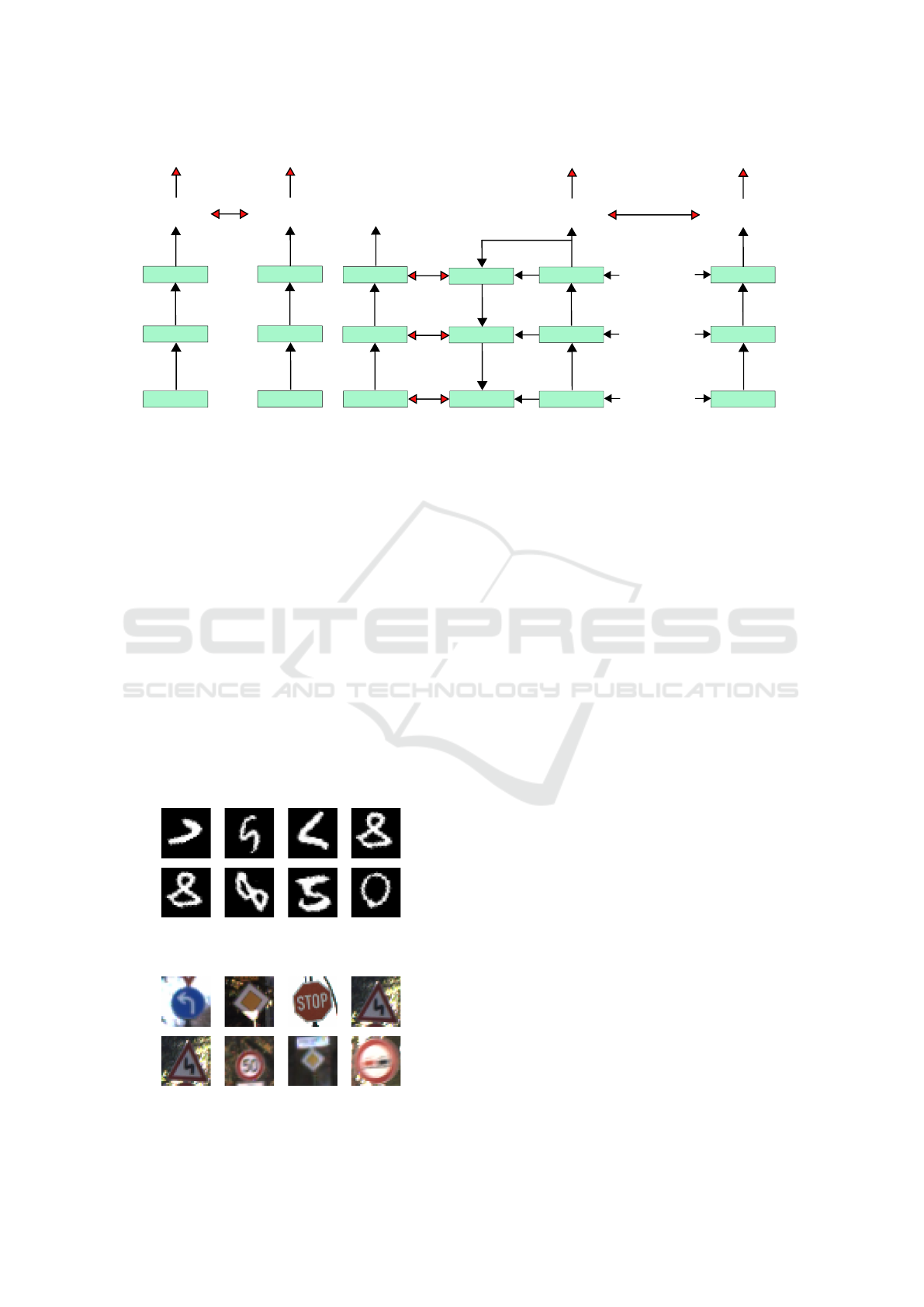
plied at the ﬁnal layer L, is illustrated in Figure 1(a).

At inference time only a single stream of the net-

work is used, keeping runtime constant with respect

to the size of the transformation space.

The similarity loss L

sim

is added to the supervised

classiﬁcation loss L

, which is applied on the output

of both network streams, to form the total loss L

total

for a data point where a weight parameter λ controls

the inﬂuence of L

sim

total

= L

+ λL

sim

(1)

Here, L

is the usual cross-entropy loss applied to the

softmax outputs σ( f

)) and σ( f

)) of the ﬁnal

network layer L for the transformed input sample:

= −

∑

i=1

logσ

( f

)) −

∑

i=1

logσ

( f

)) (2)

where σ

(x) = exp(x

∑

j=1

exp(x

) denotes the soft-

max function and y

= 1 if i is the ground truth class

and y

= 0 otherwise.

The similarity loss encourages the output of the

neural network at layer l, f

, to be similar for both

streams. It is deﬁned as the distance between the out-

puts of the transformed input pair at layer l for an ap-

propriate distance metric D(·,·):

sim

= D( f

), f

)) (3)

We propose to use a distance metric which measu-

res the correspondence between the likelihood of the

transformed input copies. More speciﬁcally, D(·,·)

is calculated by ﬂattening the network output f

at a

given layer l and applying the softmax activation:

D( f

), f

)) = −

∑

i=1

( f

))log σ

( f

)) (4)

A similar distance metric has previously been pro-

posed by Zheng et al. (2016) in order to stabilize mo-

dels against small input perturbations such as the ad-

dition of uncorrelated Gaussian noise. It is inspired by

the work of Miyato et al. (2016) on virtual adversarial

training, which showed that a distance function based

on the Kullback-Leibler (KL) divergence smoothens

the model distribution with respect to the input around

each data point. Our work extends this approach to

training models for invariance to geometric transfor-

mations of the input and is the ﬁrst to perform a de-

tailed investigation on the optimal weighing and pla-

cement of the loss.

Since the similarity loss L

sim

does not require la-

bel information, it enables semi-supervised learning

with partially labeled data. Until recently, ladder net-

works were the state-of-the-art architecture for semi-

supervised learning (Rasmus et al., 2015). Ladder

networks are denoising autoencoders with lateral con-

nections, into which the similarity loss L

sim

can be

easily integrated by duplicating the corrupted or un-

corrupted encoder path of the ladder network. The

duplicated encoder path again shares its weight with

the other encoder paths of the ladder network. A sim-

ple ladder network architecture where the corrupted

encoder path of the ladder network is duplicated and

sim

is applied on the ﬁnal output layer L is illustrated

in Figure 1(b).

As before, L

sim

is added to the total loss L

total

where it serves as a second unsupervised loss next to

the denoising loss L

denoise

, which aims to minimize

the difference between a clean layer output f

and the

output of a denoising function

given a corrupted

output

on all L layers of the network. The classiﬁ-

cation loss L

is then computed on the outputs of the

noisy encoder paths

where α is a weight parameter

of the denoising loss L

denoise

and f

) = t

total

= L

+ αL

denoise

+ λL

sim

(5)

= −

∑

i=1

logσ

(

)) −

∑

i=1

logσ

(

))

(6)

denoise

∑

l=0

|| f

) −

)||

(7)

In all models, the classiﬁcation loss L

is only ap-

plied on the labeled training samples. On the other

hand, the similarity loss L

sim

and, in case of a lad-

der network, the denoising loss L

denoise

can be applied

on both labeled and unlabeled samples of the training

data.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

sim

σ( f

))

σ( f

))

)

(a) Siamese Network

N (0,σ

)

sim

N (0,σ

)

N (0,σ

)

σ(

))

σ( f

))

denoise

σ(

))

denoise

)

(b) Ladder Network

Figure 1: Abstract network architectures considered in this work. A similarity loss L

sim

is placed on the the ﬁnal layer of the

network in order to enforce similarity between outputs of transformed copies of an input.

4 EXPERIMENTS

We ﬁrst validate our approach in terms of learning ro-

tation invariant representations on the classical rota-

ted MNIST task (Larochelle et al., 2007). Second,

we demonstrate the effectiveness of our technique on

the more challenging German Trafﬁc Sign Recogni-

tion Benchmark (GTSRB) (Stallkamp et al., 2012).

Incorporating perspective invariances using the pro-

posed similarity loss, our method leads to signiﬁcant

improvements over the baselines for this task.

4.1 Experimental Setup

The rotated MNIST classiﬁcation task (Larochelle

et al., 2007) is the standard benchmark for evaluating

Figure 2: Example images from rotated MNIST (Larochelle

et al., 2007).

Figure 3: Example images from GTSRB (Stallkamp et al.,

2012).

transformation invariance in neural networks (Sohn

and Lee, 2012; Cohen and Welling, 2016; Laptev

et al., 2016; Worrall et al., 2017), despite possible

ambiguities between rotated digits such as a rotated

6 and 9. The rotated MNIST dataset (see Figure 2)

was created by rotating MNIST digits with uniformly

sampled angles between 0 and 2π radians and consists

of 12,000 training and 50, 000 test samples. As in the

original MNIST dataset (Lecun et al., 1998), the ima-

ges are greyscale and of size 28 × 28 pixels. We split

the dataset into 10, 000 training and 2,000 validation

samples for determining the hyperparameter λ.

The German Trafﬁc Sign Recognition Benchmark

(GTSRB) (Stallkamp et al., 2012) consists of 39,209

training and 12,630 test images with 43 classes in to-

tal. We rescale the original images (see Figure 3) of

varying size to 32 × 32 pixels and normalize them.

In order to perform a fair comparison between

data augmentation and the use of a similarity loss, we

make sure that every model is being shown the same

amount of data in each training epoch. As a simila-

rity loss model utilizes each input sample x twice in

every training step under the transformations t

and

, we also present t

and t

to the data augmenta-

tion baseline in each training step. During training,

data augmentation is performed online in a randomi-

zed manner. For rotated MNIST, t

and t

rotate the

input x in every training step with an angle which is

uniformly sampled between 0 and 2π radians.

In the case of GTSRB, we train for invariance to

projective transformations, as trafﬁc signs need to be

correctly classiﬁed from different angles and distan-

ces. The augmentation with a projective transforma-

tion is performed by estimating an essential matrix

Learning Transformation Invariant Representations with Weak Supervision

using the eight-point algorithm from a set of point

correspondences between the image corners and a

randomized set of points. These points are randomly

sampled from a uniform distribution within a distance

of ±6 pixels in both dimensions of the image corners.

For all experiments we use the same randomiza-

tion seeds for model comparisons but vary the seed

across runs and for all experiments report the average

numerical results over ﬁve independent runs.

4.2 Supervised Learning on Rotated

MNIST Subset

For supervised learning, we integrate the similarity

loss L

sim

into an all convolutional network architec-

ture (Springenberg et al., 2015) and use a subset of

= 100 labeled samples of the rotated MNIST da-

taset for training, where each class is represented

equally often (i.e., 10 times).

Our network closely resembles the CNN reference

architecture for the rotated MNIST task in (Cohen and

Welling, 2016). This network is constructed from se-

ven convolutional layers, where each but the last layer

uses ﬁlters of size 3 × 3 while the last layer uses ﬁl-

ters of size 4×4. The convolutional ﬁlters are applied

with a stride of 1 × 1. A max-pooling layer of stride

and size 2 × 2 is inserted after the second convoluti-

onal layer. All but the last layer use batch normali-

zation (Ioffe and Szegedy, 2015) before ReLU nonli-

nearities, followed by dropout with a keep probability

of p = 0.7. On the last layer the softmax activation

is applied. We use the Adam optimizer (Kingma and

Ba, 2015) with a base learning rate of 0.001 and train

with 100 samples per mini-batch.

In a ﬁrst experiment, we evaluate the effect of ap-

plying the similarity loss on different layers l of the

network (see Figure 4). We ﬁnd that applying the si-

milarity loss on the last layer results in the highest

validation accuracy. This result is in line with ﬁn-

dings by Cohen and Welling (2016), which showed

that enforcing premature invariance in early layers of

the network is undesirable. For all future experiments,

we therefore only apply the similarity loss on the ﬁnal

output layer L of a network.

In addition, we perform a coarse hyperparame-

ter search with a selected set of weight parameters

λ ∈ [1.0,2.0, 3.0, 5.0,7.5,10.0,15.0,20.0]. The re-

sults are plotted in Figure 5 and show improved vali-

dation accuracies for a wide range of λ values compa-

red to using only data augmentation (λ = 0.0). While

the performance is very robust to the choice of the

weight parameter λ, we can observe a drop in valida-

tion accuracy when λ is large (λ = 20.0).

Table 1 conﬁrms performance improvements on

1 2 3 4 5 6 7

0.75

0.80

0.85

validation accuracy

Figure 4: Hyperparameter study for the similarity loss layer

l on the supervised rotated MNIST task.

0 5 10 15 20

0.84

0.85

0.86

0.87

0.88

validation accuracy

Figure 5: Hyperparameter study for the weight parameter λ

on the supervised rotated MNIST task.

the test set for the proposed similarity loss with λ =

5.0 when training for 100 epochs with N

= 100 la-

beled samples. Compared to a test error of 14.8%

when training with data augmentation, we obtain an

improved test error of 13.4% when training with

an additional similarity loss. Additionally, we also

obtain a better test error than our reimplementati-

ons of a harmonic network (Worrall et al., 2017)

and a group-equivariant P4CNN (Cohen and Wel-

ling, 2016), which replace the regular convolutions

in the network architecture with harmonic or group-

equivariant convolutions, respectively.

Table 1: Results for the supervised rotated MNIST task with

= 100.

Method Test error (%)

Worrall et al. (2017) 21.5

Data augmentation 14.8

Cohen and Welling (2016) 14.2

Similarity loss 13.4

As a baseline we also evaluate the performance on

the full dataset of 12,000 labeled examples. Here, no

signiﬁcant improvement is obtained by the similarity

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

loss compared to a data augmentation model (see Ta-

ble 2). Both data-driven methods are outperformed by

harmonic networks (Worrall et al., 2017) and a group-

equivariant P4CNN (Cohen and Welling, 2016).

Table 2: Results for the supervised rotated MNIST task with

= 12,000.

Method Test error (%)

Data augmentation 3.7

Similarity loss 3.6

Cohen and Welling (2016) 2.28

Worrall et al. (2017) 1.69

Our results suggest that applying a similarity loss

improves generalization and outperforms data aug-

mentation as well as encoded transformation invari-

ances when the number of labeled samples is small.

4.3 Semi-Supervised Learning

The unsupervised nature of the similarity loss L

sim

makes it suitable as an additional guidance for semi-

supervised learning problems in order to utilize unla-

beled data during training.

4.3.1 Rotated MNIST

As a ﬁrst architecture for semi-supervised learning

on rotated MNIST, we use the convolutional archi-

tecture from Section 4.2 and a subset of N

= 100

labeled samples. Additionally, we use the remai-

ning training samples as unlabeled data. Each mini-

batch is constructed from 100 labeled and 100 un-

labeled samples, where L

is only applied on the

labeled samples while L

sim

is applied on the full

minibatch. As before, we perform a hyperparame-

ter study of the λ weight parameter from a set λ ∈

[1.0,2.0, 3.0, 5.0,7.5,10.0,15.0,20.0] (see Figure 6).

When comparing to the λ-study for supervised lear-

ning (see Figure 5), we can now observe higher va-

lidation accuracies and again ﬁnd the performance to

be very robust.

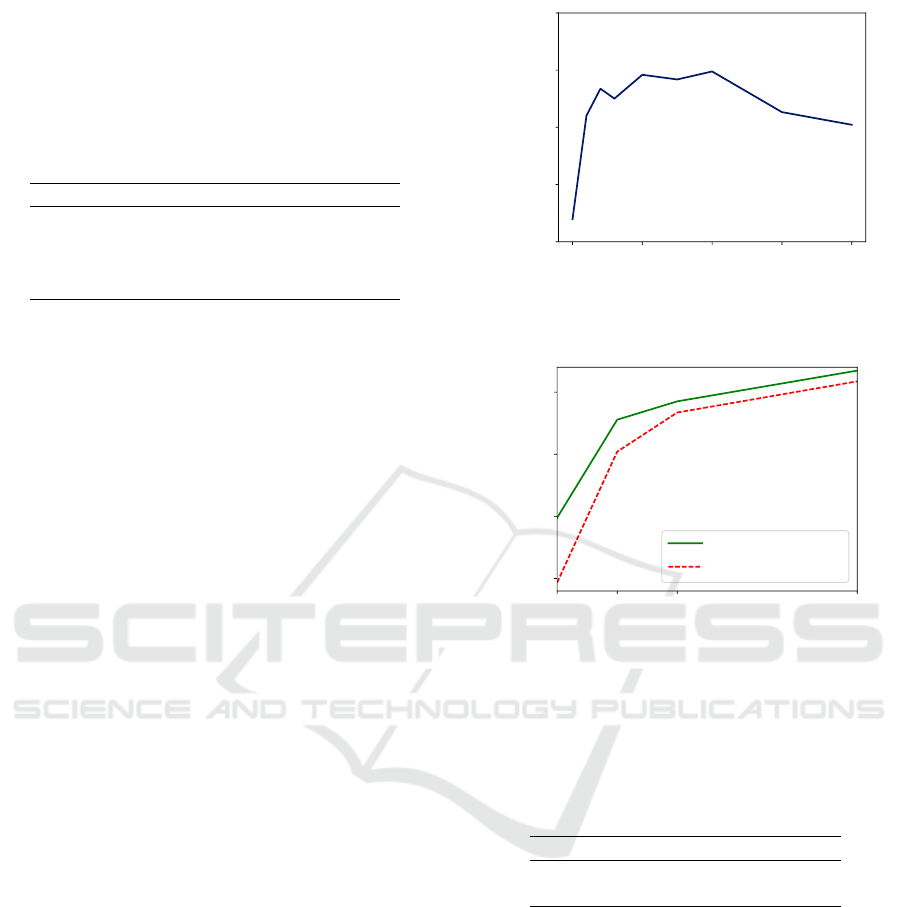
Additionally, we perform a data ablation study

where we vary the size of the labeled training set N

The results of the data ablation study are visualized

in Figure 7. The ﬁgure demonstrates that the simi-

larity loss is especially helpful when only very little

labeled data is available. The beneﬁt of a similarity

loss (for a weight parameter of λ = 10.0 and 100 trai-

ning epochs) is conﬁrmed on the test set where the

ﬁnal test error is lowered by more than 2% compared

to training only with data augmentation (see Table 3).

Furthermore, the ﬁnal test error is more than 1% lo-

wer compared to using the similarity loss on only the

0 5 10 15 20

0.84

0.85

0.86

0.87

0.88

validation accuracy

Figure 6: Hyperparameter study for λ on semi-supervised

rotated MNIST.

50 100 150 300

0.75

0.80

0.85

0.90

test accuracy

similarity loss

data augmentation

Figure 7: Accuracy vs. number of training samples on semi-

supervised rotated MNIST.

labeled images, which conﬁrms the ability of the si-

milarity loss to exploit additional unlabeled data.

Table 3: Results for the semi-supervised rotated MNIST

task with N

= 100.

Method Test error (%)

Data augmentation 14.8

Similarity loss 12.2

We also observe improved class separability when

visualizing the learned feature representations in the

last layer of the model (see Figure 8).

For a second set of semi-supervised learning ex-

periments, we incorporate the similarity loss into the

fully connected ladder network architecture proposed

by Rasmus et al. (2015) for the permutation invariant

MNIST task. It features layers of size 784-1000-500-

250-250-250-10 with respective denoising weight

parameters α = [1000.0,10.0,0.10, 0.1, 0.1,0.1,0.1].

The noisy encoder path uses Gaussian corruption

noise with standard deviation 0.3. We train the net-

work with mini-batches of 100 labeled and 256 unla-

beled samples using the Adam optimizer and a base

learning rate of 0.02 for 300 training epochs.

Learning Transformation Invariant Representations with Weak Supervision

(a) Data Augmentation (b) Similarity Loss

Figure 8: t-SNE visualizations of the learned feature representations on the ﬁnal network layer.

Table 4: Ladder network results for semi-supervised rotated

MNIST task with N

= 100.

Method Test error (%)

Data augmentation 8.0

Similarity loss (clean path) 7.6

Similarity loss (noisy path) 6.8

Table 4 displays the ﬁnal test accuracies for uti-

lizing our similarity loss in a ladder network with a

weight parameter of λ = 20.0, which was determined

in a separate hyperparameter search. We again ﬁnd

the addition of a similarity loss to be beneﬁcial. In-

corporating it in the noisy encoder path results in a

better performance of 6.8% compared to a ﬁnal test

error of 7.6% in the clean encoder path. This can be

explained by the Gaussian noise of the noisy encoder

path providing additional regularization. Our results

demonstrate that the use of a similarity loss also ena-

bles improving the performance of a previous state-

of-the-art model architecture, specially designed for

the semi-supervised learning task.

4.3.2 German Trafﬁc Sign Recognition

Benchmark

As a ﬁnal experiment, we consider the German Trafﬁc

Sign Recognition Benchmark (GTSRB) (Stallkamp

et al., 2012). The network architecture for this task is

an all-convolutional model, which resembles the All-

CNN-C architecture proposed by Springenberg et al.

(2015) for the CIFAR-10 task (Krizhevsky, 2009). It

consists of nine convolution layers. The ﬁrst four lay-

ers have 96, the, following layers 192 ﬁlters, all of

size 3 × 3. They are applied with stride 1 except in

the third and sixth layer where a stride of 2 is used.

After the ﬁnal convolutional layer average pooling is

performed. Dropout is applied on the input with a pro-

bability of 0.2 and on the convolutional feature maps

with 0.5. All layers use ReLU nonlinearities, batch

normalization and weight decay of 0.001. A softmax

activation is applied after the ﬁnal layer. The net-

work is trained with stochastic gradient descent and

Momentum with mini-batches of 100 labeled and 100

unlabeled samples. A learning rate of 0.05 is decayed

over the course of 100 training epochs.

In contrast with previous experiments on rotated

MNIST, we now train for invariance to projective

transformations. Unlike rotations, these cannot be ea-

sily encoded into the convolutional ﬁlters of a neural

network. Here, the use of a similarity loss, which re-

lies on augmenting the training data (as described in

Section 4.1), offers a simple, yet effective solution to

train CNNs for invariance to more complex geometric

transformations.

Table 5: Results for the semi-supervised GTSRB task with

= 2150.

Method Test error (%)

Data augmentation 14.8

Similarity loss 9.6

The test results for semi-supervised learning on

the GTSRB task for 50 samples per class (i.e., 2150

samples in total) and λ = 10.0 are displayed in Table

5. We observe a clear improvement in the ﬁnal test

accuracy from 14.8% to 9.6% when utilizing the si-

milarity loss, despite the model already being heavily

regularized by dropout, weight decay and batch nor-

malization, which again indicates the effectiveness of

the similarity loss when little labeled data is available.

As for rotated MNIST, we again perform a data

ablation study (see Figure 9). The study shows that

the improvement when using an additional similarity

loss is largest when N

is small, but that even for lar-

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

2150 4300 6450 8600

0.80

0.85

0.90

0.95

1.00

test accuracy

similarity loss

data augmentation

Figure 9: Accuracy vs. number of training samples on semi-

supervised GTSRB.

ger sizes of the labeled training set the similarity loss

outperforms the data augmentation model.

5 DISCUSSION

The experiments in Section 4 demonstrate the beneﬁts

of using the proposed similarity loss in both super-

vised and semi-supervised learning tasks. Data aug-

mentation works well in practice for fully supervised

problems when big labeled training sets are available.

However, in this work, we show that an additional si-

milarity loss can act as an effective regularizer, which

improves upon data augmentation when little annota-

ted training data is available. The beneﬁt of the pro-

posed similarity loss is not limited to the “toy-like”

rotated MNIST task but extends to more complex ge-

ometric transformations of natural images where even

larger improvements can be obtained.

In addition, another contribution of our work con-

cerns the fact that the proposed similarity loss can

be utilized for semi-supervised learning, where it can

help to exploit additional unlabeled data. The inclu-

sion of the similarity loss in a semi-supervised ladder

network shows particular promise. With our proposed

modiﬁcation, we further improve over an architecture

which until recently was the state-of-the-art approach

for semi-supervised learning. As the rotated MNIST

dataset has not been commonly used to evaluate semi-

supervised learning architectures we do not claim to

set a new state-of-the-art but consider the ladder net-

work using an additional similarity loss to have highly

competitive performance.

In general, the use of an unsupervised similarity

loss is a surprisingly simple idea which can easily be

integrated into any deep learning model. All it re-

quires is to duplicate the classiﬁcation stream of the

network and tune the λ hyperparameter. In our ex-

periments, we found the performance to generally be

very robust to the choice of the weight parameter λ.

The similarity loss can be additionally combined with

methods which encode invariances directly into con-

volutional ﬁlters (Cohen and Welling, 2016; Worrall

et al., 2017; Zhou et al., 2017) and with architectu-

res which enable neural networks to handle geometric

transformations more easily (Jaderberg et al., 2015;

Dai et al., 2017).

6 CONCLUSIONS

This work proposes an unsupervised similarity loss

which penalizes differences between the predictions

for transformed copies of an input for improved le-

arning of transformation invariance in deep neural

networks on the rotated MNIST and German Trafﬁc

Sign Recognition Benchmark classiﬁcation tasks. We

show that our similarity loss acts as an effective re-

gularizer, which improves model performance when

little annotated data is available, in both supervised

and semi-supervised learning. Future work could in-

vestigate the application of the proposed similarity

loss on a combination of network layers or an adjus-

tment of the weight parameter λ over the course of

training.

While this work improves the use of data-driven

methods based on augmenting training data for lear-

ning transformation invariance, there still remains a

gap to techniques which encode invariances to trans-

formations directly into the ﬁlters of a convolutional

neural network when training on the full set of labels

on rotated MNIST (Cohen and Welling, 2016; Worrall

et al., 2017; Zhou et al., 2017). However, unlike the

proposed similarity loss, which can easily be applied

for a wide variety of transformations, these methods

are currently limited to simple geometric transforma-

tions such as rotations or mirror reﬂections.

A promising avenue for future research is there-

fore the development of approaches which encode in-

variances to more complex geometric transformations

directly into the architecture of deep neural networks

and combine them with soft constraints as presented

in this paper in order to further improve the data efﬁ-

ciency of deep neural networks.

REFERENCES

Agrawal, P., Carreira, J., and Malik, J. (2015). Learning

to see by moving. In Proc. of the IEEE International

Conf. on Computer Vision (ICCV).

Bruna, J. and Mallat, S. (2013). Invariant scattering convo-

Learning Transformation Invariant Representations with Weak Supervision

lution networks. IEEE Trans. on Pattern Analysis and

Machine Intelligence (PAMI), 35(8):1872–1886.

Cohen, T. S. and Welling, M. (2016). Group equivariant

convolutional networks. In Proc. of the International

Conf. on Machine learning (ICML).

Dai, J., Qi, H., Xiong, Y., Li, Y., Zhang, G., Hu, H., and

Wei, Y. (2017). Deformable convolutional networks.

Arxiv tech report.

Doersch, C., Gupta, A., and Efros, A. A. (2015). Unsu-

pervised visual representation learning by context pre-

diction. In Proc. of the IEEE International Conf. on

Computer Vision (ICCV).

Haeusser, P., Mordvintsev, A., and Cremers, D. (2017).

Learning by association - a versatile semi-supervised

training method for neural networks. In Proc. IEEE

Conf. on Computer Vision and Pattern Recognition

(CVPR).

Ioffe, S. and Szegedy, C. (2015). Batch normalization:

Accelerating deep network training by reducing inter-

nal covariate shift. In Proc. of the International Conf.

on Machine learning (ICML).

Jaderberg, M., Simonyan, K., Zisserman, A., and Kavuk-

cuoglu, K. (2015). Spatial transformer networks. In

Advances in Neural Information Processing Systems

(NIPS).

Kingma, D. P. and Ba, J. (2015). Adam: A method for

stochastic optimization. In Proc. of the International

Conf. on Learning Representations (ICLR).

Kivinen, J. J. and Williams, C. K. I. (2011). Transformation

equivariant boltzmann machines.

Krizhevsky, A. (2009). Learning multiple layers of featu-

res from tiny images. Master’s thesis, Department of

Computer Science, University of Toronto.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).

Imagenet classiﬁcation with deep convolutional neu-

ral networks. In Advances in Neural Information Pro-

cessing Systems (NIPS).

Laptev, D., Savinov, N., Buhmann, J. M., and Pollefeys, M.

(2016). TI-POOLING: transformation-invariant pool-

ing for feature learning in convolutional neural net-

works. In Proc. IEEE Conf. on Computer Vision and

Pattern Recognition (CVPR).

Larochelle, H., Erhan, D., Courville, A., Bergstra, J., and

Bengio, Y. (2007). An empirical evaluation of deep

architectures on problems with many factors of varia-

tion. In Proc. of the International Conf. on Machine

learning (ICML).

Lecun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998).

Gradient-based learning applied to document recogni-

tion. Proc. of the IEEE, 86(11):2278–2324.

Miyato, T., Maeda, S., Koyama, M., Nakae, K., and Ishii,

S. (2016). Distributional smoothing by virtual advers-

arial examples. In Proc. of the International Conf. on

Learning Representations (ICLR).

Noroozi, M. and Favaro, P. (2016). Unsupervised learning

of visual representations by solving jigsaw puzzles.

In Proc. of the European Conf. on Computer Vision

(ECCV).

Oyallon, E. and Mallat, S. (2015). Deep roto-translation

scattering for object classiﬁcation. In Proc. IEEE

Conf. on Computer Vision and Pattern Recognition

(CVPR).

Rasmus, A., Valpola, H., Honkala, M., Berglund, M., and

Raiko, T. (2015). Semi-supervised learning with lad-

der networks. In Advances in Neural Information Pro-

cessing Systems (NIPS).

Sajjadi, M., Javanmardi, M., and Tasdizen, T. (2016). Regu-

larization with stochastic transformations and pertur-

bations for deep semi-supervised learning. In Advan-

ces in Neural Information Processing Systems (NIPS).

Sifre, L. and Mallat, S. (2013). Rotation, scaling and defor-

mation invariant scattering for texture discrimination.

In Proc. IEEE Conf. on Computer Vision and Pattern

Recognition (CVPR).

Simard, P. Y., Steinkraus, D., and Platt, J. C. (2003). Best

practices for convolutional neural networks applied to

visual document analysis.

Sohn, K. and Lee, H. (2012). Learning invariant represen-

tations with local transformations. In Proc. of the In-

ternational Conf. on Machine learning (ICML).

Springenberg, J. T., Dosovitskiy, A., Brox, T., and Ried-

miller, M. A. (2015). Striving for simplicity: The all

convolutional net. In International Conf. on Learning

Representations (ICLR) (workshop track).

Stallkamp, J., Schlipsing, M., Salmen, J., and Igel, C.

(2012). Man vs. computer: Benchmarking machine

learning algorithms for trafﬁc sign recognition. Neu-

ral Networks, 32:323–332.

Worrall, D. E., Garbin, S. J., Turmukhambetov, D., and

Brostow, G. J. (2017). Harmonic networks: Deep

translation and rotation equivariance. In Proc. IEEE

Conf. on Computer Vision and Pattern Recognition

(CVPR).

Zheng, S., Song, Y., Leung, T., and Goodfellow, I. (2016).

Improving the robustness of deep neural networks via

stability training. In Proc. IEEE Conf. on Computer

Vision and Pattern Recognition (CVPR).

Zhou, Y., Ye, Q., Qiu, Q., and Jiao, J. (2017). Oriented

response networks. In Proc. IEEE Conf. on Computer

Vision and Pattern Recognition (CVPR).

VISAPP 2018 - International Conference on Computer Vision Theory and Applications