Bifocal Parallel Coordinates Plot for Multivariate Data Visualization

Gurminder Kaur and Bijaya B. Karki

School of Electrical Engineering and Computer Science, Louisiana State University, Baton Rouge, Louisiana 70803, U.S.A.

Keywords: Parallel Coordinates Plot, Multivariate Data, High Dimensions, Information Visualization, Focus + Context.

Abstract: Visualization of multivariate data using parallel coordinates plot (PCP) becomes overwhelming as the

number of dimensions/variables increases beyond one dozen or so. Here we propose bifocal parallel

coordinates plot (BPCP) based on the focus + context approach. BPCP splits vertically the overall rendering

into the focus and context regions whose sizes can be adjusted to optimize the use of the available space.

The focus area maps a few selected dimensions of interest, referred to as priority axes, at sufficiently wide

spacing. The remaining dimensions are represented in the context area in a compact way so as to retain

useful information and provide the data continuity. The focus display can be further enhanced with various

options, such as axes overlays, scatterplot, and nested juxtaposed PCPs. In order to accommodate an

arbitrarily large number of dimensions, the context display supports multi-level stacked view, each PCP

level mapping a subset of the context axes. With flexible interactivity, BPCP can manage the priority axes

and data rendering with respect to the corresponding dimensions to support exploratory visualization while

providing useful context on the same visualization display.

INTRODUCTION

Parallel coordinates plot (PCP) is a popular

technique for multivariate data visualization (Avidan

and Avidan 1999; Few 2006; Inselberg, 2009;

Heinrich and Weiskof, 2013). It maps data points in

a multidimensional space to a 2D display surface by

laying out all dimensions/variables/attributes as

parallel vertical axes at uniform spacing. Each data

item is rendered as a polygonal line with its vertices

on these axes. PCP visualization helps us quickly

reveal patterns, trends, relationships, anomalies in

the multivariate data. Generally, static visualization

is not much of practical use because the data lines

quickly fill up the display space often resulting in

visual clutter. To generate insights into the

multivariate information requires appropriate ways

of interacting with the data samples and dimensions

(Siirtola and Raiha, 2006; Inselberg, 2009). Once

regions of interest are identified, the interactivity

helps perform more focused analysis.

PCP is expected to accommodate arbitrarily large

numbers of dimensions and data lines in a finite

display area. More dimensions require adding more

axes in a linear order. Such tightly packed axes

degrade visual resolution and make navigating the

data space difficult. Each data line simply consists of

many segments which are short so it is difficult for

the user to read the data lines. From a practical

viewpoint the user is not able to visually

comprehend all dimensions at a time or the user may

not be even interested to analyse all dimensions on

equal footing. It thus makes sense that only a subset

of the dimensions be better examined at a time. For

example, only five variables for 25-dimensional

automobile dataset (Figure 1) might be of the user’s

current interest. If we render the data with respect to

the five selected dimensions only, we will have

widely placed parallel axes. Visual clarity improves

considerably and the corresponding data segments

become fairly long and are easy to read.

The problem is that the data information with

respect to all other dimensions that are not mapped

into the current PCP is completely lost. One may

toggle between all-axes plot (an overview) and the

selected-axes plot (a detailed view) or use a

miniature PCP as overview and a regular plot as

detail together (Gruendl et al., 2016). Another option

is to support a regular plot (main view) and maintain

an axis repository to hold axes currently of less

importance (Riehmann et al., 2012). Such overview-

detail or detail-on-demand approaches suffer from a

(time) disconnect issue between the two views

tending to divide the user’s attention.

176

Kaur, G. and Karki, B.

Bifocal Parallel Coordinates Plot for Multivariate Data Visualization.

DOI: 10.5220/0006549901760183

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages

176-183

ISBN: 978-989-758-289-9

Figure 1: Parallel coordinates plot of 25-dimensional

automobile data. Five axes representing origin, weight,

horsepower, city mpg and price are widely spaced in the

left half space (focus display) and the remaining axes are

squeezed in the right half space (context display).

In this paper, we propose bifocal parallel

coordinates plot (BPCP) based on the focus +

context approach (Spence and Apperley, 2013).

BPCP represents the parallel axes corresponding to a

few priority dimensions at sufficiently wide spacing

and maps the remaining dimensions in a compact

way (Figure 1). It renders data line segments with

respect to the selected dimensions at high visual

resolution (providing a focus view which can be

further enhanced using available extra space) while

retaining at the same time the information with

respect to all other dimensions for context. The aim

is to produce a good visualization by effectively

using a finite display without much losing valuable

information. The focus + context approach was

previously applied in parallel coordinates for

highlighting certain axes groups (Brodbeck and

Girardin, 2003) and data clusters (Novotny and

Hauser, 2006). Our work is expected to serve as a

systematic bifocal presentation of parallel

coordinates. We present a novel design of the

proposed BPCP method to effectively split the total

parallel coordinates plot area into two parts. We then

explore various ways of enriching data visualization

in the “focus” part and also the ways of simplifying

rendering in the “context” part.

RELATED WORK

Parallel coordinates plot has been a subject of

extensive investigation due to its applications in

visualization of multivariate data and high-

dimensional geometry. PCP helps discover the

multivariate relations by transforming the problem

into 2D pattern recognition problem involving 2

subsets, and also has relative merits for tasks like

clustering and outlier detection (Inselberg, 1997;

Zhou et al., 2008). Due to the visual clutter caused

by over-plotting of data polylines and closely spaced

coordinate axes, PCP visualization may be confusing

and even intimidating at first, but with interactivity it

can actually be very approachable.

When the number of dimensions (k) increases,

the axes arrangement is crucial for finding and

understanding complex multivariate relations. To

compare different variables side-by-side requires the

reorder of axes and the trial of multiple

arrangements. For instance, the parallel coordinates

matrix plot (Heinrich et al., 2012) shows all layouts

simultaneously. A good axes order can be found

using the contribution- and similarity-based

reordering methods (Lu et al., 2016; Peltonen and

Lin, 2017). If k is large, only a subset of important

axes can be included in the main PCP view

(Riehmann et al., 2012; Gruendl et al., 2016).

Dimension spacing which is the gap between

adjacent axes is also important. The default spacing

is chosen to be uniform. The dimensions are not

equivalent to each other, and one way of conveying

this information is to vary dimension spacing (Yang

et al., 2003). For instance, similar dimensions are

mapped closer than the unrelated dimensions. Extra

space between the adjacent axes allows the user to

explore the pattern in detail. Horizontal zooming

in/out and panning or distortion can be used to adjust

the spacing of the concerned axes or to even collapse

a group of axes (Brodbeck and Girardin, 2003).

Specifying such local changes is difficult because of

narrow axial spacing when k becomes large.

One or more polylines to emphasize the selected

data samples can be highlighted with the rest still in

the background. Data lines can be pinched from the

above and below so that they are picked up

(Inselberg, 2009). Alternatively, a subset of data

items is selected by means of brush. Axis-aligned

brush picks a range on an axis corresponding to an

interval on the respective dimension in the data

domain (Turkey et al., 2011). Visual clutter can be

reduced by data filtering or clustering so as to reveal

patterns and anomalies (Fua et al., 1999; Peng et al.,

2004; Zhou et al., 2008).

With increasing k, various tasks related to

dimension management and interacting with data

samples become impractical at some point both

effectiveness- and performance-wise. Inselberg

(2009) has questioned the number of dimensions

PCP can handle. The answer is not “many” on a

single display. It is not possible to map a large

number of dimensions at the same time without

cluttering the display. Reduction techniques like

principal component analysis and multidimensional

scaling condense many dimensions to a few

Bifocal Parallel Coordinates Plot for Multivariate Data Visualization

177

dimensions (Jolliffe, 1986; Mead, 1992). Similar

dimensions may be grouped together and mapped as

closely-spaced axes or even as a single

representative axis. A more direct solution is

dimension filtering, which is to eliminate the

repetitive variables or remove unimportant axes

(Yang et al., 2003).

Our proposed bifocal PCP technique exploits

several of the above-mentioned ideas for its design

and effectiveness for multivariate data visualization.

Both “focus” and “context” display areas can

support various ways of interacting with the axes

and data samples. Our tests used the automobile

dataset (25 variables and 200 observations) and the

cardiac arrhythmia medical dataset (280 variables of

which are 130 used here, and 452 records) available

from the UCI machine learning repository

(http://archive.ics.uci.edu/ml).

DESIGN OF BIFOCAL PCP

In parallel coordinates plot, all dimensions

(variables) are laid out as vertical axes at uniform

spacing. If k dimensions are mapped on the display

surface of width X and height Y, the axial spacing is

given by X = X/(k-1). If k increases, the axes are

packed more compactly so as to fit all of them

within a given finite area. In the proposed bifocal

parallel coordinates plot (BPCP), the overall display

is vertically split into two regions corresponding to

“focus” and “context”, which use different axial

spacing (Figure 1). It thus applies a one-dimensional

focus + context across the axis dimension (i.e., in the

horizontal direction). The focus region maps a few

axes of interest at wider interval than the average X

enabling a detailed view of the data with respect to

the corresponding dimensions. On the other hand,

the context region accommodates all remaining axes

by packing them tightly to retain full information

about the data as much as possible. To explain the

design of the proposed BPCP, we consider three

parameters as follows:

3.1 Focus Area

The total display area spanned by parallel

coordinates and data lines is usually extended

horizontally more than vertically, i.e., X > Y. For a

large number of dimensions, it makes sense to

consider the total parallel coordinates plot width of

X = 2Y (Figure 2). The 2:1 display area can use the

horizontal spread of the computer screen fully for

PCP while leaving extra space in the vertical

direction for displaying axes labels, user controls,

and other features. When the display region is

divided into the focus and context parts, the

questions arise about their sizes and locations. The

default option is to have each part as a square

(Figure 2, middle) such that X

= Y (focus width) and

= Y (context width). To accommodate more

dimensions in the focus area, we need to increase its

width. There is a limitation because the remaining

axes must be mapped as well. We limit the

horizontal spread of the focus area to the three-

fourth of total display width (X

= 1.5Y) so the

minimum context area width is 0.5Y.

Figure 2: Axes layout of BPCP in a display area of width

X and height Y. Top: All k axes are placed at equal

spacing. Middle: The plot consists of two equal parts: the

focus part showing three axes and the context part

showing remaining k-3 axes. Bottom: The focus area maps

seven axes. Three orientation cases (low, mid and high tilt

angles with the horizontal direction) of data line segment

between the adjacent axes are shown.

The left position of the focus area with the

context area on the right as shown in Figures 1 and 2

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

178

perhaps works well. Another option is to focus

symmetrically about the centre so that its left and

right sides together provide the context display.

Moreover, the focus region can be allowed to glide

along the horizontal direction to any position in an

interactive manner, and the affected axes and data

lines need to be redrawn accordingly (Brodbeck and

Girardin, 2003).

3.2 Priority Axes

The dimensions which are represented in the focus

display with wider spacing than the average spacing

are referred to as priority (focus) axes. We need, at

least, two priority axes to focus on so that the lines

joining the data values on the corresponding

variables can be drawn with better visual resolution

and the relationships can be explored in detail.

Practically it makes more sense to have three

priority axes (Figure 2, middle). We can explore the

relationships of a central axis with two other axes,

one on the left and one on the right and then provide

a flexible option of making one of three axes the

central axis. The maximum number of the priority

axes, however, can vary depending on the focus

display and the total number of dimensions, but it

must be kept small. The priority axes can be selected

manually by the user as important

dimensions/variables/attributes. Or, they can be

automatically found based on some measures, for

instance, as highly correlated dimensions using

Pearson correlation. The priority axes can be

manipulated interactively by adding to and deleting

the axis from the focus display.

3.3 Axes Spacing

It is important that the parallel axes be laid out in the

focus region sufficiently wide from each other. The

data polygonal lines consist of segments between

successive adjacent axes. The visual impression of

these data lines depends on various angles the

component segments make while moving from left

to right. Generally, a unity slope (that is, angle 45

with the horizontal direction) of a line is considered

to give the best visual representation (von Huhn,

1931). Obviously, the unity slope is unachievable for

all data line segments. The lines connecting the

opposite ends of the adjacent axes make tilt angles

of 45

and cross each other at 90

if the horizontal

gap between the axes is equal to the axis length (i.e.,

the vertical plot extent). We have X

= Y, which

should be taken as the widest gap as it is the case

with focus width of Y for two priority axes.

However, it makes more sense to consider 45

tilt

angle for average situations where the difference

between the data marks on two adjacent axes is

equal to the half of the axis length (Figure 2,

middle). We have X

= 0.5Y, which is the case with

focus width of Y for three priority axes. The data

lines between two successive axes make tilt angles

in the range 0

(when the lines connect the data

marks at the same height) to 63.4

(when the lines

connect the opposite ends of the axes).

One issue still is that the line segments for small

differences in the data marks between two adjacent

axes appear almost horizontal. Further decreasing

the dimension spacing can increase such low-angle

tilts. For X

= 0.25Y, the lines connecting the

opposite ends of the axes make 76

so the angle of

extreme line crossing becomes 28

, which is visually

discernable. Assuming 0.25Y as the minimum axial

spacing for the largest focus display width of X

1.5Y (Figure 2, bottom), the maximum number of

the priority axes we should allow is given by k

= 1+

/X

= 7. The maximum seven dimensions to

focus on make sense with the general notion that

parallel coordinates plot is the most effective for the

datasets with fewer than one dozen dimensions

(Inselberg, 1997; Few 2006).

The focus axial spacing (X

) is the main

parameter controlling the design of the proposed

BPCP. As discussed above, we recommend that the

gap between adjacent focus axes be between 0.25Y

and Y

where Y is the vertical display extent (height)

set for the overall plot. A spacing value outside this

range either results in very closely packed axes or

very wide focus coverage. Our design strictly

imposes the focus axial spacing range. It then

constrains the number of the priority dimensions (k

)

between 2 and 7. Finally, it adjusts the focus display

width (X

) between 0.25Y (when X

= Y for two

priority axes) to 1.5Y (when X

= 0.25Y for seven

priority axes) for the 2:1 display. If the number of

dimensions is very large, we need a wider plot. We

set X = 3Y when k is greater than 31, but the average

spacing is still less than one tenth of the vertical

extent. For the minimum focus axes spacing (0.25Y),

we can now map up to nine priority axes supporting

the widest focus display of 2Y.

The above design is such that bifocal parallel

coordinates plot is ineffective when k is less than

four for the 2:1 display. For k between four and nine,

the focus area with only axial spacing greater than

the average X can be supported. For k > 9, the

average axial spacing is smaller than 0.25Y and the

full range of X

values can be exploited. This is the

situation with the number of dimensions greater than

13 for the 3:1 display.

Bifocal Parallel Coordinates Plot for Multivariate Data Visualization

179

ENHANCING FOCUS DISPLAY

The focus display can be further enriched with

additional rendering and analysis options to enable

an in-depth, interactive visualization of multivariate

data with respect to the priority dimensions.

4.1 Axes Management

Understanding data dimensions in PCP involves the

manipulation of the corresponding parallel axes,

which enable us to read off the values and ranges of

data samples. To facilitate the visual perception of

data distributions on the respective dimensions, the

axes can encode additional information using

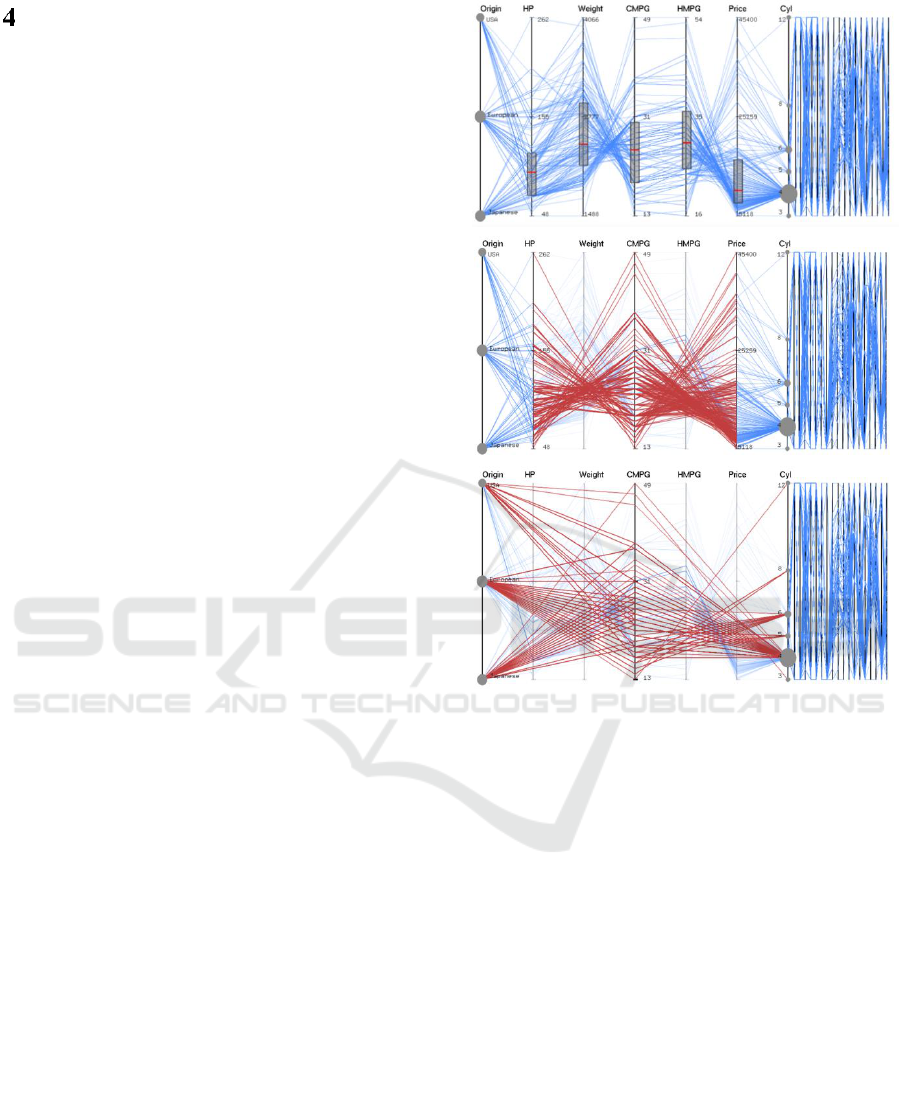
overlays like circle and box plots (Figure 3, top).

This can be helpful in deciding the priority axes.

Axes reordering option enables the user to detect

patterns within the data and pay more attention to

important dimensions (Johansson et al., 2008; Lu et

al., 2016; Peltonen and Lin, 2017). The pair-wise

relationships among the dimensions are easier to

interpret when the corresponding axes are adjacent

to each other. To explore the relationships of a

priority axis with all other priority axes, the

concerned axis is first brought to the central part

with the data lines redrawn. The central axis

represents CMPG with its adjacent axes representing

weight and HMPG in Figure 3. City mpg is

negatively correlated with weight and positively

correlated with highway mpg. To relate the central

axis to non-adjacent axes (on its left and right), the

data lines are drawn directly connecting to the

respective coordinates while suppressing or even

removing the intermediate axes and line segments

(Figure 3). This helps examine the relationships of

city mpg with four more variables including origin,

horse power, price, and the number of cylinders.

Only the focus axes and the corresponding data

segments are affected so these operations are fast.

4.2 Data Presentation

A large dataset can be better understood by breaking

it into subsets/groups and then performing inter- and

intra-group analyses. The user can choose a priority

axis (referred to as active axis drawn first) to map

the dataset into multiple subsets. If the active axis

represents categorical variable, the data samples

corresponding to each coordinate value form

asubset. For instance, the automobile dataset has

three values for the origin variable which result in

three subsets: American, European, and Japanese

cars (shown by red, green and blue in Figure 4). For

Figure 3: Focus PCP (2Y/3 wide) of 7 priority axes on left

and context PCP (Y/3 wide) on right. Circle plot for

categorical variable and boxplots for continuous variables

are shown. The data lines are directly drawn (red) from the

central axis to next-nearest neighbours (middle) and next-

next-nearest neighbours (bottom).

a continuous variable, data groups correspond to

different, non-overlapping ranges of data values.

For instance, three groups can represent low 1/4,

mid 1/2 and high 1/4 intervals on the axis

representing, say price variable. Different clustering

techniques (Fua et al., 1999; Zhou et al., 2008) can

be used to identify groups for a multiple-set

mapping of a given dataset.

Scatterplot is effective in correlation perception

and similarity detection (Huamin et al., 2012;

Kanjanabose et al., 2015). We add scatterplot for all

priority axes pair directly below their respective PCP

(Figure 4). The width and height of the scattered plot

is adjusted based on the focus axial gap X

. In each

scatter plot, the vertical axis is the same as the

priority axis just above it and the horizontal axis is

the right adjacent priority axis. The data lines in the

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

180

PCP and data points in the scatterplot can be brushed

in a consistent way so that two plots can

complement each other. The focus display can be

also appended with a data table instead to show the

actual data values on the priority axes.

Figure 4: Focus region showing three nested PCPs, one for

each subset of the automobile data: American (red),

European (green), and Japanese (blue). The nested plots

are symmetrically placed in between adjacent priority

axes. The context region shows a normal compact PCP.

Scatter plots are for the adjacent priority axes pairs.

4.3 Nested PCP

The nested parallel coordinates plot method has

recently been proposed to perform comparative

visualization of two or more datasets (Wang, 2016).

It helps in exploring both intra-set and inter-set

correlations among different variables/parameters

from a single visualization when multiple datasets

need to be analyzed together. We adopt this method

to visualize multiple subsets (groups/clusters) of the

data with respect to the priority axes (Figure 4). We

treat these subsets as if they were different datasets

and visualize them as different PCPs by embedding

juxtaposed plots within in the normal plot. The

original priority axes are globally scaled and the data

lines for different groups are superimposed

(overlapped) in the regions near the axes thereby

enabling direct intergroup comparison. The nested

axes are locally scaled and laid out in the central

region between the adjacent original axes pairs

thereby enabling visualization of different data

subsets in distinct PCPs. The left and right axes in

each nested plot are the same as the original priority

axes on its left and right.

The default width of a nested PCP is set at one-

third of the focus axial spacing (X

) symmetrically

about the middle line between the original adjacent

axes pair. The horizontal spread can be adjusted by

calculating the positions of two axes in the i

nested

pair as (i – 0.5)X

± x, where i = 1, 2, …, k

-1

(from the left to the right), and x can vary between

0.1X

and 0.4X

. The vertical extents and

positions of the embedded plots are determined by

uniformly dividing the original display height Y. If

is the number of data subsets/groups (n

= 3 in

Figure 4), the end positions of the j

nested axes (j =

1, 2, …, n

counting from the bottom) are given by (j

– 0.5)Y/n

± y, where y can vary between 0.2Y/n

and 0.5Y/n

. Our design assures that the nested axes

never overlap with each other horizontally or

vertically. The nested plot count should be kept

small, not more than five. Explicit encodings, such

as bundling and distorting can further aid the visual

perception of the data lines (Wang et al., 2016).

SIMPLIFYING CONTEXT

DISPLAY

The proposed bifocal PCP packs all non-priority

axes (that is, context axes) much more closely than

in the normal plot. As long as they do not overlap

with each other, individual dimensions should be

readable. However, the data lines depending on their

count can clutter the display to varying degree. The

goal is to retain the relevant information in the

context display and maintain the data continuity. For

instance, when brushing is applied, the user should

see the effects on the selected data samples not only

in focus but also in context (Figure 5). We can add

appropriate axes overlays for showing aggregates or

distributions of the data samples along the respective

dimensions while removing the data lines (if needed)

to minimize visual clutter. It supports interactive

ways of translating and reversing the axes.

Figure 5: Focus PCP (2Y/3 wide) of 5 priority axes and

context PCP (Y/3 wide) with a two-level stacking of 20

context axes for the automobile data. The last priority axis

(price) is repeated in the first level. The last context axis

(width) in the first level is repeated at the beginning of the

second level. Two data items are highlighted in red (light

car) and blue (heavy car).

Bifocal Parallel Coordinates Plot for Multivariate Data Visualization

181

To visually discern the dimensions requires that

a minimum gap be maintained between the adjacent

axes in the context display. This gap depends on the

screen resolution and zooming level. The user can

set a minimum gap in the number of the pixels such

that it can be, say, three times wider than the pixel

width of the axes. For total PCP display of the aspect

ratio 2:1, such minimum axial spacing is achievable

even for the worst situation where 28 axes (out of

total maximum 31 axes allowed) are packed in the

context display of width 0.5Y (with the widest focus

area containing only three priority axes). The 3:1

display does not impose an upper bound on the total

number of dimensions so the axial spacing in the

context area can be arbitrarily small.

To avoid the spacing problem with an arbitrarily

large number of dimensions, we propose a multi-

level parallel coordinates plot. A similar approach

has been previously proposed in the case of the star

plot technique (Sangli et al., 2016). The context axes

are divided into multiple groups and the context plot

area is horizontally partitioned into the equal number

of parts or levels. Each axes group is then mapped to

a different level subarea which is vertically

compressed. It thus represents a vertical stacking of

context axes. The width of each subarea is the same

as before the split so the axial spacing increases but

the axes get shorter. The number of levels (m) in the

stacked view can be adjusted interactively but

should be kept small. The multi-level axial spacing

(when m >1) is constrained to be smaller than

0.25Y/m

(that is, the minimum spacing allowed in

the focus display divided by m

), where Y is the

focus display height. Only two-level plot is allowed

for the 2:1 display (Figure 5) but more levels are

allowed for the 3:1 display. For example, if the

context width X

= Y for the data containing total

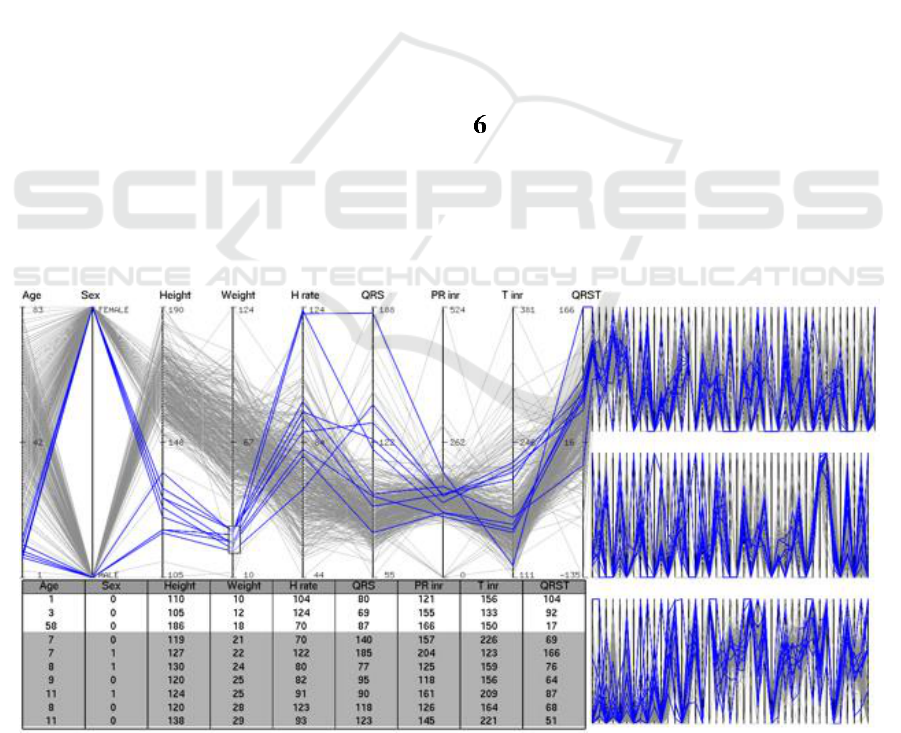
130 dimensions (Figure 6), m = 3 is allowed. Nine

are the priority axes and the remaining 121 axes are

distributed among three PCP levels. The context

axial spacing X

= X

/41 = 0.025Y, being smaller

than 0.25Y/9. Assuming that the context display

width is 500 pixels, we have X

= 12 pixels (that

also includes axial width) for a three-level plot. For

400 axes, m = 4 is allowed. For this four-level

stacked plot, the axial spacing is 5 pixels wide if X

= 500 pixels. In Figure 6, the data lines taking low

weight values tell that the heart rate varies

considerably among small children (7 to 11 years

old). In the context area, these lines mostly remain

close, but they are quite scattered on some axes.

CONCLUSIONS

The parallel coordinates plot becomes less effective

when the dimensionality of the data becomes too

high. To overcome this problem, we have proposed

bifocal parallel coordinates plot (BPCP) to provide

Figure 6: The focus region (2Y wide) showing 9 priority axes and the context region (Y wide) showing three-level PCPs for

the medical dataset consisting of 130 variables. The overall PCP display aspect ratio is 3:1. Each level accommodates 41

context axes. The last priority axis also appears as the first context axis. The first axis in each level is the last axis of the

level above it. The data items using a low-weight brush are highlighted in the PCPs and data table.

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

182

“focus” and “context” views on a single

visualization display by partitioning the overall

rendering into two regions with flexible widths. The

focus PCP renders the data with respect to priority

dimensions (whose number is kept small, below 10)

so that the corresponding axes are widely spaced.

The display can be enriched by adding ancillary

visualizations including axes overlays, embedded

parallel coordinates, and scatter plots. The context

PCP renders the same data with respect to all

remaining axes, which are tightly packed in a single

plot or a multi-level stacked layout. By

experimenting on two datasets consisting of 25 and

130 dimensions, we have demonstrated the potential

effectiveness of BPCP in visually exploring

high/ultra-high dimensional multivariate data, which

are on a rise in today’s big data world.

REFERENCES

Avidan, T. and Avidan, S. (1999). Parallax – a data

mining tool based on parallel coordinates.

Computational Statistics, 14:79-90.

Few, S. (2006). Multivariate analysis using parallel

coordinates. Perceptual Edge.

Inselberg, A. (2009). Parallel coordinates: visual

multidimensional geometry and its application.

Springer, New York.

Heinrich, J. and Weiskopf, D. (2013). State of the art of

parallel coordinates. In STAR Proceedings of

Eurographics, pages 95–116.

Siirtola, H. and Raiha, K. (2006). Interacting with parallel

coordinates. Interacting Computers, 18:1278-1309.

Gruendl, H., Riehmann, P., Pausch, Y., and Froehlich, B.

(2016). Time-series plots integrated in parallel

coordinates displays. In Eurographics/IEEE VGTC

Conference on Visualization, pages 321-330.

Riehmann, P., Opolka, J., and Froehlich, B. (2012). The

product explorer: Decision making with ease. In

International Working Conference on Advanced

Visual Interfaces, pages 423-432.

Spence R. and Apperley, M. D. (2013). A bifocal display.

The Encyclopedia of Human-Computer Interaction.

Ed., Interaction Design Foundation.

Brodbeck, D. and Giradin, L. (2003). Design study: Using

multiple coordinated views to analyse geo-referenced

high-dimensional datasets. In International

Conference on Coordinated and Multiple Views in

Exploratory Visualization, pages 104-111.

Novotny, M. and Hauser, H. (2006). Outlier-preserving

focus + context visualization in parallel coordinates.

IEEE Transactions on Visualization and Computer

Graphics, 12:893-900.

Inselberg, A. (1997). Multidimensional detective. In IEEE

Symposium on Information Visualization, pages 100-

107.

Zhou, H., Yuan, X., Qu, H., Cui, W., and Chen, B. (2008).

Visual clustering in parallel coordinates. Computer

Graphics Forum, 27:1047-1054.

Heinrich, J., Stasko, J., and Weiskopf, D. (2012). The

parallel coordinates matrix. In Eurographics

Conference on Visualization, pages 37–41.

Lu, L. F., Huang, M. L., and Zhang, J. (2016). Two axes

re-ordering methods in parallel coordinates plots.

Journal of Visual Languages & Computing, 33:3–12.

Peltonen, J. and Lin, Z. (2017). Parallel coordinates plots

for neighbour retrieval. In 12

Joint International

Conference on Information Visualization Theory and

Applications, pages 40-51.

Yang, J., Peng, W., Ward, M. O., and Rundensteiner, E.

A. (2003). Interactive hierarchical dimension ordering,

spacing and filtering for exploration of high

dimensional datasets. In IEEE Symposium on

Information Visualization, pages 105-112.

Turkey, C., Filzmoser, P., and Hauser, H. (2011).

Brushing dimensions: a dual visual analysis model for

high-dimensional data. IEEE Transactions on

Visualization and Computer Graphics, 17:2591-2599.

Fua, Y. H., Ward, M. O., and Rundensteiner, E. A. (1999).

Hierarchical parallel coordinates for exploration of

large datasets. In IEEE Visualization, pages 43–50.

Peng, W., Ward, M. O., and Rundensteiner, E. A. (2004).

Clutter reduction in multi-dimensional data

visualization using dimension reordering. IEEE

Symposium on Information Visualization, pages 89-96.

Jolliffe, J. (1986). Principal component analysis. Springer

Verlag.

Mead, Al. (1992). Review of of the development of

multidimensional scaling methods. The Statistician,

33:27-35.

Von Huhn, R. (1931). A trigonometrical method for

computing the scales of statistical charts to improve

visualization. Journal of the American Statistical

Association, 26:319-324.

Johansson, J., Forsell, C., Lind, M., and Cooper, M.

(2008). Perceiving patterns in parallel coordinates:

determining thresholds for identification of

relationships. Information Visualization, 7:152-162.

Huamin, Q., Xiaoru, Y., Hong, Z., Peihong, G., and He, X.

(2009). Scattering points in parallel coordinates. IEEE

Transactions on Visualization and Computer

Graphics,15:1001-1008.

Kanjanabose, R., Rahman, A. A., and Chen, M. (2015). A

multitask comparative study on scatter plots and

parallel coordinates plots. In Eurographics Conference

on Visualization, 34:261-270.

Wang, J., Liu, X., Shen, H. W., and Lin, G. (2016).

Multiresolution climate ensemble parameter analysis

with nested parallel coordinates plots. IEEE

Transactions on Visualization and Computer

Graphics, 23:81-90.

Sangli, S. S., Kaur, G., and Karki, B. B. (2016). Star plot

visualization of ultrahigh dimensional multivariate

data. In International Conference on Advances in Big

Data Analytics, pages 91-97.

Bifocal Parallel Coordinates Plot for Multivariate Data Visualization

183