Optical Graph Edge Recognition

Rudolfs Opmanis

Institute of Mathematics and Informatics of University of Latvia, Raina bvld. 29., LV-1459, Riga, Latvia

Keywords:

OGR, Optical Graph Recognition, Graph Vectorization, Graph Edge Recognition Algorithm.

Abstract:

Optical graph recognition is a process that from an input raster image extracts a graph topology. Graph

recognition is interesting for not only because it allows reusing information from other diagrams, but also it

is a tool that can measure the readability of a graph diagram visualisation or help with a testing of automatic

graph visualisation engines. In this paper, we propose an optical graph edge recognition algorithm that can

recognise edges with arbitrary edge routing style, handle drawings with many edge crossings and process

edges that are rendered as polylines using a solid or dashed stroke. To evaluate the proposed algorithm we

have developed comprehensive test suite with 2400 graphs of various sizes, edge densities, edge routing styles

and edge rendering strokes.

1 INTRODUCTION

Graph drawing and optical graph recognition (OGR)

are very closely related disciplines. Graph drawing

considers problems related to a graph transformation

into readable drawing, while OGR considers prob-

lems related to the inverse transformation. OGR can

be considered both as a pre-processing step before the

graph drawing or as a post-process after the graph

drawing. If we look at the optical graph recognition as

a pre-process, we can imagine a use-case when we ac-

quire a drawing of a graph and we need to make some

adjustments either in its graph layout or topology. On

the other hand, if we look at the optical graph recog-

nition as a post-process after a graph drawing step

then it can be used as a tool to enable an automatic

quality assurance. With an OGR tool we can perform

completely automatic testing of a graph visualisation

solution that validates a graph layout and rendering

results simultaneously. While using an OGR we can

cover many more tests when compared to a manual

testing process.

Our OGR solution for generic graph drawings is

split into three phases: background extraction, node

recognition and edge recognition. To limit the scope

of this paper we are investigating only the edge recog-

nition step from a full optical graph recognition so-

lution. From our experience edge recognition is the

most challenging phase especially if they are rendered

using dashed patterns. The background of a typical

graph drawing is ﬁlled with a solid colour so its ex-

traction is very easy. Node recognition seems sim-

pler than edge recognition because node recognition

usually can be done using a context-free approach

(each node can be processed independently), but edge

recognition requires a context-sensitive solution be-

cause while untangling edge crossings other edges

need to be considered as well. We feel that our so-

lution, that can handle both dashed and solid edges

independent of their colour would be applicable to the

majority of graph renderings.

Others have also worked in the ﬁeld of optical

graph recognition. (Auer et al., 2013; Krishnamoor-

thy et al., 1996) have proposed algorithms for a

generic graph recognition. Solution proposed by (Kr-

ishnamoorthy et al., 1996) seems to be limited to only

black and white graph drawings with straight edges.

(Auer et al., 2013) supports more generic drawings

but uses morphological operations for edge thinning

which produces an information loss at the edge cross-

ings that is critical for resolving edge crossings with

small angular resolution or locations where multiple

edges are crossing in a small vicinity. Also if edges

are rendered using dashed lines then algorithm pro-

posed by (Auer et al., 2013) is not applicable and

there is no simple way to ﬁx it. Dashed lines are typi-

cal in UML diagrams which also can be considered as

graph drawings. If the user knows that only speciﬁc

types of graph drawings will have to be processed

then an OGR algorithm for speciﬁc diagram types

is more practical and could easier lead to acceptable

recognition results. An optical graph recognition al-

gorithm for speciﬁc diagram types, when compared to

a generic algorithm, can make additional assumptions

184

Opmanis, R.

Optical Graph Edge Recognition.

DOI: 10.5220/0006550401840191

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages

184-191

ISBN: 978-989-758-289-9

about an input image and therefore gain an advantage.

Others have proposed speciﬁc graph recognition al-

gorithms for UML diagrams (Lank et al., 2001; Ham-

mond and Davis, 2006; Lank et al., 2000) and also

electrical schematics (Bailey et al., ). Another way

to limit the scope of recognisable graph drawings is

to limit the way how the drawing is produced. There

are on-line graph recognition algorithms that in ad-

dition to the produced graph drawing requires a list

of atomic draw actions that were used to produce it.

CAD diagram recognition or line drawing vectorisa-

tion (Dori and Wenyin, 1999; Dori and Liu, 1999;

Von Gioi et al., 2008) are similar ﬁelds and tries to

solve similar problems to optical graph recognition,

but does not convert recognised graphical primitives

into consistent graph topology.

This paper is organised as follows. In Section 2

we deﬁne basic concepts that are used in this paper,

Section 3 explains details of the proposed optical edge

recognition algorithm. Section 4 is dedicated to the

performance analysis and the testing process of the

proposed algorithm. Finally, Section 5 contains the

summary and conclusions.

2 PRELIMINARIES

In this paper we consider a graph to be an undirected

multi-graph with possible self-loops. By a graph

layout, we mean a process that assigns 2D geometry

to graph objects. For nodes, it assigns their centre po-

sitions, but for edges, it might assign a list of points.

Edges are routed as polylines from the centre of one

end-node, through the list of assigned points and to

the centre of the other end-node. We assume that

graphs in input images are laid out and rendered con-

sidering the common graph drawing aesthetics crite-

ria as described in (Di Battista et al., ) such as node-

node and node-edge overlap-free drawings and also

reasonable spacing and angular resolution between

graph objects. Since this paper is focused only on

the edge recognition step, we allow any node render-

ing style as long as they can be reliably detected by

the node recognition pre-processing algorithm. In our

benchmark tests, we use a circle to represent a node.

In this paper, an image or a graph drawing rep-

resents a bit-mapped raster image of a laid out graph.

The image can be provided as a png ﬁle or in any other

ﬁle format as long as it is possible to retrieve colour

information for every pixel. We don’t make any as-

sumptions about how the image was retrieved.

3 EDGE RECOGNITION

ALGORITHM

The edge recognition algorithm is designed to run af-

ter a node recognition algorithm so the input of the al-

gorithm consists of the input image, detected node ge-

ometry information and a image background colour.

Each node geometry should contain its centre location

and either its width and height or a set of pixels that

are considered to belong to the node. Image back-

ground colour is used to split all input image pixels

into three distinct classes: node pixels (pixels deter-

mined by node geometries), graph background pix-

els and potential edge pixels. It is important to note,

that if the graph drawing contains labels or noise then

at this point their pixels will be classiﬁed as poten-

tial edge pixels, however, after the edge recognition

step, they will be ﬁltered out in a separate set. Graph

background pixels are those pixels that are in the same

colour as graph background colour. The edge recog-

nition algorithm works only with the pixels from the

potential edge pixel class.

The edge recognition algorithm consists of three

consecutive phases: the image vectorization, the

building of segment graph, and the edge detection.

The ﬁrst phase has access to the input data of the

whole edge recognition algorithm, but each of the fol-

lowing phases has access to the algorithm input data

and also to any output information that any of the pre-

vious phases have produced.

The output of edge recognition algorithm contains

a set of recognised edges and a set of input image pix-

els which belong to the recognised edges. After the

edge recognition algorithm is ﬁnished it is possible to

divide all input image pixels into four distinct classes:

background, node, edge, and other pixels. The other

pixel set could be used as an input for other algorithms

to recognise labels or other visual elements.

Figure 1 illustrates the input this edge recogni-

tion algorithm receives. The input image is pre-

processed, the white pixels are background pixels, the

gray dashed rectangles show bounding boxes of the

detected nodes and the remaining black pixels belong

to the potential edge pixel set.

3.1 Image Vectorization

The image vectorization is the ﬁrst phase of the edge

recognition algorithm. It uses potential edge pixels to

produce a set of line segments. For the actual segment

detection, we use the Sparse Pixel Vectorization (SPI)

algorithm (Dori and Liu, 1999). SPI searches through

the set of potential edge pixels to ﬁnd clusters of pix-

els that deﬁnes line segments with consistent width

Optical Graph Edge Recognition

185

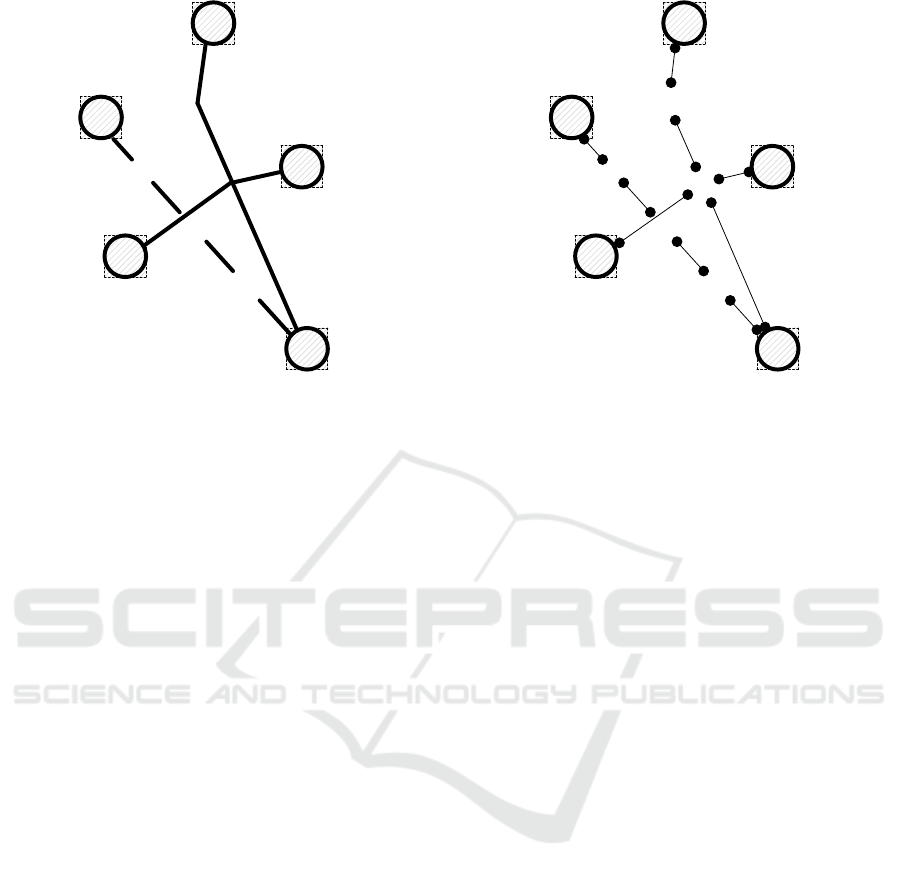
Figure 1: Input image with detected nodes.

and direction properties through the whole length of

detected segment. This strict consistency requirement

means that if some edge in the original drawing is

drawn with bend points or curves then SPI will re-

turn a set of segments that approximate that shape

(because direction changes at bends or curves) or if

there are edge crossings, then SPI will split segments

at the edge crossing point (because segment thickness

changes at the crossing). For each segment, SPI re-

turns coordinates of both end points of medial axis

and detected thickness. If an edge in the input image

is rendered using a dashed line pattern, then each dash

would be a separate segment. At this point, we are not

making any assumptions about the dashing pattern so

we will be able to handle edges with arbitrary dash

patterns and also uncommon edge renderings when

different parts of the same edge are rendered using

different dash patterns. SPI algorithm can process a

noisy input so even if the input image has some noise

it will be able to handle it.

Figure 2 shows the concept of detected edge seg-

ments.

3.2 Building of Segment Graph

The segment graph building phase is used to build a

graph which would store the segment neighbour in-

formation. The segment graph is a graph where nodes

are the endpoints of the segments detected in the pre-

vious image vectorization phase and node centres that

are speciﬁed in the input of the edge recognition algo-

rithm. A segment graph contains an edge between two

of its nodes (geometric points) if both points are geo-

metrically close to each other. The closeness thresh-

old is a parameter that can be customised before the

edge recognition starts. A segment graph contains

Figure 2: Detected line segments.

only two kinds of edges: edges between segment ends

and edges between a segment end and the centre of a

previously detected node.

To build a segment graph it is necessary to solve

common computational geometry problem for the

given point p, the distance parameter value d and the

set of points S: ﬁnd q ∈ S : p.distance(q) ≤ d. The

set S contains all node centre points and end points of

all detected edge segments. A segment graph is built

by solving this computational geometry problem for

every point in S and adding an edge between each

pair of points p and q. To reduce the number of edges

in a segment graph two different distance threshold

values were used during the segment creation. The

node neighbour distance (nd) threshold is used for

ﬁnding node centre point neighbours, but the edge

neighbour distance (ed) threshold is used to ﬁnd

neighbours of edge segment end points. The value

of ed should be greater than the greatest acceptable

gap in a edge rendering (caused by noise in drawing

or edge dash pattern) and also greater than the edge

thickness because detected segments might be split

next to crossing points. The value of nd determines

how far away an edge segment can start from the

node to still be considered connected to the node. nd

should be greater than the greatest acceptable gap in

an edge and ensure that at the distance nd from a node

all connected edges are distinguishable from each

other. Solid lines in Figure 3 illustrates generated

segment graph edges, but the dotted lines are the

detected segments. The segment graph edges are:

),(O

,J), (O

,A), (O

),(O

,H),(O

,D),

(K,J),(F, G), (B,I), (B, E), (B,C), (C, I),(C, E),

),(K

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

186

Figure 3: Created segment graph.

3.3 Edge Detection

The edge detection phase is the ﬁnal phase that using

the previously detected segments and the created seg-

ment graph ﬁnds chains of consecutive segments that

start in a node and end in a node and reports them as

edges. Segment end point coordinates can be used as

bend points for the created edges.

The edge detection algorithm works under the as-

sumption that each detected edge segment can belong

to a single detected edge so we introduce the used

segment set which initially is empty, but is dynami-

cally populated with the segments that makes up each

detected edge. The edge detection algorithm iterates

through all segments and if at least one end of the seg-

ment is close to a node (the segment graph contains

an edge between the segment end and the node cen-

tre) then it starts the edge tracking with this segment

in the direction away from the detected node.

The edge tracking step is captured in the Algo-

rithm 1. In the input it receives two objects: a) the

current segment with direction information, and b)

the set of used segments to know which of the de-

tected segments can and can not be used for the edge

tracking. While tracking an edge it iteratively builds

a chain of segments until it ﬁnds an acceptable end

node or the target end of the last segment in the built

chain doesn’t have any acceptable neighbours in the

segment graph. If target end of the last segment in

the chain has multiple valid neighbours in the seg-

ment graph then we use cost calculation function to

ﬁnd the neighbour with the smallest cost. The cost

calculation function is designed to favor neighbouring

segments that continue in the general direction of the

already built chain of segments. If the last segment

Figure 4: Next segment cost calulation.

in the chain is long enough (larger than the speciﬁed

threshold) then it is used as the general edge direction,

otherwise, we step back along the built chain until the

distance to the to the target point of the last segment

exceeds the threshold. Stepping back is very impor-

tant in dashed line recognition, because each dash on

its own might not deﬁne the correct edge direction.

On the other hand if the target end of the last segment

in the built chain doesn’t have any acceptable neigh-

bours then we cancel the edge tracking process and

return to iterating through not processed segments.

The cost calculation function receives a segment

showing the general edge direction as the ﬁrst param-

eter and a neighbour segment for which the cost value

needs to be computed as the second parameter. In Fig-

ure 4 segment AB is the general edge direction and CD

is the neighbour segment. If |BC| is shorter than the

edge thickness approximation eT value then the cost

value is angle β. If |BC| > eT then the BC direction

is as important as the direction of CD and we use the

sum of angles α and β as the cost value and in case

segments AB, BC, and CD creates ’S’ turn then we

add an additional penalty of 3π to the cost value. This

additional penalty helps with the parallel edge track-

ing.

4 EXPERIMENTAL RESULTS

To gain understanding about the quality of the pro-

posed algorithm not only it is important to understand

the details about the algorithm itself, but equally im-

portant it is to know how the quality is measured. To

Optical Graph Edge Recognition

187

Algorithm 1: Track Edge.

Input: initialSegmentStartEnd,

initialSegmentOtherEnd, Set of used

vectors usedSegments

begin

initialize list of segments segmentList

currentSegment ←

initialSegmentStartEnd.segment()

result ← NORESULT

while result = NORESULT do

nextSegment ←

getNextSegment(currentSegment,

SegmentGraph)

if currentSegmentEnd is connected to

recognized node n in SegmentGraph

and line of currentSegment crosses

bounding-box of n then

result ← SUCCESS targetNode ←

end

else if nextSegment 6= null then

segmentList.add(currentSegment)

end

else

result ← FAILURE

end

currentSegment ← nextSegment

end

get fair measurements we designed a test suite and

performed an automatic testing on more than 2400

test cases with various properties. The following sec-

tions will cover decisions and reasoning made while

designing the test suite, the algorithm testing and ﬁ-

nally the produced results. All tests used for the test-

ing are accessible at (Opmanis, 2017).

4.1 Design of Benchmark Tests

When we look at a graph drawing there are at least

three important aspects inﬂuencing our ability to read

it and recognise the graph. These aspects are: vi-

sualised graph properties (size, a number of nodes,

edges, average node degree, etc.), the graph layout,

and its rendering style. To measure the quality of the

proposed algorithm we created benchmark tests with

variations in all three aspects. Each test consisted of

a raster image with the graph rendering and a text

ﬁle with the graph topology for the validation of the

recognition result.

4.1.1 Graph Properties

To cover various graph types we generated random,

connected graphs with 10, 20, 50 and 100 nodes.

Graph connectivity was ensured by ﬁrst generating a

random tree and then adding 0.3, 0.1, 0.05 or 0.025

of all possible edges. Smaller ratio values were ap-

plied to bigger graphs. The graph sizes were chosen

to cover typical manually created graph sizes and also

reach automatically generated graph sizes.

4.1.2 Graph Layout

The graph layout is important because its properties

determines if edges will be routed with bends (or as

straight lines), what is the guaranteed node-edge spac-

ing (or there will be node-edge overlaps), how likely

are crossings of more than two edges in the same point

or close vicinity, etc. To prove that the edge recogni-

tion algorithm is not ﬁne-tuned to a particular layout

style it was tested on graphs laid out with a spring-

embedder style symmetrical layout algorithm and a

Sugiyama-style hierarchical (Sugiyama et al., 1981)

layout algorithm.

4.1.3 Symmetric Layout Style

Symmetric (spring-embedder) layout is very widely

used because of its performance and reasonably easy

readable layouts of sparse graphs. We chose to use

this layout style to generate part of our test cases be-

cause there are no dominating edge directions so it

would allow us to validate the claim that proposed

edge recognition algorithm does not depend on a par-

ticular edge direction properties. Also, edge crossings

happen randomly, therefore, there are no assumptions

about the edge crossing angles and how many edges

are crossing at the same point or close vicinity. The

symmetric layout has some properties that limit its us-

ability for edge recognizer testing such as: it routes

edges as straight line segments between the source

and target nodes and node-edge overlaps are also very

common. Straight path rendering is considered bad

for our test suite test generation because it does not al-

low us to verify if edge recognizer is capable of recog-

nising edges with bends. Node-edge crossings are bad

because they make drawings ambiguous and the pro-

posed algorithm is designed for node-edge crossing

free drawings. To solve both of these problems we

added pre-layout and post-layout steps. In the pre-

layout step, we split each edge into three segments

and added two dummy nodes to link those segments

together. In post-layout step, we substituted them

with edge bends and removed all edges that created a

node-edge crossing. Pre- and post-processing allowed

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

188

us to produce symmetric style drawings with polyline

edge routing without node-edge crossings. Test suite

contains post-processed graphs.

Figure 5 illustrates one of the test graphs with 10

nodes which is laid out using symmetric layout style

and edges are rendered using dashed line pattern, but

Figure 7 shows a test case with 100 nodes and edge

density 0.025.

Figure 5: 10 node test graph laid out with symmetric

layout and rendered using dashed pattern.

Figure 6: 10 node test graph laid out with hierarchical

layout and rendered using solid lines.

Figure 7: 100 node test graph with density 0.025 rendered

using solid lines.

4.1.4 Hierarchical Layout Style

Hierarchical (Sugyama) layout style is popular be-

cause it shows hierarchical and ﬂow properties.

Strengths of the hierarchical layout include edge rout-

ing feature that ensures an appropriate spacing be-

tween graph visual objects, therefore, it can guarantee

node-edge overlap-free drawings. When compared to

the previously mentioned symmetric layout in the hi-

erarchical layout results edges are routed with a vari-

able number of bend points, but their directions are

typically aligned with the direction of the main ﬂow,

therefore the edge crossing angles and the edge an-

gular resolution around nodes are not as random and

uniformly distributed as for symmetric layout.

Figure 6 illustrates one of the test graphs with 10

nodes which is laid out using hierarchical layout style

and edges are rendered using solid lines.

4.1.5 Graph Rendering

Each of the previously described graph size and graph

layout combination was rendered in two edge ren-

dering styles: black anti-aliased 1 pixel wide lines

with solid and dashed line patterns. These line styles

were chosen because they are commonly used for

various graph drawings and included in various di-

agram standards (such as UML, SysML) so ability

to support them is important. Also the recognition

of dashed edges is very hard (if not impossible) with

morphology-based approaches.

4.2 Testing

The whole generated test suite consists of multiple

test groups, but each group contains tests with similar

properties. Two test cases from the same group con-

tain images of graphs with the same number of nodes,

edge density, layout style and edge rendering style.

Group name follows the pattern: ’graphN-D-S-L’ to

encode all of these parameters, N describes the num-

ber of nodes, D – the edge density, S – the edge ren-

dering style where ’s’ stands for the solid lines and ’d’

–the dashed line patterns, last token L denotes the lay-

out style, where ’hier’ means a hierarchically laid out

graph, but a group name with empty style means that

it is laid out using the symmetric layout algorithm.

The automatic testing is performed on all test

cases from the test suite. All tests are executed with

the same recognition algorithm conﬁguration so algo-

rithm input parameters were not adjusted to the graph

size, the layout style or the edge rendering style.

After the image of each test case is recognised by the

graph recognition algorithm, the recognised graph

topology is validated against the graph topology

Optical Graph Edge Recognition

189

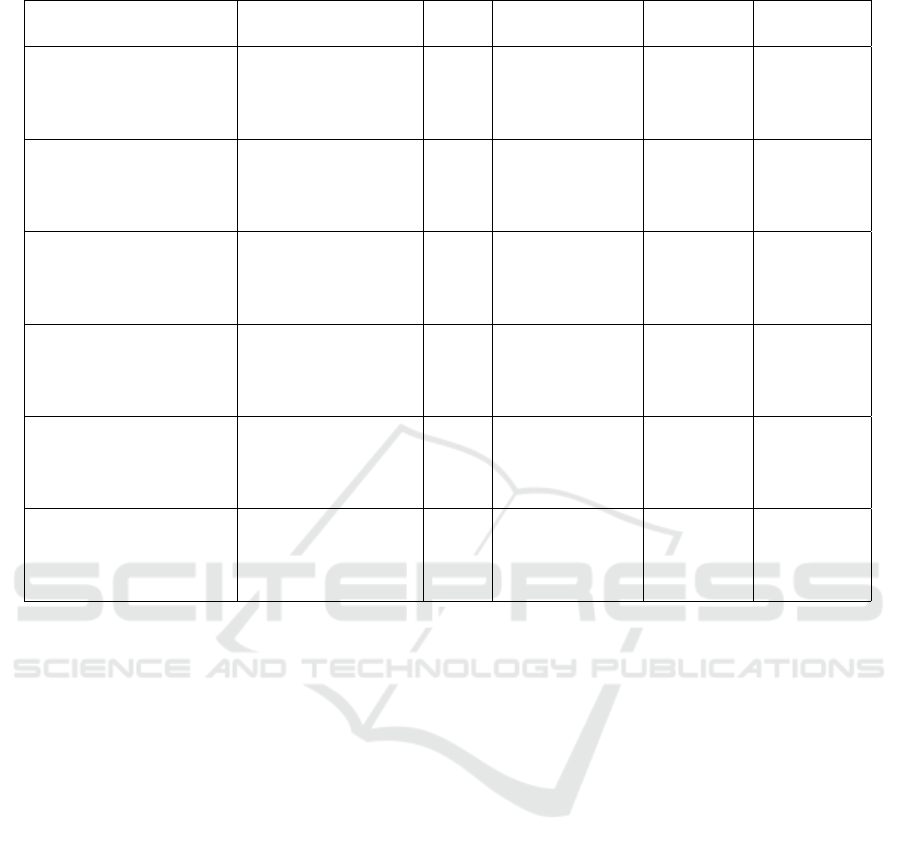
Table 1: Grouped testing results of the edge recognition algorithm (24 groups, 100 tests per group).

test group average(min, max) stdev average number ghost edge approx. test

code success rate of edges ratio time (sec)

graphs10-0.3-d 0.983 (0.875, 1.000) 0.032 19.62 0.014 4

graphs10-0.3-d-hier 0.981 (0.850, 1.000) 0.040 19.62 0.126 1

graphs10-0.3-s 0.994 (0.895, 1.000) 0.021 19.62 0.003 3

graphs10-0.3-s-hier 0.991 (0.882, 1.000) 0.028 19.62 0.013 1

graphs20-0.3-d 0.868 (0.726, 1.000) 0.054 58.04 0.092 10

graphs20-0.3-d-hier 0.938 (0.794, 1.000) 0.041 58.04 0.147 10

graphs20-0.3-s 0.934 (0.830, 1.000) 0.036 58.04 0.032 4

graphs20-0.3-s-hier 0.958 (0.853, 1.000) 0.032 58.04 0.020 5

graphs50-0.05-d 0.955 (0.861, 1.000) 0.029 97.97 0.024 46

graphs50-0.05-d-hier 0.923 (0.792, 1.000) 0.044 97.97 0.171 27

graphs50-0.05-s 0.964 (0.906, 1.000) 0.022 97.97 0.016 32

graphs50-0.05-s-hier 0.954 (0.828, 1.000) 0.033 97.97 0.033 9

graphs50-0.1-d 0.854 (0.752, 0.934) 0.038 138.49 0.088 75

graphs50-0.1-d-hier 0.869 (0.717, 0.955) 0.048 138.49 0.197 71

graphs50-0.1-s 0.891 (0.827, 0.975) 0.030 138.49 0.054 43

graphs50-0.1-s-hier 0.895 (0.794, 0.962) 0.034 138.49 0.061 23

graphs100-0.025-d 0.927 (0.870, 0.978) 0.025 182.76 0.045 130

graphs100-0.025-d-hier 0.886 (0.795, 0.982) 0.037 182.76 0.193 70

graphs100-0.025-s 0.935 (0.874, 0.989) 0.023 182.76 0.034 75

graphs100-0.025-s-hier 0.925 (0.848, 0.988) 0.027 182.76 0.053 25

graphs100-0.05-d 0.794 (0.710, 0.884) 0.037 236.04 0.141 190

graphs100-0.05-d-hier 0.808 (0.678, 0.927) 0.046 236.04 0.253 460

graphs100-0.05-s 0.849 (0.764, 0.916) 0.032 236.04 0.083 71

graphs100-0.05-s-hier 0.855 (0.761, 0.949) 0.037 236.04 0.098 94

that is stored separately from the image. During the

topology validation, both graphs (one from the graph

recognizer and the reference graph) are compared.

Nodes are matched by their centre coordinates, but

edges are matched based on their end nodes. If an

edge from the reference graph is also present in the

recognised graph then it is marked as recognised. If

an edge in reference graph cannot be matched with

an edge in the recognised graph then it is marked as

not-recognized. All edges in the recognised graph

that does not have a matching edge in the reference

graph are marked as ’ghost edges’. Each test result

can be described by three numbers: recognized edges,

not recognized edges, ghost edges, which can be used

to calculate the total number of edges (edgesTotal =

recognizedEdges + notRecognizedEdges), the

normalized successfully recognized edge ra-

tio successRate = recognizedEdges/edgesTotal

and the ghost edge ratio (ghostedgeratio =

ghostedges/edgesTotal).

Results of all tests in the same group are aggre-

gated into seven values: the maximal, minimal, av-

erage recognised edge ratio, its standard deviation,

an average number of edges, the ghost edge ratio

and the number of tests in a group. Since the mini-

mal, maximal, average and median values are relative

values they are numbers in the range [0, 1], where 1

means that everything is successfully recognised, but

0 means that no edges were recognised. The ghost

edge ratio can be any non-negative number.

4.3 Results

Table 1 shows testing results grouped by a test group.

Each group contains 100 test cases. Average edge

number is the same for all test groups with the same

number of nodes and edge density value because they

share the same topology but different edge rendering

and graph layout styles. We can observe that the stan-

dard deviation value is small so the average value ac-

tually shows the success rate that we can expect from

these kinds of tests. As a number of nodes increases

recognition quality decreases, but even for the largest

and the most complicated graphs recognition results

are good enough for automatic graph drawing quality

assurance solutions. By goodenough we mean that

we think that an automatic quality assurance environ-

ment equipped with the proposed algorithm would be

able to validate the quality of a graph drawing solu-

tion faster and more reliably than a manual process.

The solid edge rendering style recognition produces

better results when compared to the dashed edge ren-

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

190

dering style. The ghost edge ratio is comparable to the

doubled ratio of not-recognized edges which proves

that recognition result is not ﬁlled with an arbitrary

number of ghost edges (which would make it unus-

able), but rather all reported ghost edges are created

because of the ambiguous patterns in input images.

The hierarchically laid out graphs are recognised bet-

ter than the same graphs laid out using the symmetric

layout style, this could be explained by the fact that

the hierarchical layout has the poly-line edge routing

opposed to the symmetric layout style so in hierarchi-

cal layout drawings edges will not have edges routed

over bend points of other edges therefore there will be

less ambiguity.

5 SUMMARY AND FUTURE

WORK

The testing results revealed that although the dashed

edge recognition rate is worse than the solid edge

recognition the proposed solution could be useful for

automatic graph rendering and layout algorithm test-

ing. Since we used the same conﬁguration for all tests

in the test suite, the results should allow to expect

similar results on graph drawings with mixed edge

rendering styles and other graph layout styles as long

as they guarantee similar minimal node-edge spacing

values as the graph layout styles in our test cases. The

next steps in the performance analysis would be op-

timising algorithm conﬁguration for each group sep-

arately, investigate edge thickness inﬂuence on pro-

duced results, and detailed examination of test param-

eter impact on the running time.

In future, it would be interesting to try to adjust the

proposed algorithm to recognise graphs without dis-

tinguishable nodes which are typically found in im-

ages of biological networks and where the main in-

formation is stored in edges.

ACKNOWLEDGEMENTS

This work was supported by Latvian State Research

programme NexIT project No.2

REFERENCES

Auer, C., Bachmaier, C., Brandenburg, F. J., Gleiner, A.,

and Reislhuber, J. (2013). Optical graph recogni-

tion. In Didimo, W. and Patrignani, M., editors, Graph

Drawing, number 7704 in Lecture Notes in Computer

Science, pages 529–540. Springer Berlin Heidelberg.

Bailey, D., Norman, A., Moretti, G., and North, P. Elec-

tronic Schematic Recognition.

Di Battista, G., Eades, P., Tamassia, R., and Tollis, I. Graph

drawing. 1999.

Dori, D. and Liu, W. (1999). Sparse pixel vectorization:

An algorithm and its performance evaluation. IEEE

Transactions on pattern analysis and machine Intelli-

gence, 21(3):202–215.

Dori, D. and Wenyin, L. (1999). Automated cad conversion

with the machine drawing understanding system: con-

cepts, algorithms, and performance. IEEE Transac-

tions on Systems, Man, and Cybernetics-part A: sys-

tems and humans, 29(4):411–416.

Hammond, T. and Davis, R. (2006). Tahuti: A geometrical

sketch recognition system for uml class diagrams. In

ACM SIGGRAPH 2006 Courses, page 25.

Krishnamoorthy, M., Oxaal, F., Dogrusoz, U., Pape, D.,

Robayo, A., Koyanagi, R., Hsu, Y., Hollinger, D., and

Hashmi, A. (1996). Graphpack: Design and features.

Software visualization, 7:83–100.

Lank, E., Thorley, J., Chen, S., and Blostein, D. (2001).

On-line recognition of UML diagrams. In Document

Analysis and Recognition, 2001. Proceedings. Sixth

International Conference on, page 356360.

Lank, E., Thorley, J. S., and Chen, S. J.-S. (2000). An

interactive system for recognizing hand drawn UML

diagrams. In Proceedings of the 2000 conference of

the Centre for Advanced Studies on Collaborative re-

search, page 7.

Opmanis, R. (2017). Benchmark test suite. [On-

line https://drive.google.com/open?id=

0B7EhFSCsLEv9Rm9VMjBXeVNEanc; accessed 11-

June-2017].

Sugiyama, K., Tagawa, S., and Toda, M. (1981). Methods

for visual understanding of hierarchical system struc-

tures. Systems, Man and Cybernetics, IEEE Transac-

tions on, 11(2):109125.

Von Gioi, R. G., Jakubowicz, J., Morel, J.-M., and Randall,

G. (2008). On straight line segment detection. Journal

of Mathematical Imaging and Vision, 32(3):313–347.

Optical Graph Edge Recognition

191