Context Dependent Action Affordances and their Execution using an

Ontology of Actions and 3D Geometric Reasoning

Simon Reich, Mohamad Javad Aein and Florentin W

org

otter

Third Institute of Physics - Biophysics, Georg-August-Universit

at G

ottingen,

Friedrich-Hund-Platz 1, 37077 G

ottingen, Germany

Keywords:

Action Affordances, Action Ontology, Planning, 3D Geometric Reasoning.

Abstract:

When looking at an object humans can quickly and efﬁciently assess which actions are possible given the

scene context. This task remains hard for machines. Here we focus on manipulation actions and in the ﬁrst

part of this study deﬁne an object-action linked ontology for such context dependent affordance analysis.

We break down every action into three hierarchical pre-condition layers starting on top with abstract object

relations (which need to be fulﬁlled) and in three steps arriving at the movement primitives required to execute

the action. This ontology will then, in the second part of this work, be linked to actual scenes. First the

system looks at the scene and for any selected object suggests some actions. One will be chosen and, we use

now a simple geometrical reasoning scheme by which this action’s movement primitives will be ﬁlled with

the speciﬁc parameter values, which are then executed by the robot. The viability of this approach will be

demonstrated by analysing several scenes and a large number of manipulations.

1 INTRODUCTION

From every day life we know that different scenes

suggest different actions, e.g. a plate, an apple, and

a knife – as shown in Fig. 1 – suggests a “cutting the

apple” action. However, assessing whether or not a

robot could actually do this, whether it should/could

do rather something else or whether not much can be

done at all given such scenes remains a difﬁcult pro-

blem. It amounts to estimating the affordance of cer-

tain actions given the context provided by the scene.

One approach to solving this problem is to analyse

a scene and derive from it a symbolic representation,

which can then be used to ﬁnd possible actions and/or

to do planning.

To achieve this, in (Rosman and Ramamoorthy,

2011) a complex network of geometrical relations

in the spatial and temporal domains is used. Via

Support-Vector-Machines (SVMs) topological featu-

res and symbolic meanings are learned. In (Sjoo and

Jensfelt, 2011) patterns of functional relationships are

deﬁned, e.g. the object “work surface” with the action

“manipulate”. Similar, in (Liang et al., 2009) posture

templates are applied to the input data of each frame.

The resulting series of templates eventually forms a

library of actions. The authors use variable-length

Markov models for learning. In (Paul et al., 2016)

Figure 1: This scene contains a simple snack scenario. We

ask: what actions can be performed by the robot?

a common representation for abstract spatial relati-

ons and natural language is investigated. However,

(Konidaris et al., 2014) state that there cannot be one

perfect representation, but rather that “actions must

play a central role in determining the representational

requirements of an intelligent agent: a suitable sym-

bolic description of a domain depends on the actions

available to the agent.”

Staying closer to the actual motion patterns one

can also break down actions into segments, using –

for example – principal component analysis (PCA) as

in (Yamane et al., 2011). A motion sequence is here

218

Reich, S., Aein, M. and Wörgötter, F.

Context Dependent Action Affordances and their Execution using an Ontology of Actions and 3D Geometric Reasoning.

DOI: 10.5220/0006562502180229

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

218-229

ISBN: 978-989-758-290-5

projected into a state space, which is then mapped

to the ﬁrst n principal components. In that reduced

state space a threshold is applied and the action is di-

vided into two parts. The same is iteratively applied

to each subspace until some exit criteria is met. The

resulting segments could then be interpreted as mea-

ningful action parts.

There are also non-vision based methods availa-

ble, for example in (Jamali et al., 2015) and (Jamali

et al., 2014), but these methods will not be discussed

any further, as we are focusing on vision here.

All these approaches are problematic, because it

remains difﬁcult to smoothly link sensor signals (e.g.

from scene analysis) to symbolic action concepts and

then back to the signal domain for creating the trajec-

tories needed for the execution of an action by a ro-

bot. There is a danger of too strongly focusing on the

symbolic side or of remaining too close to the signal

domain.

Here we focus on manipulation actions and one

goal of the current study is to improve on this by intro-

ducing a deeper hierarchy of several layers between

signals and symbols for analysing a scene in a given

action context. We ask: What is needed to push (or

pick, or cut, etc.) a certain object? Which are the ge-

neral preconditions required for this regardless of the

actual objects in the scene? And – if those hold – are

also the speciﬁc conditions met to actually do it?

We build on the Semantic Event Chains (SECs)

framework (Aksoy et al., 2011) but we extend them

in several ways. SECs are matrices that show how

touching relations between pairs of objects change

during an action. The entries of the SEC matrix are

(“T”) for Touching, (“N”) for Not touching and (“A”)

for Absent relation. A manipulation action is segmen-

ted at keyframes which are moments that a touching

relation changes. The original SEC framework did

not much care about objects. Here, based on an ol-

der study (W

org

otter et al., 2012), we will now incor-

porate (still abstract) object roles to build an object-

action-linked ontology of manipulations, where these

object roles deﬁne the general preconditions that need

to be met to perform a certain action at all. On top of

this, we introduce a simple framework for geometric

reasoning, which allows the machine to check speciﬁc

preconditions, too, to ﬁnally execute an action.

In this study the robot selects one object in a scene

and asks – like a child during play – what could I do

with it? The framework will then analyse the situa-

tion and suggest possible manipulation actions, the-

reby addressing the problem of context dependent af-

fordances.

2 METHOD

This section divides into two parts: 1) deﬁnition of the

ontology and 2) algorithm to arrive at robotic execu-

tion of manipulation actions using the ontology given

an observed scene. We start with the ﬁrst aspect.

2.1 Ontology of Manipulation Actions

We use all manipulation actions deﬁned in (W

org

otter

et al., 2012) and create a new ontology by incorpora-

ting three layers: 1) abstract object relations (SEC),

2) object topologies and also 3) action primitives. Be-

fore doing this we need to deﬁne the roles of an object

in a more general way.

Deﬁning Object Roles: Those are determined by the

changes that occur following an action in the rela-

tion of an object to other objects. An action invol-

ves at least two objects: a hand and a main object.

Resulting object categories (hand, main, primary, se-

condary, etc.) and their abstract roles are deﬁned as

follows:

• Hand (The object that performs the action): not

touching anything at the beginning and the end of

action. It touches at least one object.

• Main (The object which is directly in contact with

the hand): not touching the hand at the beginning

and the end of action. It touches the hand at least

once.

• Primary (The object from which the main ob-

ject separates): initially touches the main object.

Changes its relation to not-touching during the

action.

• Secondary (The object to which the main object

joins): initially does not touch the main object.

Changes its relation to touching during the action.

• Load (The object which is indirectly manipu-

lated): does not touch the hand. During the

action either touches/untouches the main and un-

touches/touches container.

• Container (The object whose relation with load

changes and it is not the main object): touches or

untouches the load object.

• Main support (The object on which the main ob-

ject is located): touching the main object all the

time.

• Primary support (The object on which the pri-

mary object is located): touching the primary ob-

ject all the time.

• Secondary support (The object on which the se-

condary object is located): touching the secondary

object all the time.

Context Dependent Action Affordances and their Execution using an Ontology of Actions and 3D Geometric Reasoning

219

1 2 3 4 5

Pushing.

p.s = m.s = s.s

(a) Action 1: Pushing.

1 2 3 4 5

Pick & Place.

p.s

s.s

p.s

s.s

p.s

s.s

p.s

s.s

p.s

s.s

(b) Action 2: Pick and place.

1 2 3 4 5

Unloading.

p.s

s.s

Cont

p.s

s.s

Cont

p.s

s.s

Cont

p.s

s.s

Cont

p.s

s.s

Cont

p.s

s.s

Cont

p.s

s.s

Cont

Figure 2: Schematic of actions in the ontology are shown for the three categories. From each category only one action is

shown. The objects are marked using the following convention: h = hand, m = main m.s = main support, p = primary,

p.s = primary support, s = secondary, s.s = secondary support, L = Load, and Cont = Container.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

220

• Tool (The object which is used by the hand to en-

hance the quality of some actions): touching the

hand all the time.

Action categories are based upon the objects,

which the hand interacts with. These fall into three

categories:

1. Actions with main support: In this category the

main object is always in touch with the main sup-

port; An example is shown in Fig. 2a.

2. Actions without main support: In this category the

main object is lifted from the main support; Nn

example is shown in Fig. 2b.

3. Actions with load and container: In this category a

container with load, e.g. a glass ﬁlled with water,

is used; An example is shown in Fig. 2c.

and several actions usually exist for each group. A

more detailed list of actions is shown in Tab. 1. The

full deﬁnition of the ontology is shown elsewhere

Now we can deﬁne the layers of the ontology.

Layer 1) SEC based Object Relations at Start: The

individual graphical panels in Fig. 2 represent the co-

lumns of a Semantic Event Chain ( which reﬂect the

transition of object relations and are the necessary

conditions for successful execution). Fig. 2b shows a

pick and place action; its corresponding SEC is shown

in the upper part of Fig. 3. The ﬁrst column shows

the SEC-deﬁned pre-conditions. If and only if these

touching relations are not violated, the action could

commence. But this is not yet sufﬁcient.

Layer 2) Object Topologies: All actions are always

performed at the main object and this will only be

possible if the SEC-pre-condition hold and if the

main object appears in the scene with certain topolo-

gical connections to other objects. The middle part of

Fig. 3 shows which topologies are permitted for pick

and place.

Remarkably there are only three possible topolo-

gical relations to which all scenes that include the

main object can be reduced. To achieve this the

complete connectivity graph of who-touches-whom

will be reduced into those subgraphs that contain the

main object. Each subgraph consists of at least the

main object and the support, and, if directly touching

neighbors exist, only one directly touching neighbor

(Fig. 4). There are three cases:

1. The main object has only one touching relation.

The touched object is a support, e.g. a table (see

Fig. 4, left). A real world example is shown in

Fig. 7b; the blue plate is on top of the board and

the board becomes the support.

http://www.dpi.physik.uni-goettingen.de/cns/

index.php?page=ontology-of-manipulation-actions

2. The main object has two touching relations. One

is a support, the second one is another object,

which is also touching the support (see Fig. 4,

middle). In Fig. 7b, the apple touches its support

(green plate) and the yellow pedestal which is on

the same support.

3. The main object has two touching relations. It

touches its support and another object, which does

not touch the support (see Fig. 4, right). In Fig. 7b,

the pedestal is on top the green plate and the jar

is on top of the pedestal (but does not touch the

green plate).

These subgraphs determine the remaining precon-

ditions. For example, a tower structure as shown in

Fig. 4 (right graph) is not allowed for pick and place

and pushing actions.

Layer 3) Movement Primitives: SEC pre-conditions

and topological pre-conditions deﬁne the ﬁrst two lay-

ers of the ontology. The third and last layer is a set of

movement primitives, which are needed to execute the

action.

For the pick and place action, the primitives are

shown at the bottom of Fig. 3. The complete list of

primitives for all actions is shown on the web page.

How to ﬁll these abstract primitives with execution

relevant parameters will be described later and the

process of execution of actions is then the same as

in (Aein et al., 2013).

One primitive shall be explained in more detail:

The move(ob ject, T ) primitive sends a command to

the robot to move to a pose which is determined by

applying transform T to the pose of ob ject. The trans-

form T has two parts, a vector p which shows the

translation, and a matrix R which shows the rotation.

For example, when we want to grasp the main object,

we perform a move(main, T ) primitive to move the

robot arm end effector to a proper pose for grasping.

Since we want the end effector to reach the main ob-

ject, the vector p in this case is equal to zero. Ho-

wever, the rotation part R needs to be set such that

the robot approaches the main object from a proper

angle. This is necessary to avoid possible collisions

with other objects near the main.

2.2 Algorithm for

Execution-Preparation

Fig. 5 shows an overview of the algorithm used for

robotic execution of the above deﬁned actions. Most

components rely on existing methods and will not be

described in detail.

We start with (1) an RGB-D recorded scene which

is (2) segmented using the LCCP algorithm (Stein

Context Dependent Action Affordances and their Execution using an Ontology of Actions and 3D Geometric Reasoning

221

Table 1: Summary of ontology of actions. Actions are divided into three categories and further into sub-categories. There can

be more than one action in each sub-category.

Category Sub-Category Example Actions

Actions with main support

Actions with hand, main and main support push, punch, ﬂick

Actions with hand, main, main support and primary push apart, cut, chop

Actions with hand, main, main support and secondary push together

Actions with hand, main, main support, primary and se-

condary

push from a to b

Actions without main

support. (These action have

primary, secondary and their

supports)

primary 6= secondary and primary support 6= secondary

support

pick and place, break

off

primary 6= secondary and primary support = secondary

support

pick and place, break

off

primary 6= secondary and primary = secondary support put on top

primary 6= secondary and primary support = secondary pick apart

primary = secondary

pick and place, break

off

Actions with load

and container

The relation of load and main changes from N to T (lo-

ading)

Pipetting

The relation of load and main changes from T to N (un-

loading)

Pour, Drop

et al., 2014) into different objects from which (3) a

graph is created with edges between objects that touch

each other. (4) Then we randomly choose one ob-

ject as main. (5) The complete list of all conside-

red manipulation actions, of which there are 29 (see

Tab. 2), is derived from (W

org

otter et al., 2012) (only

3 are indicated in Fig. 5) and (6) for all of them we

use the ﬁrst layer of the ontology to check whether

the main object in this scene fulﬁlls their SEC pre-

conditions. This leads to (7) computation of all pos-

sible subgraphs for main and for those we check (8)

with the second layer of the ontology the topological

pre-conditions by which the list gets reduced. Now

we can (9) use the third layer and extract from the on-

tology the required action primitives. This concludes

the preparation stage and this information is sent to

the execution engine.

2.3 Execution-Parameterization:

Geometric Reasoning

In order to execute any of the in-principle-possible

actions we need to parameterize them. In general

we use our action library from (Aein et al., 2013)

where the required parameters are all deﬁned. They

directly map to the action primitives from stage (9)

of the above described algorithm. Thus, we need to

now consider the actual scene layout to ﬁnd possi-

ble parameter ranges for these movement primitives.

For this we employ geometric reasoning. The goal

of this is that given an action and its main object we

want to ﬁnd the directions which are free to manipu-

late this object. These directions are directly used to

deﬁne parameter ranges of the action primitives (e.g.

move(ob ject, T )) for action execution.

A step-by step explanation of the geometric rea-

soning algorithm is shown in Fig. 6. For visualization

purposes we will analyze the relative position of two

cubes to each other: one green and one blue. In a very

simple approach, one could reduce the objects to one

point in space, for example the mean or average po-

sition. This however will ignore object sizes as well

as shapes. Instead, we want a more general solution,

which does not depend on object size, shape, or dis-

tance.

First, we compute the distance from each voxel

from one cube to each voxel in the other cube and

bin the distance as shown in Fig. 6b. For two sym-

metrical objects we expect a poisson shaped distribu-

tion. We will use all voxels, which are below the ﬁrst

maximum and belong to the green cube; these points

are marked red in the histogram. The corresponding

voxels are marked in Fig. 6c in red, too. Next, we

compute the normals of these voxels. They will, as

per deﬁnition, point away from the green cube. These

normals are clusterd using a k-means clustering algo-

rithms. While undersegmentation will be harmful –

as not all directions are found – but oversegmentation

is not, a k that is greater than the expected number of

directions is used. We found k ≈ 8 leads to good re-

sults for most real-world examples. Lastly, we spawn

a half sphere around each resulting cluster (half cir-

cle in 2d as shown in the example in Fig. 6d). The

union of all spheres points to the blocked directions,

which is marked in red in the example – the direction

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

222

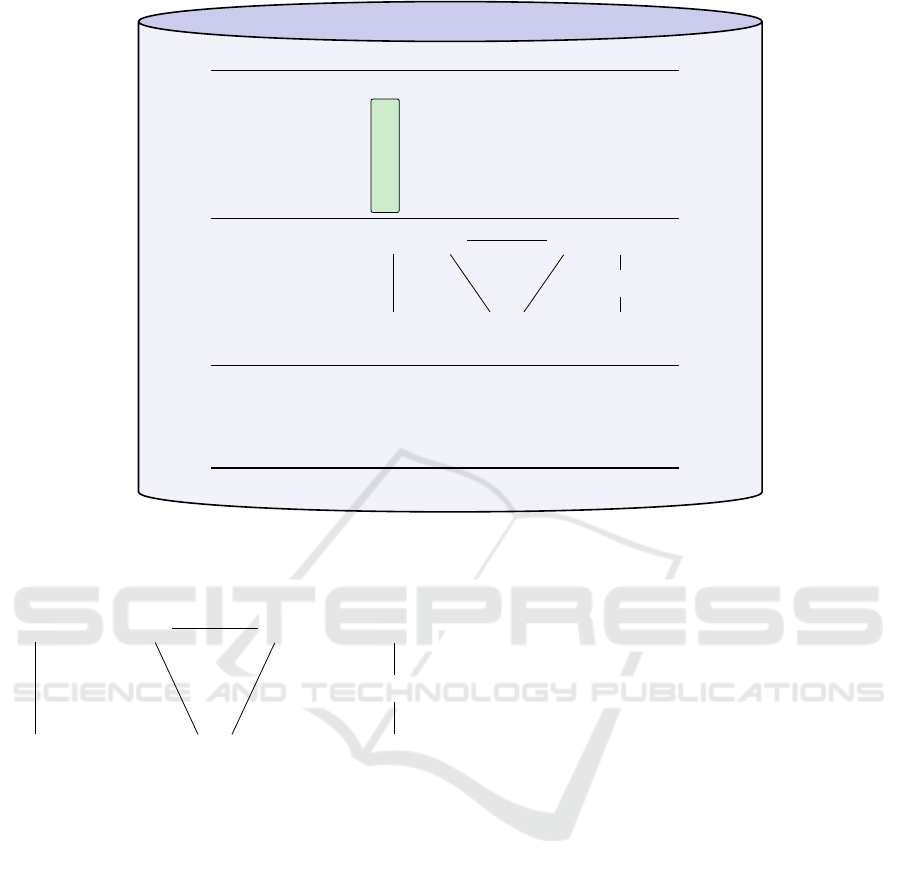
Ontology Repository

State 1 2 3 4 5

hand, main N T T T N

main, primary T T N N N

main, secondary N N N T T

main, p.s N N N N N

main, s.s N N N N N

Primitive 1

move move move

ungrasp

(main) (prim.) (sec.)

Primitive 2 grasp

move

(free)

M O

permitted permitted non-permitted

Figure 3: This ﬁgure shows one example action, pick and place, in the proposed ontology repository, which is also shown

in Fig. 2b. It consists of three parts: the SECs (top), including the SEC precondition (top with green bar), topological

preconditions (middle), and primitives (bottom). “M” is the main object; “O” depicts other objects in the scene, and “S”

stands for support.

M O

Figure 4: All complex graph structures can be reduced to

one of these three graphs. “M” is the main object; “O” de-

picts other objects in the scene on which there are no further

information. The support is “S”.

where the blue cube is located at. This computation

is performed for each object, which is in a certain ra-

dius around the main object. The radius is hardware

dependent and deﬁned by how much space the robot

hand needs to safely grasp or push an object.

The results of this type of reasoning on real scenes

will be shown in Section 3.

3 EXPERIMENTS

3.1 Setup and Experiments

We tested the algorithm in a ROS based system. A

Microsoft Kinect collects image and depth informa-

tion, in addition a high resolution Nikon DSLR ca-

mera is used for image reﬁnement. We use (Schoeler

et al., 2014) for object recognition and pose estima-

tion. For model tracking (Papon et al., 2013) is used.

Our robot is a Kuka LWR arm which executes actions

as described in (Aein et al., 2013). Fig. 7 shows three

scenes that are used for testing:

1. A cup is next to a box and an apple is on top of a

pedestal.

2. The scene that we used in previous sections: a

plate on top of a cutting board, and an apple on a

plate. Touching the apple there is a pedestal with

a jar on top

3. A cluttered kitchen scene with many objects.

3.2 Results

Using these scenes, we analyse ﬁrst the effect of the

top two layers of the ontology asking: Given a main

object, which actions are in principle permitted. Next,

we will consider the third ontology layer and perform

geometric reasoning on some examples to show how

actual action parameterization can be performed and

ﬁnally we will perform some actions with the robot.

Context Dependent Action Affordances and their Execution using an Ontology of Actions and 3D Geometric Reasoning

223

Scene

Segmentation Graph computation

Select main object, e.g. Apple

List of all candidate

actions from ontology

Check SEC preconditions

for all candidate actions

Create subgraph for main obj.

Check topological preconditions

for all candidate actions

Select one allowed action

Table

Green plate

Pedestal

Apple

Jar

Board

Blue plate

Table

Green plate

PedestalMain

Jar

Board

Blue plate

pick&

place

apple

green

plate

blue

plate

cut apple

pick&

place

apple jar

green

plate

. . . . . . . . . . . .

pick&place X

cut X

pick&place X

main must

touch

primary

. . . . . .

Support

Primary

Main

pick&place X

cut X

main must

not touch

any objects

pick&place X

. . . . . .

Combine primiti-

ves and geometrical

reasoning, execute

selected action on robot.

1 2

5 6

Figure 5: The steps of our proposed framework for scene affordances and execution are summarized here. Starting with a

real world scene (1), we perform object segmentation (2), object recognition, and graph calculation (3). The user selects a

main object, for example the apple (4). Afterwards, a list of candidate actions based on the ontology is produced (5). The

possibility of performing these actions is investigated in two steps by using the preconditions inside the ontology. First,

we check preconditions based on the SEC domain; in the example “pick&place the apple from green plate to blue plate is

allowed”, also cutting. However, “pick&place the apple from the jar to the green plate” is not, since the apple does not touch

the jar (6). We create the subgraphs around the main object, as shown in Fig. 4 (7). Afterwards, we check for topological

restrictions (8). Here, the action “cut the apple” fails, as the main object must not touch any other objects. This results in a

list of allowed actions. One action is selected (either by algorithm, or human), the primitives are read from the ontology and

sent to the execution engine. In case of move(ob ject) primitives, we perform the proposed geometric reasoning to get the

parameters.

3.2.1 Action Affordances

The results of action affordances for the three scenes

are calculated by using the preconditions of the onto-

logy and analysis of subgraph structures. The results

are summarized in Tab. 2. Each column shows the

possibility of performing different actions in the on-

tology for a speciﬁc selection of main, primary and

secondary objects.

Here, we can see some limitations of the SEC

domain. Some actions require additional high level

object knowledge (e.g. stirring or levering) and are

marked with “n”; for example stirring is always de-

nied as it requires a liquid and a container shaped ob-

ject (non-permanent objects pose a big problem for

SECs or planning in general). These properties can-

not be measured in the SECs domain. One could ar-

gue that also cutting, kneading, or scooping needs ad-

ditional high level object knowledge, but on the tou-

ching relations level these preconditions can be ensu-

red.

3.2.2 3D Geometrical Reasoning

Qualitative results of geometric reasoning are shown

in Fig. 8, Fig. 9, and Fig. 10. These results show

that by processing the low level point clouds one can

detect the blocked and free directions of a given ob-

ject. Some limitations can be found in Fig. 9a, which

shows the spatial relation between an apple and a

green plate. We expect that we can compute the nor-

mals of the point cloud, but at corners, e.g. at the

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

224

(a) Two blocks serve as an example for geome-

tric reasoning. The possible movement direction

of the green cube without touching the blue one is

of interest.

5 10 15

Count

Binned distance

(b) The distances from all voxels of the green block to all voxels from

the blue block are binned. In the next step all voxels of the green

block, which are below the maximum, are used. They are marked in

red in the above histogram.

marked in red. The normals of these voxels are

computed and clustered using k-means..

(d) A half sphere around each of the k resulting vectors is spawned

(here: half circle for visualization) and the union of all spheres com-

puted. The union, above marked in red, marks the “forbidden” di-

rections.

Figure 6: Step-by-step explanation of the geometric reasoning algorithm.

(a) Scene 1. (b) Scene 2.

Figure 7: These three scenes are used to test the algorithms.

Figure 8: Qualitative results for the geometrical reasoning

method. The algorithm is applied to the object pair apple

and red pedestal. For graphical purposes only the largest

cluster is shown with a red arrow. The computational steps

for the arrow are detailed in Fig. 6d. Here, the arrow points

from the apple downwards to the pedestal, which is the “for-

bidden” direction.

border of object point clouds, this assumption is not

always met and the resulting access angles are off. In

Fig. 9a, the apple is captured with only few points into

the direction downwards to the green plates and the

resulting vector goes off to the side and barely through

the plate.

Another problem can be seen in scene 3. In

Fig. 10c, the relations between the orange spoon and

the black spoon in the spoon holder (black spoon

and spoon holder are recognized as one object) form

one unexpected cluster downwards, all others point

towards the spoon. Careful examinations show that

there actually are some points belonging to the spoon

base below the orange spoon and that the arrow down-

ward is justiﬁed. However, the resulting access angle

is very small.

3.2.3 Action Execution

The results of action execution are presented in the

video attachment of the paper (please see aforemen-

tioned web page). The execution of three different

Context Dependent Action Affordances and their Execution using an Ontology of Actions and 3D Geometric Reasoning

225

(a) Scene 2: Apple and green plate. (b) Scene 2: Apple and jar. (c) Scene 2: Apple and pedestal.

Figure 9: Qualitative results for the geometrical reasoning method. For graphical purposes only the largest cluster is shown

with a red arrow.

(a) Scene 3: Blue cup and apple. (b) Scene 3: Orange and board. (c) Scene 3: Orange and black spoon.

Figure 10: Qualitative results for the geometrical reasoning method for a cluttered scene. For graphical purposes only the

largest cluster is shown with a red arrow. In (c) the two largest clusters are depicted using red arrows.

actions is shown: “pushing”, “pick and place”, and

“put on top”. Selected frames of these experiments

are shown in Fig. 11. Shown are the actions “pus-

hing” (left), “pick and place” (middle), and “put on

top” (right).

4 CONCLUSION

The goal of this study was to address the problem of

affordances given the scene context. We speciﬁcally

wanted to create a system that can look at objects

in a scene and suggest actions which are very likely

possible. For this we ﬁrst deﬁned a novel and hope-

fully quite complete ontology of manipulation actions

which considers objects, too, but still from a rather

abstract viewpoint. The main point here is that this

allows generalizing the same action across quite dif-

ferent scenes. Combined with geometrical reasoning

this system can analyse scenes and suggest and per-

form many actions.

Thus, essentially the proposed system acts like a

multi-layered planner with several levels of pre- and

post-conditions. This may indeed ease robotic plan-

ning problems by allowing the system to check all

conditions in a hierarchy and to ﬁnally proﬁt from the

geometrical link to the actual scene layout.

Of course, situations may exist that cannot be cor-

rectly disentangled this way. The resulting permit-

ted movement directions are always based on parts of

the 3D space that had been derived from straight di-

rection vectors. Hence if there is a complex shaped

object that hooks-around some other object this type

of geometric reasoning will fail. Also, if objects are

topologically linked (physically connected) in com-

plex ways to other objects the approach will fail. Our

system does not attempt to solve all these problems.

Rather, like a child after some experience, here we

have arrived at a system that produces very reasona-

ble suggestions about how to modify its world using

different manipulations. This is the main strength of

this approach. We have here a quite powerful bottom-

up decision framework, which does not rely on high-

level knowledge but could be extended by this (for

example using learned models of some aspects of the

world) without problems.

ACKNOWLEDGEMENTS

The research leading to these results has received

funding from the European Communitys H2020 Pro-

gramme under grant agreement no. 680431, Recon-

Cell.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

226

Figure 11: Execution results of three different scenarios: “pushing” (left), “pick and place” (middle), and “put on top” (right).

The top row shows the results of the geometrical reasoning. The allowed direction is marked with a green arrow, the forbidden

one with a red arrow. The full scene is also shown in the video attachment of the paper.

Context Dependent Action Affordances and their Execution using an Ontology of Actions and 3D Geometric Reasoning

227

Table 2: Results of the action affordances for different scenes and objects. The different scenes are also depicted in Fig. 7.

Objects corresponding to the computed affordances are listed below the table heading. Please note that we cannot check the

preconditions for some actions, e.g. stirring, knead which are related to the material of objects. These actions are denoted

with “n”; they require high level object knowledge. For example you need a liquid and a container object for stirring. This

knowledge is not provided in the SEC domain. A “X” denotes the successful execution of the action; the actions “-” were

correctly computed as not possible to execute.

Scene 1 Scene 2 Scene 2 Scene 3 Scene 3

Main Object cup apple yellow pedestal orange apple

Primary Object box yellow pedestal green plate board cup

Secondary Object red pedestal blue plate blue plate cup board

1 punch X X X X X

2 ﬂick X X X X X

3 poke X X X X X

4 chop - - - X -

5 bore X X X X X

6 cut - - - X -

7 scratch X X X X X

8 scissor-cut - - - X -

9 squash X X - X X

10 draw X X X X X

11 push X X - X X

12 stir n n n n n

13 knead X X - X X

14 rub X X X X X

15 lever n n n n n

16 scoop X X - X X

17 take down - - - X -

18 push down - - - X -

19 rip off - - - X -

20 break off n n n n n

uncover by

n n n n n

pick&place

uncover by

n n n n n

pushing

23 put on top - X - X -

24 push on top - - - - -

25 put over n n n n n

26 push over n n n n n

27 grasp X X - X X

28 push apart X X - - X

29 push together - - - - -

REFERENCES

Aein, M. J., Aksoy, E. E., Tamosiunaite, M., Papon, J., Ude,

A., and W

org

otter, F. (2013). Toward a library of ma-

nipulation actions based on semantic object-action re-

lations. In IEEE/RSJ International Conference on In-

telligent Robots and Systemsn.

Aksoy, E. E., Abramov, A., D

orr, J., Kejun, N., Dellen, B.,

and W

org

otter, F. (2011). Learning the semantics of

object-action relations by observation. The Internati-

onal Journal of Robotics Research, 30:1229–1249.

Jamali, N., Kormushev, P., and Caldwell, D. G. (2014).

Robot-object contact perception using symbolic tem-

poral pattern learning. In IEEE International Con-

ference on Robotics and Automation (ICRA), pages

6542–6548.

Jamali, N., Kormushev, P., Vias, A. C., Carreras, M.,

and Caldwell, D. G. (2015). Underwater robot-

object contact perception using machine learning on

force/torque sensor feedback. In IEEE International

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

228

Conference on Robotics and Automation (ICRA), pa-

ges 3915–3920.

Konidaris, G., Kaelbling, L. P., and Lozano-Perez, T.

(2014). Constructing symbolic representations for

high-level planning. In AAAI, pages 1932–1938.

Liang, Y.-M., Shih, S.-W., Shih, S.-W., Liao, H.-Y., and Lin,

C.-C. (2009). Learning atomic human actions using

variable-length markov models. IEEE Transactions

on Systems, Man, and Cybernetics, Part B: Cyberne-

tics, 39(1):268–280.

Papon, J., Kulvicius, T., Aksoy, E. E., and W

org

otter, F.

(2013). Point cloud video object segmentation using

a persistent supervoxel world-model. In IEEE/RSJ In-

ternational Conference on Intelligent Robots and Sys-

tems (IROS), pages 3712–3718.

Paul, R., Arkin, J., Roy, N., and Howard, T. M. (2016). Efﬁ-

cient grounding of abstract spatial concepts for natural

language interaction with robot manipulators. In Ro-

botics: Science and Systems.

Rosman, B. and Ramamoorthy, S. (2011). Learning spa-

tial relationships between objects. The International

Journal of Robotics Research, 30(11):1328–1342.

Schoeler, M., Stein, S., Papon, J., Abramov, A., and

org

otter, F. (2014). Fast self-supervised on-line trai-

ning for object recognition speciﬁcally for robotic ap-

plications. In International Conference on Computer

Vision Theory and Applications (VISAPP).

Sjoo, K. and Jensfelt, P. (2011). Learning spatial relati-

ons from functional simulation. In IEEE/RSJ Interna-

tional Conference on Intelligent Robots and Systems

(IROS), pages 1513–1519.

Stein, S. C., Schoeler, M., Papon, J., and Worgotter, F.

(2014). Object partitioning using local convexity. In

IEEE Conference on Computer Vision and Pattern Re-

cognition (CVPR), pages 304–311.

org

otter, F., Aksoy, E. E., Kr

uger, N., Piater, J., Ude, A.,

and Tamosiunaite, M. (2012). A simple ontology of

manipulation actions based on hand-object relations.

IEEE Transactions on Autonomous Mental Develop-

ment.

Yamane, K., Yamaguchi, Y., and Nakamura, Y. (2011). Hu-

man motion database with a binary tree and node tran-

sition graphs. Autonomous Robots, 30(1):87–98.

Context Dependent Action Affordances and their Execution using an Ontology of Actions and 3D Geometric Reasoning

229