AngioUnet

A Convolutional Neural Network for Vessel Segmentation in Cerebral DSA Series

Christian Neumann

, Klaus-Dietz T

onnies

and Regina Pohle-Fr

ohlich

Institute for Pattern Recognition, Hochschule Niederrhein University of Applied Sciences, Krefeld, Germany

Department of Simulation and Graphics, Otto-von-Guericke University of Magdeburg, Germany

Keywords:

CNN, Cerebral, DSA Series, Vessel Segmentation.

Abstract:

The U-net is a promising architecture for medical segmentation problems. In this paper, we show how this

architecture can be effectively applied to cerebral DSA series. The usage of multiple images as input allows

for better distinguishing between vessel and background. Furthermore, the U-net can be trained with a small

corpus when combined with useful data augmentations like mirroring, rotation, and additionally biasing. Our

variant of the network achieves a DSC of 87.98% on the segmentation task. We compare this to different

conﬁgurations and discuss the effect on various artifacts like bones, glue, and screws.

1 INTRODUCTION

In the past, segmentation tasks have been solved with

a wide variety of methods and combinations of those.

In the medical image processing context, one speciﬁc

task is the segmentation of single organs, homogene-

ous structures like bones or – in our case – vessels.

The difﬁculty of medical applications lies in the usage

of a lot of modalities. Between a pair of modalities,

the gray values rarely show any correspondence. This

means that we still have to build or adapt methods to

every single new modality in order to solve the given

task successfully.

In the context of vessel segmentation, the gene-

rally used scheme consists of preprocessing, enhance-

ment, thresholding, and possibly postprocessing. The

preprocessing commonly is needed to reduce noise

and transform the data globally e.g. normalization.

The threshold can be for example a single value or

adaptive to a small region. In summary, the segmen-

tation task consists of three major parts. These are

edge detection, noise suppression, and non linear con-

trast enhancement. All these tasks would have multi-

ple parameters, if solved with conventional methods.

By using deep learning, we can train a neural network

that is optimal for a given dataset.

The segmentation is part of the preprocessing in a

medical 2D/3D-registration project. For the treatment

of arteriovenous malformations (AVM) using radio-

surgical devices careful planning of the radiation cen-

troids is necessary in order to protect healthy tissue

and successfully embolize the nidus. In our project,

the available modalities are a digitally subtraction an-

giography (DSA) and a partial MRI of the head. The

DSA series will be some days old and may have diffe-

rent absolute gray values due to different imaging de-

vices and settings. The MRI on the other hand is made

on the same day as the treatment, in fact the gamma

knife treatment can start less than an hour later, while

the planning is done manually. For the registration

task, it is important to segment the vessels that are

visible in both modalities and to keep the spatial reso-

lution of the result as high as possible. In this paper,

we will look at the detection of vessels in the DSA

series. Besides, we plan to adapt the same network

to the MRI images as well i.e. train the same network

end-to-end on two different modalities by using a dif-

ferent dataset and possibly tuning of hyperparameters,

only.

Here we apply the U-net (Ronneberger et al.,

2015) architecture to our segmentation task. We dis-

tinguish two classes – vessels and background. Addi-

tionally, we are mostly interested in the arteries, be-

cause most veins will not be visible in a correspon-

ding MRI. Therefore vein suppression is important,

too. The given modality generally gives a good con-

trast between vessels and the background. The pro-

blem of separating the vessels (dark) from the back-

ground (bright) seems to be easy at ﬁrst. But the clas-

ses are not separable by a single threshold. The back-

ground is noisy and there is a slight shadow of bones

and more left. In order to classify images from this

Neumann, C., Tönnies, K-D. and Pohle-Fröhlich, R.

AngioUnet - A Convolutional Neural Network for Vessel Segmentation in Cerebral DSA Series.

DOI: 10.5220/0006570603310338

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages

331-338

ISBN: 978-989-758-290-5

331

modality, some kind of adaptive thresholding is nee-

ded. Especially in regions with ﬁne vessels, the con-

trast is very low. The U-Net provides us a high degree

of non-linearity to solve this problem as well as some

other advantages.

In the following sections, we will demonstrate

how the time aspect of the DSA can be exploited.

Then we discuss the changes we made to the network

architecture and which data augmentations are useful.

Finally we present the quantitative evaluation on our

dataset followed by an analysis of the effects on dif-

ferent artifacts present in the image sets.

1.1 Related Work

(Ronneberger et al., 2015) presented a convolutio-

nal neural network (CNN) architecture that provi-

des a pixelwise segmentation of neuronal structures

in electromagnetic microscopic recordings. The net-

work consists of a contracting path and an expanding

path. While the former decreases the spatial resolu-

tions with max-pooling and increases the number of

feature channels each time, the latter aims to do the

opposite by upsampling the images. Additionally out-

puts from the ﬁrst half are concatenated to the out-

puts of corresponding size in the second half. They

showed that a network like this can be trained with a

small data set by extensive usage of data augmentati-

ons. Besides shift and rotation invariance, they found

elastic deformations to be essential for microscopy

images. The U-net classiﬁes a complete tile in one

inference. This reduces the number of redundant cal-

culations compared to previous works that used a sli-

ding window patch based pipeline.

The U-net and similar encoder-decoder architec-

tures have been used to great success on classiﬁca-

tion tasks. The networks differ in the speciﬁc im-

plementation of the skip connections and the “up”-

operation. One example is the SegNet (Badrinaray-

anan et al., 2015), a fully convolutional network for

semantic pixel-wise segmentation. The encoder is a

pretrained VGG-16 network, while the work focuses

on the decoder part. The network propagates the pool-

ing indices instead of the complete output through the

skip connections. Another network similar to the U-

net is described in (Brosch et al., 2016). In this case,

multiple sclerosis lesion is segmented in magnetic re-

sonance images. They use transposed convolutions

instead of upsampling and again, the pooling indices

for unpooling.

2 DATA

The dataset consists of multiple cerebral DSA series.

Each series contains around ten DSA images, sho-

wing the dispersion of a marker ﬂuid. A single DSA

image is calculated by subtracting two consecutive x-

ray images. This allows the bones to be nearly com-

pletely invisible, while the marker ﬂuid gives a strong

contrast of the vessels. It has to be noted that the re-

ference image is only partially subtracted. This is ne-

cessary as in our case the patients have a stereotactic

frame mounted and the nine markers needed to be vi-

sible for the original purpose of an extrinsic registra-

tion. This results in multiple irrelevant things being

visible. These are bones like the top of the skull and

the eye sockets (see Figure 1), the screws that hold

the stereotactic frame (see Figure 2) and the markers

on the box (see Figure 3), and possibly glue from a

previous embolization (see Figure 4). We can ignore

all effects related to the stereotactic frame but we aim

at suppressing the remaining things. Another effect

is the appearance of white borders along edges with

a strong contrast (see Figure 5). This is visible al-

ong all larger arteries. As it overlays the vessels, it

makes some vessels look disconnected. Lastly, Fi-

gure 6 shows the same artery ﬁlled with the marker

and with it ﬂowing off a short time later. In the left

image we can discover lighter regions from inhomo-

geneous occlusion and from the second image we see

how the marker ﬂuid mixed with the blood and the

ﬂow creates fadings along the vessel boundaries.

The perspective as well as the patient’s position

are constant during a series. A single image has a re-

solution of 1024× 1024 with 10 bit of dynamic range.

Figure 1: Example for the skull and a eye socket remaining

visible in the DSA.

Figure 2: Examples for screws that hold the stereotactic

frame.

2.1 Time Context

For our dataset, we selected four images per DSA se-

ries, showing the same dispersion state. The images

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

332

Figure 3: Examples for the markers on the box mounted to

the stereotactic frame.

Figure 4: Examples for previous glue embolizations.

Figure 5: Example for white borders along contrast rich ed-

ges.

Figure 6: Example for inhomogeneous occlusion due to the

marker ﬂowing off from one image to the next.

are selected based on the following state descriptions:

1. the large arteries are visible

2. the complete artery tree is visible

3. the marker has ﬂown off the largest arteries

4. no arteries, but mainly veins are visible

Arteries and veins are not connected directly in a

healthy person’s head. The transition is done via ca-

pillaries which are not visible through an x-ray. Provi-

ded the images are taken at the right moment, we have

an image right before the capillaries are active and im-

mediately afterwards. So, the usage of multiple time

points is key to distinguishing arteries and veins. Also

the separation of vessels and background is greatly

improved (see Table 2). Using multiple time points

can be described as giving the network a time context

Table 1: Probability for the occurrence of an instance of a

given class.

No. Arteries Fine

Arteries

Veins Other

1 high low very low medium

2 high high very low medium

3 low high medium medium

4 very low low high medium

to work with but we can describe the data more preci-

sely. For this, we further split the classes into arteries,

ﬁne arteries, veins, and others. Now we can see that

we are providing multiple images with different a pri-

ori known (fuzzy) probabilities for the classes. The

mapping to the images is shown in Table 1. By choo-

sing the images based on these criteria, we enable the

network to learn to discriminate arteries better, and

effectively include a vein suppression capability.

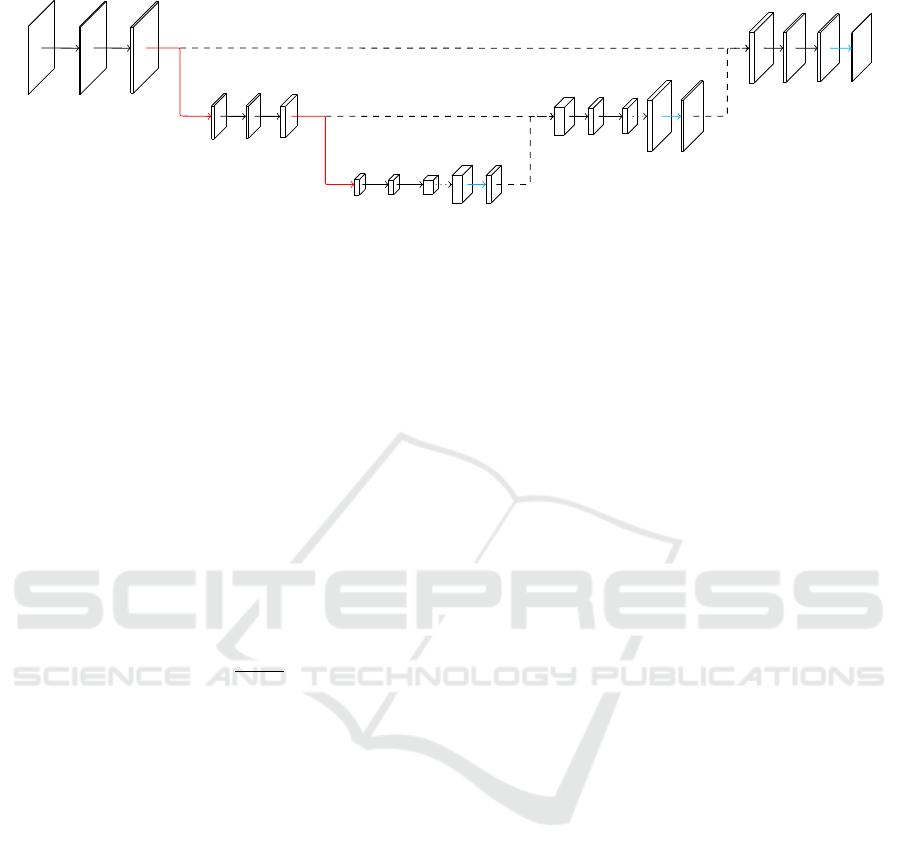
3 NETWORK ARCHITECTURE

Our network is build based on the U-net architecture.

Now we will describe the architecture that we chose

and all changes we made to it. The complete architec-

ture is depicted in Figure 8.

3.1 Building Block

The basic building block of the network consists of

two convolutional layers followed by a pooling or an

unpooling layer, respectively. The convolutions are

all non-padded in order to prevent artifacts along the

borders due to missing input values and use 3 × 3

kernels. Thus the image size decreases by two with

every convolutional layer. Every convolution is acti-

vated with a ReLU layer. The pooling layers use max-

pooling over an 2× 2 area, effectively halving the spa-

tial dimensions. In the original U-net the number of

channels is doubled with the following convolutions,

while we are doubling the number of channels before

the max-pooling layer. This is done to respect the ge-

neral rule that bottlenecks should be prevented in the

early layers of a convolutional neural network, as sug-

gested by (C¸ ic¸ek et al., 2016; Szegedy et al., 2016).

The unpooling unit consists of multiple layers. First

the image is upsampled by the factor two, then Ronne-

berger et al., analogues to the max-pooling layer, ap-

ply a 2 × 2 convolution. The convolution also halves

the number of channels. This is followed by an acti-

vation layer. Additionally, the non-pooled output of

the layer of corresponding size from the contracting

path is now cropped to the current image size and

AngioUnet - A Convolutional Neural Network for Vessel Segmentation in Cerebral DSA Series

333

Figure 7: Example for a selection of four input images.

concatenated to the channels. This provides the ne-

cessary spatial information that was lost through the

max-pooling layers. In our network we use a 1 × 1

convolution. By visual inspection, we found that this

change results in less direction dependence of the seg-

mentation.

3.2 Tile Size

These two aforementioned variants of the building

blocks are repeated multiple times and in equal num-

ber. The U-net used four max-pooling layers, which

encoded an 572 × 572 image into 1024 channels of

the size 32 × 32. The decoded output had a size of

388 × 388. For our AngioUnet, we reduced the num-

ber of max-pooling layers to two. This decision is ba-

sed on the consideration of the receptive ﬁeld as well

as the number of redundant calculations done while

training. We calculated the receptive ﬁeld of the full

net to be 40 × 40. Manual evaluation of the dataset

showed that the largest vessels are usually less than 40

pixels wide. Consequently, every neuron should see

data based on both classes – vessel, and background.

While this network allows the segmentation of one

complete tile at once, there is a trade-off between re-

dundancy and peak memory load. Ronneberger et al.

also described the “overlap-tile strategy for seamless

segmentation of arbitrary large images”. This strategy

states that in order to segment an image larger than the

tile size, we extract tiles that overlap by half the num-

ber of pixels that are lost along a given dimension.

For the AngioUnet, we use 144 × 144 tiles, which are

rather small but due to the shallower architecture, the

ratio of the output size to the input size is even bet-

ter. The resulting output size is 104 × 104, thus we

extract one 144 × 144 tile every 104 pixels in every

dimension and we can use 72.2% of every tile. The

small tile size is necessary, because of text annotati-

ons in the DSA images that we excluded for training.

This way, we have to leave less tiles out that include a

part of the masked areas. It would also be possible to

change the loss function to ignore all masked pixels

but we think that this is not worth the effort, since ti-

ling and batching should not hinder the segmentation

performance.

3.3 Training

The network is trained using gradient descent. The

loss function is the cross entropy of the softmax acti-

vation of the last layer. Every epoch the learning rate

is reduced by a constant factor. The momentum is

chosen so that the initial and ﬁnal learning rates α

and α

are respected:

m =





E−1

(1)

4 DATA AUGMENTATIONS

(Ronneberger et al., 2015) reported that data augmen-

tations were crucial for successful training of the U-

net. In our case, we use ﬁve different augmentati-

ons giving 2

· 3 = 24 variations of every tile. The

augmentations are mirroring along the x-axis, mirro-

ring along the y-axis, transposition, and addition and

subtraction of a bias. The ﬁrst three operations pro-

vide rotation invariance by 90

◦

. One might argue that

the angiographies should be mirrored along the x-axis

only, because the images always show the vessel tree

upwards. But, we think that mirroring along the y-

axis is reasonable too, because the receptive ﬁeld is

small enough and no positional information is given,

so that the network can not learn location-dependent

features but it learns to better segment thin vessels

near the bottom, which indeed run downwards.

4.1 Bias

The addition and subtraction of a bias is useful for the

given modality. A DSA image is calculated by sub-

tracting two consecutive x-ray images. This means

the gray value in the image depends on the amount

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

334

144×144

70×70

33×33

128

58×58

108×108

32 2

104×104

Figure 8: AngioUnet Architecture with four input images and 16 feature channels in the ﬁrst convolution layer (red: max-

pooling, dotted: upsampling, cyan: 1x1 convolution, dashed: crop and concat).

of change in marker density, which itself depends on

many factors e.g. the blood ﬂow and the quality of the

marker ﬂuid. Introducing a constant bias is an attempt

to reduce the impact of such effects. Given an input

image I, we can describe this augmentation for every

pixel I(x, y) as follows. The simplest way is to use a

ﬁxed bias b set to 5% of the dynamic range

b =



0.05 · 2



= 51 (2)

that we apply to all pixels in the inputs by addition

and clipping

(x, y) = min



max(0, I(x, y) ± b), 2

− b − 1



(3)

Another option is to apply a gamma correction with

γ = 0.2

(x, y) = 2



I(x, y)



1+γ

(4)

which requires no clipping and puts emphasis on the

mid range of the gray values.

4.2 Rotation Invariance

While inspecting classiﬁed images, we noticed that

the sensibility of the detection depends on the di-

rection of vessels. This is especially noticeable in

areas with synthetic shapes, e.g. text. It should be no-

ted that the effect is not symmetric along the x- or

y-axis, despite the fact that we used mirroring and ro-

tation as data augmentations. Instead, some speciﬁc

directions show a different segmentation result. Gi-

ven the small corpus for training, we think that the

segmentation should not depend on the direction, as

the network would be too speciﬁc to the dataset. We

did an experiment to make all kernels rotation sym-

metric. This can be achieved by constructing every

3 × 3 kernel from only 3 weights i.e. center w

, edge

and corner w









(5)

The idea behind this is that the network can not learn

to differentiate directions as a whole when every sin-

gle convolution is rotation invariant. Our tests showed

that the output is indeed independent of any direction

but at the same time the segmentation performance

is severely limited. Also this network was harder to

train i.e. it did not converge with the default learning

rate. Looking further by picking a single trained ker-

nel from the normal network, we found a ﬁlter mask

that was, in a simpliﬁed view, of the form





0 1 α

1 0 −1

0 −1 0





(6)

with α ≈ 1. This mask alone is very effective in sepa-

rating fore- and background visually. It can be noticed

that this mask is basically calculating the gradient in

a 135

◦

direction. Throughout the whole network, the

kernels are asymmetric. This suggests that the net-

work learns to encode different directions and their

combinations within the channels. Therefore, choo-

sing a smaller number of channels should lead to less

directivity. Naturally, further reduction of the number

of channels decreases performance, too.

5 EVALUATION

We evaluate all network conﬁgurations with our da-

taset. It consists of four DSA series each with four

1024 × 1024 images and a corresponding binary seg-

mentation map. The segmentation maps are hand-

labeled images. From these images, we cut 144× 144

tiles and apply all data augmentations. As described

in Section 4, the ﬁrst augmentation is the addition and

subtraction of a ﬁxed bias of 5%. Then all images are

successively transposed, mirrored along the x-axis,

and ﬁnally mirrored along the y-axis. This gives us

a total amount of 3576 tiles with four channels and a

label each. We use 80% of the tiles for training, 10%

AngioUnet - A Convolutional Neural Network for Vessel Segmentation in Cerebral DSA Series

335

for validation and 10% for testing. Additionally, we

classiﬁed an “unknown” series to conﬁrm the genera-

lization. The training was done on a NVIDIA Quadro

K2200 within four hours.

In Table 2, the statistics for multiple conﬁgurati-

ons are presented. The standard conﬁguration is a

network with 16 channels and a learning rate from

1· 10

−2

to 1 · 10

−6

falling exponentially over 128 epo-

chs. Conﬁgurations marked with a star needed a lo-

wer learning rate that was held constant over training

in order to be successfully trained. We gather accu-

racy, precision, and recall, and also calculate the Dice

similarity coefﬁcient (DSC) (Dice, 1945). The DSC

is the harmonic mean of the precision and the recall:

DSC = 2 ·

precision · recall

precision + recall

(7)

As an overlap metric, it describes the total segmenta-

tion performance well, by incorporating the true posi-

tives as well as the false positives and false negatives.

It is our primary measurement when comparing dif-

ferent network conﬁgurations. The value of the cross

entry loss function is also useful to predict the achie-

vable performance earlier during training. In Figure 9

the typical convergence characteristic is shown. Ge-

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 1000 2000 3000 4000 5000

accuracy

precision

DSC

recall

cross entropy

Figure 9: Statistics of the standard conﬁguration during the

ﬁrst 5000 training steps (≈ 29 epochs). These values are

reported on the validation set.

nerally the precision starts high while the recall stays

lower. With increasing number of epochs, the re-

call improves by some percent and the precision only

decreases slightly, thus increasing the DSC slowly.

Every conﬁguration was retrained ﬁve times. The re-

sults were averaged and the empiric standard devia-

tion was calculated. This way we can better compare

the conﬁgurations and decide if a variation is an im-

provement or due to a good random initialization.

5.1 Quantitative Evaluation

First, we will look at the different inputs. Table 2

shows the results for a network trained with the image

for state two only versus a network trained with all

four images. It is clear that the network with four

images has more information to base its decision on

and thus outperforms the single image network by

16.97%.

The next step is to compare the different vari-

ants of incorporating a bias as a data augmentation.

From Table 3 we can see that the network trained wit-

hout augmentation of the gray values performs signi-

ﬁcantly worse. The ﬁxed bias variant and the gamma

variant result in similar DSC values with a slight ad-

vantage for the ﬁxed bias. It can be noted that the sta-

tistics of the network trained with a gamma correction

spread substantially more.

Finally, we tested some variations and impro-

vements proposed for different deep learning tasks:

1. Our architecture uses a 1 × 1 convolution in the

upconv operation. As described earlier, we aim at

decreasing the inﬂuence of the direction in which

a vessel is captured. When we compare the re-

sults, we can see a slight improvement in all me-

trics. This suggests that for a given number of

channels the 1 × 1 convolution is less speciﬁc

i.e. more abstract.

2. Building symmetric kernels from three weights,

as shown in Section 4.2, makes the segmentation

decision mostly invariant to the vessel direction

and reduces the number of trained parameters but

it also decreases the total performance by more

than a percent. This conﬁguration needed a lear-

ning rate as low as 5 · 10

−4

to converge, still two

out of the ﬁve runs did not produce any positives

and thus are excluded from the statistics.

3. The number of channels in the network deﬁnes

the amount of generalization the network has to

learn by restricting the number of different featu-

res available at any given stage. Here k denotes

the number of channels after the ﬁrst convolution.

In the following layers the number of channels al-

ways is a multiple of k using the scheme shown

in Figure 8. The standard conﬁguration uses 16

channels. Halving it to eight increases the pre-

cision minimally but in total the performance is

slightly lower. Increasing k to 32 required redu-

cing the learning rate to 1 · 10

−3

and results in a

network with a DSC that is marginally lower.

5.2 Qualitative Evaluation

We can further evaluate the performance by looking

at the classiﬁcation of images that are unknown to the

network. One example is given in Figure 10.

All large vessels are segmented and many ﬁner

vessels are visible, too. One visible problem are lo-

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

336

Table 2: Statistics of different conﬁgurations reported on the test set after training. All values are given in percent.

conﬁguration accuracy precision recall DSC

standard 94.77 ± 0.08 89.41 ± 0.47 86.59 ± 0.45 87.98 ± 0.18

one image 89.13 ± 0.07 86.52 ± 0.59 60.22 ± 0.58 71.01 ± 0.27

2 × 2 upconv 94.72 ± 0.13 89.18 ± 0.98 85.96 ± 0.94 87.53 ± 0.28

k = 8 94.54 ± 0.19 89.90 ± 0.52 84.10 ± 1.56 86.90 ± 0.59

symmetric kernels* 93.99 ± 0.16 88.47 ± 3.23 83.96 ± 4.11 86.05 ± 0.67

k = 32* 94.65 ± 0.07 89.59 ± 0.64 85.76 ± 0.58 87.63 ± 0.12

Table 3: Statistics of the standard network trained with different biasing data augmentations. All values are given in percent.

conﬁguration accuracy precision recall DSC

no bias 93.22 ± 0.20 87.23 ± 1.61 80.89 ± 1.60 83.92 ± 0.44

ﬁxed bias 94.77 ± 0.08 89.41 ± 0.47 86.59 ± 0.45 87.98 ± 0.18

gamma 94.73 ± 0.07 88.91 ± 0.80 87.04 ± 0.96 87.96 ± 0.19

Figure 10: Example classiﬁcation using the standard con-

ﬁguration. Shown are the second input image and the seg-

mentation.

cal true positives on ﬁne vessels that are disconnected

from the main vessel tree. These can easily be remo-

ved by an optional postprocessing step. In order to do

so, we could enumerate all components using ﬂood

ﬁlling and only keep components whose number of

pixels is greater than a threshold.

At this point, we can look at all the requirements

we discussed earlier and see how well the network

fulﬁlled these based on some example patches:

1. suppression of bones (skull and eye socket)

2. suppression of glue

3. effect on screws

4. effect on stereotactic markers

5. white borders along contrast rich edges

6. inhomogeneous occlusion by the marker

The ﬁrst four items have in common that the inﬂuence

on the DSA is constant over time i.e. the effect on the

gray values is the same in all input images and thus

can be easily removed by subtraction. The network

fulﬁlled Item 1 and Item 2 in all our experiments. For

Item 3 and Item 4 we can note that those do get seg-

mented partially, if the contrast is high (see images on

the left side of Figure 2 and Figure 3). As mentioned

before, this is not relevant for our application. The

white borders (Item 5) still pose a problem because

they disrupt the segmentation of ﬁner vessels. An ex-

ample is shown in Figure 11. The small vessel paral-

lel to the large artery disappears inside the occlusion

of the latter in the DSA image. The artifact is additive

so that it should be possible to keep the vessel compo-

nents connected. The segmentation output shows that

the vesssel stops before the border, therefore missing

a possible connection. Item 6 seems to be no issue, so

that only in one segmentation output of the conﬁgura-

tion using one image as input an elongated hole was

visible in the largest artery.

Figure 11: Example for the white border along a large ar-

tery. The contrast of DSA images is enhanced for better

visibility.

6 CONCLUSION

We demonstrated how the U-net architecture can be

effectively applied to the segmentation of DSA series.

By basing the classiﬁcation on multiple images of a

time series, we can greatly improve the segmentation

performance. For our dataset, training the network on

four images, selected for speciﬁc timepoints, gives a

DSC of 87.98% which is 16.97% better than using a

single image. As noted by (Ronneberger et al., 2015),

data augmentations proved to be helpful for impro-

ving the network’s performance while using a very

small corpus of training data. Besides rotation and

mirroring, we used biasing instead of elastic deforma-

tions so that the spatial context does not get degraded.

Overall the network produces usable segmentation re-

AngioUnet - A Convolutional Neural Network for Vessel Segmentation in Cerebral DSA Series

337

sults with the main drawback of having many isolated

true positives in regions with ﬁne vessels.

ACKNOWLEDGEMENT

We would like to thank the Gamma Knife Krefeld

Centre for providing us with DICOM datasets and

medical expert knowledge.

REFERENCES

Badrinarayanan, V., Kendall, A., and Cipolla, R. (2015).

Segnet: A deep convolutional encoder-decoder ar-

chitecture for image segmentation. arXiv preprint

arXiv:1511.00561.

Brosch, T., Tang, L. Y., Yoo, Y., Li, D. K., Traboulsee, A.,

and Tam, R. (2016). Deep 3d convolutional encoder

networks with shortcuts for multiscale feature integra-

tion applied to multiple sclerosis lesion segmentation.

IEEE transactions on medical imaging, 35(5):1229–

1239.

C¸ ic¸ek,

O., Abdulkadir, A., Lienkamp, S. S., Brox, T., and

Ronneberger, O. (2016). 3d u-net: learning dense vo-

lumetric segmentation from sparse annotation. In In-

ternational Conference on Medical Image Computing

and Computer-Assisted Intervention, pages 424–432.

Springer.

Dice, L. R. (1945). Measures of the amount of ecologic

association between species. Ecology, 26(3):297–302.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. arXiv preprint arXiv:1505.04597.

Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wo-

jna, Z. (2016). Rethinking the inception architecture

for computer vision. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 2818–2826.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

338