Introduction of a Bayesian Network Builder Algorithm

Personalized Infectious Disease Risk Prediction

Retno Aulia Vinarti and Lucy Hederman

School of Computer Science and Statistics, Trinity College Dublin, The University of Dublin, Ireland

Keywords: Ontology, Knowledge-Base, Bayesian Network, Risk Prediction, Infectious Disease Risk.

Abstract: We introduce an algorithm for auto-generating a Bayesian Network (BN) structure from a knowledge-base

represented as an ontology with rules. The ontology and rules represent the assumptions of infectious disease

risk in the epidemiology domain. The resulting BN will be the computational model for an infectious disease

risk prediction service. The BN structure consists of one child node, to represent the chosen infectious disease,

with multiple parent nodes to represent the contexts which affect infection risk. Thus, this BN generation

algorithm is constrained to a relatively simple structure. The algorithm generates a BN using the API of BN

modeler software, Netica-J. We evaluate two aspects of the generated BN: the network structure and the

conditional probability tables (CPTs). The validation result shows that the algorithm generates an isomorphic

BN compared with the ontology and the CPTs are populated with consistent ratios from epidemiological rules.

Furthermore, the generated BN has resulted in a personalized infectious disease risk prediction based on the

personal attributes and their environments.

1 INTRODUCTION

Risk prediction is an estimation of the chance of a

person having an adverse event. Infectious disease

risk prediction is considered as adverse event in this

article since it is a major cause of deaths worldwide

(Aiello, et al., 2016). Conventionally, infectious

disease risk prediction deals with whether a new

infectious disease outbreak is likely to happen (1),

how fast an infection is likely to spread and the

specific location affected (2), and how likely it is that

certain measures will change the course of an

epidemic if certain measures are taken (3). The

system, for which this paper develops the algorithm,

takes a different approach by calculating a personal

risk of getting infected based on certain personal and

environmental attributes (Rev2, 2017). Adding

person properties to the prediction model allows it to

account for human susceptibility to certain diseases,

which differs from person to person (Shirai, et al.,

2004) (Shirai, et al., 2002).

Besides personalization, environment also plays

an important part in determining infection risk. The

environment is represented by the user location and

climate, including weather and season. Both

environment and climate have been proven to have

specific roles in boosting or limiting certain

pathogens (Fisman, 2008) (Monath & Vasconcelos,

2015) (WHO, 2003) (Wu, et al., 2016) (Yi, et al.,

2014). For example, children below five years old or

male adolescents or soldiers who live in Indonesia or

any countries between 30

N and 30

S are at twice the

risk for Tuberculosis in summertime than others

(Wertheim, et al., 2012). These predictors (person,

location, weather and season) will be represented as

knowledge to predict infectious disease risk in a

person at a place and time.

As epidemiological knowledge develops, more

predictors may need to be taken into consideration in

order to improve accuracy of prediction. In the

previous example, to predict Tuberculosis risk, the

person predictors, demographic risk factors (e.g. age,

occupation and gender), are included in an initial risk

prediction model. While Tuberculosis risk is now

well understood, knowledge of newer predictor,

behavioural risk factor (e.g. habit), is discovered.

Therefore, an infectious disease risk prediction

system that can be renewed to take account of new

diseases, new predictors and new data is required.

Knowledge about infectious disease predictors is

available from authorized health agencies (e.g. WHO,

CDC) in the Atlas of Human Infectious Diseases

(AHID) and epidemiological journals in declarative

form. Ontologies are used to represent this knowledge

Vinarti, R. and Hederman, L.

Introduction of a Bayesian Network Builder Algorithm - Personalized Infectious Disease Risk Prediction.

DOI: 10.5220/0006573301150126

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 5: HEALTHINF, pages 115-126

ISBN: 978-989-758-281-3

115

(Ruttenberg, et al., 2016) (Third, 2014). Meanwhile,

the predicted risk values need to be presented in

numerical form. So, both ontology and rules need to

be converted into a quantitative model that calculates

the risk prediction.

In this paper, we implement knowledge-driven

model generation which focuses on Bayesian

Networks (BN) as the generated model. We start by

building a knowledge-base that becomes the main

source of BN generation, Infectious Disease Risk

Ontology (IDR), by accumulating the declarative

knowledge manually. The IDR consists of general

infectious disease risk knowledge structure and

epidemiological rules. We introduce and validate an

algorithm that allows the automatic generation of a

BN, including populating the Conditional Probability

Tables (CPTs), directly from the knowledge-base.

The structure of the paper is as follows. Section 2

discusses related work. Section 3 presents the main

components of the Infectious Disease Risk Prediction

service including the BN generation algorithm.

Section 4 describes the evaluation of the generated

BN. Section 5 presents the evaluation results. Section

6 discusses the limitations and the advantages of

using this algorithm to generate a BN. Section 7

summarizes the contributions of the current work and

outlines future plans.

2 RELATED WORK

Knowledge-driven model generation has several

advantages in the context of continuously growing

knowledge rather than the former approach, data-

driven model generation. The knowledge-driven

system facilitates experts to contribute their best

knowledge without ruling out data and the given

contexts (Baumeister & Striffler, 2015). The

knowledge-driven modelling approach relies mainly

on the given domain knowledge (Fan, et al., 2015).

Domain knowledge for this research (i.e. infectious

disease risk) is available from various knowledge

sources and structures. Although some basic

knowledge structure is provided by BioPortal in

Ontology form (e.g. Epidemiology Ontology – EPO,

Infectious Disease Ontology – IDO and ClinicAl Risk

factoRs, Evidence and observables – CARRE)

(Ruttenberg, et al., 2016) (Third, 2014), a significant

body of relevant knowledge is gathered from the

Atlas of Human Infectious Diseases in declarative

form (Wertheim, et al., 2012).

Some quantitative models, in the public health risk

prediction domain, allow this knowledge

incorporation, such as Rule-based prediction model,

Logistic Regression, Fuzzy Cognitive Map and

Bayesian Networks (BN) (Lopman, et al., 2009)

(Blake, et al., 2016) (Jiang, et al., 2014) (Semakula,

et al., 2016) (Onisko, et al., 2001) (Jombart, et al.,

2014) (Austin & Onisko, 2015) (Douali, et al., 2014)

(Kunjunninair, 2012). BNs are able to incorporate

personal factors as nodes and connect to other nodes

without difficulties (e.g. data training, model fitting).

Also, BNs have been used in both personalization and

risk prediction research (Gao, et al., 2010).

Our previous work looked out at whether BNs that

built from declarative knowledge gathered from

AHID, CDC, and WHO fact sheets had a promising

risk prediction result (Vinarti & Hederman, 2017).

The paper predicted risk prediction result in Anthrax

disease compared with real patient data records. The

Anthrax BN was built manually, neither learnt from

historical datasets nor generated automatically by a

specific mechanism – which this paper now presents.

Rule1: The type of neighbourhood someone

lives in influences whether their house will

be burglarized.

IF: Neighbourhood(x): {bad, average, good}

THEN: Burglary(x): {true, false}

Matrix: (6 entries)

Rule2: Both a burglary and an earthquake can

cause someone’s alarm to go off.

IF: Burglary(x): {true, false} AND

EarthQuake: {tremor, moderate, severe}

THEN: Alarm(x): {true, false}

Matrix: (12 entries)

Rule2: An earthquake is often reported on the

radio.

IF: EarthQuake: {tremor, moderate, severe}

THEN: Radio: {true, false}

Matrix: (6 entries)

......

Figure 1: Probability Logic Knowledge-base.(Haddawy,

1994).

Generating a Bayesian Network from a probabilistic

knowledge-base was pioneered by Peter Haddawy

(Haddawy, 1994). He used Horn clauses to form a

probabilistic knowledge-base (Figure 1). The

knowledge-base used rules to define predictors, and

matrix to define conditional probability tables. By

using these clauses, he generated an isomorphic

Bayesian Network automatically. Whereas Haddawy

used random values in order to generate the BN, this

article seeks to populate these tables with appropriate

conditional probability values.

HEALTHINF 2018 - 11th International Conference on Health Informatics

116

3 THE PERSONALIZED

INFECTIOUS DISEASE RISK

PREDICTION

The infectious disease risk prediction web service is

designed to serve client applications which advise

users when and how to protect themselves from

infections. The service computes a person’s risk of

being infected by a specified disease today (or this

week or season depending on the disease), given their

demographic details and location. The service uses

geocodes to find weather, season and location

features (e.g. swamp, forest, river). For example, a 3-

year old female located at (40.440625, -79.995886) is

looking for their risk of Anthrax on the day

(04/07/2017, 07:55:45).

This section explains the components of the

service that are needed for predicting infectious

disease risk: (1) an ontology and rules that describes

the main elements of infectious disease risk to

represent the relationships between risk predictors

and a disease; (2) a main engine to predict the risk, a

quantitative prediction model (BN), which represents

the newest knowledge for each infectious disease; (3)

packages that support the BN to predict accurately

(weather, location APIs, health surveillance APIs and

simple functions to accommodate inputs/outputs).

The service will contain multiple independent BNs,

one per infection.

When epidemiologists find new knowledge or

new predictors about infectious disease risk, new

objects will be added to the ontology and rules, and

the BN model needs to be renewed. The renew

process makes use of the algorithm proposed in this

article to auto-generate the BN so that the prediction

model is isomorphic with the knowledge-base that

stores newest information. In this system, the

generated BN is isomorphic if all individuals and sub-

classes in the IDR Ontology have been transformed.

The individuals become the states and their sub-

classes become their nodes in the BN.

At runtime, the Live APIs tier collects current

contexts of the environment based on user’s location

and sends the retrieved values to the Context

Collector in the Logic tier. The BN model, also in the

Logic tier, takes the person’s demographics and

values from the Context Collector as inputs (i.e.

beliefs). Thereafter, the BN uses the CPT to yield the

risk prediction which is passed to the client through

the Presentation layer. In Figure 2, the separation

between runtime (left-side) and BN build time (right-

side) is illustrated by a dashed line.

The BN used at runtime is initially generated, and

further rebuilt every time there is something new

added to the knowledge-base (ontology and rules). In

order to generate a BN, nodes and states need to be

extracted from the ontology. Also, the child node’s

CPT needs to be populated by computing numerical

values from the rules. This is the main role of the BN

Builder package. For parent nodes, marginal

probability data is retrieved from sources such as the

United Nations (UN) Data API by MarginalProb

Supplier. Then, they are loaded to form parent nodes’

CPTs.

3.1 Structure of the Knowledge Base

and the Generated Bayesian

Network

An ontology is used to represent the relationship

between predictors and infectious disease risk.

Existing ontologies related to this subject and some

declarative knowledge sources have been studied and

reused to create the Infectious Disease Risk (IDR)

ontology (Figure 3). The main classes (e.g. Person,

Infectious Disease, Environment) are denoted by

rectangles. Sub-classes represent the risk factors of an

infectious disease for each class (e.g. age, gender in a

person); they are denoted by ellipses. Individuals are

the instances of the sub-classes (e.g. female and male

in gender).

Some individuals are different for each disease,

for example, age in Tuberculosis will have different

categorization with age in Anthrax. But, some other

individuals are same (e.g. female and male as

instances of gender). The individuals are not

illustrated in Figure 3. The IDR ontology is used to

support epidemiological rules in Semantic Web Rule

Language (SWRL). The SWRL rules refer to the IDR

classes, sub-classes and individuals.

Rules are used to define statements about the

factors of a person, and their environment, that affect

whether they get infected by a disease. These rules are

manually encoded from declarative knowledge

sources: Atlas of Human Infectious Disease (AHID),

Centres of Disease Control and Prevention (CDC).

They are written in SWRL form by a knowledge

engineer using numerical inputs (x1, x2, y, z in Table

1) from Health Surveillance Reports and journals

related to epidemiology of infectious diseases.

The common composition of rules is antecedent

(A), consequent (B) and denoted as (A → B). The

antecedent covers the predictors and the consequent

covers the disease. CARRE project and its related

publications introduce the clinical risk model to

describe a disease risk in a person (Third, 2014). They

Introduction of a Bayesian Network Builder Algorithm - Personalized Infectious Disease Risk Prediction

117

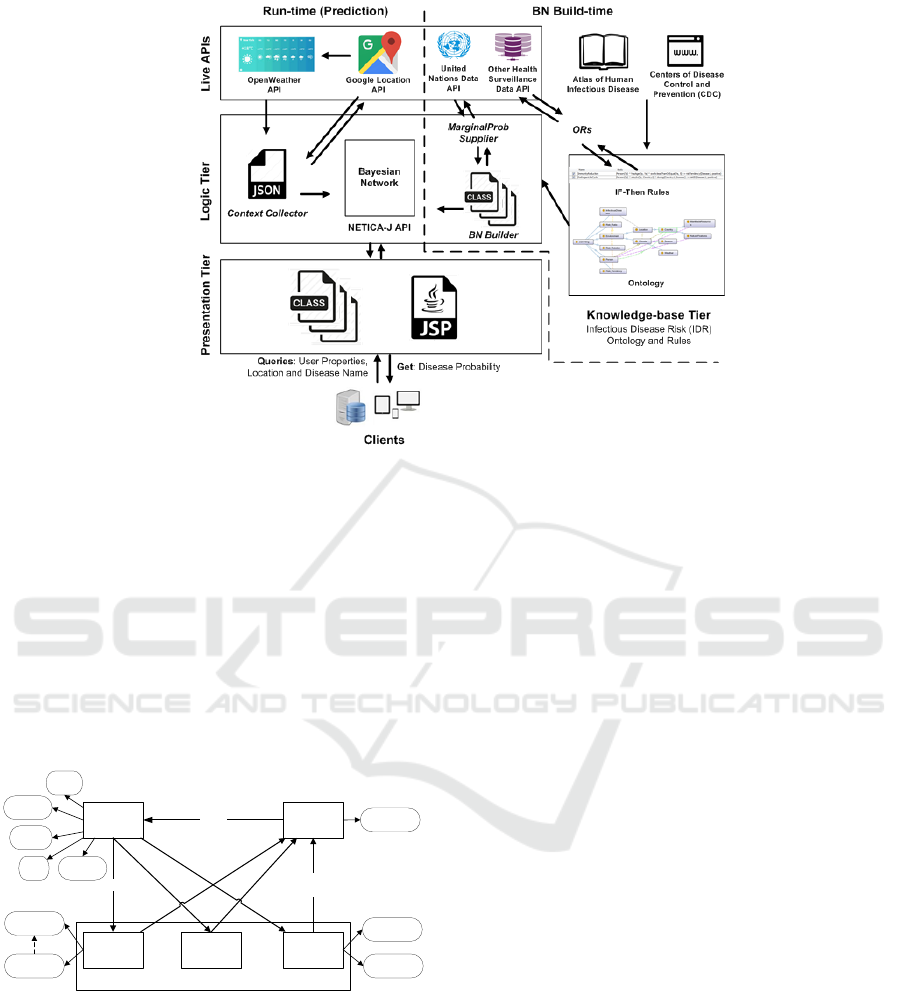
Figure 2: The Infectious Disease Risk Prediction Service Architecture.

involved risk quantification as risk ratio (i.e. Odds

Ratio – OR or Relative Risk – RR) for each risk

factor. Therefore, for the algorithm introduced in this

research, each antecedent load personal attribute(s) as

risk factor (e.g. vegan, farmers, or adult in Table 1).

Whereas its consequent has two components: the

disease name and the numerical value that shows the

significance of the risk factor to the infectious disease

risk. The numerical value is either an OR/RR or a

prevalence rate or zero (in the case of pathogen

dormancy).

Person

Infectious

Diseases

Location Climate

risk of

live in

pathogen

lifecycle

prevalence

Environment

Age

Gender

Disease

Name

Season

Weather

Existing

Illness

Features

Country

Occupation

Geocodes

live around

access date

Habit

Figure 3: The Generic Infectious Disease Risk Ontology

(IDR).

For Anthrax, these numerical values are expressed in

%K units (K=0.001), which show the risk of a disease

per 100,000 population in a particular location. Other

diseases may use different units. These values will be

inputted by the epidemiologist by identifying them

from the declarative knowledge sources. Later, the

CPT will be populated from these values by following

several procedures and computations. The

computation is embedded in the BN generation

algorithm.

There are three types of rule for representing

infectious disease risk: the first, stores OR values for

each state, the second type stores prevalence or

incidence rate for each disease, and the third type

describes the pathogen availability in specific

conditions (e.g. location, weather, season). The key

difference between OR and prevalence-type rules is

the predicate at the consequent part. An OR-type rule

has alterRisk while the prevalence-type rule has

setRisk predicate (bold letters in Table 1). Therefore,

one disease ontology has multiple OR-type rules and

at least one prevalence-type rule.

In this version of algorithm, the pathogen-type

rule uses the same predicate as prevalence-type rule

(setRisk), but the numerical value of the pathogen-

type rule is zero. This follows the assumption that the

pathogen is always considered as active unless there

is a declaration of inactivity (dormancy).

The numerical values which are stored in the rules

bring important epidemiological parameters to

populate the child node’s CPT. Meanwhile, these

rules depend on the ontology structure (classes, sub-

classes and individuals). So, both ontology and

SWRL rules inside the knowledge-base tier need to

be transformed carefully into a prediction model

(Bayesian Network).

HEALTHINF 2018 - 11th International Conference on Health Informatics

118

Table 1: Sample SWRL Rule Encoding for Anthrax Risk.

Simplified Declarative Knowledge

Rules

Rule Type

Anthrax prevalence in the US is 12 per 100,000

population per year.

Person(?all) ^ liveIn(?all, US) ->

setRisk(Anthrax, 1.12)

Prevalence

An analysis of seven studies estimated a pooled

odds ratio for Anthrax risk in non-vegan

compared with vegan is doubled.

Person(?all) ^ hasHabits(?all, vegan) ->

alterRisk(Anthrax,x1)

Person(?all) ^ hasHabits(?all, carnivore) ->

alterRisk(Anthrax,x2)

Farmers are at the highest risk.

Person(?all) ^ hasOccupation(?all, farmers) ->

alterRisk(Anthrax,y)

Children are at less risk of Anthrax compared to

Adult or Elderly

Person(?all) ^ hasDevelopmentStage(?all,

Children) -> alterRisk(Anthrax,z)

Anthrax pathogens are dormant during winter.

Person(?all) ^ accessDuring(?all, Winter) ->

setRisk(Anthrax,0)

Pathogen

3.2 The BN Builder Package

A basic BN consists of parent and child nodes. In this

system, the predictors become parent nodes and the

disease whose risk is being predicted becomes the

child node. Each node contains a CPT which consists

of states and probabilities. Parent nodes’ CPTs need

marginal probability values (e.g. the probability of a

person being a child). These values are loaded from

UN Data API. The child node’s CPT stores all

parent’s states combinations and their conditional

probabilities (e.g. the probability of a female child

getting Anthrax).

The BN Builder package aims to generate code to

call Netica-J built-in functions that generate an

isomorphic BN from the knowledge-base. The BN

Builder has two tasks: (1) create the network

structure, and (2) fill in the parent and child nodes’

CPTs. To fulfil these objectives, two algorithms are

introduced in this article: Network Construction and

CPT Population algorithm. The Network

Construction algorithm is used to create the BN

structure while the CPT Population algorithm is used

to transform rules into child node’s CPT. Both

algorithms use intermediate representations (Table 2

and Table 3 in the next sub-section).

It is also useful for the algorithm to have a

specification of impossible combinations of parent

nodes’ states as done by (Das, 2004). For example,

(e.g. pregnant – male, male – pregnant). By having

this, some unnecessary work can be reduced in the

later stage (CPT Population).

Software for managing the knowledge-base,

Protégé, is used to create the IDR and write the

SWRL rules. In general, there are two ways of using

an ontology in the context of knowledge-driven

model generation: exporting it to RDF representation

and using XML technology to query the RDF, or

directly by querying the knowledge-base using

SPARQL. This research uses XPath to retrieve items

in the knowledge-base then store them into

intermediate representations.

3.2.1 Intermediate Representation of

Network Structure and Rules

The creation of a network structure needs some

information needed to create a BN structure. The

information is obtained from the knowledge-base

representation, RDF (Figure 4). XPath queries are

then used to select the items by locating their paths in

the RDF.

Figure 4: RDF Structure.

The bold tags show the sections needed to build a BN.

The information about nodes and states to construct a

BN are stored in <Individuals> tags, while resources

about OR, prevalence and other information needed

to populate child node’s CPT are stored in <Rules>

tags. An example of a line in <Individuals>

expressing a state named female belonging to a node

named gender is given below.

IDR:Female rdf:type owl:NamedIndividual ,

IDR:Gender .

XPath queries are used to obtain all nodes and states

from the <Individuals> tags (given below). The

results of these queries are then stored in the

Introduction of a Bayesian Network Builder Algorithm - Personalized Infectious Disease Risk Prediction

119

intermediate representation in a fixed order as

presented in Table 2.

nodesQuery = "/rdf:RDF/owl:NamedIndividual/

rdf:type/@rdf:resource";

statesQuery = "/rdf:RDF/owl:NamedIndividual/

@rdf:about";

Table 2: Sample Content of the Nodes and States.

Order

Nodes

States

Age

Child

Adult

Elderly

Gender

Female

Male

Occupation

Farmers

Soldiers

For the rules, the intermediate representation uses

five components: name, disease, attribute value,

predicate and the numerical value (Table 3). Since our

rules each only refer to one attribute, this

representation is sufficient.

Table 3: Sample of the Rule Components.

name

disease

attribute

value

predi

cate

num.

values

AntLoc1

Anthrax

set

1.12

AntEnv3

Anthrax

Winter

set

AntPrson2

Anthrax

Children

alter

0.85

Table 3 shows examples of Prevalence, Pathogen and

OR-type rules, respectively. Each numerical value

represents OR, prevalence rate or pathogen dormancy

depending on the rule type. To fill Table 3, antecedent

and consequent of a rule is identified by swrl:body

and swrl:head tags, respectively. The queries are

given below Table 3.

ruleName = "/rdf:RDF/rdf:Description/

rdfs:label";

ruleDisease = "/rdf:RDF/rdf:Description/

swrl:head/.//swrl:argument1/@rdf:resource";

ruleAtt = "/rdf:RDF/rdf:Description/

swrl:body/.//swrl:argument2/@rdf:resource";

rulePredicate = "/rdf:RDF/rdf:Description/

swrl:head/.//swrl:propertyPredicate/@rdf:res

ource";

ruleNum = "/rdf:RDF/rdf:Description/

swrl:head/.//swrl:argument2";

These intermediate representations are used to

construct the Network and populate the child node’s

CPT as explained in the following sub-sections.

3.2.2 Constructing the Network

A BN structure consists of nodes and states. Referring

to the Table 2 as example, age, gender, occupation,

and Anthrax are nodes, while the items on the right-

side column are their states. These details are

obtained from the intermediate representation (Table

2). For the disease prediction BN, the predictors (age,

gender, occupation) form the parent nodes, and the

disease (e.g. Anthrax) is the child node.

In order to construct the network, the BN Builder

closely follows the Netica-J procedure in Pseudocode

1 (Norsys, 1995-2017). The bold items represent the

automation this paper presents.

Pseudocode 1: Network Construction

1. Create and set the Netica environment

2. Declaration and assignment of a child

node

3. Declaration of parent nodes

4. Loading resources from intermediate

representations

5. foreach node do

a. Assign each parent node using three

input parameters: node name,

stateString (result from Statenames

Concatenation), Netica environment

b. Construct the marginal probability

of each parent node using two input

parameters: node name, MarginalProb

array (result from MarginalProb

Concatenation)

c. Save the order of parent node into

nodequeue

d. Connect parent with child node

6. Construct the conditional probability

of the child node using nodequeue.

7. Write the network into Netica readable

file (.dne file)

The automation of Pseudocode 1 begins with parent

node assignment (line 3 and 5). The Netica-J built-in

function to assign a node is given as follows:

Node temporary = new Node (String nodename,

String statenames, net);

The declaration of a temporary node starts in line 3

and it is initialized with null value. In line 5a, the

temporary node will be assigned with real nodes and

states taken from the intermediate representation. The

assignment of this node is called for as many nodes

as found in the Table 2.

Pseudocode 2: Statenames Concatenation

1. Create a stateString

2. foreach state in a parent node do

a. Append the the state name to

stateString, followed by a comma.

3. end

HEALTHINF 2018 - 11th International Conference on Health Informatics

120

Pseudocode 3: MarginalProb Concatenation

1. Create a MarginalProb array

2. foreach state in a parent node do

a. Append the MarginalProb array with

related marginal probability.

3. end

Marginal probabilities, for example the ratio of Male

to Female in a specific region, are provided by the

MarginalProb Supplier package (see Figure 2).

Information to fill MarginalProb is usually found in

UN Data API. In Netica, the assignment of the

marginal probability to a node uses a statement:

parentNode.setCPTable(MarginalProb[]);

However, if no marginal probability data is provided,

Netica-J, by default, assigns equal fractions based on

number of states in the node. For instance, the default

MarginalProb of a two-state node is <0.5, 0.5>.

Once the nodes and their states are defined, the

order of parent nodes must be saved (line 5c) before

connecting the parents with child node (line 5d). The

order will be used by CPT Population algorithm. Line

6 in Pseudocode 1 handles the CPT population for the

child node. The details are explained in the next sub-

section.

3.2.3 Populating the CPT

The child node’s CPT is calculated from the

numerical parameters in the intermediate

representation of rule (Table 3). This involves first,

generating all combinations of the relevant states and

then computing the conditional probability for each

combination. See Figure 9 for sample extract of the

CPT for Anthrax in Netica.

To illustrate, the needed state combinations are

presented in Figure 5. The number of combinations is

∏

𝑠

𝑖

𝑛

𝑖=1

where s

is number of states in node i, and n is

number of nodes.

Age, Gender, Occupation

Children, Male, Farmers

Children, Male, Soldiers

Children, Female, Farmers

Children, Female, Soldiers

Adult, Male, Farmers

...

Figure 5: Sample of the StateCombination.

To calculate a conditional probability (condProb), for

a state combination, we apply Pseudocode 4 using the

intermediate representation for rules as in Table 3.

The algorithm can distinguish rule types as follows:

pathogen-type rules are those where the predicate is

setRisk and the value is 0; prevalence-type rules are

those whose predicate is setRisk and the value is

non-zero; OR-type rules are those with predicate

alterRisk. Then, the numerical values of each rule

type are used in different part in the process of

populating the CPT.

The algorithm checks for conditions that result in

zero disease risk (line 2 in Pseudocode 4): either there

is matching a pathogen-type rule attribute or there is

an impossible combination. By filtering these

conditions upfront, only combinations that need

calculation of conditional probabilities is left.

After the prevalence rate is obtained and set as the

condProb (line 3a), for each OR-type rule, if the

attribute value is contained in the state combination,

the rule is considered “a match”. For example, each

of ‘Adult’, ‘Male’, ‘Farmers’ in the ‘Children,

Male, Farmers’ combinations, only Farmers is

considered as “match” with AntPerson1 rule. Then,

the conditional probability is calculated by

multiplying the ORs of the matched rule by the

existing condProb (line 4a).

Pseudocode 4: CondProb Calculation

1. Initialize condProb to 1

2. IF there is a matching pathogen-type

rule attribute or IF the combination is

impossible

a. Set the condProb to 0

3. ELSE IF there is a matching prevalence-

type rule attribute,

a. Set the condProb to that value

(Prevalence)

4. ELSE for each matching OR-type rule

attribute

a. condProb = condProb * OR

5. end

4 EVALUATIONS

The algorithm’s main functions are converting the

IDR into an isomorphic BN, and populating its CPT

based on the inputted OR and prevalence values.

Therefore, the evaluation of the algorithm’s

correctness will consider the BN result and the child

node’s CPT values.

The BN generation algorithm described above

was tested on two diseases along with their risk

factors as predictors: Anthrax and Tuberculosis. The

Anthrax BN has 13 parent nodes, 36 states in total,

and 248,832 state combinations, of which only

96,768 combinations are possible. The Tuberculosis

has 12 parent nodes, 34 states in total and 138,240

state combinations, and all are possible combinations.

An OntoGraf, a common layout for organizing an

ontology structure in Protégé, is used to present the

Introduction of a Bayesian Network Builder Algorithm - Personalized Infectious Disease Risk Prediction

121

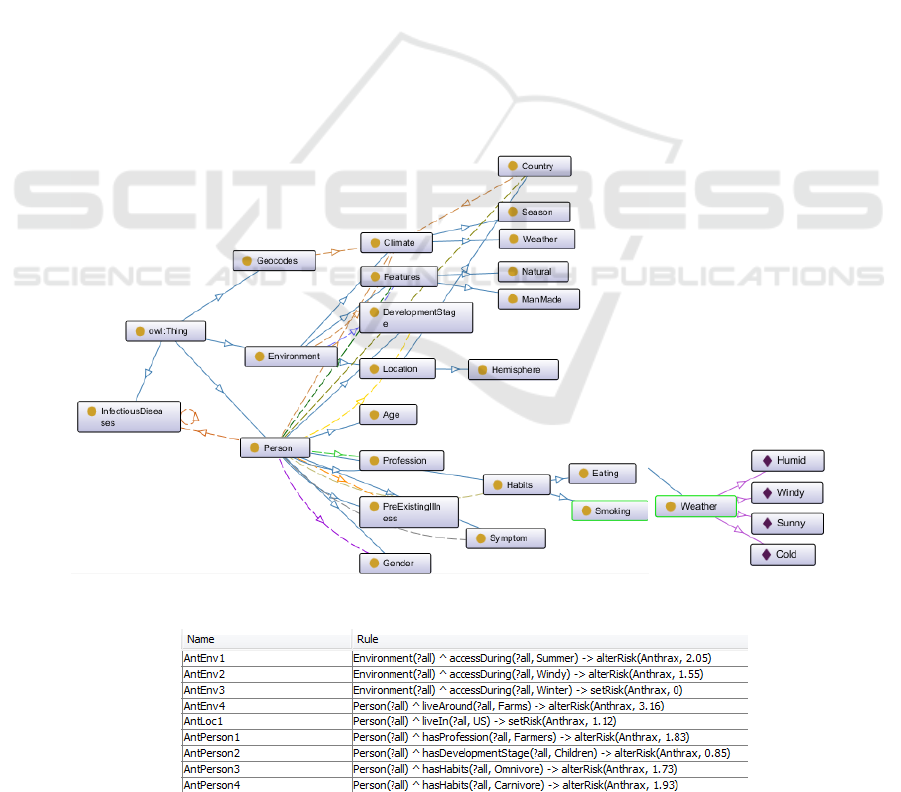
created IDR (Figure 6). The class and subclasses are

marked with circle symbol, while, individuals are

symbolized by diamonds. The example of Weather’s

individuals (Humid, Windy, Sunny, Cold) are given

in the right-hand side of Figure 6. The solid and

dashed lines represent direct and indirect relationship

in a class, respectively.

In Figure 7, SWRL rules for Anthrax are

presented. For OR-type rules, the numerical values

less than one show a decreased risk (AntPerson2), and

those of more than one show an increased risk of the

disease (AntEnv1). These rules use the alterRisk

predicate. Meanwhile, the setRisk rules can have

two options: zero and non-zero.

For AntEnv3, the zero value means the pathogen

is inactive, thus, it represents a pathogen-type rule.

The non-zero values mean prevalence or incidence

rates of the disease in the certain location (e.g.

AntLoc1), thus, it represents prevalence-type rules.

Figure 8 shows the generated BN for Anthrax; the

number of states per node varies and all states are

successfully added to its node. Also, the parent nodes

are all connected to the child node, as expected from

the algorithm. The marginal probabilities for all

parent nodes are set to default. This happens because

for this test we did not provide exact values for the

marginal probabilities but let the program use the

default uniform distribution setting.

Figure 9 shows a small extract of the generated CPT

for the child node. It consists of state combinations

(left-side of the table) which are generated by

StateCombination Generation and a conditional

probability value for each child node’s state (i.e.

AtRisk) (right-side of the table) which are calculated

by CondProb Calculation.

The last two rows in Figure 9 shows that a

function to check impossible permutations is working

for <<Indonesia> <Autumn>> – they have AtRisk

values of 0. The middle four rows show that the

pathogen-type rule works properly on all state

combinations that contain “Winter” – they have

AtRisk values of 0.

A computer with specification Intel Core i3 CPU

1.7GHz with 4GB of memory was used to generate

the BNs and populate the CPTs. It took 17 to 19

minutes approximately. The generation of state

combinations accounts for most of the time.

Figure 6: OntoGraf of the IDR.

Figure 7: SWRL rules for Anthrax used to populate CPT.

HEALTHINF 2018 - 11th International Conference on Health Informatics

122

Figure 8: The generated isomorphic BN.

5 EVALUATION RESULTS

Results of the validation will be justified by the

correctness of the algorithm. The algorithm is correct

when it generates an isomorphic BN and populates

the CPT as given odds ratios.

5.1 Evaluation on the Generated BN

Not all classes or sub-classes in the IDR will be

transformed into nodes in the BN; only classes that

have at least one individual are converted. To

compare the generated BN with the IDR, a

mechanism to retrieve all the individuals with their

corresponding classes and sub-classes directly from

the Protégé is needed. A SPARQL query is used in

the Protégé environment to execute the required

mechanism.

SELECT *

WHERE {?individual rdf:type ?type .

OPTIONAL {?type rdfs:subClassOf ?class}}

ORDER BY ?type

Thereafter, the results of this query were compared

with the generated BN (Figure 8). It can be seen from

Fig. 6 that all sub-classes are transformed into nodes

and all individuals are transformed into states.

Furthermore, the node-state arrangements in the BN

follow exactly the sub-classes and individuals’

arrangements in the ontology. Other cases have been

checked, for example, having empty sub-classes or

non-referenced data or object properties in the IDR.

Those conditions have no impact on the generated

BN. Thus, it has been shown that the generated BN is

isomorphic with the IDR.

5.2 Evaluation of the Populated CPT

To show that the algorithm correctly represents the

SWRL rules presented in Figure 7 in the child node’s

CPT, an evaluation of the CPT is carried out.

The numerical values stored in the SWRL rules

reveal the behaviour (e.g. inclination or declination)

of the disease risk. The CPT population algorithm

makes use of these numerical values to produce the

conditional probabilities. Thus, all rules are taken as

inputs and the related conditional probabilities are

taken as outputs of this evaluation.

Then, the correctness of the CPT population

algorithm is analysed by observing the outputs in two

aspects: (1) the behaviour of the conditional

probabilities has a consistent ratio with the given

numerical values in the rules, and (2) the generated

probabilities have different values for different

personal and environmental conditions.

Table 4 shows validation for all Anthrax rules

shown in Figure 7. Two countries are involved in this

evaluation: US and Indonesia. All results for

correspondent country are given for each OR-type

and pathogen-type rules. The aggregated ratio for

each state is given in the Result column. Then, to

observe the ratio of prevalence between two

countries, all ratios for OR-type rules are aggregated

and placed on the Ratio column (e.g. 1.12043 for the

AntLoc1 rule). From this process, the algorithm

populates the child node’s CPT automatically from

the SWRL rules as presented in Figure 7. Also, they

produce the comparable ratios with the given

numerical values in the SWRL rules.

Introduction of a Bayesian Network Builder Algorithm - Personalized Infectious Disease Risk Prediction

123

Furthermore, the resulting conditional

probabilities show that these conditions result in

different prediction results as stated on the rules.

(a) different personal attributes (e.g. Age,

Gender) which are taken as different person

(b) the same person living in a country during

different season (e.g. Winter, Spring)

location features (e.g. Lake, Farms) within a

country

Thus, we see that the populated CPT yield a

personalized infectious disease risk prediction based

on the personal and environmental attributes.

6 DISCUSSION

The algorithm describes about a mechanism to

convert a knowledge-base (ontology and rules)

representing an infectious disease to a risk prediction

model (BN and its CPT). Since this paper introduces

a BN generation algorithm, the comparative

evaluation is of the functional requirements of the

standard BNs. The requirements are generating BN

structure (1), and populating the CPT (2). However,

the algorithm makes some assumptions which lead to

some limitations that are discussed in this section.

States in a node are assumed to be unique and

discrete. Some possibilities that makes a node

become non-unique are (1) continuous states, and (2)

non-unique individual names across classes. Netica-

BN allows continuous numerical forms as states but

later any continuous nodes taking part in an equation

must first have been discretized (Norsys, 1995-2017).

However, no need for continuous nodes for modelling

infectious disease risk prediction. In addition,

continuous numerical forms of predictor rarely use a

BN as the prediction model. A Logistic Regression or

Bayesian Logistic Regression is more suitable for this

kind of forms (Koop, et al., 2013).

Rules in the IDR are assumed to have one attribute

per rule. For most diseases, the OR usually represents

one risk factor (e.g. male) which is independent of the

disease risk. However, other diseases may have two

or more risk factors for one OR (e.g. male, adult) or

dependent risk factors. This condition is not equal

with multiplying OR for male and adult. The current

version of the algorithm cannot handle more than one

attribute in one rule.

Figure 9: Extract of the child node’s CPT.

Table 4: Evaluation of generated model.

DESIGN

RESULT

Rule Names

Type of

attribute

Numerical Values given on

the Rules

Rule Type

Generated conditional probability values

Ratio

Context: People living in the US and Indonesia during rainy season seek for Anthrax risk disease

AntLoc1

Country

US = 1.12, Indonesia = 1

Prevalence

Indonesia

1.12043

AntPerson1

Personal

Farmers = 1.83 x Military or

Jobless

Farmers = 0.06476

Military = 0.03539

Jobless = 0.03539

Farmers = 0.05782

Military = 0.03159

Jobless = 0.03159

1.83005

AntPerson2

Personal

Children = 0.85 x Adult or

Elderly

Adult = 0.03539

Children = 0.03008

Elderly = 0.03539

Adult = 0.03159

Children = 0.02686

Elderly = 0.03159

0.85005

AntPerson3

Personal

Omnivore = 1.73 x Vegan

Vegan = 0.03539

Omnivore = 0.06128

Carnivore = 0.06831

Vegan = 0.03159

Omnivore = 0.05466

Carnivore = 0.06098

1.7309

AntPerson4

Personal

Carnivore = 1.93 x Vegan

1.93025

AntEnv4

Feature of

Location

Farms = 3.16 x Lake

Farms = 0.03539

Lake = 0.0112

Farms = 0.03159

Lake = 0.00999

3.16095

AntEnv1

Season

Summer = 2.05

Winter = 0,

Spring = 0.03539

Summer = 0.0725

Autumn = 0.03539

Rain = 0.03159

Dry = 0.03159

2.0486

AntEnv3

Climate

Winter = 0

Pathogen

HEALTHINF 2018 - 11th International Conference on Health Informatics

124

Another limitation of this algorithm is on handling

non-unique individual names. For example, an

individual none belong to vaccinated and symptoms

sub-classes. For now, if this situation happens, the

knowledge engineer should concatenate the names

with attribute values (e.g. notVaccinated).

The underlying assumption of the generated BN

is no intermediate nodes between parent and child

nodes, and all predictors are assumed to be

independent of each other. Most interdisciplinary

research takes this assumption to simplify the

network and prediction model (Fenton, et al., 2016).

The current system only allows for pathogen to be

active and inactive (set risk to 0). A support for more

complex pathogen model (Kilianski, et al., 2015)

(Huang, et al., 2012) would be beneficial.

Finally, for the requirements to predict a

personalized infectious disease risk, some critical

features are already facilitated in initial version in this

paper. Further development related to detailed

specification can be accommodated without

significant changes to either the knowledge-base or

the generation algorithm.

7 CONCLUSIONS AND FUTURE

WORKS

This paper has described an algorithm for generating

a Bayesian Network from the declarative infectious

disease knowledge stored in an Ontology and SWRL

rules. This algorithm allows additions or

modifications to the ontology and will generate an

isomorphic Bayesian Network and populate its child

node’s CPT automatically. However, the algorithm is

a preliminary result with several limitations.

This paper uses the IDR, an Infectious Disease

Risk Ontology and SWRL rules, as main reference of

BN generation. This IDR will have numerous

individuals for each disease as the knowledge

becomes available in the future. Three types of rules

have been introduced in this paper: OR, prevalence,

pathogen-type rules. In this algorithm version, the

pathogen availability is considered as always active,

unless there is a declaration of pathogen inactivity.

Another progressing work is ready to be published in

a separated article.

The algorithm introduced in this paper only

covers one possible source of OR and prevalence

values – explicitly provided by experts within rules.

There is another source that is possible to access:

WHO data sources in UN Data or Health Surveillance

API. By opting in these sources, there will be an

automated process that aims to put the numerical

values in the rule. This leads to some possibilities that

are not covered by this algorithm for now, such as

contradicting the established rules. A procedure to

manage the rules might be a substantial improvement

in the future.

Some other further works be (1) modifying the

intermediate representation and the XPath queries for

accommodating more than one dependent attribute in

one rule, (2) observing relevant time period for

predicting various infectious disease risks; this will

impact on the conditional probabilities given to a

client and thus will slightly modify the CPT

Population algorithm.

To sum up, from the evaluation section, it can be

concluded that the Network Creation algorithm has

successfully generated an isomorphic BN from the

Ontology structure. In addition, the CPT Population

algorithm has auto-populated the child node’s CPT

and the ratio of the conditional probability results are

consistent with the inputted OR. Furthermore, the BN

Builder package has resulted in a personalized

infectious disease risk prediction based on the

personal attributes and their environments.

ACKNOWLEDGEMENTS

The research for this paper is financially supported by

Islamic Development Bank (IDB) through Merit

Scholarship Programme for High Technology.

REFERENCES

Aiello, A. E., Simanek, A. M., Eisenberg, M. C. & Walsh,

A. R., 2016. Design and methods of a social network

isolation study for reducing respiratory infection

transmission. Vol. 15.

Aliferis, C. F., Tsamardinos, I., Statnikov, A. R. & Brown,

L. E., 2005. A Causal Probabilistic Network Learning

Toolkit for Biomedical Discovery. Las Vegas, Nevada,

Mathematics and Engineering Techniques in Medicine

and Biological Sciences.

Austin, R. M. & Onisko, A., 2015. Increased cervical

cancer risk associated with extended screening intervals

after negative human papillomavirus test results 1(1).

Baumeister, J. & Striffler, A., 2015. Knowledge-driven

systems for episodic decision support. Knowledge-

based systems, Volume 88, pp. 45-56.

Blake, I. M., Chenoweth, P., Okayasu, H., 2016. Detection

of poliomyelitis outbreaks to support polio eradication.

Emerging Infectious Diseases, 22(3), pp. 449-456.

Introduction of a Bayesian Network Builder Algorithm - Personalized Infectious Disease Risk Prediction

125

Chang, T. S., Gangnon, R. E., Page, D., 2015. Sparse

modeling of spatial environments associated with

asthma. Volume 53.

Das, B., 2004. Generating Conditional Probabilities for

Bayesian Networks: Easing the Knowledge Acquisition

Problem. CoRR, pp. 1-24.

Douali, N. et al., 2014. Comparison between case-based

fuzzy cognitive maps and bayesian networks. 113(1).

Fan, X.-R.et al., 2015. A knowledge-and-data-driven

modeling approach for simulating plant growth: A case

study on tomato growth. Ecological Modelling, Vol

312, pp. 363-373.

Fenton, N., Neil, M. & Lagnado, D., 2016. How to model

mutually exclusive events based on independent causal

pathways in Bayesian network models. Volume 113.

Fisman, D. N., 2008. Seasonality of viral infections:

Mechanisms and unknowns. American Journal of

Preventive Medicine, 18(10), pp. 946-954.

Gao, M., Liu, K. & Wu, Z., 2010. Personalisation in web

computing and informatics. Information Systems

Frontiers, 12(5), pp. 607-629.

Giabbanelli, P. J., Torsney-Weir, T. & Mago, V. K., 2012.

A fuzzy cognitive map of the psychosocial

determinants of obesity. 12(12).

Haddawy, P., 1994. Generating Bayesian Networks from

Probability Logic Knowledge Bases. Seattle, Morgan

Kaufmann Publishers Inc. San Francisco, CA, USA.

Huang, Z., Das, A., Qiu, Y., 2012. The vector-borne disease

airline import. risk (VBD-AIR) tool. Vol. 11.

Jiang, Q., Zhou, J. T., Jiang, Z. B. & Xu, B., 2014.

Identifying risk factors of avian infectious diseases at

household level in Poyang Lake region, China.

Preventive Veterinary Medicine, 116(2), pp. 151-160.

Jombart, T., Aanensen, D. M., Baguelin, M., 2014. A

platform for disease outbreak using the R. Vol. 7.

Kahn Jr., C. E., Roberts, L. M., Shaffer, K. A. & Haddawy,

P., 1997. Construction of a BN for mammographic

diagnosis of breast cancer. Computers in Biology and

Medicine, 27(1), pp. 19-29.

Kilianski, A., Carcel, P., Yao, S. & Roth, P., 2015.

Pathosphere.org: pathogen detection and

characterization through a web-based. BMC

Bioinformatics, 416(16), pp. 1-12.

Koop, G. et al., 2013. Risk factors for subclinical

intramammary infection in dairy goats in two

longitudinal field studies evaluated by Bayesian logistic

regression. 108(4).

Kunjunninair, A. P., 2012. Clinical decision support

system: risk level prediction of heart disease using

weighted fuzzy rules and decision tree rules. Central

European Journal of Computer Science, 2(1).

Laskey, K. B. & Mahoney, S. M., 2000. Network

Engineering for Agile Belief Network Models. IEEE

Transactions on Knowledge and Data Engineering,

12(4), pp. 487-499.

Lopman, B., Armstrong, B., Atchison, C., 2009. Host,

weather and virological factors drive norovirus epid.

PLoS One, 4(8).

Monath, T. P. & Vasconcelos, P. F. C., 2015. Yellow fever.

Journal of Clin. Viro., Volume 64, pp. 160-173.

Ngo, L. & Haddawy, P., 1995. Probabilistic logic

programming and Bayesian networks. Lecture Notes in

Computer Science, Volume 1023, pp. 286-300.

Norsys, 1995-2017. https://www.norsys.com/netica-

j/examples/SimulateCases.html.

Onisko, A., Lucas, P. & Druzdzel, M. J., 2001. Comparison

of Rule-Based and Bayesian Network Approaches in

Medical Diagnostic Systems. Portugal.

Rev2, 2017. HealthInformatics Conference: Reviewer

comment #2. Unknown: Primoris.

Ruttenberg, A. et al., 2016. Infectious Disease Ontology.

http://purl.obolibrary.org/obo/ido.owl.

Semakula, H. M., Song, G., Achuu, S. P., 2016. A Bayesian

belief network modelling of household factors

influencing the risk of malaria. Vol 75.

Shirai, O., Tsuda, T. & Kitagawa, S., 2002. Alcohol

stimulates mosquito. Journal of the American Mosquito

Control Association, 18(2), pp. 91-96.

Shirai, Y., Funada, H. & Seki, T., 2004. Landing preference

of Aedes albopictus on human skin among ABO blood

groups, secretors or nonsecretors. Journal of Medical

Entomology, 41(4), pp. 796-799.

Third, A., 2014. BioPortal: CARRE Risk Factor Ontology.

https://bioportal.bioontology.org/ontologies/CARRE.

Vinarti, R. A. & Hederman, L. M., 2017. Personalization

of Infectious Disease Risk Prediction Towards

automatic generation of a Bayesian Network.

Thessaloniki, Greece.

Wertheim, H. F. L., Horby, P. & Woodall, J. P., 2012. Atlas

of Human Infectious Diseases. Oxford: Wiley-

Blackwell.

WHO, 2003. Climate Change and Human Health - Risks

and Responses Summary, Geneva: WHO.

Wu, X. et al., 2016. Impact of climate change on human

infectious diseases. Vol. 86.

Yi, H., Devkota, B. R. & Yu, J.-s., 2014. Effects of global

warming on mosquitoes & mosquito-borne

diseases and the new strategies for mosquito control.

Entomological Research, 44(6), pp. 215-235.

HEALTHINF 2018 - 11th International Conference on Health Informatics

126