MultiVisA: Visual Analysis of Multi-run Physical Simulation Data using

Interactive Aggregated Plots

Alexey Fofonov

and Lars Linsen

1,2

Jacobs University, Bremen, Germany

Westf

alische Wilhelms-Universit

at, M

unster, Germany

Keywords:

Ensemble Visualization, Multi-run Simulation Analysis.

Abstract:

Physical simulations aim at modeling and computing spatio-temporal phenomena. As the simulations depend

on initial conditions and/or parameter settings whose impact is to be investigated, a larger number of simulation

runs is commonly executed. Analyzing all facets of such multi-run multi-ﬁeld spatio-temporal simulation

data poses a challenge for visualization. It requires the design of different visual encodings that aggregate

information in multiple ways and at multiple abstraction levels. MultiVisA is a tool for the interactive visual

analysis of multi-run data from physical simulations based on a number of aggregated plots and coordinated

interactions. A histogram-based plot allows for the investigation of the distribution of function values within

all simulation runs. A density-based time-series plot allows for the detection of temporal patterns and outliers

within the ensemble of multiple runs for single and multiple ﬁelds. A similarity-based plot allows for the

comparison of multiple or individual runs and their behavior over time. Coordinated views allow for linking

the plots to spatial visualizations in physical space. We apply MultiVisA to physical simulations from the ﬁeld

of climate research and astrophysics. We document the analysis process, demonstrate its effectiveness, and

provide evaluations involving domain experts.

1 INTRODUCTION

Simulations of time-varying phenomena over a 2D or

3D spatial domain are widely used in the ﬁeld of phy-

sics (among others) to test the respective mathema-

tical or computational models. The simulations ty-

pically depend on a number of parameter settings or

initial conditions. Since one of the research tasks is

to understand how the input settings inﬂuence the si-

mulation result, the simulations are run multiple ti-

mes with varying settings. Thus, researchers gather

multi-run spatio-temporal data with many runs and

many time steps, where each time step of each run

represents planar or volumetric data ﬁelds. The ana-

lysis of such a data set raises the challenges of efﬁ-

ciently handling the large amount of data and effecti-

vely comparing the outcome of multiple simulation

runs. Since it is not feasible to analyze all time steps

of all runs individually, one needs to aggregate infor-

mation about the entire ensemble of simulation runs.

Currently, in research communities dealing with

simulation ensembles, there is the lack of a uniﬁed ap-

proach for processing, navigation, feature detection,

and comparative analysis of entire ensembles. It is

common practice that researchers develop their own

ad-hoc solutions to their analysis tasks by develo-

ping scripts that stitch together existing tools for sol-

ving subproblems. Visualization methods are typi-

cally only used for the rendering of phenomena in

physical space, i.e., at the very end of the analysis

process. In this paper, we present MultiVisA, an ap-

proach to the interactive visual analysis of multi-run

spatio-temporal physical simulations that supports a

top-down analysis process of entire ensembles.

MultiVisA is based on three types of aggregated

plots linked with physical space visualizations and a

portfolio of interaction mechanisms. The plots in-

tuitively provide comprehensive information of the

simulation ensemble at different aggregation levels.

The ﬁeld distribution histogram aggregates ﬁeld value

occurrences over all time steps and all runs. This ﬁrst

overview allows the user to identify the relevant data

range for further analysis. The function plots aggre-

gated over all runs support multiple analysis steps re-

lated to time series. First, they allow for the detection

of relevant time steps and the synchronization of fea-

tures in multiple runs. This feature detection and se-

lection step restricts the subsequent analysis steps to

the relevant time intervals, which often reduces the

amount of data to be analyzed tremendously. Second,

Fofonov, A. and Linsen, L.

MultiVisA: Visual Analysis of Multi-run Physical Simulation Data using Interactive Aggregated Plots.

DOI: 10.5220/0006574300620073

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages 62-73

ISBN: 978-989-758-289-9

the function plots intuitively depict behavioral pat-

terns over time. The governing patterns and outliers

within the ensemble or within individual runs can be

detected. And, multiple coordinated function plots al-

low for an intuitive comparative analysis of multiple

ﬁelds. Finally, the function plots exhibit the range of

activity, which allows the user to identify representa-

tive isovalues for further analysis. This further ana-

lysis is supported by the multi-run plot, which is a

similarity plot based on isocontour similarity of dif-

ferent time steps of different runs. Hence, it allows

for a comprehensive understanding of the entire en-

semble of simulation runs by depicting each of them

as a polyline, where divergence or convergence of the

polylines indicate how much simulations differ over

time. Our plots are incorporated in one interactive

analysis tool using coordinated views, which includes

brushing and linking to physical space renderings.

The visual encodings and interaction mechanisms

provided by MultiVisA are described in Section 3,

while Section 4 is dedicated to documenting how

MultiVisA is applied to a top-down analysis of physi-

cal simulations. We chose two application scenarios

of quite different data characteristics. The ﬁrst appli-

cation provides multiple runs of astrophysical smoot-

hed particle hydrodynamics (SPH) simulations over

3D point-based spatial domains, where the runs differ

by setting different initial parameters. The second ap-

plication provides ensembles of climate simulations

over 2D gridded spatial domains with a set of diffe-

rent initial conditions. We show the effectiveness of

our analysis tool by documenting the processing pi-

peline of our approach, discussing the ﬁndings that

can be obtained at the various analysis stages, and re-

porting the feed-back from domain scientists.

2 RELATED WORK

Many approaches for the exploration and visualiza-

tion of time-varying data exist. They are based on

novel visual representations (Moere, 2004), exploring

derived spaces (Busking et al., 2010), volume visua-

lizations (Woodring and Shen, 2006), or coordinated

views (Akiba and Ma, 2007; Lee and Shen, 2009).

However, all these approaches only address single-

run data.

Recently, in (Phadke et al., 2012) some techni-

ques to support ensemble exploration and comparison

were proposed. These techniques are limited to com-

paring a small number of ensemble members at any

given time. The pairwise sequential animation techni-

que begins to suffer when more than three members

are shown. For the estimation of the uncertainty re-

presented by the simulations within an ensemble, in

othkow et al., 2011) authors proposed a method for

quantifying spatial uncertainty of isocontours consi-

dering arbitrary spatial correlations of the probability

distributions of the input data. In an approach presen-

ted by (Potter et al., 2009b), a collection of statistical

descriptors is used for analyzing ensemble data sets.

The same authors also presented “Ensemble-Vis”, a

framework consisting of a collection of overview and

linked statistical displays (Potter et al., 2009a). Si-

milarly, the “Noodles” approach has been developed

to interactively visualize ensemble output and asso-

ciated uncertainty of weather event datasets (Sanyal

et al., 2010). All these approaches are based on dis-

playing statistical information like mean and standard

deviation, which supports important analysis aspects,

but does not cover all analysis needs. In particular, the

inﬂuence of initial conditions cannot be evaluated.

In (Preston et al., 2016) authors present an inte-

ractive linked-view visualization system that focuses

on simultaneously exploring dark matter halos. De-

aling with large particle based simulation data it has

very narrow specialization on cosmology data look-

ing for a hierarchical tree-based structures. An appro-

ach for uncertainty-aware multidimensional ensemble

data visualization and exploration was recently pre-

sented by (Chen et al., 2015). Both approaches do

not allow for comparing behavior patterns of indivi-

dual simulations over time. An interactive approach

to enable a continuous analysis of a sampled parame-

ter space with respect to multiple target values was

investigated by (Berger et al., 2011). It is a suitable

approach for a certain frame analysis, but it does not

tackle spatio-temporal data. Follow-up studies such

as the one by (Konyha et al., 2012) looking into fami-

lies of curves also provide methods for the analysis of

non-spatial multi-run data.

In (Kehrer and Hauser, 2013) authors presented a

survey on multi-run multi-ﬁeld data visualization and

referred to the data as multi-faceted. They concluded

in their paper that: “The majority of the approaches

discussed in this survey speciﬁcally address one or

two facets of scientiﬁc data. What is often missing

are general concepts for handling the heterogeneity

of multi-faceted data (e.g., multi-run data are often

spatio-temporal and multi-variate as well)”. An ap-

proach presented by (Fofonov et al., 2016) tackles the

aspect of multi-run multi-ﬁeld spatio-temporal data

visualization and analysis, which allows for an explo-

ration of the parameter space in conjunction with the

physical space of the ﬁelds. For that an isosurface si-

milarity between the ﬁelds of different time steps and

different runs is used. However, to successfully apply

the approach, one needs to ﬁnd representative isole-

MultiVisA: Visual Analysis of Multi-run Physical Simulation Data using Interactive Aggregated Plots

vels sufﬁcient for capturing relevant information from

all simulation time steps.

Despite the availability of existing techniques,

most researchers who are trying to analyze their en-

semble simulations spend days or weeks to prepare

and analyze simulated data for further analysis. Usu-

ally they implement their own scripts (customized to

their needs) for data management, ﬁltering, naviga-

tion, feature detection, pattern detection, outlier de-

tection, etc. Quite frequently this even involves some

manual or semi-automatic steps. Hence, it is desi-

red to develop visual approaches that support such a

processing pipeline for an intuitive and more efﬁcient

analysis. After discussions with domain scientists of

different research areas within physics (namely, geo-

sciences and astrophysics) we identiﬁed general re-

quirements for the tools and methods for multi-run

data analysis, which led to the techniques and work-

ﬂow below.

3 VISUAL ANALYSIS OF

MULTI-RUN SIMULATION

DATA

Since the main purpose of executing multi-run simu-

lations is to capture the variety in the model with re-

spect to different initial settings or parameter selecti-

ons, an ensemble can consist of tens or even hundreds

of simulations. Despite the same nature of all runs

within an ensemble, their outcome may have high dis-

persion that needs to be investigated. Independent of

the simulation method (Eulerian or Lagrangian), the

spatial data structure (gridded or point-based), and the

purpose (impact of simulation parameters or model

evaluation), the visualization tasks can be identiﬁed

as (1) deﬁning visual encodings in the form of plots

that exhibit the proper level of aggregation and (2) de-

ﬁning interaction methods for operating on differently

aggregated plots and physical space renderings using

coordinated views. The MultiVisA system is shown

in Figure 1(a).

For the development of a successful analysis tool,

several characteristics of multi-run spatio-temporal

simulation have to be considered. First, the data size

frequently exceeds hundreds of Gigabytes, i.e., the

data set does not ﬁt into the main memory of a system.

Thus, every access to the entire data is extremely time

consuming. Even simple computations such as com-

puting the mean can take up to hours. Hence, aggre-

gated information plays an important role and being

able to concentrate on a region of interest (part of the

data) can substantially reduce the computational load.

Second, due to the multiple facets of multi-run data

(Kehrer and Hauser, 2013), different representations

are required to shed light on different aspects. Finally,

it is of interests to compare the simulations’ behavior

and evolution over time, which is complex task due to

the large number of simulation runs. Computing me-

ans is often not sufﬁcient, as behaviors of individual

runs may not be reﬂected anymore.

Having pointed out the challenges we are facing,

the analysis of multi-run spatio-temporal data can be

executed according to the following workﬂow:

1. Overview analysis of ﬁeld range distribution. In a

ﬁrst stage, one is interested in getting an overview

of the ensemble, which can be achieved by inves-

tigating the range of the considered data ﬁeld and

the distribution of ﬁeld values within the simula-

tion runs. Respective histograms allow for ﬁrst

conclusions and to narrow down the ﬁeld range

for subsequent analysis stages (see Section 3.1).

2. Analysis of ﬁeld distribution over time. In this

stage, one would like to investigate the change

within the simulation runs over time, which sup-

ports multiple important tasks. First, one can de-

tect features and the time intervals they occur,

which narrows down the time interval for further

analysis steps. Second, one can identify indivi-

dual ﬁeld values of interest, which can be furt-

her examined, e.g., by choosing them as isova-

lues. Third, one can detect overall patterns in the

ensemble as well as outliers. A run identiﬁed to

be of interest can also be observed individually as

well as in further analyses with physical domain

visualizations. Finally, one can also compare and

correlate different ﬁelds of a multi-ﬁeld data set at

this level (see Section 3.2).

3. Comparative analysis of individual runs. While

the second stage was operating on an aggregation

over multiple runs, this stage shall allow for a de-

tailed understanding of the behavior of individual

runs in a comparative view. Making appropriate

selections in the preceding stage (i.e., identifying

time interval and ﬁeld value of interest) allows for

an accurate and efﬁcient analysis approach (see

Section 3.3).

The overall structure of MultiVisA is illustrated

in Figure 1(b): Starting with the given data, the ana-

lysis pipeline is shown using orange arrows. First,

one extracts the ﬁeld histogram. Then, after selecting

a region of interest and a desired ﬁeld range, one

computes the function plots. Finally, after choosing

a representative time interval, the desired simulation

runs, and representative isovalues, one can generate

the multi-run plot. All the possible interactions bet-

ween different data representations including spatial

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

(a) Screenshot of MultiVisA (b) System structure

Figure 1: (a) MultiVisA: Interactive visual analysis system for physical simulations: (left) interaction panel for options and

data settings; (top middle) transfer function used for function plots; (top right) plot view used for ﬁeld distribution histograms

or function plots; (bottom right) similarity plot; (bottom middle) domain visualization. (b) System structure: orange arrows

show analysis pipeline, black arrows show possible interactions between different components.

domain rendering are shown using black arrows. Ba-

sed on this structure, we have designed our applica-

tion as shown in Figure 1(a).

3.1 Field Distribution Histogram

Assuming that the data to be analyzed have not

been studied yet and the simulation results are still

unknown, we propose to start with a simple overview

plot based on the estimation of the range of the inves-

tigated data ﬁeld and the analysis of the probability

distribution of the occurrence of the ﬁeld values. This

step allows us to detect simulations with outstanding

ﬁeld values and to deﬁne the main global data features

such as global ﬁeld range, shared ﬁeld range (i.e., the

intersection of the ranges of all simulation runs), or

values with high and low frequencies of occurrence.

The visual encoding is implemented by building a

histogram with ﬁeld values on the horizontal axis and

normalized frequencies of occurrence on the vertical

axis. The histogram aggregates information from all

points in space and time for all simulation runs. The

ﬁeld values from the intersection of the ranges of all

time steps of all runs are colored in green, values from

the intersection of ranges of all runs (but not from all

their time steps) are colored in blue, and values that do

not occur in all runs are colored in red, see Figures 3

and 12 (a) for examples discussed in Section 4.

The interaction mechanisms that support the ana-

lysis allows for the selection of individual ﬁeld va-

lues (using a vertical line), which reports back all si-

mulation runs where this ﬁeld value occurs, which is

particularly useful for investigating outliers. Also, it

is possible to visualize frequencies of occurrence of

the selected ﬁeld value over spatial domain (see Fi-

gure 12 (b,c)). Vice versa it is possible to select a

spatial region of interest and show the corresponding

ﬁeld histogram only for the selected region (see Fi-

gure 12 (d,e)). Moreover, the user can select a ﬁeld

range for further investigations by cutting intervals to

be neglected, which narrows down the analysis to a

region of interest.

3.2 Function Plot

At the next analysis stage, we aim at investigating

change over time. We propose to use function plots

that record how the ﬁeld values at the spatial data

samples vary over time for the simulation runs. The

plot represents the function values of each spatial data

sample of each simulation run as a piece-wise linear

graph of a time series. For the visual encoding, we ag-

gregate the time series lines over a 2D grid leading to

a 2D density histogram (effectively aggregating over

spatial positions and simulation runs). Then, we can

apply a transfer function to map the accumulated den-

sity values to color. An example of a function plot is

shown in Figure 1(a) (top right) when applying the

transfer function shown in Figure 1(a) (top middle).

We use this transfer function throughout the paper.

Note that the transfer function is applied to the range

of interest that was selected using the ﬁeld distribu-

tion histogram, i.e., the selection in the ﬁeld distribu-

tion histogram makes the visual representation of the

function plot more effective.

Function plots (or time histograms) have been

used before for time-varying scalar ﬁelds (Akiba

et al., 2006; Akiba and Ma, 2007; Buono et al., 2005;

Kehrer et al., 2008). We extend their application to vi-

sualize ensembles of simulations. Moreover, we want

MultiVisA: Visual Analysis of Multi-run Physical Simulation Data using Interactive Aggregated Plots

to point out that the underlying data structure is that

of piecewise linear curves that represent time series.

Consequently, we do not generate static histograms,

but can perform interactions on our plot. More preci-

sely, we can brush on the function plots to interacti-

vely select all curves that traverse a selected region

of interest and interactively update the plot to only

render the aggregated selected curves (see Figure 13).

Furthermore, we can interactively switch between ag-

gregating over all runs, a selected subset of runs, or

individual runs. When rendering function plots of

individual runs, brushing on the plot (see Figure 5)

triggers linked physical space visualizations of the

selection (see Figure 6). Vice versa, we can select

a spatial region of interest and report the respective

function plot only for the selected region. When ob-

serving multi-ﬁelds, we can produce one function plot

per ﬁeld, compare and correlate them with each other,

and have coordinated brushing and linking between

the multiple function plots (see Figure 13). Finally,

we can also select a speciﬁc region of interest for furt-

her analysis. In particular, when detecting a feature,

one can cut the time axis to a time interval that con-

tains the feature, which makes the subsequent analy-

sis steps more efﬁcient and effective. Also, we can

select a ﬁeld value for further analysis purposes (ba-

sed on similarity plots, see below) using a horizontal

line (see Figure 9).

Since we are typically dealing with a large amount

of runs with a high spatio-temporal resolution, we

have to accumulate many curves with many time steps

for the generation of a plot. To allow for their genera-

tion at interactive frame rates, we use a level-of-detail

representation of the curves coupled with progressive

rendering. The level-of-detail (LOD) approach uses

a hierarchical representation based on 1D Haar wave-

lets, where a sequence of values is successively de-

composed into a sequence of a coarser representation

and a sequence of detail coefﬁcients. The progres-

sive rendering approach accumulates all curves ﬁrst

at their coarsest resolution and reﬁnes the represen-

tation iteratively until the ﬁnest resolution is reached.

Moreover, using the LOD representation it is also pos-

sible to compute similarities between time series such

that when selecting a spatial region of interest we can

compute all other regions of the spatial domain with a

similar behavior (similar ﬁeld values) over the whole

simulation time (see Figure 15). This is possible by

setting a threshold for a maximum ﬁeld value devi-

ation from the values at the selected domain points

(e.g., in absolute ﬁeld values or in a relative percen-

tage of the ﬁeld range), such that points which have

their ﬁeld values for all the time steps within the deﬁ-

ned corridor are considered to be similar.

Figure 2: Schematic illustration of the similarity plot idea.

Curves represent simulation states over time, where distan-

ces between points on the curves represent dissimilarity of

corresponding simulation states.

3.3 Similarity Plot

In our third stage, we want to generate a visual enco-

ding that allows us to perform a comparative analysis

between the runs of an ensemble. Hence, we should

not anymore aggregate over the runs. The idea of the

proposed approach is to use time lines in a similarity

plot (or multi-run plot), where the similarity is measu-

red by looking at (2D or 3D) isocontours of individual

time steps. This plot is based on the work by (Fofonov

et al., 2016). Isocontours are known to be effective

ﬁeld descriptors and can capture the simulation states

within the physical domain for the runs at each point

in time. Since data are spatio-temporal, we investi-

gate for each ensemble member a sequence of discrete

time steps. The simulation state for every time step

is represented by an isocontour, where the respective

isovalue was identiﬁed in the preceding stage using

the function plots. Considering the isocontours of the

selected scalar ﬁeld, every ensemble member is repre-

sented by one thread, where the threads represent the

change of isocontours over time. Deﬁning an appro-

priate isocontour distance function, we can use pro-

jection methods to generate a similarity (or distance)

plot of all the samples to visualize the data. The points

in the projection can be connected by polylines accor-

ding to the threads they belong to. Figure 2 sketches

the idea by showing four polylines for four different

simulation runs in different colors (e.g. color-coded

according to a parameter value of the simulation). The

four polylines start from the same point, but diverge

over time, where proximity in the plot encode simila-

rity of the isocontours. Points which represent similar

simulation states are expected to be located closely

(i.e., occurrence in one simulation will cause a self-

intersection), while a great distance between points

represents a high dissimilarity.

To compute isocontour similarity, we use a quasi-

Monte Carlo (qMC) approach to estimate a degree of

volume matching between two isocontours. Based on

the volumes enclosed by the isocontours, we use a

Jaccard distance d(A, B) between isosurfaces A and B

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

deﬁned by

d(A, B) = 1 −

A∧B

A∨B

The qMC approach allows for fast computations by

evaluating the ﬁelds at a number of quasi-random

points. Then, M

A∧B

denotes the number of points

inside both isocontours (logical and) and M

A∨B

the

number of points inside of, at least, one of the isocon-

tours (logical or).

Having deﬁned a proper distance function, it is

possible to build a distance matrix (or dissimilarity

matrix) D = [d

i, j

] with pairwise distances between

isosurfaces of all time steps of all simulation runs.

Based on the distance matrix, we can apply a pro-

jection method to map the high-dimensional binary

vectors to a 2D or 3D visual space for the multi-run

plot, where the high-dimensional binary vectors re-

present the inside-outside information for each of the

qMC points. Many projection methods exist. Since

we want to create the plots at interactive rates, we took

the simplest and, thus, fastest multi-dimensional sca-

ling (MDS) approach by (Wickelmaier, 2003). The

detailed discussion of the similarity-plot generation

can be found in (Fofonov et al., 2016).

We also support a number of interaction mecha-

nisms on the similarity plot. First, instead of sho-

wing all runs, we can show a subset or even indivi-

dual ones (see Figure 11(c)). Also, parts of the plot

can be selected and a new projection of the selected

part can be generated. Since the precomputed simi-

larity matrix can be re-used, this remains interactive.

In particular, we can select one time step such that

the time lines reduce to points (see Figure 11(b)). We

can also select individual points on the time lines to

trigger a physical-space visualization either in a coor-

dinated view (see Figure 10) or in an embedded view

(see Figure 11(b)). Furthermore, we allow for swit-

ching between projections to 2D and 3D visual space

using two or three principal components. Alternati-

vely, one can only use one principal component as a

vertical axis in a 2D plot, where the horizontal axis

represents time (see Figure 11(a)).

4 CASE STUDIES

4.1 Astrophysical Simulations

To test the effectiveness of MultiVisA for the ana-

lysis of multi-run physical simulations, we executed

two case studies, where we apply the methods and

workﬂow as described above. The ﬁrst case study is

concerned with an astrophysical two-stars system of

Figure 3: Field distribution histogram (for astrophysical si-

mulation). Field values from the intersection of all time

steps’ ranges of all runs are colored in green, from the inter-

section of all simulations’ ranges (but not for all time steps)

in blue, otherwise red.

Figure 4: Function plot of the simulation of two stars both

with masses equal to 1.05 of the solar mass. Time steps

around 300 contain outliers in ﬁeld values and exhibit a sig-

niﬁcant change in the simulation structure, while before and

after this change almost steady patterns can be observed.

White Dwarfs. The ensemble consists of 45 simulati-

ons with two main parameters representing the mas-

ses of the two stars. Each simulation run consists from

400 to 1,300 time steps. Overall this data set contains

about 36, 000 time steps, which sums to approxima-

tely 170 GB of data.

Stage 1 - Field Distribution Histogram. We start

our analysis by computing the ﬁeld distribution histo-

gram for the scalar ﬁeld of Internal Energy as shown

in Figure 3. It is a simple plot, but nevertheless allows

for some ﬁrst interesting observations: (1) The distri-

bution is skewed towards the lower values. In fact,

only very few values are populating the upper half of

the histogram. The respective simulation runs can im-

mediately be identiﬁed as outliers by selecting the re-

spective regions in the histogram. (2) After having

identiﬁed the outliers, further analysis steps shall be

applied to a narrowed (more saturated) ﬁeld interval

that excludes the outliers. This will make the automa-

tic application of the transfer function in Stage 2 more

effective. (3) Higher values do not occur in all simu-

lation runs (red). The intersection areas (green and

blue) are rather small. Still, due to the smooth tran-

sition, the entire range up to the dashed line seems to

be of interest.

Stage 2 - Function Plot. In the second stage, we ope-

rate on the function plots. Figure 4 shows the function

plot for a single simulation run that was identiﬁed as

an outlier in Stage 1. In this simulation run, both stars

have the same mass. To observe the outlier values, we

did not apply the narrowing of the ﬁeld range from

MultiVisA: Visual Analysis of Multi-run Physical Simulation Data using Interactive Aggregated Plots

Figure 5: Function plot of the simulation of two stars with

different masses equal to 0.65 and 1.05 of the solar mass.

Same three phases can be distinguished as in Figure 4, but

additional feature can be observed for a hot matter. Inte-

ractive selection (shown in green) for coordinated view to

the linked physical domain visualization.

(a) (b) (c) (d)

Figure 6: Linked views of selections in Figure 5 in physical

domain. Selection (a) represents two separated stars. Se-

lection (b) shows that the shell of the core of one star is in

the same condition, while selection (c) shows that the mat-

ter of the other star is absorbed by the ﬁrst one. Selection

(d) shows the merged structure. Note that the representation

of the heavier star seems smaller, as it represents data points

with higher internal energy and therefore is only a core.

Stage 1. We can observe that there are very few ﬁeld

values with an internal energy greater than 3.0 and

that they occur around time step 300. Selecting those

outliers and investigating them in a coordinated phy-

sical space visualization, one can observe that they

belong to particles that transition from one star to the

other. When hitting the other star the internal energy

of these particles suddenly rises to high values, but

also very quickly drops down again.

Apart from the investigation of the outliers, Fi-

gure 4 clearly indicates that we can distinguish three

phases during the simulation. First, there is relati-

vely steady state up to a short period, where things

are changing (around time step 300), which is follo-

wed by another relatively steady state. Looking at

other simulation runs from the same ensemble, we

can observe a similar behavior pattern consisting of

three phases, but the distributions of ﬁeld values du-

ring the simulations are different. Figure 5 shows the

function plot for a simulation run where one of the

stars is much larger than the other (now the ﬁeld range

is cropped according to the observations in Stage 1).

When comparing Figures 4 and 5, we can observe an

additional feature. To further analyze this, we again

brush on the plot and investigate what corresponds to

those features in a coordinated physical space, see Fi-

gure 6. We observe that initially we have two stars (a)

in the ﬁrst phase. In the second phase, for the hea-

Figure 7: Function plot aggregated from all 45 astrophysi-

cal multi-run simulations without synchronization. General

structure cannot be recognized. Vertical discontinuities in-

dicate ends of simulations.

Figure 8: Result of automatic function plot synchronization

for the astrophysical multi-run simulation data. As opposed

to the unsynchronized representation in Figure 7, details of

the general structure (three phases) can be observed.

vier one we have a slightly increasing internal energy

(b), while the lighter star loses its mass and internal

energy (c). At these time steps when the stars are mer-

ging, the function plot allows us to easily and clearly

separate the matter of the two stars according to their

ﬁeld values. Finally, the lighter star is completely ab-

sorbed by the heavier star in the third phase (d).

As mentioned above, the three phases occur in

every simulation run. Moreover, the initial and the

ﬁnal phase are pretty static. Not much is happening

there. Indeed, from an astrophysical point of view, the

transitions between the phases is of interest. Hence,

one can crop most of the initial phase and the ﬁnal

phase without losing valuable information. Using our

function plots, we can interactively cut the simulation

runs to a small time interval that fully captures the

merging phase and only the end of the initial phase

and the beginning of the ﬁnal phase. Hence, it still

includes all transitions. Identiﬁcation of such time in-

tervals for multi-run simulations is crucial and usually

takes a signiﬁcant amount of time. With our tool, it

is possible to visually identify the time intervals and

manually crop to the desired time interval.

Using side-by-side comparisons, we can intuiti-

vely compare the function plots of two simulation

runs. When trying to get an overview of the entire

ensemble, we proposed to aggregate the information

of all runs in one plot. When comparing the two plots

in Figures 4 and 5 we observe that the merging pha-

ses occur at different time steps during the simulation.

This lies in the nature of the simulation, as the runs are

not synchronized and different runs even have diffe-

rent amount of time steps. Thus, when aggregating all

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

Figure 9: Function plot representing standard deviation

from Figure 8. Despite of similar structure of the ﬁeld dis-

tribution in all simulation runs in the ensemble, this plot

shows high deviations for lower ﬁeld values. Green hori-

zontal line indicates selection of representative ﬁeld value

used for isocontour similarity computation.

45 simulation runs without synchronization, we can-

not observe any general pattern, see Figure 7. Using

the manual cutting of our function plots as described

above, a manual synchronization of all runs is intui-

tively possible. Although this just requires a single

selection for each run, we still need to go through

all plots once. Hence, we considered that it may be

useful to automate this step. The idea is to synchro-

nize the plots by the merging phase and to apply a

respective shifting. The advantage of our method is

that such features can be estimated using image-based

processing. We simply identify the highest gradient

of the plot density, as it is reached in the merging

phase. Since the duration of this phase is different for

the runs, we take the center of the time interval of 20

time steps with the highest sum of gradients as our sy-

nchronization point. Figure 8 shows the function plot

aggregated over all simulations runs after automatic

synchronization. Now, we can also clearly observe

the three phases in this function plot.

Another feature of our function plot approach is

that it is not restricted to create this one representa-

tion of the data ﬁeld, but we can also derive further

ﬁelds. For example, when taking the function plot

aggregated over all synchronized runs as the average

mean, we can compute a plot representing the stan-

dard deviation. Figure 9 shows the result of such a

computation. We can see the beneﬁt of such a stan-

dard deviation plot. While the plot in Figure 8 did

not exhibit strong differences, the standard deviation

plot exhibits more clearly visible structures. Despite

the similar structure of the ﬁeld distribution in all the

simulation runs over the simulation time, we can ob-

serve that the highest deviation is present in the lowest

ﬁeld values. The reason is that in every simulation run

there is the same total number of data points, but des-

cribing different simulation states the proportion of

data points representing the considered ﬁeld range is

different. It means that a more detailed comparative

analysis is required to investigate, how the simulation

states differ in terms of physical structure. To do so,

we proceed to Stage 3 by choosing a representative

(a) Projection 3D view (b)

Figure 10: 3D similarity plot (a) with selected keyframes

displayed in linked views to the domain visualization (b-d).

ﬁeld value, i.e., a ﬁeld value which describes best the

important data features in each individual simulation

run. Selecting the ﬁeld value around 0.3, as shown

by the green horizontal line in Figure 9, we cover the

main part of the structure with the highest deviation

for all three simulation phases.

Stage 3 - Similarity Plot. Having cropped the time

intervals in Stage 2, which signiﬁcantly reduces the

amount of data to be handled, and having identiﬁed

a representative ﬁeld value, we can make use of that

ﬁeld value as the selected isovalue for the isosurface

similarity computation. Having computed the iso-

surface similarity matrix, we generate the similarity

plot. For the given application, we decided to gene-

rate a 3D similarity plot (see Figure 10 (a)), which can

be visually inspected using rotation and zooming. It

shows all 45 astrophysical simulations. The polylines

are color-coded using a continuous transfer function

that maps the simulation parameter of the star’s mass

to the hue of the color. Increasing ratio between the

stars’ masses leads to changing the color towards yel-

low. We can observe a clear structure in the 3D si-

milarity plot. Figure 10 (a) conﬁrms the ﬁnding from

Stage 2 that we have three simulation phases. When

selecting a point in the plot, the ﬁeld of the respective

time step of the respective run is displayed in the phy-

sical space visualization. Figures 10 (b-d) show the

physical space visualization of the selections made in

Figure 10 (a). The linked views represent the initial

phase (b), the merging phase (c), and the ﬁnal phase

(d). Moreover, when looking at the projection, we

can see that beside of the main behavior pattern there

is another repeating pattern, which produces a rotatio-

nal structure in the upper part of the projection. Inves-

tigating this feature using linked views for different

MultiVisA: Visual Analysis of Multi-run Physical Simulation Data using Interactive Aggregated Plots

(a) Projection, by time (b) MDS, one time step

Figure 11: (a) Plotting ﬁrst principal component of pro-

jection over time. (b) 2D similarity plot for one selected

time step with embedded physical space visualizations. (c)

Similarity plot of one selected simulation run after cropping

time interval. (d) Similarity plot of same selected simu-

lation run for the full time series but skipping every other

time step, which leads to down-sampling artifacts.

projection points it becomes clear, that this pattern is

due to the rotation of the stars around their center of

masses during the simulation.

Since we are displaying all simulation runs toget-

her, it is obvious that the visual complexity of the

plot increases with increasing number and duration

of the simulation runs. The similarity plot including

all geometry is meant to give an overview and exhi-

bit the main patterns. Interaction mechanisms such

as selecting, ﬁltering, navigating, and linking to the

physical space support further analysis purposes. Fi-

gure 11 (c) shows the selection of an individual run in

the similarity plot. We observe that the simulation re-

mains for longer time in the initial and the ﬁnal phase,

while the merging phase is represented by a short time

interval with a rapid change.

Another option we provided was to plot the ﬁrst

principal component of our projection against the

time dimension, see Figure 11 (a). The red-to-yellow

color map encodes the increasing value of the simula-

tion’s input parameter reﬂecting the ratio of the stars’

masses. Now, we can easily see that increasing ratio

between the stars’ masses leads to a shift of the lines

to lower positions in the projection. Hence, there is

a straight dependence between initial parameter and

a simulation behavior, which is documented by the

continuous color transition in the plot.

To investigate this phenomenon, we propose to

operate with the projections interactively. We can se-

lect certain parts of the similarity plot and recompute

the projection only considering the selection, i.e., not

selected points do not affect the projection result. Fi-

gure 11 (b) shows a recomputed projection for a se-

lected single time step from the end of simulation.

There is a clear triangular structure shown, where the

yellow points, which are representing stars with big-

gest mass difference (i.e. with the highest ratio), have

been grouped in the right corner, while more reddish

points are located on the opposite edge of the triangle.

In between, there is a color transition visible. To cor-

relate that to physical space, we chose the option of

embedded views, i.e., the physical space visualizati-

ons of selected points are embedded as small icons in

the similarity plot.

Domain Expert Feedback. We discussed the Multi-

VisA tool and its components with the domain expert

who generated the data set. We asked for advantages

and limitations of our approach and to comment on

the effectiveness or usefulness of our approach. The

main ﬁndings were:

• To identify simulation features within a whole en-

semble, researchers are using their own scripts

and subroutines, as even advanced applications

such as SPLASH (Price, 2007) do not provide

enough functionality. With our tool a multi-run

simulation analysis becomes easy to visualize and

it allows for a faster data investigation.

• The task of time alignment is one of the most time

consuming for the researchers. From expert’s ex-

perience to perform the alignment on an ensemble

of 250 runs one needs to spend couple of weeks,

while with our tool one can do it by a single click.

• Correct and precise time deﬁnition of the analyzed

features leads to increased accuracy of the analy-

sis steps. For example, one can signiﬁcantly in-

crease the quality of the MDS projection when

narrowing down the time interval. Figure 11 (d)

shows the same similarity plot as in (c), where in

ter time interval, while in (d) one could only use

every other time step of the full time series.

• The domain expert has been working on this data

set for a long time and knows it very well. Using

our tools he was able to recognize most of the

known data features in one session. Moreover, he

even identiﬁed some additional features for furt-

her investigation.

4.2 Climate Simulations

In the second application scenario we investigate an

ensemble simulation using a global climate simula-

tion model over one to three years with different ini-

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

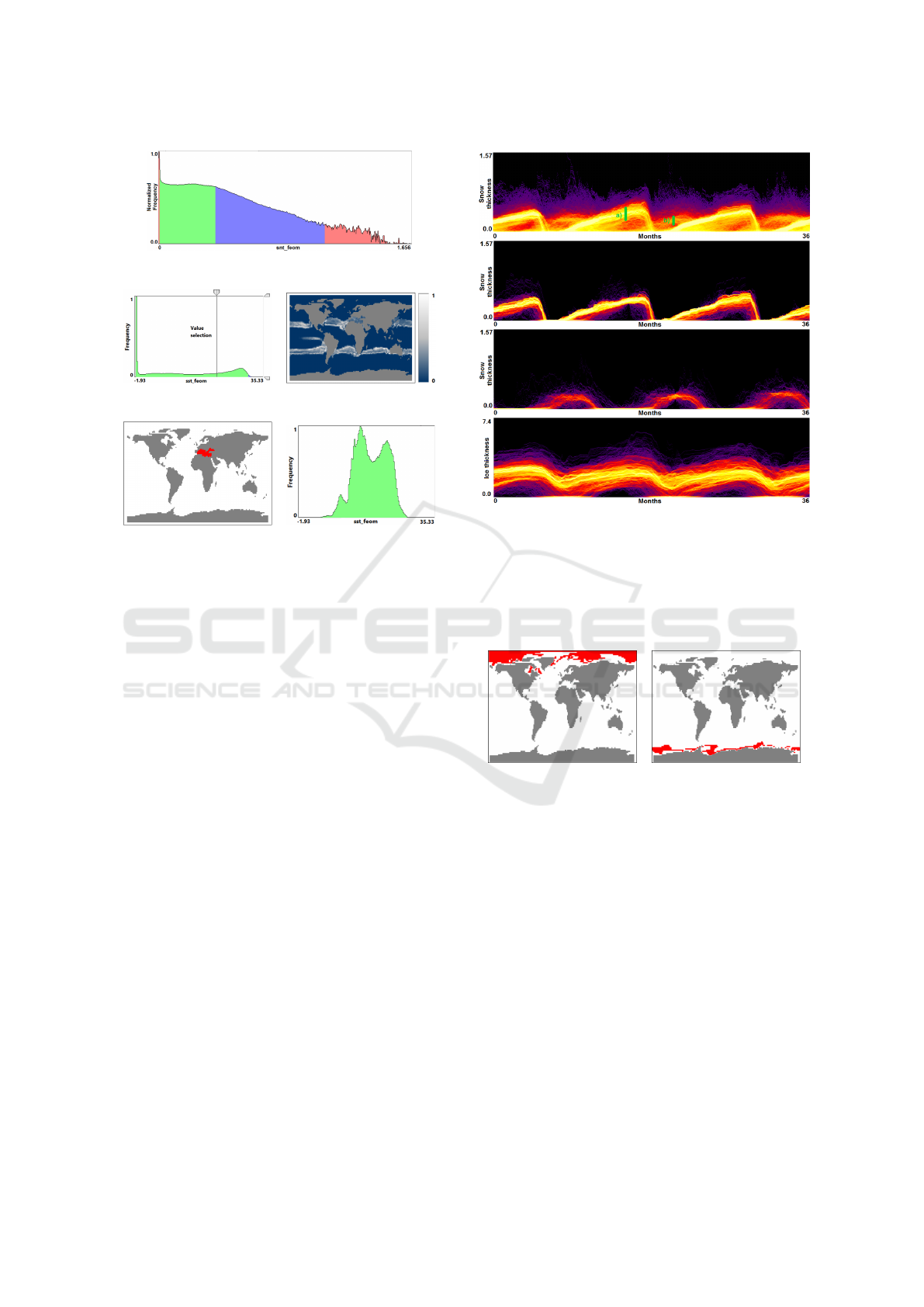
(a) Field histogram

(b) Value selection (c) Value’s appearance

(d) Area selection (e) Area’s histogram

Figure 12: (a) Field distribution histogram for sea snow

thickness in global climate simulation. (b) Interactive se-

lection of a ﬁeld value and linked visualization (c) of its

distribution of appearance. (d) Interactive selection of a

domain area and linked visualization (e) of its ﬁeld histo-

gram.

tial conditions. The 11 simulation runs have a dura-

tion of 1, 460 to 4, 380 time steps. The simulations

start at the same initial time, but are based on diffe-

rent initial conditions. The total data size is 23, 5 GB

and includes four different scalar ﬁelds: sea surface

temperature, sea ice thickness, sea ice concentration,

and sea snow thickness.

Computing of the ﬁeld distribution histogram for

sea snow thickness does not allow us to identify any

outlier (see Figure 12 (a)). Hence, we consider the

whole ﬁeld range for further analysis. When a cer-

tain ﬁeld value is of interest, it can be selected (see

Figure 12 (b)) and the distribution of the frequency of

occurrence of this value over spatial domain is rende-

red (see Figure 12 (c)). Vice versa, we can select a

spatial region of interest and show the histogram only

for that region (see Figures 12 (d, e)). Such interacti-

ons allow to estimate where and which isovalues can

be representatively used in a further analysis.

As it is of interest to analyze the multi-ﬁeld aspect,

we generate function plots for multiple ﬁelds. Since

the simulations are synchronized, we can immedia-

tely aggregate over all runs. Figure 1(a) shows the

function plot for sea ice thickness, Figure 13 (top) the

respective plot for sea snow thickness. In both plots

Figure 13: (top) Function plot for snow thickness aggrega-

ted over all climate simulation runs exhibits annual patterns

of 3 years, which are selected as shown in green. (middle)

Function plots for snow thickness when ﬁltering the trajec-

tories according to selections (a) and (b). (bottom) Function

plots for ice thickness (as in Figure 1) when ﬁltering the tra-

jectories according to selection (a).

(a) (b)

Figure 14: Coordinated views to physical space visualizati-

ons of selections in Figure 13 exhibit that selections corre-

spond to arctic region (a) and antarctic region (b).

we can observe the repeating annual pattern, but the

overall structure of the plots is different. To investi-

gate the plot in Figure 13, we made two selections.

We rendered the selected trajectories in the function

plot, see Figures 13 (middle) and in a coordinated

physical domain visualization, see Figure 14 (a, b).

We observe that the selections exhibit two annual pat-

terns, which correspond to high snow thickness va-

lues for the winter season in the arctic and antarctic

region, respectively. Our tool also allows for brushing

and linking between multiple function plots. Thus, in

Figure 13, the selection for snow thickness (second

from top) is transferred to ice thickness (bottom). We

can clearly observe the correlation between the two

patterns, yet there are visible differences. Another ap-

MultiVisA: Visual Analysis of Multi-run Physical Simulation Data using Interactive Aggregated Plots

Figure 15: (top) Function plot for sea surface temperature

aggregated over all climate simulation runs exhibits annual

patterns of 3 years. (middle) Interactive selection of spatial

region of interest (red) and display of similarly behaving

spatial regions (green) using information from the function

plot. (bottom) Function plot for sea surface temperature

when ﬁltering the trajectories according to selected area.

plication of the information from the function plots is

a search of similarly behaving points. In Figure 15

we select domain points which belong to Hudson Bay,

and using a small threshold for a desired deviation we

ﬁnd all the points with a similar change of the ﬁeld

value over the whole simulation time.

We also generate similarity plots for the ensem-

ble, see Figure 1 (bottom right). Annual patterns can

be observed again, but we also see that the runs differ

quite a bit for certain months (to the left), while they

are similar for other months (to the right). It is of inte-

rest to analyze, where in physical space the differen-

ces occur. We use the ﬁrst principal component of the

MDS projection plotted against time and compute the

plots considering arctic and antarctic regions separa-

tely, see Figure 16. One can observe that both regions

exhibit a seasonal pattern, but in the arctic (a) there

is no activity during the summer season, while in the

antarctic (b) there is activity throughout the year. Mo-

reover, the plot in (b) has higher variance and outliers,

which are candidates for further investigations.

Again, we discussed the application of our tool

with the domain expert who generated the data and

had the following ﬁndings:

• Visualization of the entire ensemble at once al-

lows for estimating the diversity of the simula-

tions’ behavior and identifying patterns and out-

liers.

(a) (b)

Figure 16: Plotting principal component of projection (ver-

tical axis) over time (horizontal axis) for all 11 simulations

when selecting arctic (a) and antarctic (b) region separately.

For isocontour similarity, we considered isovalue 0.25 of

sea snow thickness. We observe no activity during summer

months in (a), but activity throughout the year in (b). Note

that the metric for the distance computation returns absolute

values such that both plots are oriented the same way.

• A strong advantage is the option to easily estimate

activities of subregions. Usually one would need

to look at some physical domain visualization for

some selected time steps. Our tools leads to incre-

ased accuracy of feature detection.

• Estimating the inﬂuence of initial conditions to

the simulation result is usually performed in sen-

sitivity studies. A large number of statistical des-

criptors needs to be used. While it is complicated

to capture the behavioral differences with a sin-

gle value descriptor, our approach captures them

in a multidimensional fashion and allows for inte-

raction and navigation.

5 DISCUSSION AND

CONCLUSION

We presented MultiVisA, a visual analysis approach

for multi-run spatio-temporal data analysis in the con-

text of physical simulations. We identiﬁed the needs

of domain scientists to have a visualization tool that

supports early steps of the analysis process. Multi-

VisA uses plots at different aggregation levels to sup-

port the analysis workﬂow in a top-down manner. We

applied our tool for case studies in climate research

and astrophysics. We were able to perform effective

and efﬁcient analyses and got encouraging feedback

from the domain scientists saying that MultiVisA can

indeed improve their analysis tasks. All the proposed

algorithms were efﬁciently implemented using paral-

lelization on CPU and GPU where applicable, which

allowed for a smooth user experience during the inte-

ractive sessions using standard PCs or laptops.

The methods described in this paper scale quite

well, where steps early in the pipeline scale even bet-

ter than later ones, as the idea of the pipeline is to

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

reduce the amount of data to be analyzed from step

to step, which is important for a successful compara-

tive visualization at high interactivity. Hardware limi-

tations such as data reading speed from hard disk or

GPU memory size are the main bottle necks of our sy-

stem. One of the features of our system is that it works

equally well with data of any type and any spatial con-

ﬁguration. Thus, our general tools can be amended

for speciﬁc purposes.

ACKNOWLEDGMENTS

This work was funded by the Deutsche Forschungs-

gemeinschaft (DFG) under contract LI 1530/21-1.

REFERENCES

Akiba, H., Fout, N., and Ma, K.-L. (2006). Simultaneous

classiﬁcation of time-varying volume data based on

the time histogram. In Proceedings of the Eighth Joint

Eurographics / IEEE VGTC Conference on Visualiza-

tion, pages 171–178.

Akiba, H. and Ma, K.-L. (2007). A tri-space visualiza-

tion interface for analyzing time-varying multivariate

volume data. In Proceedings of the 9th Joint Euro-

graphics / IEEE VGTC conference on Visualization,

EUROVIS’07, pages 115–122.

Berger, W., Piringer, H., Filzmoser, P., and Gr

oller, E.

(2011). Uncertainty-aware exploration of continuous

parameter spaces using multivariate prediction. Com-

puter Graphics Forum, 30(3):911–920.

Buono, P., Aris, A., Plaisant, C., Khella, A., and Shnei-

derman, B. (2005). Interactive pattern search in time

series. In Proceedings of SPIE, volume 5669, pages

175–186.

Busking, S., Botha, C. P., and Post, F. H. (2010). Dynamic

multi-view exploration of shape spaces. In Procee-

dings of the 12th Eurographics / IEEE - VGTC confe-

rence on Visualization, EuroVis’10, pages 973–982.

Chen, H., Zhang, S., Chen, W., Mei, H., Zhang, J., Mer-

cer, A., Liang, R., and Qu, H. (2015). Uncertainty-

aware multidimensional ensemble data visualization

and exploration. IEEE Transactions on Visualization

and Computer Graphics, 21(9):1072–1086.

Fofonov, A., Molchanov, V., and Linsen, L. (2016). Vi-

sual analysis of multi-run spatio-temporal simulati-

ons using isocontour similarity for projected views.

IEEE Transactions on Visualization and Computer

Graphics, 22(8):2037–2050.

Kehrer, J. and Hauser, H. (2013). Visualization and vi-

sual analysis of multifaceted scientiﬁc data: A sur-

vey. IEEE Transactions on Visualization and Com-

puter Graphics, 19(3):495–513.

Kehrer, J., Member, S., Ladst

adter, F., Doleisch, H., Steiner,

A., and Hauser, H. (2008). Hypothesis generation in

climate research with interactive visual data explora-

tion. In IEEE Transactions on Visualization and Com-

puter Graphics, pages 1579–1586.

Konyha, Z., Le

z, A., Matkovi

c, K., Jelovi

c, M., and Hauser,

H. (2012). Interactive visual analysis of families of

curves using data aggregation and derivation. In Pro-

ceedings of the 12th International Conference on Kno-

wledge Management and Knowledge Technologies, i-

KNOW ’12, pages 24:1–24:8.

Lee, T.-Y. and Shen, H.-W. (2009). Visualization and explo-

ration of temporal trend relationships in multivariate

time-varying data. IEEE Transactions on Visualiza-

tion and Computer Graphics, 15(6):1359–1366.

Moere, A. (2004). Time-varying data visualization using

information ﬂocking boids. In IEEE Symposium on

Information Visualization, INFOVIS 2004, pages 97–

104.

Phadke, M. N., Pinto, L., Alabi, O., Harter, J., Taylor II,

R. M., Wu, X., Petersen, H., Bass, S. A., and Healey,

C. G. (2012). Exploring ensemble visualization. In

Proc. SPIE, volume 8294, pages 1–12.

othkow, K., Weber, B., and Hege, H.-C. (2011). Proba-

bilistic marching cubes. Computer Graphics Forum,

30(3):931–940.

Potter, K., Wilson, A., Bremer, P.-T., Williams, D., Dou-

triaux, C., Pascucci, V., and Johnson, C. (2009a).

Ensemble-vis: A framework for the statistical visuali-

zation of ensemble data. In IEEE Workshop on Kno-

wledge Discovery from Climate Data: Prediction, Ex-

tremes., pages 233–240.

Potter, K., Wilson, A., Bremer, P.-T., Williams, D., Dout-

riaux, C., Pascucci, V., and Johnson, C. (2009b). Vi-

sualization of uncertainty and ensemble data: Explo-

ration of climate modeling and weather forecast data

with integrated visus-cdat systems. Journal of Phy-

sics: Conference Series, 180(1).

Preston, A., Ghods, R., Xie, J., Sauer, F., Leaf, N., Ma,

K. L., Rangel, E., Kovacs, E., Heitmann, K., and Ha-

bib, S. (2016). An integrated visualization system

for interactive analysis of large, heterogeneous cos-

mology data. In 2016 IEEE Paciﬁc Visualization Sym-

posium (PaciﬁcVis), pages 48–55.

Price, D. J. (2007). Splash: An interactive visualisation

tool for smoothed particle hydrodynamics simulati-

ons. Publications of the Astronomical Society of Au-

stralia, 24:159–173.

Sanyal, J., Zhang, S., Dyer, J., Mercer, A., Amburn, P., and

Moorhead, R. J. (2010). Noodles: A tool for visua-

lization of numerical weather model ensemble uncer-

tainty. IEEE Transactions on Visualization and Com-

puter Graphics, 16(6):1421 – 1430.

Wickelmaier, F. (2003). An introduction to MDS. Aal-

borg Universitetscenter. Institut for Elektroniske Sy-

stemer. Afdeling for Kommunikationsteknologi. Rap-

port. Aalborg Universitetsforlag.

Woodring, J. and Shen, H.-W. (2006). Multi-variate, time

varying, and comparative visualization with contex-

tual cues. IEEE Transactions on Visualization and

Computer Graphics, 12(5):909–916.

MultiVisA: Visual Analysis of Multi-run Physical Simulation Data using Interactive Aggregated Plots