
The Shape of an Image
A Study of Mapper on Images
Alejandro Robles
1
, Mustafa Hajij
2
and Paul Rosen
2
1
Department of Electrical Engineering, University of South Florida, Tampa, U.S.A.
2
Department of Computer Science and Engineering, University of South Florida, Tampa, U.S.A.
Keywords:
Mapper, Contour Tree, Topological Data Analysis.
Abstract:
We study the topological construction called Mapper in the context of simply connected domains, in particular
on images. The Mapper construction can be considered as a generalization for contour, split, and joint trees on
simply connected domains. A contour tree on an image domain assumes the height function to be a piecewise
linear Morse function. This is a rather restrictive class of functions and does not allow us to explore the topology
for most real world images. The Mapper construction avoids this limitation by assuming only continuity on the
height function allowing this construction to robustly deal with a significantly larger set of images. We provide
a customized construction for Mapper on images, give a fast algorithm to compute it, and show how to simplify
the Mapper structure in this case. Finally, we provide a simple procedure that guarantees the equivalence of
Mapper to contour, join, and split trees on a simply connected domain.
1 INTRODUCTION
Recently, the study of data has benefited from the
introduction of topological concepts (Carlsson, 2009;
Carlsson et al., 2008; Carlsson et al., 2005; Collins
et al., 2004), in a process known as Topological Data
Analysis (TDA).
One of the most successful topological tools for
shape analysis is the contour tree (Boyell and Ruston,
1963). The contour tree of a scalar function, defi-
ned on a simply connected domain, can be thought of
as an efficient topological summary of that domain.
This structure is obtained by encoding the evolution of
the connectivity of the level sets induced by a scalar
function defined on the domain. Contour trees are of
fundamental importance in computational topology,
geometric processing, image processing and computer
graphics.
Contour trees are particularly useful for processing
massive data. Contour trees, and their more general
version Reeb graphs (Reeb, 1946), have been used
in numerous applications including shape understan-
ding (Attene et al., 2003), visualization of isosurfa-
ces (Bajaj et al., 1997), contour indexing (Boyell and
Ruston, 1963), image processing (Kweon and Kanade,
1994), data simplification (Carr et al., 2004; Rosen
et al., 2017b), and many other applications. Contour
tree algorithms can be found in many papers such as
(Takahashi et al., 2009; Rosen et al., 2017a) and Reeb
graphs algorithms are studied in (Shinagawa and Kunii,
1991; Doraiswamy and Natarajan, 2009).
Singh et al. proposed a method to understand the
shape of data using a topology-inspired construction
called Mapper (Singh et al., 2007). Since then, Mapper
has became one of the most popular tools used in TDA.
It has been applied successfully for various data related
problems (Lum et al., 2013; Nicolau et al., 2011) and
studied from multiple points of view (Carri
`
ere and
Oudot, 2015; Dey et al., 2017).
The construction of Mapper is closely related to
Reeb graphs and contour trees (Singh et al., 2007).
Indeed this construction can be considered as a genera-
lization of Reeb graph under some technical conditions
(Munch and Wang, 2015). The relation between Reeb
graph and Mapper has recently been made precise in
(Carri
`
ere and Oudot, 2015).
The true power of Mapper lies in its general des-
cription in terms of topological spaces and maps on
them. This abstract version of the construction is usu-
ally called topological Mapper. In the original work
where Mapper was introduced (Singh et al., 2007),
Mapper was applied to study the shape of point clouds.
This version of Mapper is now referred to as statistical
Mapper (Stovner, 2012). While topological Mapper
allows one to introduce the main ideas of Mapper in
general terms, statistical Mapper deals with aspects
Robles, A., Hajij, M. and Rosen, P.
The Shape of an Image - A Study of Mapper on Images.
DOI: 10.5220/0006574803390347
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages
339-347
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
339

related to point clouds, such as clustering and noise.
Similar technical aspects arise when trying to apply
Mappers on other domains, such as images.
The purpose of this article is to study Mapper on
specific domains, namely simply connected domains
and apply this study to images. While the focus of this
article is Mapper on images, we state the results whe-
never possible on a general simply connected domain.
1.1 Contribution
Mapper construction on images operates on a height
function defined on the image domain. The height
function can be a color channel or luminance of the
input image itself or the gradient magnitude of the
image, which is typically a compact and connected
region in
R
2
. After discussing the topological and
statistical versions of Mapper construction on image
domains, we relate this construction to the contour
tree algorithm that enables Mapper to realize contour,
merge, and split trees.
The method we propose here has multiple advan-
tages. Beside being theoretically justified, the con-
struction of Mapper is flexible and applicable to conti-
nuous scalar function defined on a simply connected
domain in any dimension. Contour tree algorithms on
simply connected domains assume the height function
on the domain to be piecewise linear Morse function.
While this class of function is useful for a wide vari-
ety of applications, it is rather restrictive for images
and it does not allow us to explore the topology for
most real world images without heavy preprocessing
of the image height function. Mapper construction
avoids this limitation by assuming only continuity on
the height function allowing this construction to ro-
bustly deal with a significantly larger class of images.
Moreover, Mapper naturally gives a multi-resolution
hierarchical understanding of topology of the under-
lying domain.
The approach we take to Mapper here is geared for
simply connected domains and, in particular, for ima-
ges. Using the properties of such domains, we provide
a fast construction algorithm. Finally, we provide a
simple algorithm that guarantees the equivalence of
Mapper construction to contour, join, and split trees
on a simply connected domain.
2 PRELIMINARIES AND
MOTIVATION
As mentioned in the introduction, Mapper is closely
related to the contour tree. This related structure moti-
vates the construction of Mapper.
(c)(b)(a) (d)
Figure 1: (a) Scalar function is segmented into (b) topologi-
cal regions by converting that scalar field into a (c) landscape,
using the intensity value for height. The connection of those
regions can be converted into a contour tree (d) that describes
the topology.
Contour Trees.
The contour tree of a scalar field, de-
fined on a simply connected domain, tracks the evolu-
tion of contours in that field and stores this information
in a tree structure. Each node in the tree represents a
critical point where contours appear, disappear, merge,
or split. Each edge corresponds to adjacent and topo-
logically equivalent contours. In essence, the contour
tree forms a topological skeleton that connects critical
points (i.e. local minima, maxima, and saddle points).
Figure 1 shows an example of the contour tree of a
scalar field defined on a 2d domain.
In practice, we usually want to compute contour
trees on a piecewise linear Morse function defined on
a simplicial complex. The mathematical framework
specified for contour tree does not apply directly on
such domains. The difficulty rises when one tries
to extract isosurfaces for a scalar value as the pre-
images of an scalar values may not be an isosurface
(Szymczak, 2005). Nonetheless several contour tree
algorithms have been proposed, but they all depend
some method of isosurface extraction. Hence two
different methods of isosurface extraction might lead
to two different contour trees.
Mapper.
The construction of Mapper avoids the pro-
blem of dealing with isosurfaces all together by fo-
cusing on portions of the range of the scalar field.
To illustrate this, consider the simple scalar function
f : X −→ [a, b]
example given in Figure 2. Cover
the range
[a, b]
by two overlapping intervals
A :=
(a −ε, c + ε)
and
B =: (c − ε, b + ε)
such that
c ∈ [a, b]
and
ε > 0
. Note the interval
A
and
B
cover the interval
[a, b] in the sense : [a, b] ⊂ A ∪ B.
Now, consider the inverse images
f
−1
(A)
and
f
−1
(B)
. Figure 2 (c) illustrates that
f
−1
(A)
consists of
two connected components
α
1
and
α
2
and
f
−1
(B)
con-
sists of a three connected components
β
1
,
β
2
and
β
3
.
Moreover, there are some overlaps between these con-
nected components. Namely, the intersections
α
1
∩ β
1
,
α
1
∩β
2
,
α
1
∩β
2
and
α
2
∩β
3
are non-empty. We record
the information of the connected components and their
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
340

b
a
X
f
B
A α
1
α
2
β
1
β
2
β
3
α
1
α
2
β
1
β
2
β
3
(a) (b) (c) (d)
Figure 2: The construction of Mapper on a 1d function. (a) A scalar function
f : X −→ [a, b]
. (b) The range
[a, b]
is covered by
the two intervals A, B. (c) This gives a decomposition of the domain X. (d) Mapper is constructed.
non-empty overlap by a graph structure. The nodes of
this graph represent the connected components and the
edges represent the non-empty intersection between
these components. The Mapper construction is the
graph associated to the function
f
and the cover
A, B
in this manner.
Mapper’s Relationship to Contour Trees.
One
can notice that this graph is very related to the contour
tree. Both the contour tree and Mapper essentially
track the same topological information in the scalar
field, but the way this information is encoded in each
one of them is different. The nodes of the contour
tree of a scalar field are represented by the critical
points the field and the edges represent the regions in
the domain where the are no topological change in
the contours. On the other hand the nodes in Map-
per represent connected regions in the domain and the
edges represent the connection between two different
connected components. Hence, the combination stores
when a topological change occur to the contour.
3 TOPOLOGICAL MAPPER
We now give the general definition of Mapper for a
continuous scalar function defined on a simply con-
nected domain.
Let
X
be a simply connected domain in
R
n
. We
will assume that
X
is compact and connected. A cover
of
X
is a collection of open sets
U = {U
i
}
i∈I
such
that
X ⊂ ∪
i∈I
U
i
.
I
here is any indexing set. The com-
pactness condition implies that we can always find
a finite cover for
X
. In the case of an image,
X
is a
compact simply connected subset of
R
2
. The
1
-
nerve
of
N
1
(U, X )
of
X
induced by the covering of
U
is a
graph with nodes are represented by the elements of
U
and edges represented by the pairs
A, B
of
U
such that
A ∩ B 6=
/
0
. The nerve of a space
X
can be thought of
as a topological skeleton of the underlying space. The
main idea of Mapper lies in the way of constructing
this cover using the range of a function
f
defined
on
X
. More precisely, a continuous scalar function
f : X −→ [a, b]
on
X
and a cover for the range of
f
give rise to a natural cover of
X
in the following way. A
cover for an interval
[a, b]
is finite collection of open in-
tervals
U = {(a
1
, b
1
), ..., (a
n
, b
n
)}
that cover
[a, b]
, i.e.
[a, b] ⊂ ∪
n
i=1
(a
i
, b
i
)
. Now take the inverse images of
each open set in
U
under the function
f
. The result is
U( f ) := { f
−1
((a
1
, b
1
)), ..., f
−1
((a
n
, b
n
))}
is an open
cover for the space
X
. The open cover
U( f )
can now
be used to obtain the
1
-nerve graph
M(X, f , U) :=
N
1
(X, U( f ))
. The Mapper construction is by defini-
tion the graph M(X, f , U).
3.1 Cover Resolution
For a fixed function
f
the graph
M(X, f , U)
depends
on the choice of the cover
U
of the interval
[a, b]
. This
idea of Mapper resolution can be made precise via
the notion of cover refinement (Munkres, 2000). Let
X
be a space and let
A
and
B
be two covers of
X
.
The cover
B
is a refinement a cover
A
if for each
element of
B
of
B
there is at least one element
A
of
A
such that
B ⊆ A
. If
B
is a refinement a cover
A
,
there is a embedding of the graph
N
1
(X, A)
inside the
graph
N
1
(X, B)
. That is there is one-to-one function
φ
that maps between the vertices sets
N
1
(X, A)
and
N
1
(X, B)
together with an assignment that assigns to
every edge
e = (u, v)
in
N
1
(X, A)
a path in
N
1
(X, B)
between
φ(u)
and
φ(v)
. See (Munkres, 2000). Figure 8
show examples
4
nested sequences of cover refinement
along with their corresponding graphs. This simple,
effective, way to give a multi-resolution Mapper is one
of its main advantages over contour tree.
4 TOPOLOGICAL MAPPER ON
IMAGES
In this section, we discuss the details of topologi-
cal Mapper on images that will be used in our algo-
The Shape of an Image - A Study of Mapper on Images
341

Figure 3: The two types of pixel adjacency relation.
rithm for the statistical Mapper on images discussed
in section 5. We assume that
f : X −→ [a, b]
is con-
tinuous height function defined on the image domain
X ⊂ R
2
.
4.1 Choosing the Cover
While the choice of cover for the Mapper construction
is flexible, certain covers that give rise to a non-
desirable tree structure. We describe an effective way
to construct the cover for the domain that will help in
computing Mapper efficiently.
Start by splitting the interval
[a, b]
into n subin-
tervals
[c
1
, c
2
], [c
2
, c
3
], ..., [c
n−1
, c
n
]
such that
c
1
= a
and
c
n
= b
. Choose
ε > 0
and construct a cover
U(ε, n) = {U
i
= (c
i
− ε, c
i+1
− ε)}
n−1
i=1
for the inter-
val
[a, b]
. We want to choose
ε
so that only adjacent
intervals intersect. The choice of
ε
should satisfies the
following conditions:
1.
The intersection
U
i
∩U
j
=
/
0
unless
j ∈ {i − 1, i, i +
1} for 2 ≤ i, j ≤ n − 2.
2. U
1
∩U
j
=
/
0
unless
j ∈ {1, 2}
and finally
U
n−1
∩
U
j
=
/
0 unless j ∈ {n − 2, n − 1}.
This choice of
ε
ensures that only adjacent inter-
vals intersect with each other. We denote
U
odd
to the
subset of
U
consisting of intervals with odd indices.
Similarly we define
U
even
to be the collection of open
sets
U
i
∈ U
such that index
i
is even. These cover
choices minimize the number of overlaps between the
cover elements.
4.2 Determining the Nodes
A node in Mapper is a connected component of
f
−1
((c, d))
, where
(c, d)
is an open interval in the
cover
U
of the range of
f
. Given a range
(c, d)
, in the
case of an image
X
, we want to find the those pixels in
X
whose pixel value lie in
(c, d)
. Given a region
R
in
an image
X
consisting of a collection of pixels whose
pixel value lie within the range
(a, b)
, we want to de-
termine the connected components in the
R
. Here one
needs to specify what exactly is meant by a connected
component in this context. The image
X
induces a
graph structure with nodes being the pixels and the
edges are determined by the local pixel adjacency rela-
tion. There are two common types of pixel adjacency
relations shown in Figure 3.
Using the graph on an image with either one
of the pixel adjacency relation conventions, we can
now consider the connected components of subgraph
consists of the pixels in a region
R
. A walk on
a graph
G
is a sequence of vertices and edges
(v
0
, e
0
, v
1
, e
1
, ··· , e
l−1
, v
l
)
such that
e
i
= [v
i−1
, v
i
] ∈
E(G)
. A graph is said to be connected if there is a
walk between any two vertices. A connected compo-
nent in a graph is a maximal connected subgraph. Fin-
ding connected components of a graph is well-studied
in graph theory and it can be found by in linear time
using either breadth-first search or depth-first search
(Hopcroft and Tarjan, 1971).
4.3 Determining the Edges
An edge in Mapper is created whenever two connected
components have non-trivial intersection. The cover
that we described for the range
[a, b]
in section 4.1 was
chosen to minimize the number of sets we check for
intersection. Namely the condition that we impose
on the cover of
[a, b]
ensures that only adjacent open
interval overlap. In other words, if
U
i
and
U
j
are two
open sets in the cover of
U(ε, n)
of the interval
[a, b]
,
then by the choice of the cover specified in section 4.1,
we check if the connected components of
f
−1
(U
i
)
and
f
−1
(U
j
)
intersect only when we know that
U
i
and
U
j
are adjacent to each other. This significantly reduces
the number of set intersections checked.
5 ALGORITHM
The creation of the Mapper graph is done in three
stages. First, all pixels in the image are labeled by the
cover they map to. Pixels with the same label are then
grouped by searching for all connected components
with the same label. This provides the nodes for the
Mapper graph. Next, the connected component regions
are scanned for overlaps. Every pair of overlapping
regions in the image corresponds to an edge connecting
the nodes in the Mapper graph. Finally, the third stage
simplifies the Mapper graph by removing nodes with
two valencies.
5.1 Node Finding
In our approach, pixel labeling is done using a pair of
lookup tables, one for the even cover
U
even
and one for
the odd cover
U
odd
. When a lookup table maps outside
of its set of covers, it returns a value that signifies that
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
342

Region 1
Region 2
Candidate Pixels
in Region 2
Figure 4: Line scanning for candidate pixels.
the pixel does not map to a cover in this table. This
even/odd separation has an important benefit that when
one lookup table is applied to the image, none of the
resulting regions overlap. This means that instead of
processing the image for each covering one-by-one,
the image only needs to be processed twice, once for
U
even
and once for
U
odd
, to find all the connected
regions.
Breadth-first search (BFS) is used to find connected
regions once the pixels have been labeled. By taking
advantage of the queue structure of BFS, every pixel
in a connected region can be traversed before moving
onto the next region as long as only the top of the
queue is being modified. This continuity of the search
allows us to add pixels in other regions to the same
queue, thus allowing processing many regions with
one search. As a region is traversed, pixels are marked
with an identification unique to that region. In our
implementation, this identification is created using the
position of the first pixel in the region touched during
the search.
Input EvenOdd Overlap
Figure 5: Region search is done twice, once for even and
once for odd covers. Here, each region identified during the
search is given a unique color. If a pixel is not found to map
to a cover during the search the, pixel is not colored (these
are the pixels colored in black in the middle two images).
This shows how splitting the covers gives a pair of images
which do not contain overlapping regions. Regions in one
image will, however, overlap with regions in the other image,
as shown in the image on the bottom right.
Our approach initializes the BFS queue with can-
didate pixels which are pixels found by scanning each
row in the image from left to right until a pixel, which
differs in label from the previous pixel is found (see
Figure 4). This gives the pixels that start a region along
every line in the image. Since a region needs at least
one pixel to be in the queue at the start of the search,
the use of candidate pixels ensures each region in the
Figure 6: Simplification of the mapper graph.
image will be traversed, while reducing the number of
pixels in the queue at the start of the search.
At the end of the search, every pixel will have an
associated identification that represents the connected
component region it belongs to. Finally, these regions
define the nodes in the Mapper graph. See Figure 5
for illustration of the process of node finding done on
an example image.
5.2 Edge Finding
Once the regions in the image have been identified
for both the even and odd covers, overlaps between
regions need to be found. A naive approach would be
to create a set of pixel locations for every region in
both sets of coverings, and check whether pairs of sets
are disjoint. This type of approach, however, requires
every pair of sets to be tested for disjointness, making
it inefficient.
To determine region overlap, we take advantage
of the candidate pixels found during node finding, see
Figure 4. Since these pixels signifies the entrance of a
region with a different labeling, this means that there
are two different regions from the two opposing covers
overlap. Notice that this method takes advantage of
the way we construct the cover in section 4.1.
5.3 Graph Simplification
The resulting Mapper graph can contain thousands
of nodes. Many of these nodes can be removed as
they do not indicate topological events. In the Mapper
graph, a node with valency equal to
2
corresponds to
a region where no topological event occur. In other
words, such a node is not a merge, split, creation, or
termination of a region. These nodes are analogous to
regular points in the contour tree. Hence, these nodes
can be safely removed to obtain a simplified graph,
such as in Figure 6.
6 REALIZING THE CONTOUR
TREE
The Mapper construction can be used to realize the
contour tree. Here we give a choice of covering that
The Shape of an Image - A Study of Mapper on Images
343

guarantees that Mapper gives rise to all the topological
information encoded in the contour tree. We need to
assume that the given function is a piecewise linear
Morse function
f : X −→ [a, b]
on a simply connected
domain
X
. The assumption of piecewise linear Morse
is necessary in order to work with a contour tree. For
precise definitions related to Morse theory on simpli-
cial complex see (Pascucci et al., 2004).
Recall that every node in the contour tree corre-
sponds to a critical point. The critical point of a
function signifies a topological change in the space
X
with respect the scalar function. Moreover, if
t
1
and
t
2
are two consecutive critical values
f
then for
any two values
c
1
, c
2
∈ (t
1
,t
2
)
the number of connected
components of both
f
−1
(c
1
)
and
f
−1
(c
2
)
are the same.
In other words, a topological change that occur to the
space only when as we sweep though a critical value.
Hence, in order for Mapper to give us the information
encoded in the contour tree, it is sufficient to make a
choice of the covering on
[a, b]
, so that we store the
following information:
1.
The number of connected components between
every two consecutive critical values of f .
2.
The way the connected components merge, split,
appear, and disappear when passing through a cri-
tical point.
The following procedure gives a choice of covering
for [a, b] that satisfies the previous two criteria:
1.
Let
t
1
,t
2
, ...,t
n
be the critical values for
f
ordered
in an ascending order. Let
p
1
, p
2
, ..., p
n
be the
corresponding critical points of f .
2.
For each
1 ≤ i ≤ n − 1
, we choose four numbers
a
i
b
i
, c
i
and
c
i
in the interval
[t
i
,t
i+1
]
such that
a
i
<
d
i
< c
i
< b
i
.
3. Let c
0
= a − ε and let d
n
= b + ε for some ε > 0.
4.
Let
U
be the covering of
[a, b]
consisting of
the intervals
(a
1
, b
1
), ..., (a
n−1
, b
n−1
)
as well as
(c
0
, d
1
),(c
1
, d
2
),...,(c
n−1
, d
n
).
Notice that the Mapper construction obtained using
the covering
U
stores all the topological information
encoded in the function
f
. Hence, any further refine-
ment of the covering
U
will not produce any further
details in the Mapper construction as far as the topo-
logy of the original domain is concerned. In other
words, the above construction gives the highest Map-
per resolution that one could obtain on a piecewise
linear Morse function.
7 JOIN AND SPLIT TREES
The previous sections describe how Mapper can be
used to obtain a contour tree. The Mapper construction
is general and can be used to realize other structures
such as the join and split trees (Carr et al., 2003).
The only change one needs to make to the previous
setup is making a different choice for the shape of the
open interval that makes covering of the range. These
choices will be justified after we illustrate the basic
ideas of join/split trees.
For a continuous scalar function
f : X −→ [a, b]
defined on a simply connected domain
X
the split tree
ST ( f , X)
of
f
on
X
tracks the topological changes
occur of the set
{p ∈ X | f (p) ≥ c}
of a value
c
as this
value is swept from
∞
to
−∞
. Similarly, the join tree
JT ( f , X)
of
f
on
X
tracks the topological changes
occur to the topology of the set
{p ∈ X| f (p) ≤ c}
as
the value
c
goes from
−∞
to
∞
. The Mapper con-
struction can be used to compute both split and join
trees on any simply connected domain. The only thing
that must be chosen to obtain these structures is the
shape of the open intervals for the covering
U
of range
[a, b].
The choice of covering for a join tree should be
of a collection of open intervals of the form
(−∞, c)
that covers the interval
[a, b]
. That is, the cover
must be a finite set
{(−∞, c
1
), ..., (−∞, c
n
)}
such that
[a, b] ⊂ ∪
n
i=1
(−∞, c
i
)
. As the values to
c
i
increases,
only merging events occur in the set
{p ∈ X| f (p) ≥ c}
,
which is reflected in the resulting Mapper graph. On
the other hand, the choice of covering needed to con-
struct the split tree is a collection of open intervals of
the form (c, ∞).
8 RESULTS
To demonstrate how our work performs we run a few
experiments on some images with various complexi-
ties. Figure 7 shows the illustrative examples on some
images. The height functions chosen on these images
are the input images themselves. The figure shows
the images along with the Mapper graph on drawn on
the top of them. The vertical position of the node is
chosen to be the average of the pixel values of the re-
gion that corresponds to that node. On the other hand
the
(x, y)
position of a node is the center mass of the
pixel positions of the pixels in the region. The size of
the node is proportional to the number of pixels in the
corresponding connected component.
In Figure 8 we show how multiple refinement of
covering give rise to a hierarchy of Mapper on the
same image. The graphs in the figure, shown from left
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
344
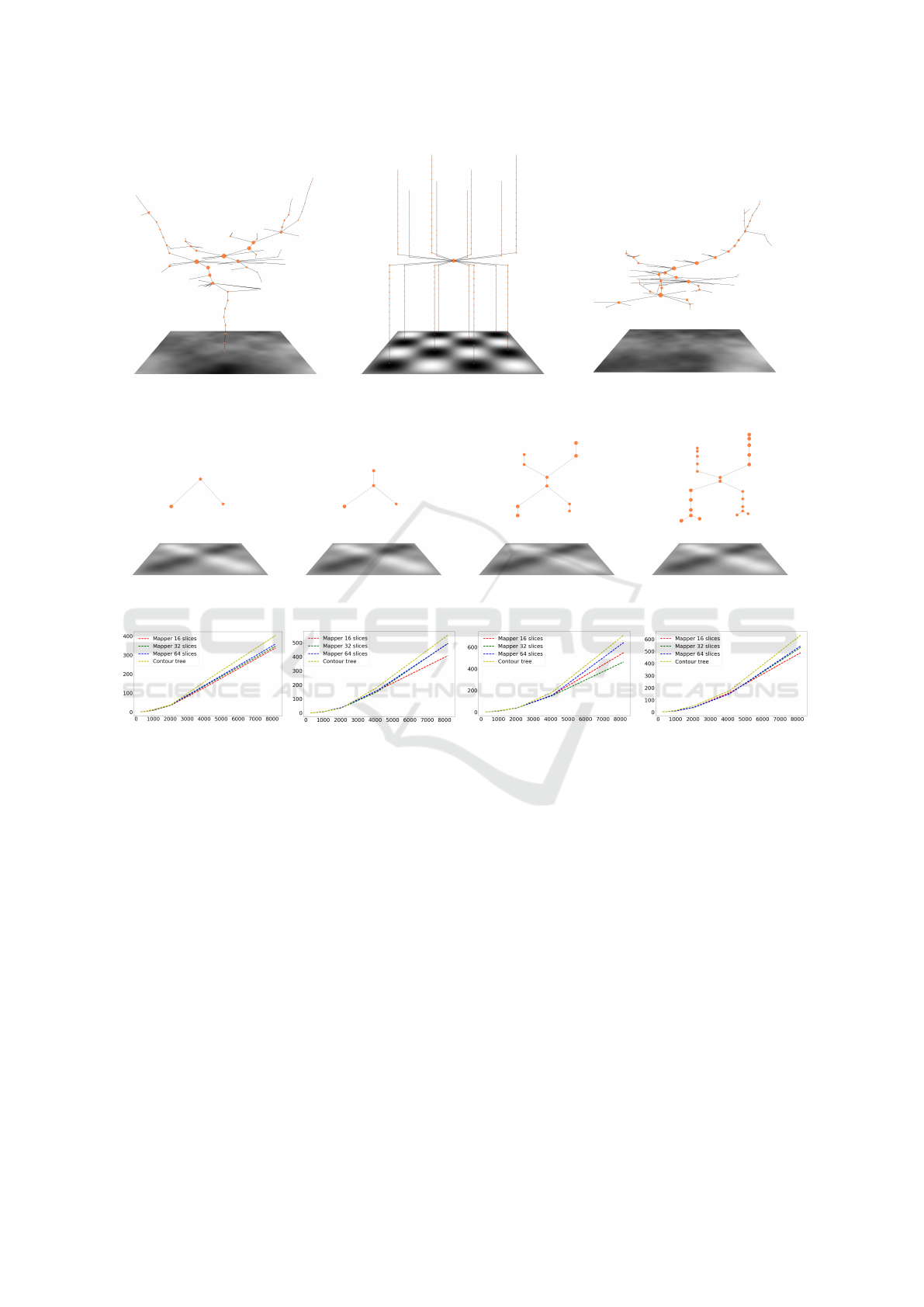
Figure 7: Examples of Mapper on images using pixel values as the height function. The range of these images was covered by
a cover of 32 open sets.
Figure 8: Multi-resolution of Mapper using different covering resolutions. The graphs are constructed from left to right by
using 2, 4, 8, 16 slices of the range covering.
Figure 9: Performance analysis of Mapper in comparison with contour tree on procedurally and non-procedural images. Each
image was done with the resolutions :
256
2
, 512
2
, 1024
2
, 2084
2
, 4096
2
,
and
8192
2
. Each resolution was tested against Mapper
and contour tree. Mapper was tested using
16
,
32
, and
64
cover slices. The
x
-axis represents the square root of the resolution of
the image. The y-axis represents the running time in milliseconds.
to right, are generated by using
2, 4, 8, 16
slices of the
covering. The figure shows immediately the effect of
cover refinement of the resolution and level of details.
8.1 Running Time
We tested our algorithm on a
3.7
GHs AMD with
a
16
GB of memory. We implemented the results
shown in Figures in Java and tested them on the Win-
dows platform. We tested the running time of the
algorithm against two parameters : changing number
of slices in the covers and increasing the resolution of
the image. We performed the tests on procedural and
non-procedural images. See Figure 9 for the perfor-
mance analysis. We also ran a comparison between
the Mapper algorithm we present here and a contour
tree algorithm. The contour tree algorithm we used is
a version of algorithm given in (Carr et al., 2003).
While both contour tree and Mapper give almost
identical performance for images with small resoluti-
ons, Mapper outperforms contour tree as we increase
the resolution of on the image. See Figure 9.
One can notice here that the performance computa-
tion time of Mapper increase linearly with the increase
of number of slices in the cover. Moreover, observe
in Figure 9 that Mapper computes faster than contour
tree even when we choose to calculate it on the highest
resolution.
9 LIMITATIONS
Mapper assumes the underlying height function to be
continuous. If the provided function is not continuous
The Shape of an Image - A Study of Mapper on Images
345

Figure 10: Mapper on an image with a discontinuous height
function is not guaranteed to produce a tree.
Mapper still produces a graph, but it is no longer gua-
ranteed that this graph is a tree. Figure 10 an example
of an image whose height function is discontinuous.
Depending on the application at a hand this limi-
tation of Mapper could potentially be used for image
understanding. As illustrated in Figure 10 the graph
captures the ”shape” in the underlying image.
10 CONCLUSIONS
We introduce the study of Mapper on simply connected
domains, in particular 2d images. On simply con-
nected domains, the Mapper construction generalizes
contour, split, and join trees. Our work here uses the
properties of the image domain to obtain a customi-
zed algorithm for Mapper on images, which we show
to have advantages in making the graph calculation
more efficient. The algorithmic aspects to deal with
additional domains have also been addressed in this
work. We plan to investigate such directions more in
the future.
ACKNOWLEDGEMENTS
This work was supported in part by a grants from
the National Science Foundation (IIS-1513616) and
(OAC-1443046).
REFERENCES
Attene, M., Biasotti, S., and Spagnuolo, M. (2003). Shape
understanding by contour-driven retiling. The Visual
Computer, 19(2):127–138.
Bajaj, C. L., Pascucci, V., and Schikore, D. R. (1997). The
contour spectrum. In Proceedings of the 8th Confe-
rence on Visualization’97, pages 167–ff. IEEE Compu-
ter Society Press.
Boyell, R. L. and Ruston, H. (1963). Hybrid techniques
for real-time radar simulation. In Proceedings of the
November 12-14, 1963, fall joint computer conference,
pages 445–458. ACM.
Carlsson, G. (2009). Topology and data. Bulletin of the
American Mathematical Society, 46(2):255–308.
Carlsson, G., Ishkhanov, T., De Silva, V., and Zomorodian,
A. (2008). On the local behavior of spaces of natu-
ral images. International journal of computer vision,
76(1):1–12.
Carlsson, G., Zomorodian, A., Collins, A., and Guibas, L. J.
(2005). Persistence barcodes for shapes. International
Journal of Shape Modeling, 11(02):149–187.
Carr, H., Snoeyink, J., and Axen, U. (2003). Computing con-
tour trees in all dimensions. Computational Geometry,
24(2):75–94.
Carr, H., Snoeyink, J., and van de Panne, M. (2004). Sim-
plifying flexible isosurfaces using local geometric me-
asures. In Visualization, 2004. IEEE, pages 497–504.
IEEE.
Carri
`
ere, M. and Oudot, S. (2015). Structure and sta-
bility of the 1-dimensional mapper. arXiv preprint
arXiv:1511.05823.
Collins, A., Zomorodian, A., Carlsson, G., and Guibas, L. J.
(2004). A barcode shape descriptor for curve point
cloud data. Computers & Graphics, 28(6):881–894.
Dey, T. K., Memoli, F., and Wang, Y. (2017). Topological
analysis of nerves, reeb spaces, mappers, and multis-
cale mappers. arXiv preprint arXiv:1703.07387.
Doraiswamy, H. and Natarajan, V. (2009). Efficient algo-
rithms for computing reeb graphs. Computational Ge-
ometry, 42(6):606–616.
Hopcroft, J. and Tarjan, R. (1971). Efficient algorithms for
graph manipulation. Technical report, STANFORD
UNIV CALIF DEPT OF COMPUTER SCIENCE.
Kweon, I. S. and Kanade, T. (1994). Extracting topographic
terrain features from elevation maps. CVGIP: image
understanding, 59(2):171–182.
Lum, P., Singh, G., Lehman, A., Ishkanov, T., Vejdemo-
Johansson, M., Alagappan, M., Carlsson, J., and Carls-
son, G. (2013). Extracting insights from the shape
of complex data using topology. Scientific reports,
3:1236.
Munch, E. and Wang, B. (2015). Convergence between
categorical representations of reeb space and mapper.
arXiv preprint arXiv:1512.04108.
Munkres, J. R. (2000). Topology. Prentice Hall.
Nicolau, M., Levine, A. J., and Carlsson, G. (2011). To-
pology based data analysis identifies a subgroup of
breast cancers with a unique mutational profile and ex-
cellent survival. Proceedings of the National Academy
of Sciences, 108(17):7265–7270.
Pascucci, V., Cole-McLaughlin, K., and Scorzelli, G. (2004).
Multi-resolution computation and presentation of con-
tour trees. In Proc. IASTED Conference on Visualiza-
tion, Imaging, and Image Processing, pages 452–290.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
346

Reeb, G. (1946). Sur les points singuliers d’une forme
de pfaff completement intergrable ou d’une fonction
numerique. Comptes Rendus Acad.Science Paris,
222:847–849.
Rosen, P., Tu, J., and Piegl, L. (2017a). A hybrid solution to
calculating augmented join trees of 2d scalar fields in
parallel. In CAD Conference and Exhibition.
Rosen, P., Wang, B., Seth, A., Mills, B., Ginsburg, A., Ka-
menetzky, J., Kern, J., and Johnson, C. R. (2017b).
Using contour trees in the analysis and visualiza-
tion of radio astronomy data cubes. arXiv preprint
arXiv:1704.04561.
Shinagawa, Y. and Kunii, T. L. (1991). Constructing a reeb
graph automatically from cross sections. IEEE Com-
puter Graphics and Applications, 11(6):44–51.
Singh, G., M
´
emoli, F., and Carlsson, G. E. (2007). Topo-
logical methods for the analysis of high dimensional
data sets and 3d object recognition. In SPBG, pages
91–100.
Stovner, R. B. (2012). On the mapper algorithm: A study of
a new topological method for data analysis. Master’s
thesis, Institutt for matematiske fag.
Szymczak, A. (2005). Subdomain aware contour trees and
contour evolution in time-dependent scalar fields. In
Shape Modeling and Applications, 2005 International
Conference, pages 136–144. IEEE.
Takahashi, S., Fujishiro, I., and Okada, M. (2009). Ap-
plying manifold learning to plotting approximate con-
tour trees. IEEE Transactions on Visualization and
Computer Graphics, 15(6):1185–1192.
The Shape of an Image - A Study of Mapper on Images
347
