
Graph-Cut Segmentation of Retinal Layers from OCT Images
Bashir Isa Dodo, Yongmin Li, Khalid Eltayef and Xiaohui Liu
Department of Computer Science, Brunel University, U.K.
Keywords:
Retinal Layer Segmentation, Optical Coherence Tomography, Graph-Cut.
Abstract:
The segmentation of various retinal layers is vital for diagnosing and tracking progress of medication of var-
ious ocular diseases. Due to the complexity of retinal structures, the tediousness of manual segmentation and
variation from different specialists, many methods have been proposed to aid with this analysis. However
image artifacts, in addition to inhomogeneity in pathological structures, remain a challenge, with negative in-
fluence on the performance of segmentation algorithms. Previous attempts normally pre-process the images or
model the segmentation to handle the obstruction but it still remains an area of active research, especially in re-
lation to the graph based algorithms. In this paper we present an automatic retinal layer segmentation method,
which is comprised of fuzzy histogram hyperbolization and graph cut methods to segment 8 boundaries and
7 layers of the retina on 150 OCT B-Sans images, 50 each from the temporal, nasal and centre of foveal re-
gion. Our method shows positive results, with additional tolerance and adaptability to contour variance and
pathological inconsistency of the retinal structures in all regions.
1 INTRODUCTION
Segmentation is the separation of images into more
meaningful information based on similarity or differ-
ence, continuity or discontinuity. Segmentation using
graph cut methods, depends on assignment of appro-
priate weight. The paths obtained by the default short-
est path algorithms, have no optimal way of handling
inconsistencies (such as the irregularity in OCT im-
ages), as thus it sometimes obtains the wrong paths,
which we call the ”wrong short-cuts”. To avoid the
wrong short-cuts, we reassign the weights to promote
the homogeneity between adjacent edges using fuzzy
histogram hyperbolization. In other words, the edges
with high value get higher weights, while those with
low values become lower. The idea behind this is that,
the transition between layers of OCT images which
are from dark to light or vice versa are improved. This
means we can better identify the layers by searching
for the changes or transitions between layer bound-
aries. Additionally, we take into account the transition
between the layers is in most cases very smooth, mak-
ing it quite difficult to segment the layers. Now if we
re-emphasize on this changes, such that they become
clearer, this aids the algorithm in successful segmen-
tation and avoiding wrong short-cuts.
In this paper we take into account the effect of pro-
moting continuity and discontinuity, in addition to
adding hard constraints based on the structure of
retina to segment 7 retinal layers including the Nerve
Fibre Layer (NFL), the Ganglion Cell to Layer-Inner
Plexiform Layer(GCL+IPL), the Inner Nuclear Layer
(INL), the Outer Plexiform Layer (OPL), the Outer
Nuclear Layer to Inner Segment (ONL+IS), the Outer
Segment (OS) and the Retinal Pigment Epithelium
(RPE) by detecting eight (8) layer boundaries. The
locations of these layers and boundaries in an OCT
image are illustrated in Fig.1.
This paper is organized as follows. In Section 2,
we review background information on the Graph-Cut
segmentation method and the previous work in retinal
layer segmentation. Section 3 describes the proposed
segmentation method. Section 4 presents experimen-
tal results on 150 OCT images. Finally conclusions
are drawn in Section 5.
2 BACKGROUND
2.1 The Graph-Cut Method
Graph-Cut is an optimization method used in solving
many image processing and computer vision prob-
lems, as first reported by (Seheult et al., 1989), where
the problem is represented as a graph. A graph G is
a pair (ν, ε) consisting of a vertex set ν (referred to
as nodes in 2D or Vertex 3D nested grid) and an edge
Dodo, B., Li, Y., Eltayef, K. and Liu, X.
Graph-Cut Segmentation of Retinal Layers from OCT Images.
DOI: 10.5220/0006580600350042
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 2: BIOIMAGING, pages 35-42
ISBN: 978-989-758-278-3
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
35
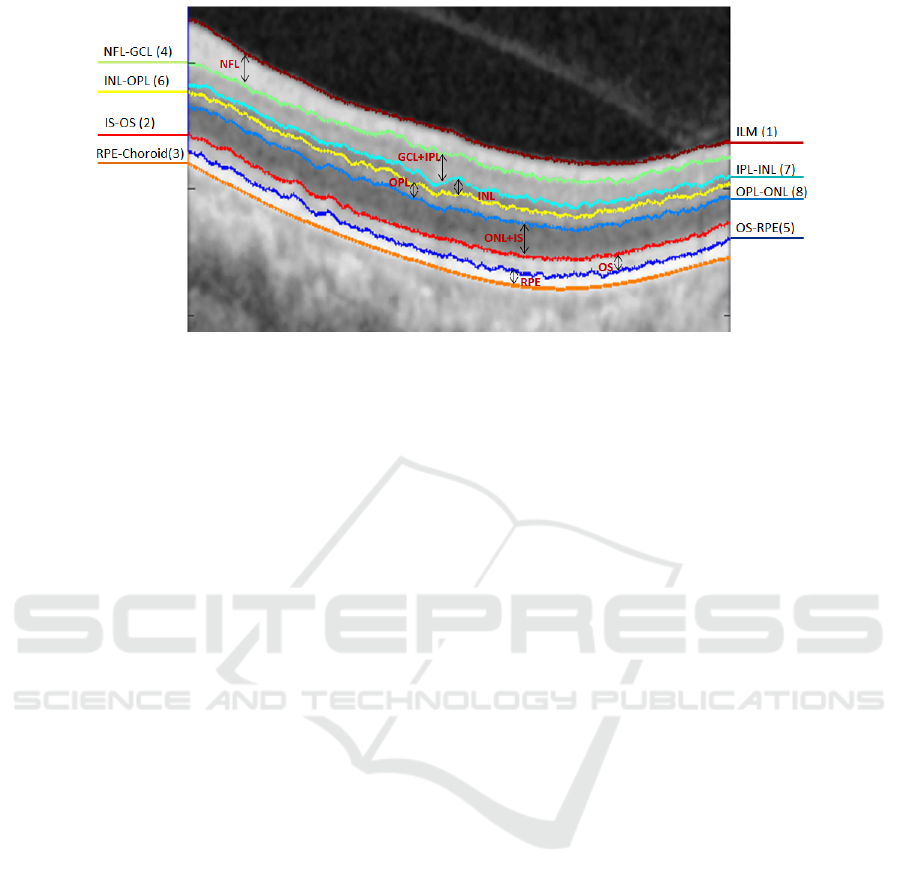
Figure 1: Illustration of the 8 boundaries and 7 retinal layers segmented in the study. The numbers in brackets are the
sequential order of the segmentation.
set ε ⊂ ν x ν. There are two main terminal vertices,
the source s and the sink t. The edge set comprises of
two type of edges: the spatial edges en = (r, q), where
r, q ∈ ν\{s \ t}, stick to the given grid and link two
neighbour grid nodes r and q except s and t; the ter-
minal edges or data edges, i.e. e
s
= (s, r) or e
t
= (r, t),
where r ∈ ν\{s \ t}, link the specified terminal s or
t to each grid node p respectively. Each edge is as-
signed a cost C(e), assuming all are non-negative i.e.
C(e) ≥ 0. A cut partitions the image into two disjoint
sets of s and t, also termed the s-t cut. it divides the
spatial grid nodes of Ω into disjoint groups, whereby
one belongs to source and the other belongs to the
sink, such that
ν = ν
s
[
ν
t
, ν
s
\
ν
t
=
/
0 (1)
We then introduce the concept of max-flow/min-
cut(Ford and Fulkerson, 1956). For each cut, the en-
ergy is defined as the sum of the costs C(e) of each
edge e ∈ ε
st
⊂ ε, where its two end points belong to
two different partitions. Hence the problem of min-
cut is to find two partitions of vertices such that the
corresponding cut-energy is minimal,
min
ε
st
⊂ε
∑
e∈ε
st
C(e) (2)
while on the other hand the max-flow is used to calcu-
late the maximal flow allowed to pass from the source
s to the sink t, and is formulated by
max
p
s
∑
v∈ν\{s,t}
p
s
(v) (3)
Graph-Cut has been an active area of research since
its introduction to image processing, in particular
some popular methods utilizing its concept includes
(Boykov and Jolly, 2001; Kolmogorov and Zabih,
2004; Yuan et al., 2010).
2.2 Segmentation of Retinal Layers
The segmentation of retinal layers has been an area
of active research and has drawn a large number of
researches, since the introduction of Optical Coher-
ence Tomography (OCT) (Huang et al., 1991). Vari-
ous methods have been proposed, some with focus on
number of layers, others on the computational com-
plexity, graph formulation and mostly now optimiza-
tion approaches. Segmentation of retinal images is
challenging and requires automated analysis methods
(Baglietto et al., 2017). In this regard a multi-step ap-
proach was developed by (Baroni et al., 2007). How-
ever the results obtained were highly dependent on the
quality of images and the alterations induced by reti-
nal pathologies. A 1-D edge detection algorithm us-
ing the Markov Boundary Model (Koozekanani et al.,
2001), which was later extended by (Boyer et al.,
2006) to obtain the optic nerve head and RNFL. Seven
layers were obtained by (Cabrera Fern
´
andez et al.,
2005) using a peak search interactive boundary detec-
tion algorithm based on local coherence information
of the retinal structure. The Level Set method was
used by (Novosel et al., 2013; Wang et al., 2015b;
Wang et al., 2015a; Wang et al., 2017) which were
computationally expensive compared to other opti-
mization methods. Graph based methods in (Salazar-
Gonzalez et al., 2014; Kaba et al., 2015; Zhang et al.,
2015; Haeker et al., 2007; Garvin et al., 2009) have
reported successful segmentation results, with vary-
ing success rates.Recently, (Dodo et al., 2017) pro-
posed a method using the Fuzzy Histogram Hyper-
bolization (FHH) to improve the image quality, then
embedded the image into the continuous max-flow to
simultaneously segment 4 retinal layers.
Moreover, the use of gradient information derived
from the retinal structures has in recent years been
BIOIMAGING 2018 - 5th International Conference on Bioimaging
36

of interest to OCT segmentation researchers. It was
utilised by (Chiu et al., 2010) with the Graph-Cut
method, where the retinal structure is employed to
limit search space and reduced computational time
with dynamic programming. This method was re-
cently extended to 3D volumetric analysis by (Tian
et al., 2015) in OCTRIMA 3D with edge map and
convolution kernel in addition to hard constraints in
calculating weights. They also exploited spatial de-
pendency between adjacent frames to reduce process-
ing time. Edge detection and polynomial fitting was
yet another approach proposed to derive boundaries
of the retinal layers from gradient information by (Lu
et al., 2011), and machine learning by (Lang et al.,
2013) with the use of random forest classifier. The
utilization of gradient information on OCT images
is largely based on the changes that occur at layer
boundaries in the vertical direction, thereby attract-
ing segmentation algorithms to exploit this advan-
tage. Our method takes into account the retinal struc-
ture and gradient information, but more importantly,
the re-assignment of weights in the adjacency matrix,
which contributes largely to the success of our graph-
cut approach.
3 THE PROPOSED METHOD
In this section we provide the details of our approach
to segmenting 8 retinal layer boundaries from OCT B-
Scan images.A schematic representation of the over-
all method is illustrated in Fig. 4
3.1 Pre-processing
The speckle noise is very common in OCT images,
which has negative effects on further processing, for
example, the retinal OCT images have low Signal to
Noise Ratio (SNR) due to the strong amplitude of
speckle noise.
Various methods have been used to handle the
presence of noise. In this work, we pre-process the
images with a Gaussian filter to suppress the speckle
noise and enhance the retinal layer boundaries, which
is important for the weight calculation in the next
stage. This also reduces false positive in the segmen-
tation stage. We show example of a pre-processed im-
age compared to its original in Fig. 2 .
3.2 Weight Calculation
In this stage we obtain the vertical gradient of the
image, normalize the gradient image to values in the
range of 0 to 1, and then we obtain the inverse of the
normalized image gradient as shown in Fig. 3.
These two normalized gradient images are then used
to obtain two separate undirected adjacency matrices,
where Fig. 3(a) contains information of light-dark
transitions while 3(b) contains information for tran-
sition from dark-light. The adjacency matrices are
formulated with the following equation (Chiu et al.,
2010):
w
ab
= 2 − g
a
− g
b
+ w
min
(4)
where w
ab
, g
a
, g
b
and w
min
are the weights assigned
to the edge connecting any two adjacent nodes a and
b, the vertical gradient of the image at node a, the
vertical gradient of the image at node b, and the mini-
mum weight added for system stabilization. To im-
prove the continuity and homogeneity in the adja-
cency matrices they are hyperbolized, firstly by cal-
culating the membership function with the fuzzy sets
equation (5) (Tizhoosh et al., 1997) and then trans-
formed with equation (6).
w
0
ab
=
w
ab
− w
mn
w
mx
− w
mn
(5)
where w
mn
and w
mx
represents the maximum and min-
imum values of the adjacency matrix respectively, the
adjacency matrices are then transformed with the fol-
lowing equation:
w
00
ab
= (w
0
ab
)
β
(6)
where w
0
ab
is the membership value from (5), and β,
the fuzzifier is a constant. Considering the number
of edges in an adjacency matrix, we use a constant
β instead of calculating the fuzziness. The main rea-
son is to reduce computational time and memory us-
age. The resulting adjacency matrices are such that
the weights are reassigned, and the edges with high
weights get higher values while those with low val-
ues get lower edge weights. Our motive here is that,
if continuity or discontinuity is re-emphasized the al-
gorithm will perform better. Where in this case we
improve both, the region of the layers get values close
to each other, while that of the background gets lower
along the way, this is more realistic and applicable in
this context (as the shortest path is greedy search ap-
proach), because at the boundary of each layer there
is a transition from bright to dark or dark to bright,
and therefore improving it aids the algorithm in find-
ing correct optimal solutions that are very close to the
actual features of interest.
The weight calculation is followed by several se-
quential steps of segmentation that are discussed in
the next few subsections. We adopt layer initializa-
tion from (Chiu et al., 2010), where two columns
are added to either side of the image with minimum
Graph-Cut Segmentation of Retinal Layers from OCT Images
37
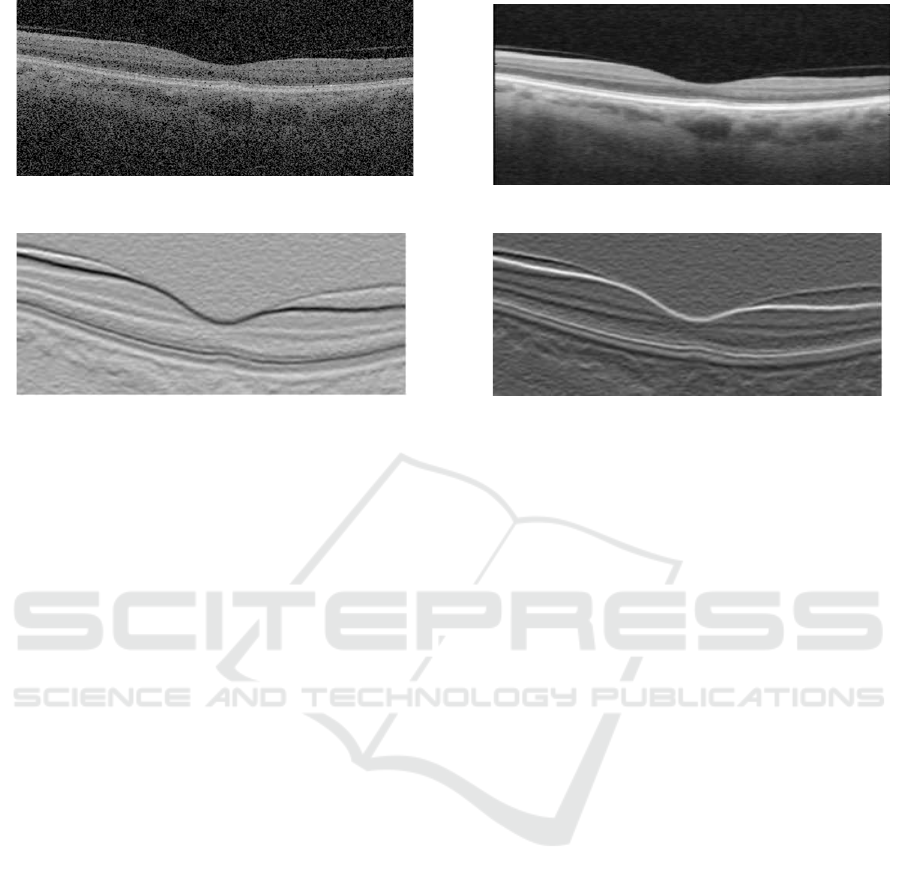
Figure 2: Image pre-processing. (a) Original image corrupted with speckle noise, and (b) filtered image by Gaussian.
Figure 3: Image gradients used in generating (a) dark-bright adjacency matrix and (b) bright-dark adjacency matrix.
weights (w
min
), to enable the cut move freely in those
columns. This is based on the understanding that
each layer extends from the first to last column of
the image, i.e. dividing the image horizontally at
each layer boundary, and that the Graph-Cut method
prefers paths with minimum weights. We use Djik-
stra’s algorithm (Dijkstra, 1959) in finding the min-
imum weighted path in the adjacency matrix (other
optimization methods utilizing sparse adjacency ma-
trices might be used in finding the minimum path).
Graph-Cut methods are optimal at finding one bound-
ary at a time, and therefore to segment multiple re-
gions in most cases, requires an iterative search in
limited space. Limiting the region of search is a com-
plex task, it requires prior knowledge and is depen-
dent on the structure of the features or regions of
interest. Some additional information on automatic
layer initialization and region limitation are discussed
in (Chiu et al., 2010) and (Kaba et al., 2015).
3.3 ILM and IS-OS Segmentation
It is commonly accepted that the NFL, IS-OS and
RPE exhibits high reflectivity in an OCT image (Chiu
et al., 2010; Lu et al., 2011; Tian et al., 2015).
Taking into account this reflectivity and the dark-
bright adjacency matrix we segment the ILM and IS-
OS boundaries using Dijkstras algorithm (Dijkstra,
1959). The ILM (vitreous-NFL) boundary is seg-
mented by searching for the highest change from dark
to light, this is because there is a sharp change in
the transition, additionally it is amidst extraneous fea-
tures, above it is the background region in addition to
no interruption of the blood vessels, as can be seen
in the gradient image. All of the above reasons make
it easier to segment the ILM than other layers. We
then limit the region below ILM and search for the
next highest change from dark-bright in order to seg-
ment the IS-OS boundary. In most cases the ILM is
segmented, but to account for uncertainties, i.e to dif-
ferentiate or confirm which layer was segmented, we
use the mean value of the vertical axis of the paths to
determine the layer segmented, as the ILM is above
the IS-OS (similar to (Chiu et al., 2010).
3.4 RPE and NFL-GCL Segmentation
As mentioned in the previous subsection, RPE is one
of the most reflective layers. Using the bright-dark ad-
jacency matrix, the RPE-Choroid boundary exhibits
the highest bright-dark layer transition as can be seen
in Fig.3(a). Additionally based on experimental re-
sults, it is better to search for the transition from bright
to dark for the RPE, due to the interference of blood
vessels and the disruption of hyper-reflective pixels
in the choroid region. Therefore searching for the
bright-dark transition is ideal for the RPE most es-
pecially to adapt to noisy images. To segment the
NFL-GCL boundary,we limit the search space be-
tween ILM to IS-OS, and utilize the bright-dark ad-
jacency matrix to find the minimum weighted path.
The resulting path is the NFL-GCL boundary, as it
is one of the most hyper-reflective layers. Addition-
ally if we limit our search space to regions below the
ILM and above the RPE, the resulting bright-dark and
dark-bright minimum paths are the NFL-GCL and IS-
OS respectively (i.e the NFL-GCL and IS-OS bound-
aries exhibits the second highest bright-dark and dark-
BIOIMAGING 2018 - 5th International Conference on Bioimaging
38

Figure 4: Main steps of segmentation algorithm schematic representation.
bright transition respectively in an OCT image).
3.5 OS and IPL to ONL Segmentation
To segment the OS-RPE and three other boundaries
(IPL-INL, INL-OPL, and OPL-ONL) from IPL to
ONL, we use the prior segmented layers as bench-
marks for search space limitation. We obtain the OS-
RPE region by searching for the dark-bright short-
est path between IS-OS and the RPE-Choroid. For
the remaining boundaries, first we segment the INL-
OPL, because it exhibits a different transition among
the three. This is done by searching for the short-
est path between NFL-GCL and IS-OS on the dark-
bright adjacency matrix. Consequently the IPL-INL
and OPL-ONL boundaries are obtained by limiting
the region of path search between INL-OPL and NFL-
GCL, and INL-OPL and IS-OS regions respectively,
on the bright-dark adjacency matrix.
4 EXPERIMENTAL RESULTS
We evaluated the performance of the proposed
method on a set of 150 B-scan OCT images centred
on the macular region. This data set was collected
in Tongren Hospital with a standard imaging protocol
for retinal diseases such as glaucoma. The resolution
of the B-scan images are 512 pixels in depth and 992
pixels across section with 16 bits per pixel. We man-
ually labelled all the retinal layers in the dataset under
the supervision of clinical experts. This serves as the
Graph-Cut Segmentation of Retinal Layers from OCT Images
39

ground truth in our experiments. Prior to segment-
ing the images, 15% percent of the image height was
cropped from the top to remove regions with low sig-
nal and no features of interest. We segment seven reti-
nal layers automatically using MATLAB 2016a soft-
ware. The average computation time was 4.25 sec-
onds per image on a PC with Intel i5-4590 CPU, clock
of 3.3GHz, and 8GB RAM memory.
The method obtains the boundaries in the or-
der from ILM(Vitreous-NFL), IS-OS, RPE-Choroid,
NFL-GCL, OS-RPE, INL-OPL, IPL-INL to OPL-
ONL respectively. The locations of these boundaries
and the sequential order of the segmentation is shown
in Fig. 1. Sample results of the 8 retinal layer bound-
aries and the underlying 7 layers are shown in Fig. 5.
Figure 5: Segmentation results of 8 boundaries and 7 lay-
ers. Boundaries from top to bottom, the segmented bound-
aries are ILM, NFL-GCL, IPL-INL,INL-OPL, OPL-ONL,
IS-OS, OS-RPE and RPE-Choroid.
To evaluate the proposed method we calculate the
Root Mean Squared Error (RMSE), and Mean Abso-
lute Deviation (MAD) by (7). Table 1 shows the mean
and standard deviation of both MAD and RMSE, for
the seven layers targeted in this study.
MAD(GT, SEG) =
0.5 ∗
1
n
n
∑
i=1
d(pt
i
, SEG) +
1
m
m
∑
i=1
d(ps
i
, GT )
!
RMSE =
s
1
n
n
∑
i=1
(SEG
i
− GT
i
)
2
Dice =
2 | GT
i
∩ SEG
i
|
| GT
i
| + | SEG
i
|
(7)
where SEG
i
is the pixel labelled as retinal Layer by
the proposed segmentation method and GT
i
is the true
retinal layers pixel in the manually annotated image
(ground truth) image. pt
i
and ps
i
represent the coordi-
nates of the images, while d(pt
i
, SEG) is the distance
of pt
i
to the closest pixel on SEG with the same seg-
mentation label, and d(ps
i
, GT ) is the distance of ps
i
to the closest pixel on GT with the same segmenta-
tion label. n and m are the number of points on SEG
and GT respectively. For all layers our method has
performed well. Especially considering the low value
of NFL for both MAD and RMSE. The high value
in ONL+IS is due to the presence of high noise and
lower reflectivity of the boundaries within the region,
however, this is still considerably low.
Furthermore, We evaluated the retinal nerve fi-
bre layer thickness (RNFLT) (the area between ILM
and NFL-GCL) with additional criteria, due to its
high importance in the diagnosis of ocular dis-
eases, including glaucoma. This is evaluated with
four criteria, namely, accuracy, sensitivity(true pos-
itive rate(TPR)), error rate(FPR) and the Dice in-
dex(coefficient). These measurements are computed
with the following equations while the Dice is com-
puted from (8):
Accuracy =
T P + T N
(T P + FP + FN + T N)
Sensitivity(T PR) =
T P
(T P + FN)
ErrorRate(FPR) =
FP
(FP + T N)
(8)
where T P, T N, FP and FN refers to true positive,
true negative, false positive and false negative respec-
tively. T P represents the number of pixels which are
part of the region that are labeled correctly by both
the method and the ground truth. T N represents the
number of pixels which are part of the background
region and labeled correctly by both the method and
the ground truth. FP represents the number of pixels
labeled as a part of the region by the method but la-
beled as a part of the background by the ground truth.
Finally, FN represents the number of pixels labeled
as a part of the background by the system but labeled
as a part of the region in ground truth. The results of
applying the above criteria on the RNFLT are shown
in Table 2.
5 CONCLUSIONS
We have presented an automatic segmentation method
for retinal OCT images that is capable of segment-
ing 7 retinal layers with 8 boundaries. The core of
BIOIMAGING 2018 - 5th International Conference on Bioimaging
40

Table 1: Performance evaluation with mean and standard deviation of RMSE and MAD for 7 retinal boundaries. 150 SD-OCT
B-Scan images (Units in pixels).
RetinalLayer MeanMAD MeanRMSE ST DMAD ST DRMSE
NFL 0.2689 0.0168 0.0189 0.0121
GCL+IPL 0.5938 0.0432 0.0592 0.0382
INL 0.6519 0.0387 0.0792 0.0612
OPL 0.5101 0.0446 0.0410 0.0335
ONL+IS 0.6896 0.0597 0.0865 0.0329
OS 0.4617 0.0341 0.0360 0.0150
RPE 0.4617 0.0341 0.0360 0.0150
Table 2: Mean accuracy, sensitivity, error rate, Dice and
Root Mean Squared Error (RMSE) of the Retinal Nerve
Fibre Layer Thickness (RNFLT) and standard deviation
(STD).
Measure ST D
Mean Accuracy 0.9816 0.0375
Mean Sensitivity 0.9687 0.0473
Mean Error Rate 0.0669 0.0768
Mean Dice 0.9746 0.0559
the method is a Graph-Cut segmentation using Dijk-
stra’s algorithm (Dijkstra, 1959). More importantly,
the adjacency matrices from vertical gradients and a
sequential process of segmentation, as two key ele-
ments of the study, are integrated into the Graph-Cut
framework. We have applied the proposed method to
a dataset of 150 OCT B-scan images, with successful
segmentation results. Further quantitative evaluation
indicates that the segmentation measurement is very
close to the ground-truth.
The main contributions of this work are as fol-
lows:
1. We have presented a method to automatically
identify 7 retinal layers across 8 layer boundaries,
so far one of the most comprehensive studies in
this area;
2. The adjacency matrices are effectively integrated
into the Graph-Cut framework with better weight
calculation;
3. Based on the unique characteristics of reflectivity
of different retinal layers and their changes across
layers, a sequential process of segmentation has
been developed.
REFERENCES
Baglietto, S., Kepiro, I. E., Hilgen, G., Sernagor, E.,
Murino, V., and Sona, D. (2017). Segmentation of
retinal ganglion cells from fluorescent microscopy
imaging. In Proceedings of the 10th International
Joint Conference on Biomedical Engineering Systems
and Technologies (BIOSTEC 2017), pages 17–23.
Baroni, M., Fortunato, P., and La Torre, A. (2007). Towards
quantitative analysis of retinal features in optical co-
herence tomography. Medical engineering & physics,
29(4):432–441.
Boyer, K. L., Herzog, A., and Roberts, C. (2006). Auto-
matic recovery of the optic nervehead geometry in op-
tical coherence tomography. IEEE Transactions on
Medical Imaging, 25(5):553–570.
Boykov, Y. and Jolly, M.-P. (2001). Interactive Graph Cuts
for Optimal Boundary & Region Segmentation of Ob-
jects in N-D Images. Proceedings Eighth IEEE Inter-
national Conference on Computer Vision. ICCV 2001,
1(July):105–112.
Cabrera Fern
´
andez, D., Salinas, H. M., and Puliafito, C. A.
(2005). Automated detection of retinal layer structures
on optical coherence tomography images. Optics Ex-
press, 13(25):10200.
Chiu, S. J., Li, X. T., Nicholas, P., Toth, C. a., Izatt, J. a., and
Farsiu, S. (2010). Automatic segmentation of seven
retinal layers in SDOCT images congruent with expert
manual segmentation. Optics express, 18(18):19413–
19428.
Dijkstra, E. W. (1959). A note on two problems in connex-
ion with graphs. Numerische mathematik, 1(1):269–
271.
Dodo, B., Li, Y., and Liu, X. (2017). Retinal oct image seg-
mentation using fuzzy histogram hyperbolization and
continuous max-flow. In IEEE International Sympo-
sium on Computer-Based Medical Systems.
Ford, L. R. and Fulkerson, D. R. (1956). Maximal
flow through a network. Journal canadien de
math
´
ematiques, 8:399–404.
Garvin, M. K., Abr
`
amoff, M. D., Wu, X., Russell, S. R.,
Burns, T. L., and Sonka, M. (2009). Automated 3-
D intraretinal layer segmentation of macular spectral-
domain optical coherence tomography images. IEEE
transactions on medical imaging, 28(9):1436–1447.
Haeker, M., Wu, X., Abr
`
amoff, M., Kardon, R., and Sonka,
M. (2007). Incorporation of regional information
in optimal 3-D graph search with application for in-
traretinal layer segmentation of optical coherence to-
mography images. Information processing in medical
Graph-Cut Segmentation of Retinal Layers from OCT Images
41

imaging : proceedings of the ... conference, 20:607–
618.
Huang, D., Swanson, E. A., Lin, C. P., Schuman, J. S.,
Stinson, W. G., Chang, W., Hee, M. R., Flotte, T.,
Gregory, K., and Puliafito, C. A. (1991). Optical
coherence tomography. Science (New York, N.Y.),
254(5035):1178–81.
Kaba, D., Wang, Y., Wang, C., Liu, X., Zhu, H., Salazar-
Gonzalez, a. G., and Li, Y. (2015). Retina layer
segmentation using kernel graph cuts and continuous
max-flow. Optics express, 23(6):7366–84.
Kolmogorov, V. and Zabih, R. (2004). What Energy Func-
tions Can Be Minimized via Graph Cuts? IEEE Trans-
actions on Pattern Analysis and Machine Intelligence,
26(2):147–159.
Koozekanani, D., Boyer, K., and Roberts, C. (2001). Reti-
nal thickness measurements from optical coherence
tomography using a Markov boundary model. IEEE
Transactions on Medical Imaging, 20(9):900–916.
Lang, A., Carass, A., Hauser, M., Sotirchos, E. S., Cal-
abresi, P. a., Ying, H. S., and Prince, J. L. (2013).
Retinal layer segmentation of macular OCT images
using boundary classification. Biomedical optics ex-
press, 4(7):1133–52.
Lu, S., Yim-liu, C., Lim, J. H., Leung, C. K.-s., and Wong,
T. Y. (2011). Automated layer segmentation of op-
tical coherence tomography images. Proceedings -
2011 4th International Conference on Biomedical En-
gineering and Informatics, BMEI 2011, 1(10):142–
146.
Novosel, J., Vermeer, K. A., Thepass, G., Lemij, H. G., and
Vliet, L. J. V. (2013). Loosely Coupled Level Sets
For Retinal Layer Segmentation In Optical Coherence
Tomography. IEEE 10th International Symposium on
Biomedical Imaging, pages 998–1001.
Salazar-Gonzalez, A., Kaba, D., Li, Y., and Liu, X. (2014).
Segmentation of the blood vessels and optic disk in
retinal images. IEEE journal of biomedical and health
informatics, 18(6):1874–1886.
Seheult, A., Greig, D., and Porteous;, B. (1989). Exact
Maximum A Posteriori Estimation For Binary Images.
Journal of the Royal Statistical Society, Vol. 51(No.
2):271 –279.
Tian, J., Varga, B., Somfai, G. M., Lee, W. H., Smiddy,
W. E., and DeBuc, D. C. (2015). Real-time automatic
segmentation of optical coherence tomography vol-
ume data of the macular region. PLoS ONE, 10(8):1–
20.
Tizhoosh, H. R., Krell, G., and Michaelis, B. (1997). Lo-
cally Adaptive Fuzzy Image Enhancement. In Inter-
national Conference on Computational Intelligence,
pages 272–276. Springer.
Wang, C., Kaba, D., and Li., Y. (2015a). Level set segmen-
tation of optic discs from retinal images. Journal of
Medical Systems, 4(3):213–220.
Wang, C., Wang, Y., Kaba, D., Wang, Z., Liu, X., and Li,
Y. (2015b). Automated Layer Segmentation of 3D
Macular Images Using Hybrid Methods. Image and
Graphics, 9217:614–628.
Wang, C., Wang, Y., and Li, Y. (2017). Automatic choroidal
layer segmentation using markov random field and
level set method. IEEE journal of biomedical and
health informatics.
Yuan, J., Bae, E., Tai, X.-C., and Boykov, Y. (2010). A study
on continuous max- flow and min-cut approaches.
2010 IEEE Conference, 7:2217–2224.
Zhang, T., Song, Z., Wang, X., Zheng, H., Jia, F., Wu, J.,
Li, G., and Hu, Q. (2015). Fast retinal layer segmenta-
tion of spectral domain optical coherence tomography
images. Journal of Biomedical Optics, 20(9):096014.
BIOIMAGING 2018 - 5th International Conference on Bioimaging
42
