
Grammar-based Compression for Directed and Undirected Generalized
Series-parallel Graphs using Integer Linear Programming
Morihiro Hayashida
1
, Hitoshi Koyano
2
and Tatsuya Akutsu
3
1
National Institute of Technology, Matsue College, 14-4, Nishiikumacho, Matsue, Shimane 690–8518, Japan
2
Quantitative Biology Center, Riken, 2-2-3, Minatojima-minamimachi, Chuo-ku, Kobe, Hyogo 650–0047, Japan
3
Institute for Chemical Research, Kyoto University, Gokasho, Uji, Kyoto 611–0011, Japan
Keywords:
Generalized Series-parallel Graph, Grammar-based Compression, Integer Linear Programming.
Abstract:
We address a problem of finding generation rules from biological data, especially, represented as directed and
undirected generalized series-parallel graphs (GSPGs), which include trees, outerplanar graphs, and series-
parallel graphs. In the previous study, grammars for edge-labeled rooted ordered and unordered trees, called
SEOTG and SEUTG, respectively, were defined, and it was examined to extract generation rules from glycans
and RNAs that can be represented by rooted tree structures, where integer linear programming-based methods
for finding the minimum SEOTG and SEUTG that produce only given trees were developed. In nature and or-
ganisms, however, there are various kinds of structures such as gene regulatory networks, metabolic pathways,
and chemical structures that cannot be represented as rooted trees. In this study, we relax the limitation of
structures to be compressed, and propose grammars representing edge-labeled directed and undirected GSPGs
based on context-free grammars by extending SEOTG and SEUTG. In addition, we propose an integer linear
programming-based method for finding the minimum GSPG grammar in order to analyze more complicated
biological networks and structures.
1 INTRODUCTION
Data compression for a structure is related with the
amount of information that it contains. The amount of
information would be large if the size of compressed
data is still large. Otherwise, the data include redun-
dant data, and the amount of information is small. Our
purpose is to extract useful information and knowl-
edge from data through compression. In particular,
we focus on biological structured data constructed in
nature. Such structures could be often explained by
several simple generation rules.
In previous studies, biological data represented by
rooted trees such as glycans and RNAs were com-
pressed and analyzed (Zhao et al., 2010; Zhao et al.,
2015). It is known that glycans are composed of mul-
tiple monosaccharides bound by glycosidic bonds,
take various structures in accordance with biosyn-
thetic reactions, and the function of a glycan depends
on its structure. Hence, it is important to analyze the
glycan structures, and to extract rules of the biosyn-
theses. They developed integer linear programming-
based methods, called the minimum SEOTG and
SEUTG, for finding the minimum grammar that pro-
duces only given single ordered and unordered rooted
trees, and applied them to biological data such as gly-
cans with up to 36 nodes and 5 distinct labels, where
these methods are based on a kind of tree grammar,
the simple elementary ordered (unordered) tree gram-
mar (SEO(U)TG) (Akutsu, 2010). Furthermore, they
extended the methods to multiple rooted trees be-
cause generation rules are commonly utilised among
these multiple trees. It, however, is considered that
structures generated in nature cannot be always rep-
resented by rooted trees. In this paper, we extend
their grammar to directed and undirected generalized
series-parallel graphs (GSPGs), which include trees
and outerplanar graphs. In addition, we propose an
integer linear programming-based method for finding
the minimum GSPG grammar that produces only a
given generalized series-parallel graph.
A series-parallel graph is defined by two proce-
dures, called series and parallel compositions, and
two special nodes in the graph are labeled with source
and sink as terminal nodes (Eppstein, 1992; Eikel
et al., 2015). A generalized series-parallel graph is
defined by the addition of another series-type compo-
sition, called generalized series composition, where
Hayashida, M., Koyano, H. and Akutsu, T.
Grammar-based Compression for Directed and Undirected Generalized Series-parallel Graphs using Integer Linear Programming.
DOI: 10.5220/0006583001050111
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 3: BIOINFORMATICS, pages 105-111
ISBN: 978-989-758-280-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
105

the shared node between two composed graphs is la-
beled with a terminal node (Korneyenko, 1994). Ho
et al. proposed a decomposition method for GSPGs
using many processors in parallel (Ho et al., 1999).
However, it is not guaranteed that their method al-
ways finds the minimum decomposition tree. It has
been proved that the problem of finding the mini-
mum SEO(U)TG for a given rooted tree is NP-hard
(Akutsu, 2010). Hence, the problem of finding the
minimum grammar for a given GSPG is also NP-hard,
and it means that there does not exist any polynomial
time algorithm for finding the minimum GSPG gram-
mar.
Since production rules of a SEO(U)TG can be re-
garded as two types of series compositions in GSPGs,
we define a grammar by adding a production rule
corresponding to the parallel composition to their
grammar, and developan integer linear programming-
based method for finding the minimum GSPG gram-
mar.
2 METHOD
We briefly review the simple elementary ordered (un-
ordered) tree grammar (SEO(U)TG) and the integer
linear programming-based methods for finding the
minimum SEOTG and SEUTG, and propose gram-
mars for edge-labeled directed and undirected gen-
eralized series-parallel graphs (GSPGs) and an inte-
ger linear programming-based method for finding the
minimum GSPG grammar.
2.1 SEOTG and SEUTG
SEOTG and SEUTG are context-free grammar
(CFG)-like grammars for edge-labeled ordered and
unordered rooted trees, respectively. In CFG,
a nonterminal symbol is replaced with several
(non)terminal symbols (Hopcroft et al., 2001). In
SEO(U)TG, an edge having a nonterminal symbol is
replaced with one or two edges having (non)terminal
symbols. SEOTG and SEUTG are defined as follows.
Definition 1 (Simple Elementary Ordered Tree Gram-
mar (SEOTG)). A SEOTG is defined as 4-tuple (Σ, Γ,
S, ∆), where Σ is a set of terminal symbols, Γ is a set
of nonterminal symbols, S is a start nonterminal sym-
bol in Γ, and ∆ is a set of production rules (R1), (R1t),
(R2), (R2t), (R3), (R3r), (R3l) as shown in Fig. 1.
Definition 2 (Simple Elementary Unordered Tree
Grammar (SEUTG)). A SEUTG is defined as 4-tuple
(Σ, Γ, S, ∆) where Σ is a set of terminal symbols, Γ is
a set of nonterminal symbols, S is a start nonterminal
A
a
A
B
C
A
B
C
(R1) (R1t)
(R2)
(R3)
A
B
C
(R3r)
A
B
C
(R3l)
A
B
C
(R2t)
A
a
Figure 1: Three main types (R1), (R2), (R3) of production
rules of SEOTG for rooted ordered trees. A black circle
denotes a tag.
D
b
S
A
B
A
C
B
C
a
B
D
E
E
c
S
A
B
C
B
B
C
D
E
D
E
a
b
c
b
c
(a)
(b)
Figure 2: Example of a SEOTG with
({a,b,c},{S,A, B,C, D, E}, S,∆) and the tree gener-
ated by this grammar. (a) Production rules of ∆. (b) The
derivation of the generated tree.
symbol in Γ, and ∆ is a set of production rules (R1),
(R1t), (R2), (R2t), (R3), (R3r).
It is noted that (R3r) becomes equivalent to (R3l)
because the edge order is ignored.
These production rules do not construct any cycle
but trees. A tree generated from a nonterminal sym-
bol by SEOTG and SEUTG has at most two special
nodes, its root and a tag node, where a tag means a
terminal node to which another tree structure can be
attached.
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
106

Fig. 2 shows an example of a SEOTG with
({a,b,c},{S,A, B,C, D,E},S,∆), and the tree gener-
ated by the grammar, where ∆ is shown in Fig. 2(a).
The generation starts from S, production rules are
applied to edges with nonterminal symbols, and the
tree with only terminal symbols is generated (see Fig.
2(b)).
2.2 The Minimum SEOTG and SEUTG
We can obtain a clue of generation mechanisms of bi-
ological structures by finding the minimum grammar.
For a rooted ordered tree T, the following integer lin-
ear programming problem was formulated for finding
the minimum SEOTG that produces only the tree T.
Minimize
∑
u∈U
p
u
Subject to
x
i,ε, j, j
= 1 for all i, j ∈ ch(i) (|ch( j)| = 0),
x
i, j, j, j
= 1 for all i, j ∈ ch(i) (|ch( j)| > 0),
x
1,ε,lch(1),rch(1)
= 1,
x
i,ε,h,k
≤
k−1
∑
l=h
y
i,ε,h,l,k
+
∑
t∈I(T
i,ε,h,k
)
z
i,ε,h,k,t
for all i, h ≤ k ∈ ch(i),
y
i,ε,h,l,k
≤
1
2
(x
i,ε,h,l
+ x
i,ε,l+1,k
)
for all i, h ≤ l < k ∈ ch(i),
z
i,ε,h,k,t
≤
1
2
(x
i,t,h,k
+ x
t,ε,lch(t) ,rch(t)
)
for all i, h ≤ k ∈ ch(i),t ∈ I(T
i,ε,h,k
),
x
i, j,h,k
≤
k−1
∑
l=h
y
i, j,h,l,k
+
∑
t∈anc( j)
z
i, j,h,k,t
for all i, h ≤ k ∈ ch(i), j ∈ I(T
i,ε,h,k
),
y
i, j,h,l,k
≤
1
2
(x
i,ε,h,l
+ x
i, j,l+1,k
)
for all i, h ≤ l < k ∈ ch(i), j ∈ I(T
i,ε,l+1,k
),
y
i, j,h,l,k
≤
1
2
(x
i, j,h,l
+ x
i,ε,l+1,k
)
for all i, h ≤ l < k ∈ ch(i), j ∈ I(T
i,ε,h,l
),
z
i, j,h,k,t
≤
1
2
(x
i,t,h,k
+ x
t, j,lch(t),rch(t)
)
for all i, h ≤ k ∈ ch(i), j ∈ I(T
i,ε,h,k
), t ∈ anc( j),
p
u
≥
1
|S(u)|
∑
T
i, j,h,k
∈S(u)
x
i, j,h,k
for all u ∈ U,
p
u
< 1 +
1
|S(u)|
∑
T
i, j,h,k
∈S(u)
x
i, j,h,k
for all u ∈ U,
x
i, j,h,k
,y
i, j,h,l,k
,z
i, j,h,k,t
, p
u
∈ {0,1},
where lch(i), rch(i), and ch(i) denote the leftmost
child of the node v
i
in T, the rightmost child of v
i
,
and the set of child nodes of v
i
, respectively. T
i,t,h,k
denotes the subtree rooted at v
i
, with the child nodes
v
j
(h ≤ j ≤ k) and v
t
labeled with a tag in T, which
does not have a tag when t = ε. I(T) denotes the set
of internal nodes, except for the root and leaves of
tree T. anc( j) denotes the set of ancestor nodes of v
j
,
where j /∈ anc( j) and anc(ε) =
/
0.
Each variable of x
i, j,h,k
,y
i, j,h,l,k
,z
i, j,h,k,t
takes ei-
ther 0 or 1. x
i, j,h,k
= 1 if T
i, j,h,k
is generated by the
grammar, x
i, j,h,k
= 0 otherwise. y
i, j,h,l,k
= 1 if both of
T
i, j,h,l
and T
i, j,l+1,k
are generated, y
i, j,h,l,k
= 0 other-
wise. z
i, j,h,k,t
= 1 if both of T
i,t,h,k
and T
i, j,lch(t),rch(t)
are generated, z
i, j,h,k,t
= 0 otherwise.
In this formulation, the Euler string es(T) is used
to determine if two edge-labeled rooted trees T
1
and
T
2
are isomorphic to each other, where es(T) for a tree
T is defined by the sequence of edge labels l and its
opposite
¯
l, along the depth-first search traversal of T
(Akutsu, 2010). It is noted that for two edge-labeled
rooted trees T
1
and T
2
, T
1
is isomorphic to T
2
if (and
only if) es(T
1
) = es(T
2
). U denotes the set of all Euler
strings for all connected subtrees of T. S(u) denotes
the set of all subtrees T
i, j,h,k
of T such that es(T
i, j,h,k
)
is equivalent to u. Then, p
u
= 1 means that the mini-
mum grammar generates the subtree corresponding to
u, and
∑
u∈U
p
u
represents the number of nonterminal
symbols.
Similarly to the minimum SEOTG, the minimum
SEUTG was formulated.
2.3 Directed and Undirected
Generalized Series-parallel Graph
Grammars (GSPGGs)
Let G(V,E) be an undirected GSPG with a set V of
nodes and a set E of edges labeled with l(e) for e ∈ E.
For example, Fig. 4(a) shows the benzene ring, which
is regarded as an undirected GSPG with six nodes and
six edges, and is constructed by several series compo-
sitions after one parallel composition.
We define an undirected generalized series-
parallel graph grammar (GSPGG) as follows.
Definition 3 (Undirected generalized series-parallel
graph grammar). An undirected GSPGG is defined as
4-tuple (Σ, Γ, S, ∆), where Σ and Γ are sets of nonter-
minal and terminal symbols, every terminal symbol is
an undirected labeled edge, S is a start nonterminal
symbol, and ∆ is a set of production rules as shown in
Fig. 3.
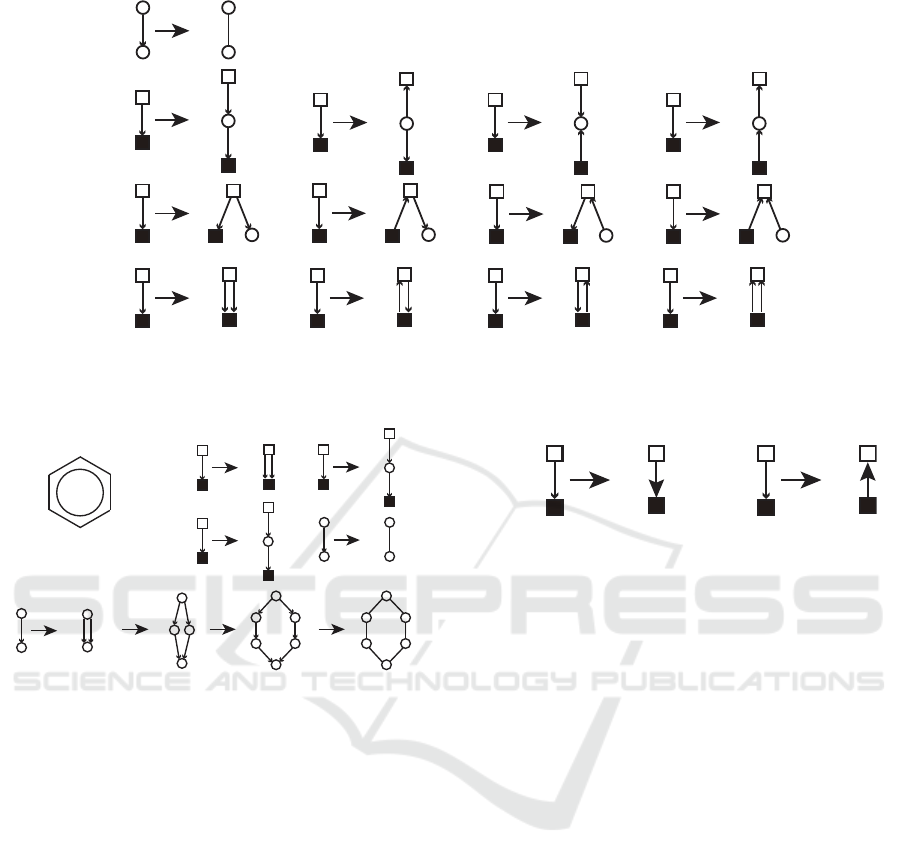
In Fig. 3, a head and a tail of each arrow denote
two terminal nodes of its edge. If the graph with only
terminal symbols generated from a nonterminal sym-
bol is symmetric, then the source and sink nodes can
be changed to each other. White and black squares
mean that in a production rule, the node with a white
(black) square in the left-hand side corresponds to the
node with a white (black) square in the right-hand
Grammar-based Compression for Directed and Undirected Generalized Series-parallel Graphs using Integer Linear Programming
107
A
a
A
B
C
A
B
C
(R1)
(R2a)
(R3a)
A
B
(R4a)
C
A
B
C
(R2b)
A
B
C
(R2c)
A
B
C
(R2d)
A
B
C
(R3b)
A
B
C
(R3c)
A
B
C
(R3d)
A
B
(R4b)
C
A
B
(R4c)
C
A
B
(R4d)
C
Figure 3: Four main types of production rules of undirected GSPGGs. A head and a tail of each arrow denote two terminal
nodes of its edge. White and black squares mean that the node with a white (black) square in the left-hand side corresponds
to the node with a white (black) square in the right-hand side.
S
A
A
S
A
A
B
C
C
A
B
C
B
C
B
C
C C
C C
C C
C
a
a a
a a
a a
(a)
(c)
(b)
Figure 4: Example of an undirected generalized series-
parallel graph and its grammar. (a) The benzene ring. (b)
An undirected GSPGG of the benzene ring. (c) The deriva-
tion of the benzene ring using the grammar, where terminal
symbol ’a’ denotes a bond with order 1.5 of the benzene
ring.
side. In the production rule (R4a-d), an edge between
the source and sink nodes is replaced with two edges,
and a cycle is generated.
Fig. 4(b) shows an example of an undirected
GSPGG that produces the benzene ring (Fig. 4(a)),
where each bond in the benzene ring is represented as
an edge with label ’a’ because six bonds are equiv-
alent to each other. Fig. 4(c) shows the derivation
of the benzene ring using the undirected GSPGG.
The start symbol ’S’ is replaced with two nontermi-
nal symbols ’A’ making a cycle. ’A’ is replaced with
’B’ and ’C’. ’B’ is replaced with two ’C’s. ’C’ is
replaced with ’a’. Then, the number of production
rules is equal to the number of nonterminal symbols,
|Σ| = 4 (Σ = {S, A,B,C}). For finding the minimum
GSPGG, it is enough to find GSPGGs with the mini-
mum number of nonterminal symbols.
A
a
(R1a)
A
a
(R1b)
Figure 5: Production rules of replacement of a nontermi-
nal symbol with a terminal symbol in directed GSPGGs. In
each production rule, the arrow in the right-hand side de-
notes a directed edge.
Similarly to the definition of undirected GSPGGs,
we define a directed GSPGG as follows.
Definition 4 (Directed generalized series-parallel
graph grammar). A directed GSPGG is defined as 4-
tuple (Σ, Γ, S, ∆), where Σ and Γ are sets of nonter-
minal and terminal symbols, every terminal symbol is
a directed labeled edge, S is a start nonterminal sym-
bol, ∆ is a set of the same types of production rules of
undirected GSPGGs except (R1), and (R1) is replaced
with (R1a-b) as shown in Fig. 5.
Fig. 6 shows an example of a directed GSPG and
its grammar that produces only the graph, where the
chemical structure of the purine (Fig. 6(a)) is trans-
formed to a directed graph as shown in Fig. 6(b).
If it is transformed to an undirected graph, two end-
points of a terminal symbol cannot be distinguished,
and atom types are not determined in the graph pro-
duced by an undirected GSPGG.
2.4 The Minimum Directed and
Undirected GSPGGs
Let G(V,E) be a directed (undirected) GSPG with a
set V of nodes and a set E of labeled edges. To con-
sider all combinations of compositions of subgraphs
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
108

n
n
n
n
n
n
h
n
n
c
c
N
N
N
N
H
S
A
B
E
D
G
A
B
D
E
C
C
C
F
F
H
F
I
G
C
H
D
c
F
n
J
h
(c)
(a) (b)
I
F
J
Figure 6: Example of a directed generalized series-parallel
graph and its directed GSPGG. (a) The purine. (b) A trans-
formed directed graph. (c) A directed GSPGG that gener-
ates the graph (b).
of G, we repeatedly partition subgraphs into two con-
nected components until only edges remain. A GSPG
has two terminal nodes, whereas G does not have any
terminal node. Hence, we require that a partitioned
subgraph has at most two terminal nodes. Suppose
that G
i,S, j,T
represents a connected subgraph with ter-
minal nodes i and j, where S and T are subsets of ad-
jacent nodes of i and j, respectively. If a partitioned
subgraph has one terminal node, we represent the sub-
graph as G
i,S
, G
i,S,ε,
/
0
, or G
ε,
/
0,i,S
. G is also represented
as G
ε,
/
0,ε,
/
0
. If G
i,S, j,T
is isomorphic to G
i
′
,S
′
except
node j, and is generated by a production rule, then
G
i
′
,S
′
is also generated by the same production rule.
A subgraph with at most two terminal nodes can
be partitioned into two subgraphs with one or two ter-
minal nodes.
Fig. 7 shows an example of an undirected GSPG
1
2
3
4
5
1
2
3
4
1
2
3 3
4
4
5
2
1
3
1
3
1
3
4
5
3
4
5
(a)
(b)
(c)
(d)
(e)
G
G
4,{3}
G
3,{1,2}
G
3,{4}
G
1,{2},3,{2}
G
1,{3},3,{1,4}
G
4,{5}
G
3,{4},4,{3}
G
1,{3},3,{1}
Figure 7: Example of an undirected GSPG and its partition-
ing. (a) An example graph G with five nodes. (b) The parti-
tioned graphs G
4,{3}
and G
4,{5}
at node 4 of G. (c) The par-
titioned graphs G
3,{1,2}
and G
3,{4},4,{3}
at node 3 of G
4,{3}
.
(d) The partitioned graphs G
1,{2},3,{2}
and G
1,{3},3,{1,4}
at
nodes 1 and 3 of G. (e) The partitioned graphs G
1,{3},3,{1}
and G
3,{4}
at node 3 of G
1,{3},3,{1,4}
. A black circle denotes
a terminal node.
G with five nodes and its partitioning. G is partitioned
into two subgraphs G
4,{3}
and G
4,{5}
at node 4 that
does not belong to any cycle as shown in Fig. 7(b).
If a node to be partitioned does not belong to any cy-
cle, only the node can be a new terminal node. Then,
production rules of (R2) and (R3) can be constructed,
and G is generated from G
4,{3}
and G
4,{5}
by series
compositions. In Fig. 7(c), we cannot partition G
4,{3}
at node 1 or 2 because two connected components are
not generated. G
4,{3}
is partitioned into G
3,{1,2}
and
G
3,{4},4,{3}
at node 3. Then, production rules of (R2)
and (R3) can be constructed, and G
4,{3}
is generated
from G
3,{1,2}
and G
3,{4},4,{3}
by series compositions.
On the other hand, if a node to be partitioned belongs
to only a cycle, another node belonging to the cycle is
needed. In Fig. 7(d), G is partitioned into G
1,{2},3,{2}
and G
1,{3},3,{1,4}
at nodes 1 and 3. Then, a production
rule of (R4) can be constructed, and G is generated
from G
1,{2},3,{2}
and G
1,{3},3,{1,4}
by parallel com-
position. In Fig. 7(e), G
1,{3},3,{1,4}
cannot be parti-
tioned at node 4 because only subgraphs with at most
two terminal nodes are allowed. Hence, G
1,{3},3,{1,4}
is partitioned into G
1,{3},3,{1}
and G
3,{4}
at node 3.
Then, a production rule of (R3) can be constructed,
and G
1,{3},3,{1,4}
is generated from G
1,{3},3,{1}
and
G
3,{4}
by generalized series composition.
Suppose that I (G) is a set of indices (i,S, j,T)
of all subgraphs G
i,S, j,T
of G obtained by re-
peatedly partitioning, S (G) is a set of all distinct
subgraphs G
i,S, j,T
, and E(u) is a set of all sub-
Grammar-based Compression for Directed and Undirected Generalized Series-parallel Graphs using Integer Linear Programming
109

graphs G
i,S, j,T
that are isomorphic to u. Consider
the case that G
i,S, j,T
(V
i,S, j,T
,E
i,S, j,T
) is correctly
partitioned into G
i
′
,S
′
, j
′
,T
′
(V
i
′
,S
′
, j
′
,T
′
,E
i
′
,S
′
, j
′
,T
′
)
and G
i
′′
,S
′′
, j
′′
,T
′′
(V
i
′′
,S
′′
, j
′′
,T
′′
,E
i
′′
,S
′′
, j
′′
,T
′′
). Let
C (G
i,S, j,T
) be a set of all index com-
binations (i
′
,S
′
, j
′
,T
′
,i
′′
,S
′′
, j
′′
,T
′′
) that
V
i
′
,S
′
, j
′
,T
′
∪ V
i
′′
,S
′′
, j
′′
,T
′′
= V
i,S, j,T
, V
i
′
,S
′
, j
′
,T
′
∩
V
i
′′
,S
′′
, j
′′
,T
′′
= {i, j}, E
i
′
,S
′
, j
′
,T
′
∪ E
i
′′
,S
′′
, j
′′
,T
′′
= E
i,S, j,T
,
E
i
′
,S
′
, j
′
,T
′
∩ E
i
′′
,S
′′
, j
′′
,T
′′
=
/
0, E
i
′
,S
′
, j
′
,T
′
6=
/
0, and
E
i
′′
,S
′′
, j
′′
,T
′′
6=
/
0 in such cases. Then, we propose the
following integer linear programming formulation
for finding the minimum directed and undirected
GSPGGs that produce only a given generalized
series-parallel graph G.
Minimize
∑
u∈S ( G)
p
u
Subject to
x
ε,
/
0,ε,
/
0
= 1, (1)
x
i,S, j,T
= 1
for all (i,S, j,T) ∈ I (G) s.t. |E
i,S, j,T
| = 1, (2)
x
i,S, j,T
≤
∑
(i
′
,S
′
, j
′
,T
′
,i
′′
,S
′′
, j
′′
,T
′′
)∈C (G
i,S, j,T
)
y
i
′
,S
′
, j
′
,T
′
,i
′′
,S
′′
, j
′′
,T
′′
for all (i,S, j,T) ∈ I (G) s.t. |E
i,S, j,T
| ≥ 2, (3)
y
i
′
,S
′
, j
′
,T
′
,i
′′
,S
′′
, j
′′
,T
′′
≤
1
2
(x
i
′
,S
′
, j
′
,T
′
+ x
i
′′
,S
′′
, j
′′
,T
′′
)
for all (i
′
,S
′
, j
′
,T
′
,i
′′
,S
′′
, j
′′
,T
′′
) ∈ C (G
i,S, j,T
),(4)
p
u
≥
1
|E|
∑
G
i,S, j,T
∈E (u)
x
i,S, j,T
for all u ∈ S (G), (5)
p
u
< 1+
1
|E|
∑
G
i,S, j,T
∈E (u)
x
i,S, j,T
for all u ∈ S (G),(6)
x
i,S, j,T
,y
i
′
,S
′
, j
′
,T
′
,i
′′
,S
′′
, j
′′
,T
′′
, p
u
∈ {0,1}.
In this formulation, x
i,S, j,T
= 1 if G
i,S, j,T
is gen-
erated by the minimum GSPGG, otherwise 0. In the
minimum SEO(U)TG, the Euler string is used to de-
termine whether or not partitioned subtrees are iso-
morphic. However, it cannot be used for GSPGs,
and we must investigate whether or not G
i,S, j,T
is
isomorphic to G
i
′
,S
′
, j
′
,T
′
. Eqs. (5) and (6) represent
that p
u
= 1 for u ∈ S (G) if and only if a subgraph
G
i,S, j,T
isomorphic to u is generated by the mini-
mum GSPGG, otherwise 0. The objective function
indicates the number of nonterminal symbols in the
grammar, and the integer linear programming prob-
lem finds the minimum GSPGG. Eq. (1) represents
that G is constructed by the grammar. Eq. (2) repre-
sents that each edge in G is constructed by the gram-
mar. Eq. (3) represents that G
i,S, j,T
is constructed
by some production rule. Eq. (4) represents that a
production rule can be candidate in the grammar if
both of G
i
′
,S
′
, j
′
,T
′
and G
i
′′
,S
′′
, j
′′
,T
′′
are constructed by
the grammar. Since the problem of finding the mini-
mum directed and undirected GSPGGs that produce
only a given GSPG is NP-hard, it is reasonable to
solve it by utilising integer linear programs.
3 CONCLUSION
In this paper, we proposed the definition of di-
rected and undirected generalized series-parallel
graph (GSPG) grammars, and an integer linear
programming-based method for finding the minimum
GSPG grammar that produces only a given GSPG.
It has been proved that any outerplanar graph is a
GSPG. We can find the minimum grammar for trees,
outerplanar graphs, and GSPGs. As future work, we
would like to apply our method to biological struc-
tured data, and extract production rules to construct
the structure. Our integer linear programming for-
mulation can take exponential time of the size of a
GSPG. Hence, we would like to analyze the time
complexity for the case that the degree of every node
is less than a constant value. Furthermore, we would
like to uncover what kind of graphs other than trees
and outerplanar graphs can be handled by directed
and undirected GSPGGs.
ACKNOWLEDGEMENTS
This work was partially supported by Grants-in-Aid
#16K00392, #16KT0020, and #26240034 from JSPS,
Japan.
REFERENCES
Akutsu, T. (2010). A bisection algorithm for grammar-
based compression of ordered trees. Information Pro-
cessing Letters, 110:815–820.
Eikel, M., Scheideler, C., and Setzer, A. (2015). Minimum
linear arrangement of series-parallel graphs. Lecture
Notes in Computer Science, 8952:168–180.
Eppstein, D. (1992). Parallel recognition of series-parallel
graphs. Information and Computation, 98:41–55.
Ho, C., Hsieh, S., and Chen, G. (1999). Parallel decompo-
sition of generalized series-parallel graphs. Journal of
Information Science and Engineering, 15:407–417.
Hopcroft, J., Motwani, R., and Ullman, J. (2001). Introduc-
tion to Automata Theory, languages, and Computa-
tion, chapter Chapter 5: Context-Free Grammars and
Languages, pages 169–218. Addison-Wesley, Boston,
2 edition.
Korneyenko, N. (1994). Combinatorial algorithms on
a class of graphs. Discrete Applied Mathematics,
54:215–217.
Zhao, Y., Hayashida, M., and Akutsu, T. (2010). Inte-
ger programming-based method for grammar-based
tree compression and its application to pattern extrac-
tion of glycan tree structures. BMC Bioinformatics,
11(Suppl 11):S4.
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
110

Zhao, Y., Hayashida, M., Cao, Y., Hwang, J., and Akutsu,
T. (2015). Grammar-based compression approach to
extraction of common rules among multiple trees of
glycans and RNAs. BMC Bioinformatics, 16:128.
Grammar-based Compression for Directed and Undirected Generalized Series-parallel Graphs using Integer Linear Programming
111
