Adaptive Filtering for Electromyographic Signal Processing in Scoliosis
Indexes Estimation
Eleonora Sulas
1
, Luigi Raffo
1
, Marco Monticone
2
and Danilo Pani
1
1
Dept. of Electrical and Electronic Engineering, University of Cagliari, Cagliari, Italy
2
Dept. of Medical Sciences and Public Health, University of Cagliari, Cagliari, Italy
Keywords:
Scoliosis, EMG, Adaptive Filters, RLS, ECG.
Abstract:
Adolescent idiopathic scoliosis is defined as a three-dimensional deformity of the spine and trunk occurring
in about 2.5% of most populations. It is usually analyzed radiographically, but electromyography (EMG)
can be also used, since muscles activity is correlated to deformity progression. EMG ratio is a numerical
index used in the literature to provide information about scoliosis progression. Trunk EMG recordings are
strongly affected by the electrocardiogram (ECG) of the subject. Previous studies removed this interference
from the EMG signal by blanking the QRS complexes of the ECG but, as a consequence, several segments
of the signal are removed. Furthermore, the other relevant ECG waves such as P and T are not cancelled and
can invalidate the computation of parameters such as the EMG ratio. The aim of this study is to evaluate the
possibility, by means of a modified recording protocol including further electrodes, to completely remove the
ECG interference by adopting a multi-reference recursive least square (RLS) adaptive filter. The results of
the study reveal how the complete clearing of the ECG from the EMG channels leads to different numerical
values of the index, compared to the QRS blanking, more reliable and meaningful for the clinicians.
1 INTRODUCTION
Scoliosis is commonly referred to as a lateral curva-
ture of the spine, but the deformity is much more com-
plex. Indeed, it is a three-dimensional deformity of
the spine and trunk (M. A. Asher et al.).
Adolescent idiopathic scoliosis (AIS) occurs in
healthy pubertal children and the prevalence of AIS
with an angle of the spinal curve larger than 10
◦
is ap-
proximately 2.5% in the general population (M. Mon-
ticone et al.).
The etiology is still poorly defined, even if the
main causes could be recognized as: genetic predis-
position, skeletal, muscular and neurological distur-
bances during growth, connectivity tissue abnormali-
ties (M. Monticone et al.).
The primary treatment goal for adolescents is to
reduce progression in order to decrease the risk of
back pain, disability, breathing problems and cos-
metic deformities, and improve their health-related
quality of life during adulthood.
The condition of subjects with idiopathic scolio-
sis is usually analyzed radiographically. However,
electromyography (EMG) can be also exploited, since
abdominal and paravertebral muscles are essential to
maintain or modify the shape of the spine. EMG is
the recording of the bio-electrical activity of muscle
fibers. For this reason, it has been investigated over
few decades to observe which relation could be rec-
ognized between paraspinal muscles activity and sco-
liosis deformity. Some studies (J. Cheung et al) show
that the paraspinal muscle activity ratios at the lower
end vertebra are correlated to increased axial rotation
of the spine, and provide a valuable tool to predict
a rapid increase of its curvature. The EMG ratio in-
dex involves measurements of the EMG activity on
the convex and concave sides of the scoliotic curve,
identified from a radiographic image on the coronal
plane.
Trunk muscle EMG is contaminated by the elec-
trical activity of the heart (electrocardiogram, ECG),
due to its position in the chest close to the record-
ing site. Other noise sources, such as motion arti-
facts, mains interference, etc., contaminate the EMG
making it difficult to obtain the information of interest
without appropriate signal processing methods.
Notch filters can remove mains interference from
the recorded surface EMG signals very effectively,
whereas high-pass filters with a cut-off frequency
between zero and 5 Hz may be used to remove
Sulas, E., Raffo, L., Monticone, M. and Pani, D.
Adaptive Filtering for Electromyographic Signal Processing in Scoliosis Indexes Estimation.
DOI: 10.5220/0006586001610167
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 4: BIOSIGNALS, pages 161-167
ISBN: 978-989-758-279-0
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
161

R
Q
P
S
T
Figure 1: Main epochs of the cardiac cycle as visible in one
ECG lead (synthetic data).
Figure 2: Positioning of the 12 electrodes for the 6-channel
EMG recordings following the protocol adopted for this
study.
Figure 3: ECG electrodes sites following the protocol
adopted for this study.
movement-induced baseline wandering artifacts.
Different methods have been proposed to remove
the ECG artifact from EMG signals. This problem is
usually solved by blanking the QRS complexes from
the ECG signal (J. Cheung et al). QRS is the epoch
of the ECG related to the ventricular depolarization,
originating the heart systole, and it represents the
sharpest and tallest waveform of the ECG, as clearly
visible from Fig. 1. This approach is challenged in
this paper, since it leads to the cancellation of useful
s(k)+n(k)
ñ(k) x(k)
e(k)
d(k)
y(k)
-
+
ŝ(k)
Figure 4: Typical scheme of an adaptive noise canceler.
Figure 5: Multichannel adaptive filter.
segments of the EMG signal and, at the same time,
it does not solve the problem of removing the other
ECG waves (P and T, see Fig. 1).
In a previous work (Lu G. et al), a single-channel
adaptive noise canceler based on the recursive least
square (RLS) approach was evaluated as effective
and efficient for ECG cancellation in surface EMG
recordings. In this work, we propose the adoption of
multi-reference RLS adaptive filters for ECG interfer-
ence cancellation in EMG ratio indexes computation
(J. Cheung et al), comparing the results with those
achievable by using QRS blanking. The results high-
light the better quality of the signal processed with the
proposed method and, consequently, a more reliable
estimation of the EMG ratio.
2 MATERIALS AND METHODS
The acquisition protocol for the EMG signal is first
described in this section. Then, the two different al-
gorithms used to cancel the ECG interference from
the EMG signals are presented, along with the study
population.
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
162

2.1 Signal Acquisition Protocol
From a radiographic image of the trunk, in a coronal
projection, it was possible to define which were the
upper and lower vertebrae and the apex vertebra of the
curve deformity. This is important to define the elec-
trodes placement sites. Furthermore, the Cobb angle
(i.e. the angle formed between a line drawn parallel
to the upper border of the upper vertebral body and a
line drawn parallel to the lower border of the lowest
vertebra of the scoliotic curve; then erecting perpen-
diculars from these lines to cross each other, the angle
between these perpendiculars being the angle of cur-
vature”, see Fig. 2) was determined.
To measure the activity of the paraspinal mus-
cles, in particular of the multifidus muscles, six
pairs of disposable adhesive surface EMG electrode
(CDES000024 by Spes Medica srl) were placed sym-
metrically with respect to the superficial spinae mus-
cles at three different levels, corresponding to the
upper-end, apex and the lower-end vertebrae of the
curve. An example of this electrode positioning is
shown in Fig. 2. The electrodes were chosen focus-
ing on the performance in terms of signal recording
and children’s comfort due to the light adhesive prop-
erties of the solid hydrogel.
The EMG measurements were performed at rest
in standing position, for 60 s. Four electrode were
placed on the torso, as it can been seen from Fig. 3,
in order to collect the ECG along three orthogonal
axes in space. This enables the reconstruction of the
electrical activity of the heart in the three dimensions,
yielding a better projection of this activity in possibly
any place on the body surface.
Signal acquisition was performed by using a 32-
channels physiological recording device, namely the
Porti7 by TMSI BV. It is a general purpose record-
ing instrument providing unipolar and bipolar elec-
trophysiological inputs and auxiliary inputs. In this
application, 16 unipolar channels were used and the
bipolar leads were obtained digitally post-processing
the unipolar leads. The sampling frequency was set
to 2048 Hz for each channel and the digital data res-
olution was 22 bits, 71.526 nV per bit, with a gain of
50 mV/V. No analog filtering is present in the signal
chain. Decimation and linear phase digital low-pass
filtering is performed inside the analog to digital con-
verter (cut-off frequency is 553 Hz).
2.2 ECG Cancellation by
Multi-reference RLS Adaptive
Filter
Fig. 4 shows the block diagram of an adaptive noise
canceller. The aim of an adaptive filter used in an in-
terference cancellation configuration, is to extract a
clean version of the signal of interest s(k). This sig-
nal is corrupted by the additive noise component n(k).
Employing a reference signal strongly correlated to
the noise but not to the signal of interest, the adap-
tive filter adjusts its coefficients in order to obtain an
output y(k) that approximates n(k), forcing the error
signal e(k) to resemble s(k).
d(k) = s(k) + n(k) (1)
x(k) ≈ n(k) (2)
y(k) = w
T
x(k) (3)
Adaptation of the filter coefficients follows a min-
imization procedure of a particular objective or cost
function. The classical linear Wiener filter minimises
the mean-square error (MSE):
ξ(k) = E[e
2
(k)] (4)
ξ(k) = E[d
2
(k)] − 2w
T
p + w
T
Rw (5)
Equating the gradient vector of ξ respect to the
adaptive filter coefficient w to zero minimizes the
MSE cost function:
∆
w
ξ
D
(k) = −2p(k) + 2R(k)w (6)
obtaining:
w(k) = R
−1
(k)p(k) (7)
where R is the input signal correlation matrix and
p the crosscorrelation vector between the reference
signal and the input signal. To be able to solve the
Wiener solution, R must be non-singular. If the filter
length is greater than that required to reduce the error
to zero, R(n) will become singular.
RLS filter family uses the weighted least-squares
objective function, instead of the MSE cost function,
defined as:
ξ
D
(k) =
k
∑
i=0
λ
k−1
[d(i) − w
T
x(i)] (8)
The forgetting factor λ, which is a real valued pa-
rameter in the range from 0 to 1, allows to emphasize
the most recent error samples, giving to the objective
Adaptive Filtering for Electromyographic Signal Processing in Scoliosis Indexes Estimation
163

function the ability of modelling non-stationary pro-
cesses.
The RLS algorithm adaptively updates the coeffi-
cient vector to minimize the summation of weighted
least-square errors. In particular, it defines the R and
p parameters, introducing the forgetting factor λ:
R(k) =
k
∑
i=0
λ
k−1
x(i)x
T
(k) = X
T
(k)X(k) (9)
p(k) =
k
∑
i=0
λ
k−1
d(i)x(i)0X
T
(k)d(k) (10)
Consequently, the optimum solution takes the
form:
w(k) = R
−1
(k)[x(k)e(k) + R(k)w(k − 1)] (11)
The computation of the inverse matrix of R can
be reduced significantly by using the matrix inversion
lemma, obtaining:
R
−1
=
1
λ
[R
−1
(k − 1) − κ(k)k
T
(k)] (12)
where:
κ(k) = R
−1
(k)x(k) (13)
k(k) = R
−1
(k − 1)x(k) (14)
At each step, the RLS algorithm estimates R and
P based on all past data and updates the weight vector
using the matrix inversion lemma. The filter coeffi-
cient update equation becomes:
w(k) = w(k − 1) + e
∗
(k)κ(k) (15)
The RLS filter does not attempt to solve the
Wiener solution at each step, that would require the
calculation of repeated inverted R matrix, but updates
R
−1
(k) using R
−1
(k − 1), the inverted R matrix of the
previous step. In this case, no matrix inversion is re-
quired, as it is shown in Eq. 15. The only invertible
matrix that is required to be calculated is R
−1
(0).
In this application, a multireference RLS adaptive
filter is used to process each EMG channel d(k) for
ECG interference cancellation. The three projections
of the ECG along the three orthogonal axes described
by the combination of the four electrodes on the torso
represent the three different components of x(k). In
the particular case of multi-reference, the block dia-
gram presents a difference in the x(k) input signal, as
it is shown in Fig. 5, where the input vector at k instant
does not present only one sample, but the samples at
k instant of all the inputs considered by the system.
For the RLS filter computation, at k = 0, the initial
instant, two variables must be chosen from the user:
the initial coefficient vector w and the inverse matrix
of R. If there are some a priori information, they can
be used to set the first values of the w vector, if not,
w(0) is set as an array of zeros. Moreover, the for-
getting factor λ has to be chosen. It impacts on the
ability to track the input signal and on the stability
of the filter coefficient. To this aim, λ was empirically
fixed at 0.98. As the number of the processed samples
increases, the effect of this initialization error will de-
crease because of the effect of the weighting factor
λ.
It is not simple to choose the length of data re-
quired for ensuring invertibility of R. The RLS
method uses an approximate initialization, so it does
not require matrix inversion. At k = 0, the coefficient
vector w is inizialized to an array of 0, of the length
3 (the length of each of the three reference channel
was chosen equal to 1). The initial correlation matrix
R
−1
(0) was set equal to the identity matrix of 3 × 3,
because of the channel length of 1 and the use of 3
channels. The trick behind the chosen R
−1
(0) is that
it could be defined as:
R
−1
(0) = δI (16)
where δ is the regularization parameter, to which
should be assigned a small value for high signal-to-
noise ratio (SNR) and a large value for low SNR,
which may be justified on regularization grounds
(Haykin S.).
To sum up, Alg. 1 presents the pseudocode of this
method, where the invR, R
−1
(k), is the result of the
combination of the past invR, R
−1
(k − 1). Moreover,
in the case of multireference adaptive filter, the error
vector E is the result of the difference between d, the
raw EMG signal, that presents the signal of interest
and the noise, and the scalar product of the coefficient
vector w and the three reference signals x.
Before feeding the signals to the multi-reference
RLS adaptive filter, they have been high-pass filtered
in order to remove large baseline wandering artifacts.
To this aim, a linear-phase equiripple finite impulse
response (FIR) filter (order 1124, 80 dB attenuation)
with a cut-off frequency of 5 Hz was designed. Be-
ing an offline processing, no special care was paid to
the filter order, preferring to achieve a linear phase
response associated with filter causality.
Even though the adaptive filter is able to cancel
the whole ECG interference, not only the QRS com-
plexes, their attenuation can be used to evaluate the
cancellation performance, since it is the highest com-
ponent of the ECG signal.
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
164

2.3 ECG Cancellation by QRS Blanking
QRS blanking (M. Monticone et al.) was performed
on each EMG channel, pre-processed using the same
FIR filter adopted for the previous method. In this
way, variability in the ECG cancellation performance
cannot be biased by a different pre-processing stage.
Algorithm 1 : Pseudocode of the multireference RLS
algorithm.
for each sample of the X matrix x do
//X contains the x inputs
κ = invR · X;
k = κ/(λ + X
0
· κ);
invR = (1/λ) · (invR − κ · κ
0
/(λ + X
0
· κ));
E = d −W
0
· X;
W = W + E
∗
· k;
end for
However, for QRS blanking, the 50 Hz noise was
eliminated by using a notch filter. Afterwards, a peak
detection algorithm was used to find the R peak of the
ECG waves. The peak detection algorithm applied
in this work is the Pan-Tompkins algorithm (J. Pan
et al.). Pan-Tompkins method filters the ECG signal
through a band-pass filter to emphasize the QRS com-
plex band. The filtered signal goes through a deriva-
tive filter, then it is squared and a moving window in-
tegration is applied. Finally, R peaks detection is per-
formed by means of an adaptive thresholding mecha-
nism. The QRS complexes were removed by deleting
the samples in an interval of 125 ms around the R
peaks.
No other waves of the ECG signal (i.e., P and T)
are removed or attenuated by this approach.
2.4 Paraspinal Activity Ratio
The paraspinal activity EMG ratio is defined as the
absolute summated EMG amplitudes, over the total
EMG recording time, of an electrode pair on the con-
vex side divided by the same quantinti of a contralat-
eral electrode pair on the concave side. EMG is re-
ferred to the erector spinae muscles.
In this way, an activity EMG ratio of one means
that the EMG activities on the convex and concave
sides of the scoliotic curve are the same. An EMG
activity ratio higher than one means that the EMG ac-
tivity on the convex side is greater than that on the
concave side. Finally, an EMG activity ratio lower
than one stands for less EMG activity on the con-
vex side than on the concave side (J. Cheung et al).
The study (J. Cheung et al) correlates both spinal
speed and muscle activity asymmetry to the progres-
sion of the idiopathic scoliosis. The evidences from
that study reveal that, in the standing condition, the
lower end vertebra index values are recognized in the
non-progressive groups if they fall in the range [0.43
1.64], while the range [0.80 7.86] is recognized as a
progressive idiopathic scoliosis.
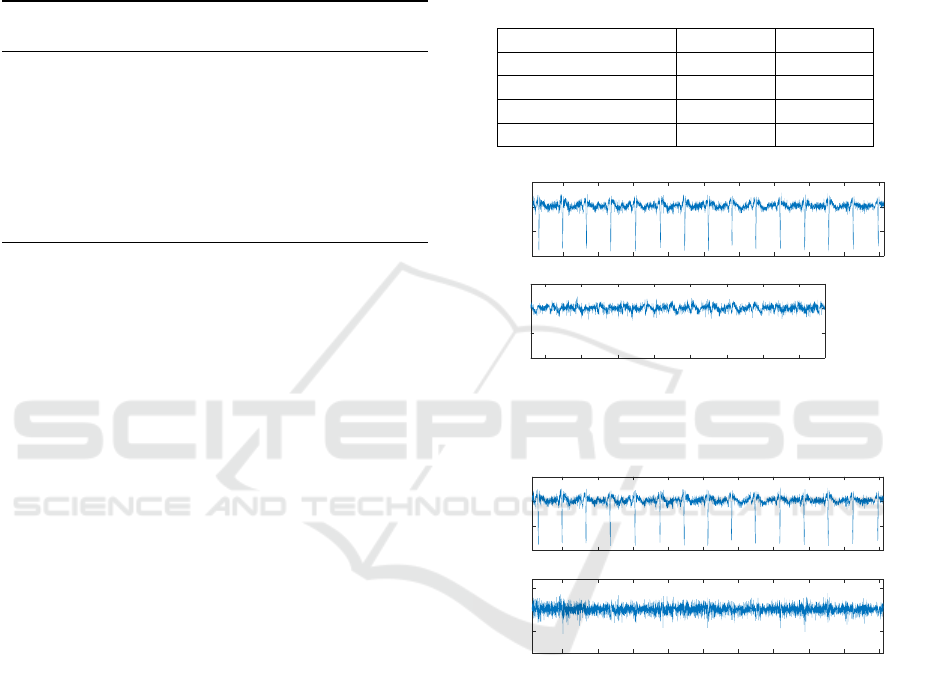
Table 1: Study Population.
Subject 1 Subject 2
Upper end vertebra D11 D10
Lower end vertebra L4 L3
Apex vertebra L2 L1
Cobb angle 14
◦
19
◦
45 46 47 48 49 50 51 52 53 54
time [s]
-200
-100
0
100
Amplitude [uV]
36 37 38 39 40 41 42 43
time [s]
-200
-100
0
100
Amplitude [uV]
Figure 6: From top to bottom: 5 Hz high-pass filtered signal
and processed signal by QRS blanking.
45 46 47 48 49 50 51 52 53 54
time [s]
-200
-100
0
100
Amplitude [uV]
45 46 47 48 49 50 51 52 53 54
time [s]
-100
-50
0
50
Amplitude [uV]
Figure 7: From top to bottom: 5 Hz high-pass filtered signal
and RLS adaptive filtered signal.
2.5 Study Population
In order to test the algorithms on real signals, two fe-
male subjects, with a right dorso-lumbar adolescent
idiopathic scoliosis, were enrolled in the study. The
study was performed following the principles out-
lined in the Helsinki Declaration of 1975, as revised
in 2000.
In Table 1, the principal characteristics of the two
enrolled subjects are presented. The Upper, Lower
and Apex vertebra are referred to the anatomical name
of each spine vertebra(C, cervical; D dorsal, thoracic;
L, lumbar; S, sacral).
Adaptive Filtering for Electromyographic Signal Processing in Scoliosis Indexes Estimation
165

1 2 3 4 5 6
EMG signals
-20
-15
-10
-5
0
Attenuation dB
Figure 8: Boxplots of the six signals of Subject 1.
1 2 3 4 5 6
EMG signals
-20
-15
-10
-5
0
Attenuation dB
Figure 9: Boxplots of the six signals of Subject 2.
3 RESULTS
3.1 ECG Cancellation Results
The raw signals were first preprocessed by using the
5 Hz high pass filter, mainly introduced to remove the
baseline wandering artefact, and then processed ac-
cording to the two algorithms described above. As
it can be seen from Fig. 6, when QRS blanking al-
gorithm is used, the P and T waves keep to stay in
the processed signal, despite they are mainly charac-
terized by low frequency components. Moreover, the
processed signal is shortened compared to the original
one, also losing the EMG information present in the
blanked parts. This can be also seen in Fig. 6, where
10 seconds of the original signal correspond to about
8 seconds of the QRS blanked signal.
Conversely, as it can be seen from Fig. 7, by us-
ing the RLS adaptive filter, P and T waves are also
attenuated without any sample loss.
The attenuation of the QRS complexes provided
by the adaptive filter was evaluated for the six EMG
channels recorded on each subject. The results of
such an analysis are reported in the boxplot in Fig. 8
and Fig. 9. In such figures, the median is highlighted,
the box defines the 50% of the samples between the
first and third quartile, and the whiskers range from
the minimum to the maximum value, excluding the
outliers (represented with crosses). The outliers are
defined as data larger than q3 + 1.5(q3 - q1) or smaller
than q1 - 1.5(q3 - q1), where q1 and q3 are the 25
th
and 75
th
percentiles, respectively, corresponding to
approximately ± 2.7σ and 99.3 coverage, if the data
are normally distributed.
Table 2: Paraspinal activity ratio results (LE Lower End,
UE Upper End).
Blanking Adaptive ∆
Filter
Subject Apex Vertebra 0.77 0.63 0.14
1 LE Vertebra 0.82 1.05 0.23
UE Vertebra 0.08 0.77 0.69
Subject Apex Vertebra 0.88 1.2 0.32
2 LE Vertebra 0.81 1.04 0.23
UE Vertebra 0.8 0.98 0.18
3.2 Paraspinal Activity Ratio Results
The EMG activity ratio was evaluated on the signals
processed using the two methods. The results are
summarized in Table 2.
The absolute difference ∆ between the two in-
dexes is quite large, up to 0.69. The achieved results
can be ascribed to the poor cancellation of the ECG
signal with the QRS blanking methods, as depicted in
Fig. 6. In this case, the contribution of P and T waves
still affects the EMG signals. Despite the QRS com-
plex is the highest component of the ECG, the other
waves exhibit a wider support, so that QRS blank-
ing is not sufficient to obtain an ECG-independent
signal for the computation of the EMG activity ra-
tio. The limitation of this study is the small study
population, requiring the acquisition of a larger one.
Moreover, ∆ is remarkably too high, also compared to
the typical range of variability of this parameter pre-
sented in (J. Cheung et al) and in 2.4. Such a big ∆
make the two groups, non-progressive and progres-
sive idiopathic scoliosis, possible to confuse the two
population. In order to evaluate the significance of
the paraspinal ratio recognizing those two groups, a
larger dataset composed by healthy and AID subjects
is needed.
4 CONCLUSION
In this work, two processing methods for the reduc-
tion of the ECG signal in EMG recordings for the
evaluation of the EMG activity ratio index have been
presented. QRS blanking and multi-reference RLS
adaptive filtering have been used to process real data
from subjects with AID. Despite the state of the art
in the field only exploits QRS blanking for EMG pre-
processing, the results presented in this work suggest
that the non-complete removal of the ECG interfer-
ence could hamper the achievement of a meaningful
value for this index.
In the light of the results achieved in this work,
we are currently acquiring a larger dataset including
BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing
166

healthy subjects and patients affected by AID. This
will strengthen the evidences of the present study in
terms of EMG activity ratio index pre-processing.
Furthermore, with a larger dataset, homogeneous
groups composed of a significant number of subjects
can be formed. Such an approach is needed to study
the effectiveness of the EMG activity ratio index with
the improved pre-processing.
ACKNOWLEDGEMENTS
The authors wish to thank the physiotherapist and the
subjects who took part in the study. Eleonora Sulas
is grateful to Sardinia Regional Government for sup-
porting her PhD scholarship (P.O.R. F.S.E., European
Social Fund 2014-2020).
REFERENCES
M. A. Asher and D. C. Burton (2006) Adolescent idiopathic
scoliosis: natural history and long term treatment ef-
fects. Scoliosis, vol. 1, no. 1, p. 2.
M. Monticone, E. Ambrosini, D. Cazzaniga, B. Rocca, and
S. Ferrante (2014) Active self-correction and task-
oriented exercises reduce spinal deformity and im-
prove quality of life in subjects with mild adoles-
cent idiopathic scoliosis. Results of a randomised
controlled trial. Eur. Spine J., vol. 23, no. 6, pp.
12041214.
J. Cheung et al. (2005) A preliminary study on electromyo-
graphic analysis of the paraspinal musculature in id-
iopathic scoliosis. Eur. Spine J., vol. 14, no. 2, pp.
130137.
Lu G., Brittain J., Holland P., John Yiannib J., Greenb A.L.,
Stein J.F., Aziz T.Z., Wang S. (2009) Removing ECG
noise from surface EMG signals using adaptive filter-
ing. Neurosci Lett. vol. 462, no. 1, pp.9-14.
J. A. Apolin
´
ario (2009) QRD-RLS adaptive filtering.
J. Pan and W. J. Tompkins (1985) A Real-Time QRS Detec-
tion Algorithm. IEEE Trans. Biomed. Eng., vol. BME-
32, no. 3, pp. 230236.
Haykin S.(2014) Adaptive Filter Theory. Pearson Education
Limited 2014.
Adaptive Filtering for Electromyographic Signal Processing in Scoliosis Indexes Estimation
167