Knee Kinematics Feature Selection for Surgical and Nonsurgical

Arthroplasty Candidate Characterization

M. A. Ben Arous

1,6

, M. Dunbar

, S. Arfaoui

3,6

, A. Mitiche

, Y. Ouakrim

4,6

, A. Fuentes

G. Richardson

and N. Mezghani

4,6

Collège Bois de Boulogne, Montreal, Quebec, Canada

Dalhousie University, Halifax, Nova Scotia, Canada

Collège Jean-de-Brébeuf, Montreal, Quebec, Canada

LICEF Research Center, TELUQ University, Montreal, Quebec, Canada

INRS Énergie, Matériaux et Télécommunications, Montreal, Quebec, Canada

Laboratoire de Recherche en Imagerie et Orthopédie (LIO), ETS/CRCHUM, Montreal, Quebec, Canada

Keywords:

Knee Kinematic, Biomechanical Data, Feature Selection, Complexity Measures, Arthroplasty.

Abstract:

The purpose of this study is to investigate a method to select a set of knee kinematic data features

to characterize surgical vs nonsurgical arthroplasty subjects. The kinematic features are generated from

3D knee kinematic data patterns, namely, rotations of ﬂexion-extension, abduction-adduction, and tibial

internal-external recorded during a walking task on a dedicated treadmill. The discrimination features are

selected using three types of statistical complexity measures: the Fisher discriminant ratio, volume of overlap

region, and feature efﬁciency. The interclass distance measurements which the features thus selected induce

demonstrate their effectiveness to characterize surgical and nonsurgical subjects for arthroplasty.

1 INTRODUCTION

Knee kinematic data during locomotion, which

can be easily acquired in clinical settings (Lustig

et al., 2012), provide useful information about

knee function and can serve the development of

objective methods of computer aided diagnosis to

assist surgical decisions and treatment.

Preoperative knee conditions, prosthesis design,

and surgical techniques all inﬂuence knee kinematics

following an arthroplasty. However, kinematic

studies have primarily focused on postoperative

knee kinematics (Seon et al., 2011). Preoperative

investigations have been scarce (Casino et al., 2009;

Casino et al., 2008; Mihalko et al., 2007) in great part

due to knee kinematic data complexity (Mezghani

et al., 2008), which are high-dimensional vectors and

of high variability. The studies in (Casino et al.,

2009; Casino et al., 2008; Mihalko et al., 2007)

investigated knee kinematic data of osteoarthritis

patients and (Mezghani et al., 2016) speciﬁcally

addressed surgical vs nonsurgical discrimination of

candidates for arthroplasty.

High kinematic data variability and

dimensionality are illustrated in Figure 1, which

shows the graph of a sample of one hundred

ﬁfty-three (153) participants curves and their

average curves. The intra-class high variability and

inter-class proximity, which are evident in the ﬁgure,

make discriminating feature extraction notoriously

difﬁcult. In spite of the importance of this problem,

there has been no investigation of feature extraction

in terms of objective metrics. By reducing the

dimension of the data representation vector, feature

selection affords a means of escape from the curse of

dimensionality while maintaining a good description

of the data. The feature selection methods are usually

evaluated using the classiﬁcation rate of a chosen

classiﬁer. However, these methods are classiﬁer

dependent. Our goal is to investigate measures for

feature selection independent of classiﬁers design.

In this study, we propose a knee kinematics

feature selection method based on statistical

complexity measures, namely, the Fisher

discriminant ratio, volume of overlap region,

and feature efﬁciency. The purpose is to select the

most discriminant features from a feature set of

interest in a classiﬁcation task.

176

Arous, M., Dunbar, M., Arfaoui, S., Mitiche, A., Ouakrim, Y., Fuentes, A., Richardson, G. and Mezghani, N.

Knee Kinematics Feature Selection for Surgical and Nonsurgical Arthroplasty Candidate Characterization.

DOI: 10.5220/0006586601760181

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 4: BIOSIGNALS, pages 176-181

ISBN: 978-989-758-279-0

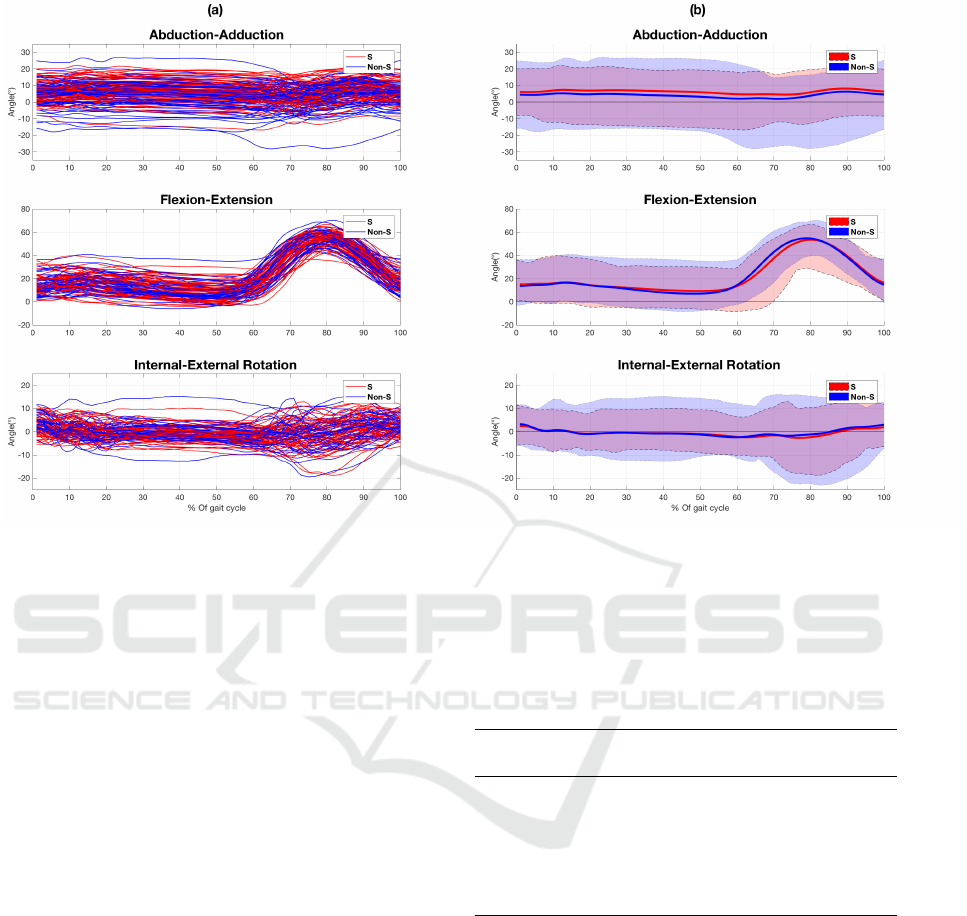
Figure 1: (a) Kinematic gait signals (of the database) during a gait cycle: Abduction-adduction (line1), Flexion-extension

(line 2), and Internal-external rotation (line3). The signals were interpolated and resampled from 1% to 100% (100 points)

of the gait cycle. Each red curve represents a surgical participant (S) and each blue one represent a Non-Surgical (Non-S)

participant (b) The mean and standard deviation of the kinematic gait signals. The blue and red lines represent respectively

the S and Non-S group average patterns.

2 METHODS

2.1 Database

The database was provided by the Division of

Orthopedic Surgery in Halifax QEII Health Sciences

Center (Nova Scotia, Canada). The one hundred

ﬁfty-three (153) participants enrolled for the research

had a diagnosis of knee osteoarthritis ranging from

moderate to severe condition and were all scheduled

for an arthroplasty consult. All participants also

went through an orthopedic physical assessment

by one of two experienced orthopedic surgeon

and were consequently assigned to surgical (S) or

nonsurgical (Non-S) groups. Table 1 summarizes

the principal demographic characteristics of the

participants. A t-test was performed to examine the

general participant characteristic differences between

the two groups. The statistical analysis was conducted

using SPSS 20.0 (Statistical Package for Social

Sciences). The P-value of 0.05 was set as level of

statistical signiﬁcance.

All participants underwent physiotherapy

assessment and patients reported outcome

questionnaires. Three-dimensional (3D) knee

Table 1: Demographic characteristics of S and Non-S

groups (BMI design the mean body mass index).

Groupe S Groupe Non-S

N =80 N = 73

Age (year) 64, 7 ± 9, 3 64.2 ± 9.2

Height(m) 1.67 ± 0.1 1.69 ± 0.1

Weight (kg) 92.8 ± 23.7 90.9 ± 19.3

BMI (kg / m

) 33.13 ± 7.0 31.5 ± 6, 0

Proportion of

men / group

37% 50%

kinematics data, namely, rotation measurements

for ﬂexion-extension, abduction-adduction, and

tibial internal-external, in the sagittal, frontal,

and transverse planes, respectively, were recorded

while each participant walked on a treadmill at a

self-selected, comfortable speed. A validated knee

marker attachment system, the KneeKG system

(Emovi Inc, Montreal, Canada) (Figure. 2), was

installed on the participant’s knee to record the 3D

kinematics data during gait trials of 45 sec on an

instrumented treadmill at a comfortable self-speed.

This motion capture device is composed of a

harness and a tibial plate ﬁxed quasi rigidly onto

Knee Kinematics Feature Selection for Surgical and Nonsurgical Arthroplasty Candidate Characterization

177

the femoral condyles and tibial crest, and provides

accurate, repeatable, and reliable measurements

(Lustig et al., 2012). A number of representative

gait cycles, generally 15, were averaged to obtain

a means pattern per subject. This was followed by

interpolation and resampling from 1% to 100% of the

gait cycle, therefore giving 100 measurement points

for each participant (Figure. 1).

Figure 2: Knee kinematic acquisition system.

2.2 Kinematic Feature Extraction

Sixty-nine (69) biomechanical parameters were

extracted from the 3D kinematic signals. These were

chosen from the common variable in clinical

biomechanical studies of knee osteoarthritis

populations (Astephen et al., 2011; Bytyqi et al.,

2014; Mezghani et al., 2017), such as maxima,

minima, varus and valgus thrusts, angles at initial

contact, mean value and range of motion (ROM)

throughout gait cycles, and sub-phases (stance phase,

swing phase) as illustrated in Figure 3.

Figure 3: Gait cycle phases and sub-phases.

2.3 Kinematic Feature Selection using

Statistical Measures of Complexity

Statistical measures of complexity, which evaluates

class ambiguity, were used to afford an evaluation

of the discriminant power of the class representation

features, i.e., the features capacity to distinguish data

samples from distinct classes. For each individual

feature, the complexity measure examines the range

and spread of the values of instances of different

classes and verify the discriminant power of a single

feature.

Let D = {x

, x

, ....., x

} a data set containing

n elements, each belonging to one of two distinct

classes c

and c

. In our case, c1 corresponds to

the surgical group (S) and c

to nonsurgical group

(Non-S). Each element x is characterized by a feature

vector ( f

, f

, ... f

), where p is the dimension of the

feature space (p = 69 biomechanical parameters).

The overlap is evaluated according to the

following measures:

2.3.1 Fisher Discriminant Ratio (F1)

This measure computes the maximum discriminative

power of each feature. For a two-class data set, the

Fisher discriminant ratio F1(i) of a feature f

, (i =

1, ..., p), is deﬁned as:

F1(i) =

(µ

− µ

)

(σ

+ σ

)

, (1)

where µ

, µ

, σ

are the means and variances

of the two classes, respectively, according to the i

feature, (i = 1, 2, . . . , p).

A high value of the Fisher’s discriminant ratio

indicates that the feature enables to separate the data

set of different classes with partitions that are parallel

to an axis of the feature space.

2.3.2 Volume of Overlap Region (F2)

This measure estimates the amount of relative overlap

of the bounding regions of two classes (Lorena and

de Souto, 2015). For each feature f

, (i = 1, ..., p),

where p is the dimension of the feature space, the

Volume of overlap region (F2) is deﬁned as:

F2(i) =

MinMax(i) − MaxMin(i)

MaxMax(i) − MinMin(i)

(2)

MinMax(i) = min(max( f

, c

), max( f

, c

))

MaxMin(i) = max(min( f

, c

), min( f

, c

))

MaxMax(i) = max(max( f

, c

), max( f

, c

))

MinMin(i) = min(min( f

, c

), min( f

, c

))

where f

is the i-th feature. c

and c

refer to

the two classes and max( f

, c

) and min( f

, c

) are,

respectively, the maximum and minimum values of

the feature f

for class c

. In other words, the volume

BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing

178

of overlap is evaluated using the ratio of the width of

the overlap interval MinMax(i) − MaxMin(i) to the

width of the entire interval MaxMax(i) − MinMin(i).

A low value of the volume of overlap region

means that the feature can discriminate the examples

of different classes.

2.3.3 Feature Efﬁciency (F3)

The feature efﬁciency measure is particularly relevant

when dealing with high-dimensional data. It

informs on how much each feature contributes to

the separation of the classes. The contribution is

called efﬁciency. For each feature, the ambiguous

(overlapping) regions are removed so that only

non-overlapping regions remain.

Let MinMax

= min(max( f

, c

), max( f

, c

)) and

MaxMin

= max(min( f

, c

), min( f

, c

)). For each

feature f

, the feature efﬁciency F3(i) is given by the

following ratio:

F3(i) =

| f

∈ [MinMax

, MaxMin

, (3)

where | | denotes the number of non-overlapping

elements and n is the total number of elements in both

classes.

2.3.4 Thresholds of Class Ambiguity Measures

To be used to select the discriminant feature, the class

ambiguity measures require, for each measure, the

estimation of a threshold to decide if a speciﬁc feature

is whether discriminant or not.

We investigated thresholds estimation using

the probability distribution of the class ambiguity

measures. For each measure, i.e., the Fisher

discriminant ratio F1(i), the volume of overlap region

F2(i) and the feature efﬁciency F3(i), a probability

distribution has been determined. The thresholds are

estimated using the 95th quantile of the probability

distribution.

2.4 Evaluation of the Selected Features

Several studies have addressed feature selection

evaluation. The methods of evaluation can be divided

in two major groups: individual feature evaluation

and feature subset evaluation. A subset evaluation is

relevant in our case. We evaluated the efﬁciency of

the selected feature subset using interclass distance.

This measure was compared to the interclass distance

using the original set of all features (consisting of

69 biomechanical features). A high value of the

interclass distance indicates that the features are

relevant.

3 RESULTS AND DISCUSSION

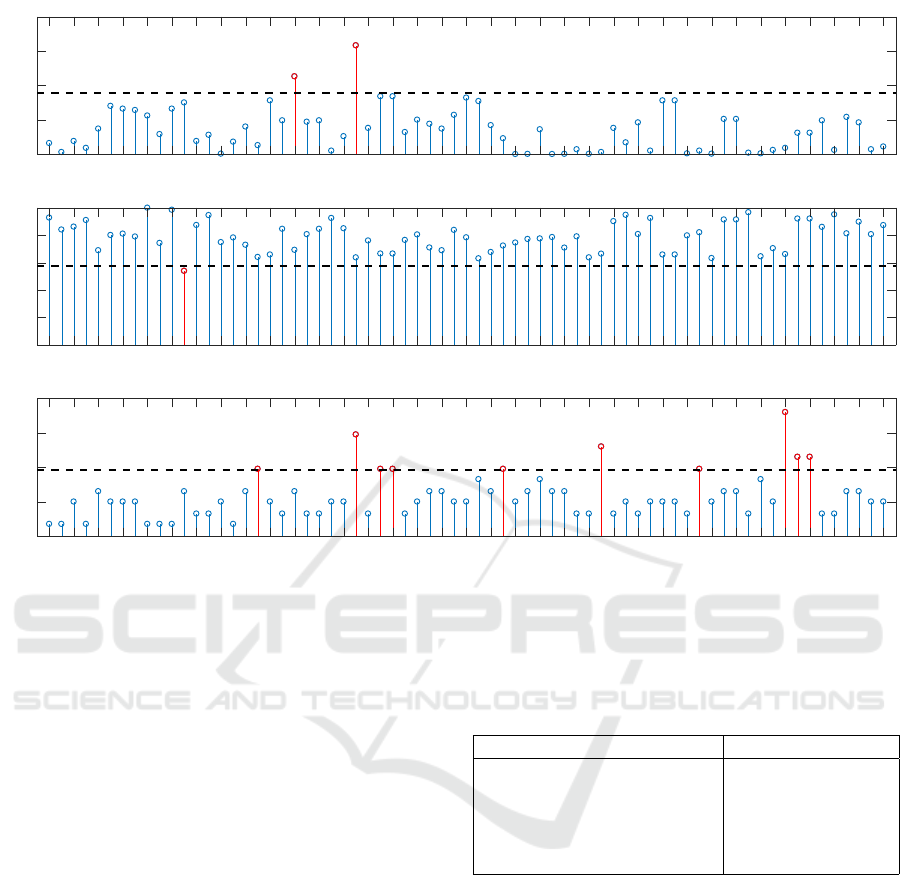
The class ambiguity measures of each feature taken

individually and the corresponding thresholds are

represented in Figure. 4. The thresholds are estimated

using the 95th quantile of the probability distribution

of each complexity measure as explained in the

Section 2.3.4.

Table 2: Selected features.

Selected features

: Minimum frontal plan angle during

mid-stance, where abduction is negative and

adduction is positive

: Maximum axial plane angle, where internal

rotation is negative and external rotation is

positive

: Maximum ﬂexion angle during the loading

phase

: Mean adduction/adduction angle during the

stance phase

: Maximum ﬂexion angle

: % of GC where the maximum angle of

ﬂexion occurs

: Maximum frontal plan angle, where

abduction is negative and adduction is positive

: Frontal plane angle at 54 % of the GC

: Mean transverse plane rotation during the

swing phase

: Transverse plane rotation angle at the end of

the terminal swing

: ROM of the internal/external rotation

: Maximum ﬂexion angle (absolute value)

during loading

Figure 4 (a) represents the discriminant ratio

F1(i) for each feature f

(i = 1, 2, ..., 69) computed

according to Eq. 1. The threshold was set to 0.08.

The selected feature set contains { f

, f

}. In Figure

4(b), we represented the ratio of the width of the

overlap interval F2(i) of each feature. The threshold

here was set to 0.57 and we were interested in low

values of F2(i). The only retained feature is { f

Finally, in Figure 4(c), we represented the individual

feature efﬁciency which describes the ratio of the

number of samples that are not in the overlapping

region to the total number of samples. The threshold

was set to 0.38. The combination of the features

identiﬁed as a result of the complexity analysis

forms the following set of the selected features are:

{ f

, f

}. Table 2

Knee Kinematics Feature Selection for Surgical and Nonsurgical Arthroplasty Candidate Characterization

179

0.05

0.1

0.15

0.2

(a) Fisher discriniminant ratio F1

0.2

0.4

0.6

0.8

(b) Volume of overlap region F2

0.02

0.04

0.06

0.08

(b) Feature efficiency F3

Knee Kinematic feature

Figure 4: Measures of class ambiguity for each feature f

(i = 1, 2, ..., 69): (a) The Fisher discriminant Ratio F1(i); a high

value of F1(i) indicates that the feature is discriminant. (b) The ratio of the width of the overlap interval F2(i); a low value of

F2(i) measure means that the feature can discriminate the samples of different classes. (c) The individual feature efﬁciency

F3(i); a high value of F3(i) indicates a good efﬁciency. The horizontal dashed black lines correspond to the threshold values

and the retained features are in red.

summarizes the selected features and their clinical

meaning.

This result supports previous studies on

biomechanical data and their association with

knee pathologies. Indeed f

, which corresponds

to the ROM of the Internal-external rotation, has

been identiﬁed as a characteristic of improvement

following a total knee replacement surgery (Jones

et al., 2006). Also, f

, which is the mean of

abduction-adduction angle during the stance

phase, has been identiﬁed discriminant for knee

osteoarthritis severity assessment.

The efﬁciency of the subset of selected features

have been measured using the interclass distance

measure (Table 3). This measure is higher when

compared to interclass distance using the whole

feature data set (1832.2 and 987.8 respectively) which

show that the selected features discriminate better the

two classes.

The statistical analysis reveals no differences in

the general characteristics between the two groups

(as described in Table 1), which means that these

characteristics are not involved in the characterization

of surgical and nonsurgical arthroplasty candidates.

Table 3: Surgical and nonsurgical interclass distances.

Data set Inter class distance

Feature data set (69

biomechanical features)

987.8

Selected feature data set

(12 retained biomechanical

features)

1832.2

4 CONCLUSION

In this study, we developed a feature selection method

for 3D knee kinematic data using statistical measures

of class ambiguity. We investigated each feature

taken individually using the Fisher discriminant ratio,

volume of overlap region, feature efﬁciency. Within

the original 69 biomechanical features extracted

from the 3D kinematic signals, 12 features have

been selected that contain pertinent information

to characterize surgical vs nonsurgical arthroplasty

subjects. This set of discriminant features can also

help in future clinical studies to identify biomarkers

for knee surgical arthroplasty candidate treatment.

BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing

180

In a subsequent study, the selected features will

serve as input to build classiﬁcation models to help

discriminate automatically surgical from nonsurgical

arthroplasty subjects.

ACKNOWLEDGEMENTS

This research was supported in part by the Natural

Sciences and Engineering Research Council Grant

(RGPIN-2015-03853) and the Canada Research Chair

on Biomedical Data Mining (950-231214). The

authors would like to thank Hilary Mac Donald and

Tim Parlee for the kinematic data collection.

REFERENCES

Astephen, J., Deluzio, K., Dunbar, M., Caldwell, G., and

Hubley-Kozey, C. (2011). The association between

knee joint biomechanics and neuromuscular control

and moderate knee osteoarthritis radiographic

and pain severity. Osteoarthritis Cartilage,

26(3):186–193.

Bytyqi, D., Shabani, B., Lustig, S., Cheze, L.,

Karahoda Gjurgjeala, N., and Neyret, P. (2014). Gait

knee kinematic alterations in medial osteoarthritis:

three dimensional assessment. Int. Orthop.,

38(6):1191–1198.

Casino, D., Martelli, S., and Zaffagnini, S. (2009). Knee

stability before and after total and unicondylar knee

replacement: In vivo kinematic evaluation utilizing

navigation. Journal of Orthopaedic Research,

27(2):202–207.

Casino, D., Zaffagnini, S., and Martelli, S. (2008).

Intraoperative evaluation of total knee replacement:

kinematic assessment with a navigation system.

Knee Surgery, Sports Traumatology, Arthroscopy,

17(4):369–373.

Jones, L., Beynon, M., Holt, C., and Roy, S. (2006). An

application of the dempster-shafer theory of evidence

to the classiﬁcation of knee function and detection of

improvement due to total knee replacement surgery. J

Biomechanics, 39(13):2512–2520.

Lorena, A. C. and de Souto, M. C. P. (2015). On

Measuring the Complexity of Classiﬁcation Problems,

pages 158–167. Springer International Publishing,

Cham.

Lustig, S., Magnussen, R., Cheze, L., and Neyret, P. (2012).

The kneekg system: a review of the literature. Knee

Surg. Sport. Traumatol. Arthrosc., 20(4):633–638.

Mezghani, N., Husse, S., Boivin, K., Turcot, K., Aissaoui,

R., Hagemeister, N., and de Guise, J. (2008).

Identiﬁcation of knee frontal plane kinematic patterns

in normal gait by principal component analysis.

Journal of Mechanics in Medicine and Biology,

13(3):r1230–1232.

Mezghani, N., Ouakrim, Y., Fuentes, A., Mitiche, A.,

Whynot, S., Richardson, G., and M, D. (2016).

Biomechanical signal classiﬁcation of surgical and

non-surgical candidates for knee arthroplasty. The

IEEE International Symposium on signal, Image,

Video and Communication (ISIVC).

Mezghani, N., Ouakrim, Y., Fuentes, A., Mitiche, A.,

Whynot, S., Richardson, G., and M, D. (2017).

Mechanical biomarkers of medial compartment knee

osteoarthritis diagnosis and severity grading:

Discovery phase. Journal of biomechanics,

52(1):106–112.

Mihalko, W., Ali, M., Phillips, M., Bayers-Thering, M.,

and KA, K. (2007). Passive knee kinematics before

and after total knee arthroplasty. The Journal of

Arthroplasty, 23(1):57–60.

Seon, J., Park, J., Jeong, M., Jung, W., Park, K., Yoon, T.,

and EK, S. (2011). Correlation between preoperative

and postoperative knee kinematics in total knee

arthroplasty using cruciate retaining designs. Int

Orthopedic, 35(4):515–520.

Knee Kinematics Feature Selection for Surgical and Nonsurgical Arthroplasty Candidate Characterization

181