
Apoptotic Regulatory Module as Switched Control System
Analysis of Asymptotic Properties
Magdalena Ochab, Andrzej Swierniak, Jerzy Klamka and Krzysztof Puszynski
Institute of Automatic Control, Silesian University of Technology, Akademicka 16, 44-100 Gliwice, Poland
Keywords:
Biological System, Piece-wise Linear Model, Switchings.
Abstract:
Switching control systems are getting increased interests due to their capability to exhibit simultaneously
several kinds of dynamic behaviour in different parts of the system. Such hybrid systems can be applied in
many different fields. We present the application of the switched control systems in modelling a biological
system, precisely a p53-dependent apoptotic intercellular pathway. Biological experiments show that cells
exhibit variety of different behaviours for the same external stimuli. Differences in cell responses lead to
population split into fractions. We present the analysis of asymptotic properties of the apoptotic regulatory
module with respect to a parameter which describes an effect of an external stress. Results show that the
system can exhibit two types of behaviour: stabilization or oscillation near the equilibrium point.
1 INTRODUCTION
Switched control systems are a class of systems that
consist of several linear subsystems and set of switch-
ing rules among them. Such systems are character-
ized by different models in dependence on the state
of the system. As a result even simple model can
have various types of dynamic behaviour for speci-
fied states of the system, which can result in chaos
or multiple limit cycles. On the other hand, switched
systems are relatively easy to analyse due to its par-
tially linear properties (Klamka et al., 2013).
Among many other applications of switched sys-
tems, they can be applied to modelling the biological
processes (Swierniak and Klamka, 2014). Biologi-
cal and biochemical reactions usually are not sponta-
neous but are regulated by variety of regulatory fac-
tors, and consequently the process rates are described
by the step-like function. To retain the switching be-
haviour majority of biological models are highly non-
linear, which implies difficulties in their analysis. The
piece-wise linear models are easier to create, because
values of the parameters correspond directly to the
observed processes rates. Moreover the switched sys-
tems enable analysis of the properties, which are com-
patible with biological observations. Comparison of
the nonlinear model results and the ones from piece-
wise linear model shows that the basic dynamics is
the same (Ochab et al., 2016). Switched systems can
be efficiently applied to modelling biological gene-
protein networks, systems with complex dynamics.
Apoptosis is intercellular process of programmed
cell death. It occurs in every multicellular organism
in damaged, defective or no longer required cells.
One of the key players in the apoptotic response to
the DNA damage is the protein p53, which activates
production of proteins responsible for apoptosis. The
proper activity of the apoptotic pathway is crucial for
the whole organism, because it enables elimination of
the damaged cells and prevents carcinogenesis (Vous-
den and Lu, 2002; Schmitt and Lowe, 1999). Huge
interest of the protein p53 and its regulatory network
among the researchers is a result of high contribution
of the cell with its p53 abnormalities in the cancer
cells.
The main activity of the p53 is regulation protein
production by acting as transcription factor. In nor-
mal healthy cell the low p53 level is maintained by
the negative coupling with MDM2. The p53 activates
MDM2 production, which in turn induces p53 degra-
dation. External stress, such as DNA damage, induces
MDM2 degradation. Decrease of the MDM2 results
in stabilization of p53 and activation of the proteins
production which are responsible for cell cycle block-
ade, damaged DNA repair and apoptosis. Results of
biological experiments show that, depending on the
stress level, the p53 can be maintained on different
levels (Kracikova et al., 2013). In case of low stress,
the normal cell division is blocked by the medium
level of the p53 and processes of DNA repair are ini-
Ochab, M., Swierniak, A., Klamka, J. and Puszy
´
nski, K.
Apoptotic Regulatory Module as Switched Control System - Analysis of Asymptotic Properties.
DOI: 10.5220/0006593601190126
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 3: BIOINFORMATICS, pages 119-126
ISBN: 978-989-758-280-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
119

tiated. However in this state the p53 level is not high
enough to induce the process of apoptosis. Top level
of external stress activates the positive feedback loop,
which works through protein PTEN. Protein PTEN is
induced by p53, and after accumulation in cytoplasm
is able to block the negative feedback by blocking the
MDM2 transport to nucleus. As a result the p53 in-
creases to high level and apoptosis is activated (Jonak
et al., 2016). Due to the great significance of the
p53-dependent apoptotic pathway a wide range of ex-
periments, both biological and mathematical, are per-
formed to acquire fully knowledge about this process.
In our previous research we have examined the
system behaviour for three different stress levels: 0,
4 and 9 a.u. (Ochab et al., 2017a). In present paper
we study possible system responses and thus we focus
our attention on the asymptotic properties of the con-
trol system for the whole range of parameter R, which
stands for a level of stress.
2 METHODS
2.1 PLDE Model Analysis
Piece-wise linear differential equation models (PLDE
models) consist of set of linear differential functions
and set of rules defining the subset of functions, which
is used for a specified state. For biological systems the
general equation is defined as:
dx
i
dt
= p
i
(X) − d
i
(X)x
i
, i = 1, 2,..., n (1)
where x
i
is a protein, p
i
is a production rate, d
i
is a
degradation rate and X is a state of the system de-
scribed by the set of boolean functions. The phase
space is divided by thresholds into regulatory do-
mains. In each domain the system is described by a
linear (affine) model. The boundaries of the domains
are defined by threshold values denoted by θ
i j
, where
i is the variable (protein) and j is a number of the
threshold for the given variable. On the boundaries,
values of the parameters can switch and consequently
the system is not continuous. Additionally the sys-
tem contains switching variables, which define if the
specific variable is above or below its threshold. The
switching variables are boolean and are denoted by
Z
i
, where i indicates a number of the variable. The
boolean variables are applied to define the regulatory
domains. Each domain is defined by a boolean vec-
tor B which specifies relation of all the variables to its
threshold. Moreover relation between variables and
thresholds defines the values of the parameters in the
model.
In the piece-wise linear models two types of sta-
tionary points are distinguished: regular stationary
points and singular stationary points.
2.1.1 RSP
The regular stationary points, shortly RSPs, exist in-
side the regulatory domain. The RSPs are localized
by application of steady state condition for each do-
main. If the calculated point lies inside boundaries of
the considered domain, it is asymptotically stable and
is called RSP. A method determining RSP can be de-
scribed as follows:
for each subsystem described by linear equation
model
• calculate steady state dx
i
/dt = 0
• check localization of the point, if the point lies
inside the boundaries, it is the RSP.
2.1.2 SSP
Localization of the singular stationary points, shortly
SSPs, is much more challenging, because they exist
when at least one of the variables lies on its threshold.
In our analysis we use the method proposed for gene
regulatory networks (Plahte et al., 1994; Mestl et al.,
1995; Plahte et al., 1998). In the simplest case only
one variable is equal to its threshold which means that
the SSP is located on the boundary.
The SSPs can be described by a number of the
variables which lie on the threshold. In the simplest
case only one variable is located on the boundary and
the other variable values are not restricted. It is wor-
thy to notice that such case is possible only if the vari-
able is directly dependent on its own threshold value.
To be precise, the SSP lies on the threshold θ
i j
for
variable x
i
= θ
i j
, if the derivative ∂F
i
/∂Z
i j
is greater
than 0, where F
i
is the time derivative dx
i
/dt and Z
i j
is switching variable.
The switched system is not continuous on the
thresholds, so to calculate the derivatives, we replace
the step function by the continuous sigmoid function
with the limit [0,1]. Thus the switching function is a
monotonic mollifier defined as Z
i j
= Z(x
i
,θ
i j
,δ):
Z
i j
=
0 for x
i
≤ θ
i j
− δ,
increases from 0 to 1 for x
i
∈ hθ
i j
− δ,θ
i j
+ δi
1 for x
i
≥ θ
i j
+ δ
Parameter δ denotes the distance from the threshold,
so with δ tending to zero, the monotonic mollifier ap-
proaches the step function.
In order to determine existence of the SSP in
the case when two or more variables are equal to
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
120

their thresholds, we apply the procedure described by
Mestl et al. (Mestl et al., 1995). For all sets of the
threshold variables:
• replace values of the variables by corresponding
thresholds
• determine values of the switching variables,
which are not related to the analysed thresholds,
as 0 or 1
• set time derivatives to 0
• solve the set of equations to calculate values of
switching variables related to the analysed thresh-
olds
• check assumptions: values of switching variables
must be included in the range [0,1] and values
of remaining variables must be in the specified
range, if yes, there is a SSP
In the system with SSP localized on the crossing
of boundaries oscillations can be observed, because
there exist a limit cycle around the SSP.
2.2 p53-Dependent Apoptotic Model
A piece-wise linear model of the p53 regulatory mod-
ule was presented in our previous paper, where we
compared its results with the results obtained by the
nonlinear model (Ochab et al., 2016). The model
consists of 4 variables, which correspond to different
types of proteins: P - p53, C - cytoplasmic MDM2,
N - nuclear MDM2, T - PTEN. Production of p53
(P) is constant and its degradation is increased by nu-
clear MDM2 (N). Production of cytoplasmic MDM2
(C) and PTEN (T ) is induced by p53 (P). Nuclear
MDM2 (N)results from nuclear import of the cyto-
plasmic form (C), which is regulated by T . Conse-
quently in this system two feedback loops exist. The
first one is negative and it exists between P, C and
N, because p53 (P) induces production of its own in-
hibitor. The second one is positive, due to blockade of
the negative feedback by PTEN (T ), which is induced
by p53 (P). All the dependencies between proteins
are presented on the diagram (Fig. 1).
We introduce 4 threshold to divide phase space
into regulatory domains. There is one threshold value
for p53 in order to model the activation of MDM2 and
PTEN production (parameters p
∗
2
and p
∗
3
respectively)
by accumulated p53. One threshold for PTEN is used
to model the blockade of the MDM2 transport to nu-
cleus. PTEN level exceeding the threshold value sig-
nifies decrease of the MDM2 transport rate (k
∗
1
). Ad-
ditionally there are two threshold values for nuclear
MDM2, which separates the three levels of p53 degra-
dation: low, medium and high. There are no threshold
Figure 1: Model of the p53 regulatory core. Symbols of
the variables, switching variables and model parameters are
taken from the model (2).
for cytoplasmic MDM2, because none of the analysed
processes are dependent on its level. Due to existence
of four thresholds, the model contains four switching
variables Z
P
, Z
T
, Z
N1
, Z
N2
, which define if the spe-
cific variable is above or below its threshold. More-
over each domain is defined by a vector B = [P,N, T ],
where P, N and T are the boolean-like states denoting
if the corresponding variable is below (0) or above (1
in case of P and T and 1 or 2 in case of N) its thresh-
old. For example domain [110] denotes the subspace,
where P > θ
P
, θ
N1
< N < θ
N2
and T < θ
T
. Please,
note that parameters which are dependent on the sys-
tem state are marked with
∗
.
The control system is linear, precisely affine, with
a constant input. The general linear differential state
equation can be written in the following form:
˙
x(t) = Ax(t) + b, t ∈ [0, +∞) (2)
where the x(t) ∈ R
n
is a state vector, A is a given n ×n
- dimensional control matrix and b ∈ R
n
is a constant
input. They are defined below:
x(t) =
P(t)
C(t)
N(t)
T (t)
b =
p
1
p
∗
2
0
p
∗
3
.
Moreover,
A =
−d
∗
1
0 0 0
0 −(k
∗
1
+ d
2
(1 + R)) 0 0
0 k
∗
1
−d
2
(1 + R) 0
0 0 0 −d
3
where
p
∗
2
= p
20
+ p
21
Z
P
p
∗
3
= p
30
+ p
31
Z
P
d
∗
1
= d
10
+ d
11
Z
N1
+ d
12
Z
N2
k
∗
1
= k
10
− k
11
Z
T
Apoptotic Regulatory Module as Switched Control System - Analysis of Asymptotic Properties
121

Z
P
=
0 if P < θ
P
1 if P > θ
P
Z
N1
=
0 if N < θ
N1
1 if N > θ
N1
Z
N2
=
0 if N < θ
N2
1 if N > θ
N2
Z
T
=
0 if T < θ
T
1 if T > θ
T
The degradation of the MDM2, both cytoplasmic
and nuclear, is increased by stress factor denoted by
R. The values of the parameters given above are pre-
sented in Table 1 and the values of threshold are pre-
sented in Table 2 Values of the parameters base on our
previous research (Ochab et al., 2016) and the biolog-
ical results (Jonak et al., 2016).
3 RESULTS
As we showed in our previous paper (Ochab et al.,
2017a), for different size of stress - reflected by dif-
ferent values of the parameter R, the system response
can be significantly different. In order to check all
possible realizations of the system for whole range
of stress, we examine existence of the different RSPs
and SSPs for R ∈ [0, +∞i. The system behaviour for
specified values of R can be visualized by the transi-
tion diagram. The domains are marked by the rect-
angles with vectors determining their states. The ar-
rows show the directions of the transitions between
domains. Transition diagrams show in which domain
the RSPs exist and are useful in localizing the closed
sequences between domains, which can contain the
SSPs around which the systems response can oscil-
late. The simplest way to create transition diagram is
calculation of the RSP in each domain and determine
whether the solution stay in the analysed domain or
move to another. Exemplary, for stress R = 5, there is
one RSP in the system in the domain [101] and one
possible limit cycle between domains [010], [110],
[120] and [020] (Fig. 2).
3.1 Regular Stationary Point - RSP
In this section we determine ranges of the R in which
the RSP exists in any domain. For each domain we
write the model equations and equal them to 0. Then
we solve the system of equation to find values of
R, which assures that the stationary point lays inside
analysed domain. In the apoptotic switched model the
Figure 2: State transition diagram for the apoptotic model
for R = 5. Gray domain contains RSP, bold arrows empha-
size the closed sequence around the SSP.
regular stationary points can exist only in 3 domains.
The RSPs exist:
• in domain [020] for R ∈ [0,0.8635i
• in domain [111] for R ∈ h1.0322,1.9154i
• in domain [101] for R ∈ h1.9154,+∞i.
The values of the variable P in the steady states
in each domain are presented in table 3. For R ∈
[0.8635,1.0322i there is no RSP in the system, so the
system response does not stabilize on one value but
oscillates in a limit cycle.
The regular stationary points correspond to the
asymptotically stable cell response in different cases.
For low stress the RSP exists in domain [020] and cor-
responds to the low p53 level and the high nuclear
MDM2 level, which agrees with biological observa-
tion of normal cells, where low p53 level is main-
tained by high degradation rate and, in turn by high
MDM2 level. An increase of the parameter R results
in disappearing of the RSP in domain [020] and aris-
ing in domain [111] and afterwards in [101]. The in-
crease of the R corresponds to higher external stress
level, which induces cell damages, the MDM2 degra-
dation and consequently accumulation of the p53 (see
Table 3 with increasing values of p53 in stationary
points).
In biological experiments after high stress level
the increased p53 level is observed. The p53 level in
cell determines the cell response, the medium average
p53 level can be assigned to the cells with repairable
damages and excluded proliferation, whereas the high
p53 level indicates cells with unrepairable damages
and apoptosis activation.
3.2 Singular Stationary Point - SSP
In the apoptotic model thresholds exist for 3 vari-
ables: P, N and T, and consequently, the SSP can
exist in 3 types of subspaces: on the plane where one
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
122

Table 1: The values of the model parameters.
Parameter Description Value Unit
p
1
spontaneous P production rate 8.8 1/sec
p
20
spontaneous C production rate 2.4 1/sec
p
21
P-induced C production rate 21.6 1/sec
p
30
spontaneous T production rate 0.5172 1/sec
p
31
P-induced T production rate 3.6204 1/sec
d
10
spontaneous P degradation rate 9.8395 ∗ 10
−5
1/sec
d
11
N-induced P degradation rate 6.5435 ∗ 10
−5
1/sec
d
12
N-induced P degradation rate 1.6283 ∗ 10
−4
1/sec
d
2
spontaneous C and N degradation rate 1.375 ∗ 10
−5
1/sec
d
3
spontaneous T degradation rate 3 ∗ 10
−5
1/sec
k
10
spontaneous N transport rate 1.5 ∗ 10
−4
1/sec
k
11
T -inhibited N transport rate 1.4713 ∗ 10
−4
1/sec
Table 2: The values of the thresholds for variables.
Thresholds Description Value Unit
θ
P
P threshold value 4.5 ∗ 10
4
molecules
θ
N1
1
st
N threshold value 4 ∗ 10
4
molecules
θ
N2
2
nd
N threshold value 8 ∗ 10
4
molecules
θ
T
T threshold value 1 ∗ 10
5
molecules
Table 3: Values of p53 (P) in regular stationary point for
different values of stress R.
R Domain P
s
0 - 0.8635 [020] 3.3559 ·10
4
1.0322 - 1.9154 [111] 5.3714 · 10
4
1.9154 - +∞ [101] 8.9435 ·10
4
variable lies on its threshold, on the crossing of the
planes, where two variables lie on thresholds, and on
the point, where all three variables lie on their thresh-
olds.
In order to check if the model can contain the
SSP on the plane, we calculate the derivatives of all
the variables with respect to its switching variables
∂F
i
/∂Z
i j
. In this model partial derivatives for all the
variables P, C, N and T do not directly depend on
their switching variables Z
i j
so all ∂F
i
/∂Z
i j
are equal
to zero. Consequently in this system there is no SSP
on the surface of the single boundary.
To determine an existence of the SSP on the cross-
ing of two boundaries we analyse all the existed cases.
For all combinations of two thresholds from θ
P
, θ
T
and θ
N1
or θ
N2
the procedure described in section
2.1.2 was applied with attitude to determine values of
the stress R, for which the assumptions are satisfied.
For the whole range of the parameter R, the SSP can
exist only in two subspaces.
3.2.1 SSP 1: [θ
P
, θ
N2
, T < θ
T
]
The SSP exists on the crossing of the threshold of the
p53 and the MDM2, precisely for P equal to θ
P
, N
equal to θ
N2
and T smaller than θ
T
. The model equa-
tions describing the steady state in this subspace are
as follows:
0 = p
1
− (d
10
+ d
12
Z
N2
)θ
P
,
0 = p
20
+ p
21
Z
P
− (k
10
+ d
2
(1 + R))C ,
0 = k
10
C − d
2
(1 + R)θ
N2
,
0 = p
30
+ p
31
Z
P
− d
3
T. (3)
The switching parameters Z
P
and Z
N2
are in the
range [0,1] and the value of the T variable is smaller
than θ
T
for R ∈ h0.8635, 7.7038i.
3.2.2 SSP 2: [θ
P
, θ
N2
, T > θ
T
]
The second SSP in the system exists for P equal to
θ
P
, N equal to θ
N2
and T greater than θ
T
. The model
equations describing the steady state are presented be-
low:
0 = p
1
− (d
10
+ d
12
Z
N2
)θ
P
,
0 = p
20
+ p
21
Z
P
− (k
10
− k
11
+ d
2
(1 + R))C ,
0 = (k
10
− k
11
)C − d
2
(1 + R)θ
N2
,
0 = p
30
+ p
31
Z
P
− d
3
T. (4)
Apoptotic Regulatory Module as Switched Control System - Analysis of Asymptotic Properties
123
The switching parameters Z
P
and Z
N2
are in the
range [0, 1] and the value of the T variable is greater
than θ
T
for R ∈ h0.7059, 1.0322i.
The last possible case, is localization of the SSP
in the crossing of three boundaries. In this model two
such points exist and should be analyzed: [θ
P
, θ
N1
,
θ
T
] and [θ
P
, θ
N2
, θ
T
]. In both cases the values of the
switching variables Z
P
, Z
N1
(or Z
N2
) and Z
T
are not
included in the range [0,1] so independently of the
parameter R, the SSP cannot exist there.
Due to an existence of the SSPs in two subspaces,
two types of oscillations can be observed. Signifi-
cantly wider range of the parameter R have the SSP
in the region [θ
P
, θ
N2
, T < θ
T
]. This SSP results
in undamped oscillations between low and high p53
level and medium and high MDM2 level. Such os-
cillations are a consequence of the negative feedback
loop, and are related to the delayed cell response in
case of the repairable damages. Biological experi-
ments show that for the low stress level a cell makes
an attempt to repair its damages and comes back to the
normal state. The oscillation of the p53 level prevents
cell division but in the same time does not induce
cell elimination (Geva-Zatorsky et al., 2006; Bar-Or
et al., 2000). Consequently if the damages are not un-
repairable, the cell has got time to come back to the
normal state.
The second SSP indicates an existence of the cy-
cle between the p53 and the MDM2 for high PTEN
level. Such situation occurs only for a very narrow
range of R parameters. This case is possible for low
external stress, when the initial high PTEN level is
maintained over the θ
T
threshold by oscillation be-
tween low and high p53 level. However in biological
cells high PTEN level is observed only after p53 ac-
tivation, so such situation is not probable concluding
from the biological results.
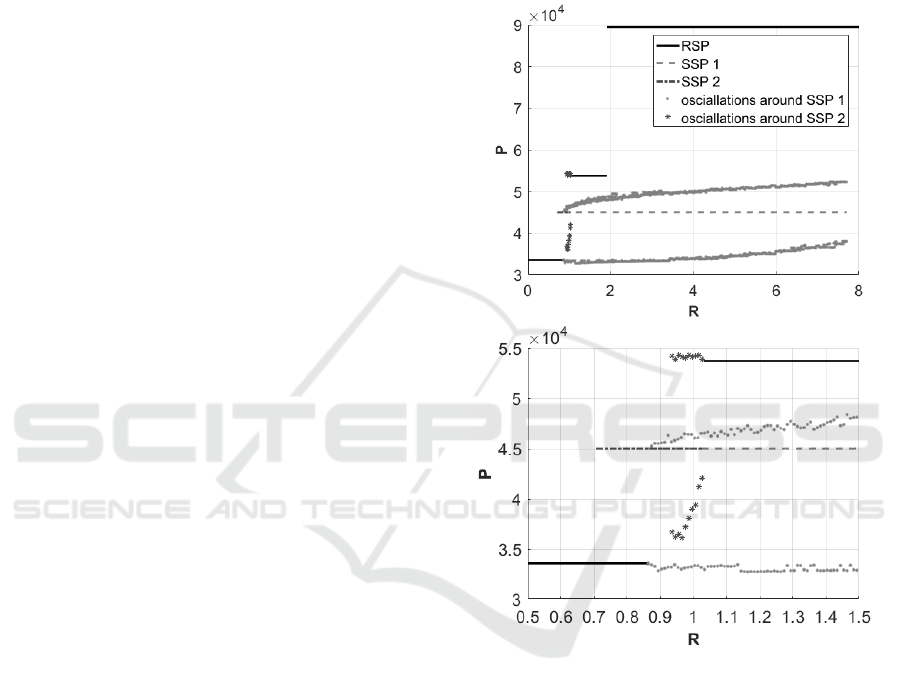
3.3 Bifurcation Diagram
Depending on the R parameter value, the stationary
points exist in different domains or on the different
boundaries. For small R the RSP exists in domain
[020] and the P level is low. With increase of the R
value, in the system the second stationary point, SSP,
appears. Depending on the initial conditions the sys-
tem can stabilize in the domain [020] or oscillate be-
tween domains with low and high P and medium and
high N. With further increase of the R, in the system
any RSP does not exist, so the only possible system
response is oscillation. In quite narrow range of the R
parameter values, in the system two singular station-
ary points exist, which results in two different cycles
and different levels of proteins. With further increase
of R, in the system the RSP in the domain [111] arises,
which is characterized by the medium P level. For R
greater than 1.9154 in the system the RSP arises in the
domain [101] with the high P level. The SSP exists in
the system for R smaller than 7.7038 which means,
that depending on the initial conditions, in the system
two types of response can be observed: stabilization
or oscillations (see Fig. 3).
Figure 3: Level of the variable P in dependency on the pa-
rameter R. Top figure: results for the whole range of R.
Bottom figure: magnification of the figure for R = h0.51.3i.
SSP 1 - values of P in the SSP with T < θ
T
, SSP 2 - values
of P in the SSP with T > θ
T
. Please notice the lack of os-
cillations around SSP 2 for R ∈ h0.8635, 0.95i - see text for
explanation.
The dependency between variables N and R is pre-
sented on the Fig. 4. With increase of R, the N level is
decreased. For a wide range of the R parameter, in the
system two types of result exists, stabilization in the
steady state or oscillation of the protein levels, which
are a consequence of the simultaneous existence of
the two stationary points: SSP and RSP.
Notice the lack of oscillations around SSP for R ∈
h0.8635,0.95i on Fig. 3 (bottom panel). It is caused
by the close proximity of the SSP to the θ
T
bound-
ary which causes that the trajectories escape from the
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
124
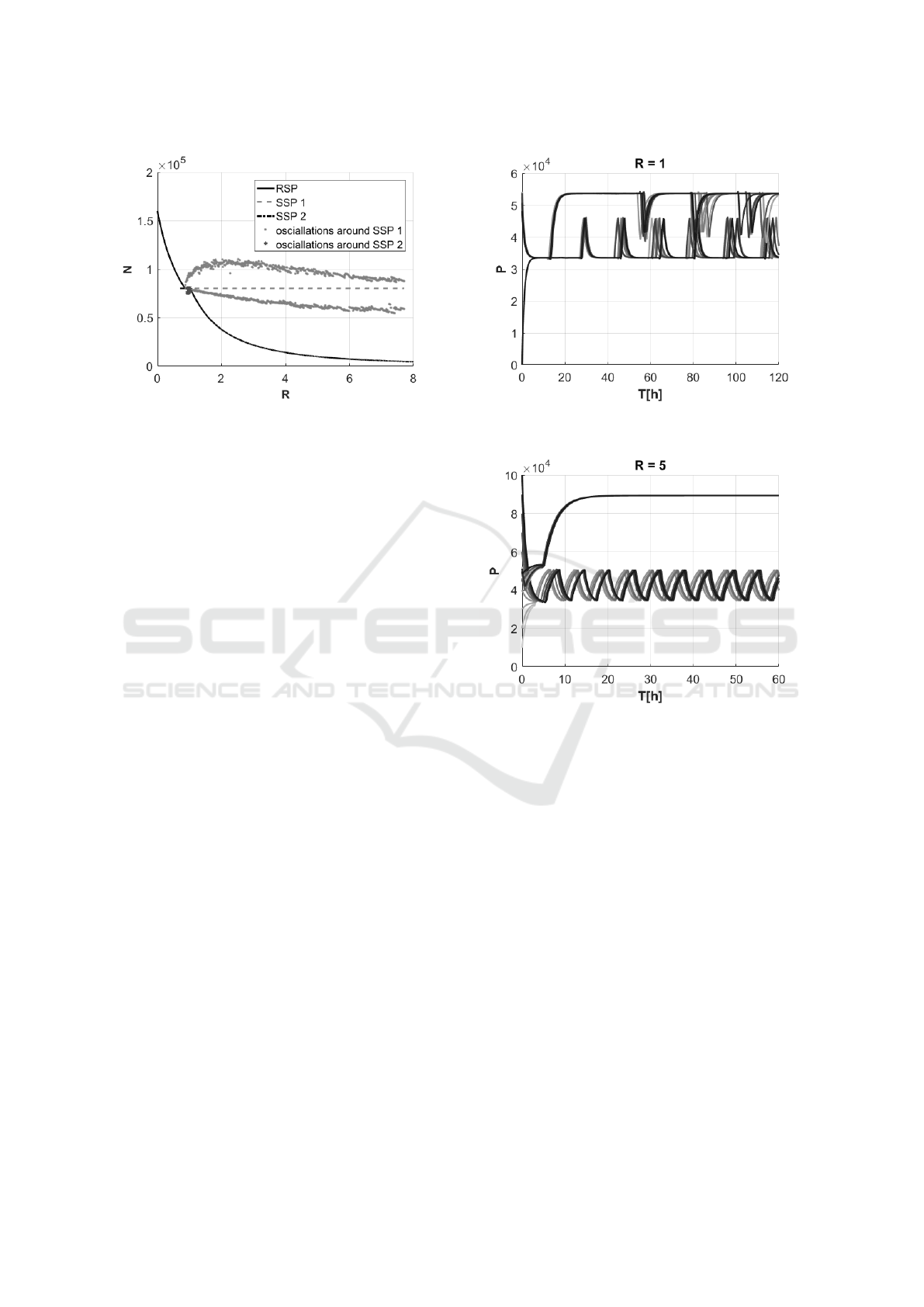
Figure 4: Level of the variable N in dependency on the pa-
rameter R. SSP 1 - values of N in the SSP with T < θ
T
, SSP
2 - values of N in the SSP with T > θ
T
.
oscillatory mode. With the increasing R, SSP recedes
from the θ
T
boundary and with R greater than 0.95,
trajectories do not cross the threshold θ
T
thus oscil-
lations appear. Nevertheless the presented method is
unable to detect analytically this phenomenon which
is its weakness.
More generally the weakness of the presented
method is impossibility to analytically determine the
attraction pools for the calculated stationary points.
The numerical simulation for different initial condi-
tions shows, that in the case of [θ
P
, θ
N2
, T > θ
T
] the
attraction pool is very small.
3.4 Numerical Results
To testify the achieved results we calculated the sys-
tem response for two values of parameter R for differ-
ent initial conditions. For R equals 1, in the system
two SSPs exist and consequently on the time courses
the two types of oscillations are observed. Interest-
ingly both SSPs are on the same borders, precisely
for subspaces with P = θ
P
and N = θ
N2
, but one point
is under θ
T
threshold and the second one is above.
Consequently, even if the values of the variable P in
the stationary points are the same, the time courses are
significantly different (Fig. 5). For the higher value of
R, in the system one RSP and one SSP exist. Conse-
quently, depending on the initial conditions, the sys-
tem can approach the steady point in the domain [101]
or oscillate in the limit cycle around the singular sta-
tionary point (Fig. 6). In the case of modelling cell
population using stochastic approach, different types
of responses are received. Consequently the cell pop-
ulation is divided into several fractions, which present
different behaviours (Ochab et al., 2017b).
Figure 5: Time course of the variable P for different initial
conditions for value of parameter R equals 1.
Figure 6: Time course of the variable P for different initial
conditions for value of parameter R equals 5.
4 CONCLUSIONS
Analysis of the switched system demonstrate the
properties of the apoptotic intercellular pathway. The
localization and the types of the existing stationary
points correspond with the biological results. The
presented method can be efficiently applied to piece-
wise linear systems to examine properties of the
protein regulatory networks, nevertheless the results
show that this method is not free from imperfections.
Lack of the analysis of the attraction pools can lead to
false determination of the system behaviour based on
existence of the singular stationary points without at-
traction pools. In the future we want to overcome this
difficulty and improve the proposed methodology.
Apoptotic Regulatory Module as Switched Control System - Analysis of Asymptotic Properties
125

ACKNOWLEDGEMENT
The research presented here was partially supported
by the National Science Centre in Poland granted
with decision number DEC-2016/23/B/ST6/03455
(for KP), DEC-2014/13/B/ST7/00755 (for AS and
JK) and BKM- 508 /RAU1/2017 t. 6 (MO).
Calculations were performed on the Ziemowit
computational cluster created in the EU Innovative
Economy Operational Programme (POIG).02.01.00-
00-166/08 project (BIO-FARMA) and expanded in
the POIG.02.03.01-00-040/13 project (Syscancer)
(http://www.ziemowit.hpc.polsl.pl).
REFERENCES
Bar-Or, R. L., Maya, R., Segel, L. A., Alon, U., Levine,
A. J., and Oren, M. (2000). Generation of oscilla-
tions by the p53-mdm2 feedback loop: a theoretical
and experimental study. Proceedings of the National
Academy of Sciences, 97(21):11250–11255.
Geva-Zatorsky, N., Rosenfeld, N., Itzkovitz, S., Milo, R.,
Sigal, A., Dekel, E., Yarnitzky, T., Liron, Y., Polak, P.,
Lahav, G., et al. (2006). Oscillations and variability in
the p53 system. Molecular systems biology, 2(1).
Jonak, K., Kurpas, M., Szoltysek, K., Janus, P., Abramow-
icz, A., and Puszynski, K. (2016). A novel mathemat-
ical model of atm/p53/nf-κ b pathways points to the
importance of the ddr switch-off mechanisms. BMC
systems biology, 10(1):75.
Klamka, J., Czornik, A., and Niezabitowski, M. (2013).
Stability and controllability of switched systems. Bull.
Pol. Acad. Sci., Tech. Sci. (Online), 61(3):547–555.
Kracikova, M., Akiri, G., George, A., Sachidanandam, R.,
and Aaronson, S. (2013). A threshold mechanism me-
diates p53 cell fate decision beteen growth arrest and
apoptosis. Cell Death Differ, 20:576–588.
Mestl, T., Plahte, E., and Omholt, S. W. (1995). A mathe-
matical framework for describing and analysing gene
regulatory networks. Journal of Theoretical Biology,
176(2):291–300.
Ochab, M., Puszynski, K., and Swierniak, A. (2016). Appli-
cation of the piece-wise linear models for description
of nonlinear biological systems based on p53 regula-
tory unit. In Proc. XXI National Conference on Ap-
plications of Mathematics in Biology and Medicine,
Sandomierz, pages 85–90.
Ochab, M., Puszynski, K., Swierniak, A., and Klamka, J.
(2017a). Variety behavior in the piece-wise linear
model of the p53-regulatory module. In International
Conference on Bioinformatics and Biomedical Engi-
neering, pages 208–219. Springer.
Ochab, M., Swierniak, A., Klamka, J., and Puszynski, K.
(2017b). Influence of the stochasticity in threshold
localization on cell fate in the plde-model of the p53
module. In Polish Conference on Biocybernetics and
Biomedical Engineering, pages 205–217. Springer.
Plahte, E., Mestl, T., and Omholt, S. W. (1994). Global
analysis of steady points for systems of differential
equations with sigmoid interactions. Dynamics and
Stability of Systems, 9(4):275–291.
Plahte, E., Mestl, T., and Omholt, S. W. (1998). A method-
ological basis for description and analysis of systems
with complex switch-like interactions. Journal of
mathematical biology, 36(4):321–348.
Schmitt, C. A. and Lowe, S. W. (1999). Apoptosis and ther-
apy. J. Pathol, 187:127–137.
Swierniak, A. and Klamka, J. (2014). Comparison of con-
trollability conditions for models of antiangiogenic
and combined anticancer therapy. In Proc. 19th World
Congress The International Federation of Automatic
Control, Cape Town.
Vousden, K. H. and Lu, X. (2002). Live or let die: the cell’s
response to p53. Nature, 2:594–604.
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
126
