Object Oriented Structure from Motion: Can a Scribble Help?

Rahaf Rahal

, Daniel Asmar

, Elie Shammas

and Bernard Ghanem

Department of Mechanical Engineering, American University of Beirut, Beirut, Lebanon

King Abdullah University of Science and Technology, Thuwal, Saudi Arabia

Keywords:

Structure from Motion, Interactive Image Segmentation, Object Reconstruction.

Abstract:

The concept of anywhere anytime scanning of 3D objects is very appealing. One promising solution to extract

structure is to rely on a monocular camera to perform, what is well-known as Structure from Motion (SfM).

Despite the signiﬁcant progress achieved in SfM, the structures that are obtained are still below par the quality

of reconstruction obtained through laser scanning, especially when objects are kept as part of their background.

This paper looks into the idea of treating points in the scene non-uniformly, in an attempt to give more weight

to the objects of interest. The system presented utilizes a minimal user interaction, in the form of a scribble,

to segment the pertinent objects from different views and focus the reconstruction on them, leading to what

we call Object Oriented SfM (OOSfM). We test the effect of OOSfM on the reconstruction of speciﬁc objects

by formulating the bundle adjustment (BA) step in three novel manners. Our proposed system is tested on

several real and synthetic datasets, and results of the different formulations of BA presented are reported and

compared to the conventional (vanilla) SfM pipeline results. Experiments show that keeping the background

points actually improves the reconstructed objects of interest.

1 INTRODUCTION

From the early ages, humans have always striven to

capture and reproduce the shapes of objects around

them; whether for religious or artistic purposes, the

millions of sculptures of both animate and inanimate

objects that abound around us are proof of this natu-

ral desire. In our modern day, this desire is ever so

strong and, in addition to its artistic appeal, the de-

sire to generate 3D models is product-driven. With

the advent of 3D scanners, Computer Aided Design,

and Computer Aided Manufacturing, the replication

of 3D objects has become accessible to the general

public. Example applications include the burgeoning

ﬁeld of augmented and virtual reality, in which accu-

rate scans of the as-is object is required before aug-

menting it with any virtual addition.

Lasers have typically been the instruments of

choice for scanning objects. They are relatively accu-

rate, and robust to varying lighting conditions; howe-

ver, lasers are not readily available everywhere and

they are relatively expensive. Furthermore, for large

scenes, the setup of lasers at different vantage points

necessary for covering the entire scene can be quite

time-consuming. Stereo cameras can also be used

for scanning objects, but usually do not produce very

good results because of the inevitable holes that are

Figure 1: Concept of object oriented SfM (OOSfM): by fo-

cusing on different parts in the image, does SfM produce

better or worse quality objects than the vanilla SfM? The

objects selected and shown in focus (bunny on the left, cube

on the right) and their corresponding sought-after recon-

structions (bottom row).

left in the models because of the frequent unrelia-

ble disparity values obtained in stereopsis. As anot-

her alternative, monocular cameras can also be used

for scanning, using a technique commonly known as

Structure from Motion (SfM), where both the scene

structure and the camera trajectory inside the scene

during scanning are estimated. SfM offers many ad-

vantages: ﬁrst, it relies on a single camera; most pe-

ople today have access to a camera in their smart pho-

nes, and by adding the required software, these devi-

ces easily turn into low-cost 3D scanners. Secondly,

monocular cameras possess a relatively large ﬁeld of

Rahal, R., Asmar, D., Shammas, E. and Ghanem, B.

Object Oriented Structure from Motion: Can a Scribble Help?.

DOI: 10.5220/0006596005410548

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

541-548

ISBN: 978-989-758-290-5

541

view, both in depth and width, which ultimately re-

sults in the ability to scan large areas (Frahm et al.,

2010). Unfortunately, SfM also suffers from many

disadvantages. First, since the technique relies on a

monocular camera, the models that are obtained are

to an unknown scale. Second, applying the vanilla

SfM to an entire image generates reconstructions with

low accuracies, which, in their untouched form, are

not accurate enough to be built upon for applications

in computer graphics, such as in building the compu-

ter models for 3D printing, or for scanning outdoor

structures in augmented reality applications. In many

cases, manual labor-intensive post-processing of the

point cloud is necessary before it can be really used

in practice.

The objective of this work is to tackle the idea of

focused reconstruction. To do so, we suggest different

SfM variants, which will use a minor input from the

user with the aim of reconstructing speciﬁed objects

in the scene, while maintaining an acceptable recon-

struction quality for the remaining parts in the scene.

We qualify this concept as an Object-Oriented SfM

and refer to it hereafter as OOSfM (see Fig. 1).

This paper thus presents a set of object oriented

SfM variants, and studies whether it is possible to im-

prove the structure estimate of select objects in the

scene, while maintaining the background, albeit at a

lower (yet controlled) quality. There are three main

contributions in this work. (1) We present an object

tracking system that is developed for localizing the

object of interest in each image of a sequence of ima-

ges. After the user manually identiﬁes the object of

interest in the ﬁrst image, it is automatically detected,

and its boundaries segmented in subsequent images.

(2) By formalizing the bundle adjustment part of SfM

in three different ways, we attempt to put more weight

in the solution on the object of interest, and compare

the output to the traditional SfM result to test whether

the scribble could be of a help to the reconstruction

process. (3) Based on the results of our experiments,

we prove the inability of the re-projection error me-

tric to capture the actual reconstruction error when the

object of interest is considered rather than the entire

scene.

2 RELATED WORK

Object oriented SfM and Visual SLAM (simultaneous

localization and mapping)–a close relative of SfM,

born out of robotics–have recently gained popula-

rity, given the breadth of information that seman-

tics can carry in the guidance of 3D reconstruction

underhauf et al., 2015). In the context of SLAM, Fi-

oraio and Di Stefano (Fioraio and Di Stefano, 2013)

proposed a new semantic bundle adjustment frame-

work to jointly estimate camera positions and object

poses through a global semantic optimization. Their

system relies on a database of seven objects, and it si-

multaneously tackles the object detection and SLAM

problems. Galvez-Lopez et al. (G

alvez-L

opez et al.,

2016) used a larger database of objects, and a modi-

ﬁed bundle adjustment formulation, taking the size of

these objects into account to recover the scale parame-

ter of the output SLAM map. Frost and Murray (Frost

and Murray, 2016) also took it a step further and re-

lied on object detections to resolve both the scale am-

biguity and the drift problem in SLAM without the

need to add additional sensors. For all these SLAM

systems, the primary objective is motion estimation;

objects are detected but not reconstructed, in contrast

to what SfM strives to do.

On the other hand, in the ﬁeld of object-based

SfM, Bao et al. (Bao et al., 2012) introduced what

is known as semantic SfM. While their work focused

on camera pose estimation and the improvement of

object detection, the target of OOSfM is the evalua-

tion of the resulting 3D structure of an object of any

category. A recent paper by Crocco et al. (Crocco

et al., 2016) proposed extending SfM to using ob-

jects instead of points. While their algorithm is ap-

plied to factorization based SfM, our modiﬁcation is

to the numerical optimization, which results in more

freedom in the choice of the number of images. In

fact, the numerical method is usually better suited

than factorization, as discussed in (Sch

onberger and

Frahm, 2016). Another difference is that while they

mainly focus on recovering the position of objects in

the scene, OOSfM focuses on the structure itself.

Incorporating user interactions in the 3D recon-

struction process has been explored before, in works

such as (Debevec et al., 1996), (Cipolla and Robert-

son, 1999), (Oh et al., 2001), and (Van den Hengel

et al., 2007), but most of them require extensive hu-

man interaction, such as manual feature extraction

and matching, or rely on predeﬁned primitives, and

are thus not extendible to general object models.

Other works, like that of Sinha et al. (Sinha et al.,

2008) require less user interaction, but rely on the out-

put of SfM to guide the process. This might not be a

good idea because any mistakes in the SfM will pro-

pagate to the ﬁnal model. SfM is particularly suscep-

tible to homogeneous or repetitive background, which

could adversely affect the reconstruction of the ob-

jects of interest.

The work of Kowdle et al. (Kowdle et al., 2010)

is the closest in spirit to OOSfM, where user guided

segmentation of an object of interest is used to iden-

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

542

tify the objects to reconstruct. OOSfM differs from

this work in that it only requires one user scribble to

segment the object of interest in the scene. In addi-

tion, while we introduce the object emphasis at the

level of SfM, they rely on shape from silhouette, and

on the camera output from vanilla SfM, to get a tex-

tured model of the object. Finally, the background in

their system is completely discarded and they focus

only on the object of interest.

Existing user guided segmentation methods have

been summarized in (Zhu et al., 2016) which clas-

siﬁes the current segmentation methods into three

groups: unsupervised methods that rely on low

level features such as color and texture, weakly-

supervised methods which include interactive seg-

mentation and co-segmentation techniques, and fully-

supervised methods, which encompass object propo-

sals and use fully labeled data to ﬁnd a segmentation

model of speciﬁc object classes. The segmentation

that we propose combines the three different techni-

ques. Guided with a small amount of user interaction,

it uses both object proposals (Kr

ahenb

uhl and Koltun,

2014) and low level features to make the segmenta-

tion more object oriented, while allowing for a wider

range of objects that could consist of simple homoge-

neous regions in the scene.

3 OBJECT ORIENTED

STRUCTURE FROM MOTION

In the ﬁrst part of OOSfM, the image is segmen-

ted using any off-the shelf object proposal techni-

que. Next, the user scribbles on the object of inte-

rest in the ﬁrst image. Assuming we have an ordered

photo collection, the selected object is automatically

selected in subsequent frames as will be discussed be-

low. OOSfM is then applied to the group of images,

to test the effect of emphasizing the object of interest.

3.1 Segmentation and Object Selection

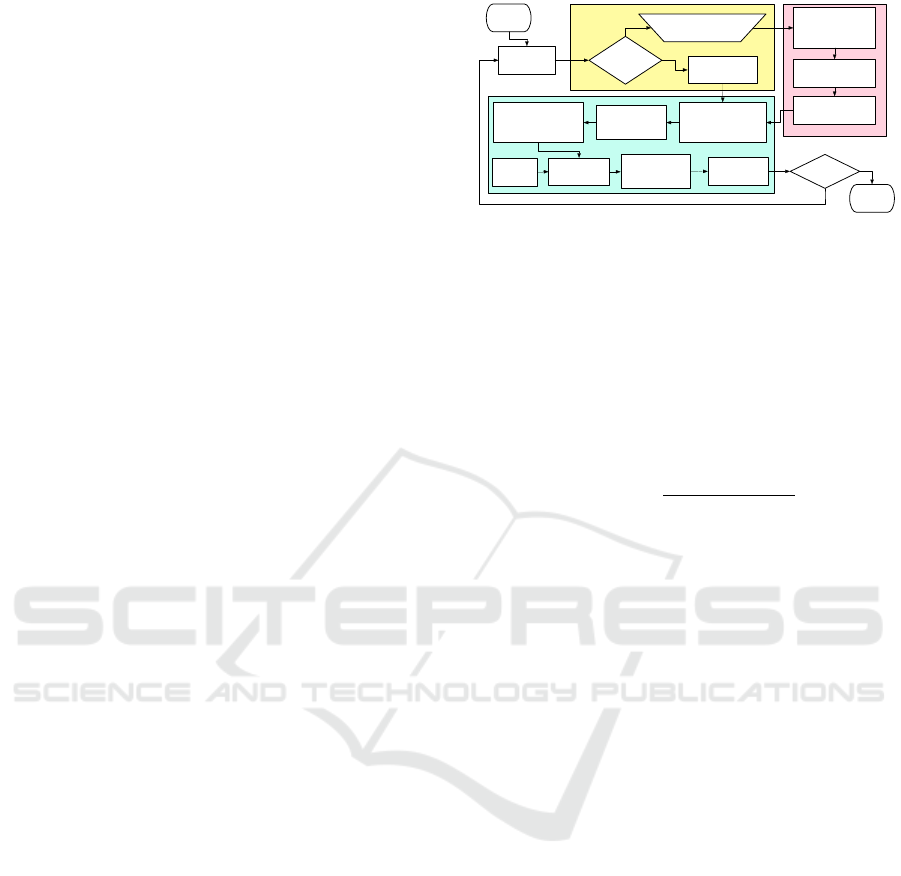
The details of the segmentation part of OOSfM are

shown in Fig. 2. OOSfM inputs images and ex-

tracts object hypotheses using the Geodesic Object

Proposals (GOP) method of Kr

ahenb

uhl and Koltun

(Kr

ahenb

uhl and Koltun, 2014). Then, the user is

prompted to scribble on the object of interest in only

the ﬁrst image, and the initial segmentation is perfor-

med by choosing the GOP having the most similarity

and the least difference with the scribble in terms of

pixels spanned. The segmentation produced by object

proposals is coarse, with a high likelihood of several

object proposals covering different areas of the same

START

Load Img1,

Img2

Generate Mixture

Model 1 (MM1)

driven by OD

Select largest blob in

Img1 as object

Select Object

using blob

Segment Img2

using MM2

Choose blob with most

SIFT features matched

to those in blob of Img1

Scribble in Img1 on Object

Desired (OD)

Img1 = First

Image?

YES

Last Image

pair?

STOP

Reﬁne segmentation

of Img1 using MM1

Generate Mixture

Model 2 (MM2) driven

by Img1 segmentation

GOP on

Img2

Select largest

blob in Img2 as

object

Reﬁne

segmentation on

Img2 using GOP

Use Object from

previous iteration

YES

Figure 2: Detailed ﬂowchart of the segmentation in

OOSfM.

object. Therefore, in order to better delineate the

boundaries of the sought-after object, an appearance-

based segmentation is implemented, using the appea-

rance of the selected object proposal to guide the pro-

cess.

The segmentation relies on the following Maxi-

mum A Posteriori (MAP):

p(c

) =

p(x

)p(c

)

∑

p(x

)p(c

)

(1)

This formulation relies on a mixture model of the

image, where each pixel is generated by ﬁrst choo-

sing the mixture component, or image segment, and

then generating the item from this component. The

prior probability p(pixel = c

), or simply p(c

), is the

probability of the pixel being generated from either

the object of interest or from background clutter. It

is calculated as p(c

) = n

/n, where n

is the number

of pixels belonging to cluster l, based on the object

proposal chosen before, and n is the total number of

pixels.

The likelihood p(x|c

) of generating a pixel with a

feature vector x, given a segment l, is computed using

the output of the GOP method. Here, we assume the

feature vector to be Gaussian with mean µ

and cova-

riance Σ

. It contains (1) the R,G, and B color values

at each pixel location; (2) the row (u) and height (v)

positions in the image; and (3) the local entropy para-

meters.

The new probabilities lead to an updated segmen-

tation for the ﬁrst image. To ensure the object consists

of connected components and remove possible noisy

regions, we choose, as the ﬁnal version of the object

of interest in the ﬁrst image, the blob with the largest

number of connected pixels belonging to the object

cluster (see Fig. 3 to better clarify this step).

Once the different objects of interest are segmen-

ted in the ﬁrst image, the segmentation can be pro-

pagated to the subsequent images, and is performed

according to a MAP, which is now conditioned on the

previous segmentation S

t−1

, in addition to the feature

Object Oriented Structure from Motion: Can a Scribble Help?

543

(a)

(c)(b)

(d) (e)

Figure 3: Sample segmentation results in OOSfM, (a) user

scribble, (b) selected GOP, (c) p(pixel label=object |x

), (d)

M.A.P. segmentation, (e) segmentation into connected regi-

ons (blobs) and selection of largest blob.

vector of the current frame. Blobs are extracted by re-

gion growing pixels labelled as objects. To match to

the selected blob in the ﬁrst image, we choose, in the

new image, the blob containing the largest number of

SIFT features matched to those in the selected object

in the ﬁrst image:

Blob

c,q

= argmax

i∈I

{| f (Blob

) ∩ f (Blob

)|;q ∈ I

}

(2)

where subscripts c and q are used to refer to the ‘cor-

responding’ and ‘query’ blobs respectively and f (.) is

the ensemble of features belonging to a blob. I

and I

refer to two different images in which blobs are being

matched, and |.| refers to the cardinality of the inter-

section.

The chosen blob is matched again to the closest

object proposal in image t, and the segmentation is ﬁ-

nally reﬁned by introducing a new mixture model and

MAP detector which are based, this time, on the last

segmentation of the image itself S

. The largest con-

nected area of pixels, labeled as object, is then ﬁnally

chosen as our object of interest.

3.2 Object Oriented Structure from

Motion

After the ﬁrst step of OOSfM is complete and objects

are segmented in each image, we aim to extract the

structure and the motion by implementing a modiﬁed

version of SfM, which uses the objects’ segmentation.

Most steps are identical to those in the traditional SfM

pipeline, except for the bundle adjustment, as will be

explained below.

First, each pair of frames are considered sequenti-

ally, and SIFT features are detected and matched in

order to extract the Essential matrix relating image

pairs. Here, we assume each camera is already ca-

librated off-line. Then, a ﬁrst estimate of rotation

and translation is obtained using least-squares (Hart-

ley and Zisserman, 2003). After that, the information

from successive frames is combined, while keeping

track of the common features. Each time a new image

is added, the 2D features are triangulated to their 3D

position using our ﬁrst guess of camera rotations and

translations. After looping over all images, the com-

plete set of structure and motion parameters are then

optimized for, in the bundle adjustment step (Triggs

et al., 1999), using the ﬁrst triangulation as an initial

guess for the Levenberg-Marquardt algorithm. The

structure and camera positions, which we optimize

for, are parameterized by a single state vector v. The

simplest formulation of the bundle adjustment step

aims to minimize the sum of the squared re-projection

errors of all the points in the scene, re-projected onto

all cameras in which they are observed:

min

∑

cam.

∑

3D pts.



(x − x

rep

(v))

+ (y − y

rep

(v))



, (3)

where, the measured row and column positions

of image features are represented by (x,y), while

the predicted values of these features are denoted

rep

(v),y

rep

(v)).

Assuming the measurement noise is Gaussian, this

minimization gives the Maximum Likelihood (ML)

solution, which represents the jointly optimal struc-

ture of the scene and the motion parameters of the

cameras (Hartley and Zisserman, 2003).

In the formulation of (3), the terms inside the sum

are equally weighted, and as such, points belonging

to the objects and others belonging to the background

equally contribute to the optimization results. The ﬁ-

nal re-projection error of the structure is in this case

minimized, such that it compromises the error attri-

butable to both the objects and background. For this

reason, we propose to introduce the change in the SfM

pipeline at the level of the bundle adjustment in a way

to give more weight to the object of interest, which in

general contains less noisy feature matching than the

background.

3.2.1 Minimizing the Object Error, with a

Bound on the Background Error

To minimize the negative effect of errors in back-

ground estimation on the accuracy of the estimated

structure of objects, the ﬁrst method we propose is to

reformulate the bundle adjustment step as a constrai-

ned optimization problem, where the new objective

function aims to minimize the sum of squared re-

projection errors of points exclusively belonging to

the selected objects of interest, rather than the entire

scene. In the optimization, we bound the background

re-projection error and include it as a hard constraint.

The upper bound for the background re-projection er-

ror is denoted by threshold n. The optimization is ex-

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

544

pressed mathematically as follows:

min

∑

cam.

∑

3D pts.∈obj



(x − x

rep

(v))

+ (y − y

rep

(v))



subject to:

∑

cam.

∑

3D pts.∈back



(x − x

rep

(v))

+ (y − y

rep

(v))



≤ n

(4)

The value chosen for n greatly affects the results of

the optimization. In order to improve on the object

re-projection error resulting from the vanilla version

of SfM in (3), n should be larger than the background

error resulting from the normal bundle adjustment,

where all points are considered uniformly. Therefore,

the minimum value of n is estimated by running nor-

mal SfM.

3.2.2 Object-Only SfM

In the previously described method, we formulate BA

as a constrained optimization and solve for all para-

meters at once. However, the background constraint

does not only involve the background structure points.

It also inﬂuences the camera positions, and thus it

might be negatively affecting the object structure pa-

rameters despite the decrease in the total object re-

projection error. For this reason, we try to investigate

the effect of background points on the optimization.

The next BA variant eliminates completely the

background points from the objective function (Eq.

5). It minimizes the total re-projection error of object

points, without any consideration to the background

points, which are kept however part of the optimiza-

tion parameters for comparison purposes.

min

∑

cam.

∑

3D pts.∈obj



(x − x

rep

(v))

+ (y − y

rep

(v))



(5)

3.2.3 Weighted Bundle Adjustment

Removing background points completely from the

cost function of the optimization could have nega-

tive effects on the output structure of the object. In

fact, as it will be shown in the results section, more

points in the optimization usually lead to a better re-

construction. For this reason, the next formulation

keeps the background points as part of the objective

function, but with a lower weight. Note that this idea

is similar in spirit to the covariance-weighted bundle

adjustment formulation (Triggs et al., 1999).

min

∑

cam.

∑

3D pts.∈obj



(x − x

rep

(v))

+ (y − y

rep

(v))



∑

cam.

∑

3D pts.∈back.



λ(x − x

rep

(v))

+ (y − y

rep

(v))



(6)

λ is a weight factor (less than 1), whose role is to de-

crease the effect of the background on the results. By

keeping the background points inside the optimiza-

tion, we avoid overﬁtting the camera parameters to

the object of interest.

4 EXPERIMENTS AND RESULTS

The different OOSfM versions were tested on a num-

ber of publicly available real and synthetic datasets,

consisting of multi-view images of different scenes,

each with a different number of images of different

resolutions. Since OOSfM is designed to reconstruct

objects and not large-scale scenes, we observe that a

relatively small number of images is sufﬁcient to eva-

luate its performance. Although our SfM variants can

be bootstrapped off of any SfM implementation, we

choose to build off the implementation of SFMedu

(Xiao, 2014). For the constrained bundle adjustment

step, a ﬁrst-order interior-point algorithm was used

with an appropriate function tolerance. Sequential

quadratic programming was also used on some da-

tasets where convergence was not met through the

interior-point method.

4.1 Results on the Segmentation Part of

OOSfM

The ﬁrst part of our SfM formulation involves the seg-

mentation of the object of interest, starting with the

user scribble on the ﬁrst image.

Fig. 4, 5 and 6 present the results of the interactive

segmentation, and the propagation of the segmenta-

tion across images of the Clocktower (Kowdle et al.,

2010), Stone (Kowdle et al., 2010) and fountain-P11

(Strecha et al., 2008) datasets. The algorithm does

well even on difﬁcult datasets like Stone. For Clock-

tower, the segmentation is still capable of detecting

the tower in spite of it being severely occluded by a

tree in many of the frames.

4.2 Performance of OOSfM

After the segmentation, the remaining components

of OOSfM, with the different modiﬁed versions of

BA, are applied to every dataset, focusing the recon-

struction on a speciﬁc object with a random shape in

the scene. The ﬁrst metric that we use to evaluate the

three variants we present is the average re-projection

error, which is deﬁned as (2

∑

residuals

|residuals|

), for the ob-

ject points alone since our aim is to test the effect of

OOSfM on the object structure.

Object Oriented Structure from Motion: Can a Scribble Help?

545

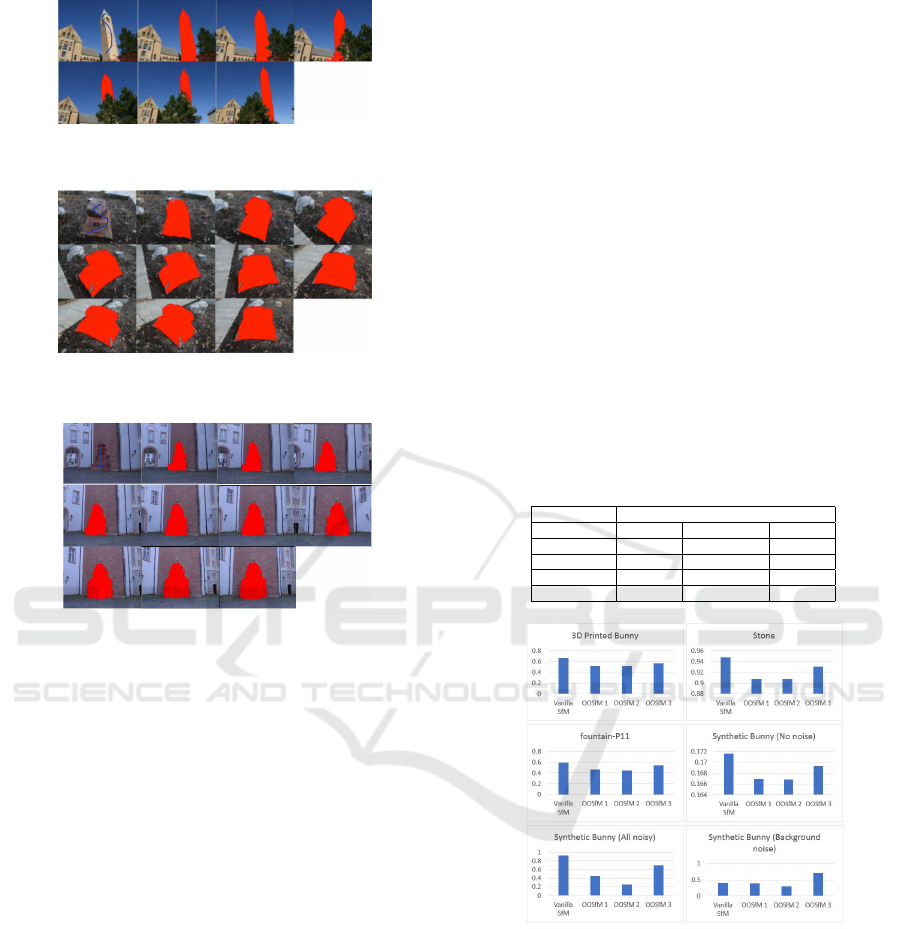
Figure 4: Results on the Clocktower dataset; images are

ordered from left to right on each row.

Figure 5: Results on the Stone dataset; images are ordered

from left to right on each row.

Figure 6: Results on the fountain-P11 dataset; images are

ordered from left to right on each row.

We choose real datasets with a rich number of fe-

atures to test our algorithms: ”3D Printed Bunny”,

”Stone” and ”fountain-P11”, where the interactive

segmentation has been successful to delimit the ob-

ject of interest in the scene. SIFT features are used

to perform the matching at the level of these datasets.

A synthetic dataset, ”Synthetic Bunny”, is also crea-

ted with the Stanford Bunny (Turk and Levoy, 2005)

as the object of interest. Ray tracing from the ground

truth point cloud is used in this case to recover the 2D

features, to eliminate the errors that could be induced

by the SIFT matching.

Artiﬁcial noise is added to the 2D matched points

of the ”Synthetic Bunny” dataset, to end up with three

scenarios: ”Synthetic Bunny (No noise)”, with no

added noise to the matches. The SfM result in this

case is already good (average total re-projection error

of 0.177653). ”Synthetic Bunny (All noisy)”, where

noise is added on the re-projections of 1 in 5 points

of both object and background points. ”Synthetic

Bunny (Background noise)”, with added noise on the

re-projections of the background points to account for

the variability in the background.

The different variants of BA will be numbered as

follows in the rest of the paper:

1. Minimizing the Object Error, with a Bound on the

Background Error

2. Object-Only SfM

3. Weighted Bundle Adjustment (with a chosen

background weight λ = 0.5)

The re-projection errors for the ”3D Printed

Bunny” are ﬁrst reported in details in Table 1. Fig.

7 then summarizes, for all the datasets, the change

in the re-projection error of the object alone as for-

mulations 1-3 are applied. For method 1, we set the

parameter n in the constraint to the background error

resulting from the vanilla SfM, added by 1 then roun-

ded to the nearest half-integer. The initial guess for

the optimization is the output of vanilla SfM for met-

hods 1 and 2, as for method 3, it is the triangulation

result.

Table 1: Average re-projection errors for the object, back-

ground, and total scene using the vanilla SfM and OOSfM

on the 3D printed Bunny dataset.

Re-projection Error

SfM variant Object Background Total

Vanilla SfM 0.659979 1.955798 1.299734

OOSfM 1 0.51802 2.941184 1.835419

OOSfM 2 0.51802 5.832184 3.570761

OOSfM 3 0.567647 2.043443 1.321943

Figure 7: Graphical comparison of the re-projection errors

of the object for both regular SfM and OOSfM (1-3). Note

the obvious drop in error for OOSfM variants on all datasets

except the last.

The ﬁrst observation that we can make is that the

object re-projection error decreases compared to the

vanilla SfM output, as a result of all three BA modi-

ﬁcations, for all datasets except the last. In addition,

optimizing the cost function over the object alone wit-

hout any consideration to the background always gi-

ves the lowest object re-projection error. This ideally

should mean a better reconstruction for the object of

interest. Therefore, based on the re-projection error

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

546

metric alone, the result of the BA optimization on the

object is best when the object is taken alone (met-

hod 2). Since our original aim was to keep the object

within context by maintaining an acceptable estimate

of the background, it seems that methods 1 and 3 give

the results that we are looking for.

However, the re-projection residual alone is not

a good indicator of the quality of the reconstruction.

For instance, in (Ma et al., 2015), a better cylindri-

cal structure was actually at the cost of an increase in

the re-projection error of the scene. In our formula-

tion, constraining the bundle adjustment step to ob-

ject points only could lead to overﬁtting the camera

parameters to the object of interest. This can be in-

ferred from the high re-projection error that results on

the background points compared to vanilla SfM, for

the same 3D points positions. The idea is similar in

concept to the case of ﬁtting a line to points, where fe-

wer points could lead to an erroneous representation

of the global picture. It is also hard to visually assess

whether any method is performing better than the ot-

her in terms of improving the object’s structure (Fig.

8).

Figure 8: Point clouds of the fountain-P11 object, using the

different SfM methods: Vanilla SfM result of the fountain

(object) overlaid on the ground truth point cloud of the en-

tire scene (top left), OOSfM 1 (top right), OOSfM 2 (bottom

left) and OOSfM 3 (bottom right) results of the object.

A comparison to ground truth data is therefore

performed to assess the different methods presented,

and to ﬁnd out whether it is indeed possible to im-

prove the reconstruction of the object of interest. This

is done on the ﬁrst scenario of the ”Synthetic Bunny”

dataset, without any added noise. For the compari-

son, the object of interest is segmented from the out-

put point cloud that each OOSfM generates, as well

as, from the ground truth point cloud. The two object

point clouds are manually aligned using three anchor

points, while allowing for optimization of scale, rota-

tion, and translation between them. The iterative clo-

sest point (ICP) (Besl and McKay, 1992) algorithm is

then applied to minimize the root mean square error.

This error is reported for each method in Table 2.

Table 2: Comparison of the RMS error with the ground truth

object using the vanilla SfM and OOSfM for the Synthetic

Bunny (No noise) dataset.

Synthetic Bunny (No noise)

RMS error

Vanilla SfM 0.0144957

OOSFM 1 0.0186764

OOSfM 2 0.0194392

OOSfM 3 0.0147708

While the RMS error is small for all methods , the

vanilla SfM result still shows the lowest error with the

ground truth point cloud of the object. The object-

only result (OOSfM 2) shows the highest RMS er-

ror; it is explained by the fact that the camera para-

meters obtained from the optimization are overﬁtting

the object. This in turns causes the object’s points in

3D to move, leading to a worse object point cloud in

spite of the lower re-projection error. In OOSfM 1

as well, allowing for a higher error in the background

while decreasing the object’s error does not guarantee

a better structure. On the other hand, keeping back-

ground points in the optimization, even with a lower

weight (OOSfM 3), gives an RMS error very close to

the vanilla result. This brings us to the conclusion that

keeping background points as part of the optimization

improves the ﬁnal reconstruction of the object.

Figure 9 shows the 3D points found through va-

nilla SfM and each variant of OOSfM, overlaid on the

Stanford Bunny from the synthetic dataset.

Figure 9: Results showing the Stanford bunny from the

synthetic dataset with the overlay of 3D points resulting

from vanilla SfM (top left), OOSfM 1 (top right), OOSfM 2

(bottom left), and OOSfM 3 (bottom right). Here the change

is more prominent; note how point clouds using vanilla SfM

and OOSfM 3 (weighted BA) ﬁt the model better, because

they take background points into consideration.

5 CONCLUSIONS

We introduced a system that automatically tracks ob-

jects through a sequence of images, based on an initial

user scribble. We then tested different bundle adjust-

ment formulations that attempted to give more weight

on the object of interest. While we decreased the to-

tal object re-projection error using the three BA vari-

Object Oriented Structure from Motion: Can a Scribble Help?

547

ants, we demonstrated that vanilla SfM outperforms

the other formulations in terms of accuracy of the re-

constructed objects. The main conclusion that we can

make is that a lower re-projection error does not ne-

cessarily correspond to a better structure, which puts

into question the accuracy of this metric as a measure

of the structure estimate when dealing with speciﬁc

objects, rather than the entire scene. In the future,

we will study the effect of semantics on the recon-

struction of the object of interest, and whether additi-

onal prior information about the nature of the object

could improve on the vanilla result of the SfM pro-

blem.

ACKNOWLEDGEMENTS

This work was supported by the Lebanese National

Council for Scientiﬁc Research (LNCSR).

REFERENCES

Bao, S. Y., Bagra, M., Chao, Y. W., and Savarese, S. (2012).

Semantic structure from motion with points, regions,

and objects. In IEEE Conference on Computer Vision

and Pattern Recognition (CVPR), pages 2703–2710.

Besl, P. J. and McKay, N. D. (1992). A method for regis-

tration of 3-d shapes. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 14(2):239–256.

Cipolla, R. and Robertson, D. (1999). 3d models of ar-

chitectural scenes from uncalibrated images and va-

nishing points. In Image Analysis and Processing,

1999. Proceedings. International Conference on, pa-

ges 824–829.

Crocco, M., Rubino, C., and Del Bue, A. (2016). Struc-

ture from motion with objects. In IEEE Conference

on Computer Vision and Pattern Recognition (CVPR).

Debevec, P. E., Taylor, C. J., and Malik, J. (1996). Mo-

deling and rendering architecture from photographs:

A hybrid geometry-and image-based approach. In

Annual conference on Computer graphics and inte-

ractive techniques, pages 11–20.

Fioraio, N. and Di Stefano, L. (2013). Joint detection,

tracking and mapping by semantic bundle adjustment.

In IEEE Conference on Computer Vision and Pattern

Recognition (CVPR), pages 1538–1545.

Frahm, J. M., Fite-Georgel, P., Gallup, D., Johnson, T., Ra-

guram, R., Wu, C., and Pollefeys, M. (2010). Building

rome on a cloudless day. In European Conference on

Computer Vision (ECCV), pages 368–381.

Frost, D. P. and Murray, D. W. (2016). Object-aware bundle

adjustment for correcting monocular scale drift. In

IEEE International Conference on Robotics and Au-

tomation (ICRA), pages 4770–4776.

alvez-L

opez, D., Salas, M., Tard

os, J. D., and Montiel,

J. M. M. (2016). Real-time monocular object slam.

Robotics and Autonomous Systems, 75.

Hartley, R. and Zisserman, A. (2003). Multiple view geome-

try in computer vision. Cambridge University Press.

Kowdle, A., Batra, D., Chen, W. C., and Chen, T. (2010).

imodel: interactive co-segmentation for object of in-

terest 3d modeling. In European Conference on Com-

puter Vision (ECCV), pages 211–224.

ahenb

uhl, P. and Koltun, V. (2014). Geodesic object pro-

posals. In European Conference on Computer Vision,

pages 725–739.

Ma, T., Sun, Z., Zhang, W., and Chen, Q. (2015). Three-

dimensional reconstruction of a cylinder surface based

on constrained bundle adjustment. Optical Engineer-

ing, 54(6):063101–063101.

Oh, B. M., Chen, M., Dorsey, J., and Durand, F. (2001).

Image-based modeling and photo editing. In Annual

conference on Computer graphics and interactive

techniques, pages 433–442.

Sch

onberger, J. L. and Frahm, J. M. (2016). Structure-from-

motion revisited. In IEEE Conference on Computer

Vision and Pattern Recognition (CVPR).

Sinha, S. N., Steedly, D., Szeliski, R., Agrawala, M., and

Pollefeys, M. (2008). Interactive 3d architectural mo-

deling from unordered photo collections. ACM Tran-

sactions on Graphics, 27(5):159.

Strecha, C., Von Hansen, W., Van Gool, L., Fua, P., and

Thoennessen, U. (2008). On benchmarking camera

calibration and multi-view stereo for high resolution

imagery. In Computer Vision and Pattern Recognition,

2008. CVPR 2008. IEEE Conference on, pages 1–8.

Ieee.

underhauf, N., Dayoub, F., McMahon, S., Eich, M., Up-

croft, B., and Milford, M. (2015). Slam–quo vadis?

in support of object oriented and semantic slam. In

Robotics and Systems (RSS) Workshop, Rome, Italy.

Triggs, B., McLauchlan, P. F., Hartley, R. I., and Fitzgibbon,

A. W. (1999). Bundle adjustment—a modern synthe-

sis. In Hieidelberg, S. B., editor, International works-

hop on vision algorithms., pages 298–372.

Turk, G. and Levoy, M. (2005). The stanford bunny.

Van den Hengel, A., Dick, A., Thorm

ahlen, T., Ward, B.,

and Torr, P. H. (2007). Videotrace: rapid interactive

scene modelling from video. ACM Transactions on

Graphics (ToG), 26(3):86.

Xiao, J. (2014). Sfmedu. http://vision.princeton.edu/

courses/SFMedu/.

Zhu, H., Meng, F., Cai, J., and Lu, S. (2016). Beyond pixels:

A comprehensive survey from bottom-up to seman-

tic image segmentation and cosegmentation. Journal

of Visual Communication and Image Representation,

34:12–27.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

548