Visibility based WSPD for Global Illumination

M. Maria

, N. Mustafa

, T. Bardoux

, J. Defaye

and V. Biri

University of Paris-Est, LIGM, France

Ubisoft Motion Pictures, Montreuil, France

Keywords:

Ray Tracing, Many-light, VPL Clustering.

Abstract:

In the context of rendering production, and especially for indirect diffuse global illumination, many-light

techniques can be used to quickly render noise free images. In this paper, we propose a view-independent

algorithm, based on Well Separated Pair Decomposition (WSPD), to handle efﬁciently clustering of virtual

point lights. Our clustering, the Visibility based WSPD (V-WSPD) consider both geometric and visibility

information of two sets of points, allowing an improved rendering time with a similar image quality.

1 INTRODUCTION

In computer graphics industry, computing accurately

global illumination (GI) in complex scenes, like those

illustrated in Figure 1, remains really challenging

since the size of the assets and the number of lights

are massive. In such productions, path tracing or point

based GI methods are generally used to compute the

ﬁnal image (K

riv

anek et al., 2010). But their rende-

ring engine also computes separated layers of this ﬁ-

nal image such as glossy reﬂection/refraction or indi-

rect diffuse lighting. The latter is a particular GI pro-

blem that could be handled with Virtual Point Light

(VPL) based techniques (Dachsbacher et al., 2014).

Visibility queries between pairs of points remain

one of the main cost of all GI algorithms (Dutr

et al., 2006). Thus, the knowledge of the overall

scene structure is a key to compute indirect illumi-

nation more efﬁciently, especially for a full sequence

of images of the same scene. Recent works, for in-

stance Imperfect Shadow Maps (Ritschel et al., 2008),

have followed this way. They approximate visibility

for indirect illumination by rendering a low-resolution

shadow map from a rough point-based representation

of the scene geometry. This approximation is then

used to achieve real-time GI on GPU.

Deﬁned in the many-light framework, our work is

also based on visibility approximation but handles a

considerably larger number of VPL, for ofﬂine ren-

dering. It focuses on the visibility of two different

point sets, created along light paths vertices (such as

VPL). We redeﬁne the work of (Bus et al., 2015a)

on the Well-Separated Pair Decomposition (WSPD)

method. While they use a pure geometric criterion

to build their structure, we drive the construction di-

rectly with visibility queries, along with the existing

geometric factor, while remaining view-independent.

The result is a new data structure, the Visibility ba-

sed WSPD (V-WSPD), that handles visibility to furt-

her reduce the number of shadow rays needed to com-

pute indirect illumination. We show that this additio-

nal visibility criterion allows to signiﬁcantly speed up

rendering while keeping a similar image quality.

Therefore, our main contributions can be summa-

rized as follows:

• an efﬁcient data structure, the V-WSPD, optimi-

zed for fast rendering with a large number of VPL;

• a view-independent construction algorithm, allo-

wing to reuse the V-WSPD for a full sequence of

images in case of static scenes;

• an analysis of the performance scalability w.r.t.

the visibility approximation accuracy.

This paper is organized as follows: Section 2 re-

views the existing many-light rendering techniques

related to our approach; Section 3 gives the theore-

tical background introducing our work; Section 4 de-

tails our new data structure, the V-WSPD; Section 5

presents and discusses experimental results; Section 6

concludes and gives several future work lines.

Maria, M., Mustafa, N., Bardoux, T., Defaye, J. and Biri, V.

Visibility based WSPD for Global Illumination.

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages

81-90

ISBN: 978-989-758-287-5

Figure 1: Examples of VPL rendering with the V-WSPD: rendered image, indirect illumination and error ×128. The scenes

(GEEKROOM and MARKET) come from the TV Series Rabbids Invasion of Ubisoft.

2 RELATED WORK

During this last decade, many-light methods have be-

come very attractive since they allow to render high-

quality, almost artifact-free, but biased images in a

fraction of the time taken by Monte-Carlo methods

to converge to a noise-free image. Thus, a lot of re-

cent researches focus on this topic (Simon et al., 2015;

Hedman et al., 2016; O’Donnell and Chajdas, 2017)

In this section, we focus on global illumination

in many-light methods, especially on techniques de-

signed to compute (or approximate) efﬁciently the

contribution of large amount of VPL. For real-time

techniques, improvements on VPL distribution or lig-

hting, and a detailed state-of-the-art report, the reader

is referred to (Dachsbacher et al., 2014).

Generating a high-quality image with many-light

algorithms usually requires from thousands to milli-

ons of VPL. A naive method, such as the original In-

stant Radiosity (Keller, 1997), which evaluates line-

arly the contribution of each VPL for each point to

shade, would be prohibitively time-consuming to be

used in practice. To overcome this problem, several

methods, called scalable methods, have been propo-

sed to accurately approximate the computation with a

sub-linear complexity. We review the most relevant

ones next.

2.1 VPL Clustering

Clustering methods aim at partitioning the set of VPL

into clusters w.r.t. their contribution to the image. The

goal is to store important VPL into small clusters and

negligible ones into largest clusters. Then, each clus-

ter is represented by a single representative light with

adapted intensity. When rendering, for each point to

shade, a subset of clusters (a clustering) is selected

to approximate the radiance. Thus, the number of

evaluations becomes drastically smaller than the total

amount of VPL and the computation is much faster.

The idea of VPL clustering has been introduced

in (Paquette et al., 1998). They build a hierarchical

octree on the set of VPL and then extract a clustering

of VPL for each point to be shaded. Their method

signiﬁcantly speeds up the process but is not robust,

leading to badly chosen clustering. Since then, a lot of

methods have been presented. We propose to classify

them into two main families: tree-based methods and

matrix-based methods.

Tree-based Methods. Lightcuts (Walter et al.,

2005) is the ﬁrst practical VPL clustering method.

It is based on a binary tree, called light tree, from

which a clustering is selected for each point to be

shaded. This selection is performed by reﬁning the

tree from the root to minimize the error upper bound

until it is below a given perceptual threshold. Many

extensions of Lightcuts have followed this ﬁrst work.

Multidimensional Lightcuts (MDLC) (Walter et al.,

2006) uses a shading point tree to handle distributed

effects such as anti-aliasing or motion blur. Bidirecti-

onal Lightcuts (Walter et al., 2012) extends MDLC to

handle more materials, such as glossy reﬂections or

subsurface scattering. (Wang et al., 2011) aim at im-

proving the clustering selection efﬁciency by exploi-

ting cluster coherence. IlluminationCut (Bus et al.,

2015b) uses two trees to cluster both pixels and VPL

and to further minimize the radiance evaluation cost

per pixel. (Rehfeld and Dachsbacher, 2016) propose

to compute the lightcuts only for a sparse subsam-

pled image and then to interpolate between these lig-

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

htcuts for all others point to be shaded. As part of

GPU computing, (Davidovi

c et al., 2012) address the

problem of adapting Lightcuts to the GPU. Recently,

(Bus et al., 2015a) introduced a view-independent

VPL clustering method, built on a Well-Separated

Pair Decomposition (WSPD) structure. As the struc-

ture we propose is based on this work, it is described

with more details in Section 4.1.

Matrix-based Methods. Other methods directly

study the light transport matrix: rows of the matrix

represent the pixels of the image and columns cor-

respond to the VPL so that each row/column combi-

nation encodes the contribution of a VPL to a pixel.

(Ha

san et al., 2007) ﬁrst introduce the Matrix Row-

Column Sampling (MRCS) to generate a single glo-

bal clustering for the whole image. MRCS has been

adapted for animation using tensors and exploiting

temporal coherence (Ha

san et al., 2008). The main

drawback of these methods is that they fail to cap-

ture local lighting. (Davidovi

c et al., 2010) address

this problem by capturing separately the global and

local lighting and combining them to get the ﬁnal

image. With the same goal, Lightslice (Ou and Pel-

lacini, 2011) partitions the image into slices and then

reﬁnes the global clustering for each slice. This solu-

tion consumes prohibitively too much memory to be

used with a large number of VPL. (Huo et al., 2015)

use a matrix separation technique to reduce the num-

ber of shadow rays needed. These methods are in-

herently view-dependent (they have to be performed

for each image to render) since they need the know-

ledge of (some) shading points. In this paper, we pro-

pose a structure that is fully view-independent. Thus,

it could be computed once, and reused for a full se-

quence of images.

2.2 VPL Sampling and Caching

Another way to reduce the algorithm complexity is

by choosing a relevant subset of VPL (or rejecting

negligible ones) w.r.t. their contribution to the ﬁnal

image. For instance, Importance Sampling (Georgiev

and Slusallek, 2010) rejects VPL while Importance

Caching (Georgiev et al., 2012) builds a probability

function by computing and recording the contribution

of all VPL for a sparsely distributed shading points

into caches, called Importance Records. Then, for a

given point to shade, the closest Importance Records

are used to sample the VPL. Later, (Yoshida et al.,

2015) extend this work by proposing an adaptive ca-

che insertion to further reduce variance.

Once again these methods are view-dependent and

have to be performed for each image to render.

3 THEORETICAL BACKGROUND

Let S be the set of VPLs, and P be the set of points

to be shaded. The radiance caused by the direct illu-

mination of a single light source s ∈ S , for a surface

point p ∈ P observed from the direction ω is deno-

ted L

(p, ω) and deﬁned as the product of its mate-

rial (M), geometric (G), visibility (V ) and intensity

(I) terms (cf. (Walter et al., 2005)):

(p, ω) = M

(p, ω) · G

·V

(p) · I

(1)

Then, for each point p to be shaded, the total radiance

(p, ω) is computed by summing all light contribu-

tions:

(p, ω) =

∑

s∈S

(p, ω) (2)

For a single cluster C ⊆ S, let rep(C) ∈ C be the

representative light of C. Then, the radiance can be

approximated as:

(p, ω) = M

rep(C)

(p, ω) · G

rep(C)

·V

rep(C)

(p) · I

rep(C)

(3)

The representative light’s intensity is usually precom-

puted once, as I

rep(C)

∑

s∈C

, and stored within the

cluster. Thus, rep(C) has to be chosen carefully to mi-

nimize the error caused by V

rep(C)

, G

rep(C)

and M

rep(C)

computation.

Then, for a clustering ζ = {C

, . . . ,C

} of S the

radiance can be approximated as:

(p, ω) =

∑

C∈ζ

(p, ω) (4)

Rendering an image means solving Equation 2 for

each p ∈ P . This can be seen as a graph scan pro-

blem on the complete bipartite graph G = (P , S , E

in which each edge (p, s) ∈ E

has a weight induced

by the Equation 1. The naive rendering method to

solve this problem would be to cast all the |P | · |S |

rays, a prohibitive number.

To reduce the complexity of this problem, as seen

in Section 2, several methods can be employed. For

instance, Importance sampling (Georgiev and Slusal-

lek, 2010) rejects some lights of S according to their

contribution on the image while LightSlice (Ou and

Pellacini, 2011) clusters both P and S to improve ren-

dering time while keeping good image quality.

But, to approximate the problem in a view-

independent way, and thus to get the same structure

for all images to be rendered, only the S set can be

considered. The goal is to get a clustering of S for

each s ∈ S. Then, the problem can be rephrased as

a scan of the complete Euclidean graph K = (S , E

)

on S and can be trivially solved in O(|S |

) since

| = Θ(|S |

). Once again, given the usual huge

Visibility based WSPD for Global Illumination

number of lights in a scene, the graph is too dense

to be used in this way.

The Well-Separated Pair Decomposition

(WSPD) (Callahan and Kosaraju, 1995) is a

fundamental structure in computational geometry,

that provides a compact representation of K in O(|S |)

space. In other words, it is a partition of the





edges

of K into O(|S |) subsets. Each subset of the partition

is represented by two point sets (or clusters) A, B ⊆ S

that are well-separated.

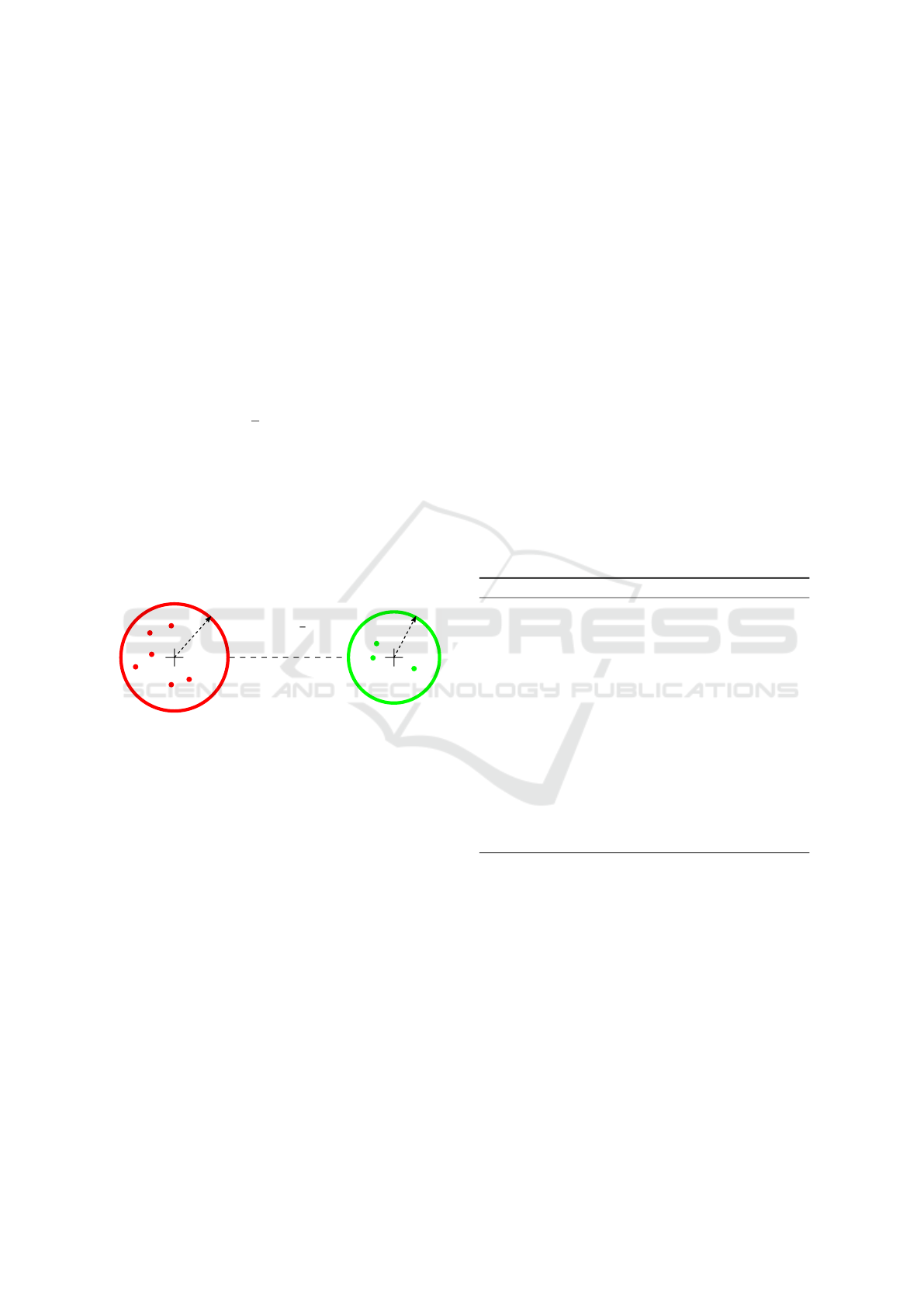
Let us denoted b(C) the smallest enclosing ball

containing all the points of the cluster C and r(C) its

radius. Two clusters A and B are well-separated if, for

a separation parameter 0 < ε ≤ 1:

d(A, B) >

· max(r(A), r(B)),

where d(A, B) is the distance between b(A) and b(B)

(cf. Figure 2). We say that A and B are ws-clusters.

From that, we can deﬁne a WSPD of a point set S

with separation parameter ε as a set of pairs W =

{{A

, B

}, . . . , {A

, B

}} such that, ∀i:

, B

⊂ S ; A

∩ B

and B

are well-separated w.r.t. ε.

r(A)

r(B)

d(A, B) >

· r(A)

Figure 2: The clusters A and B are well-separated according

to the separation parameter ε.

(Bus et al., 2015a) show that the WSPD struc-

ture can pre-compute ws-clusterings of S in a view-

independent way and be used efﬁciently during ren-

dering to extract ws-clustering for each point to be

shaded. This pure geometric WPSD approximates

only the geometric G and intensity I terms of the

Equation 3. In their work, visibility is handled using

additional structures. In this paper, we avoid using ad-

ditional structures to approximate the visibility term

V by driving the WSPD construction using visibility

queries between ws-clusters candidates.

4 VISIBILITY BASED WSPD

In this section we describe our algorithm based on

VPL rendering with WSPD. We ﬁrst recall some ba-

sics about WSPD clustering, then we focus on the

major improvement taking into account visibility bet-

ween clusters of points.

4.1 WSPD Clustering Basics

Here we recall some basics about the use of WSPD

for VPL rendering. More details can be found on (Bus

et al., 2015a).

Construction. The structure construction is sum-

marized in Algorithm 1. From a set of VPLs S , we

build a compressed octree in which a node represents

an axis-aligned bounding box containing a non-empty

subset of S. Each leaf contains one and only one

VPL and each node represents a cluster C deﬁned by

a single representative light with an adapted intensity.

Then, the WSPD is constructed with a top down scan

of the tree. In the end, each node A of the octree sto-

res a list of nodes, denoted pairs(A), with whom it

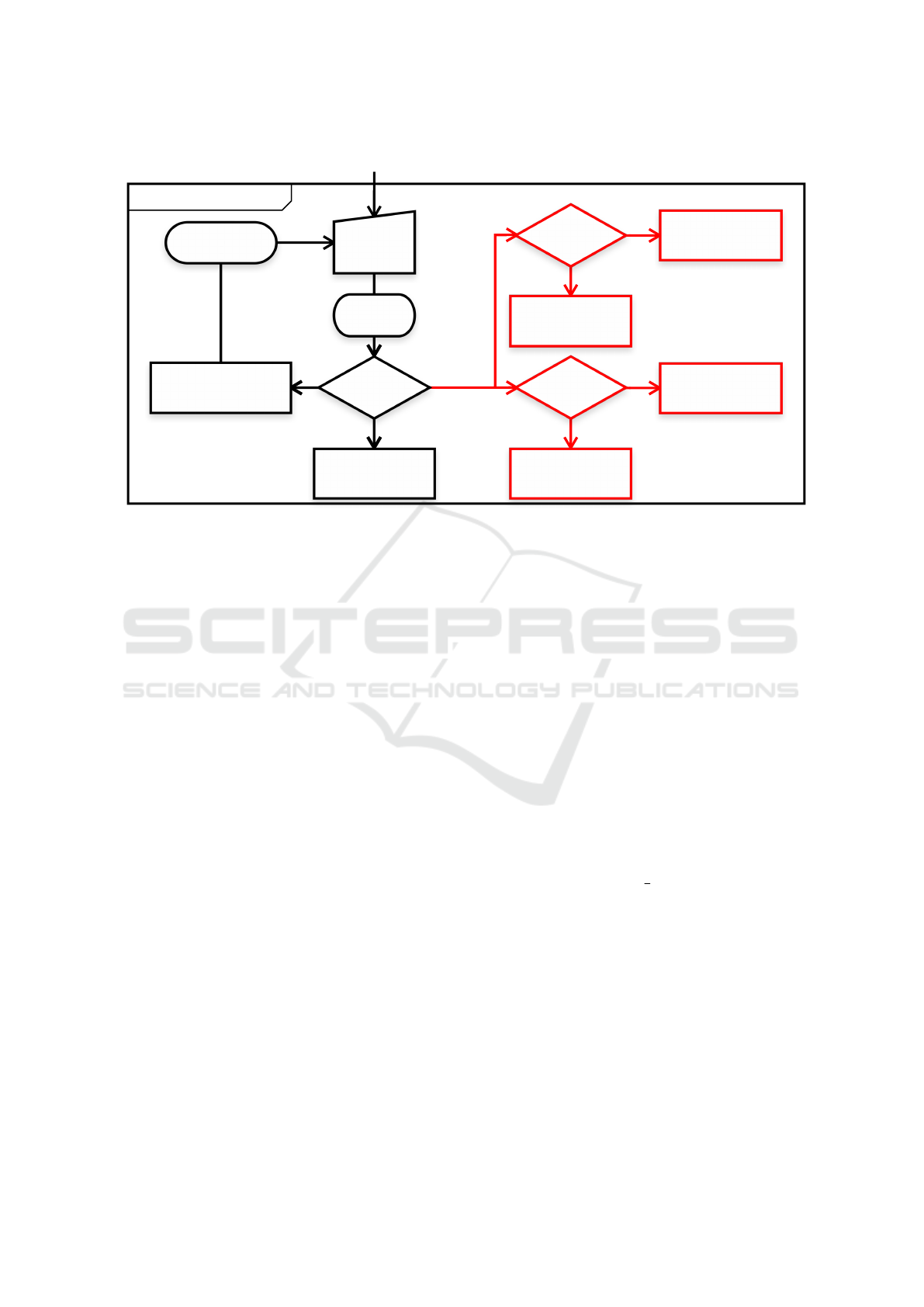
forms a pair. In its pure geometric form, the function

checkPair (cf. Alg. 1, line 8) works as follows (cf.

Figure 3, left): if the two nodes are well-separated

then they form a ws-pair; else, the process recursively

goes on with the children of the biggest node. This

function, checkPair, is the one we improve, as descri-

bed in Section 4.2, to take into account visibility.

Algorithm 1: Build a WSPD from a set of point.

Require: S : set of points;

1: O ← buildCompressOctree(S );

2: S: stack of nodes of S ;

3: S.push(O.root);

4: while S.notEmpty() do

5: C ← S.pop();

6: for i ∈ {1..8} do

7: for j ∈ {1..(i − 1)} do

8: // . . . . . . . . . . . . . . . . . . . . . . . . . cf. Figure 3

9: checkPair(C.child(i),C.child( j));

10: end for

11: S.push(C.child(i));

12: end for

13: end while

Precomputation of Clusterings of S . The goal is

to precompute, for each s ∈ S , a clustering ζ

, . . . ,C

} of S \{s}. In fact, these clusterings are

implicitly encoded in the WSPD structure. Given that

each node contains the list of its well-separated clus-

ters, ζ

corresponds to the union of the pairs of all no-

des from the leaf containing s to the root of the octree.

Extraction of Clusterings of P during Rendering.

The ﬁnal goal is to get, for any point p ∈ P , a cluste-

ring ζ

of S . This can be efﬁciently extracted from the

WSPD. First, we search for the (approximated) nea-

rest light s to p, with distance d. Then, from the pre-

computed clustering ζ

, ζ

is constructed as follows:

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

While Stack not empty

checkPair(A, B)

Stack

POP

PUSH

(V-WSPD)

{children(X),Y }

{A, B}

X = maxRadius(A, B)

Y = other

Reﬁne biggest radius

Pure geometric WSPD Visibility WSPD

pairs(A).insert(B)

pairs(B).insert(A)

pairs(A).insert(B)

YES

B.visible(A) ?

YES

(WSPD)

isW S(A, B) ?

YES

re ject{A, B}

pairs(B).insert(A)

YES

A.visible(B) ?

re ject{B, A}

Figure 3: Schematic algorithm for function checkPair(A, B) (Algorithm 1, line 8): left, pure geometric WSPD; right, additio-

nal process for visibility based WSPD.

∀C

∈ ζ

, if d(s,C

) ≥ d, add C

to ζ

, else repeat with

children(C

This pure geometric WSPD approximates only the

geometric term of the rendering equation but ignores

the others. To answer this issue, (Bus et al., 2015a)

use two additional structures. First, they compute

sub-groups of lights in each clusters w.r.t. their nor-

mals. Second, they pre-compute, for each cluster, a

small cube map to handle inner visibility inside this

cluster. These cube maps are used directly during ren-

dering, along with a single shadow test between p and

the cluster C, to estimate the contribution. This appro-

ach leads to two drawbacks:

• its construction needs two passes, one for the pure

geometric WSPD and another to compute visibi-

lity information and build the additional structu-

res;

• the computation of the cube maps for each cluster

is memory and time consuming;

Our purpose is to drive directly the WSPD con-

struction using visibility queries in order to have a

uniform data structure, easy to implement, and com-

puted in one pass.

4.2 Driving Construction with Visibility

To make the WSPD approximate the visibility term

of the rendering equation, we propose a new criterion

to decide on pair creation. Our method is illustrated

in Figure 3, the new part being in red, on the right.

In this section, we explain how we check visibility

between nodes and how this information can be used

to optionally reﬁne the WSPD. Beneﬁts from this new

method are presented and discussed in Section 5.

Visibility Checking. To reduce the number of

shadow rays needed to compute indirect illumination,

we use visibility queries to reject some pairs in the

WSPD.

Let A and B be two nodes, respectively represen-

ted by their enclosing ball b(A) and b(B). In the

pure geometric WSPD, two nodes form a pair if they

are well-separated i.e. if, for a separation parame-

ter 0 < ε ≤ 1, d(A, B) >

· max(r(A), r(B)), where

d(A, B) is the distance between b(A) and b(B) and r is

the radius. Here, we ﬁrst check for well-separateness

and then pairs are created w.r.t. their visibility.

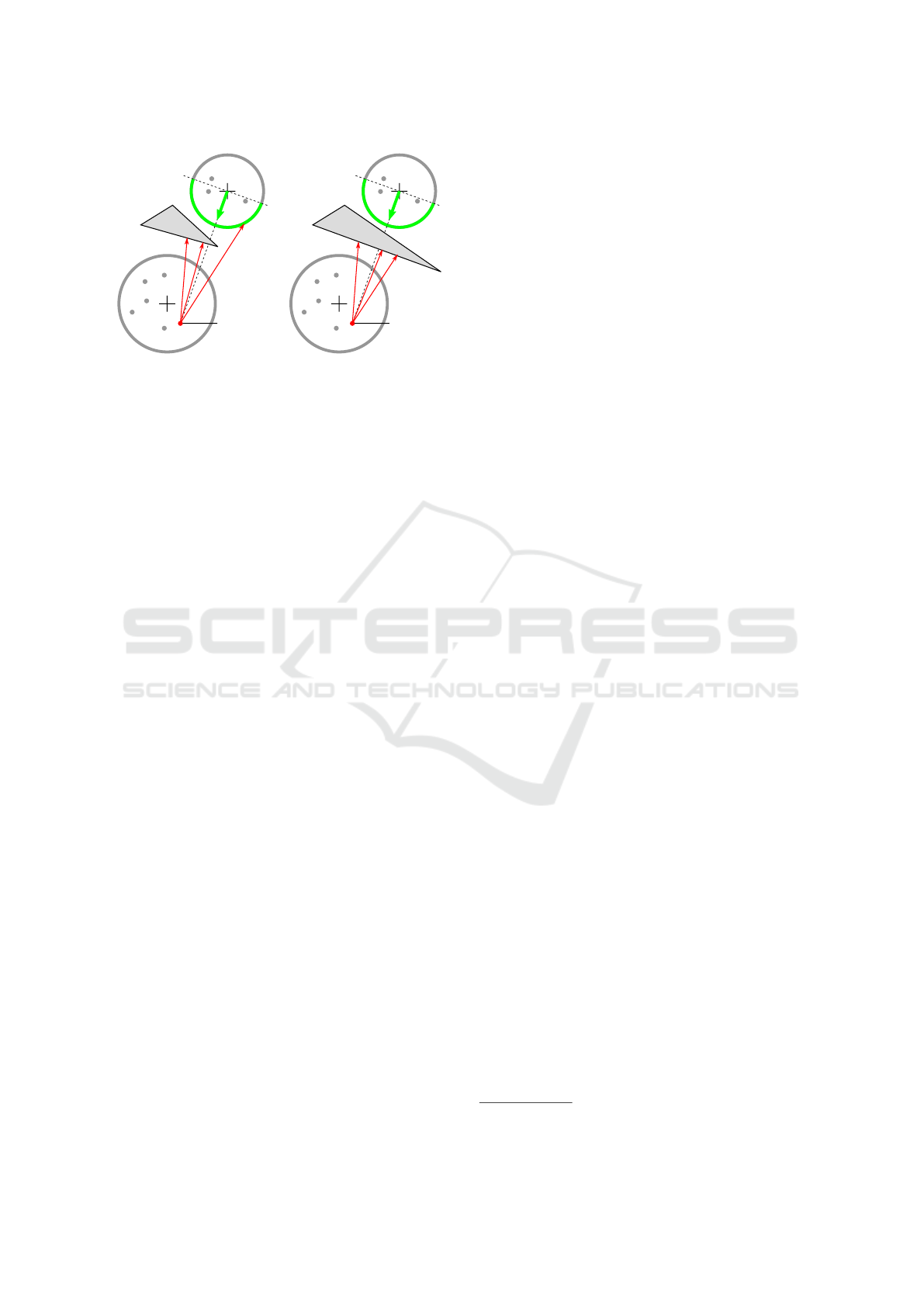
First, we consider A as a shading node and B as a

light node. B will belong to pairs(A) if its representa-

tive light rep(B) is potentially visible from any point

p ∈ A (cf. Figure 4). We approximate the compu-

tation by checking the visibility between rep(B) and

some points H sampled on the hemisphere of b(A) fa-

cing rep(B). If each h

∈ H is not visible from rep(B),

then the pair is rejected. Then, the same process is re-

peated, considering B as a shading node and A as a

light node.

Visibility based WSPD for Global Illumination

rep(B)

Figure 4: Visibility checking: A is the shading node and B

the light node; left: rep(B) is potentially visible from any

point p ∈ A; right: rep(B) is not visible.

We have to process differently the case where the

shading node is a leaf. When building the pure geo-

metric WSPD, leaves are considered with no radius.

In our case, a shading node represents a subset of P

so that if it is a leaf, we cannot ignore its radius. Thus,

for a leaf shading node P and a light node S, the pair

is automatically accepted if rep(S) is inside b(P).

The number of samples picked up on the shading

node hemisphere (denoted spv) is set by the user. The

higher spv is, the lower the error becomes, but with

an increase in precomputation time. We discuss the

impact of this parameter in Section 5. Now, we show

how this visibility information could be used to reﬁne

the WSPD.

Visibility Reﬁnement. The visibility check allows

to discard pairs according to their visibility. One

could think that these visibility queries could be used

to improve the WSPD quality: if the test fails, then

reﬁne with shading node children. In practice, expe-

riments reveal that this strategy is not relevant for two

reasons.

First, it increases signiﬁcantly the V-WSPD con-

struction time: for a unique reﬁnement, it requires

to perform up to 8×spv additional visibility queries.

Moreover, in the worst case, when a shading node is

not visible at all, this strategy will conduct to reﬁne

the full subtree, without any acceptation.

Second, the improvement on the overall image

quality is negligible. Indeed, since the clusters are

geometrically coherent due to the well-separation cri-

terion, the probability for a shading node to be visible

from a light while its parent has not been accepted is

very low.

5 RESULTS AND DISCUSSION

In this section, we present our experimental results on

four different scenes, illustrated in Table 2, with num-

ber of triangles given in Table 1. The ﬁrst two, CON-

FERENCE and MUSEUM are commonly used scenes

in computer graphics. The two others, GEEKROOM

and MARKET are production scenes used for the TV

series Rabbids Invasion by Ubisoft. All scenes con-

tain roughly 600k VPL.

Timings are measured on an Intel Xeon E5-

2670 running at 2,3Ghz with 32GB of RAM, for

1024×1024 pixels images without anti-aliasing. We

use Embree for our ray tracing kernel (

Afra et al.,

2016). For WSPD based methods, ε is ﬁxed at 0.25.

The inﬂuence of this parameter is detailed in (Bus

et al., 2015a). We compare the V-WSPD with the pure

geometric WSPD and with the state-of-the-art met-

hod IlluminationCut (Bus et al., 2015b) without adap-

tive sampling. We used the implementation provided

on the IlluminationCut author’s website

. We set the

maximum error bound to have roughly similar rende-

ring times, and we do not provide any limit for the

maximal cut size. Unfortunately, we could not com-

pare with Lightslice (Ou and Pellacini, 2011) since it

uses too much memory to be run on our machine.

5.1 Performance

Table 1 shows statistics about preprocess time, indi-

rect illumination rendering time and error averaged

from several points of view. We measure the normali-

zed RMSE in LAB color space to compute the nume-

rical difference with the naive VPL reference image

for indirect illumination. We choose to compare in

LAB color space because it is designed to represent

the human eye perception better than RGB. The er-

ror images shown in Table 2 are generated by com-

puting the channel-wise Euclidean distance in LAB

color space with the reference image and multiplying

it by 128 (to be visible). We ﬁrst evaluate the per-

formance of the V-WSPD by comparing it with the

pure geometric WSPD in terms of rendering and con-

struction times. Then we compare it with the state-of-

the-art i.e. with IlluminationCut.

Rendering. As part of rendering, the V-WSPD al-

lows to reduce computation times by 45% (cf. Table 1)

while keeping a similar RMSE. This improvement

can be explained by analyzing the number of shadow

rays shot to compute indirect illumination. Indeed,

since the visibility checking rejects a lot of potenti-

ally non visible pairs, the number of shadow rays is

https://busnorbert.bitbucket.io/

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

Table 1: Results and comparison for four scenes with 600k VPL: timing and error for naive method (VPL), pure geometric

WSPD, visibility based WSPD (V-WSPD) with 5 spv and IlluminationCut (IC) (Bus et al., 2015b).

CONFERENCE MUSEUM GEEKROOM MARKET

(262.3k tr.) (1.53M tr.) (39.04M tr.) (46.06M tr.)

Naive VPL Render (s) 2316.74 3579.62 3661.81 3845.64

WSPD

Preproc. (s) 2.85 3.65 4.63 6.51

Render (s) 12.83 19.74 24.24 29.91

RMSE 0.000450607 0.000695289 0.000602983 0.00189347

# pairs (×10

) 204.38 252.88 269.09 327.06

Preproc. (s) 12.75 19.61 34.95 63.96

V-WSPD Render (s) 8.64 11.12 13.68 13.87

(5 spv) RMSE 0.000462769 0.000712769 0.000604522 0.001998

# pairs (×10

) 96.89 80.82 113.46 100.64

Preproc. (s) 105.94 218.51 249.91 290.49

Render (s) 8.53 10.86 13.88 13.71

RMSE 0.000266304 0.000504664 0.00046284 0.00131467

Err. bound (%) 1 4 1 1.2

WSPD V-WSPD

0 2000 4000 6000

CONF.

MUSEUM

GEEK.

MARKET

(a)

WSPD V-WSPD - 5 spv

0 600050004000300020001000

#shadow rays per pixel

(b)

Figure 5: Number of shadow rays for WSPD and V-WSPD: (a) average number of shadow rays per pixel for each scene (same

points of view as Table 2); (b) false-colored images of the MUSEUM scene.

highly reduced and rendering performance are higher

(cf. Figure 5). We can notice that for the MARKET

scene, the improvement on rendering times is much

better, due to the high level of occlusion brought for

instance by the shelves. For a shading node located

near the shelves, a lot of pairs are rejected so a lot of

shadow rays are avoided. For the same scene, we can

see some blocking artifacts in the false-colored image

in Table 2, due to the visibility approximation. These

artifacts are visible because error is multiplied by 128

but are not perceptible in the ﬁnal image.

Construction. As expected, V-WSPD construction

times are higher than pure geometric WSPD ones.

This is due to the visibility queries needed to drive

the construction. In this way, the complexity does

not only depend on the number of VPL but also on

the number of polygons making up the scene: one

visibility query requires to scan the geometry in or-

der to determine if there is an intersection. Moreover,

the higher the occlusion degree of a scene, the higher

the construction time because more visibility queries

have to be performed before rejecting a pair.

One should consider that, since the V-WSPD

structure is completely view-independent, it has to be

constructed only once for a full sequence of images.

This is a concrete advantage in case of walk-through

system or even to compute static layer in animation

production. Indeed, the time lost when constructing

the structure is negligible w.r.t. the time earned when

rendering: for instance, with MARKET scene, con-

struction time is amortized from the fourth image.

Visibility based WSPD for Global Illumination

Comparison State-of-the-Art. For similar rende-

ring time, we can notice that IlluminationCut gene-

rates images with a lower RMSE. In counterpart, pre-

processing times are considerably higher (about 7 ti-

mes). This shows that the way to build the WSPD ba-

sis structure is not necessarily the best and that some

work has to be done to achieve better quality. Indeed,

for now, the space partition used to build the WSPD

is just a regular octree and does not rest on a speciﬁc

metrics as the light tree of IlluminationCut.

5.2 Visibility Checking

As stated in Section 4.2, the number of samples (spv)

used to approximate the potential visibility between a

shading node and a light node can be tweaked to in-

ﬂuence both performance and precision of our algo-

rithm. In practice, for a shading cluster P and a light

cluster S, the ﬁrst visibility check corresponds to the

direct visibility between rep(S) and b(P). Following

points on b(P) are determined with stratiﬁed hemis-

phere sampling. Figure 6 shows the impact of this

parameter, spv, on construction time, rendering time

and image quality, for the MUSEUM scene.

0.6

1.1

0.7

0.8

0.9

spv:

2 4 6 8 10 12 14 16

RMSE (×10

−3

) T (s)

Error T

build

render

Figure 6: Error (RMSE), construction time (T

build

) and ren-

dering time (T

render

) w.r.t. number of samples per visibility

check (spv), for the MUSEUM scene.

As expected, construction time grows linearly

with spv since more visibility queries are performed.

But it does not inﬂuence rendering time. Of course

the RMSE is improved by the growth of spv, but it

tends to converge rapidly. Therefore, we noticed, in

all our scenes, that a 4 to 6 value for spv is a good

trade-off between speed and quality.

6 CONCLUSION AND FUTURE

WORK

We have presented a new data structure for VPL clus-

tering: the Visibility based WSPD (V-WSPD). It rede-

ﬁnes the work of (Bus et al., 2015a) on the WSPD by

driving the construction with visibility queries (along

with the existing geometric factor), while remaining

view-independent.

We have shown that the V-WSPD allows to

achieve far better rendering times than the pure ge-

ometric WSPD while keeping a similar image qua-

lity. This improvement implies an increase in con-

struction times, since it requires to cast rays to deter-

mine visibility. But, given that the V-WSPD is view-

independent, it could be reused for a full sequence

of images, so that the loss in construction times is

quickly amortized.

Compared to the state-of-the-art method, Illumi-

nationCut (Bus et al., 2015b), our method generates

images with higher error even if these errors are not

visible to the naked eye (cf. table 2). In counterpart,

IlluminationCut preprocessing time is far higher. To

improve the accuracy of our method, we could change

the basis structure of the V-WSPD, trying different

partition structures such as a kd-tree (as it has been

done in physics for N-body simulation (Lopes et al.,

2014)) or a Multi-BVH (Ernst and Greiner, 2008). In

that case, these partitions should be constructed cle-

verly w.r.t. VPL distribution and contribution.

Another idea would be to compact the V-WSPD

with the space partition used as acceleration struc-

ture for the scene geometry. Thus, rendering times

could be further improved since only one structure

scan would be necessary for both primary ray casting

and indirect illumination.

Finally, we plan to use the concept of pair de-

composition for different kinds of set of points: light

source points, importance records (points viewed

from the camera) and even pure geometrical points.

The latter implies a good point sampling for the scene

geometry. All these combinations of pair of point sets

can be used for both points clustering, points sam-

pling and points rejection. This drives us toward a

framework for clustering, rejecting or selecting pair

of points that can be useful in several situations in

rendering (coarse evaluation of visibility, driving light

transport in path tracing. . . ).

ACKNOWLEDGEMENTS

This work has been supported by the BPI France PA-

PAYA grant, from the Programme d’Investissement

d’Avenir. Authors would like to thank Ubisoft Motion

Pictures Montreuil for giving us for the GEEKROOM

and MARKET scenes, and K. Renaudeau for English

language reviewing.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

Table 2: Comparison for same rendering time: pure geometric WSPD, visibility based WSPD (V-WSPD), Illumination-

Cut (Bus et al., 2015b) and false-colored image for error (Euclidean distance ×128 in LAB color space).

WSPD V-WSPD IlluminationCut

CONFERENCE

MUSEUM

GEEKROOM

MARKET

Visibility based WSPD for Global Illumination

REFERENCES

Afra, A. T., Wald, I., Benthin, C., and Woop, S. (2016).

Embree ray tracing kernels: Overview and new fea-

tures. In ACM SIGGRAPH 2016 Talks, SIGGRAPH

’16, pages 52:1–52:2, New York, NY, USA. ACM.

Bus, N., Mustafa, N. H., and Biri, V. (2015a). Global il-

lumination using well-separated pair decomposition.

Computer Graphics Forum, 34(8):88–103.

Bus, N., Mustafa, N. H., and Biri, V. (2015b). Illumina-

tionCut. Computer Graphics Forum (Proceedings of

Eurographics 2015), 34(2):561 – 573.

Callahan, P. B. and Kosaraju, S. R. (1995). A decomposition

of multidimensional point sets with applications to k-

nearest-neighbors and n-body potential ﬁelds. J. ACM,

42(1):67–90.

Dachsbacher, C., K

riv

anek, J., Ha

san, M., Arbree, A., Wal-

ter, B., and Nov

ak, J. (2014). Scalable realistic ren-

dering with many-light methods. Computer Graphics

Forum, 33(1):88–104.

Davidovi

c, T., Georgiev, I., and Slusallek, P. (2012). Pro-

gressive lightcuts for gpu. In ACM SIGGRAPH 2012

Talks, SIGGRAPH ’12, New York, NY, USA. ACM.

Davidovi

c, T., K

riv

anek, J., Ha

san, M., Slusallek, P., and

Bala, K. (2010). Combining global and local virtual

lights for detailed glossy illumination. ACM Trans.

Graph., 29(6):143:1–143:8.

Dutr

e, P., Bala, K., Bekaert, P., and Shirley, P. (2006). Ad-

vanced Global Illumination. AK Peters Ltd.

Ernst, M. and Greiner, G. (2008). Multi Bounding Volume

Hierarchies. In IEEE Symposium on Interactive Ray

Tracing, RT ’08, pages 35–40.

Georgiev, I., K

riv

anek, J., Popov, S., and Slusallek, P.

(2012). Importance caching for complex illumination.

Computer Graphics Forum, 31(2pt3):701–710.

Georgiev, I. and Slusallek, P. (2010). Simple and Robust Ite-

rative Importance Sampling of Virtual Point Lights. In

Lensch, H. P. A. and Seipel, S., editors, Eurographics

2010 - Short Papers. The Eurographics Association.

san, M., Pellacini, F., and Bala, K. (2007). Matrix row-

column sampling for the many-light problem. ACM

Trans. Graph., 26(3).

san, M., Vel

azquez-Armendariz, E., Pellacini, F., and

Bala, K. (2008). Tensor clustering for rendering

many-light animations. In Proceedings of the Nine-

teenth Eurographics Conference on Rendering, EGSR

’08, pages 1105–1114, Aire-la-Ville, Switzerland. Eu-

rographics Association.

Hedman, P., Karras, T., and Lehtinen, J. (2016). Sequential

monte carlo instant radiosity. In Proceedings of the

20th ACM SIGGRAPH Symposium on Interactive 3D

Graphics and Games, I3D ’16, pages 121–128, New

York, NY, USA. ACM.

Huo, Y., Wang, R., Jin, S., Liu, X., and Bao, H. (2015).

A matrix sampling-and-recovery approach for many-

lights rendering. ACM Trans. Graph., 34(6):210:1–

210:12.

Keller, A. (1997). Instant radiosity. In Proceedings of

the 24th Annual Conference on Computer Graphics

and Interactive Techniques, SIGGRAPH ’97, pages

49–56, New York, NY, USA. ACM Press/Addison-

Wesley Publishing Co.

riv

anek, J., Fajardo, M., Christensen, P. H., Tabellion, E.,

Bunnell, M., Larsson, D., and Kaplanyan, A. (2010).

Global illumination across industries. In ACM SIG-

GRAPH 2010 Courses, SIGGRAPH ’10, New York,

NY, USA. ACM.

Lopes, R. H. C., Reid, I. D., and Hobson, P. R. (2014). A

well-separated pairs decomposition algorithm for k-d

trees implemented on multi-core architectures. Jour-

nal of Physics: Conference Series, 513(5):052011.

O’Donnell, Y. and Chajdas, M. G. (2017). Tiled light trees.

In Proceedings of the 21st ACM SIGGRAPH Sympo-

sium on Interactive 3D Graphics and Games, I3D ’17,

pages 1:1–1:7, New York, NY, USA. ACM.

Ou, J. and Pellacini, F. (2011). Lightslice: Matrix slice

sampling for the many-lights problem. ACM Trans.

Graph., 30(6):179:1–179:8.

Paquette, E., Poulin, P., and Drettakis, G. (1998). A light

hierarchy for fast rendering of scenes with many lig-

hts. Computer Graphics Forum, 17(3):63–74.

Rehfeld, H. and Dachsbacher, C. (2016). Lightcut interpola-

tion. In Proceedings of High Performance Graphics,

HPG ’16, pages 99–108, Aire-la-Ville, Switzerland.

Eurographics Association.

Ritschel, T., Grosch, T., Kim, M. H., Seidel, H.-P., Dachs-

bacher, C., and Kautz, J. (2008). Imperfect Shadow

Maps for Efﬁcient Computation of Indirect Illumina-

tion. ACM Trans. Graph. (Proc. of SIGGRAPH ASIA

2008), 27(5).

Simon, F., Hanika, J., and Dachsbacher, C. (2015). Rich-

vpls for improving the versatility of many-light met-

hods. Comput. Graph. Forum, 34(2):575–584.

Walter, B., Arbree, A., Bala, K., and Greenberg, D. P.

(2006). Multidimensional lightcuts. ACM Trans.

Graph., 25(3):1081–1088.

Walter, B., Fernandez, S., Arbree, A., Bala, K., Donikian,

M., and Greenberg, D. P. (2005). Lightcuts: A sca-

lable approach to illumination. ACM Trans. Graph.,

24(3):1098–1107.

Walter, B., Khungurn, P., and Bala, K. (2012). Bidirectional

lightcuts. ACM Trans. Graph., 31(4):59:1–59:11.

Wang, G., Xie, G., and Wang, W. (2011). Efﬁcient search

of lightcuts by spatial clustering. In SIGGRAPH Asia

2011 Sketches, SA ’11, pages 26:1–26:2, New York,

NY, USA. ACM.

Yoshida, H., Nabata, K., Iwasaki, K., Y., D., and T., N.

(2015). Adaptive importance caching for many-light

rendering. Journal of WSCG, 23(1):65–72.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications