Objective Evaluation of Bradykinesia in Parkinson’s Disease using

Evolutionary Algorithms

Siti Anizah Muhamed

, Rachel Newby

2,3,4

, Stephen L. Smith

, Jane Alty

3,4

Stuart Jamieson

3,4

and Peter Kempster

2,5

Department of Electronic Engineering, University of York, York, U.K.

Neurosciences Department, Monash Medical Centre, Victoria, Australia

Department of Neurology, Leeds General Infirmary, Leeds, U.K.

Hull York Medical School, University of York, U.K.

Department of Medicine, Monash University, Victoria, Australia

Keywords: Parkinson’s Disease, Evolutionary Algorithms, Cartesian Genetic Programming, Bradykinesia, Finger

Tapping, Hand Pronation-Supination, Hand Opening-closing.

Abstract: Bradykinesia, a slowing of movement, is the fundamental motor feature of Parkinson’s disease (PD) and the

only physical sign that is obligatory for diagnosis. The complex nature of Bradykinesia makes it difficult to

reliably identify, particularly as the early stages of the disease. This paper presents an extension of previous

studies, applying evolutionary algorithms to movement data obtained from the standard clinical finger tapping

(FT) test to characterise Bradykinesia. In this study, hand pronation-supination (PS) and hand opening-closing

(HO) tasks are also considered. Cartesian Genetic Programming (CGP), is the evolutionary algorithm used to

train and validate classifiers using features extracted from movement recordings of 20 controls and 22 PD

patients. Features were selected based on the current clinical definition of Bradykinesia. The results show the

potential of HO and PS to be used as effective classifiers with an accuracy of 84%. Discriminative features

were also investigated with the possibility of informing clinical assessment.

1 INTRODUCTION

Bradykinesia, meaning slowness of movement, is

the only clinical sign that is mandatory for the

diagnosis of Parkinson’s Disease (PD) (Heldman et

al. 2011). The terms akinesia (absence of movement),

bradykinesia (slowness of movement), and

hypokinesia (decreased amplitude), are all used

interchangeably to describe the most prominent

phenomena of Parkinsonism. The conditions they

describe are usually referred to collectively as

bradykinesia (Figure 1). This symptom might have

the highest potential as a motor progression marker of

Parkinson’s disease (Maetzler et al. 2009). The

complex nature of Bradykinesia itself is one of the

reasons that makes it difficult for clinicians and

neurologists to be certain of its existence in the early

stages of Parkinson’s disease. Clinicians look for

signs of bradykinesia by observing a patient’s ability

to perform rapid, repetitive, alternating movements of

the hand using tasks such as finger taps, toe taps, hand

grips and hand pronation–supination (Jankovic

2008). The gold standard for clinical evaluation is the

Unified Parkinson’s Disease Rating Scale, UPDRS,

and its modified version, MDS-UPDRS (Goetz et al.

2008). It remains unclear how slowed movements due

to physiological ageing are different from the

bradykinesia seen in parkinsonian conditions. A

better understanding of characteristics of

bradykinesia and how it differs between these groups

can be used to inform clinical assessments towards

conforming early diagnosis.

Finger tapping (FT) is a popular task that has been

used many times in studies to evaluate Bradykinesia

in PD. Several methods have been used to optimise

FT data recorded by movement sensors in studies that

use statistical tests to compare movement features of

PD patients against healthy controls (Dunnewold et

al. 1997) (Jobbágy et al. 2005) (Yokoe et al. 2009)

(Espay et al. 2011) or with other movement disorders

(Ling et al. 2012). Alternatively, popular statistical

machine learning methods such as support vector

machine (SVM) is claimed to achieve better

classification on FT movement data. (Martinez

Manzanera et al. 2015) (Patel et al. 2009).

Muhamed, S., Newby, R., Smith, S., Alty, J., Jamieson, S. and Kempster, P.

Objective Evaluation of Bradykinesia in Parkinson’s Disease using Evolutionary Algorithms.

DOI: 10.5220/0006601700630069

In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 4: BIOSIGNALS, pages 63-69

ISBN: 978-989-758-279-0

Figure 1: Descriptions of Bradykinesia. (Fernandez et al.

2014).

Our group have successfully used Evolutionary

Algorithm (EA) to evolve high accuracy classifiers

that differentiate Parkinson's disease patients from

healthy controls (Lones et al. 2012) (Smith and

Timmis 2008). Further investigation into classifiers

evolved was able to characterise movement disorder

in PD (Lacy et al. 2013) and inform clinical

assessment (Lones et al. 2013). Based on the success

of using FT data, we believe that EAs can also be used

on other motor tasks to achieve the same if not better

results. Specifically, this study extends our work to

other common clinical motor tasks; pronation-

supination (PS) and hand opening-closing (OC) tasks.

FT was also included in this study for validation and

comparison purposes.

Cartesian Genetic Programming (CGP), a type of

EA was used to train classifiers. CGP was introduced

by Miller and Thomson (Miller and Thomson n.d.)

where the candidate solutions are represented as a

string of integers of fixed length that is mapped to a

non-cyclic directed graph. CGP and its variants have

shown excellent ability in the classification of a range

of medical applications including the classification of

mammograms for the detection of breast cancer

(Hope et al. 2007) and diagnosis of Alzheimer’s

disease (Hazell and Smith 2008). Additionally, there

were also classifications using bio-signals such as

spectral data for evaluation of cancerous thyroid cell

lines (Lones et al. 2010), digital images of the cells to

differentiate benign and malignant breast mass cells

(Ahmad et al. 2012) and electrocardiography (ECG)

signals to classify cardiac arrhythmia types (Ahmad

et al. 2013).

A distinct advantage of EAs is that the classifiers

evolved can be scrutinised to discover which features,

or even, which parts of the movement data were used

in their construction. Although statistical machine

learning methods such as SVM usually able to

generate comparable classifiers, it requires extra steps

to identify most discriminating inputs. A technique

such as forward-selection wrapper approach or other

feature ranking methods had to be integrated to

achieve the same objective.

The main objectives of this paper are to look into

the potential of applying EAs to evolve classifiers

using movement data of PS and HO tasks and

evaluate possible Bradykinesia characteristics that

later can be used to inform clinical assessments.

2 METHODOLOGY

After obtaining informed written consent, 20 controls

and 22 patients with idiopathic Parkinson’s disease

were tested using the Movement Disorders Society

Unified Parkinson’s Disease Rating Scale (MDS-

UPDRS) in a conventional clinical setting at the

Monash Medical Centre, Melbourne, Australia. The

finger tapping, pronation-supination and hand

opening-closing components of the MDS-UPDRS

were assessed both clinically and using an objective

motion tracking system.

2.1 Movement Data Collection

The motion tracking system used for movement

recording employ Polhemus Patriot Electromagnetic

(EM) tracking sensors (Polhemus 2016). The system

consists of electronic system unit (SEU), a magnetic

transmitter and two EM tracking sensors. Each

participant wears the EM sensors on index finger and

thumb when they perform the specified assessments.

The EM sensors record position and orientation

relative to the transmitter in six degrees of freedom

with an update rate of 60 Hz per sensor. The system

returns three Cartesian coordinates (X, Y, and Z) and

three orientation Euler Angles: azimuth, elevation

and roll.

2.2 Movement Features

Features were extracted based on the current clinical

definition of bradykinesia and the nature of the

movement in each task.

2.2.1 Finger Tapping

In this study, patients were asked to perform the

standard clinical finger tapping test as defined by the

Movement Disorders Society Unified Parkinson’s

Disease Rating Scale (MDS-UPDRS). This instructs

patients to perform ten finger taps as fast and as wide

as possible. As one of the final objectives of this study

is to inform clinical assessment, it is important for the

BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing

task to be performed identically with standard clinical

evaluation.

The separation distance between the finger and

the thumb during the finger tapping action was

computed by first calculating the difference between

the x, y and z coordinate values for the respective

sensors, and then, the Euclidean distance, or overall

positional separation, between index finger and

thumb. Speed and acceleration were calculated as

the first and second derivatives of the distance,

respectively. The raw movement data was also

preprocessed to remove noise using Low Pass 5Hz

Butterworth filter. Butterworth filter is most common

filter used in biomechanics data analysis due to its

excellent passband response (Christodoulakis et al.

2010).

Patients often have difficulties in performing the

exact number of the cycles as instructed. Therefore,

cycles frequency is one of the features selected

instead of time taken to finish the task. Other features

were quantified for the opening and closing phases of

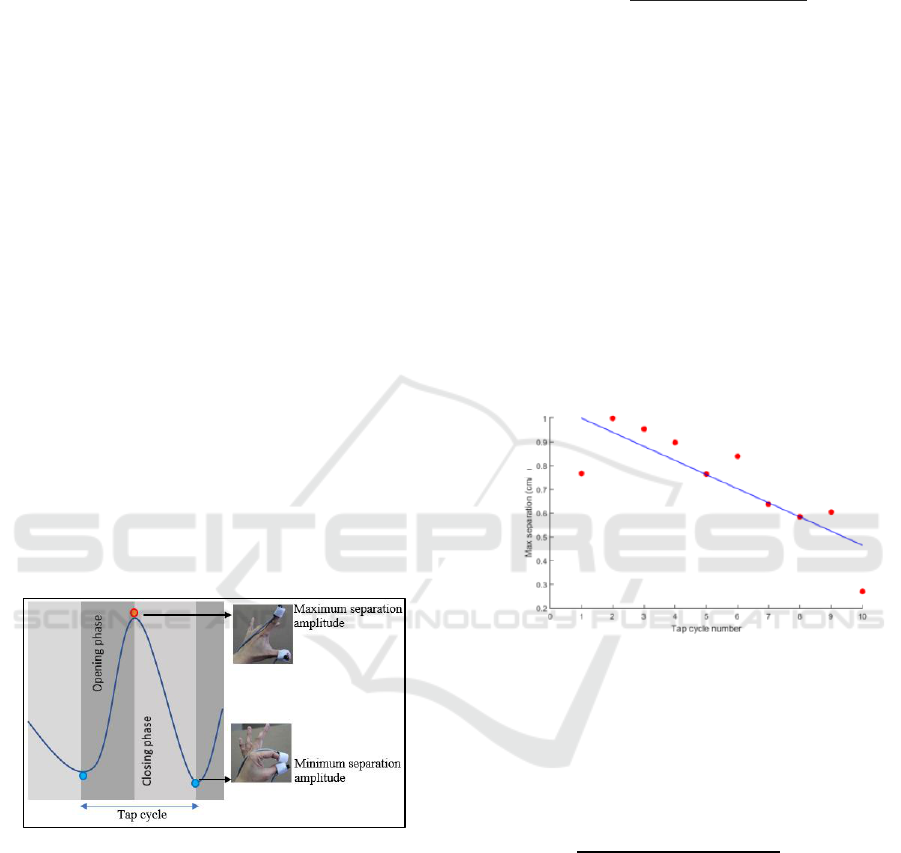
the cycle. The opening phase begins once the fingers

are separated, from an initially closed position –

equating to a minimal distance between the sensors –

to when they are maximally separated; the closing

phase begins once the sensors move towards one

another after the point of maximal separation and

finishes when the sensors have achieved a minimum

separation.

Figure 2: Separation data showing opening and closing

phases of a tapping cycle.

Figure 2 provides a representation of positional

separation data, showing opening and closing phases

of a cycle. Minimum, maximum and average of

normalised speed and acceleration of both cycle

phases were computed according to (Lacy et al.

2013). To measure rhythm, Coefficient of Variation

(COV) was used. COV reflects how much a

movement component measure varies over a defined

period. It may be considered a measure of how

rhythmic the repetitive movements are. COV of

amplitude was calculated over a period of tapping

cycles as follows:

 







To calculate the decrementing trend, maximum

separation amplitude or speed for each tap cycle was

linearly regressed against the number of cycles. A

negative slope indicates that the overall trend of a

movement component measure is decrementing and a

zero or positive slope indicates that the amplitude is

not decrementing. Figure 3 provides examples of

linear regression plots of maximum amplitude to

obtain the slope indicating a trend of separation

amplitude. Measures of amplitude and speed alone

may not have captured the real movement patterns of

subjects. To capture the relationship between these

components a variable called periodicity was

calculated.

    

Figure 3: An example of tap decrementing trend for a

patient with slope = -0.6.

Other features extracted are halts, hesitation and

amp*freq. Halts were measured by calculating the

percentage of the tap cycle duration spent at ‘zero’ (<

5% of the maximum) speed:

 

    



 

When the movement showed smaller peaks

between tapping cycle phases (Figure 4), it is treated

as hesitation.

Objective Evaluation of Bradykinesia in Parkinson’s Disease using Evolutionary Algorithms

Figure 4: The smaller peaks counted as four hesitations.

Bigger amplitude with greater frequency during

finger tapping means faster finger movement. This is

considered as better performance. Alternatively, the

movement can be executed faster with smaller

amplitude. The amplitude × frequency of tapping is

suggested in (Jobbágy et al. 2005) to characterise the

speed. This feature is determined for each tapping

cycle and then averaged over the whole test. Table 1

summarises all features used as inputs to the CGP

classifier.

Table 1: Finger tapping extracted features.

Feature

(0)

Cycles frequency

(1)

Max overall amplitude

(2)

Mean amplitude

(3)

Maximum overall speed

(4)

Max opening speed

(6)

Max closing speed

(7)

Max opening acceleration

(8)

Max opening deceleration

(9)

Max closing acceleration

(10)

Max closing deceleration

(11)

Periodicity

(12)

COV amplitude

(13)

COV speed

(14)

Decrementing amplitude

(15)

Decrementing speed

(16)

Halts

(17)

Hesitation

(18)

Amp*freq

2.2.2 Hand Pronation-supination

For the hand pronation-supination task (PS), the

MDS-UPDRS requires the participant to extend the

arm out in front of their body with the palms face

down and then turn the palm up and down alternately

10 times as fast and fully as possible.

After some experimentation, it was concluded that

the most useful data in our pronation-supination

recordings came from the movement of the thumb.

Since only one sensor is used, the amplitude is

defined as the Euclidean distance between thumb

sensor and Patriot transmitter.





















 





Velocity was calculated by differentiation of each

Cartesian coordinate component (x, y, z) over the

sampling time period to compute the respective

velocity components 











. The total velocity

was computed from the sum of its components and its

magnitude, the speed





























 









Acceleration is obtained by differentiating the

velocity, using the same sampling time. The same

features in Table 1 were used for PS classifiers by

replacing opening and closing phases with pronation

and supination phases respectively.

Since PS involves angular movements, movements

were computed using Euler angles. Average,

minimum and maximum of angular velocity and

angular acceleration values were calculated

according to (Picardi et al. 2010), giving the

additional six angular features shown in Table 2.

Table 2: Hand pronation-supination features.

Feature

(19)

Mean angular speed

(20)

Max angular speed

(21)

Min angular speed

(22)

Mean angular acceleration

(23)

Max angular acceleration

(24)

Min angular acceleration

2.2.3 Hand Opening-closing

For the hand opening-closing task (HO), the MDS-

UPDRS requires the participant to make a tight fist

with the arm bent at the elbow so that the palm faces

the examiner and then requires the participant to open

the hand ten times as fully and as quickly as possible.

Sensors were placed at the same positions as in finger

tapping task. However, unlike finger tapping, which

is a simultaneous movement of thumb and fingers, the

hand-opening task involves two steps movements.

Therefore, the features extracted were also taking into

account the measurements of both sensors separately,

instead of just considering the distance between the

two sensors. The thumb sensor (TS) and finger

sensor (FS) movement data were used to compute the

total of seventeen features. (Table 3).

BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing

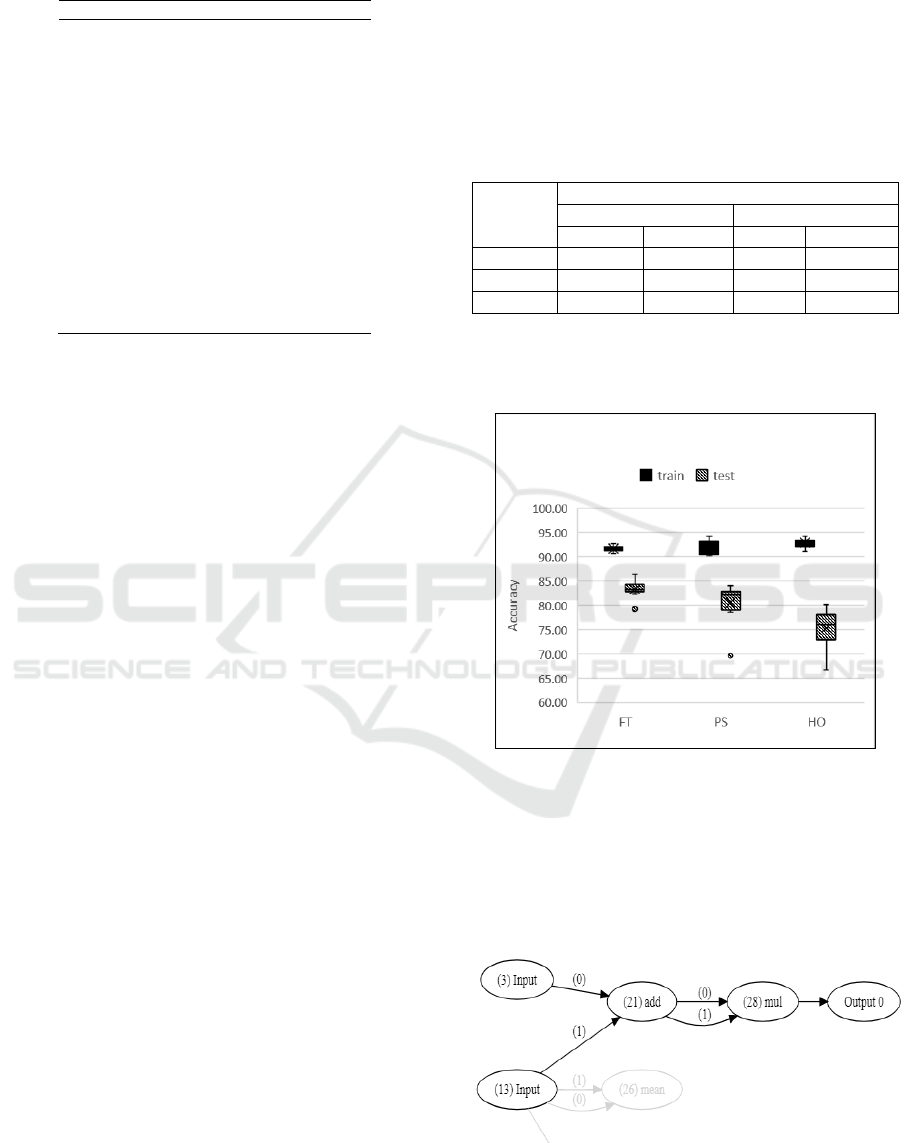
Table 3: Hand opening-closing extracted features.

Feature

(0)

HO frequency

(1)

Maximum opening

(2)

COV opening

(3)

TS average speed

(4)

TS minimum speed

(5)

TS maximum speed

(6)

TS minimum acceleration

(7)

TS maximum acceleration

(8)

TS COV speed

(9)

TS Halts

(10)

FS average speed

(11)

FS minimum speed

(12)

FS maximum speed

(13)

FS minimum acceleration

(14)

FS maximum acceleration

(15)

FS COV speed

(16)

FS Halts

2.3 Classification

Classification used a typical CGP evolutionary

strategy which selects one parent from each

generation and uses mutation to produce four

children. The next generation then comprises the

parent and the four children, giving a population of

size five - four children plus one parent: (1+4) - ES.

Three sets of classifiers were evolved, one for each

movement task. The input data consists of floating

point values representing selected Bradykinesia

features extracted from the patient’s movement (as

defined in section 2.2).

The fitness assigned to each classifier is simply

the proportion of samples correctly classified.

Previous CGP classifiers in FT studies (mentioned in

the introduction) used the area under a ROC Curve

(Fawcett 2006) as fitness function, but in this study,

classification accuracy is used for simplicity and

direct comparison. Through experimentation, the

following CGP parameters values were adopted:

number of nodes available 15, nodes arities of 2,

mutation rate of 0.05 and number of generations

10000. The function set comprised



 

   



. Data from each class was

divided into training and test sets. To compensate for

any effect on results caused by small amounts of

training and test data, 5-fold cross validation was

used. Results are averaged over ten runs for statistical

significance. The best classifier model is used to

determine those features that are most discriminative.

3 RESULTS

With numbers of subjects relatively low compared to

our previous FT studies, the classifications accuracies

in this study are surprisingly good. For the finger

tapping task, averaged accuracy of the test set across

ten runs is 82.66%. For the pronation-supination task,

80.54%, and for the hand opening task, 75.32%. Best

and average accuracies of all tasks are summarised in

table 4.

Table 4: Average and best accuracies of classifiers evolved

for all motor tasks.

Task

Accuracy

Averaged ten runs

Best run

train

test

train

test

91.69

83.3

91.79

87.20

92.04

80.54

94.34

84.03

92.92

75.32

94.27

80.21

Figure 5 showing the distribution of cross-

validated classification accuracies for ten runs of each

task.

Figure 5: Distribution of accuracies across ten runs.

As mentioned in the introduction, one of the main

advantages of using GP method is the ability to

recognise which inputs were used to evolve the

strongest classifier. For example, the PS classifier

with 85% accuracy is visualised in figure 6, showing

only the active nodes.

Figure 6: Visualisation of a PS classifier.

In this example, the inputs used are maximum

Objective Evaluation of Bradykinesia in Parkinson’s Disease using Evolutionary Algorithms

overall speed and speed rhythm (COV). All features

used to evolve the best classifier of each task are

summarised in table 5.

Table 5: Most discriminating features for each task.

Task

Features

(4)(7)(9) (14) from Table 1

(0)(2)(3)(4)(5)(6) (14) from Table 2

(8) (13) (14) (16) (17) (20) from Table 1*

and Table 2

* replaced opening phase with pronation phase and closing

phase with supination phase.

4 CONCLUSIONS

It is clear from the classification results that hand

opening-closing and hand pronation-supination have

the same potential as finger tapping to be used as a

tool in the characterisation of Bradykinesia using GP

to inform clinical assessment. The overall accuracy

was lower than shown in previous studies of GP

classifications using finger tapping data, but we

believe this is due to smaller numbers of subjects.

Almost all classifiers across ten runs for all tasks are

consistent with good accuracies above 70%.

Although the most discriminative movement features

in this study may not be generalised to inform clinical

assessment because of the small sample numbers, it

was demonstrated that by using GP, it could easily be

acquired.

Movement features are computed based on the

current clinical definition of Bradykinesia. However,

CGP has the ability to accept raw positional or speed

data points and perform an unbiased search that will

not be constrained by pre-defined characteristics.

Future work will process PS and HO data using a

sliding window, similar to FT acceleration data in

continuous time series adopted by (Lones et al. 2014).

By using raw data points to induce classifiers, it opens

the possibility of finding new features of

Bradykinesia from the movement tasks.

REFERENCES

Ahmad, A.M. et al., 2012. Breast cancer detection using

cartesian genetic programming evolved artificial neural

networks. Proceedings of the fourteenth international

conference on Genetic and evolutionary computation

conference - GECCO ’12, p.1031.

Ahmad, A.M., Khan, G.M. & Mahmud, S.A., 2013.

Classification of Arrhythmia Types Using Cartesian

Genetic Programming Evolved Artificial Neural

Networks. , pp.282–291.

Christodoulakis, G. et al., 2010. On the filtering and

smoothing of biomechanical data. Communication

Systems Networks and Digital Signal Processing

(CSNDSP), 2010 7th International Symposium on,

pp.512–516.

Dunnewold, R.J., Jacobi, C.E. & van Hilten, J.J., 1997.

Quantitative assessment of bradykinesia in patients

with Parkinson’s disease. Journal of neuroscience

methods, 74, pp.107–112.

Espay, A.J. et al., 2011. Differential response of speed,

amplitude, and rhythm to dopaminergic medications in

Parkinson’s disease. Movement Disorders, 26(14),

pp.2504–2508.

Fawcett, T., 2006. An introduction to ROC analysis.

Pattern Recognition Letters, 27, pp.861–874..

Fernandez, H.H., Machado, A.G. & Pandya, M., 2014. A

Practical Approach to Movement Disorders: Diagnosis

and Management., Demos Medical Publishing.

Goetz, C.G. et al., 2008. Movement Disorder Society-

Sponsored Revision of the Unified Parkinson’s Disease

Rating Scale (MDS-UPDRS): Scale presentation and

clinimetric testing results. Movement Disorders,

23(15), pp.2129–2170.

Hazell, A. & Smith, S.L., 2008. Towards an Objective

Assessment of Alzheimer â€

s Disease : The

Application of a Novel Evolutionary Algorithm in the

Analysis of Figure Copying Tasks. , pp.2073–2079.

Heldman, D. a et al., 2011. The modified bradykinesia

rating scale for Parkinson’s disease: reliability and

comparison with kinematic measures. Movement

disorders : official journal of the Movement Disorder

Society, 26(10), pp.1859–63.

Hope, D.C., Munday, E. & Smith, S.L., 2007. Evolutionary

Algorithms in the Classification of Mammograms.

2007 IEEE Symposium on Computational Intelligence

in Image and Signal Processing, (CIISP), pp.258–265.

Jankovic, J., 2008. Parkinson’s disease: clinical features

and diagnosis. Journal of neurology, neurosurgery, and

psychiatry, 79(4), pp.368–76.

Jobbágy, A. et al., 2005. Analysis of finger-tapping

movement. Journal of neuroscience methods, 141(1),

pp.29–39.

Lacy, S.E., Lones, M. a & Smith, S.L., 2013.

Characterisation of Movement Disorder in Parkinson 's

Disease using Evolutionary Algorithms Categories and

Subject Descriptors., (August 2009), pp.1479–1485.

Ling, H. et al., 2012. Hypokinesia without decrement

distinguishes progressive supranuclear palsy from

Parkinson’s disease. Brain, 135, pp.1141–1153.

Lones, M.A. et al., 2013. Evolving Classifiers to Inform

Clinical Assessment of Parkinson ’ s Disease. , pp.76–

82.

Lones, M.A. et al., 2012. Evolving Classifiers to Recognise

the Movement Characteristics of Parkinson’s Disease

Patients. , pp.1–18.

Lones, M.A. et al., 2014. Evolving Classifiers to Recognize

the Movement Characteristics of Parkinson’s Disease

Patients. , 18(4), pp.559–576.

BIOSIGNALS 2018 - 11th International Conference on Bio-inspired Systems and Signal Processing

Lones, M. a. et al., 2010. Discriminating normal and

cancerous thyroid cell lines using implicit context

representation Cartesian genetic programming. IEEE

Congress on Evolutionary Computation, pp.1–6.

Maetzler, W., Liepelt, I. & Berg, D., 2009. Progression of

Parkinson’s disease in the clinical phase: potential

markers. The Lancet Neurology, 8(12), pp.1158–1171.

Martinez Manzanera, O. et al., 2015. A method for

automatic and objective scoring of bradykinesia using

orientation sensors and classification algorithms. IEEE

Transactions on Biomedical Engineering, 9294(c),

pp.1–1.

Miller, J.F. & Thomson, P., 2000. Cartesian genetic

programming. Genetic Programming, Proceedings of

the Third European Conference on Genetic

Programming (EuroGP2000)., 1802, pp.121–132.

Patel, S. et al., 2009. Monitoring Motor Fluctuations in

Patients With Parkinson’s Disease Using Wearable

Sensors. IEEE Transactions on Information

Technology in Biomedicine, 13(6), pp.864–873.

Picardi, C. et al., 2010. Objective Assessment of Cognitive

Impairment in Parkinson’s Disease Using Evolutionary

Algorithm C. Di Chio et al., eds., Berlin, Heidelberg:

Springer Berlin Heidelberg.

Polhemus motion tracking company. (2016).

http://polhemus.com.

Smith, S.L. & Timmis, J., 2008. An immune network

inspired evolutionary algorithm for the diagnosis of

Parkinson’s disease. Bio Systems, 94(1–2), pp.34–46.

Yokoe, M. et al., 2009. Opening velocity, a novel

parameter, for finger tapping test in patients with

Parkinson’s disease. Parkinsonism & related disorders,

15(6), pp.440–4.

Objective Evaluation of Bradykinesia in Parkinson’s Disease using Evolutionary Algorithms