Retrieving 3D Objects with Articulated Limbs by Depth Image Input

Jun-Yang Lin

, May-Fang She

, Ming-Han Tsai

, I-Chen Lin

, Yo-Chung Lau

and Hsu-Hang Liu

Department of Computer Science, National Chiao Tung University, Hsinchu City, Taiwan

Telecommunication Laboratories, Chunghwa Telecom Co., Ltd, Taoyuan City, Taiwan

Keywords:

3D Object Retrieval, Depth Image Analysis, Shape Matching.

Abstract:

Existing 3D model retrieval approaches usually implicitly assume that the target models are rigid-body. When

they are applied to retrieving articulated models, the retrieved results are substantially inﬂuenced by the model

postures. This paper presents a novel approach to retrieve 3D models from a database based on one or few

input depth images. While related methods compared the inputs with whole shapes of 3D model projections

at certain viewpoints, the proposed method extracts the limbs and torso regions from projections and analyzes

the features of local regions. The use of both global and local features can alleviate the disturbance of model

postures in model retrieval. Therefore, the system can retrieve models of an identical category but in different

postures. Our experiments demonstrate that this approach can efﬁciently retrieve relevant models within a

second, and it provides higher retrieval accuracy than those of compared methods for rigid 3D models or

models with articulated limbs.

1 INTRODUCTION

With the popularity of 3D modeling tools, more and

more 3D models are designed and uploaded by cre-

ators and vendors. Therefore, various kinds of meth-

ods were proposed to improve the efﬁciency of 3D

model retrieval from a large dataset. Searching by

keywords is the most common way to search desired

information, but it can be difﬁcult for a user to ﬁg-

ure out appropriate keywords describing the variety of

model shapes. Therefore, most successful 3D model

retrieval systems adopted content-based search and

required users to input sketches or images as queries.

Funkhouser et al. (Funkhouser et al., 2003) presented

a shape-based query engine, supporting queries based

on keywords, 2D sketches, 3D sketches, and 3D mod-

els. The LightField descriptor proposed by Chen et

al. (Chen et al., 2003) projects each 3D model onto

silhouette images from vertices of an enveloping do-

decahedron. It then evaluates the similarities between

query images and silhouettes of database models.

Nevertheless, most existing methods assume that

the 3D models are rigid or the viewpoint of input im-

ages are axis-aligned, e.g. the frontal or side views.

In the case of querying by views, they compared two

projected shapes based on shape features extracted

from the whole projected silhouette or depth images.

If a user takes a 3D model with articulated limbs as

the input, the retrieved results can be substantially

inﬂuenced by the limb postures of models or view

points. Accordingly, we propose evaluating not only

the global projected shapes but also local features. As

shown in Figure 1, if we only considered the global

shapes, it led to the result 1(a). However, if we fur-

ther compared the local information extracted from

torso and limb regions, more relevant models can be

retrieved as shown in 1(b).

Based on the aforementioned concept, we mea-

sured different combinations of global and local fea-

tures and developed a prototype system. Given one or

multiple depth images as query inputs, the proposed

system can efﬁciently retrieve relevant models from

a dataset extended from publicly used databases. Our

experiments also demonstrate that it can retrieve more

accurate results than results by comparative methods,

for not only 3D models with limbs but also rigid mod-

els.

2 RELATED WORK

To intuitively assign input queries, several research

works adopted view-based matching methods to re-

trieve models from sketch or image inputs. View-

based retrieval systems usually assume that 3D shapes

can be represented by several 2D projections from dif-

Lin, J-Y., She, M-F., Tsai, M-H., Lin, I-C., Lau, Y-C. and Liu, H-H.

Retrieving 3D Objects with Articulated Limbs by Depth Image Input.

DOI: 10.5220/0006609601010111

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 1: GRAPP, pages

101-111

ISBN: 978-989-758-287-5

101

Figure 1: (a) Retrieval results from the global shape only. (b) Retrieval results of our proposed method. (c) Top 20 retrieval

results of our method for articulated models and non-rigid quadruped animal models in random view.

ferent views. Chen et al. (Chen et al., 2003) thought

that if two 3D models are similar, their projected

views from various angles are similar as well. They

compared the Zernike moment (Canterakis, 1999) and

the Fourier descriptor between two projected silhou-

ettes. Daras and Axenopoulos (Daras and Axenopou-

los, 2010) extended the view-based concept and mea-

sured multiple shape features and their combinations.

However, the models in the database and from input

queries need to be aligned in a standard viewpoint

set. Wu et al. (Wu et al., 2016) used the view-based

matching for object pose tracking. In our work, we

allow users to record depth images of an input in an

arbitrary viewpoint.

Existing view-based systems usually analyze the

global shapes of projections. It implicitly assumes

that the models in the same category have simi-

lar poses, but in reality there are plenty of models

with joints and their limb postures are changeable.

Skeleton-based measures are capable of dealing with

the deformation and articulation of shape data. Bai

and Latecki (Bai and Latecki, 2008) computed skele-

ton similarity by comparing geodesic paths between

skeleton endpoints, and did not consider the topolog-

ical structure of the skeleton graphs or trees. Shen et

al. (Shen et al., 2013) extended the previous work (Bai

and Latecki, 2008) to do shape clustering according to

the similarity of each shape. They proposed the dis-

tance measurement between shapes and clusters ac-

cording to the correspondence of skeleton endpoints

and junction points.

To extract skeleton from 2D contours, Igarashi

et al. (Igarashi et al., 1999) presented an extraction

method in the famous Teddy system . The method

ﬁrst performs Delaunay triangulation to generate tri-

angles covering the shape. Then, it approximates

the medial axis and extracts the skeleton of the con-

tour according to the connectivity between triangles.

However, skeleton extraction is usually sensitive to

the boundary noise. In order to prune the spurious

skeleton branches, Shen et al. (Shen et al., 2011)

evaluated the contribution of contour segment to the

whole shape, and presented a novel method for skele-

ton reﬁnement. In the case of 3D skeleton extraction,

Hasler et al. (Hasler and Thorm, 2010) inspected ex-

amples of different subjects at the same time, and then

improved the robustness of shape skeleton estimation.

Wang and Lee (Wang and Lee, 2008) applied iterative

least squares optimization to shrink models and pre-

serves their geometries and topologies.

Several works decompose a 3D model into parts

or skeletons for similarity measures or other applica-

tions. Mohamed and Hamza (Mohamed and Hamza,

2012) matched two 3D shapes by comparing their rel-

ative shortest paths between the skeleton endpoints.

Kim et al. (Kim et al., 2013) partitioned a collec-

tion of models into clusters and generated consis-

tent segmentations and correspondences for all the

models with similar parts. Instead of analyzing ge-

ometric structures of shapes, Kim et al. (Kim et al.,

2014) and Xie et al. (Xie et al., 2014) analyzed 3D

shapes based on the interactions between 3D mod-

els and human postures. These methods can be ex-

tended for 3D shape retrieval and correspondence es-

timation. Kleiman et al. (Kleiman et al., 2015) pre-

sented a novel approach to quantify shape similar-

ity based re-arrangements, additions, and removals

of parts. L

opez-Sastre et al. (L

opez-Sastre et al.,

2013) employs a 3D spatial pyramid representation

for 3D shape categorization and classiﬁcation. Sipi-

ran et al. (Sipiran et al., 2013) represents a 3D shape

by its global descriptions and partition descriptions.

However, these methods were designed for 3D shape

matching, and they cannot be directly applicable to

sparse depth image inputs, since the 3D parts or limbs

can partially be occluded during projection.

3 OVERVIEW

Our goal is to efﬁciently search 3D models with one

or few input images, especially for 3D objects with ar-

ticulated limbs. In order to acquire more information

and details of the object surfaces, we selected depth

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

102

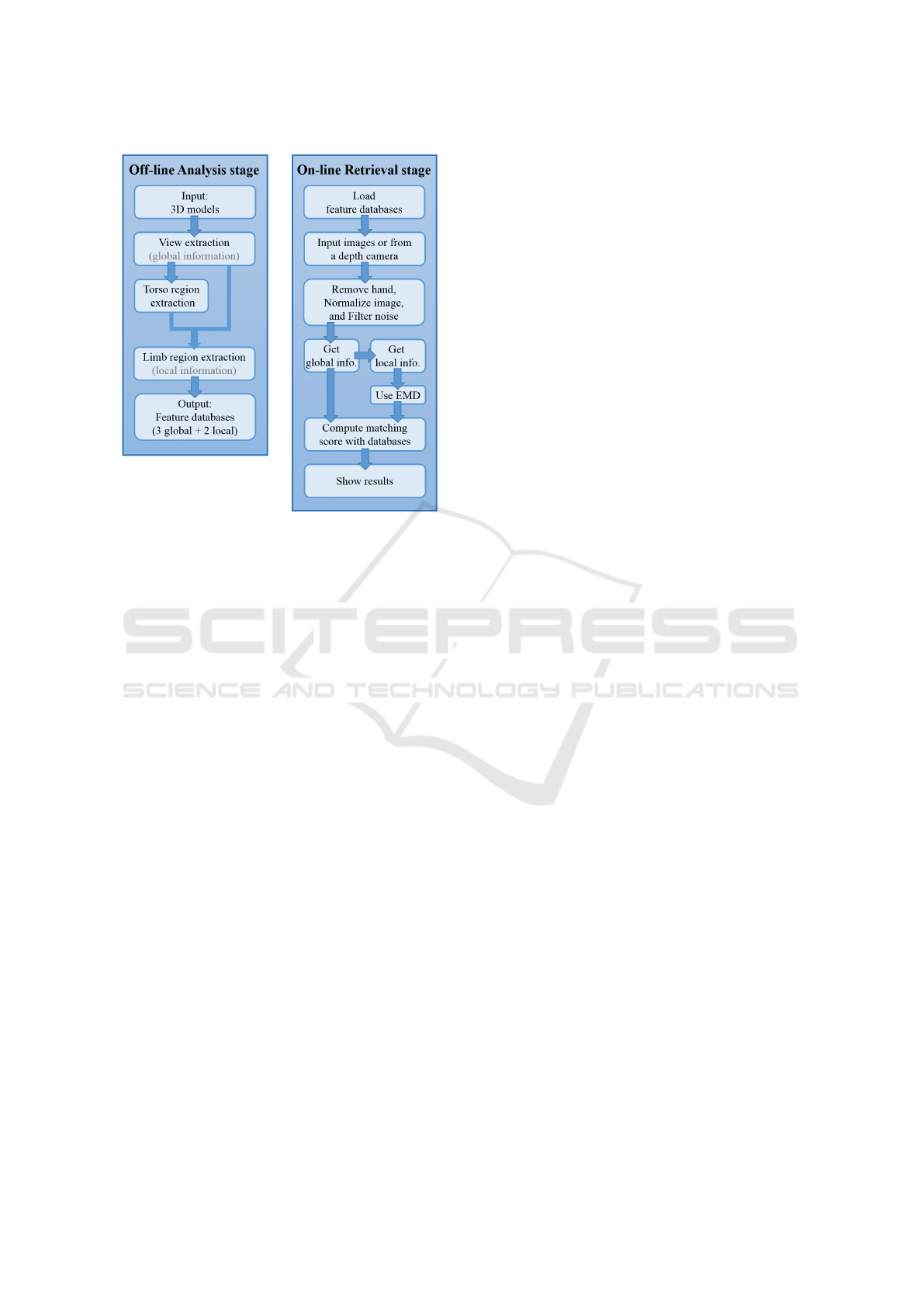
Figure 2: The ﬂow chart of the proposed system.

images as our inputs rather than silhouette binary im-

ages in related methods. We used Xtion PRO (ASUS

Inc., ) as our live depth image capture device, and it

can be replaced by other low-cost depth cameras off

the shelf, such as Kinect (Microsoft Corp., ).

The ﬂow chart of our proposed method is shown in

Figure 2. For more efﬁcient online retrieval, we sepa-

rated our system into two stages: ofﬂine analysis and

online retrieval. In the ofﬂine analysis stage, for each

model in the database, we generated a set of 2D pro-

jected depth images. Then, we extracted features with

rotation-invariant and perspective-insensitive proper-

ties for these projected images. These feature coef-

ﬁcients were regarded as the global information. We

then further decomposed each projected depth images

into the main torso (body) and limb regions. These

parts (torso and limb regions) can provide local infor-

mation, respectively. Finally, we can get three global

and two local features to build our feature database.

In the online retrieval part, our system ﬁrst loads

the descriptor databases, and then a user can input

one or multiple depth images captured from a real

3D object. The proposed system then evaluates the

minimum matching distance between the input and

each model in database according to global and local

features. The retrieval results are sorted according to

their scores. A complete online retrieval process can

be ﬁnished within a second for the database contain-

ing about 18,000 images.

4 OFFLINE ANALYSIS

This section describes how we extract different shape

descriptors to represent the complex 3D models and

the properties of these shape features are introduced

as well. Figure 3 shows the ﬂowchart of our ofﬂine

analysis.

4.1 Extraction of Projected Views and

Regions

The pioneer view-based matching method by Chen

et al. (Chen et al., 2003) extracted features from the

whole projected silhouette images. By contrast, we

make use of projected depth images to acquire more

details from the model surfaces, and segment parts

from the whole shape for local information analysis.

Figure 4 shows an example of a 3D horse model and

ﬁve of its projected depth images.

For a model with limbs, there are usually obvious

limb regions in global projected images. Therefore,

we ﬁrst ﬁnd the body part from the projected image.

Our initial thought is to apply the mathematical mor-

phology operations (erosion and dilation) to the whole

projected image, and leave the torso region. Then, we

can obtain the preliminary limb regions by subtract-

ing the torso region form the global region. However,

we found that the limbs may be still connected with

the torso or other limbs by such a method.

As shown in Figure 5(c), because the projected

limb regions may be overlapped. We have to further

analyze the preliminary limb region for more accurate

region separation. The depths within each limb region

are similar, abrupt depth differences (gaps) usually

occur in the boundary between different limb regions.

Therefore, we use Canny edge detection to the pre-

liminary limb images, and get the edge map as shown

in Figure 6(a). Then, we remove the edge points from

the preliminarily separated image and the result limb

regions are not connected to each other as shown in

Figure 6(b). Since the limbs and torso are most sep-

arated, we adjust a ﬂood ﬁll algorithm to gather each

limb region as shown in Figure 6(c). The ﬂood-ﬁll

method selects a few points as seeds and propagates

labels from a point to its neighbors when their prop-

erties are similar. We would like to emphasize that

since there is noise and the projected depth maps vary

from models, the segmented regions may not always

be perfect. This issue can be mended by using an

error-tolerable distance during online matching.

Retrieving 3D Objects with Articulated Limbs by Depth Image Input

103

Figure 3: Overview of ofﬂine analysis.

Figure 4: An example of a horse model and its projected

depth images at vertices of a dodecahedron.

4.2 Extraction of Features

After getting the whole projected views of 3D models

and segmenting them into the torso and limb regions,

we then extract features from these depth regions. In

our trial, we found that three different features are dis-

tinct for matching the global depth images. The three

features are Zernike moments, Histogram of Depth

Gradient (HODG), and 2D-polar Fourier Transform.

The Zernike moments and 2D-polar Fourier Trans-

form descriptor approximate image shape structure by

polynomials and transformed bases. They are also

recommended in Chen et al. (Chen et al., 2003)

and Daras and Axenopoulos (Daras and Axenopou-

los, 2010). We further apply the HODG to distinguish

Figure 5: Extracting the preliminary limb regions. (a) Input

depth images. (b) The torso region by mathematical opera-

tions. (c) The preliminary limb regions by subtraction.

Figure 6: (a) The edge map of the preliminary limb regions.

(b) The results of subtracting the edge points from the pre-

liminarily separated image. (c) The ﬁnal results of limb re-

gions.

the contours and surface of models which have dis-

tinct gradient vectors.

For the part regions (torso and limb region), we

found that Zernike moments and 2D-polar Fourier

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

104

features are still capable of approximating the shapes

of local regions. However, the areas of limbs are rel-

atively small and it makes the HODG occasionally

sensitive to noise or segmented region boundaries.

Therefore, two features are applied to local regions.

In short, three global features and two local features

are applied to analyze depth images in the database.

We brieﬂy introduce and discuss about their proper-

ties in the following paragraphs and the experiment

section.

Zernike moments are a class of orthogonal mo-

ments. They have the properties of rotation invariance

and efﬁcient construction. Moreover, they can effec-

tively resist image noise. Due to the above properties,

Zernike moments are ideal features for shape repre-

sentation in shape classiﬁcation problems. Please re-

fer to (Canterakis, 1999) and (Chen et al., 2003) for

details.

2D-polar Fourier Transform is a variant of the

Discrete Fourier Transform (DFT). This approach

ﬁrst transforms an input image into a 2D-polar im-

age by mapping the (θ, r) onto the (x, y) coordinate.

We can then apply popularly used Fast Fourier Trans-

form (FFT) to the 2D-polar image. It is also applied

in (Daras and Axenopoulos, 2010).

Histogram of depth gradients (HODG) is vari-

ant of histogram of image gradients (HOG) com-

monly used for object detection. It counts the occur-

rences of gradient orientation in a depth image. The

principal thought for HODG is that the shape and sur-

face of an object in a certain view can be approxi-

mately described by the distribution of the depth gra-

dients. To evaluate the HODG, we ﬁrst use Sobel op-

erator in a depth image to get the depth gradient of

each pixel, and evaluate the gradient orientation and

magnitude.

We divide the orientation space into 36 bins, and

accumulate the gradients for each bin. The descriptor

is the concatenation of these bins. To keep this de-

scriptor rotation-invariant, we align the bin with the

maximum value as the primary one, and rotate the fol-

lowing bins according to the order. When we want to

match two histograms, we can compare the primary

bin ﬁrst, and then compute the following bins sequen-

tially. The HODG is suitable to describe the various

changes of surface appearance and contours.

4.3 Descriptor Database

In order to keep the images scale and translation in-

variant, when we generate the depth images which

are projected from the dodecahedron vertices, we

translate the depth images to the center of an im-

age and normalize their sizes. Moreover, the afore-

Figure 7: The left is the input image. The middle and the

right are the searching results of Zernike moments.

Figure 8: Different retrieval results by using Zernike mo-

ments with and without HODG.

mentioned descriptors are all rotation-invariant. We

then use these features to produce the compact fea-

ture databases.

Zernike moments are useful in discriminating the

whole appearance of images in these three descrip-

tors. However, as shown in Figure 7, while only

using Zernike moments, sometimes we may retrieve

some unexpected results when the poses of articulated

models, such as human beings or animals, are simi-

lar to that of a plane. In order to reduce the failure

results, we apply the 2D-polar Fourier Transform. It

can retain more detailed contour shapes. By constrast,

HODG is suitable for analyzing the surface orienta-

tion and sharp contour changes as shown in Figure 8.

In summary, our global feature set is composed of

Zernike moments, Histogram of Depth Gradient, and

2D-polar Fourier Transform; our local feature set con-

sists of Zernike moments and 2D-polar Fourier Trans-

form for torso and limb regions. The recommended

combination of these features is analyzed in the ex-

periment section.

5 ONLINE MODEL RETRIEVAL

This section introduces our interactive 3D model re-

trieval system. Figure 9 shows the ﬂow chart about

our online retrieval system.

5.1 Acquiring Input Depth Images

After the system initialization, a user can input one or

multiple depth image ﬁles or live capture inputs from

a depth camera. Figure 10 shows different ways to

get the query inputs. Before capturing the live depth

Retrieving 3D Objects with Articulated Limbs by Depth Image Input

105

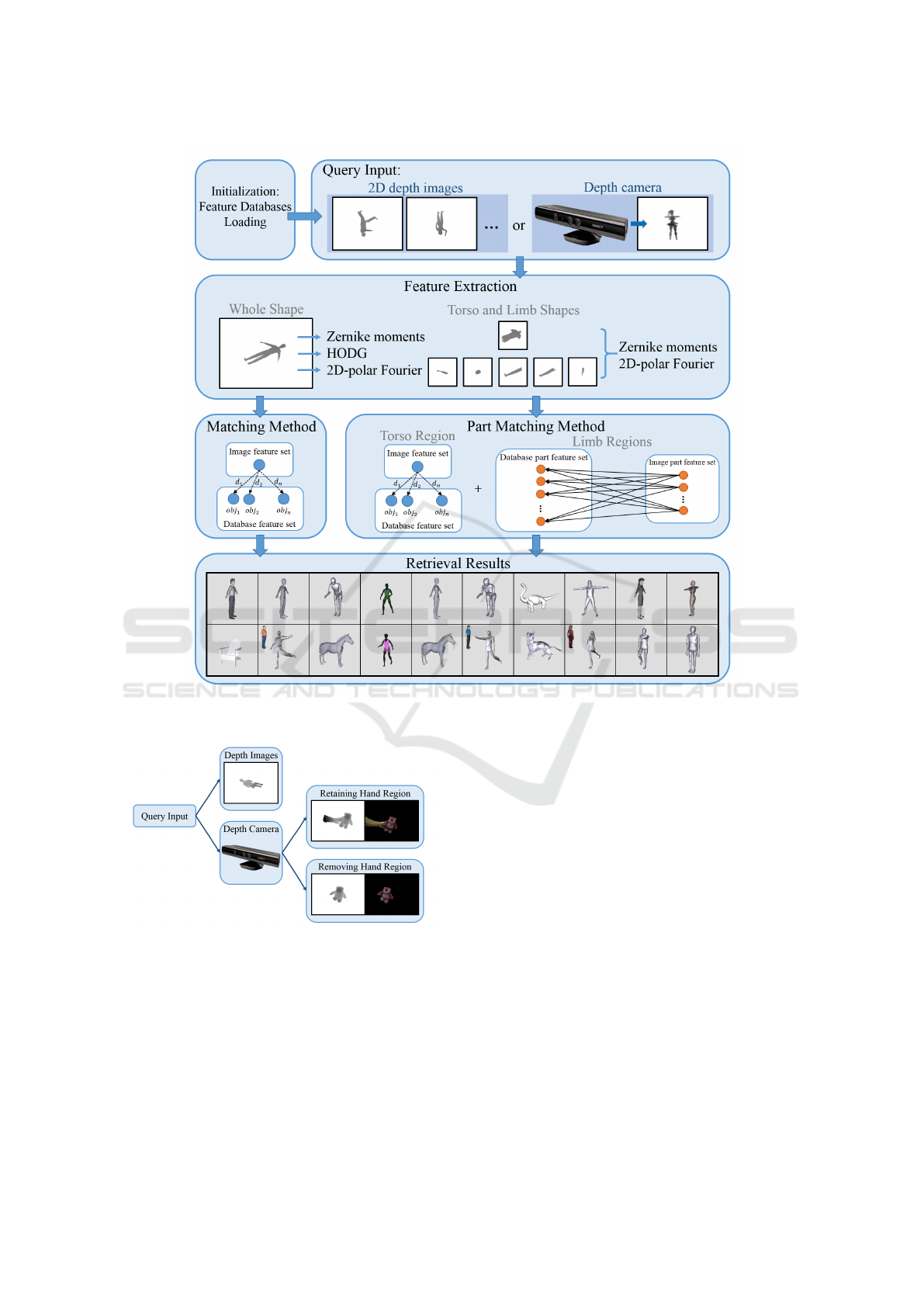
Figure 9: Overview of online model retrieval.

Figure 10: Different ways to acquire input depth images.

images, we need to take an initial frame as the back-

ground region. Pixels with large depth differences be-

tween the initial and current frames are regarded as

the foreground. This step can be improved by ad-

vanced segmentation methods, e.g. (Rother et al.,

2004), (Lin et al., 2015). For the live captured depth

images, a user can hold an object in front of the cam-

era in hand. According to the recorded color his-

togram, our system can detect and remove users hand

region and leave the grabbed object for model query.

Since there is always noise disturbing a live captured

image, we apply connected component labelling to

gather pixels and omit the scattered groups without

sufﬁcient pixel numbers.

5.2 Matching Distances

After acquiring the reﬁned depth images, similar to

4.1, our system automatically segments the torso and

limb regions from the whole shape, and extracts the

global and local feature descriptors. Then, it com-

putes the distances of global and local features among

the input and model projections in the database.

Figure 11 shows the overview of our matching

method. We can see that there are twenty views for

each 3D model and ﬁve (three for global information

and two for local information) feature sets for each

view. Then, we describe the distance terms for each

descriptor.

The distances for Zernike moments, 2D-polar

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

106

Figure 11: Overview of the matching method. Ψ is the set

of all 3D models in our database. ψ

is one of the 3D mod-

els.

Fourier are denoted by d

Zernike

and d

PolarFourier

respec-

tively. These two distances can be formulated by

equation 1.

set

,set

ob j

∑

i=1



− f

ob j



, (1)

where f

is the i

feature coefﬁcient of a query im-

age, f

ob j

is the i

coefﬁcient of one of the objects

in our 3D model database, and N is 35 for Zernike

moments and 78 for 2D-polar Fourier descriptors.

The distance for Histogram of Depth Gradient is

denoted by d

HODG

, and it is formulated as follows:

HODG:set

,set

ob j

∑

i=1



∩ f

ob j



+ ε

, (2)

where f

is the i

feature coefﬁcient of a query im-

age, f

ob j

is the i

coefﬁcient of one of the objects

in our 3D model database, and we set ε to 0.001, N

to 36. The denominator of equation 2 is the sum of

intersection operations for histogram bin values.

On the other hand, the local feature sets

(ZernikePart and PolarFourierPart) comprise features

for torso and limb regions. For example, if a whole

projected depth image can be divided into one torso

and three limb regions, there are four parts in this

shape. Since a torso and limbs have different prop-

erties, these two kinds of regions are handled and

matched separately. The distances for torso and limb

regions are denoted by d

Torso

and d

Limb

, and the dis-

tance between two feature sets are formulated as fol-

lows:

Torso:set

,set

ob j

∑

i=1



− f

ob j



Limb:set

,set

ob j

= EMD



, f

ob j



Part

Torso

+ n × d

Limb

n + 1

(3)

where f

is the i

feature coefﬁcient of query image,

ob j

is the i

coefﬁcient of one of the objects in our

3D model database, and N is 35 for ZernikePart and

78 for PolarFourierPart. The computing way between

Zernike moments and ZernikePart for torso region is

the same because there is only a torso region in each

shape, and so do 2D-polar Fourier Transform and Po-

larFourierPart for the torso region. f

is a sequence

of limb features of query image, and f

ob j

is a se-

quence of limb features of an object in our 3D model

database. The EMD function is the earth movers dis-

tance proposed by Rubner et al. (Rubner et al., 2000).

n is the number of limb regions in a projected image,

and d

Part

is weighted average of d

Torso

and d

Limb

The earth movers distance (EMD) is a method

to evaluate dissimilarity (distance) between two

multi-dimensional distributions, and here we use

ZernikePart and PolarFourierPart. The EMD esti-

mates the minimum moving distance between two

feature sets, and the EMD is formulated as follow:

∑

i=1

∑

j=1

i j

= min

∑

i=1

∑

j=1

EMD(P, Q) =

∑

i=1

∑

j=1

i j

∑

i=1

∑

j=1

i j

(4)

where P is the ﬁrst feature set with m limb regions, Q

is the second feature set with n limb regions, a

i j

is the

optimal work amount between P and Q, and d

i j

is the

ground distance between P and Q.

Finally, the distance between two views (input and

a projected view of a database model) becomes:

view:set

,set

= w

Zernike

+ w

HODG

+ w

ZPart

+ w

PFPart

(5)

where w

Zernike

, w

HODG

, w

ZPart

, and w

PFPart

are

the normalized weights for corresponding distances.

These distances have the same weights by default. If

a user turns off one of the distances, the corresponding

weight term is set to zero.

5.3 Model Query

Since our system does not constrain the viewing angle

of the query input, we do not have information about

the viewpoints or other spatial relationship among the

input images. Therefore, the distance between an in-

put depth image and a database model is set as the dis-

tances between the inputs and the most similar view

of that model. The equation is as follows:

ob j = argmin

∑

i=1

min



view:in, j



, (6)

Retrieving 3D Objects with Articulated Limbs by Depth Image Input

107

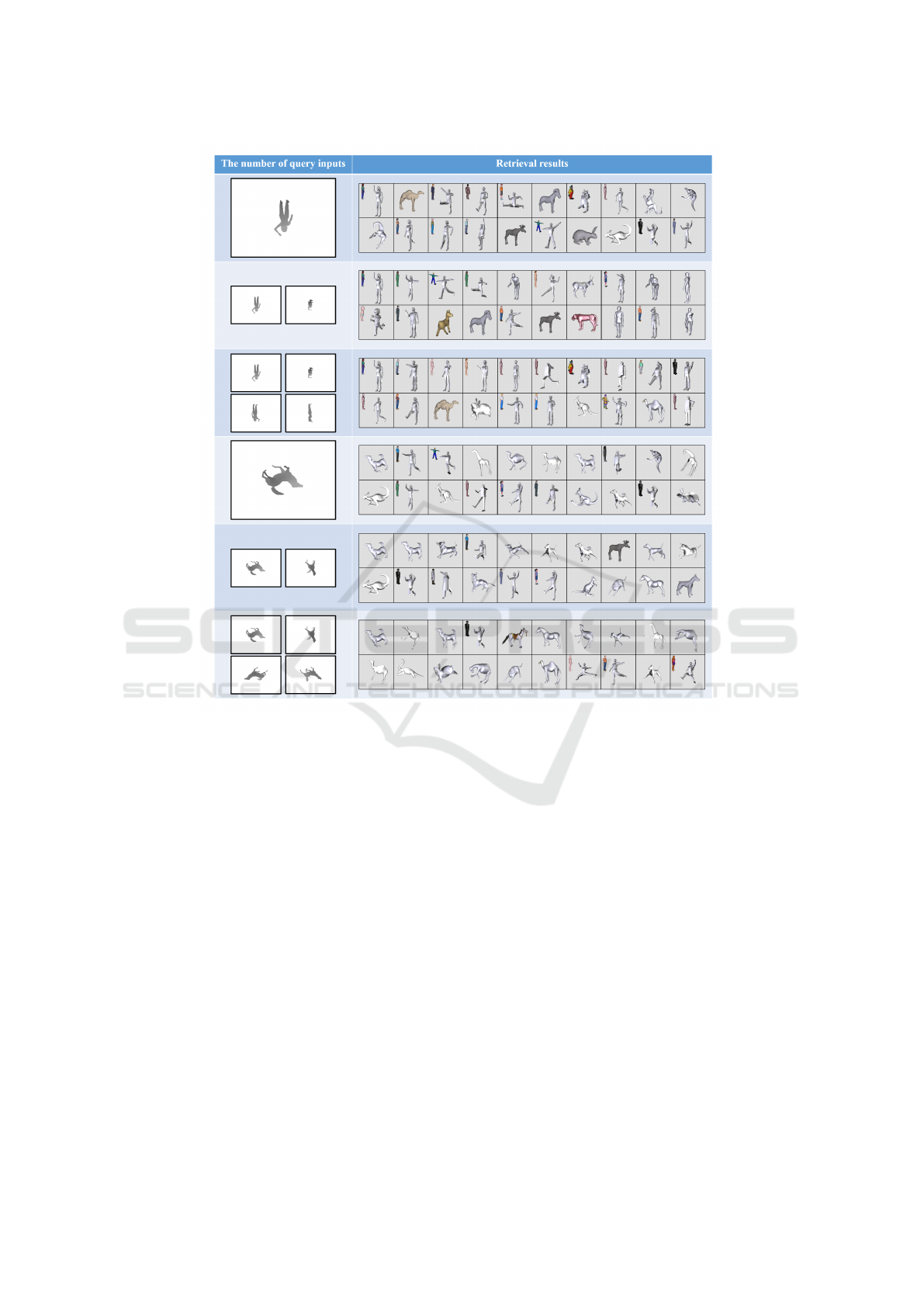
Figure 12: Left: Examples of query by different numbers of input images. Right: The corresponding retrieval results.

where o represents the index of an object model in

database; i is the index of an input image; j is the

index of a view belonging to o; N

is the number of

input images.

Our system allows users inputting one or more

query images. Figure 12 shows different results with

one, two, and four query inputs, and we can ﬁnd that

the results are more accurate with more input views.

6 EXPERIMENT

6.1 Retrieval System

Our prototype system is developed in C/C++ lan-

guage, with OpenCV, OpenGL, and OpenNI libraries.

The experimental database derived from two famous

3D model datasets. The NTU dataset is published by

Chen et al. (Chen et al., 2003), and SHREC15 (Lian

and Zhang, 2015) dataset contains a variety of non-

rigid 3D models. Since one of our comparison meth-

ods, shape clustering proposed by Shen et al. (Shen

et al., 2013), is only suitable for retrieving the sil-

houette images with extractable skeletons, we chose

573 models from NTU database which have complete

and noiseless meshes. Since there are few postured

models in NTU dataset, we therefore chose 42 hu-

man models and required users to edit their postures

with Maya (Autodesk Inc., ). Each human model has

5 different postures. Several examples are shown in

Figure 13. Also, we take 97 non-rigid quadruped ani-

mal models from SHREC15 (Lian and Zhang, 2015).

There are 880 models in total. In Table 1, we list

the time spending in the ofﬂine and online stages. It

shows that our method is efﬁcient in online retrieval.

Please refer to the supplementary video to see the

demo for online retrieval.

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

108

Figure 13: Left: The original human models from NTU

database (Chen et al., 2003). Right: The corresponding

models in random postures.

Table 1: The spending time in the ofﬂine and online stages.

Process Time (seconds)

Extract projected views 309.685

Extract local info. and features 1746.443

Load feature databases 4.366

Retrieve per image 0.539

6.2 Performance Evaluation

We compared three different methods. The method

proposed by Shen et al. (Shen et al., 2013) is denoted

by “SC”. SC computes the similarity between two

skeleton paths of silhouette images. It ﬁnds the corre-

spondence of endpoints and junction points, and cal-

culates path distances as the similarity measurement

of shapes. SC can advantageously retrieve shapes

with the presence of joint movement, stretching, and

contour deformation, so we took this method as one

of our comparisons for retrieving models with artic-

ulated limbs. The feature set proposed by Chen et

al. (Chen et al., 2003) is denoted by “LFD”. LFD

feature set is combination of Zernike moments and

Fourier Transform, and it is known for its capability

for searching 3D models with sparse inputs. Our pro-

posed method is denoted by “Our Method”. However,

since the two related methods do not consider the

depth information, during our experiments we also

turned off the HODG term to demonstrate the capa-

bility without using depth information. Our method

without HODG is denoted by “Our Method (without

HODG)”.

Before the precision-recall analysis, we demon-

strate the results of articulated and rigid model re-

trieval. Since the articulated models may have diverse

motions of torso parts or limbs, we want to retrieve

models which have diverse motions compared to the

input. Figure 14 shows the retrieved results. Since

our method includes not only global but also local

information, the proposed method can get human or

quadruped animal models in different postures.

Figure 14: The results of retrieving articulated models and

rigid objects.

In order to evaluate these methods, we use three

popularly used measures: precision-recall diagram,

the area under precision-recall curve, and F-measure.

To calculate the Precision-Recall, we separated the

dataset into 32 categories, and used the leave-one-out

method to evaluate the retrieval accuracy.

As shown in Table 2 and Table 3, we tried various

combinations of features, and ﬁnd the most effective

one to be our feature sets. In the following, we ab-

breviate Zernike moments as “Z”, 2D-polar fourier as

“PF”, ZernikePart as “ZPart”, and PolarFourierPart as

“PFPart”. With HODG, the best combination is ZPart

+ HODG + PF. Without HODG, the best one is ZPart

+ PFPart.

Figure 15 shows the precision-recall curves of

all models. Our method with parts gets the highest

scores at any view situation. Even without HODG,

our method still outperforms SC and LFD. Table 4

shows the corresponding precision-recall area and F-

measure. We also show the precision-recall curves of

four views and twenty views.

Retrieving 3D Objects with Articulated Limbs by Depth Image Input

109

Figure 15: The precision-recall curves of both rigid and articulated categories (32 categories). (a) random 1 view (b) random

4 views (c) all 20 views

Table 2: The precision-recall area and F-measure of top-4

feature sets with HODG.

Feature sets F-measure Area

Z+HODG+PF 0.337945 0.362754

ZPart+HODG+PF 0.353717 0.380994

Z+HODG+PFPart 0.339882 0.365623

ZPart+HODG+PFPart 0.351692 0.376325

Table 3: The precision-recall area and F-measure of top-4

feature sets without HODG.

Feature sets F-measure Area

Z+PF 0.320841 0.312618

ZPart+PF 0.352201 0.354703

Z+PFPart 0.325695 0.321335

ZPart+PFPart 0.354193 0.357654

In Figure 16 and 17, we give different numbers

of inputs, and ﬁnd that the performance improvement

converges with 8 or more inputs.

Figure 16: The F-measure scores in different numbers of

inputs.

7 CONCLUSION AND FUTURE

WORK

This paper proposes a novel method to retrieve rigid

and articulated 3D models. When most existing meth-

Table 4: The precision-recall area and F-measure of both

rigid and articulated categories (32 categories).

Random 1 view F-measure Area

Our (without HODG) 0.351801 0.352638

Our (with HODG) 0.352834 0.37696

SC (Shen et al., 2013) 0.317446 0.301876

LFD (Chen et al., 2003) 0.304962 0.286351

Random 4 views F-measure Area

Our (without HODG) 0.370055 0.40825

Our (with HODG) 0.372430 0.441786

SC (Shen et al., 2013) 0.343624 0.363110

LFD (Chen et al., 2003) 0.328067 0.34843

All 20 views F-measure Area

Our (without HODG) 0.375983 0.429935

Our (with HODG) 0.379451 0.467065

SC (Shen et al., 2013) 0.355618 0.395940

LFD (Chen et al., 2003) 0.335435 0.372276

Figure 17: The area scores in different numbers of inputs.

ods retrieved features from the whole projected views

or based on skeleton topologies, we propose using

global shapes and additional local information from

segmented torso and limb regions for 3D model re-

trieval. This method does not require a well-aligned

model posture or viewpoint. Each query can be ﬁn-

ished within a second by our current system with-

out carefully code optimization. In our experiment,

GRAPP 2018 - International Conference on Computer Graphics Theory and Applications

110

we evaluated different combinations of feature sets

and different numbers of input views. These reports

can be helpful for further view-based retrieval system.

The comparison also demonstrated that the proposed

method can get more accurate results than two known

methods.

Currently, our retrieval method is designed for

articulated objects in which the limbs are rigid.

One possible extension is to incorporate deformation

methods, e.g. (Chen et al., 2013), for retrieving ob-

jects with surface deformation. Recently, the deep

learning techniques succeed in various vision prob-

lems. Our current method is relatively low-cost in

computation, and another possible future work is to

incorporate the features extracted from learning meth-

ods, e.g.(Su et al., 2015).

REFERENCES

ASUS Inc. Xtion pro. www.asus.com/3D-Sensor/.

Autodesk Inc. Maya. www.autodesk.com/products/

maya/.

Bai, X. and Latecki, L. J. (2008). Path similarity skeleton

graph matching. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 30(7):1282–1292.

Canterakis, N. (1999). 3D Zernike moments and Zernike

afﬁne invariants for 3D image analysis and recogni-

tion. In 11th Scandinavian Conf. on Image Analysis,

In 11th Sc:85–93.

Chen, C.-H., Tsai, M.-H., Lin, I.-C., and Lu, P.-H. (2013).

Skeleton-driven surface deformation through lattices

for real-time character animation. The Visual Com-

puter, 29(4):241–251.

Chen, D.-Y., Tian, X.-P., Shen, Y.-T., and Ouhyoung, M.

(2003). On Visual Similarity Based 3D Model Re-

trieval. Eurographics, 22(3):223–232.

Daras, P. and Axenopoulos, A. (2010). A 3D Shape Re-

trieval Framework Supporting Multimodal Queries.

International Journal of Computer Vision, 89(2-

3):229–247.

Funkhouser, T., Min, P., Kazhdan, M., Chen, J., Halder-

man, A., Dobkin, D., and Jacobs, D. (2003). A search

engine for 3d models. ACM Trans. Graph., 22(1):83–

105.

Hasler, N. and Thorm, T. (2010). Learning Skeletons for

Shape and Pose. Proceedings of the 2010 ACM SIG-

GRAPH symposium on Interactive 3D Graphics and

Games - I3D ’10, 1(212):23–30.

Igarashi, T., Matsuoka, S., and Tanaka, H. (1999). Teddy:

A sketching interface for 3d freeform design. In Pro-

ceedings of SIGGRAPH, pages 409–416.

Kim, V. G., Chaudhuri, S., Guibas, L., and Funkhouser, T.

(2014). Shape2pose: Human-centric shape analysis.

ACM Trans. Graph., 33(4):120:1–120:12.

Kim, V. G., Li, W., Mitra, N. J., Chaudhuri, S., DiVerdi,

S., and Funkhouser, T. (2013). Learning part-based

templates from large collections of 3d shapes. ACM

Trans. Graph., 32(4):70:1–70:12.

Kleiman, Y., van Kaick, O., Sorkine-Hornung, O., and

Cohen-Or, D. (2015). Shed: Shape edit distance for

ﬁne-grained shape similarity. ACM Trans. Graph.,

34(6):235:1–235:11.

Lian, Z. and Zhang, J. (2015). Shrec15 non-rigid

3d shape retrieval. www.icst.pku.edu.cn/zlian/

shrec15-non-rigid/data.html.

Lin, I.-C., Lan, Y.-C., and Cheng, P.-W. (2015). SI-

Cut: Structural inconsistency analysis for image fore-

ground extraction. IEEE Transactions on Visualiza-

tion and Computer Graphics, 21(7):860–872.

opez-Sastre, R., Garc

ıa-Fuertes, A., Redondo-Cabrera, C.,

Acevedo-Rodr

ıguez, F., and Maldonado-Basc

on, S.

(2013). Evaluating 3d spatial pyramids for classifying

3d shapes. Computers & Graphics, 37(5):473–483.

Microsoft Corp. Kinect. www.xbox.com/Kinect.

Mohamed, W. and Hamza, A. B. (2012). Reeb graph path

dissimilarity for 3d object matching and retrieval. The

Visual Computer, 28(3):305–318.

Rother, C., Kolmogorov, V., and Blake, A. (2004). Grabcut:

interactive foreground extraction using iterated graph

cuts. ACM Transactions on Graphics, 23(3):309–314.

Rubner, Y., Tomasi, C., and Guibas, L. J. (2000). Earth

mover’s distance as a metric for image retrieval. Inter-

national Journal of Computer Vision, 40(2):99–121.

Shen, W., Bai, X., Hu, R., Wang, H., and Jan Latecki, L.

(2011). Skeleton growing and pruning with bending

potential ratio. Pattern Recognition, 44(2):196–209.

Shen, W., Wang, Y., Bai, X., Wang, H., and Jan Latecki, L.

(2013). Shape clustering: Common structure discov-

ery. Pattern Recognition, 46(2):539–550.

Sipiran, I., Bustos, B., and Schreck, T. (2013). Data-aware

3D partitioning for generic shape retrieval. Computers

& Graphics, 37(5):460–472.

Su, H., Maji, S., Kalogerakis, E., and Learned-Miller, E. G.

(2015). Multi-view convolutional neural networks for

3d shape recognition. In Proc. IEEE International

Confererence on Computer Vision, pages 945–953.

Wang, Y.-S. and Lee, T.-Y. (2008). Curve-skeleton extrac-

tion using iterative least squares optimization. IEEE

transactions on visualization and computer graphics,

14(4):926–36.

Wu, L.-C., Lin, I.-C., and Tsai, M.-H. (2016). Augmented

reality instruction for object assembly based on mark-

erless tracking. Proceedings of the 20th ACM SIG-

GRAPH Symposium on Interactive 3D Graphics and

Games - I3D ’16, pages 95–102.

Xie, Z., Xiong, Y., and Xu, K. (2014). Ab3d: Action-based

3d descriptor for shape analysis. Visual Computer,

30(6-8).

Retrieving 3D Objects with Articulated Limbs by Depth Image Input

111