Visual GISwaps - An Interactive Visualization Framework for Geospatial

Decision Making

Goran Milutinovic

and Stefan Seipel

1,2

Faculty of Engineering and Sustainable Development, University of G¨avle, G¨avle, Sweden

Division of Visual Information and Interaction, Department of Information Technology, Uppsala University, Uppsala,

Sweden

Keywords:

GIS, Decision Making, Interactive Visualization, GISwaps.

Abstract:

Different visualization techniques are frequently used in geospatial information systems (GIS) to support

geospatial decision making. However, visualization in GIS context is usually limited to the initial phase of the

decision-making process, i.e. situation analysis and problem recognition. This is partly due to the choice of

methods used in GIS multi-criteria decision-making (GIS-MCDM) that usually deploy some non-interactive

approach, leaving the decision maker little or no control over the calculation of overall values for the consid-

ered alternatives; the role of visualization is thus reduced to presenting the ﬁnal results of the computations.

The contributions of this paper are twofold. First, we introduce GISwaps, a novel, intuitive interactive method

for decision making in geospatial context. The second and main contribution is an interactive visualization

of the choice phase of the decision making process. The visualization allows the decision maker to explore

the consequences of trade-offs and costs accepted during the iterative decision process, both in terms of the

abstract relation between different decision variables and in spatial context.

1 INTRODUCTION

The main purpose of geographic information systems

(GIS) is providing support for decision making. The

term GIS in itself is not easily deﬁned, as it has come

to symbolize a technology, an industry, a way of doing

work etc. (Chrisman, 1999). In this paper we use the

term as deﬁned in Cowen (1988), where GIS is rec-

ognized as “a decision support system involving the

integration of spatially referenced data in a problem

solving environment”.

In the last couple of decades, a whole new in-

terdisciplinary ﬁeld of study, commonly referred to

as GIS-based multi-criteria decision analysis (GIS-

MCDA), has emerged. In Malczewski and Rinner

(2015), GIS-MCDA is deﬁned as “a collection of

methods and tools for transforming and combining

geographic data and preferences (value judgments) to

obtain information for decision making.” The most

commonly accepted generalization of the decision-

making process is suggested by Simon (1960), with

intelligence, design and choice as three major phases.

During the intelligence phase, a problem or a situation

that calls for a decision is identiﬁed and formulated.

This phase involves data collection, exploration and

preprocessing. The alternatives, or the set of possi-

ble solutions, are deﬁned in the design phase. Finally,

in the choice phase, the alternatives are evaluated and

the most appropriate alternative or set of alternatives

is selected.

There is a vibrant community within the GIS-

MCDA performing research in the ﬁeld of visual-

ization. However, Andrienko and Andrienko (2003)

point out that, while visualization plays an important

role in the initial phase of the decision-making pro-

cess, it is rarely used in the design phase and the

choice phase. GIS decision-making requires more

extensive use of visualization and interaction even

during the decision process itself, i.e. during mak-

ing the actual choices. In order to decide whether

or not a trade-off to be made is feasible or admissi-

ble, the decision maker needs to see how an option is

positioned in both the geographical and the attribute

space, as well as how it compares to other options

(Andrienko and Andrienko, 2003). Limited use of vi-

sualization in the choice-phase in geospatial decision

making is in part related to the choice of multi-criteria

decision-making methods used in GIS-MCDM. This

phase of the decision-making process in GIS con-

text is most commonly performed using some weight-

ing method to derive the weights of the criteria, i.e.

the weights associated with attribute map layers, and

236

Milutinovic, G. and Seipel, S.

Visual GISwaps - An Interactive Visualization Framework for Geospatial Decision Making.

DOI: 10.5220/0006610202360243

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages

236-243

ISBN: 978-989-758-289-9

some compensatory aggregation method to obtain the

score for each alternative in the set (Milutinovic et al.,

2017). This non-interactive approach leaves the deci-

sion maker with little or no control over the score cal-

culation once the criteria weights have been set, and

the role of visualization is thus reduced to presenting

the ﬁnal results of the computations.

The contributions of this paper in the context of

GIS-MCDA are twofold. We ﬁrst introduce GISwaps,

a novel approach to multi-criteria decision making in

geospatial applications. GISwaps is an adaptation of

the Even Swaps method (see Hammond et al. (1998,

1999)) to geospatial problems. It presents an intuitive

strategy to simplify the decision process through iter-

ative reduction of decision criteria. Following a re-

view of related work in Section 2, the mechanism of

GISwaps and its relation to EvenSwaps are described

in Section 3. The second and main contribution of

this paper, which is presented in Section 4, is an in-

teractive visualization allowing the decision maker to

explore the consequences of trade-offs and costs ac-

cepted during the iterative decision process, both in

terms of the abstract relation between different deci-

sion variables and in spatial context. In Section 5 we

discuss the beneﬁts of using this interactive visual-

ization in GISwaps for identifying situations and de-

pendencies between alternatives that would otherwise

remain unrevealed.

2 RELATED WORK

In a survey of ways of visualizing alternatives in the

context of multiple criteria decision making, Mietti-

nen (2014) gives an overview of commonly known

techniques, such as bar charts, scatterplots and value

paths, as well as a number of techniques using circles,

polygons or icons, techniques based on hierarchical

clustering and projection-based techniques. A num-

ber of different approaches to interactive visualization

in decision making have been suggested. Carenini

and Loyd (2004) propose ValueCharts, a set of in-

teractive visualization methods aimed to help deci-

sion maker in inspecting linear models of preferences

and evaluation. The concept is further developed in

Bautista and Carenini (2006), with ValueCharts re-

designed in order to support all phases of preferential

choice. A Decision Ball model, aimed to assist deci-

sion maker by visualizing decision process based on

even swaps, is presented in Li and Ma (2008). Their

study is of limited use for our method, though, as

it i) is limited to decision making in discrete choice

models (assumes small number of alternatives), and

ii) operates by cancellation of alternatives rather than

criteria, abandoning the very principle of the Even

Swaps method. Kollat and Reed (2007) present a

framework for Visually Interactive Decision-making

and Design using Evolutionary Multi-objective Opti-

mization (VIDEO). The framework is capable of vi-

sually representing up to four objectives (three on X,

Y and Z, and a fourth as a colour) and allows visual

navigation through large sets of alternatives, explor-

ing and visualizing trade-offs.

The need for interactivevisualization in spatial de-

cision making in continuous choice models is signiﬁ-

cant, due to a large number of alternatives. Andrienko

and Andrienko (2003) underline the decision maker’s

need to see how an option is positioned in both the

geographical and the attribute space, as well as how

it compares to other options. Based on that prin-

ciple, the authors have developed CommonGIS, an

own software system for exploratory analysis of spa-

tial data including spatio-temporal data (Andrienko

et al., 2003; Andrienko and Andrienko, 2003, 2004)

Also Malczewski and Rinner (2015) state the impor-

tance of interactive visualization in GIS-MCDM. The

authors make a distinction between geovisualization

of MCDA input (visualizing criteria, visualizing al-

ternatives and visualizing scaled values and criterion

weights) and geovisualization of MCDA results (vi-

sualizing combination rules and parameters and vi-

sualizing model sensitivity). Each of the aforemen-

tioned visualization objectives should assume and

support interactivity (Malczewski and Rinner, 2015).

Jankowski et al. (2001) raise the question of effec-

tive means of using maps as a support to spatial prob-

lems exploration and structuring. The main role (ob-

jective) of using maps in spatial MCDM is the con-

sideration of geographical locations in the process of

deciding trade-offs among the decision criteria. Si-

multaneous representation of both criterion and de-

cision space helps the decision maker deﬁne his/her

preferences not only on the base of the attribute data,

but also geography. Jankowski et al. (2001) ﬁnd that

highly interactive depiction of both criteria and deci-

sion spaces would be more productive for understand-

ing the structure of the decision situation than static

display. Thus, decision procedures should be facili-

tated by highly interactive visualization.

The interactive visualization framework presented

in this paper is inspired and guided by the above prin-

ciples. The framework is designed as an integral part

of GISwaps, a novel method for decision making in

continuous choice models based on Even Swaps.

Visual GISwaps - An Interactive Visualization Framework for Geospatial Decision Making

237

3 GISwaps METHOD

In this section we give a brief overview of the

GISwaps method, as well as an overview of Even

Swaps method on which GISwaps is based. This

overview should facilitate the reader in understanding

the main features of the proposed visualization frame-

work.

3.1 Even Swaps

Even Swaps is a simple, yet powerful multi-criteria

decision-making method developed by Hammond

et al. (1998). The main principle of the method is ad-

justing the consequences of considered alternatives in

order to render them equivalent in terms of the chosen

criterion. In that way, that criterion may be cancelled

out as irrelevant for further analysis. Hammond et al.

(1999) deﬁne the method by the following ﬁve steps:

1. Determine the change necessary to cancel out

chosen reference criterion (R).

2. Assess what adjustments need to be done in cho-

sen response criterion (M), in order to compensate

for the needed change.

3. Make the even swap. An even swap is a process

of increasing the value of an alternative in terms

of one criterion and decreasing the value by an

equivalent amount in terms of another. After the

swaps are performed over the whole range of al-

ternatives,all alternativeswill havethe same value

on R and it can be cancelled out as irrelevantin the

process of ranking the alternatives.

4. Cancel out the now-irrelevant criterion R.

5. Eliminate dominated alternative(s). Alternative a

is said to be dominated by alternative b if it is infe-

rior to b on at least one criterion and not superior

to b on any other criterion.

These steps are repeated until a single alternative re-

mains.

Let us consider a simple multi-criteria decision

problem. Assume that X wants to buy a house, and

is considering four alternatives: A, B, C and D. The

goal is to ﬁnd the best alternative considering price

(P), size (S) and distance from the city center (D

ist

Values for the alternatives in terms of each of the cri-

teria are presented in Table 1.

Table 1: Values for alternatives A, B, C and D.

A B C D

P (1000 $) 110 120 115 160

S (m

) 115 130 125 145

ist

(km) 4 4,5 3 2

There are no dominated alternatives to be removed,

so X proceeds and chooses P as the reference crite-

rion (R) and S as the response criterion (M). After ad-

justing P-value for all the alternatives to the minimum

price of 110000$, X modiﬁes S-value for each alter-

native in such way that, depending on X’s preferences

and judgement, this modiﬁcation compensates for the

performed adjustment on P. The result is shown in ta-

ble 2.

Table 2: The values in terms of S are adjusted in order to

compensate for the proposed change on P.

A B C D

P (1000 $) 110 110 120 110 115 110 160

S (m

) 115 120 130 118 125 115 145

ist

(km) 4 4,5 3 2

Now that all four alternatives have the same value on

P, P is cancelled out as irrelevant. Furthermore, A

is dominated by D and is eliminated. X proceeds by

choosing S as the referencecriterion and D

ist

as the re-

sponse criterion. The result after making adjustments

is given in table 3.

Table 3: The values in terms of D

ist

are adjusted in order to

compensate for the proposed change on S.

B C D

S (m

) 120 120 118 120 115

ist

(km) 4,5 3,5 3 2,8 2

As S is now cancelled out as irrelevant, alternative D

is chosen as the best alternative with the value of 2,8

in terms of D

ist

(the only remaining criterion).

3.2 GISwaps

The Even Swaps method, as presented in Section 3.1,

is only suitable for decision-making in discrete choice

models, when the number of alternatives is relatively

small. Many GIS-related decision-making situations

concern a continuous choice model, where the num-

ber of alternatives is only constrained by the limits

of the used data representation model. For example,

ﬁnding the optimal location for a certain purpose in

an area represented by a 1000 x 1000 grid, the num-

ber of alternatives could be as high as 1 000 000, de-

pending on the grid resolution and speciﬁc constraints

of the problem. If the mechanism of the Even Swaps

method is to be applied to geospatial problems, the

process of making trade-offsneeds to be automatized.

For this purpose we introduce GISwaps, an approach

that makes decision making based on even swaps in

decision problems with large number of alternatives

manageable. The method, which is described in de-

tail in Milutinovic et al. (2017), uses input from the

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

238

decision maker on a number of virtual alternatives in

order to calculate, for each alternative in the set, the

coefﬁcient of the value change (swap coefﬁcient) on

the response criterion. As the name suggests, the vir-

tual alternativesdo not need to actually exist in the set,

but are hypothetical alternatives used to ﬁne-tune the

value update function. The number of virtual alterna-

tives, as well as assigned descriptive values in terms

of each criterion, are set in each step for the current

reference and response criteria, respectively.

Unlike Even Swaps, GISwaps does not incorpo-

rate elimination of dominated alternatives. In geospa-

tial decision making we usually want to obtain an or-

dered set of all feasible alternatives, as opposed to a

single best alternative. In its basic form, our method

can be expressed by the following algorithm:

Repeat

Decide the reference criterion R

Decide the response criterion M

Set virtual alternatives

Obtain trade-off values for virtual alternatives

Calculate update coefficients for virtual alternatives

For each alternative in the set

Calculate the update coefficient for the alternative

Update the value of the alternative with respect to M

Discard R

Until a single criterion remains

Rank the alternatives

In a typical geospatial site location problem, a

number of possibly conﬂicting criteria is usually con-

sidered. Finding the optimal site location for building

a dam, for example, requires considering factors such

as water discharge, undulation, hydraulic head, dis-

tance to urban areas, distance to forests and distance

to agricultural areas. Applying GISwaps on such case

would take ﬁve swap turns, one of the criteria being

cancelled out in each turn. In the following example,

we explain our method on one possible turn, where

hydraulic head is used as the reference, and undula-

tion as the response criterion. We use 16 virtual alter-

natives in order to ﬁne-tune the value update function.

Each of the alternatives is assigned a pair of values: a

value from the arrayV

(four reference values in terms

of the reference criterion R) and a value from the array

(four reference values in terms of the response cri-

terion M). We use following reference values for the

virtual alternatives in terms of R and M, respectively:

= [R

min

+ R

min

+ 2R

min

+ 3R

]

= [M

min

+ M

min

+ 2M

min

+ 3M

max

]

(1)

where

min

: minimum value with respect to R

max

: maximum value with respect to R

= (R

max

− R

min

)/4

min

: minimum value with respect to M

max

: maximum value with respect to M

= (M

max

− M

min

)/4

For example, for hydraulic head values in range 1-

46 and undulation values in range 1-136, it gives the

following values for V

and V

, respectively:

= [1,12.3,23.5,34.8]

= [35,68,103,136]

(2)

Based on his/her judgement and preferences, the deci-

sion maker now needs to perform even swaps. He/she

chooses a compensation value M

(i, j)

of criterion M

for each virtual alternative, i.e. for each pair of ref-

erence values (V

(i)

( j)

); i, j ∈ [1..4]. Each value

(i, j)

is chosen so that the decision maker is in-

different between the differences (R

max

− V

(i)

) and

( j)

− M

(i, j)

). The compensation values are stored

in a 4x4 matrix M

(Equation 3). With the input from

the decision maker as shown in Figure 1, the M

ma-

trix contains following values:







18 40 57 87

20 44 66 91

22 50 70 95

28 59 84 106







(3)

Update coefﬁcients for each element in M

are stored

in corresponding matrix M

. Each value M

(i, j)

is cal-

culated as

(i, j)

( j)

− M

(i, j)

max

− V

(i)

(4)

For the input used in the example, the M

matrix con-

tains following values:







0.37 0.63 1.01 1.09

0.44 0.73 1.08 1.33

0.57 0.82 1.44 1.82

0.60 0.85 1.66 2.69







(5)

In order to calculate the update coefﬁcient for an al-

ternativea, we need to determine index i using a

(the

value of a in terms of the reference criterion R) and in-

dex j using a

(the value of a in terms of the response

criterion M). The indexes are determined as follows:

i = k for V

[k]

≤ a

< V

[k+1]

, k ∈ [1..3]

i = 4 for a

≥ V

[4]

j = 1 for a

≤ V

[1]

j = k for V

[k−1]

< a

≤ V

[k]

, k ∈ [2..4]

(6)

The value update coefﬁcient for any alternative a can

now be calculated as

= M

(i, j−1)

(i, j)

− M

(i, j−1)

) ·

− V

( j−1)

( j)

− V

( j−1)

(7)

Visual GISwaps - An Interactive Visualization Framework for Geospatial Decision Making

239

The remaining four turns are performed in the same

manner. After cancelling out ﬁve of six criteria, the

grid containing the values for the only remaining cri-

terion would be the de facto result of the decision pro-

cess that can be shown in an appropriate GIS soft-

ware.

While GISwaps enables interactive deﬁnition of

compensation values and a fully automatized up-

date of response criteria in a quasi-continuous multi-

criteria decision model, it requires suitable visualiza-

tions of the outcomes in the iterative process of up-

dating coefﬁcients and elimination of reference crite-

ria. In the following section we present our approach

to visualizing the complex relationships between the

choice of reference and response criteria, the design

of the update coefﬁcients, and their effect on the huge

amount of alternatives both in attribute space and ge-

ographical space.

4 VISUAL GISwaps

The GISwaps method is an interactive method for

spatial decision making. Through a semi-automatized

process explained in Section 3.2, the decision maker

sets the actual trade-off values between alternatives

with respect to a pair of criteria. Throughout the pro-

cess, the decision maker is active and in full control.

The interactive visualization presented in this sec-

tion allows the decision maker to explore the conse-

quences of trade-offs and costs accepted during each

step of the iterative decision process.

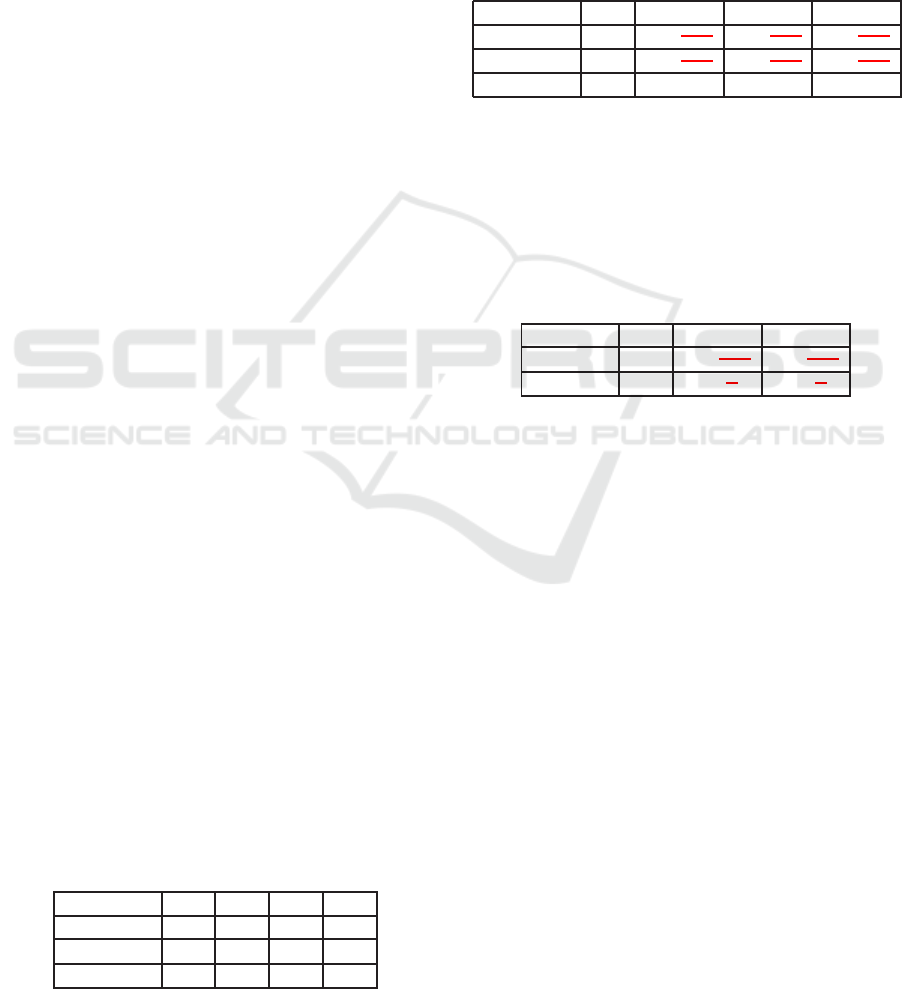
The main window of the application that imple-

ments the GISwaps method as well as the visualiza-

tion framework is given in Figure 1. The image shows

the setup of the example used in Section 3.2, after the

decision maker has selected reference (in the appli-

cation referred to as measuring stick) and response

criteria, and set compensation values in terms of the

latter. The example is used in this section with the

same trade-off values as in Section 3.2.

Our interactive visualization frameworkintegrates

fundamental visualization techniques, and consists of

three conceptual units: 1) visualization of alterna-

tives in attribute space, 2) visualization of alternatives

in geographical space, and 3) visualization of value

functions. In each step of the iterative process, ref-

erence and response criteria are selected by the deci-

sion maker. The scatterplot representing the attribute

space for the set of alternatives is constructed as a

2D-plot, with position on the X-axis determined by

the value in terms of the response criterion, and po-

sition on the Y-axis determined by the value in terms

of the reference criterion. This representation gives

the decision maker an insight into the distribution of

data in terms of the currently chosen response crite-

rion. An extra dimension may be added to the plot by

color-coding samples in order to show values of the

alternatives in terms of a third criterion, that we will

refer to as comparison criterion. Even though the val-

ues of the alternatives in terms of the comparison cri-

terion are not changed, and the comparison criterion

should not be directly considered when determining

trade-off values for the response criterion in the cur-

rent iteration, this extra information gives the deci-

sion maker a deeper insight and better understanding

of the consequences of the performed trade-offs. The

comparison criterion is chosen by the decision maker

from the list of non-cancelled criteria. An example of

a non-color-coded and a color-coded plot is given in

Figure 2. The positions of the alternatives are updated

and the plot redrawn each time the decision maker

changes a value in terms of the response criterion of

any of the virtual alternatives. In order for the deci-

sion maker to be able to explore and make judgements

regarding the consequences of a change, the original

positions of alternatives are shown in the plot in light

blue color. This gives the decision maker a better un-

derstanding of not only the magnitude of change re-

sulting from the proposed trade-off values, but even

the distribution of change, i.e. how many alternatives

are affected by the proposed trade-off. By clicking

on and highlighting a point in the plot, the decision

maker gains access to further information about the

selected alternative. A vector representing the magni-

tude of change in terms of the response criterion af-

ter the suggested trade-off is shown in the plot as the

distance between the original and current value (po-

sition), as a complement to the numeric information.

Furthermore, the selected alternative is highlighted in

the map panel, giving the decision maker information

about the position of the alternative in the geographi-

cal space. An example is shown in Figure 3. The part

of the visualization that concerns geographical space

consists of two maps of the geographic area where the

decision problem is situated. The two maps simulta-

neously show color-coding for both response criterion

and comparison criterion (if any). The geographic

distribution of the alternatives in the left map is al-

ways color-coded by values of alternatives in terms of

the response criterion. The color-coding in the right

map is related to the color-coding in the scatterplot,

i.e. it shows the values of the alternatives in terms of

the comparison criterion if there is one selected, and

is not color-coded otherwise. In Figure 3, Discharge

was chosen as comparison criterion.

Visualization of value functions is given in form

of a multi-line chart, with the number of lines de-

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

240

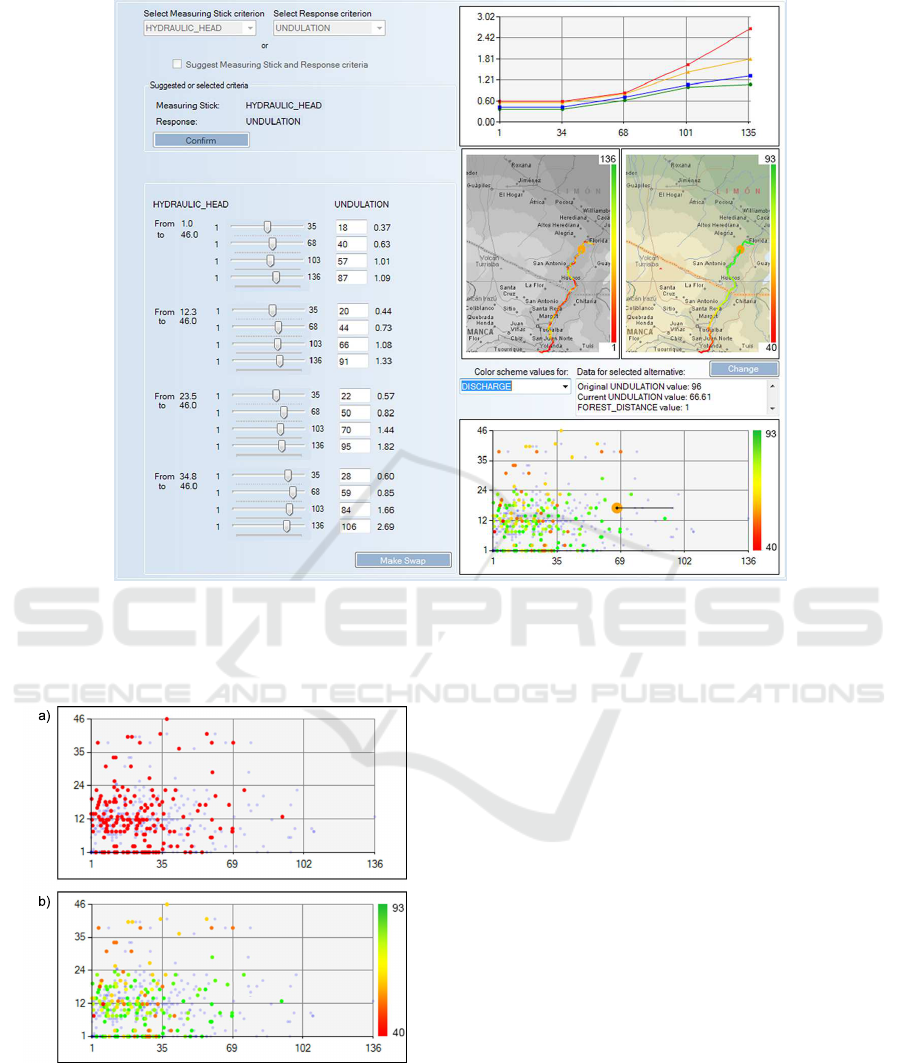
Figure 1: Main window of the application implementing GISwaps and the visualization framework. Adjusting the values in

terms of the response criterion (Undulation, in the example), in order to compensate for the changes made in the reference

criterion (Hydraulic head), is performed in the left panel. The right panel contains attribute space visualization scatterplot

(bottom), geographical space visualization maps (middle), and value functions visualization (top).

Figure 2: Scatterplot for the example decision problem with

no comparison criterion selected (a) and with Discharge se-

lected as the comparison criterion (b).

termined by the number of elements in V

and the

number of points deﬁning each line determined by the

number of elements in V

(see Equation 1 in Section

3.2). An example is given in Figure 4. This visual

representation makes potential deviations in a value

function evident, allowing the decision maker to ad-

just suggested values if the deviationis due to an error,

rather than personal preference and judgement.

5 DISCUSSION AND

CONCLUSIONS

In Keeney and Raiffa (1976), the essence of the is-

sue of trade-offs under certainty is described as “How

much achievement on objective 1 is the decision

maker willing to give up in order to improve achieve-

ment on objective 2 by some ﬁxed amount?”. As the

authors point out, the trade-off issue usually requires

subjective judgement of the decision maker. As a

trade-off method based on even swaps, GISwaps is

an intuitive and efﬁcient tool capable to address one

of the big challenges in the context of decision sup-

port systems, namely, how to handle the preferences

of the decision maker. Instead of being concerned

with the abstract concept of the relative importance of

decision criteria, using GISwaps the decision maker

Visual GISwaps - An Interactive Visualization Framework for Geospatial Decision Making

241

Figure 3: When an alternative is selected, its magnitude of

change is shown, as well as its position in the geographical

space (highlighted in the map panel).

Figure 4: Visualization of value functions. The number of

functions (lines) is determined by the number of elements

in V

works with concrete values and differences, which we

believemakes our method more ﬂexible than the com-

monly used approach of combining weighting and ag-

gregation methods.

Geospatial multi-criteria decision problems tend

to be complex, with a large number of conﬂicting cri-

teria to be taken into consideration, and thousands or

even millions of alternatives to be evaluated and com-

pared. In order for the decision maker to have a good

understanding of the consequences of his/her choices,

numeric data needs to be complemented by a visual

representation of relevant information that would be

unavailable otherwise. In an interactive decision-

making method, this needs to be done at each step

of the decision-making process.

The positiveimpact of the interactivevisualization

presented in this paper is multifaceted:

• The scatterplot representation of the alternatives

in the attribute space gives the decision maker an

insight into the distribution of data in terms of the

currently chosen response criterion. From Figure

2, for example, it is obviousthat only a small num-

ber of alternatives has the undulation value in the

upper half of the range, i.e. over 68.

• It reveals potential outliers. Outliers, both posi-

tive and negative, may have a signiﬁcant impact

on the reliability of the values interpolated from

the values assigned to virtual alternatives; for that

reason, they should not pass unnoticed.

• It gives the decision maker the possibility to get

a closer look at the alternatives of interest. Ex-

tra information available on demand includes the

original value, the current value and the magni-

tude of change in terms of the response criteria,

the value of the alternative in terms of any of the

non-cancelled criteria, and the geographic loca-

tion of the alternative. This information is of great

importance for understanding the impact of a sug-

gested trade-off.

• The map view helps the decision maker make

more sensitive choices. By being able to see the

geographic location of the selected alternative, the

decision maker can, based on his/her knowledge

and preferences, re-evaluate suggested trade-offs

that would affect the alternative(s) of interest.

• Our visualization saves the decision maker time

and effort. The prime assumption for any trade-

off based method for decision making to be suc-

cessful is that the trade-offs are balanced and care-

fully performed. Deciding trade-offvaluesfor vir-

tual alternatives that might not have any impact on

the outcome of the decision process is therefore

better avoided. By means of visual representation

of alternatives in the attribute space, the decision

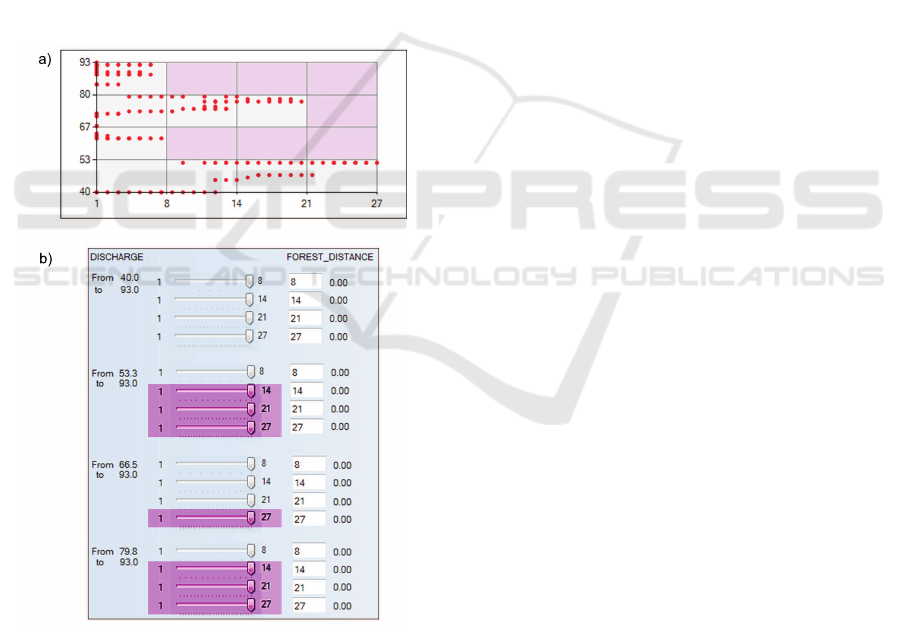
maker can see if there are empty value intervals,

i.e. value ranges with no alternatives. In the ex-

ample in Figure 5, there are seven intervals out

of sixteen with no alternatives. Consequently, it

is unnecessary to decide trade-off values for the

virtual alternatives that deﬁne those intervals.

• It helps the decision maker make consistent trade-

offs. The signiﬁcance of the value functions

chart increases with the number of virtual alter-

natives. In many cases, the decision maker wants

the trade-off values to be consistent over the set of

virtual alternatives. Making consistent trade-offs

based on numeric values only is a demanding task,

and the complexity of the task increases with the

number of virtual alternatives. Visual representa-

tion makes potential deviations in a value function

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

242

evident (see Figure 4; the function represented by

the blue line shows a deviation for x = 27), allow-

ing the decision maker to adjust suggested values

if the deviation is due to an error, rather than per-

sonal preference and judgement.

The GISwaps method and the interactive visualiza-

tion presented here are designed and developed in

close cooperation with experts in multi-criteria deci-

sion making and geographic information systems. At

this point, though, they have not been used by practi-

tioners in the ﬁeld of GIS-MCDM. In a forthcoming

study, the GISwaps method will be evaluated with re-

spect to efﬁciency and usability, in comparison with

the combination of AHP and the weighted summation

method, which is the most commonly used approach

in geospatial decision-making. Based on the results,

a second study will be carried out, where the impact

of the interactive visualization framework presented

in this paper will be evaluated.

Figure 5: a) Empty intervals, i.e. intervals that contain no

alternatives; b) Virtual alternatives for which it is unneces-

sary to set trade-off values, as they deﬁne empty intervals.

REFERENCES

Andrienko, N. and Andrienko, G. (2003). Informed spa-

tial decisions through coordinated views. Information

Visualization, 2(4):270–285.

Andrienko, N. and Andrienko, G. (2004). Interactive visual

tools to explore spatio-temporal variation. Proceed-

ings of the working conference on Advanced visual

interfaces - AVI ’04, page 417.

Andrienko, N., Andrienko, G., and Gatalsky, P. (2003). Ex-

ploratory spatio-temporal visualization: An analytical

review. Journal of Visual Languages and Computing,

14(6):503–541.

Bautista, J. and Carenini, G. (2006). An integrated task-

based framework for the design and evaluation of vi-

sualizations to support preferential choice. Proceed-

ings of the working conference on Advanced visual in-

terfaces - AVI ’06, (February):217.

Carenini, G. and Loyd, J. (2004). Valuecharts: Analyzing

linear models expressing preferences and evaluations.

Proceedings of the working conference on Advanced

visual interfaces - AVI ’04, (February):150.

Chrisman, N. R. (1999). What does ’gis’ mean? Transac-

tions in GIS, 3(2):175–186.

Cowen, D. (1988). Gis versus cad versus dbms: what are the

differences. Photogrammetric Engineering and Re-

mote Sensing, (54):1551–1555.

Hammond, J. S., Keeney, R. L., and Raiffa, H. (1998). Even

swaps: A rational method for making trade-offs. Har-

vard Business Review, 76(2):137–149.

Hammond, J. S., Keeney, R. L., and Raiffa, H. (1999).

Smart Choices - a practical guide to making better

life decisions. Broadway Books, New York, USA, 1st

edition.

Jankowski, P., Andrienko, N., and Andrienko, G. (2001).

Map-centred exploratory approach to multiple criteria

spatial decision making. International Journal of Ge-

ographical Information Science, 15(2):101–127.

Keeney, R. L. and Raiffa, H. (1976). Decisions with Multi-

ple Objectives - Preferences and Value Tradeoffs. John

Wiley & Sons, Inc., USA.

Kollat, J. B. and Reed, P. (2007). A framework for visually

interactive decision-making and design using evolu-

tionary multi-objective optimization (video). Environ-

mental Modelling and Software, 22(12):1691–1704.

Li, H. L. and Ma, L. C. (2008). Visualizing decision process

on spheres based on the even swap concept. Decision

Support Systems, 45(2):354–367.

Malczewski, J. and Rinner, C. (2015). Multicriteria De-

cision Analysis in Geographic Information Science.

Springer, New York, USA.

Miettinen, K. (2014). Survey of methods to visualize alter-

natives in multiple criteria decision making problems.

OR Spectrum, 36(1):3–37.

Milutinovic, G., Ahonen-Jonnart, U., and Seipel, S. (2017).

Giswaps - a new method for decision making in

continuous choice models based on even swaps.

Manuscript submitted for publication.

Simon, H. A. (1960). New science of management decision.

Harper, New York, USA.

Visual GISwaps - An Interactive Visualization Framework for Geospatial Decision Making

243