
Loop-loop Interaction Metrics on RNA Secondary Structures
with Pseudoknots
Michela Quadrini and Emanuela Merelli
University of Camerino, via Madonna delle Carceri, Camerino, Italy
Keywords:
Structure Comparison, RNA Secondary Structures, Interaction Distance, Pseudoknotted Structure, Loop.
Abstract:
Many methods have been proposed in the literature to face the problem of RNA secondary structures compari-
son. From a biological point of view, most of these methods are satisfactory for the comparison of pseudoknot
free secondary structures, whereas the problem of pseudoknotted motifs comparison has not been solved yet.
In this paper, we propose loop-loop interaction metrics, a new measure able to compute the distance of two
pseudoknotted secondary structures by comparing loops and their interactions. The new measure is defined
for RNA molecules whose structural and biological information is represented as algebraic expressions of
hairpin loops, so that each RNA secondary structure can be represented as a word, which describes the in-
teractions among loops and uniquely defines the intersection set, the set of pairs of loops that cross. Hence,
the interaction metrics is defined as the symmetric set difference applied to the intersection sets of molecules.
To illustrate how to apply the proposed methodology, we compare two RNA molecules, PKB66 and PKB10,
extracted from Pseudobase++ database. To test the validity of the measure, we evaluated the evolutionary
conservation of the pseudoknot domain of Vertebrate Telomerase RNA.
1 INTRODUCTION
Ribonucleic acid (RNA) is a linear polymer of nu-
cleotides arranged in a sequence referred to as a pri-
mary structure. This sequence is made of four dif-
ferent types of nucleotides, known as Adenine (A),
Guanine (G), Cytosine (C) and Uracil (U). Such nu-
cleotides are linked together by phosphodiester bonds
in a way that the orientation can be established ac-
cording to the polarity 5
0
to 3
0
of the molecule.
Neutralization of the molecule determines the initial
event of the folding process, which generates com-
plex three-dimensional shapes (Dill, 1990), (Ferr
´
e-
D’Amar
´
e and Doudna, 1999). During such process
each nucleotide can interact at most with one other
nucleotide establishing a hydrogen bond. In this
work, the phosphodiester bond between two consec-
utive nucleotides is referred to as a strong interac-
tion, while the relations dynamically created during
the folding process are called weak interactions. Both
interactions are chemical bonds: the latter, in con-
trast to the former, are weak bonds that can be eas-
ily broken, and their formation is subject to restric-
tions. In fact, each nucleotide can form a base pair by
interacting with another one performing the Watson-
Crick base pairs (G-C and A-U) and wobble base
pairs (G-U). In 2−dimensions, the folding process
can perform many RNA secondary structures; it de-
pends on the free energy of RNA configurations. The
RNA secondary structure is composed of five basic
structural elements namely hairpins, bulges, internal
loops, multi-loops and helixes (or stacks). Each struc-
tural element is generated when at least one base pair
is performed. Thus, each of them is characterized by
strong and weak interactions. We can observe that
each structure element performs a loop, therefore sec-
ondary structures are composed of loops. If no inter-
action among loops is present, the secondary structure
is pseudoknot free, as illustrated in Figure 1 (A), oth-
erwise it is pseudoknotted, as depicted in Figure 1 (B).
Pseudoknots are tertiary structures that occur
widely in RNA and they play a multitude of roles
in the cell (Staple and Butcher, 2005), including
the catalysis of various ribozymes (Rastogi et al.,
1996), and the alteration of gene expression by induc-
ing ribosomal frameshifting in many viruses (Shen
and Jr, 1995). The biological functions of an RNA
molecule depend on its structure (Laskowski and
Thornton, 2008). The presumption is that to a pre-
served function corresponds a preserved configura-
tion. In other words, the molecule cannot sustain
substantial changes to its secondary and tertiary struc-
Quadrini, M. and Merelli, E.
Loop-loop Interaction Metrics on RNA Secondary Structures with Pseudoknots.
DOI: 10.5220/0006610700290037
In Proceedings of the 11th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2018) - Volume 3: BIOINFORMATICS, pages 29-37
ISBN: 978-989-758-280-6
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
29
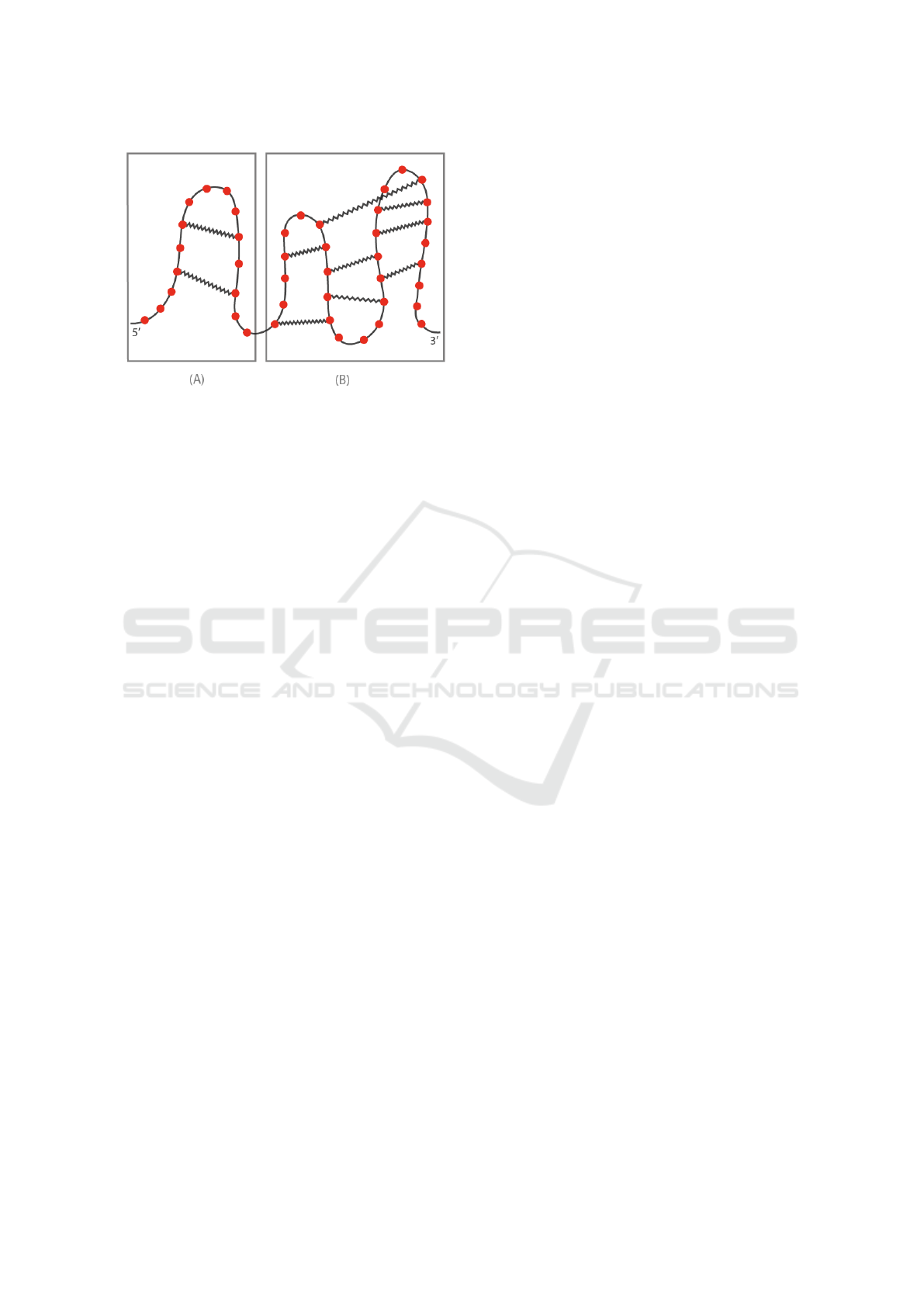
Figure 1: RNA secondary structure.
ture to preserve a particular function. Therefore, the
structure comparison is used in the classification of
RNA molecules, the prediction of the folding process
and the measurement of the evolution stability. The
comparison of RNA secondary structures is one of
the main basic computational problems regarding the
study of RNAs. In literature, many approaches have
been proposed for facing this problem. One of them
consists in the ordered trees comparison, but it works
only for RNA pseudoknot free structures, since only
this type of structure can be mapped into an ordered
tree. The method for ordered trees comparison can be
generally classified into two categories: tree edition
and tree alignment (Herrbach et al., 2010). Both are
based on the edit operations on nodes, i.e., node sub-
stitution, node insertion, and node delation. For each
operation, a cost is associated. Thus, given two trees,
through a sequence of edit operations, one changes
into the other associating a cost which is given by
the sum of the cost of each operation. In contrast to
sequences, the alignment and edition model are not
equivalent for trees. In fact, tree edition consists in
constructing a common supertree, while tree align-
ment permits to find the common subtree. Which
model is favourable depends on the biological prob-
lem of interest. It is trivial to observe that the edi-
tion problem is useful to identify the conserved struc-
tures during the folding process, while the alignment
is suitable for clustering RNA molecules purely on
the structure level. The problem of pseudoknotted
motifs comparison has not been solved yet. Only
few algorithms have been developed for studying spe-
cific cases of pseudoknots: the progress in this field
has been hindered by the complexity of the prob-
lem. From an algorithmic perspective, the problem
of comparing RNA structures is usually formalized as
the comparison of arc-annotated sequences featuring
crossing interactions. An arc-annotated sequence is
a sequence over a given alphabet, together with ad-
ditional structural information specified by arcs con-
necting pairs of positions. The problem of comput-
ing a distance between two arc-annotated sequences
was introduced in (Evans, 1999) with a model that
used only three edit operations either on single nu-
cleotides or base pairs: it has been proved by (Blin
and Touzet, 2006) that such a problem is NP-hard.
Thus, a new representation of RNA secondary struc-
tures and a new approach for their comparison are
necessary.
In this paper, we define a new measure, loop-loop
interaction metrics, able to compute the distance of
two pseudoknotted secondary structures in terms of
interactions among loops. In particular, we use an
algebraical representation of RNA secondary struc-
tures, both pseudoknot free and pseudoknotted, re-
cently introduced by (Quadrini et al., 2017), that al-
lows us to represent each RNA secondary structure as
an algebraic composition of hairpins. In our model,
the hairpin is the basic loop of such representation.
Firstly, starting from such algebraic expression, we
design an appropriate procedure to obtain the abstract
algebraic expression of the structure, which allows us
to define a proper set of functions for associating a
word to each RNA secondary structure. The word
permits the identification of interactions among loops
and to define a unique set, intersection set. Such set is
composed of all the pairs of loops that cross together.
Finally, interaction metrics is defined as the symmet-
ric set difference applied to the sets which identifies
the crossing among loops. For illustrating in detail
an application of our approach, it is applied over two
RNA molecules, PKB66 and PKB10, extracted from
Pseudobase++ database. To test the measure, we eval-
uated the evolutionary conservation of the pseudoknot
domain of Vertebrate Telomerase RNA. The most fea-
tured of this structure is the evolutionary conservation
of four structural domains: the pseudoknot domain,
the CR4-CR5 domain, the Box H/ACA domain and
the CR7 domain (Chen et al., 2000).
The paper is organized as follows. In Section
2, we present related works regarding the RNA sec-
ondary structure comparison. The measure of RNA
secondary structures with pseudoknots, that we pro-
pose, is introduced in Section 3, which in turn is or-
ganized into three subsections. In the first subsection,
we report an algebraic expression of RNA secondary
structures in terms of hairpins. In the second, start-
ing from the defined algebraic expression, we intro-
duce an appropriate procedure to obtain the abstract
algebraic expression of the structure. Moreover, a set
of functions able to associate a unique word to each
abstract algebraic expression is also defined in this
subsection. In the last subsection, the measure is de-
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
30

scribed and an example of its application is shown.
The results and some critical considerations are dis-
cussed in Section 4. The paper closes with some con-
clusions and future work in Section 5.
2 RELATED WORKS
The structure of a molecule provides a framework
for its biological functions (Laskowski and Thornton,
2008). Thus, the knowledge of structures is very im-
portant and the ability to compare them is useful in the
study of the function and evolution of RNA. In the
literature, there are several approaches to represent
RNA secondary structures which consist of formal-
izing them in terms of base pair sets, trees, graphs or
diagram representations. As a consequence, several
approaches have been proposed for RNA secondary
structure comparisons and corresponding similarity
measurements. The simplest comparison metric is the
base pair distance (Ding et al., 2005), which gives us
the number of different base pairs between two struc-
tures. Other approaches are also possible, such as the
symmetric set difference, the Hausdorff distance, and
the mountain metric (Moulton et al., 2000).
For comparing structures using tree representa-
tion, a classical approach is to first define a set of basic
and atomic operations, called edit operations, that al-
low to change a structure into another. The methods
for ordered tree comparisons can be generally classi-
fied into two categories: tree edition and tree align-
ment (Herrbach et al., 2010). In terms of alignment, a
wide amount of algorithms based on tree comparisons
have been designed (Shapiro, 1988), (Le et al., 1989),
(Corpet and Michot, 1994). In addition, several tree
edit distance metrics have been developed (Shapiro
and Zhang, 1990), (Moulton et al., 2000), (Dulucq
and Tichit, 2003). However, these approaches are not
able to take into account the pseudoknotted RNA sec-
ondary structures. Mohl et al. (M
¨
ohl et al., 2010) de-
veloped a type system for decompositions. The main
idea is that the scheme of a folding algorithm can be
transformed into a dynamic-programming algorithm
for the alignment. Rastegari and Condon in their work
(Rastegari and Condon, 2007) proposed a meta algo-
rithm, which starts by determining the class of each
structure, and then selects a suitable dynamic pro-
gramming algorithm. Song et al. (Song et al., 2015)
introduced a method for aligning two known RNA
secondary structures with pseudoknots based on the
partition function to calculate the scores of the align-
ments between bases or base pairs of the two RNAs
with a dynamic programming algorithm. Moreover,
Evans (Evans, 2011) in her work proposed a polyno-
mial time algorithm for finding common RNA sub-
structures that include pseudoknots.
3 MATERIAL AND METHODS
The new measure of RNA secondary structures with
pseudoknots, that we propose, permits us to compare
this kind of RNA structures in terms of interaction
among loops. To define it, we use the algebraic ex-
pression, introduced by (Quadrini et al., 2017). Such
algebraic expression is obtained from an appropri-
ate operator able to model interactions among loops
and the relative translation into a multiple context-
free grammar. These two concepts are reintroduced
in Section 3.1. For more details, the interested read-
ers can refer to (Quadrini et al., 2017). Starting from
this algebraic expression, we obtain its abstract alge-
braic expression through the definition of an appropri-
ate procedure in Section 3.2. Moreover, in the same
section, we also introduce a set of functions able to
associate a unique word to each abstract algebraic ex-
pression. This word permits us to design another pro-
cedure to identify interactions among loops and to de-
fine a set, where elements are pairs that represent two
crossing loops. In Section 3.3, the new measure is
introduced.
3.1 Algebraic Expression for RNA
Secondary Structures
Each RNA secondary structure is composed of loops,
which can be formalized by the operator 1
k
. The op-
erator maps two arc diagrams into another one, mod-
eling each interaction among loops. It depends on
a non-negative integer parameter, k, which indicates
that the resulting structure is obtained by attaching
the second arc diagram on the k−th nucleotides of
the first one. The operator is well-defined if each
nucleotide of the resulting structure performs at most
one weak interaction. This restriction is due to the na-
ture of RNA molecules. In other words, the situation
illustrated in Figure 2 has to be excluded.
Figure 2: Not permitted structure.
It is also well-defined if the two structures do not
share nucleotides, i.e., the first arc diagram is fol-
lowed by the second one. In other words, the two
structures are concatenated, as shown in Figure 3.
Formally, it is obtained when k is equal to 0.
Loop-loop Interaction Metrics on RNA Secondary Structures with Pseudoknots
31

Figure 3: Concatenation of loops.
Algebraically, ha
s
1
,a
s
N
i[ α ] represents an RNA sec-
ondary structure. More specifically, α is the se-
quence of nucleotides (backbone) enclosed by the
pseudoweak interaction, a fictitious weak interaction,
between the first nucleotide, a
1
, and the last one, a
N
,
identified by pair ha
s
1
,a
s
N
i. See Figure 4 (A) for an il-
lustration. Note that the molecule in Figure 4 (B) is a
special case of an RNA secondary structure, referred
to as a pseudoloop in this paper. It is an RNA sec-
ondary structure without head and tail. Algebraically,
each nucleotide that performs a weak interaction with
another one is represented by symbol ], while the un-
paired nucleotides are indicated by ε.
Figure 4: An example of secondary structure (A) and pseu-
doloop (B).
An example of the crossing operator application
is illustrated in Figure 5. The second arc diagram is
attached to the fifth nucleotide of the first arc diagram.
Figure 5: Example of a crossing operator application.
Formally, let S
1
and S
2
be two struc-
tures, where S
1
= (a
s
1
,a
s
N
)ha
s
2
...a
s
N−1
i and
S
2
= (b
s
1
,b
s
M
)hb
s
2
.. .b
s
M−1
i, the resulting structure,
S
1
1
k
S
2
, is well defined if
k = 0, s ∈ {ε,]}
S
1
1
k
S
2
→ (a
s
1
,b
s
M
)h a
s
2
.. .a
s
N−1
a
s
N
b
s
1
.. .b
s
M−1
i
k ≤N,s ∈{ε, ]},((b
1
= a
k
) ∧BC),
((b
2
= a
k+1
) ∧BC), .. ., ((b
N−k
= a
N
) ∧BC)
S
1
1
k
S
2
→(a
s
1
,b
s
M
)h a
s
2
.. .b
s
1
.. .b
s
N−k
b
s
N−k+1
.. .b
s
M−1
i
where BC expresses the biological constraint, i.e.
each nucleotide performs at most one weak interac-
tion, and it is formalized as follows:
BC : (s = ε, (¯s = ε ∨ ¯s = ])) ∨(s = ], ¯s = ε) .
This operator is translated into a Multiple Context-
Free Grammar (MCFG), introduced in (Seki et al.,
1991). This choice is due to the inadequacy of a
Context-Free Grammar to describe the crossing de-
pendence of pseudoknots; it can be proved by apply-
ing Ogdens Lemma (Harrison, 1978). Thus, a more
expressive grammar is required.
Let Σ
RNA
= {A,U,G,C} be the alpha-
bet of RNA nucleotides, and let Σ
RNA
=
{(A,U ), (U,A), (G,C),(C, G),(G,U),(U,G)} be
the alphabet of weak interactions, whose elements
represent Watson-Crick or wobble base pairs. The
first entry of each pair is the first nucleotide of the
hydrogen bond, whereas the second one represents
the corresponding complementary base pair. In
other words, the nucleotides are identified by left,
π
1
(a
1
,a
2
) = a
1
, and right, π
2
(a
1
,a
2
) = a
2
, which are
canonical projection functions of the ordered pair.
The grammar utilised is G
RNA
= (V
N
,V
T
,R, S, F),
where V
N
= {S,P,L}, V
T
= Σ
RNA
∪Σ
RNA
∪{[ , ]},
F = {f
(1,k)
} is the set of partial functions, and the set
of productions R is defined as follows:
S ::= αPα RNA secondary structure
P ::= f
(1,0)
JPα,LK Concatenation
| f
(1,k)
JP,LK Nesting or Crossing
| L Hairpin
L ::= x[α
+
]
where x ∈Σ
RNA
, α ∈ Σ
∗
RNA
and
f
(1,k)
JS, LK =
S 1
k
L if 1
k
is defined;
unde f ined otherwise.
Such multiple context-free grammar G
RNA
gener-
ates uniquely all RNA secondary structures; as a con-
sequence, each secondary structure can be uniquely
decomposed in terms of a particular loop, i.e., hairpin.
The start symbol, S, represents any RNA secondary
structure. The first production of the grammar formal-
izes the concatenation between an RNA pseudoloop
P followed by a sequence of nucleotides α, eventu-
ally empty, and a loop L, whereas the second one rep-
resents both the crossing and the nesting between a
pseudoloop P and a loop L. Finally, production P →L
generates a loop. Each loop L is a hairpin, L →x[α
+
],
i.e., a Watson-Crick or a wobble base pair encloses a
sequence of unpaired nucleotides, α
+
. For illustring
an example, we take into account the structure PKB66
obtained from Pseudobase++ database (Taufer et al.,
2008) illustrated in Figure 6.
Figure 6: The diagram of PKB66 molecule extracted from
Pseudobase++ database (Taufer et al., 2008).
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
32

It is a pseudoknot of SELEX-isolated inhibitor of
HIV-1 reverse transcriptase (Burke et al., 1996). The
head and the tail of the structure are α
1
= CAAGAAC
and α
10
= ACCA, respectively. The initial pseudoloop
involves nucleotides from the 8-th to the 36-th. The
pseudoloop is composed of crossings among weak in-
teractions. Such crossings will be formalized making
explicit hairpins. The order of choice of hairpins is
well determined and such a choice depends on the
complementary nucleotides of base pairs. In partic-
ular, the hairpin of the pseudoloop having the left-
most complementary nucleotides is selected. Thus,
the first selected hairpin is x
8
[α
9
] where x
8
= (G,C)
and α
9
= GGUGAGAACCGAGACAAACACC. In this
way, the reduced pseudoloop involves nucleotides
from the 8-th to the 35-th. In the following step, the
hairpin x
7
[α
8
] has been explicited, where x
7
= (G,C)
and α
8
= GUGAGAACCGAGACAAACAC. Moreover,
each time that a hairpin is added it is necessary to for-
malize in which nucleotide of the relative pseudoloop
the hairpin is attached. Thus, the algebraic expression
of the structure is
S = α
1
x
1
[α
2
] 1
2
x
2
[α
3
] 1
3
x
3
[α
4
] 1
6
x
4
[α
5
] 1
7
x
5
[α
6
]
1
8
x
6
[α
7
] 1
9
x
7
[α
8
] 1
10
x
8
[α
9
]α
10
(1)
where
α
1
=CAAGAAC
α
2
=GGACGGGUGAGAACC x
1
=(C, G)
α
3
=GACGGGUGAGAAC x
2
=(G,C)
α
4
=ACGGGUGAGAA x
3
=(G,C)
α
5
=AGAACCGAGACAAA x
4
=(G,C)
α
6
=GAGAACCGAGACAAAC x
5
=(G,C)
α
7
=U GAGAACCGAGACAAACA x
6
=(G,C)
α
8
=GUGAGAACCGAGACAAACAC x
7
=(U, A)
α
9
=GGUGAGAACCGAGACAAACACC x
8
=(G,C)
α
10
=ACCA
3.2 From the Algebraic Structure to the
Intersection Set
The grammar, introduced in Section 3.1, permits the
association of a unique algebraic expression for each
RNA secondary structure in terms of hairpins. Such
an algebraic expression contains the structural and bi-
ological information of the molecule. For each al-
gebraic expression, it is possible to associate an ab-
stract expression obtained by the first one by remov-
ing the nucleotides and introducing the position of the
weak interaction into the structure. More specifically,
each weak interaction divides the backbone into three
parts, as illustrated in Figure 7, which are enumerated
from left to right starting from 0.
For each algebraic expression
S = αx[α
+
] 1
k
x[α
+
] 1
k
··· 1
k
x[α
+
]α
Figure 7: Backbone divided by an arc.
by applying the procedure of Abstract Algebraic Ex-
pression, the abstract algebraic expression is ob-
tained. In other words, such procedure takes in in-
put the algebraic expression of an RNA molecule ob-
tained from the multiple context free grammar and re-
turns another algebraic expression,
S
0
= L 1
t
L 1
t
··· 1
t
L
Note that t is a non-negative integer that represents
the part of the backbone which the successive loop is
attached to. Thus, the operator 1
t
is different from
the initial crossing operator: the initial one depends
on nucleotides, whereas the second one depends on
the part of the backbone. We decided to maintain the
same symbol in order to not overload the notation.
Data: Algebraic Expression of RNA
Secondary Structure
Result: Abstract Algebraic Expression
N is the number of loops;
Let α
1
be the length of L
1
;
Let d the length P
1
−α
1
;
for i = 2 to N −1 do
Compute P
i
;
s = 0 ;
while s ≤i do
if k
i−1
= 0 then
t = 2(i −1) ;
else if k
i−1
< P
1+s
then
if k
i−1
> d then
for j = 1 to i −1 do
if k
i−1
≤ k
j
then
t = j + s ;
end
end
end
else
s = s + 1 ;
end
end
end
Algorithm 1: Abstract Algebraic Expression.
We take into account RNA molecule PKB66 in-
troduced before and illustrated in Figure 6. Start-
ing from its algebraic expression (1) and applying the
procedure of Abstract Algebraic Expression, the rel-
ative abstract algebraic expression of the considered
Loop-loop Interaction Metrics on RNA Secondary Structures with Pseudoknots
33

molecule is obtained. It is
S
0
= L
1
1
0
L
2
1
0
L
3
1
3
L
4
1
3
L
5
1
3
L
6
1
3
L
7
1
3
L
8
(2)
Let S
A
be the set of abstract algebraic expressions.
Let E : S
A
→ W
S
be a rewriting rule that associates
to each abstract expression another expression. Each
loop is indicated by its starting , x
i
, and final, x
i
points,
and a ∧
k
is associated to each 1
k
. Note that the non-
negative integer parameter k is the same for both ex-
pressions.
EJL
i
1
k
SK =
EJL
i
KEJ1
k
KEJSK if S = L
j
∨
S = L
j
1
k
S
⊥ otherwise.
EJL
i
K = x
i
x
i
i ∈ N
EJ1
k
K = ∧
k
k ∈N
Let F : W
S
→ w be a rewriting rule that for each ele-
ment of W
S
associates a word that identifies uniquely
the structure in terms of initial and final points of
loops.
F Jω ∧
k
x
j
x
i
K =
w
1
.. .w
k−1
x
j
w
k+1
.. .w
N
x
i
if length(ω) > k
⊥ otherwise.
F Jω ∧
k
x
j
x
i
∧
k
0
x
s
x
s
K =
F Jω
0
∧
k
0
x
s
x
s
K if ω
0
= F Jω ∧
k
x
j
x
i
K
⊥ otherwise.
For illustrating an application of the previous rewrit-
ing rules, we again consider the molecule PKB66.
Applying the rewriting rule E to the Abstract Alge-
braic Expression 2, the following term is obtained
ω
A
= x
1
x
1
∧
0
x
2
x
2
∧
0
x
3
x
3
∧
3
x
4
x
4
∧
3
x
5
x
5
∧
3
x
6
x
6
∧
3
x
7
x
7
∧
3
x
8
x
8
(3)
Applying the rewriting rule F to previous term, we
have
w = x
1
x
2
x
3
x
8
x
7
x
6
x
5
x
4
x
1
x
2
x
3
x
4
x
5
x
6
x
7
x
8
(4)
For each word by applying the following procedure,
the intersection Loop Set, the Intersection set is ob-
tained. Such set is composed of all the pairs of loops
that cross together.
The intersection set of the considered structure, ob-
tained applying the previous algorithm, illustrated in
Figure 6 is
V = {(L
1
,L
4
),(L
1
,L
5
),(L
1
,L
6
),(L
1
,L
7
),(L
1
,L
8
),
(L
2
,L
4
),(L
2
,L
5
),(L
2
,L
6
),(L
2
,L
7
),(L
2
,L
8
),
(L
3
,L
4
),(L
3
,L
5
),(L
3
,L
6
),(L
3
,L
7
),(L
3
,L
8
)}
Data: w, word associated to RNA secondary
strucuture
Result: Intersection set associated to the
structure
N is the number of loops;
for i = 1 to N do
Select x
i
and x
i
;
w
i
is the subword from x
i
to x
i
;
M
i
is the length of w
i
;
V = V ∪{L
i
} ;
for j = 1 to M
i
do
Select w
i
[ j] = a
j
;
if a
j
= x
k
and x
k
is an element of w
i
then
else
V = V ∪{L
k
} ;
end
end
end
Algorithm 2: Intersection Loops Set.
3.3 A Measure for Comparing RNA
Secondary Structure
Each RNA secondary structure can be represented as
an algebraic composition of hairpins, considered as
basic loops. The new measure, that we propose, is
based on the interactions among loops. Let S
1
and S
2
be two RNA secondary structures with pseudoknots.
Let V
1
and V
2
be the respective intersection sets ob-
tained applying the methodology introduced in Sec-
tion 3.2. Each element of the two sets represents an
interaction between two loops. For example, if the
pair (L
1
,L
2
) is an element of V
1
, it means that L
1
and
L
2
are two loops of structure S
1
and they cross each
other. Thus, two structures can be compared taking
advantage of the set theory. Many methods have been
proposed in literature. In this case, the symmetric set
difference is a good first approach to evaluate the dif-
ference of structures.
Definition 1: The interaction metrics d
I
is the car-
dinality of the symmetrics difference between the sets
of interaction among loops V
1
and V
2
,
d
I
(V
1
,V
2
) = |(V
1
\V
2
) ∪(V
2
\V
1
)|
where V
1
and V
2
are the intersection sets of structure
S
1
and S
2
, respectively. Note that A \B is the set
of all elements that are in A, but not in B. Hence,
we count the crossings present in either of the struc-
tures, but not in both. This interaction loop distance
is a metric. This metric is very strict: all differences
have the same weight. It does not take into account
the backbone of the two structures. For illustating an
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
34

Figure 8: The diagram of PKB66 molecule extracted from
(Taufer et al., 2008).
application of the proposed measure, we consider as
examples two structures, S
1
and S
2
. Let S
1
be PKB66
molecule illustrated in Figure 6 and let S
2
be PKB10
molecule illustrated in Figure 8. It is tRNA-like struc-
ture 3’end pseudoknot of ononis yellow mosaic virus.
Its intersection loops set is
V
2
= {(L
1
,L
4
),(L
1
,L
5
),(L
1
,L
6
),(L
1
,L
7
),(L
1
,L
8
),
(L
1
,L
9
),(L
2
,L
4
),(L
2
,L
5
),(L
2
,L
6
),(L
2
,L
7
),
(L
2
,L
8
),(L
2
,L
9
),(L
3
,L
4
),(L
3
,L
5
),(L
3
,L
6
),
(L
3
,L
7
),(L
3
,L
8
),(L
3
,L
9
)}
The distance in terms of interaction among loops of
the two considered structure is d
I
(V,V
2
) = 3. In fact,
the cardinality of the difference between V and V
2
is
0 since each element of V is also in V
2
, vice versa
the cardinality of V
2
\V is 3 because of three pairs,
(L
1
,L
9
),(L
2
,L
9
),(L
3
,L
9
), are elements of V
2
, but they
are not in V .
4 RESULTS AND DISCUSSIONS
In this paper, we introduced a measure able to com-
pare RNA secondary structures in terms of interac-
tions among loops. In order to test the measure,
we evaluated the evolutionary conservation of the
pseudoknot domain of Vertebrate Telomerase RNA.
Telomerase is a ribonucleoprotein enzyme that main-
tains telomere length by adding telomeric sequence
repeats onto chromosome ends. The essential RNA
component of telomerase provides the template for
secondary structure of telomeric repeat synthesis. The
most featured Vertebrate Telomerase RNA is the evo-
lutionary conservation of four structural domains: the
pseudoknot domain, the CR4-CR5 domain, the Box
H/ACA domain and the CR7 domain (Chen et al.,
2000). Applying the proposed methodology to the
two pseudoknots, the distance is
d
I
(V
H
,V
S
) = 0
where V
H
and V
S
are the intersection sets of the
two pseudoknots domains of human and sharpnose
shark telomerase RNAs, respectively. The result,
d
I
(V
H
,V
S
) = 0, shows that each interaction between
loops belongs to both molecules. As consequences,
the structure is conserved in accordance to the results
present in the literature (Chen et al., 2000). Moreover,
this measure, able to capture the interactions between
loops, can be also applied to classify the molecules.
Although two molecules of each pair are character-
ized by a functional similarity, the interaction among
loops can differ. For example, we take into account a
pair of molecules, extracted from (Taufer et al., 2008),
that involves structural elements for translation initia-
tion and ribosome recruitment found in the viral inter-
nal ribosome entry site (PKB223) and the V4 domain
of 18S rRNA (PKB205) (Pasquali et al., 2005). Ap-
plying the proposed methodology to the two pseudo-
knots, the distance d
I
(V
PKB223
,V
PKB205
) = 24, where
V
PKB223
and V
PKB205
are the intersection sets of the
PKB223 and PKB205 molecules, respectively. This
information can be considered as a structural con-
strain to guide the secondary structure folding. In
fact, the biological presumption is that the RNA struc-
ture folds hierarchically. During the folding pro-
cess, pseudoknot free structures are initially formed,
whereas pseudoknots motifs are generated later to
minimize the energy. Thus, a classification of the
structures is useful to understand or classify how the
structure evolves. Moreover, the measure can be also
used to detect a mutation. At a structural level, the
measure is able to capture the interactions between
the loops. Each interaction between two loops is de-
termined by a crossing of two base pairs. Taking the
crossing among base pairs in consideration permits to
define a more precise energy function than the stan-
dard one (Vernizzi et al., 2016).
The introduced measure is obtained taking advan-
tage of the set theory. In particular, the symmetric dif-
ference of sets has been used. Other similarity func-
tions can be applied to reach a more accurate measure
based on interactions among loops. A list of useble
similitarity functions is reported in Table 1.
Table 1: Similarity functions over two set X and Y .
Similarity Functions Definition
Intersection S
B
(X,Y )= |X ∩Y|
Cosine S
C
(X,Y )=
|X∩Y |
√
|X||Y |
Dice S
D
(X,Y )=
2|X∩Y |
|X|+|Y |
Hamming S
H
(X,Y )= |(X ∩Y )∪(X ∪Y )
C
|
Jaccard S
J
(X,Y )=
|X∩Y |
|(X∪Y )
From an algorithmic point of view, for each RNA
molecule, in order to define the measure, we obtained
a word that uniquely represents the secondary struc-
ture. Over this word, it is possible to define a set of
rewriting rules that permits us to obtain the shape of
Loop-loop Interaction Metrics on RNA Secondary Structures with Pseudoknots
35

each molecule. The shape is a topological concept
widely used by Bon (Bon et al., 2008) and Reydis et
al. (Reidys et al., 2011). Moreover, it is also pos-
sible to define an algorithm to compute some topo-
logical invariants, such as genus and crossing num-
ber (Vernizzi et al., 2016). Another possible proce-
dure over the word can be easily defined to detect
whether or not a pseudoknot belongs to a given class.
Understanding if two structures are characterized by
the same pseudoknots is useful for the choice of the
particular algorithm for comparing the two structures
taking into account the biological relevant operations
such as addition, deletion, and substitution of nu-
cleotides or base pairs.
5 CONCLUSIONS
The biological function of an RNA molecule depends
on its structure. As a consequence, the molecule can-
not sustain substantial changes to its secondary and
tertiary structures to preserve the particular function.
Thus, the knowledge of the structure is very important
and the ability to compare the RNA structure motifs
supports the study of function and evolution of RNA.
In this paper, we proposed a measure to compare
RNA secondary structures with pseudoknots in terms
of interactions among loops. From a biological point
of view, it is useful to identify the conserved struc-
tures during the evolution since its primary structure
is often unpreserved. In fact, this measure is able to
detect the global properties of the molecules taking
advantage of the set theory. Consequently, a bene-
fit is that it can be computed quickly. Its properties
make the measure easy to be handled theoretically. A
statistical study over a large set of molecules can be
performed in order to determine a new clusterization.
This clusterization can be compared with others taken
from differnt approaches present in the literature.
We plan to improve the developed software that
implements the measure and the whole methodology
presented in this paper in order to investigate and an-
alyze in statistical terms the correlations between the
proposed measure and the functions of RNAs. More-
over, we plan to evaluate the five similarity func-
tions in order to classify the performance of the dif-
ferent similarity functions as measured. For reach-
ing the goals, we have decided to compare molecules
extracted from the Rfam (Nawrocki et al., 2015)
database. This database classifies non-coding RNAs
in families whose member posses a similar secondary
structure, suggesting evolutionary relationships and
similar functions. Moreover, this database provides
a consensus secondary structure for each family.
ACKNOWLEDGEMENTS
We acknowledge the financial support of the Fu-
ture and Emerging Technologies (FET) programme
within the Seventh Framework Programme (FP7)
for Research of the European Commission, un-
der the FET-Proactive grant agreement TOPDRIM
(www.topdrim.eu), number FP7-ICT- 318121.
REFERENCES
Blin, G. and Touzet, H. (2006). How to compare arc-
annotated sequences: The alignment hierarchy. In In-
ternational Symposium on String Processing and In-
formation Retrieval, pages 291–303. Springer.
Bon, M., Vernizzi, G., Orland, H., and Zee, A. (2008).
Topological classification of RNA structures. Journal
of molecular biology, 379(4):900–911.
Burke, D. H., Scates, L., Andrews, K., and Gold, L. (1996).
Bent pseudoknots and novel rna inhibitors of type 1
human immunodeficiency virus (hiv-1) reverse tran-
scriptase. Journal of molecular biology, 264(4):650–
666.
Chen, J.-L., Blasco, M. A., and Greider, C. W. (2000). Sec-
ondary structure of vertebrate telomerase rna. Cell,
100(5):503 – 514.
Corpet, F. and Michot, B. (1994). Rnalign program: align-
ment of rna sequences using both primary and sec-
ondary structures. Computer applications in the bio-
sciences: CABIOS, 10(4):389–399.
Dill, K. (1990). Dominant forces in protein folding. Bio-
chemistry, 29(31):7133–55.
Ding, Y., Chan, C. Y., and Lawrence, C. E. (2005). Rna
secondary structure prediction by centroids in a boltz-
mann weighted ensemble. Rna, 11(8):1157–1166.
Dulucq, S. and Tichit, L. (2003). Rna secondary structure
comparison: exact analysis of the zhang–shasha tree
edit algorithm. Theoretical Computer Science, 306(1-
3):471–484.
Evans, P. (1999). Algorithms and Complexity for Anno-
tated Sequences Analysis. PhD thesis, University of
Victoria.
Evans, P. A. (2011). Finding common rna pseudoknot struc-
tures in polynomial time. Journal of Discrete Algo-
rithms, 9(4):335 – 343.
Ferr
´
e-D’Amar
´
e, A. and Doudna, J. (1999). Rna folds: in-
sights from recent crystal structures. Annual review of
biophysics and biomolecular structure, 28(1):57–73.
Harrison, M. A. (1978). Introduction to formal language
theory. Addison-Wesley Longman Publishing Co.,
Inc.
Herrbach, C., Denise, A., and Dulucq, S. (2010). Av-
erage complexity of the jiang–wang–zhang pairwise
tree alignment algorithm and of a rna secondary struc-
ture alignment algorithm. Theoretical Computer Sci-
ence, 411(26):2423–2432.
BIOINFORMATICS 2018 - 9th International Conference on Bioinformatics Models, Methods and Algorithms
36

Laskowski, R. and Thornton, J. (2008). Understanding the
molecular machinery of genetics through 3D struc-
tures. Nature Reviews Genetics, 9(2):41–151.
Le, S.-Y., Owens, J., Nussinov, R., Chen, J.-H., Shapiro,
B., and Maizel, J. V. (1989). Rna secondary struc-
tures: comparison and determination of frequently re-
curring substructures by consensus. Bioinformatics,
5(3):205–210.
M
¨
ohl, M., Will, S., and Backofen, R. (2010). Lifting pre-
diction to alignment of rna pseudoknots. Journal of
Computational Biology, 17(3):429–442.
Moulton, V., Zuker, M., Steel, M., Pointon, R., and Penny,
D. (2000). Metrics on rna secondary structures. Jour-
nal of Computational Biology, 7(1-2):277–292.
Nawrocki, E. P., Burge, S. W., Bateman, A., Daub, J., Eber-
hardt, R. Y., Eddy, S. R., Floden, E. W., Gardner, P. P.,
Jones, T. A., Tate, J., and Finn, R. D. (2015). Rfam
12.0: updates to the rna families database. Nucleic
Acids Research, 43(D1):D130–D137.
Pasquali, S., Gan, H. H., and Schlick, T. (2005). Modu-
lar rna architecture revealed by computational analysis
of existing pseudoknots and ribosomal rnas. Nucleic
Acids Research, 33(4):1384–1398.
Quadrini, M., Culmone, R., and Merelli, E. (2017). Topo-
logical classification of rna structures via intersec-
tion graph. Accepted to 6th International Confer-
ence on the Theory and Practice of Natural Computing
(TPNC).
Rastegari, B. and Condon, A. (2007). Parsing nucleic
acid pseudoknotted secondary structure: algorithm
and applications. Journal of computational biology,
14(1):16–32.
Rastogi, T., Beattie, T. L., Olive, J. E., and Collins, R. A.
(1996). A long-range pseudoknot is required for ac-
tivity of the neurospora vs ribozyme. The EMBO jour-
nal, 15(11):2820.
Reidys, C. M., Huang, F., Andersen, J. E., Penner, R. C.,
Stadler, P. F., and Nebel, M. E. (2011). Topology
and prediction of rna pseudoknots. Bioinformatics,
27(8):1076–1085.
Seki, H., Matsumura, T., Fujii, M., and Kasami, T. (1991).
On multiple context-free grammars. Theoretical Com-
puter Science, 88(2):191–229.
Shapiro, B. A. (1988). An algorithm for comparing multiple
rna secondary structures. Computer applications in
the biosciences: CABIOS, 4(3):387–393.
Shapiro, B. A. and Zhang, K. (1990). Comparing multi-
ple rna secondary structures using tree comparisons.
Bioinformatics, 6(4):309–318.
Shen, L. X. and Jr, I. T. (1995). The structure of an rna pseu-
doknot that causes efficient frameshifting in mouse
mammary tumor virus. Journal of molecular biology,
247(5):963–978.
Song, Y., Hua, L., Shapiro, B. A., and Wang, J. T. (2015).
Effective alignment of rna pseudoknot structures us-
ing partition function posterior log-odds scores. BMC
Bioinformatics, 16(1).
Staple, D. W. and Butcher, S. E. (2005). Pseudoknots: Rna
structures with diverse functions. PLOS Biology, 3(6).
Taufer, M., Licon, A., Araiza, R., Mireles, D., Van Baten-
burg, F., Gultyaev, A. P., and Leung, M.-Y. (2008).
Pseudobase++: an extension of pseudobase for easy
searching, formatting and visualization of pseudo-
knots. Nucleic acids research, 37(suppl 1):D127–
D135.
Vernizzi, G., Orland, H., and Zee, A. (2016). Classification
and predictions of rna pseudoknots based on topolog-
ical invariants. Physical Review E, 94(4):042410.
Loop-loop Interaction Metrics on RNA Secondary Structures with Pseudoknots
37
