Road Surface Scanning using Stereo Cameras for Motorcycles

Joerg Deigmoeller

, Nils Einecke

, Oliver Fuchs

and Herbert Janssen

Honda Research Institute Europe, Carl-Legien-Strasse 30, 63073 Offenbach, Germany

Honda R&D Europe (Germany), Carl-Legien Strasse 30, 63073 Offenbach, Germany

Keywords:

Stereo, Depth Estimation, Plane Fitting, Road Surface Reconstruction, Motorcycle, Suspension Adaptation.

Abstract:

Active and semi-active suspension systems for vehicles became quite popular in the recent years as they

allow for a smoother and safer ride compared to conventional suspension systems. The performance of an

active/semi-active suspension system can be even more improved if the road condition in front of the vehicle

is known. Currently only a few luxury cars combine fully active suspension with stereo cameras for such a

predictive adaptation. However, we are not aware of any existing system for motorcycles. In this work, we

present an algorithm that can cope with the rolling movement of a motorcycle. In addition, it can robustly

reconstruct the road proﬁle within a single time step and does not require temporal integration which allows

real-time processing up to very high speeds at a precision in the order of millimeters. The complete system

has been successfully tested on a German highway and a precise road laser scan has been used for evaluation.

1 INTRODUCTION

To use a suspension system to its full extent it is indis-

pensable to predict the road condition in front of the

vehicle and to adapt to it accordingly. For cars this

improves the comfort whereas for motorcycles this

has also an inﬂuence on the stability of the vehicle

especially at high speeds. That means, single irregu-

larities on a highway like bridge joints have a strong

impact on the handle bar. In case of semi-active sus-

pension systems, that have much faster adaptation

times than active suspension systems (approximately

30 ms (Savaresi et al., 2010)), it still requires a scan-

ning of at least 4m ahead to cope with speeds up to

200km/h. As the visual appearance of the scene dras-

tically changes at such high velocities, temporal inte-

gration is quite difﬁcult and it is required to develop a

system that can create a precise road proﬁle in as few

time steps as possible.

To detect the road in front of a vehicle, the most

promising sensors are nowadays laser scanners and

cameras. As the space for sensors is very limited on a

motorcycle, it is desirable to use one sensor for mul-

tiple applications, like sign recognition, lane assist or

collision warning, which is only achievable by cam-

eras. In addition, laser scanners would require a fairly

dense and fast one-dimensional scan arrangement to

achieve similar performance as cameras.

Using cameras for road reconstruction, one could

use a structure from motion approach (one camera)

or a stereo camera system. A major problem apply-

ing structure from motion is the optical ﬂow compu-

tation at high speeds. Because of huge displacements,

strong perspective transformations and motion blur, it

is impossible to meet the real-time requirements. In

addition, the monocular approach is limited in preci-

sion and has a higher latency compared to the stereo

vision system for this scenario.

In this work, we present a stereo vision system that

meets all the previously mentioned requirements. It is

able to work despite very strong vibrations of a mo-

torcycle which are much higher than the vibrations

of a car and caused serious problems for the stereo

processing. The biggest challenge in developing such

a system is to reach a level of sufﬁcient robustness

within a single time step while preserving precise re-

construction and the possibility to also work in lean-

ing position.

2 RELATED WORK

The closest application that is already on market is the

Magic Body Control that is available in the Mercedes

Benz S-Class. It adapts the suspension in advance by

using a stereo camera that scans the road condition in

front, which is called Road Surface Scan (Weist et al.,

2013). Details about the method are not stated, but

Deigmoeller, J., Einecke, N., Fuchs, O. and Janssen, H.

Road Surface Scanning using Stereo Cameras for Motorcycles.

DOI: 10.5220/0006614805490554

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

549-554

ISBN: 978-989-758-290-5

549

from the article it can be extracted that sparse fea-

tures are used for depth estimation. In a second step,

the ego-motion is used to integrate those features over

time and by this get a precise road surface reconstruc-

tion. It seems that Road Surface Scan does not focus

on single road irregularities, but on continuous road

shapes that might bring the vehicle into oscillating up

and down movements. This can be avoided by a pre-

dictive suspension adaptation.

A similar idea in using ego-motion information

has been published in (Sugimoto et al., 2013). They

compute the 3D surface of a ground area by minimiz-

ing the photometric error assuming that in small areas

the pixel transformation follows a homography. Com-

bining all homographies in a mesh, they optimize the

surface including a smoothness term. The ﬁnal out-

put is a Digital Elevation Map (DEM). The drawback

of this approach is the high computational effort and

as for Road Surface Scan, the precision of the recon-

struction is reached by integrating multiple time steps,

which is difﬁcult at high speeds.

In (Shen et al., 2014), the authors use a multi pur-

pose camera to also compute an elevation map of the

road in front. For this they assume a pitch angle

and height of the mounted camera. They adapt for

changes in the pitch angle from 3D coordinates from

a certain area where the road is assumed to be ﬂat.

Additionally, they cannot cope with roll angles. Nev-

ertheless, they state height measurement variances of

1.2cm at a distance of 5-8m which is too imprecise

for our application.

A combination of elevation map computation,

obstacle and curb detection has been published

in ((Oniga and Nedevschi, 2010),(Oniga et al.,

2008),(Oniga et al., 2007)). This approach focuses on

separating those three types instead of precise surface

reconstruction. For this purpose they use a quadratic

road surface model, because they are interested in a

large road area. For our purpose, as we are interested

only in a narrow path in front of the vehicle, a planar

model is enough. Nevertheless, they run there algo-

rithm in real-time and within a range of cm-precision.

The authors of (Siegemund et al., 2011) and

(Siegemund et al., 2010) also focus on curb detection

by using a third order polynomial and temporal inte-

gration. Even if the result looks promising, we cannot

rely on temporal integration and we assume a simple

planar model.

3 SYSTEM OVERVIEW

After image rectiﬁcation, the system consists of two

parts. First, the reconstruction of the road proﬁle and

second, the computation of a height map. The latter

provides the basis for the detection of road irregulari-

ties.

The disparity computation used in this work is the

Summed Normalized Cross-Correlation method (Ei-

necke and Eggert, 2010) that is a good combination

in terms of precision and computation time. The in-

formation from previous time steps about the road ge-

ometry in front is used to further improvethe disparity

precision.

Finally, an elevation map is computed by assum-

ing that the road is optimally planar and irregularities

on the road deviate from this model assumption. This

allows for a simple thresholding on the elevation map

to make a decision whether the suspension should be

adapted or not. The adaptation itself is not part of this

work. There are several ways to integrate both sys-

tems, but this is beyond the scope of this paper.

In the remainder of this paper, we focus on the

feasibility to detect bumpy road conditions in such

extreme conditions as on a motorcycle at high pre-

cision. We ﬁrst discuss the disparity computation in

Section 4. The elevation map and post processing

are discussed in Section 5. To evaluate the system,

we give an insight into its performance by comparing

against an ofﬂine generated laser scan of a German

highway road proﬁle in Section 6.

4 DISPARITY COMPUTATION

The Summed Normalized Cross-Correlation (SNCC)

method provides a dense disparity map which is very

robust against illumination changes as it is based on

the approved NCC computation. An improvement to

the standard method has been shown by reducing the

fattening effect that is caused by strong intensity con-

trasts that usually occur at depth discontinuities (Ei-

necke and Eggert, 2010). To overcome this, the cor-

relation value

at a certain pixel coordinate (x

, y

)

is estimated by summing up the correlation values of

the neighbouring pixels ρ

|N(i)|

∑

jεN(i)

. (1)

By this, the SNCC method achieves similar pre-

cision as the standard SGM (Hirschmueller, 2008)

method at lower computation time (Scharstein et al.,

2017).

The neighbourhood N(i) is deﬁned by the desired

patch dimensions used for the correlation measure. In

case of a ﬂat road, the best quantization in depth can

be achieved by using a ﬂat patch. On the other hand,

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

550

Figure 1: Correlation measure between left and right stereo image using a rectangular patch (red) along the epipolar line

(dashed line). If the motorcycle is in upright position, (top image) the search direction is aligned with the road geometry

(pixels with same disparity lie on the epipolar line). If the motorcycle is in leaning position (bottom image), the search

direction is not aligned with the road geometry. Hence, no proper match is found.

to ensure sufﬁcient statistics for the correlation mea-

sure, the patch should be wide in order to compensate

the ﬂatness (see Fig. 1, top image).

If the motorcycle is in upright position, such a

rectangular patch provides robust matches at high res-

olution in depth. This is due to the fact that the

search direction of the disparity measure - which is

the epipolar line - is aligned with the road geometry.

In other words, disparities with the same value lie one

a horizontal line on the road as the epipolar line does.

On the other hand, the good quantization in depth

by the ﬂat patch worsens the correlation measure in

leaning position of the motorcycle. This is because

the epiploar line and the pixels with same disparities

on the road are rotated against each other (see Fig. 1,

bottom image). Hence, there will be no proper match

between the left and right image.

As we will see in the next section, we estimate

the road geometry assuming a planar structure. That

means, we roughly know the rotation between epipo-

lar line and road already. With this knowledge, we

could rotate the patch - which is very inefﬁcient in

terms of computation time - or we warp the image

content.

The latter one can be done very efﬁcient by back-

ward warping and bilinear interpolation. This presup-

poses that the image content is purely planar which

is true for our application. Instead of compensating

for the rotation, which would mean that we have to

rotate both images and we would destroy the epiploar

geometry, we choose the method of warping only one

image and compensate the offset along the epipolar

line (Einecke and Eggert, 2013). Assuming we have

a rough estimate of the plane parameters q

, q

and

from a previous time step, the disparity d

between

left and right image can be expressed by:

= q

− c

) + q

− c

) + q

, (2)

where c

and c

is the principal point. This re-

lation allows to reduce the pixel offset between both

images before the correlation measure is done. This

means that d

= 0 if we have the perfect plane param-

eters. As this is usually not the case, because we use

the parameters from the previous time step, we can at

least bring both regions of interest close to each other

where the road assumption is fulﬁlled.

The reduction of disparity increases the conﬁ-

dence for the correlation measure, because both im-

ages are close to congruent instead of beeing rotated

to each other. Fig. 2 shows the effect of warping one

stereo image by the planar model compared to the

conventional approach without warping.

A nice side effect of this compensation is less

computational effort because the disparity search

range is drastically reduced.

5 ELEVATION MAP

After the disparities have been computed, we ﬁrst es-

timate the current plane parameters q

, q

and q

from

Equation 2 in the latest stereo image pair and we reuse

it for the next time step as described in Section 4.

For the model ﬁtting, the robust regression method

RANSAC is used (Fischler and Bolles, 1981). To ex-

tract the plane normal vector (n

, n

)

and distance

Road Surface Scanning using Stereo Cameras for Motorcycles

551

reconstruction of road patch without image warping

reconstruction of road patch with image warping

0.05m

0.0m

-0.05m

0.05m

0.0m

-0.05m

Figure 2: Inﬂuence of image warping in leaning position on the elevation map. The disparity is only computed within the red

rectangle marked in the image as this is the part of the road the front wheel will pass. Other areas are not of interest. In the

upper part of the image the elevation maps are shown with and without warping for distances from 3m-7m. The upper graph

illustrates the inﬂuence of leaning on the disparity computation as discussed in Fig. 1. The lower graph shows a nice and ﬂat

reconstruction because the image warping has been applied before the disparity computation.

to the plane, Equation 2 can be rewritten as fol-

lows:

= q

(x− c

) + q

(y− c

) + q

(3)

= −

(x− c

) −

(y− c

) −

where b is the baseline and f

, f

are the focal

lengths.

The elevation map can be derived by computing

the distance of each triangulated image point to the

plane which is simply d

. Rearranging Equation 3 for

gives:

p,i

= −

(x− c

) −

(y− c

) −

. (4)

To evaluate the system a thresholding is applied

on the elevation map. If the distance d

p,i

exceeds a

certain threshold t

and the number of exceeding dis-

tances hits a minimum quantity Q

, the system de-

tects an irregularity on the road. The ﬁnal output is

the maximal detected elevation d

p,max

and the corre-

sponding depth Z

max

within the current time step.

6 EXPERIMENTAL RESULTS

Many different output formats of the system are pos-

sible, starting from a single maximum value to the

whole road proﬁle or even a proﬁle model. To be able

to evaluate the system on public roads, we decided

to use Z

max

and d

p,max

and match them to our ground

truth data.

The ground truth data was a 1km long 3D laser

scan of the German highway A3 available in the open

format CRG (OpenCRG, 2017). If the system returns

a detection, we check if the ground truth 3D scan also

contains an irregularity and if the measured distance

max

matches. To localize the motorcycle within the

CRG data, we equipped the motorcycle with a GPS

sensor and a stroke sensor at the front wheel.

As the track contains three bridge joints, which are

easy to detect in the recorded stroke data and in the

CRG data, we can synchronize both data. The GPS

information is used for rough positioning at the be-

ginning and the speed information is used to localize

the motorcycle between the bridge joints.

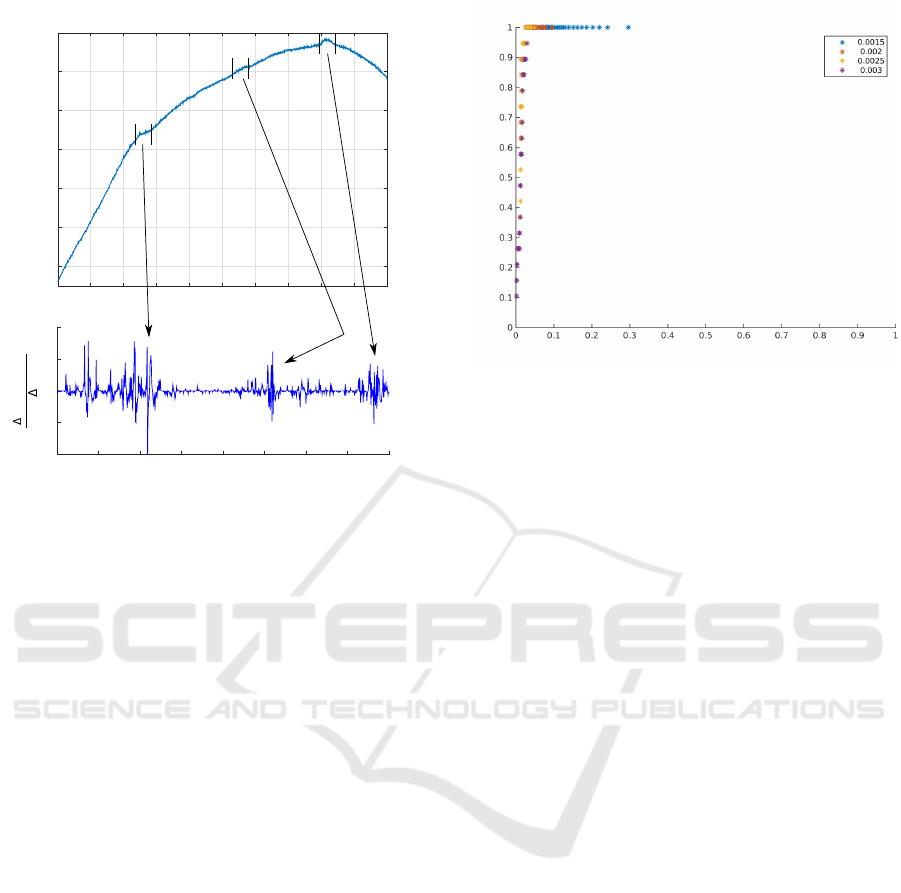
To quantify the system, we used the Receiver Op-

erating Characteristic (ROC) curve. A true positive is

deﬁned as a detected irregularity that matches with the

distance given in the CRG data. A false positive is any

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

552

100 200 300 400 500 600 700 800

-10

-5

100 200 300 400 500 600 700 800 900 1000

7.5

8.5

9.5

10.5

road profile

derivative of stroke over time

distance [m]

height [m]

stroke [mm]

samples @ 30Hz

Figure 3: CRG data of German highway A3 (top image)

and corresponding stroke data (bottom image).

detection if there is no irregularity in the CRG data.

In addition to the straight track, we used a curve at an

exit containing an irregularity that is clearly visible in

the stroke sensor. As it is difﬁcult to get comprehen-

sive CRG data sets from public roads, we were limited

to this one data set. We used one half of the recording

for parameter training and the remaining data for test-

ing. On the 1km long test track there are 19 events, in-

cluding the three bridge joints with a maximal height

of 3cm. The smallest event is in a range of 5mm. This

makes an overall number of 80 events within 8033

stereo image pairs.

The training data is used to ﬁnd the best values for

the threshold t

on the elevation map and the mini-

mum quantity threshold Q

. From the ROC curve in

Fig. 4 those corresponds to t

= 2.5mm and Q

= 40

pixels if we are interested in as many detections as

possible at low false positive rate. Applying this pa-

rameter set on the testing data gives a true positive

rate of 97.3% and a false positive rate of 2%.

The system runs on an Intel i7 processor at a run-

time of approximately 20ms on a region of interest of

50x200 pixels. The images are captured at 30 frames

per second and a resolution of 2048x1088 pixels. Our

evaluation has shown that the performance on half

resolution is similar to the full resolution at much less

computation time.

The testing data contained speeds in a range from

100-150km/h. Unfortunately, the highway section we

used for our evaluation has been renewed soon after

our ﬁrst recording session so that we could not eval-

true positive rate

false positive rate

Figure 4: ROC curves of the system for the training data.

Applying the optimal working point from the training data

on the testing data - in terms of true positive detections -

gives a true positive rate of 97.3% and a false positive rate

of 2%.

uate 200km/h, rain and night conditions. At least,

we can state that in all cases the algorithm still de-

livers plausable results. For the night riding we had

to mount a brighter front light, because the standard

light on our motorcycle was too weak for proper de-

tection by our cameras.

7 CONCLUSION

We presented a road-scanning system based on stereo

cameras for predictive suspension adaptation. It can

cope with high dynamic movementsof the motorcycle

as leaning.

To ensure low latency we did not use any tempo-

ral integration of the 3D reconstruction. The major

inﬂuence on the robustness is the big patch size for

the disparity measure. The shape of the patches have

been chosen to optimally ﬁt to the geometry of the

road at low computational effort.

The evaluation has shown that the precision of the

system is in the order of millimeters up to high speeds

of 150 km/h. The system also works at 200km/h and

higher, at night and in rainy conditions. Unfortu-

nately, we cannot provide numbers for latter scenar-

ios as the test track with ground truth has been recon-

structed during our evaluation period.

In future, the system will be integrated into a semi-

active suspension system. The extremely vibration re-

sistant camera set-up for motorcycles can also be used

for any other vision application that requires one or

two cameras.

Road Surface Scanning using Stereo Cameras for Motorcycles

553

REFERENCES

Einecke, N. and Eggert, J. (2010). A two-stage correlation

method for stereoscopic depth estimation. In DICTA,

pages 227–234.

Einecke, N. and Eggert, J. (2013). Stereo image warping for

improved depth estimation of road surfaces. In IEEE

Intelligent Vehicles Symposium, pages 89–194.

Fischler, M. A. and Bolles, R. C. (1981). Random sample

consensus: a paradigm for model ﬁtting with appli-

cations to image analysis and automated cartography.

Communications of the ACM.

Hirschmueller, H. (2008). Stereo processing by semi-global

matching and mutual information. In IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

pages 328–341.

Oniga, F. and Nedevschi, S. (2010). Processing Dense

Stereo Data Using Elevation Maps: Road Surface,

Trafﬁc Isle, and Obstacle Detection. IEEE Transac-

tions on Vehicular Technology, pages 1172–1182.

Oniga, F., Nedevschi, S., and Meinecke, M. (2008). Curb

Detection Based on a Multi-Frame Persistence Map

for Urban Driving Scenarios. In IEEE Conference on

Intelligent Transportation Systems, pages 67–72.

Oniga, F., Nedevschi, S., Meinecke, M. M., and To, T. B.

(2007). Road Surface and Obstacle Detection Based

on Elevation Maps from Dense Stereo. In IEEE Con-

ference on Intelligent Transportation Systems, pages

859–865.

OpenCRG (2017). Opencrg. http://opencrg.org. [Online;

accessed 07. November 2017].

Savaresi, S. M., Poussot-Vassal, C., Spelta, C., Sename,

O., and Dugard, L. (2010). Semi-Active Suspension

Control Design for Vehicles. Butterworth-Heinemann,

Oxford.

Scharstein, D., Szeliski, R., and Hirschmller, H.

(2017). Middlebury stereo vision page.

http://vision.middlebury.edu/stereo/. [Online;

accessed 07. November 2017].

Shen, T., Schamp, G., and Haddad, M. (2014). Stereo Vi-

sion Based Road Surface Preview. In IEEE Confer-

ence on Intelligent Transportation Systems.

Siegemund, J., Franke, U., and Forstner, W. (2011). A tem-

poral ﬁlter approach for detection and reconstruction

of curbs and road surfaces based on Conditional Ran-

dom Fields. In IEEE Intelligent Vehicles Symposium,

pages 637–642.

Siegemund, J., Pfeiffer, D., Franke, U., and Forstner, W.

(2010). Curb reconstruction using Conditional Ran-

dom Fields. In IEEE Intelligent Vehicles Symposium,

pages 203–210.

Sugimoto, S., Motooka, K., and Okutomi, M. (2013). Di-

rect Generation of Regular-Grid Ground Surface Map

from In-Vehicle Stereo Image Sequences. In 2013

IEEE International Conference on Computer Vision

Workshops (ICCVW), pages 600–607.

Weist, U., Missel, J., Cytrynski, S., Mehren, D., Schwarz,

D. T., and Kern, S. (2013). Fahrkomfort der extrak-

lasse. ATZextra, 18.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

554