
3D Adaptive Histogram Equalization Method for Medical Volumes
Paulo Amorim
1
, Thiago Moraes
1
, Jorge Silva
1
and Helio Pedrini
2
1
Division of 3D Technologies, Center for Information Technology Renato Archer, Campinas-SP, 13069-901, Brazil
2
Institute of Computing, University of Campinas, Campinas, SP, 13083-852, Brazil
Keywords:
Contrast Enhancement, Medical Images, Histogram Equalization, Volume Rendering.
Abstract:
Medical imaging plays a fundamental role in the diagnosis and treatment of several diseases, enabling the
visualization of internal organs and tissues for use in clinical procedures. The quality of medical images can
be degraded by several factors, such as noise and poor contrast. The application of filtering and contrast en-
hancement techniques is usually necessary to improve the quality of images, which facilitates the segmentation
and classification stages. In this paper, we develop and analyze a novel three-dimensional adaptive histogram
equalization method for improving contrast in the context of medical imaging. Several data sets are used to
demonstrate the effectiveness of the proposed approach.
1 INTRODUCTION
Several medical imaging modalities (Ahmad et al.,
2014; Beutel et al., 2000) have been employed in
modern medicine to aid the diagnosis and treat-
ment of diseases, such as digital radiography (DR),
magnetic resonance imaging (MRI), endoscopy (ES),
ultrasound (US), angiography (AG), mammography
(MG), computed tomography (CT) and positron emis-
sion tomography (PET). These imaging techniques al-
low visual representations of internal structures of the
body to be constructed, assisting physicians in diag-
nostic decisions (Nolden et al., 2013; Thammasitboon
and Cutrer, 2013).
During the acquisition process, the quality of
medical images can be degraded by artifacts, for in-
stance, noise and poor contrast. Techniques of im-
age filtering and contrast enhancement are necessary
to compensate such effects in order to improve the
image quality.
In the image processing field (Amorim et al.,
2013; Amorim et al., 2015; Moraes et al., 2015),
several approaches have been developed to attenuate
noise while preserving relevant features. Some com-
mon noise removal approaches (Gonzalez and Woods,
2002; Parker, 2010; Russ, 2015) include median filter,
Weiner filter, Gaussian filter, bilateral filter, among
others. Additionally, enhancement techniques (Hum-
mel, 1977; Singh and Bovis, 2005; Stark, 2000) have
been employed to emphasize features or characteris-
tics of the image, such that the resulting image has
superior quality than the original one.
Histogram equalization (Gonzalez and Woods,
2002; Hummel, 1977) is a very well known tech-
nique for enhancing the contrast of an image, whose
main goal is to better distribute the pixel intensities
based on the probability distribution of the gray lev-
els. By means of this histogram adjustment, regions
with poor contrast are enhanced, producing an overall
contrast improvement.
As main contribution of our work, we propose
and evaluate a variant of the two-dimensional con-
trast limited adaptive histogram equalization (2D
CLAHE) (Zuiderveld, 1994) to improve contrast in
medical images. It differs from the original approach
in the sense that our method operates directly on the
three-dimensional volumes, without requiring the ex-
traction of two-dimensional sections of images.
Several histograms are constructed and modified
to redistribute the pixel intensities of the images, sig-
nificantly improving their local contrast. Experiments
are conducted on different medical volumetric data
sets to demonstrate the effectiveness of the proposed
method.
This paper is organized as follows. Section 2
briefly reviews some relevant concepts and techniques
related to the topic under investigation. Section 3
describes the proposed local contrast enhancement
method. Section 4 presents and analyzes the exper-
imental results obtained with our method. Section 5
concludes the paper with some final remarks and di-
rections for future work.
Amorim, P., Moraes, T., Silva, J. and Pedrini, H.
3D Adaptive Histogram Equalization Method for Medical Volumes.
DOI: 10.5220/0006615303630370
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages
363-370
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
363

2 BACKGROUND
A common problem that occurs in medical imaging is
the generation of images with poor contrast due to a
limited exposure range, which affects the correct in-
terpretation of anatomical structures for diagnosis and
treatment procedures.
Enhancement techniques (Chen et al., 2014; Gu
et al., 2016; Huang et al., 2013; Kim et al., 1998;
Saleem et al., 2017; Stark, 2000; Wang et al., 1983)
have been developed to adjust the contrast and im-
prove quality of images in order to make their char-
acteristics more suitable for subsequent stages, such
as segmentation and classification. Therefore, after
the image enhancement process of an image, a cer-
tain component becomes more distinguishable from
other components and the background.
Several definitions of contrast have been proposed
in the literature. Weber contrast (Fechner, 1860) is
expressed as:
C
W
=
I − I
b
I
b
(1)
where I and I
b
correspond to the luminance of the ob-
jects and the background, respectively.
Michelson contrast (Michelson, 1995) is defined
as:
C
M
=
I
max
− I
min
I
max
+ I
min
(2)
where I
min
and I
max
correspond to the lowest and high-
est luminance, respectively.
Root mean square (RMS) contrast (Peli, 1990) is
defined as the standard deviation of the pixel intensi-
ties:
C
RMS
=
v
u
u
t
1
MN
M−1
∑
x=0
N−1
∑
y=0
(I
xy
−
¯
I)
2
(3)
where I
xy
are the elements with x and y coordinates of
the image with dimensions M × N, whereas
¯
I is the
average intensity of all pixel intensities in the image.
The pixel intensities of I are normalized in the range
[0,1].
Contrast stretching (Arici et al., 2009; Chang and
Wu, 1998; Yang, 2006) is a basic image enhancement
technique used to increase the dynamic range of the
gray levels present in the image. A low contrast im-
age typically has its pixel intensities concentrated on
a narrow range, such that information may be lost.
Linear contrast enhancement techniques expand
the original intensity values of the pixels linearly.
Three linear contrast enhancement techniques are
briefly described as follows. In the minimum-
maximum linear contrast stretching, the pixel values
are redistributed to a new range of values specified
by lower and upper pixel value limits over the im-
age under normalization. For 8-bit gray level im-
ages, the lower and upper limits are usually assigned
to 0 and 255, respectively. In the percentage linear
contrast stretching, the enhancement is similar to the
minimum-maximum approach, however, it employs
specified minimum and maximum values within a cer-
tain percentage of pixels from the mean of the his-
togram. In a piecewise linear contrast stretching, the
range of the image intensity is expanded in selected
areas according to linear function.
Nonlinear contrast enhancement techniques apply
non-linear transfer functions to redistribute the inten-
sity values of pixels to increase the contrast of an
image. Histogram equalization applies a monotonic
non-linear mapping to adjust the intensity values of
pixel in the image such that the resulting image con-
tains a uniform distribution of intensities. The cumu-
lative probability distribution can be used to equalize
the histogram of an image.
The histogram equalization (Abdullah-Al-Wadud
et al., 2007; Cheng and Shi, 2004; Gonzalez and
Woods, 2002; Pizer et al., 1987; Russ, 2015) is typ-
ically a global process in the sense that it applies a
function to transform the image based on the inten-
sity level distribution of the entire image. In certain
cases, it is desirable to enhance details over small re-
gions of the image, such that the equalization process
can be adapted to produce a local enhancement. In
adaptive histogram equalization, the image is divided
into a number of non-overlapping blocks, such that
the histogram equalization mapping is applied locally
within each block. In order to remove artifacts due to
block boundaries, the pixel intensities are interpolated
across the blocks using an interpolating function.
A variant of the adaptive histogram equal-
ization, known as contrast limited adaptive his-
togram equalization (2D CLAHE), was proposed by
Zuiderveld (Zuiderveld, 1994) to avoid noise to be
overamplified in homogeneous regions of the image.
This approach limits noise amplification by clipping
the histogram through a specified value before com-
puting the cumulative distribution function. Instead
of discarding the part of the histogram that exceeds
the clip limit, it is redistributed uniformly among all
histogram bins (Pizer et al., 1987).
3 PROPOSED METHOD
This section describes the main stages that compose
the proposed method for locally equalizing the his-
togram of the medical images. The method oper-
ates directly on the three-dimensional volumes, which
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
364
is an extension of the contrast limited adaptive his-
togram equalization (2D CLAHE) (Zuiderveld, 1994)
to improve contrast in medical images. Figure 1
illustrates the main components of the proposed
three-dimensional contrast limited adaptive histogram
equalization (3D CLAHE).
Initially, two-dimensional slices are stacked to-
gether to form a volume. The volume is then subdi-
vided in blocks with predefined size. The histogram is
calculated for each block and part of histogram is cut
according to a predefined value. Finally, the blocks
are joined and a trilinear interpolation function is ap-
plied to remove artifacts that may occur on the bound-
aries between blocks.
Algorithm 1 describes the main steps of the
proposed three-dimensional contrast limited adap-
tive histogram equalization (3D CLAHE). Function
CDF denotes the Cumulative Distribution Function,
whereas functions min and max return the minimum
and maximum grayscale values in the given image,
respectively. H is a vector of histograms, where each
position of the vector stores the histogram of a sub-
block, CS is an auxiliary vector to store the result of
CDF, and MAP is a vector that maps each grayscale
value to a new intensity value after the histogram
equalization.
The trilinear interpolation is expressed as
[(MAP
LUA
[v
i
] × x_inv_coe f × y_inv_coe f × z_inv_coe f )+
(MAP
RUA
[v
i
] × x_coe f × y_inv_coe f × z_inv_coe f )+
(MAP
LBA
[v
i
] × x_inv_coe f × y_coe f × z_inv_coe f )+
(MAP
LU P
[v
i
] × x_inv_coe f × y_inv_coe f × z_coe f )+
(MAP
RU P
[v
i
] × x_coe f × y_inv_coe f × z_coe f )+
(MAP
LBP
[v
i
] × x_inv_coe f × y_coe f × z_coe f )+
(MAP
RBA
[v
i
] × x_coe f × y_coe f × z_inv_coe f )+
(MAP
RBP
[v
i
] × x_coe f × y_coe f × z_coe f )]
/(size
x
× size
y
× size
z
)
where MAP
LUA
, MAP
RUA
, MAP
LBA
, MAP
LUP
,
MAP
RUP
, MAP
LBP
, MAP
RBA
, MAP
RBP
are the maps
for the 8 nearest subblocks (Figure 2). x_coe f ,
y_coe f , z_coe f are the distances from V
i
to MAP
LBA
for x, y and z, respectively. x_inv_coe f , y_inv_coe f ,
z_inv_coe f is the distance from V
i
to MAP
RU P
for x,
y and z, respectively.
To test our contrast enhancement methodology,
we employed MRI volumes, which were subdivided
into blocks with size of 8×8×8 voxels. Larger block
dimensions, such as 16×16×16 voxels, generated
much noise and decreased the peak signal noise ratio
(PSNR) values.
The histogram clip value used in our methodology
was assigned to 5, since larger values also increased
the noise level in the image, consequently decreasing
the PSNR value.
Algorithm 1: Proposed 3D CLAHE method.
1 3D_CLAHE (image, size, clip_limit, nbins)
input : image: volumetric image;
size: size of subblocks;
clip_limit: value at which the
histogram is clipped;
nbins: number of bins for
histogram;
output: image_equalized;
2 Divide image into subblocks with the given
size;
3 Create image_equalized with same size as
image;
4 for each subblock S
i
do
5 H[S
i
] ← histogram(S
i
, nbins);
6 Clip H[S
i
] according to clip_limit and
redistribute equally the excess voxels
across the histogram;
7 CS ← CDF(H[S
i
]);
8 MAP[S
i
] ← CS × (max(image) -
min(image)) + min(image);
9 for each voxel V
i
from image do
10 Find 8 closest neighboring subblocks
centers;
11 Use the pixel intensity to find the map
value at the 8 subblocks;
12 Use the 8 mapped values to interpolate
with trilinear interpolation to obtain
the V
i
mapped value and assign this
value to the corresponding voxel in
image_equalized;
13 return image_equalized;
4 EXPERIMENTAL RESULTS
Experiments were conducted on a set of five volumes
acquired through magnetic resonance imaging (MRI).
These images were extracted from the publicly avail-
able OASIS dataset (Marcus et al., 2007).
Magnetic resonance imaging was chosen since
this modality commonly generates images with het-
erogeneous contrast when compared to computed to-
mography (CT). Each volume contains 256 slices at a
resolution of 128×256 pixels.
We compared the proposed method (3D CLAHE)
against 2D CLAHE (Zuiderveld, 1994). For 2D
CLAHE, the equalization was applied to each slice
of the volume using blocks with 8 × 8 pixels. For 3D
3D Adaptive Histogram Equalization Method for Medical Volumes
365
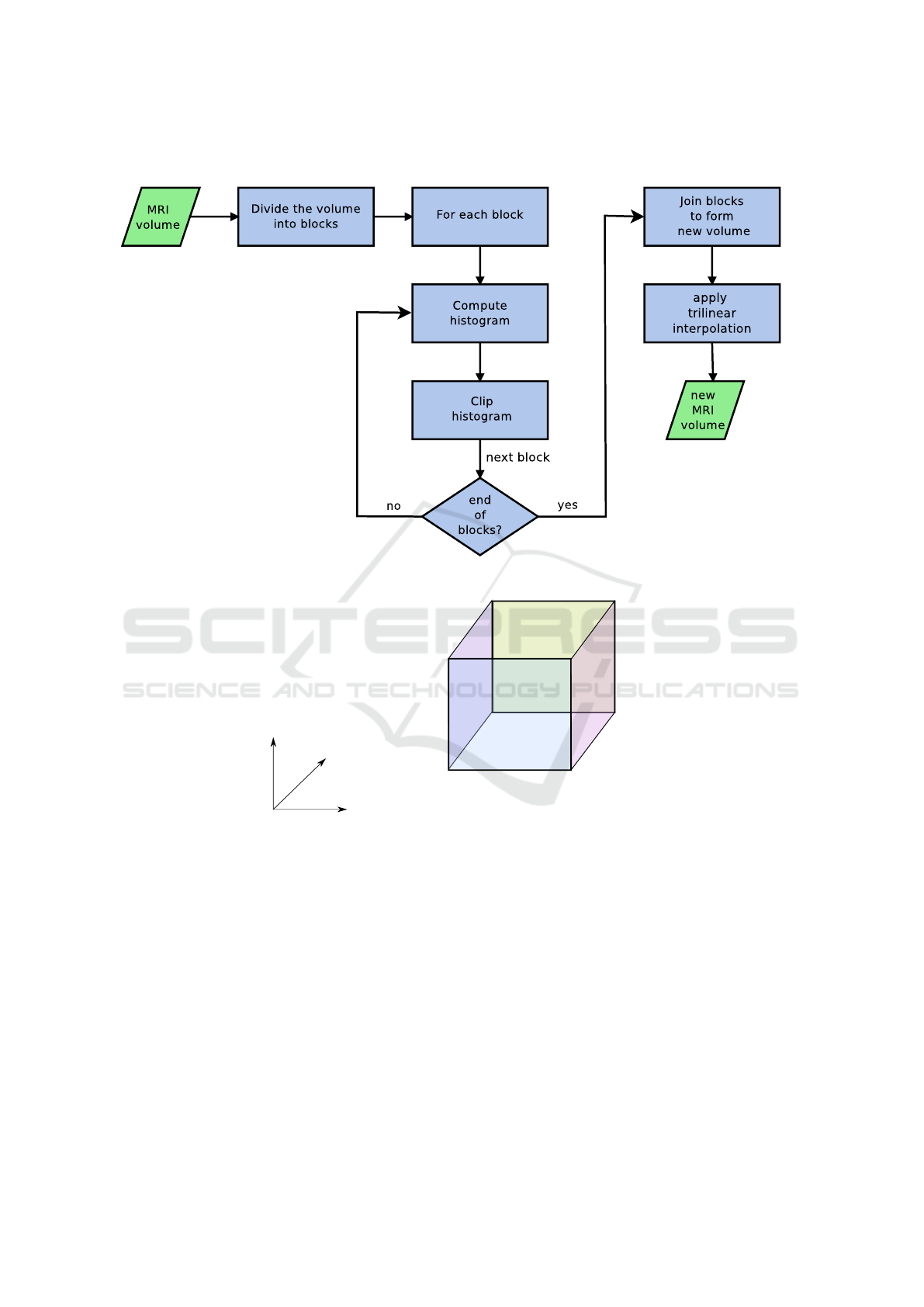
Figure 1: Proposed methodology for three-dimensional contrast limited adaptive histogram equalization.
MAP
LBP
X
Z
Y
MAP
LUA
MAP
RUA
MAP
LUP
MAP
RUP
MAP
RBA
MAP
RBP
MAP
LBA
Figure 2: Centers of the 8 subblocks form a cube, which illustrates the position of the maps used in the interpolation.
CLAHE, we used blocks with 8× 8 × 8 voxels. A his-
togram clip limit of 5 was used in both approaches.
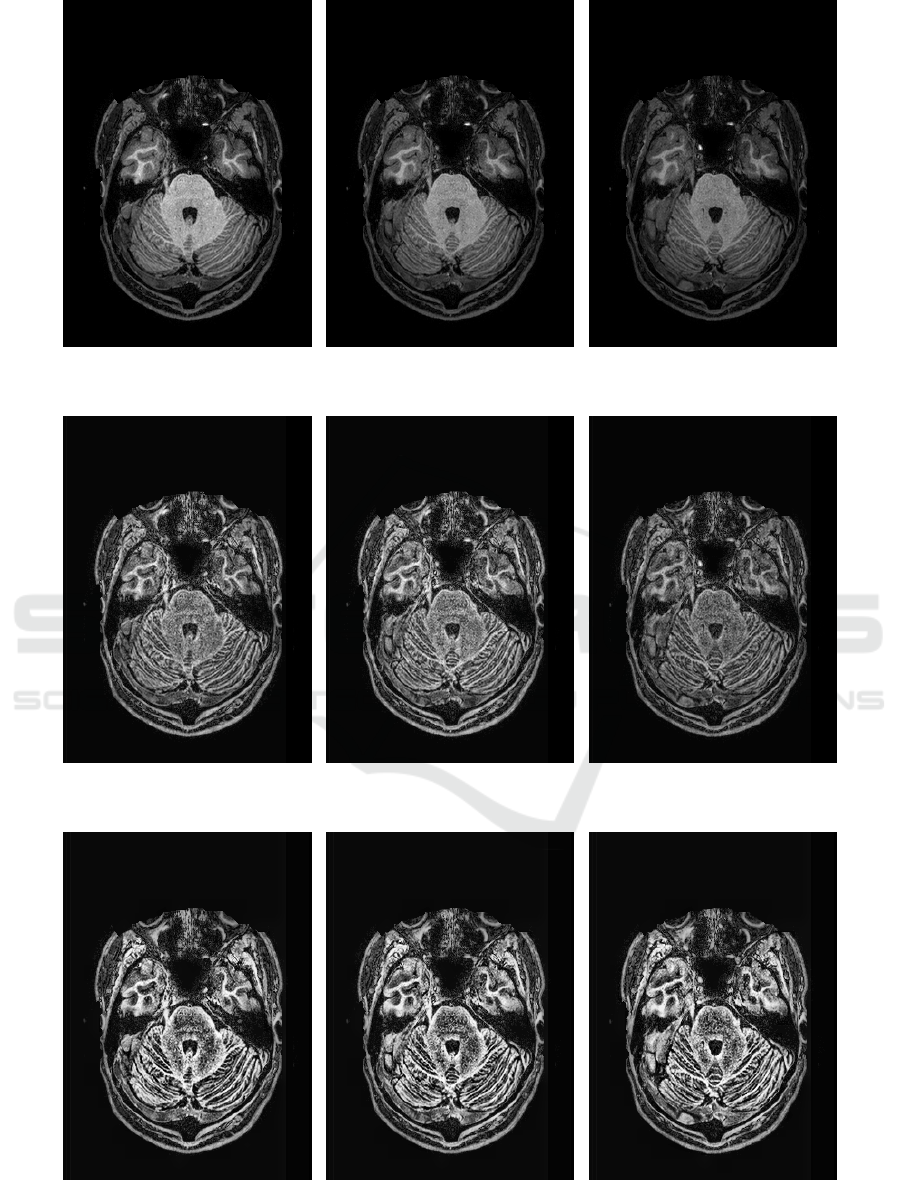
In the first row of Figures 3 and 4, all images are
non-equalized. It is possible to observe that these im-
ages have different level of contrast. Images in the
second row were equalized with the 2D CLAHE tech-
nique. They present better contrast when compared
to their corresponding original images, however, the
have different contrast between the slices which it is
not ideal for volume rendering or 3D segmentation
purpose. Finally, images in the third row of Figures 3
and 4 were equalized with the proposed 3D CLAHE
method, which present uniform contrast.
The peak signal noise ratio (PSNR) was measured
for both 2D CLAHE and 3D CLAHE methods. It
is possible to observe from Table 1 that our method
achieved higher values of PSNR for all tested images,
which means that they are closer to the original im-
age.
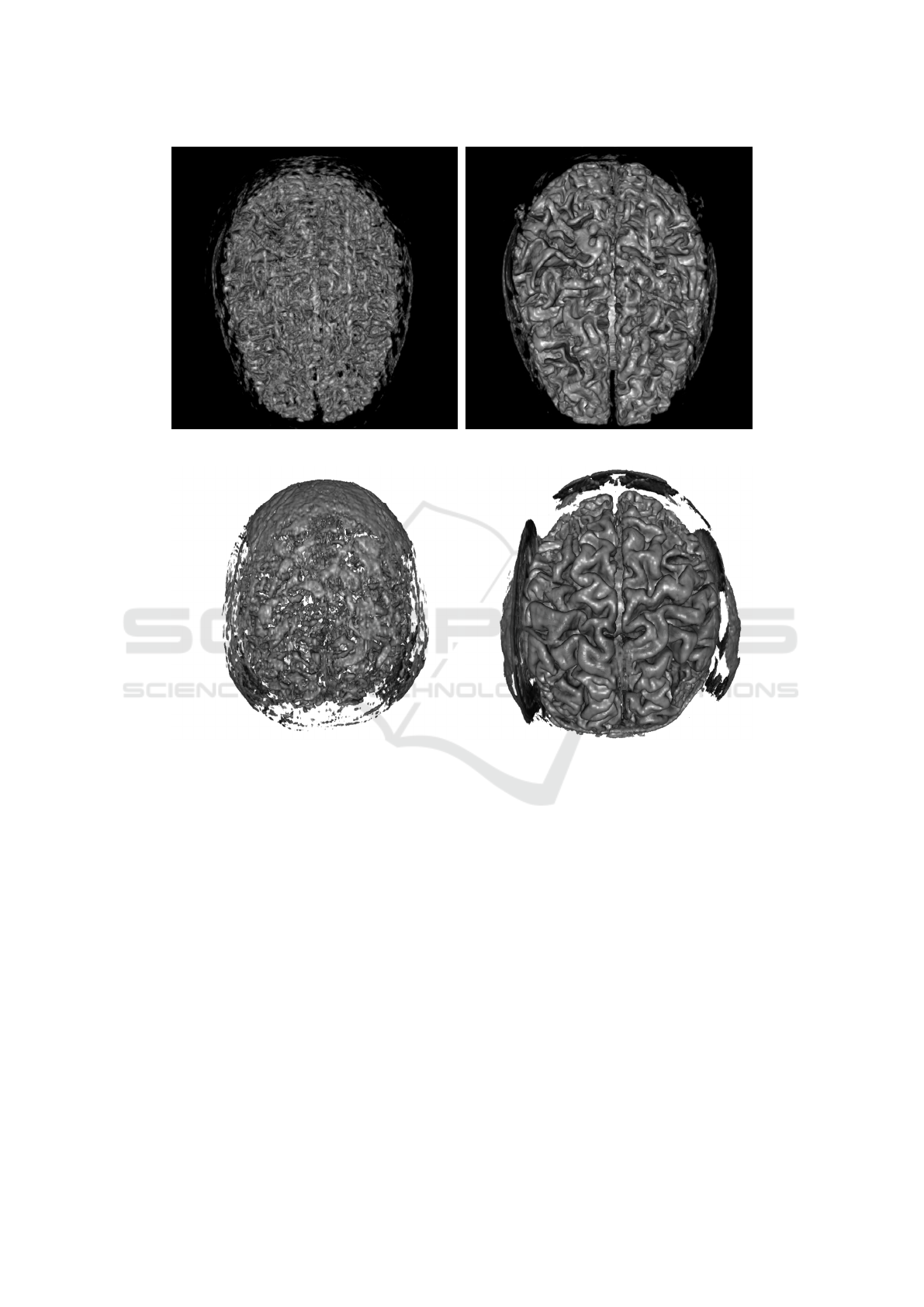
Figure 5 shows the results of volume rendering
with raycasting technique for two volumes equalized
with 2D CLAHE and with the proposed technique.
The details in the surface of the brain are clearly vis-
ible when the volumetric data sets are equalized with
the proposed method.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
366
original
slice 179
original
slice 180
original
slice 181
slice 179
equalized with 2D CLAHE
slice 180
equalized with 2D CLAHE
slice 181
equalized with 2D CLAHE
slice 179
equalized with 3D CLAHE
slice 180
equalized with 3D CLAHE
slice 181
equalized with 3D CLAHE
Figure 3: Comparison between input and equalized images with 2D CLAHE and proposed 3D CLAHE method.
3D Adaptive Histogram Equalization Method for Medical Volumes
367

original
slice 84
original
slice 85
original
slice 86
slice 84
equalized with 2D CLAHE
slice 85
equalized with 2D CLAHE
slice 86
equalized with 2D CLAHE
slice 84
equalized with 3D CLAHE
slice 85
equalized with 3D CLAHE
slice 86
equalized with 3D CLAHE
Figure 4: Comparison between input and equalized images with 2D CLAHE and proposed 3D CLAHE method.
Table 1: PSNR values for equalized volumes with 2D CLAHE and proposed method.
Dataset PSNR
2D CLAHE 3D CLAHE
OAS2_0001_MR1_RAW_mpr-1.nifti.hdr 21.01 73.98
OAS2_0002_MR1_RAW_mpr-1.nifti.hdr 22.24 66.31
OAS2_0003_MR1_RAW_mpr-1.nifti.hdr 18.63 66.86
OAS2_0004_MR1_RAW_mpr-1.nifti.hdr 25.08 68.58
OAS2_0005_MR1_RAW_mpr-1.nifti.hdr 29.01 30.13
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
368
equalized with 2D CLAHE equalized with proposed method
equalized with 2D CLAHE equalized with proposed method
Figure 5: Comparison between two volumetric data sets equalized with 2D CLAHE and proposed method.
5 CONCLUSIONS AND FUTURE
WORK
In this paper, we extended the contrast limited adap-
tive histogram equalization technique for improving
contrast in medical images. Differently from the
original method, our method operates directly on
the three-dimensional MRI volumes, where the his-
tograms are computed and transformed within blocks
extracted from the medical data.
Experiments conducted on a number of medical
volumes demonstrated that the proposed method was
capable of significantly enhancing the contrast of the
images. The resulting volumes can provide health
professionals with valuable information for diagnosis
and treatment purposes.
As directions for future work, we intend to inves-
tigate the extension of other 2D image enhacement
techniques to 3D.
ACKNOWLEDGMENTS
We are grateful to Brazilian Council for Scien-
tific and Technological Development (CNPq) for
Grant #305169/2015-7 and to São Paulo Research
Foundation (FAPESP) for the Brazilian Research
Institute for Neuroscience and Neurotechnology -
BRAINN (CEPID process #2013/07559-3) and for
the Thematic Projects (Grants #2017/12646-3 and
#2014/12236-1).
3D Adaptive Histogram Equalization Method for Medical Volumes
369

REFERENCES
Abdullah-Al-Wadud, M., Kabir, M. H., Dewan, M. A. A.,
and Chae, O. (2007). A Dynamic Histogram Equaliza-
tion for Image Contrast Enhancement. IEEE Transac-
tions on Consumer Electronics, 53(2):593–600.
Ahmad, H. A., Yu, H. J., and Miller, C. G. (2014). Medical
Imaging Modalities. In Medical Imaging in Clinical
Trials, pages 3–26. Springer.
Amorim, P., Moraes, T., Silva, J., and Pedrini, H. (2015).
InVesalius: An Interactive Rendering Framework for
Health Care Support. In International Symposium on
Visual Computing, pages 45–54, Las Vegas, NV, USA.
Springer.
Amorim, P. H., de Moraes, T. F., da Silva, J. V., and Pedrini,
H. (2013). An Out-of-core Volume Rendering Archi-
tecture. In IV ECCOMAS Thematic Conference on
Computational Vision and Medical Image Processing,
page 173. CRC Press.
Arici, T., Dikbas, S., and Altunbasak, Y. (2009). A His-
togram Modification Framework and its Application
for Image Contrast Enhancement. IEEE Transactions
on Image Processing, 18(9):1921–1935.
Beutel, J., Kundel, H. L., and Van Metter, R. L. (2000).
Handbook of Medical Imaging: Physics and Psy-
chophysics, volume 1. Spie Press.
Chang, D.-C. and Wu, W.-R. (1998). Image Contrast En-
hancement based on a Histogram Transformation of
Local Standard Deviation. IEEE Transactions on
Medical Imaging, 17(4):518–531.
Chen, Z., Jiang, T., and Tian, Y. (2014). Quality Assess-
ment for Comparing Image Enhancement Algorithms.
In IEEE Conference on Computer Vision and Pattern
Recognition, pages 3003–3010.
Cheng, H. and Shi, X. (2004). A Simple and Effective
Histogram Equalization Approach to Image Enhance-
ment. Digital Signal Processing, 14(2):158–170.
Fechner, G. (1860). Elemente der Psychophysik (Elements
of Psychophysics), volume 1. Leipzig: Breitkopf und
Härtel.
Gonzalez, R. C. and Woods, R. E. (2002). Digital Image
Processing. Prentice Hall Upper Saddle River.
Gu, K., Zhai, G., Lin, W., and Liu, M. (2016). The Anal-
ysis of Image Contrast: From Quality Assessment to
Automatic Enhancement. IEEE Transactions on Cy-
bernetics, 46(1):284–297.
Huang, S.-C., Cheng, F.-C., and Chiu, Y.-S. (2013). Effi-
cient Contrast Enhancement using Adaptive Gamma
Correction with Weighting Distribution. IEEE Trans-
actions on Image Processing, 22(3):1032–1041.
Hummel, R. (1977). Image Enhancement by Histogram
Transformation. Computer Graphics and Image Pro-
cessing, 6(2):184–195.
Kim, T. K., Paik, J. K., and Kang, B. S. (1998). Contrast
Enhancement System using Spatially Adaptive His-
togram Equalization with Temporal Filtering. IEEE
Transactions on Consumer Electronics, 44(1):82–87.
Marcus, D., Wang, T., Parker, J., Csernansky, J., Morris, J.,
and Buckner, R. (2007). Open Access Series of Imag-
ing Studies (OASIS): Cross-Sectional MRI Data in
Young, Middle Aged, Nondemented, and Demented
Older Adults. Journal of Cognitive Neuroscience,
19(9):1498–1507.
Michelson, A. A. (1995). Studies in Optics. Courier Cor-
poration.
Moraes, T. F., Amorim, P. H., da Silva, J. V., Pedrini, H.,
and Meurer, M. I. (2015). Medical Volume Render-
ing based on Gradient Information. In 5th Eccomas
Thematic Conference on Computational Vision and
Medical Image Processing, pages 181–186, Tenerife,
Spain. CRC Press.
Nolden, M., Zelzer, S., Seitel, A., Wald, D., Müller, M.,
Franz, A. M., Maleike, D., Fangerau, M., Baumhauer,
M., and Maier-Hein, L. (2013). The Medical Imaging
Interaction Toolkit: Challenges and Advances. Inter-
national Journal of Computer Assisted Radiology and
Surgery, 8(4):607–620.
Parker, J. R. (2010). Algorithms for Image Processing and
Computer Vision. John Wiley & Sons.
Peli, E. (1990). Contrast in Complex Images. Journal of the
Optical Society of America, 7(10):2032–2040.
Pizer, S. M., Amburn, E. P., Austin, J. D., Cromartie, R.,
Geselowitz, A., Greer, T., ter Haar Romeny, B., Zim-
merman, J. B., and Zuiderveld, K. (1987). Adaptive
Histogram Equalization and its Variations. Computer
Vision, Graphics, and Image Processing, 39(3):355–
368.
Russ, J. C. (2015). The Image Processing Handbook. CRC
Press.
Saleem, A., Beghdadi, A., and Boashash, B. (2017).
A Distortion-free Contrast Enhancement Technique
based on a Perceptual Fusion Scheme. Neurocomput-
ing, 226:161–167.
Singh, S. and Bovis, K. (2005). An Evaluation of Contrast
Enhancement Techniques for Mammographic Breast
Masses. IEEE Transactions on Information Technol-
ogy in Biomedicine, 9(1):109–119.
Stark, J. A. (2000). Adaptive Image Contrast Enhance-
ment using Generalizations of Histogram Equaliza-
tion. IEEE Transactions on Image Processing,
9(5):889–896.
Thammasitboon, S. and Cutrer, W. B. (2013). Diagnostic
Decision-making and Strategies to Improve Diagno-
sis. Current Problems in Pediatric and Adolescent
Health Care, 43(9):232–241.
Wang, D. C., Vagnucci, A. H., and Li, C. (1983). Digi-
tal Image Enhancement: A Survey. Computer Vision,
Graphics, and Image Processing, 24(3):363–381.
Yang, C.-C. (2006). Image Enhancement by Modified
Contrast-stretching Manipulation. Optics & Laser
Technology, 38(3):196–201.
Zuiderveld, K. (1994). Contrast Limited Adaptive His-
togram Equalization. In Graphics Gems IV, pages
474–485. Academic Press Professional, Inc.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
370
