Parallel Bubbles

Evaluation of Three Techniques for Representing Mixed Categorical and

Continuous Data in Parallel Coordinates

Rapha

el Tuor

, Florian Ev

equoz

1,2

and Denis Lalanne

Human-IST Institute, University of Fribourg, 1700 Fribourg, Switzerland

Institute of Information Systems, University of Applied Sciences Western Switzerland,

HES-SO Valais-Wallis, 3960 Sierre, Switzerland

Keywords:

Visualization, Parallel Coordinates, Categorical Data, User Study.

Abstract:

Parallel Coordinates are a widely used visualization method for multivariate data analysis tasks. In this paper

we discuss the techniques that aim to enhance the representation of categorical data in Parallel Coordinates.

We propose Parallel Bubbles, a method that improves the graphical perception of categorical dimensions in

Parallel Coordinates by adding a visual encoding of frequency. Our main contribution consists in a user study

that compares the performance of three variants of Parallel Coordinates, with similarity and frequency tasks.

We base our design choices on the literature review, and on the research guidelines provided by Johansson and

Forsell (2016). Parallel Bubbles are a good trade-off between Parallel Coordinates and Parallel Sets in terms

of performance for both types of tasks. Adding a visual encoding of frequency leads to a signiﬁcant difference

in performance for a frequency-based task consisting in assessing the most represented category. This study is

the ﬁrst of a series that will aim at testing the three visualization methods in tasks centered on the continuous

axis, and where we assume that the performance of Parallel Sets will be worse.

1 INTRODUCTION

Parallel Coordinates (Inselberg and Dimsdale, 1990;

Wegman, 1990) are a popular visualization method

for representing multivariate data. The parallel axes

represent dimensions, and each multivariate item cor-

responds to a polyline crossing the axes. This vi-

sualization method allows to reveal patterns quickly

(Siirtola et al., 2009) and is thus a good tool for ex-

ploratory analysis tasks. A recurring problem of Par-

allel Coordinates is the visual clutter that occurs with

large numbers of polylines: it hinders data analysts

from identifying clusters and trends, and from extract-

ing relevant information from the data. Moreover,

representing categorical dimensions in Parallel Coor-

dinates is not ideal since it increases the visual con-

fusion: ”either the frequency information is not vis-

ible or a ranking is imposed on the visual mapping

transformation, inﬂuencing perception of the data”

(Kosara et al., 2006). This is due to the fact that

categorical dimensions are represented in the same

way as continuous dimensions: the continuous design

model used by Parallel Coordinates does not match

the discrete user model of the data (Kosara et al.,

2006). Another problem arising from the represen-

tation of categorical data is overplotting (Dang et al.,

2010): it occurs when the discrete number of cate-

gorical values is signiﬁcantly smaller than the size of

the dataset, resulting in many samples sharing a given

categorical value. This leads to ”the increased like-

lihood of multiple lines passing successively through

the same points” (Havre et al., 2006). In the frequent

case that multiple items have identical values along

neighboring axes, their lines overlap exactly, there-

fore leaving visible only the last line segment drawn,

thus hiding the frequency information (Dang et al.,

2010; Kosara et al., 2006). In summary, clutter and

overplotting should be avoided as much as possible

since they hide frequency information and prevent

the detection of patterns. Reducing them is one of

the main challenges in the design of Parallel Coor-

dinates (Heinrich and Weiskopf, 2013). Researchers

propose several methods to address these challenges,

but very few present results form user-centered eval-

uations (Johansson and Forsell, 2016). There still

lacks an evidence of measurable beneﬁts that would

encourage the use of a variant of Parallel Coordinates

over standard ones. For example, frequency-based ap-

252

Tuor, R., Evéquoz, F. and Lalanne, D.

Parallel Bubbles - Evaluation of Three Techniques for Representing Mixed Categorical and Continuous Data in Parallel Coordinates.

DOI: 10.5220/0006615602520263

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 3: IVAPP, pages

252-263

ISBN: 978-989-758-289-9

proaches (Kosara et al., 2006) seem promising, but it

is unclear whether these techniques positively affect

the ability of users to quickly and reliably identify

patterns in the data. Do the users correctly interpret

categorical dimensions? Do these methods allow for

a better performance in typical data analysis tasks?

In this paper, we ﬁrst give an overview on the cur-

rent state of the art of clutter reduction techniques for

Parallel Coordinates. Next, we present an enhanced

version of Parallel Coordinates, Parallel Bubbles, that

aims to tackle the problem of overplotting instances

when dealing with categorical dimensions. By adding

a visual encoding of frequency, we assume that Par-

allel Bubbles will allow to detect more effectively the

most represented categorical values, and thus should

enhance the user performance in similarity and fre-

quency tasks. In order to measure the gain of per-

formance, we lead a controlled user experiment con-

sisting of three data analysis tasks. We use randomly

generated datasets composed of one continuous di-

mension and one categorical dimension. In the last

section, we describe and discuss the outcomes of this

user experiment.

2 STATE OF THE ART

Parallel Coordinates (Inselberg and Dimsdale, 1990;

Wegman, 1990) were initially designed to represent

continuous dimensions. Kosara et al. (2006) state that

when dealing with multivariate datasets, the diver-

gence between the user’s mental model and the visual

representation of the data can be eliminated by the use

of frequency-based techniques. These techniques rep-

resent categories by visual entities that are scaled pro-

portionally to their corresponding frequency (Kosara

et al., 2006). In this chapter, we give an overview

on the existing overplotting reduction methods, de-

signed to enhance the visual representation of cate-

gorical data. We group these methods in the four cat-

egories proposed by Heinrich and Weiskopf (2013),

namely ﬁltering, aggregation, spatial distortion, and

the use of colors.

2.1 Clutter Reduction Methods

2.1.1 Filtering

Filtering consists in removing signals from the in-

put. Brushing (Shneiderman, 1994) is one example:

specifying values ranges and using logical operators

(Martin and Ward, 1995), allows to render only a por-

tion of the polylines, reducing visual clutter and over-

plotting. However, brushing is of little use with non-

Figure 1: Comparison of evaluations of 26 visualiza-

tion techniques in relation to standard Parallel Coordinates

(2DPC). ”A yellow colour indicates no signiﬁcant differ-

ence in performance. A green colour means that the tech-

nique outperforms 2DPC for the speciﬁc task. A red colour

means that the technique performs worse than 2DPC. A

light blue colour shows that no evaluation has been found

in the literature. O denotes that the technique is based on

animation” (Johansson and Forsell, 2016). Source: Johans-

son and Forsell (2016).

ordered categorical dimensions: selecting a range of

categories is not useful since their order does not have

any meaning. A good way to implement ﬁltering for

non-ordered dimensions is to allow the user to select

a discrete amount of categories instead of a range, by

using checkboxes.

2.1.2 Aggregation

Aggregation techniques are based on the principle of

grouping data, and representing aggregate items in-

stead of individual samples (Heinrich and Weiskopf,

2013). Such aggregates include mean, median or

cluster centroid of a subset of samples. Density func-

tions are another method, and allow to reveal dense ar-

eas and clusters in the data: the mathematical model

of density in parallel coordinates proposed by Hein-

rich and Weiskopf (2009) is an example of this tech-

nique. The Angular Histogram (Geng et al., 2011) is

another example of this approach: a vector-based bin-

ning depicts the distribution of the data. For their part,

geometry-based techniques map the clusters to en-

velopes (Moustafa, 2011) or to bounding boxes (Fua

et al., 1999).

Frequency-based representations show the distri-

bution of data samples in each category, like the par-

allel coordinate dot plot (Dang et al., 2010), which

overcomes the problem of overplotting by adding a

dot plot to each axis. Kosara et al. (Kosara et al.,

2006) developed the Parallel Sets: they represent each

category with a parallelogram scaled according to its

corresponding frequency (Figure 2c) and connecting

Parallel Bubbles - Evaluation of Three Techniques for Representing Mixed Categorical and Continuous Data in Parallel Coordinates

253

the axes. This method is best suited for data contain-

ing exclusively categorical dimensions: it does not

provide a good way to integrate continuous data since

each continuous dimension axis is divided into bins,

”and thus, transformed into a categorical dimension.”

Moreover, outliers are impossible to detect with this

method. The authors note that ”showing continuous

axes as true Parallel Coordinates dimensions would

of course be the most useful display of this data”.

2.1.3 Spatial Distortion

Spatial distortion techniques consist in scaling the dis-

tance between the ticks on an individual axis accord-

ing to a meaningful criterion, or in modifying the dis-

tance between two axes. A few examples of spatial

distortion are the ﬁsheye view and the linear zoom

(Heinrich and Weiskopf, 2013), or the method pro-

posed by Teoh and Ma (2003) deﬁning frequency-

based intervals on categorical axes. Spatial distortion

can help in several ways: it reduces clutter, clariﬁes

dense areas and facilitates the brushing of individual

lines with a pointing device (Heinrich and Weiskopf,

2013). Rosario et al. (2003) present a way to give a

meaning to the spacing between the levels of a cat-

egorical dimension: similar levels are closer to each

other. Their approach transforms levels into numbers

with techniques similar to Multiple Correspondence

Analysis. By doing so, the spacing among levels con-

veys semantic relationships. Their method consists in

three steps:

1. The Distance step consists in identifying a set of

independent dimensions that allow to calculate the

distance between their nominal levels.

2. The Quantiﬁcation step uses the distance infor-

mation to assign order and spacing among nomi-

nal levels.

3. The Classing step uses results from the previous

step to determine which levels within a dimension

are similar to each other, grouping them together.

This method can also be used at the dimensions

scale, to assign spacing among the axes given a sim-

ilarity measure. Heinrich and Weiskopf (2013) ad-

vocate precaution regarding the use of this method at

the dimensions scale. They state that ”horizontal dis-

tortion affects angles and slopes of lines, which can

have an impact on the accuracy of judging angles”,

and hence the correlation levels. Like ﬁltering meth-

ods, spatial distortion does not restore the missing fre-

quency information since overplotting is still present.

2.1.4 Colors

Using colors is an efﬁcient way to represent and iden-

tify a small set of categories. However, this approach

does not scale well with large amounts of categories,

since it is difﬁcult for the human visual system to re-

liably distinguish more than twelve colors (Heinrich

and Weiskopf, 2013).

2.2 Research Guidelines

In a recent paper, Johansson and Forsell (2016) per-

formed a survey on 23 existing papers that present

user-centered evaluations of the standard 2D Paral-

lel Coordinates technique and its variations. They

highlight the fact that despite the large number of

publications proposing variations of Parallel Coor-

dinates, only a limited number present results from

user-centered evaluations. Figure 1 gives an overview

on the performance of 26 techniques in relation to

standard Parallel Coordinates (2DPC), for 7 tasks.

We therefore conclude that up to now, many types of

tasks have not been assessed yet (conﬁguration, visual

mining) and some visualization methods are missing

(Trellis Plot, Scatterplot matrix). Moreover, the com-

parison lacks information about the nature of the data

(continuous, categorical, mixed) that was visualized.

They categorize the evaluations as follows :

1. Evaluating axis layouts of Parallel Coordinates.

2. Comparing clutter reduction methods.

3. Showing practical applicability of Parallel Coor-

dinates.

4. Comparing Parallel Coordinates with other data

analysis techniques.

The enhancement of the visualization of mixed

categorical and continuous data falls into the cate-

gories 1 and 2. Evaluating axis layouts of Parallel

Coordinates includes ”techniques for arranging axes

in 2D Parallel Coordinates in order to highlight spe-

ciﬁc types of relationships, or for reducing clutter”.

They discuss seven studies that evaluated the axis

layouts of Parallel Coordinates. They note that ”the

2D Parallel Coordinates axis layout is both effective

and efﬁcient for tasks involving comparing relation-

ships between variables”. This layout is qualiﬁed as

intuitive ”and novice users learn it without effort”.

They underline the need to investigate and study sys-

tematically the differences between axis layouts with

different tasks and users.

To sum up, there still lacks an evidence of mea-

surable beneﬁts that would encourage the use of a

variation of Parallel Coordinates over standard ones

(Johansson and Forsell, 2016). It is unclear whether

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

254

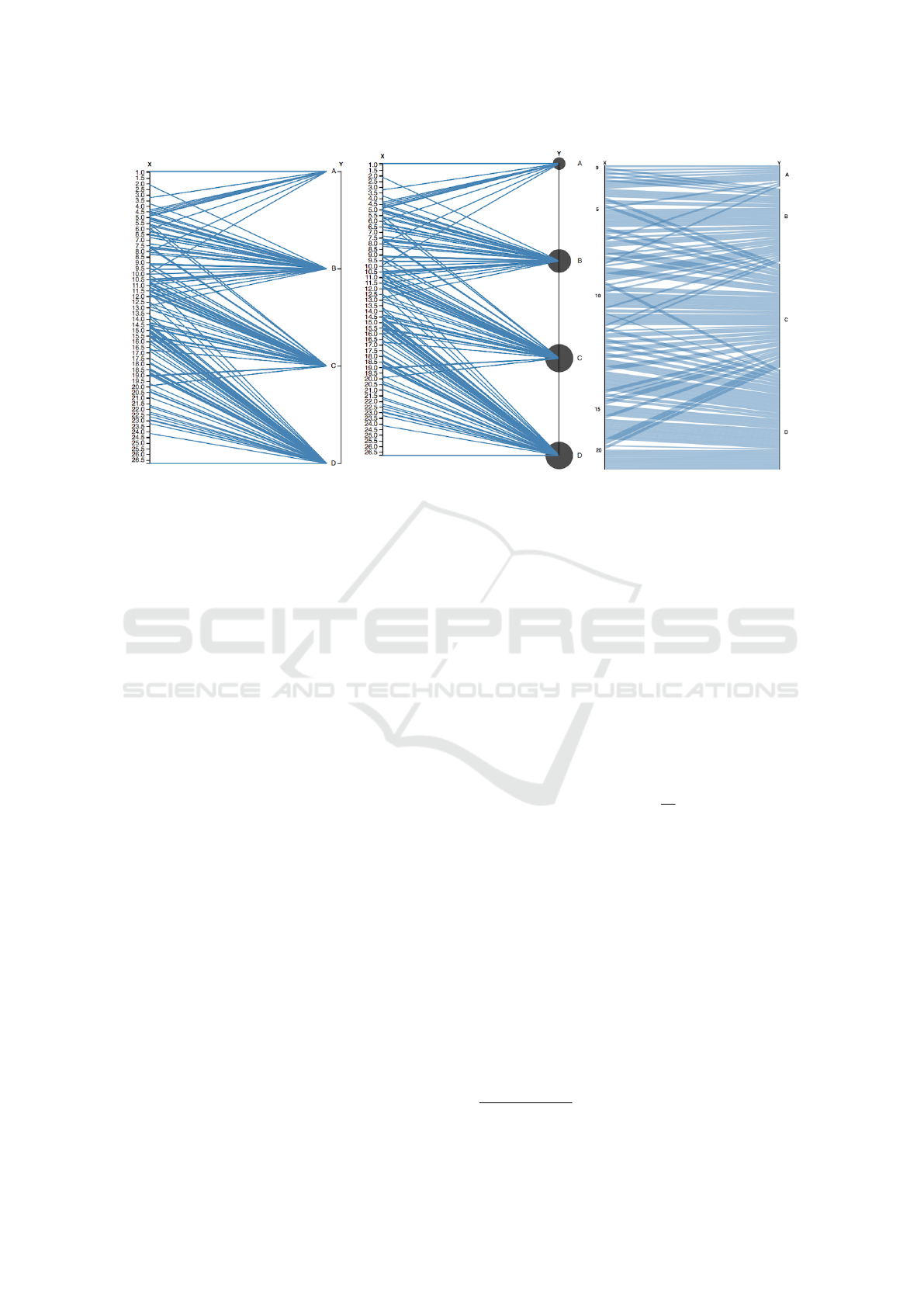
(a) Parallel Coordinates. (b) Parallel Bubbles. (c) Parallel Sets.

Figure 2: The three variants of Parallel Coordinates that we compared. The left axis is continuous, the right axis is categorical.

Here, the dataset 2 (medium correlation) is represented.

frequency-based techniques positively affect the abil-

ity of users to quickly and reliably identify patterns

in the data: do they correctly interpret categorical di-

mensions? Do these methods allow for a better per-

formance in standard data analysis tasks?

Therefore, we focus our research on testing the ef-

fect of adding a frequency encoding for categorical di-

mensions on basic data analysis tasks. The outcomes

of this study should allow to tell if a a frequency-

enhanced version of Parallel Coordinates allows the

user to accomplish conﬁguration tasks signiﬁcantly

faster than with regular Parallel Coordinates. The

next chapter describes the protocol of our user exper-

iment.

3 THE STUDY: PARALLEL

COORDINATES, PARALLEL

BUBBLES AND PARALLEL

SETS

The goal of our study is to compare the performance

of three variants of Parallel Coordinates in similarity

and frequency tasks, in order to verify if the addition

of a visual encoding of frequency results in a signiﬁ-

cant difference in performance. Our approach, Paral-

lel Bubbles, aims to enhance the visual perception of

categorical dimensions by adding a visual encoding

of frequency.

3.1 Visual Metaphor

The cornerstone of Parallel Bubbles is a ”bubble” (a

circle) of variable radius that represents a categorical

level. It was inspired by the ”bubble plot” invented

more than two centuries ago by Playfair (1801). A

similar feature has already been available in Parabox

by Advisor Solutions and is presented in Few (2006).

The area of the bubble is linearly proportional to the

amount of items that belong to the said value: the

radius r

of each bubble b is deﬁned by computing

the square root of the number of items n

belonging

to one category, and then multiplying this number by

two:

= 2

√

(1)

Sets of vertically aligned bubbles are arranged on

each categorical axis. Continuous dimensions are rep-

resented as regular Parallel Coordinates axes, and are

easily distinguishable from the categorical ones. As in

Parallel Coordinates, each data item is represented by

a polyline passing through each of the continuous and

categorical axes. This approach gives an overview of

the distribution of categories inside a dimension, and

restores the frequency information that was lost be-

cause of overplotting: the size of a bubble gives an

information about the amount of lines that intersect at

a given point on the axis.

https://www.advizorsolutions.com/articles/parabox

Parallel Bubbles - Evaluation of Three Techniques for Representing Mixed Categorical and Continuous Data in Parallel Coordinates

255

3.2 Advantages

This method offers several advantages: ﬁrst, it has

a low computational complexity when compared to

density models (Heinrich and Weiskopf, 2009) and

kernel density estimators, making it a suitable solu-

tion even for large datasets. Secondly, bubbles offer a

minimal learning curve: it is a simple add to Parallel

Coordinates, which are widely used nowadays. Third,

Parallel Bubbles are easy to implement: one bubble

has to be added to each categorical value, which is

a trivial task with today’s available data visualization

javascript libraries, like D3.js

for example.

3.3 Hypothesis

Our hypothesis is that the three types of visualizations

induce a signiﬁcant difference in performance, in fre-

quency and similarity tasks. We also formulate the

following sub-hypotheses: Parallel Coordinates (ab-

breviated ”ParaCoord”) offer the best performance for

similarity tasks, because the representation of refer-

ences as lines allow to assess the level of correlation

easily. Next, Parallel Sets (”ParaSet”) offer the best

performance for frequency tasks because of the visual

encoding of frequency they implement. Finally, Par-

allel Bubbles (”ParaBub”) should be a good compro-

mise in terms of performance for both types of tasks,

with a signiﬁcantly better performance than Parallel

Coordinates in frequency tasks due to the add of a

frequency encoding, and a signiﬁcantly better perfor-

mance than Parallel Sets in similarity tasks thanks to

the aforementioned advantages of representing links

between dimensions in the form of polylines. We de-

scribe the three tested variants of Parallel Coordinates

as follows (Figure 2):

• ParaCoord – standard Parallel Coordinates (Fig-

ure 2a). This method is sensible to clutter

and overplotting problems, making the frequency

tasks harder to complete.

• ParaBub – Parallel Coordinates, with the addi-

tion of bubbles on axes, a visual encoding of fre-

quency for categorical values (”Y” axis) (Figure

2b). This makes the frequency of categorical val-

ues easier to estimate. The similarity between di-

mensions is still easy to assess too, thanks to the

graphical representation of links between dimen-

sions in the form of polylines.

• ParaSet – a variant of Parallel Coordinates, en-

coding frequencies according to the height of the

categorical segment on the axis (Figure 2c). The

D3.js: https://d3js.org/

continuous axis, ”X”, is only showing a few val-

ues on the graduation. The height between two

given values on the continuous axis is propor-

tional to the number of items belonging to the

range. With this visualization method, similarity

tasks should be harder to complete because the

polylines are replaced by colored areas, adding

a layer of complexity (namely the height of each

area) that is not directly relevant to the task. This

visualization method should offer the best results

for frequency tasks.

In order to evaluate the performance of participants

on the three visualizations, we established three data

analysis tasks. We describe them in the next section.

3.4 Tasks

The tasks that we submitted to the participants only

represent a subset of the tasks commonly carried out

by data analysts – these include, among others, clus-

ters and outliers identiﬁcation, classiﬁcation, or selec-

tion of single data points. According to Fernstad and

Johansson (2011), ”the overall task of data analysis is

to identify structures and patterns within data. Most

patterns, such as correlation and clusters, can be de-

ﬁned in terms of similarity. Hence, the most relevant

general tasks to focus on are, in our opinion, the iden-

tiﬁcation of relationships in terms of similarity.” They

also state that ”when it comes to analysis of categor-

ical data the frequency of categories, i.e. the relative

number of items belonging to speciﬁc categories or

combinations of categories, is often of major interest

and is, as mentioned previously, the main property of

focus in categorical data visualization.” With this in

mind we deﬁned the two types of tasks as follows:

1. Similarity – identify structures in data. To suc-

ceed, the user needs to be able to estimate the

strength of the correlation (Figure 4a).

2. Frequency – the user has to estimate the amount

of items belonging to a given categorical value.

Being able to identify the single most represented

category is important too (Figures 4b and 4c).

On this basis, we deﬁned the three following data

analysis tasks:

• (T1) Similarity task – Are the X and Y axes cor-

related? Possible answers: Strongly, mildly, not

at all (Figure 4a).

• (T2) Frequency task – What proportion of lines

have the value B for the Y axis? Possible answers:

a range of values from 0% to 100%, by step of

10% (Figure 4b).

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

256

Figure 3: First task asked to participants in the tutorial. This

ﬁgure was shown to participants assigned to the Parallel

Bubbles.

• (T3) Frequency task – What is the most repre-

sented value on Y axis? Possible answers: A, B,

C, D (Figure 4c).

We reduced interaction capacities as much as pos-

sible in order to minimize the amount of dependent

variables and to obtain more robust results. Thus, we

did not allow the user to manually reorder the axes, to

change the position of categorical values on the axis

and to delete, add or group dimensions together.

3.5 Study Material

We submitted the tasks in the form of an online sur-

vey

and participants were recruited via Proliﬁc

, a

crowdsourcing platform dedicated to research sur-

veys. In total, 367 participants ﬁlled out the survey.

Each of them was paid 0.70£. A tutorial was pro-

posed in the beginning of the survey. It explained the

assigned visualization method and the two types of

SurveyMonkey: https://www.surveymonkey.com

Proliﬁc: https://www.proliﬁc.ac/

(a) Task 1: similarity.

(b) Task 2: frequency.

Figure 4: The three tasks, as asked to the participants using

the Parallel Bubbles, on the dataset 2.

Parallel Bubbles - Evaluation of Three Techniques for Representing Mixed Categorical and Continuous Data in Parallel Coordinates

257

tasks. At the end of it, participants had to complete

three questions about a ﬁctive dataset with the highest

level of correlation (the dataset and task 1 are shown

in Figure 3). These tasks allowed to screen out partic-

ipants who didn’t meet basic criteria for our study:

• (T1) Similarity task – Are the Weight and Fruit

variables correlated? Possible answers: Strongly,

mildly, not at all.

• (T2) Frequency task – How many of the fruits

do you estimate to be tomatoes (in %)? Possible

answers: a range of values from 0% to 100%, by

step of 10%.

• (T3) Frequency task – Which fruit type is

the most represented? Possible answers: Pea,

Tomato, Coconut.

We followed the design recommendations of Kit-

tur et al. (2008) in order to maximize the usefulness

of the data we collected: answers to the questions are

explicitly veriﬁable, and ﬁlling them out accurately

and in good faith requires the same amount of effort

than a random or malicious completion. In the next

part of the questionnaire, we tested the visualization

methods on three datasets presenting different levels

of correlation. Using different datasets should allow

to get more robust results. In order to fully control the

correlation levels, we generated the data ourselves:

we generated three datasets with a Python script,

with a size large enough to generate overplotting

(465 to 480 data items). We used two-dimensional

datasets because the tasks that we deﬁned are com-

parison tasks, i.e. requiring the user to assess two

dimensions at a time; this type of task focuses the

user’s attention on the smallest level of granularity

offered by Parallel Coordinates. As explained above,

multidimensional data exploration is based upon a

subset of tasks of this type. Therefore, we chose

to use one continuous dimension X and one cate-

gorical dimension Y for our datasets. The function

random.multivariate normal(mean,cov,size)

from the numpy library allowed us to generate random

samples from a multivariate normal distribution. For

each dataset we ran this function three times using

overlapping input ranges (e.g. for one dataset: [0, 20],

[10, 30] [20, 40]) in order to make the distribution

more even. The cov argument contained the covari-

ance matrix which allowed to control the variation

of the variable X in regard to the variable Y, by

multiplying the elements C

x,y

and C

y,x

by an index

taking the values 0.0 (no correlation), 0.8 (medium

correlation) and 1.0 (strong correlation) for each

dataset.

3.6 Experimental Design

We designed the study as a ”between-group”. The

independent variables were the type of visualization

(ParaCoord, ParaBub or ParaSet) and the type of data

(no correlation, medium correlation and strong corre-

lation). The presentation order of the three datasets

was counterbalanced using the Latin square proce-

dure (Graziano and Raulin, 2010), giving 6 data or-

der variants for each visualization method, for a total

of 18 questionnaires. Each participant was assigned

one visualization method. To avoid any learning bias,

each of the three datasets was shown only once to

each participant, in the order deﬁned by the Latin

square method. Each participant had to follow a tu-

torial explaining the visualization method assigned to

him, and then had to perform 9 tasks: 3 tasks on each

of the 3 datasets.

3.7 Procedure

In order to grade the visual analysis capacities of par-

ticipants on each visualization method, we placed a

written tutorial in the beginning of the survey, using

a two-dimensional dataset of fruits and vegetables,

along with their respective weights. The categorical

value was the fruit or vegetable type (pea, tomato, co-

conut, strawberry), and the continuous value was the

weight of each data item. At the end of the tutorial,

participants had to perform a set of explicitly veriﬁ-

able qualiﬁcation tasks. We used the results of these

tasks to exclude negligent participants and keep the

remaining for further analysis. Participants were in-

formed in the beginning of the survey that we would

evaluate the performance of the visualization tech-

niques rather than their individual performance. Once

the tutorial was completed, each participant had to ﬁll

in the main part of the survey. Using the selected visu-

alization method, they had to complete the three tasks

described above, for each dataset.

3.8 Results

This section aims to compare the results of the partic-

ipants who present the best expertise in data analysis

tasks. We selected the participants who completed the

tutorial questions with the highest scores. The aim is

to get the most representative results for a usage by

expert data analysts.

Before computing the results, we preprocessed the

data by deleting the answers of 5 participants who had

completed the ﬁrst task only (1 for ParaCoord and 4

for ParaSet), 10 participants who timed out, and 1 par-

ticipant who completed the questionnaire too quickly

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

258

Figure 5: Frequency histogram for the distribution of the

completion time of the full questionnaire.

(6 seconds), leaving a total of 356 participants.

We wanted to determine with which visualization

method the most ”expert” users obtained the best per-

formance. In order to keep only answers made by

users that completely understood the tasks, we re-

moved the answers of the participants who had made

at least one mistake in the questions 1 and 3 of the tu-

torial, and who answered more than 10% away from

the correct percentage in the question 2. The odds

of answering correctly by chance to the 3 questions

of the tutorial were thus 1/3 * 3/11 * 1/3, about 3%.

We then conducted a χ

test that revealed no signiﬁ-

cant difference between the three visualization meth-

ods (p < 0.05). This means that the results of the

qualiﬁcation questions were not mainly inﬂuenced by

the visualization method, but rather by the analysis

capabilities of the participants. This qualiﬁcation ﬁl-

tering left us with the answers of 241 participants’ to

analyze: 78 for Parallel Coordinates, 76 for Parallel

Bubbles and 87 for Parallel Sets.

We did not take the completion time into account

for our analysis, because too many variables can af-

fect the time spent on the questionnaire for an online

questionnaire. Establishing a threshold for the time

spent on tasks ”[...] may not adequately identify non-

conscientious participants, and may inadvertently dis-

qualify many others” (Downs et al., 2010). Figure 5

shows the distribution of completion time for all par-

ticipants. It has a positively skewed unimodal shape,

which is typical to response time distributions (Heath-

cote et al., 1991).

3.8.1 Tasks Performance

For the task T1 (similarity) and T3 (frequency),

whose answers are dichotomous (true or false), we

computed the error rate for each participant. For task

(a) Factor: Visualization method

Figure 6: The Post Hoc tests performed on the results of the

task 1.

T2 (frequency), the answer was given in %, by step

of 10%. It should be noted that the true percentage

value could only be approximated with the proposed

answers – for example, the real proportion of B was

16.77% in the Data 1, and the closest answer the user

could give was 20%. For consistency with other stud-

ies (Heer and Bostock, 2010; Skau and Kosara, 2016),

we computed the log absolute error of accuracy in this

way: log

(|judgedvalue −truevalue|+

). We per-

formed an analysis of variance (ANOVA) (Graziano

and Raulin, 2010) on the results of the three tasks,

followed by a Bayesian ANOVA and Post Hoc tests.

3.9 Task 1

The average error rate of T1 can be seen in Figure

7. The Parallel Sets returned the best error rate, fol-

lowed by the Parallel Bubbles. We performed an

ANOVA which revealed no signiﬁcant difference be-

tween the three factors ”Visualization method”, with a

p-value of 0.0809. The Parallel Sets are returning the

best performance, which is surprising considering the

fact that they present the largest visual clutter due to

their area representation. We performed a Bayesian

ANOVA followed by Post Hoc tests that conﬁrmed

the results of the ANOVA (Figure 6). For the lev-

els ”Parallel Bubbles” and ”Parallel Coordinates” of

the factor ”Visualization method”, the Bayes Factor

corresponds to substantial evidence for the null hy-

pothesis (H0). For the levels ”Parallel Bubbles” and

”Parallel Sets”, the Bayes Factor corresponds to anec-

dotal evidence for H0. For the levels ”Parallel Coordi-

nates” and ”Parallel Sets” of the factor ”Visualization

method”, the Bayes Factor corresponds to substantial

evidence for the alternative hypothesis (HA). These

results suggest that for a similarity task, there is no

signiﬁcant difference in error rate between the Par-

allel Bubbles and the two other visualization meth-

ods. There is an anecdotal evidence for an effect of

the factors ”Parallel Coordinates” and ”Parallel Sets”

for HA.

3.10 Task 2

For T2 (frequency), we computed the mean of quar-

tiles 1 and 3 for the log absolute error, and the 95%

Parallel Bubbles - Evaluation of Three Techniques for Representing Mixed Categorical and Continuous Data in Parallel Coordinates

259

ParaCoord ParaBub ParaSet

0.2

0.4

0.6

0.8

0.41

0.37

0.31

Error rate

Figure 7: Average error rate for T1 (similarity) on all

datasets. Error bars show 95% CI. The ANOVA indicates

that the means of the factor ”Visualization method” are not

signiﬁcantly different.

conﬁdence interval (Table 1 and Figure 8). We con-

structed the 95% percentile interval based on 1000

bootstrap iterations. As for the ﬁrst task, the Parallel

Sets give the minimal error rate. A decomposition by

type of data (1 = no correlation, 2 = medium correla-

tion, 3 = strong correlation) shows that the strongly

correlated data lead to the smallest error rate. We

performed a multiway ANOVA to test the effects of

the multiple factors (”visualization method”, ”data”)

on the mean of the vector ”Score”. It results that

only the mean responses for levels of the factor ”data”

are signiﬁcantly different with a p-value smaller than

0.05. The multiple comparison shows that two groups

can be made based on the factor ”data” (see Figure

9): the ﬁrst group is composed of the levels 1 and

2 (strong and medium correlation), and the second

group is composed of the level 3 (strong correlation).

The Bayesian ANOVA, followed up with a Post Hoc

test, conﬁrms these results (Figure 10). For the fac-

tor ”data”, the Bayes Factor corresponds to substan-

tial evidence for H0 for the levels 1 and 2 (inexistent

and medium correlation). Between the levels 1 and

3, and 2 and 3, there is decisive evidence for an ef-

fect of the data type for HA. The dataset 3 (strongly

correlated), with no lines intersecting, leads to a sig-

niﬁcantly lower error rate than the two other datasets.

3.11 Task 3

The average error rate of task T3 (frequency) can

be seen in Figure 11, showing the same ranking in

the visualization types as for T1 and T2. The mul-

tiway ANOVA reveals a signiﬁcant difference be-

tween the three visualization methods. The Post Hoc

test performed after the Bayesian ANOVA suggests

Table 1: T2: Average of quartiles Q1 and Q3, for the log

absolute error. 95% conﬁdence intervals. Split by visual-

ization type. ANOVA: F(39.23) = 1.880 21e−15, p < 0.01.

Type Log error CI 95%

ParaCoord 2.093 ±0.178

ParaBub 2.094 ±0.165

ParaSet 2.018 ±0.150

Figure 8: T2: Average of quartiles Q1 and Q3, for the log

absolute error, for all datasets. 95% conﬁdence intervals.

a very strong evidence for an effect of the Visual-

ization method for the levels ”Parallel Coordinates”

and ”Parallel Bubbles” for HA, and a decisive evi-

dence for the levels ”Parallel Coordinates” and ”Par-

allel Sets” for HA, and ”Parallel Bubbles” and ”Par-

allel Sets” for HA too.

3.12 Discussion

The analysis of tasks T1 and T2 did not yield any sig-

niﬁcant difference between any of the three visualiza-

tion methods. For T1, we can conclude that Paral-

lel Sets and Parallel Bubbles are suitable for similar-

ity tasks that consist in assessing the level of corre-

lation between a categorical and a continuous dimen-

sion. The same can be said for T2: the three visualiza-

tion methods are equivalent regarding the error rates.

This task was the most complex, since it required to

pick one answer out of the 11 available. For the task

T3, Parallel Sets signiﬁcantly outperformed the two

other methods, and Parallel Bubbles are signiﬁcantly

better than Parallel Coordinates. This partially con-

ﬁrms one of our sub-hypotheses: adding a frequency

encoding does have a signiﬁcant inﬂuence on perfor-

mance with a frequency task consisting in identifying

the most represented category.

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

260

Figure 9: The distribution of Log Error per chart type, for task T2. The error bars show 95% CI and the middle black lines

represent the median for each box plot. The multiple comparisons for the multiway ANOVA show a signiﬁcant effect of the

factor Data on the vector ”Log Error”. The two grouping variables are visualization method and data. Data points beyond the

whiskers are displayed using +.

(a) Factor: Visualization method

(b) Factor: data

Figure 10: The Post Hoc tests performed on the results of

the task 2.

Regarding the factor ”data”, we clearly identiﬁed

two clusters: one is composed of the data with no cor-

relation and a medium correlation, and the other clus-

ter is composed of the strongly correlated data.

We can conclude that adding a visual encoding

of frequency improves performance of the user in a

frequency task consisting in evaluating the most rep-

resented category. It does neither improve the per-

formance of the user in frequency tasks consisting in

evaluating the proportion of samples belonging to a

given category, which is somewhat surprising, nor for

a similarity task consisting in assessing the level of

correlation.

For the task T3, the better performance of Paral-

lel Sets in comparison with Parallel Bubbles might

be caused by the difference of accuracy with which

ParaCoord ParaBub ParaSet

0.2

0.4

0.6

0.8

***

0.54

0.4

0.2

Error rate

Figure 11: Average error rate for T3 (frequency) on all

datasets. Error bars show 95% CI. The ANOVA indicates

that the means of all three visualization methods are pair-

wise signiﬁcantly different.

we perceive the channels used. Parallel Bubbles use

an area encoding: the area of bubbles is linearly pro-

portional to the number of items, the radius of a bub-

ble being equal to the square root of the frequency,

multiplied by two. For Parallel Sets, we use a length

encoding: the height of the boxes was deﬁned as

linearly proportional to the frequency. The differ-

ence in performance when using these two encodings

can be explained by Steven’s Psychophysical Power

Law (Stevens, 1975a): this law states that the appar-

Parallel Bubbles - Evaluation of Three Techniques for Representing Mixed Categorical and Continuous Data in Parallel Coordinates

261

Figure 12: The psychophysical power law of Stevens

(Stevens, 1975a) for the Area and Length encodings. ”The

apparent magnitude of all sensory channels follows a power

function based on the stimulus intensity.”

ent magnitude of an area is perceptually compressed

(by a factor of 0.7), while the perception of length is

very close to the true value (see ﬁgure 12). Based on

these results, in the conclusion we propose a few ap-

proaches to improve the Parallel Bubbles.

4 CONCLUSION AND FUTURE

WORKS

Our study attempted to ﬁnd out which visualization

method gives the best performance for typical data

analysis tasks. Participants were asked to perform

three types of tasks: in the ﬁrst task (T1) participants

had to assess the level of correlation between the con-

tinuous and the categorical dimension. In the second

task (T2), they had to estimate the percentage of sam-

ples belonging to a given category. In the third task

(T3), they had to assess which of the four categories

was the most represented. Our hypothesis is invali-

dated for the tasks T1 and T2: for these two tasks,

adding a visual encoding of frequency does not em-

power the user with signiﬁcantly better data analysis

capabilities. However, the results of task T3 conﬁrm

one of our sub-hypotheses: a visual encoding of fre-

quency in the form of bubbles (Parallel Bubbles) or

lines (Parallel Sets) results in a signiﬁcant difference

in performance between all three visualization meth-

ods for a frequency tasks consisting in identifying the

most represented categorical value.

Parallel Sets delivered the best performance in all

tasks, but Parallel Bubbles present two main advan-

tages over Parallel Sets: ﬁrst, they are easier to im-

plement, requiring the simple add of a circle on each

categorical value of a Parallel Coordinates plot. Sec-

ond, they are best suited for continuous values. Thus

we recommend the use of Parallel Bubbles for basic

data analysis tasks performed on mixed categorical

and continuous datasets.

As future works, it would be interesting to further

extend the Parallel Bubbles method, implement it in a

functional system and use it in a real context. It would

be pertinent to test it in a use case. Having explicitly

veriﬁable tasks in the beginning of the survey allowed

us to ﬁlter out non-expert users. However, in a fu-

ture study, the tutorial could be improved by signal-

ing more clearly to users that their answers would be

scrutinized, as suggested by Kittur et al. (2008). This

would likely increase the time spent on tasks, and the

quality of the answers.

One way to improve the Parallel Bubbles would

be to replace the circles, that are evenly spaced,

but have variable areas, with vertically stacked bars

scaled proportionally to the frequency of the cate-

gorical value they represent. The user would assess

the length of segments, instead of areas. This would

counterbalance the psychophysical effects related to

area representation deﬁned by Stevens (1975b). The

effectiveness of this encoding would approach that of

Parallel Sets, and its performance in similarity and

frequency tasks would probably increase. Next stud-

ies will continue to focus on the categorical axis, com-

paring the area encoding of frequency (bubbles) with

alternative encodings such as density functions, his-

tograms and dot plots.

REFERENCES

Dang, T. N., Wilkinson, L., and Anand, A. (2010). Stack-

ing graphic elements to avoid over-plotting. IEEE

Transactions on Visualization and Computer Graph-

ics, 16(6):1044–1052.

Downs, J. S., Holbrook, M. B., Sheng, S., and Cranor, L. F.

(2010). Are your participants gaming the system?

Screening mechanical turk workers. Proceedings of

the SIGCHI conference on Human Factors in comput-

ing systems - CHI ’10, pages 2399–2402.

Fernstad, S. J. and Johansson, J. (2011). A Task Based Per-

formance Evaluation of Visualization Approaches for

Categorical Data Analysis. 2011 15th International

Conference on Information Visualisation, pages 80–

89.

Few, S. (2006). Multivariate analysis using parallel coordi-

nates. Perceptual Edge, pages 1–9.

Fua, Y.-H. F. Y.-H., Ward, M., and Rundensteiner, E.

(1999). Hierarchical parallel coordinates for explo-

IVAPP 2018 - International Conference on Information Visualization Theory and Applications

262

ration of large datasets. Proceedings Visualization ’99

(Cat. No.99CB37067), pages 43–508.

Geng, Z., Peng, Z., Laramee, R. S., Walker, R., and Roberts,

J. C. (2011). Angular histograms: Frequency-based

visualizations for large, high dimensional data. IEEE

Transactions on Visualization and Computer Graph-

ics, 17(12):2572–2580.

Graziano, A. M. and Raulin, M. L. (2010). Research Meth-

ods - A Process of Inquiry.

Havre, S. L., Shah, A., Posse, C., and Webb-Robertson, B.-

J. (2006). Diverse information integration and visual-

ization. volume 6060, pages 60600M–60600M–11.

Heathcote, A., Popiel, S., and Mewhort, D. J. K. (1991).

Analysis of response time distributions: An exam-

ple using the Stroop task. Psychological bulletin,

109(2):340–347.

Heer, J. and Bostock, M. (2010). Crowdsourcing Graphical

Perception: Using Mechanical Turk to Assess Visu-

alization Design. Proceedings of the 28th Annual Chi

Conference on Human Factors in Computing Systems,

pages 203–212.

Heinrich, J. and Weiskopf, D. (2009). Continuous parallel

coordinates. IEEE Transactions on Visualization and

Computer Graphics, 15(6):1531–1538.

Heinrich, J. and Weiskopf, D. (2013). State of the Art of

Parallel Coordinates. Eurographics, pages 95–116.

Inselberg, A. and Dimsdale, B. (1990). Parallel coordinates:

a tool for visualizing multi-dimensional geometry.

Johansson, J. and Forsell, C. (2016). Evaluation of Paral-

lel Coordinates: Overview, Categorization and Guide-

lines for Future Research. IEEE Transactions on Vi-

sualization and Computer Graphics, 22(1):579–588.

Kittur, A., Chi, E. H., and Suh, B. (2008). Crowdsourcing

User Studies With Mechanical Turk. CHI ’08 Pro-

ceedings of the twenty-sixth annual SIGCHI confer-

ence on Human factors in computing systems, pages

453–456.

Kosara, R., Bendix, F., and Hauser, H. (2006). Parallel

sets: Interactive exploration and visual analysis of cat-

egorical data. In IEEE Transactions on Visualization

and Computer Graphics, volume 12, pages 558–568.

IEEE.

Martin, A. and Ward, M. (1995). High Dimensional Brush-

ing for Interactive Exploration of Multivariate Data.

Proceedings Visualization ’95, pages 271–278.

Moustafa, R. E. (2011). Parallel coordinate and parallel

coordinate density plots. Wiley Interdisciplinary Re-

views: Computational Statistics, 3(2):134–148.

Playfair, W. (1801). Commercial and political atlas and sta-

tistical breviary (edited by h. wainer & i. spence).

Rosario, G. E., Rundensteiner, E. A., Brown, D. C., and

Ward, M. O. (2003). Mapping nominal values to num-

bers for effective visualization. In Proceedings - IEEE

Symposium on Information Visualization, INFO VIS,

pages 113–120.

Shneiderman, B. (1994). Dynamic queries for visual infor-

mation seeking. IEEE Software, 11(6):70–77.

Siirtola, H., Laivo, T., Heimonen, T., and R

aih

a, K.-J.

(2009). Visual Perception of Parallel Coordinate Vi-

sualizations. In 2009 13th International Conference

Information Visualisation, pages 3–9. IEEE.

Skau, D. and Kosara, R. (2016). Arcs , Angles , or Areas

: Individual Data Encodings in Pie and Donut Charts.

35(3).

Stevens, S. (1975a). Laws that govern behavior.(book re-

views: Psychophysics. introduction to its perceptual,

neural, and social prospects). Science, 188:827–829.

Stevens, S. (1975b). Psychophysics: Introduction to its per-

ceptual, neural and social prospects.

Teoh, S. T. and Ma, K.-L. (2003). PaintingClass: interactive

construction, visualization and exploration of decision

trees. Star, pages 667–672.

Wegman, E. J. (1990). Hyperdimensional Data Analysis

Using Parallel Coordinates. Journal of the American

Statistical Association, 85(411):664–675.

Parallel Bubbles - Evaluation of Three Techniques for Representing Mixed Categorical and Continuous Data in Parallel Coordinates

263