
Low Complex Image Resizing Algorithm using Fixed-point Integer
Transformation
James McAvoy, Ehsan Rahimi and Chris Joslin
Department of Systems and Computer Engineering, Carleton University, 1125 Colonel By Dr., Ottawa, ON, Canada
Keywords:
Resizing Algorithm, Image Halving and Doubling, DCT Transformation, Fixed-point Integer Transformation,
Subband Approximation, Low-complexity.
Abstract:
This paper proposes an efficient image resizing algorithm, including both halving and doubling, in the DCT
domain. The proposed image resizing algorithm works on a 4 by 4 DCT block framework with a lower
complexity compared to the similar previous methods. Compared to the images that were halved or doubled
through the bilinear interpolation, the proposed algorithm produces images with similar or higher PSNR or
SSIM values at the significantly lower computational cost. The test results also confirm that our approach
improves the current frequency domain resizing algorithms through the fixed-point integer transformation
which reduces the computational cost by more than 60% with negligible dB loss.
1 INTRODUCTION
Image resizing algorithms are often required to reduce
the memory space or the bandwidth required to store
or transmit videos or images. Usually, systems re-
size videos or images in the spatial domain by deci-
mation or interpolation of pixels; however, it is more
beneficial to resize them in the compressed domain,
which avoids the high computational overhead asso-
ciated with decompression and compression operati-
ons. Recently, video data is often stored in the com-
pressed format based on blocks of 4 ×4 discrete co-
sine transform (DCT) coefficients. Video compres-
sion standards such as H.264/AVC (ITU, 2012; ISO,
2012) and H.265/HEVC employ 4 ×4 fixed-point ap-
proximation of the popular DCT to transform frames
from the spatial to the frequency domain.
In the early days of developing resizing algorithms
in the Discrete Cosine Transform (DCT) domain, re-
searchers devoted effort to image
1
halving and dou-
bling problem. Some of the early contributors in this
field were Chang and Messerchmitt (Chang and Mes-
serchmitt, 1995), and Merhav and Bhaskaran (Mer-
hav and Bhaskaran, 1997) who developed resizing al-
gorithms that exploit linear, distributive and unitary
transform properties of DCT. Although image quality
was similar and often times superior than resizing in
1
Image and video frames will be used interchangeably
in this paper.
the spatial domain, the computational complexity was
almost same as spatial domain resizing techniques.
Dugad and Ahuja (Dugad and Ahuja, 2001) pro-
posed a simple fast computation algorithm for the
image halving and doubling by exploiting the low-
frequency DCT coefficients. Later, Mukherjee and
Mitra (Mukherjee and Mitra, 2002) proposed some
modifications to the Dugad and Ahuja’s algorithm
that improved the image quality and increased the
computational cost. It is worth mentioning that
both algorithms use subband approximation of DCT
coefficients while performing image resizing opera-
tions in the frequency domain. Jiang and Feng (Ji-
ang and Feng, 2002) formulated spatial relationships
of the DCT coefficients between a block and sub-
blocks. Their approach decomposes and recompo-
ses blocks of DCT coefficients. Mukherjee and Mitra
(Mukherjee and Mitra, 2005) also created several re-
sizing algorithms based on decomposition and re-
composition combined with subband approximation
such as IHAC, IDAD, LMDS, and LMUS algorithms.
Depending on the ordering of these operations, one
can vary the computational cost and the final image
quality for the resizing algorithm.
Among all image resizing algorithms presented
recently(Mukherjee and Mitra, 2005; Mukhopadhyay
and Mitra, 2004; Nam et al., 2010; Aggarwal and
Singh, 2015; Hung and Siu, 2014; Meher et al., 2014),
two of these algorithms are the base of others and of
McAvoy, J., Rahimi, E. and Joslin, C.
Low Complex Image Resizing Algorithm using Fixed-point Integer Transformation.
DOI: 10.5220/0006616901430149
In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 4: VISAPP, pages
143-149
ISBN: 978-989-758-290-5
Copyright © 2018 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
143

interest to us in this article. The first is the image
halving algorithm presented by Mukherjee and Mitra
in (Mukherjee and Mitra, 2005), i.e. Image hal-
ving through approximation followed by composition
(IHAC) and the second is its reverse doubling algo-
rithm, Image doubling through decomposition follo-
wed by approximation. Both of these algorithms in-
clude conversion matrix to compose and decompose
blocks of DCT coefficients when resizing images in
the DCT domain. These matrices consist of entries
that are the approximation of irrational numbers. Alt-
hough conversion matrices containe several zero en-
tries, matrix multiplication with blocks of DCT coef-
ficients contributes most of the overall computational
cost; however, both these algorithms have been shown
to provide greater efficiency compared to resizing in
the spatial domain (Mukherjee and Mitra, 2005; Muk-
hopadhyay and Mitra, 2004).
This paper aims to enhance the Mukherjee and
Mitra image and doubling algorithms by deriving a
fixed-point integer approximation of the conversion
matrices. Indeed, the proposed fixed-point integer ap-
proximation algorithm is very similar to the approach
used in H.264/AVC standard body in order to define
the default inverse transform process. H.264/AVC
deviated from previous video compression standards
by employing a 4 ×4 fixed-point integer transform
instead of the popular 8 ×8 DCT. This way, as repor-
ted by Malvar et al. (Hallapuro et al., 2002; Malvar
et al., 2003), a reduction in the complexity with the
negligible impact on image quality can be achieved.
In this paper, we describe how IHAC and IDDA
algorithms that are enhanced by deriving a fixed-point
integer conversion matrix from the floating-point con-
version matrix, in Section 2. The image quality per-
formance is assessed in Section 3 and then, the com-
putational cost of the proposed algorithms is exami-
ned in Section 4.
2 PROPOSED METHOD
Image halving is an operation that takes an image of
size N ×N and outputs an image of N/2×N/2, where
image doubling is the inverse operation to resize an
image with the resolution of 2N ×2N.
Supposing that b denotes a 8 ×8 block in the spa-
tial domain containing four adjacent blocks b
k
which
k ∈ {0,1,2,3} as illustrated in Fig. 1. Therefore, b
k
denotes a 4 ×4 block in the spatial domain whose
DCT coefficients are encoded as 4 ×4 block B
k
in the
compressed domain. Generally, to half an image one
needs to convert four adjacent DCT blocks B
1
, B
2
, B
3
and B
4
DCT blocks to a single 4 ×4 DCT block, B
d
.
In Mukherjee and Mitra’s IHAC algorithm, four 2 ×2
adjacent blocks (
ˆ
B
k
) are derived from the correspon-
ding 4 ×4 DCT blocks (B
k
) using subband approxi-
mation and then the 2 ×2 blocks
ˆ
B
k
are recomposed
to form a single 4 ×4 block B
d
using the conversion
matrix (Mukherjee and Mitra, 2005).
To double an image, Mukherjee and Mitra em-
ployed DCT block decomposition (Mukherjee and
Mitra, 2005). In the IDDA algorithm, as shown in
Fig. 2, a 4 ×4 DCT block denoted as B is first de-
composed using the conversion matrix to four 2 ×2
DCT blocks,
ˆ
B
k
. Then each of these blocks is trans-
formed into a 4×4 DCT block, B
k
, by using subband
approximation and zero-padding.
To halve this image the IHAC resizing algorithm
would contain the following composition step:
B
d
= A
"
ˆ
B
(2×2)
1
ˆ
B
(2×2)
2
ˆ
B
(2×2)
3
ˆ
B
(2×2)
4
#
A
T
= A ·
ˆ
B ·A
T
, (1)
Where · denotes matrix multiplication and the conver-
sion matrix, A, is as:
A =
1/
√
2 0 1/
√
2 0
0.6533 0.2706 −0.6533 0.2706
0 1/
√
2 0 −1/
√
2
−0.2706 0.6533 0.2706 0.6533
.
(2)
Note that the rows of A are orthogonal and have unit
norms, which is a necessary condition for an ortho-
gonal block transformation. All the entries in A re-
quire processors to approximate irrational numbers.
A fixed-point approximation is equivalent to scaling
each row of the conversion matrix, A, and rounding
to the nearest integer. To this end, the conversion ma-
trix is multiplied by 2.5 and then rounded. Therefore,
we have C defined as:
C = round(2.5 ·A)
=
2 0 2 0
2 1 −2 1
0 2 0 −2
−1 2 1 2
. (3)
We selected the scaling constant of 2.5 because it was
same one that the H.264/AVC designers used to de-
velop their fixed-point approximation of 4-point DCT
(Hallapuro et al., 2002; Malvar et al., 2003). To re-
store the orthonormal property of the original matrix
of A, all the values of c
i j
in row r are multiplied by
1
r
∑
j
c
2
r j
:
A = C •R, (4)
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
144
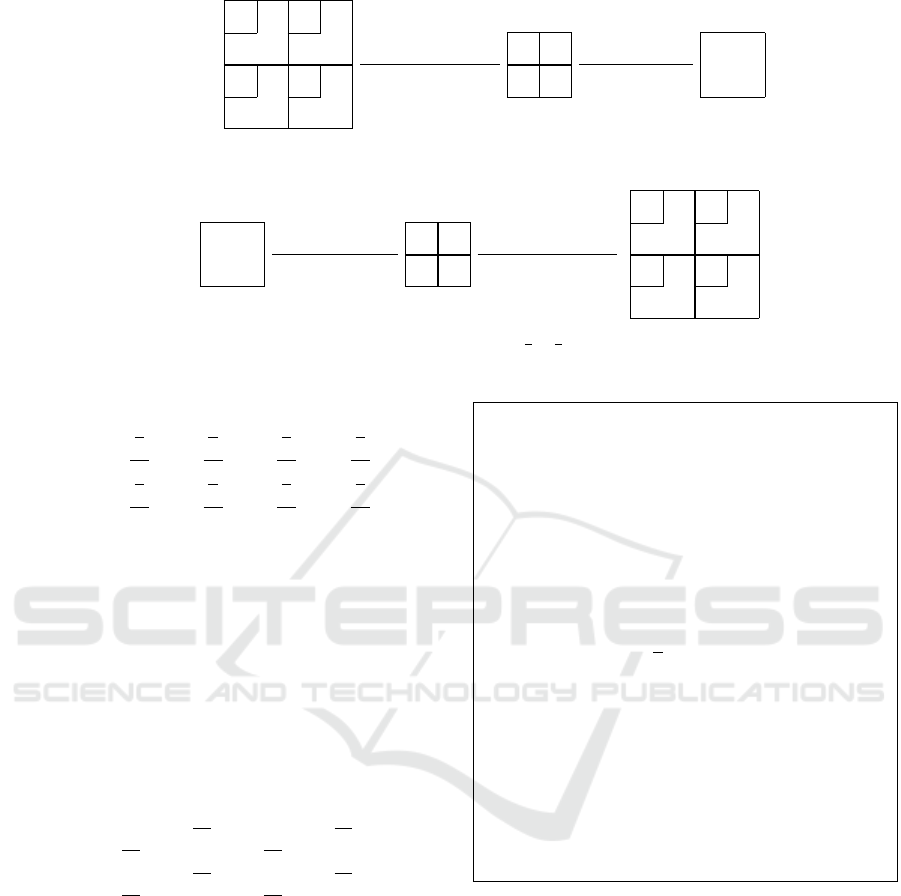
B
1
B
2
B
3
B
4
ˆ
B
1
ˆ
B
2
ˆ
B
3
ˆ
B
4
B
d
ˆ
B
3
ˆ
B
4
ˆ
B
2
ˆ
B
1
- -
Subband approximation Block composition
Block
ˆ
B
Figure 1: IHAC algorithm-Four 2 ×2 approximated DCT coefficients of adjacent blocks are composed into one 4 ×4 DCT
block (Mukherjee and Mitra, 2005).
B
ˆ
B
3
ˆ
B
4
ˆ
B
2
ˆ
B
1
ZerosZeros
ZerosZeros
ˆ
B
1
ˆ
B
2
ˆ
B
3
ˆ
B
4
- -
Block decomposition
Subband approximation
with zero-padding
Figure 2: IDDA algorithm-An 4 ×4 DCT block is decomposed into four
4
2
×
4
2
blocks where each is approximated to an 4×4
DCT block with zero-padding (Mukherjee and Mitra, 2005).
where R is defined as:
R =
1/
√
8 1/
√
8 1/
√
8 1/
√
8
1/
√
10 1/
√
10 1/
√
10 1/
√
10
1/
√
8 1/
√
8 1/
√
8 1/
√
8
1/
√
10 1/
√
10 1/
√
10 1/
√
10
,
(5)
and the operator • denotes an element-by-element
multiplication. The two-dimensional transformation
in Equation (1) can be rewritten as:
B
d
= A ·
ˆ
B ·A
T
= [C •R] ·
ˆ
B ·[C
T
•R
T
]. (6)
Rearranging to extract the scaling arrays R:
B
d
= [C ·
ˆ
B ·C
T
] •[R •R
T
]
= [C ·
ˆ
B ·C
T
] •S, (7)
Where
S = R •R
T
=
1/8 1/
√
80 1/8 1/
√
80
1/
√
80 1/10 1/
√
80 1/10
1/8 1/
√
80 1/8 1/
√
80
1/
√
80 1/10 1/
√
80 1/10
. (8)
Using the new fixed-point approximation of the con-
version matrix C with its scaling matrix S, we mo-
dified the IHAC algorithm. Fig. 3 outlines our new
proposed image halving algorithm that takes advan-
tage of these matrices in the block composition step.
Similarly, we modified the IDDA algorithm in
the decomposition step to leverage the fix-point ap-
proximation of the conversion matrix with its sca-
ling matrix. Fig 4 displays the outline of our propo-
sed fix-point approximation of the IDDA algorithm
(IDDA
f pa
).
Input: 4 ×4 block based DCT encoded image.
Output: 4 ×4 block based DCT encoded downs-
ampled image.
for every four adjacent 4×4, B
1
,B
2
,B
3
,B
4
of the
input image do
1. Subband approximation: Get correspon-
ding 2 × 2 two-point DCT blocks {
ˆ
B
(2×2)
k
},
where k ∈ {0,1, 2,3} using low-pass truncated
approximation, as follows.
ˆ
B
(i, j)
k
=
1
2
[B
(i, j)
k
], f or 0 ≤i, j ≤ 1.
2. Block composition: Convert four 2 × 2
DCT blocks to a 4 ×4 DCT block B
d
as fol-
lows.
B
d
=
C
"
ˆ
B
(2×2)
1
ˆ
B
(2×2)
2
ˆ
B
(2×2)
3
ˆ
B
(2×2)
4
#
C
T
!
•S
end for
Figure 3: Our proposed resizing algorithm, IHAC
f pa
, for
halving an image based on a 4 ×4 DCT block framework.
3 QUALITY ASSESSMENT
We developed three experiments to evaluate image
quality performance of our proposed fixed-point ap-
proximation of the IHAC and IDDA algorithms.
In the first experiment, for each image in the sam-
ple set I
orig
of size N ×N is first spatially downsam-
pled using MATLAB bicubic interpolation with anti-
aliasing to an image I
d
of size N/2 ×N/2. These
halved images provided a reference so PSNR can be
computed when comparing images produced from va-
Low Complex Image Resizing Algorithm using Fixed-point Integer Transformation
145

Input: 4 ×4 block based DCT encoded image.
Output: Upsampled image in the compressed
domain.
for each 4 ×4 blocks B do the following: do
1. Block decomposition: Convert the block to
four 2 ×2 DCT blocks as follows.
"
ˆ
B
(2×2)
1
ˆ
B
(2×2)
2
ˆ
B
(2×2)
3
ˆ
B
(2×2)
4
#
=
C
T
BC
•S
2. Subband approximation and zero pad-
ding: Compute the approximate 4 ×4-point
DCT coefficients from each of
ˆ
B
(2×2)
k
, where
k ∈{0,1, 2,3}, low-pass truncated approxima-
tion.
ˆ
B
(i, j)
k
= 2
h
ˆ
B
(i, j)
k
i
, f or 0 ≤i, j ≤ 1.
Form four 4 ×4 DCT blocks by zero padding
each of them (the high frequency components
are assigned to zero).
end for
Figure 4: Our resizing algorithm IDDA
f pa
for doubling
images based on a 4 ×4 DCT block framework.
rious halving algorithms. The original images I
orig
in
the sample set are raw grayscale (8 bits/pixel) images
with a resolution of 512 ×512 pixels. In all the expe-
riments, we applied MATLAB dct2 function to trans-
form all the images I
orig
from the spatial to the DCT
domain to represent compressed images formatted as
blocks of 4×4 DCT coefficients. We applied the DCT
resizing algorithms on the compressed I
orig
and out-
putted a compressed halved image. Using MATLAB
idct2, we transformed these newly compressed hal-
ved images back into the spatial domain where we
computed an PSNR with the reference halved images.
We also compared our proposed halving algorithm
with halved images that were resized in the spatial
domain by bilinear interpolation, which will be refer-
red as IHS. Tables 1 and 2 show the PSNR and SSIM
values computed from comparing the halved images
generated from our proposed halving algorithm with
IHAC and IHS. As can be seen in these tables, our
proposed halving algorithms produces images with
slightly lower PSNR or higher SSIM values compared
to its floating-point implementation (IHAC), which
was expected because of rounding errors associated
with integer transforms with scaling. In average, our
IHAC
f pa
algorithm generates images that are 0.13 dB
lower PSNR value or 0.0003 lower SSIM value than
ones generated from IHAC algorithm; however, ima-
ges generated from our halving algorithm have 2.27
dB higher quality than the images generated by IHS
algorithm.
Table 1: Experiment 1. PSNR values from image halving
experiment.
Image IHS IHAC IHAC
f pa
Fishing boat 39.94 42.00 41.67
Cameraman 40.47 46.09 45.47
Elaine 45.13 45.87 45.98
Goldhill 42.39 43.63 43.37
House 46.49 50.48 50.92
Jetplane 40.22 44.27 43.99
Lake 39.11 42.80 42.54
Lena 42.00 45.62 45.45
Livingroom 40.06 42.01 41.70
Mandril 36.54 36.49 36.32
Peppers 42.54 44.94 45.00
Pirate 40.83 43.25 43.07
Walkbridge 37.89 39.74 39.43
Watch 36.69 41.04 40.76
Woman blonde 41.61 42.72 42.60
Woman darkhair 48.73 51.19 51.65
mean(PSNR) 41.29 43.88 43.75
Table 2: Experiment 1. SSIM values from image halving
experiment.
Image IHS IHAC IHAC
f pa
Fishing boat 0.9920 0.9929 0.9925
Cameraman 0.9950 0.9985 0.9982
Elaine 0.9956 0.9930 0.9929
Goldhill 0.9922 0.9934 0.9931
House 0.9971 0.9992 0.9991
Jetplane 0.9951 0.9976 0.9974
Lake 0.9934 0.9958 0.9956
Lena 0.9947 0.9965 0.9963
Livingroom 0.9913 0.9935 0.9932
Mandril 0.9823 0.9845 0.9839
Peppers 0.9963 0.9960 0.9959
Pirate 0.9919 0.9949 0.9946
Walkbridge 0.9874 0.9922 0.9917
Watch 0.9952 0.9981 0.9980
Woman blonde 0.9936 0.9937 0.9935
Woman darkhair 0.9979 0.9984 0.9984
mean(SSIM) 0.9932 0.9949 0.9946
Figure 5 show the image ”Lena” generated by our
IHAC
f pa
algorithm as well as the ones obtained by
IHAC and IHS algorithms. Figure 5a is an image hal-
ved through bicubic interpolation with anti-aliasing,
which is the reference image so PSNR can be compu-
ted. Figure 5b is an image halved by our proposed al-
gorithm, IHAC
f pa
, with PSNR value of 45.45 dB. Fi-
gure 5c was downsampled through floating-point im-
plementation of the IHAC algorithm, which provide
a PSNR value of 45.62 dB. Figure 5d was a spatial
downsampled image using bilinear interpolation that
produced a PSNR value of 42.00 dB.
For the second experiment to evaluate image qua-
lity performance of our IDDA
f pa
algorithm, we first
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
146

(a) I
d
(b) IHAC
f pa
(c) IHAC (d) IHS
Figure 5: Resultant images downsampled in experiment 1.
spatially downsampled image I
orig
to create an image
I
d
that are compressed then upsampled in the DCT
domain. We used MATLAB bicubic interpolation
with anti-aliasing to halve images in the spatial dom-
ain to produce image I
d
. Using MATLAB dct2
function, we transformed the spatially halved image
I
d
to the DCT domain to represent a compressed
image formatted as blocks of 4 ×4 DCT coefficients.
Then we applied the doubling algorithms to resize
and output compressed image to the original resolu-
tion. We transformed the compressed doubled image
back into the spatial domain using MATLAB idct2
function so a PSNR value can be computed between
the upsampled image with the original image I
orig
. Si-
milar in the first experiment, we doubled the halved
image I
d
in the spatial domain using bilinear interpo-
lation for comparison, which will be referred as IDS
in the paper. Tables 3 and 3 display the results of
this experiment. As can be seen by these results, on
average our doubling approach created images only
0.07 dB lower than images that were spatially resi-
zed; however, in point of SSIM assessment there is
about 0.01 improvement. Again, our IDDA
f pa
algo-
rithm generates images with negligibly lower PSNR
and SSIM values compared to the ones generated
from IHAC algorithm; although, our IDDA
f pa
algo-
rithm is considerably less complex as shown in the
next section.
In the third experiment, an image is first halved
and then doubled. The resulting upsampled image is
compared with the original image I
orig
. We compa-
red the PSNR value computed from images genera-
ted from resizing algorithms used in tandem: spatial
resizing using IHS-IDS, IHAC-IDDA and our pro-
posed halving and doubling algorithm. The results
of this experiment are shown in Tables 5 and 6. As
can be seen from the results of this experiment, using
our proposed algorithms in tandem provides PSNR
values about 0.48 dB lower PSNR value and about
0.0048 lower SSIM value than the IHAC-IDDA pai-
ring but we observed an 1.27 dB PSNR gain or about
0.0476 SSIM gain over the spatial approach imple-
Table 3: Experiment 2. PSNR values from image doubling
experiment.
Image IDS IDDA IDDA
f pa
Fishing boat 28.94 29.40 29.11
Cameraman 33.21 33.68 32.91
Elaine 32.53 32.75 32.50
Goldhill 30.62 31.03 30.78
House 41.72 41.18 39.66
Jetplane 30.17 30.68 30.28
Lake 29.35 29.77 29.37
Lena 32.69 33.17 32.72
Livingroom 28.59 28.94 28.69
Mandril 23.05 23.49 23.38
Peppers 31.23 31.62 31.31
Pirate 29.99 30.43 30.14
Walkbridge 26.23 26.70 26.47
Watch 27.11 27.55 27.14
Woman blonde 28.99 29.38 29.19
Woman darkhair 39.84 40.04 39.44
mean(PSNR) 30.89 31.24 30.82
mented using IHS-IDS pairing.
These limited experiments demonstrated to us that
our algorithms could produced images equal or better
than resizing images in the spatial domain using bi-
linear interpolation while benefiting from the compu-
tational savings derived from our approach. The next
section will discuss how computationally efficient our
algorithms are.
4 COMPUTATIONAL COST
This section outlines the computational cost of our
proposed resizing algorithms. By using a fixed-point
approximation of the conversion matrix in our propo-
sed algorithms, we hope to decrease the computati-
onal cost. Leveraging fixed-point arithmetic, multi-
plying or dividing values that are a power of two can
be accomplished by binary shift operations. As can be
seen in Equation (3), the conversion matrix C entries
are either 0, 1’s or 2’s. Therefore, matrix multiplica-
Low Complex Image Resizing Algorithm using Fixed-point Integer Transformation
147
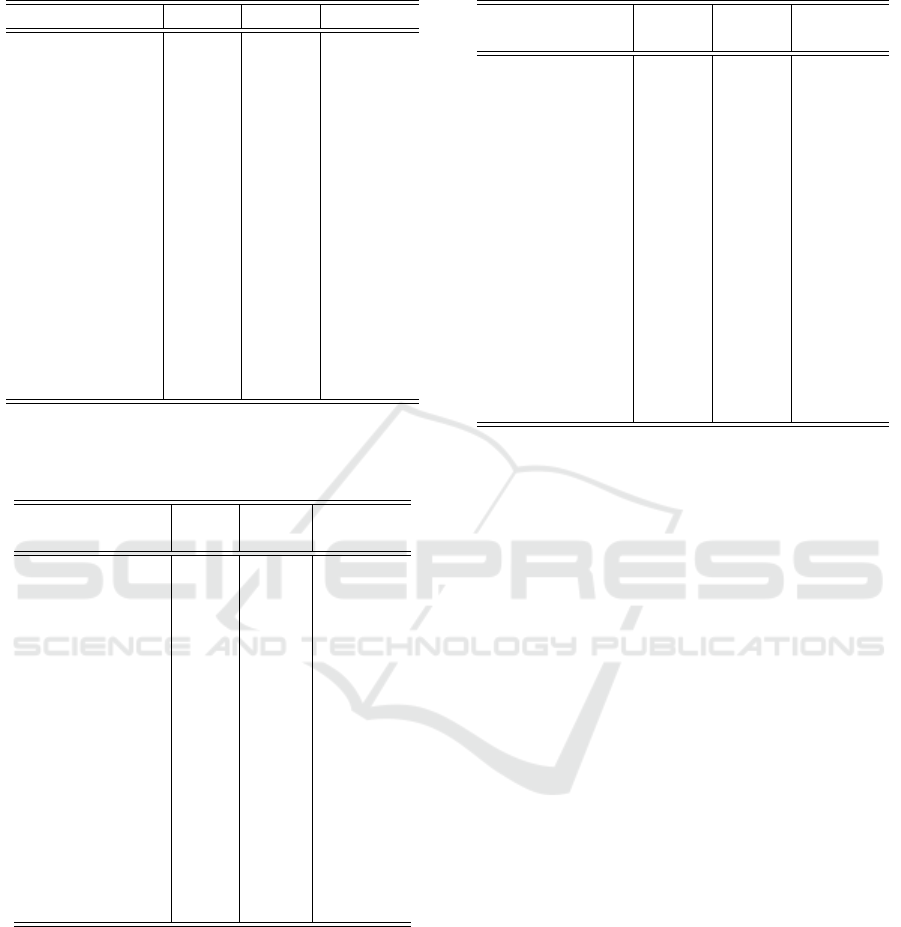
Table 4: Experiment 2. SSIM values from image doubling
experiment.
Image IDS IDDA IDDA
f pa
Fishing boat 0.8274 0.8478 0.8414
Cameraman 0.9551 0.9624 0.9539
Elaine 0.7930 0.8074 0.8038
Goldhill 0.8304 0.8527 0.8475
House 0.9838 0.9837 0.9777
Jetplane 0.9288 0.9373 0.9300
Lake 0.8610 0.8776 0.8705
Lena 0.9021 0.9140 0.9084
Livingroom 0.8194 0.8419 0.8357
Mandril 0.6576 0.7178 0.7143
Peppers 0.8829 0.8911 0.8832
Pirate 0.8565 0.8774 0.8708
Walkbridge 0.7648 0.8071 0.8009
Watch 0.9383 0.9462 0.9369
Woman blonde 0.8328 0.8526 0.8481
Woman darkhair 0.9590 0.9619 0.9587
mean(SSIM) 0.8621 0.8799 0.8739
Table 5: Experiment 3. PSNR values from image halving
followed by image doubling.
Image IHS IHAC IHAC
f pa
IDS IDDA IDDA
f pa
Fishing boat 27.99 29.64 29.37
Cameraman 31.24 33.94 33.16
Elaine 31.89 32.96 32.64
Goldhill 29.81 31.27 31.02
House 38.65 41.73 39.68
Jetplane 29.02 30.88 30.47
Lake 28.15 30.00 29.57
Lena 31.41 33.43 32.92
Livingroom 27.71 29.15 28.93
Mandril 22.52 23.71 23.62
Peppers 30.35 31.83 31.44
Pirate 29.04 30.66 30.36
Walkbridge 25.43 26.92 26.71
Watch 25.88 27.75 27.33
Woman blonde 28.34 29.59 29.40
Woman darkhair 38.43 40.39 39.48
mean(PSNR) 29.74 31.49 31.01
tions can be carried out multiplier-free.
Let assume that n
m
and n
a
are the total number of
multiplications and additions required for the image
resizing algorithm, respectively. The IHAC
f pa
algo-
rithm first performs subband approximation and mul-
tiplies each element in the input 4 ×4 DCT coeffi-
cients by half, which can be implemented as a right
shift operation; thus, there is no cost. The composi-
tion step contains two matrix multiplications by ap-
plying the conversion matrix C on input DCT coeffi-
Table 6: Experiment 3. PSNR values from image halving
followed by image doubling.
Image IHS IHAC IHAC
f pa
IDS IDDA IDDA
f pa
Fishing boat 0.7972 0.8591 0.8546
Cameraman 0.9345 0.9648 0.9586
Elaine 0.7775 0.8192 0.8158
Goldhill 0.8003 0.8644 0.8605
House 0.9728 0.9845 0.9797
Jetplane 0.9089 0.9408 0.9359
Lake 0.8335 0.8856 0.8803
Lena 0.8823 0.9200 0.9153
Livingroom 0.7854 0.8537 0.8495
Mandril 0.6038 0.7455 0.7430
Peppers 0.8678 0.8974 0.8906
Pirate 0.8260 0.8867 0.8817
Walkbridge 0.7156 0.8240 0.8197
Watch 0.9191 0.9497 0.9420
Woman blonde 0.8097 0.8635 0.8596
Woman darkhair 0.9507 0.9644 0.9609
mean(SSIM) 0.8366 0.8890 0.8842
cients twice. Since matrix multiplication with C can
be carried out multiplier-free, only additions count,
which there are n
a
= 8. An element-by-element mul-
tiplication is applied with the scaling matrix, S. As
shown in Equation (8), the scaling matrix S contains
four elements equal to 1/8, which can be implemen-
ted as a right shift operation; and twelve elements
that need to perform multiplication. thus n
m
= 12 and
n
a
= 0. Finally, the four 4 ×4 input DCT blocks re-
present 64 pixels of the input image. Therefore, on
average our method will consume n
m
= 0.1875 and
n
a
= 0.25 per pixel of the original image.
Similarly, our IDDA
f pa
algorithm contains two
matrix multiplication using the conversion matrix
C. Also, scaling matrix and subband approximation
are similar. Therefore, the proposed doubling algo-
rithm requires n
m
= 0.1875 and n
a
= 0.25 per pixel
of the upsampled image.
Table 7 and 8 compare the computational com-
plexity for the IHAC
f pa
and IDDA
f pa
algorithms
with other image halving and doubling algorithms, re-
spectively. As shown by these tables, both proposed
image halving and doubling algorithms are more effi-
cient than their floating-point implementations. When
comparing our proposed halving algorithm, IHAC
f pa
,
with its floating-point implementation, it is 63% more
efficient in n
m
and 75% in n
a
. Regarding doubling
algorithm, IDDA
f pa
, it is 91% more efficient in n
m
and 83% in n
a
when comparing with its floating-point
version, IDDA. When comparing both of our propo-
sed algorithms with spatial resizing, the computatio-
nal saving is about 85% in n
m
and 97% in n
a
.
VISAPP 2018 - International Conference on Computer Vision Theory and Applications
148

Table 7: Computational complexity of halving algorithms.
ops IHS IHAC IHAC
f pa
n
m
1.25 0.5 0.1875
n
a
8.25 1 0.25
Table 8: Computational complexity of doubling algorithms.
ops IDS IDDA IDDA
f pa
n
m
1.25 2 0.1875
n
a
8.25 1.5 0.25
5 CONCLUSION
In this paper, we developed a fixed-point approxima-
tion of a conversion matrix that is included in IHAC
and IDDA resizing algorithms. Matrix multiplications
with fixed-point approximation of the conversion ma-
trices are multiplier-free, which reduce the computati-
onal cost in the proposed resizing algorithms. Images
generated by the proposed fixed-point resizing algo-
rithms have PSNR values negligibly lower than PSNR
of those images generated by the floating-point imple-
mentations; however, the total number of multiplica-
tions and additions are substantially decreased. The
proposed fixed-point approximation also can be ex-
tended so one can resize images by integral or arbi-
trary factors. Also, there are several resizing algo-
rithms that use conversion matrices for composition
and decomposition such as IHCA, IDAD, LMDS and
LMUS, which would be good candidates for this ap-
proach.
ACKNOWLEDGEMENTS
The authors would like to acknowledge that this re-
search was supported by NSERC Strategic Project
Grant: Hi-Fit: High Fidelity Telepresence over Best-
Effort Networks.
REFERENCES
(2012). Advanced video coding for generic audiovisual ser-
vices.
(2012). Information technology – coding of audio-visual
objects – part 10: Advanced video coding.
Aggarwal, A. and Singh, C. (2015). Hybrid dct-zernike
moments-based approach for image up-sampling. In
2015 Annual IEEE India Conference (INDICON), pa-
ges 1–6.
Chang, S.-F. and Messerchmitt, D. G. (1995). Manipula-
tion and compositing of MC-DCT compressed video.
IEEE Journal on Selected Areas in Communications,
13(1):1–11.
Dugad, R. and Ahuja, N. (2001). A fast scheme for image
size change in the compressed domain. IEEE Tran-
saction on Circuits and Systems for Video Technology,
11(4):461–474.
Hallapuro, A., Karczewicz, M., and Malvar, H. S. (2002).
Low-complexity transform and quantization. In Joint
Video Team (JVT) of ISO/IEC MPEG and ITU-VCEG.
Hung, K. W. and Siu, W. C. (2014). Novel dct-based
image up-sampling using learning-based adaptive k
-nn mmse estimation. IEEE Transactions on Cir-
cuits and Systems for Video Technology, 24(12):2018–
2033.
Jiang, J. and Feng, G. (2002). The spatial relationship of
DCT coefficients between a block and its sub-blocks.
IEEE Transaction on Signal Processing, 50(5):1160–
1169.
Malvar, H. S., Hallapuro, A., Karczewicz, M., and Kerof-
sky, L. (2003). Low-complexity transform and quanti-
zation in H.264/AVC. IEEE Transaction Circuits and
Systems Video Technology, 13:598–603.
Meher, P. K., Park, S. Y., Mohanty, B. K., Lim, K. S., and
Yeo, C. (2014). Efficient integer dct architectures for
hevc. IEEE Transactions on Circuits and Systems for
Video Technology, 24(1):168–178.
Merhav, N. and Bhaskaran, V. (1997). Fast algorithms for
DCT-domain image down-sampling and for inverse
motion compensation. IEEE Transaction on Circuits
and Systems for Video Technology, 7(3):486–476.
Mukherjee, J. and Mitra, S. K. (2002). Image resizing in the
compressed domain using subband DCT. IEEE Tran-
saction on Circuits and Systems for Video Technology,
12(7):620–627.
Mukherjee, J. and Mitra, S. K. (2005). Arbitrary resizing
of images in the DCT space. In IEE Proceeding Vi-
sion, Image and Signal Processing, volume 152, pa-
ges 155–164.
Mukhopadhyay, J. and Mitra, S. (2004). Resizing of ima-
ges in the DCT space by arbitrary factors. In Image
Processing, 2004. ICIP ’04. 2004 International Con-
ference on, volume 4, pages 2801–2804.
Nam, H. M., Jeong, J. Y., Byun, K. Y., Kim, J. O., and
Ko, S. J. (2010). A complexity scalable h.264 decoder
with downsizing capability for mobile devices. IEEE
Transactions on Consumer Electronics, 56(2):1025–
1033.
Low Complex Image Resizing Algorithm using Fixed-point Integer Transformation
149
