Combined Correlation Rules to Detect Skin based on Dynamic Color

Clustering

Rodrigo Augusto Dias Faria and Roberto Hirata Jr.

Institute of Mathematics and Statistics, University of S

ao Paulo, Rua do Mat

ao 1010, S

ao Paulo, Brazil

Keywords:

Skin Detection, Human Skin Segmentation, YCbCr Color Model, Correlation Rules, Dynamic Color

Clustering.

Abstract:

Skin detection plays an important role in a wide range of image processing and computer vision applications.

In short, there are three major approaches for skin detection: rule-based, machine learning and hybrid. They

differ in terms of accuracy and computational efﬁciency. Generally, machine learning and hybrid approaches

outperform the rule-based methods, but require a large and representative training dataset as well as costly

classiﬁcation time, which can be a deal breaker for real time applications. In this paper, we propose an

improvement of a novel method on rule-based skin detection that works in the YCbCr color space. Our

motivation is based on the hypothesis that: (1) the original rule can be reversed and, (2) human skin pixels

do not appear isolated, i.e. neighborhood operations are taken in consideration. The method is a combination

of some correlation rules based on these hypothesis. Such rules evaluate the combinations of chrominance

Cb, Cr values to identify the skin pixels depending on the shape and size of dynamically generated skin color

clusters. The method is very efﬁcient in terms of computational effort as well as robust in very complex image

scenes.

1 INTRODUCTION

Skin detection can be deﬁned as the process of identi-

fying skin-colored pixels in an image. It plays an im-

portant role in a wide range of image processing and

computer vision applications such as face detection,

pornographic image ﬁltering, gesture analysis, face

tracking, video surveillance systems, medical image

analysis, and other human-related image processing

applications.

The problem is complex because of the numerous

similar materials with human skin tone and texture,

and also because of illumination conditions, ethnicity,

sensor capturing singularities, geometric variations,

etc. Because it is a primary task in image process-

ing, additional requirements as real time processing,

robustness and accuracy are also desirable.

The human skin color pixels have a restricted

range of hues and are not deeply saturated, since the

appearance of skin is formed by a combination of

blood (red) and melanin (brown, yellow), which leads

the human skin color to be clustered within a small

area in the color space (Fleck et al., 1996).

The choice of a color space is also a key point

of a feature-based method when using skin color as

a detection cue. Due to its sensitivity to illumina-

tion, the input image is, in general, ﬁrst transformed

into a color space whose luminance and chrominance

components can be separate to mitigate the prob-

lem (Vezhnevets et al., 2003).

Basically, there are three approaches for skin de-

tection: rule-based, machine learning based and hy-

brid. They differ in terms of classiﬁcation accuracy

and computational efﬁciency. Machine learning and

hybrid methods require a training set, from which the

decision rules are learned. Such approaches outper-

form the rule-based methods but require a large and

representative training dataset as well as it takes a

long classiﬁcation time, which can be a deal breaker

for real time applications (Kakumanu et al., 2007).

In this work we propose an improvement of a

novel method on rule-based skin detection that works

in the YCbCr color space (Brancati et al., 2017). Our

motivation is based on the hypothesis that the origi-

nal rule can be complemented with another rule that

is a reversal interpretation of the one proposed origi-

nally. Besides that, we also take in consideration that

a skin pixel does not appear isolated, so we propose

another variation based on neighborhood operations.

The set of rules evaluate the combinations of chromi-

Faria, R. and Jr., R.

Combined Correlation Rules to Detect Skin based on Dynamic Color Clustering.

DOI: 10.5220/0006618003090316

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

309-316

ISBN: 978-989-758-290-5

309

nance Cb, Cr values to identify the skin pixels de-

pending on the shape and size of dynamically gener-

ated skin color clusters (Brancati et al., 2017). The

method is very efﬁcient in terms of computational ef-

fort as well as robust in very complex image scenes.

2 RELATED WORK

There are a large number of works of skin detection

based on color information and there are a couple of

them comparing different techniques and classiﬁers,

mainly from the point of view of performance, color

models, skin color modeling and different datasets

(Vezhnevets et al., 2003; Kakumanu et al., 2007;

Mahmoodi and Sayedi, 2016).

In (Jones and Rehg, 2002), the authors applied

a Bayesian decision rule with a 3-dimensional his-

togram model constructed from approximately 2 bil-

lion pixels collected from 18,696 images over the In-

ternet to perform skin detection. They calculated two

different histograms for skin and non-skin in the RGB

color space. Using those histograms along with train-

ing data, a classiﬁer was derived with the standard

likelihood ratio approach of a pixel be skin to not be

skin. The best performance at an error rate of 88%

was reached for histograms of size 32.

Another method explicitly deﬁnes, through a

number of rules, the boundaries that delimit the

grouping of skin pixels in some color space (Vezh-

nevets et al., 2003). This was the approach adopted

by (Kovac et al., 2003) in the YCbCr color space,

obtaining a true positive rate of 90.66%. They (Ko-

vac et al., 2003) also performed experiments with

the chromaticity channels Cb and Cr only. The re-

sults showed that the performance of the classiﬁer is

inferior in relation to the approach using all Y, Cb

and Cr channels. The key advantage of this method

is the simplicity of skin detection rules that leads

to the construction of a very fast classiﬁer. On the

other hand, achieving high recognition rates with this

method is difﬁcult because it is necessary to ﬁnd a

good color space and empirically appropriate decision

rules (Vezhnevets et al., 2003).

Differently from (Kovac et al., 2003), the authors

of (Yogarajah et al., 2011) developed a technique

where the thresholds deﬁned in the rules are dynam-

ically adapted. The method consists of detecting the

region of the eye and extracting an elliptical region to

delimit the corresponding face. A Sobel ﬁlter is ap-

plied to detect the edges of the resulting region which

is subjected to a dilation. The resulting image is sub-

tracted from the elliptical image. As a result, there is

a more uniform skin region where the thresholds are

calculated. The technique was used as a preprocess-

ing step for (Tan et al., 2012) in a strategy combin-

ing a 2-dimensional density histogram and a Gaussian

model for skin color detection. The results showed an

accuracy of 90.39%.

(Naji et al., 2012) constructed an explicit classi-

ﬁer in the HSV color space for 4 different skin eth-

nic groups in parallel. After primitive segmentation,

a rule-based region growth algorithm is applied, in

which the output of the ﬁrst layer is used as a seed,

and then the ﬁnal mask in other layers is constructed

iteratively by neighboring skin pixels. The number of

true positive pixels reported was of 96.5%.

(Kawulok et al., 2013) combined global and local

image information to construct a probability map that

is used to generate the initial seed for spatial analysis

of skin pixels. Seeds extracted using a local model are

highly adapted to the image, which greatly improves

the spatial analysis result.

Although color is not used directly in some skin

detection approaches, it is one of the most decisive

tools that affect the performance of algorithms (Mah-

moodi and Sayedi, 2016). Despite the performance

of most skin detectors is directly related to the choice

of color space, (Albiol et al., 2001) proved that the

optimum performance of the skin classiﬁers is inde-

pendent of the color space.

RGB is the most commonly used color space

for storing and representing digital images, since the

cameras are enabled to provide the images in such

model. To reduce the inﬂuence of illumination, the

RGB channels can be normalized and the third com-

ponent can be removed, since it does not provide sig-

niﬁcant information (Kakumanu et al., 2007). This

characteristic led (Bergasa et al., 2000) to construct

an adaptive and unsupervised Gaussian model to seg-

ment skin into the normalized RGB color space, using

only the channels r and g.

In (Jayaram et al., 2004), a comparative study us-

ing a Gaussian approach and a histogram in a dataset

of 805 color images in 9 different color spaces has

been performed. The results revealed that the absence

of the luminance component, which means using only

two channels of the color space, signiﬁcantly impacts

the performance as well as the selection of the color

space. The best results were obtained in the SCT, HSI

and CIELab color spaces with histogram approach.

In (Chaves-Gonz

alez et al., 2010), the authors

compared the performance of 10 color spaces based

on the k-means clustering algorithm on 15 images

of the Aleix and Robert (AR) face image database

(Mart

ınez and Benavente, 1998). According to the re-

sults obtained, the most appropriate color spaces for

skin color detection are YCgCr, YDbDr and HSV.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

310

In (Kaur and Kranthi, 2012), an algorithm simi-

lar to that proposed by (Kovac et al., 2003) have been

implemented, where the boundaries that delimit the

grouping of skin pixels are deﬁned by explicit rules.

After segmenting the image with the explicit rules,

the algorithm also performs morphological and ﬁlter-

ing operations to improve the accuracy of the method.

The authors applied the algorithm in the YCbCr and

CIELab color spaces, ignoring the Y and L luminance

components, respectively. The results were more sat-

isfactory when the algorithm was applied on CIELab.

A similar technique was implemented in (Shaik et al.,

2015) and (Kumar and Malhotra, 2015) in the HSV

and YCbCr color spaces, the latter providing the best

results in both.

Finally, in (Brancati et al., 2017), a novel rule-

based skin detection method that works in the YCbCr

color space based on correlation rules that evaluate

the combinations of chrominance Cb, Cr values to

identify the skin pixels depending on the shape and

size of dynamically generated skin color clusters was

proposed. Geometrically, the clusters create trape-

zoids in the YCb and YCr subspaces that reﬂect in the

inversely proportional behavior of the chrominance

components. The method was compared with six well

known rule-based methods in literature outperform-

ing them in terms of quantitative performance evalu-

ation parameters. Moreover, the qualitative analysis

shows that the method is very robust in critical sce-

narios.

3 SKIN DETECTION

A state of the art skin detection method has been re-

cently developed by (Brancati et al., 2017). Here, we

review the method and extend it adding more rules to

enforce the constraints and seeking for a better perfor-

mance in terms of false positive rate without hurting

the performance of the original method.

3.1 Original Method

In order to describe the proposed extensions, we will

ﬁrst transcribe the original method that is based on the

deﬁnition of image-speciﬁc trapezoids, named T

YCb

and T

YCr

, in the YCb and YCr subspaces, respectively.

The trapezoids are essential to verify a relation be-

tween the chrominance components Cb and Cr in

these subspaces (Brancati et al., 2017).

The base of the trapezoids T

YCr

and T

YCb

(Fig. 1)

are given by (Y

min

, Cr

min

) and (Y

min

, Cb

max

) in the YCr

and YCb subspaces, respectively. The values Cr

min

133, Cb

max

= 128 were selected according to (Chai

Figure 1: Graphical representation of the trapezoids as well

as the parameters Y

min

= 0, Y

max

= 255, Y

, Y

, Cr

min

max

, Cb

min

, Cb

max

, h

, H

), H

). Adapted

from (Brancati et al., 2017).

and Ngan, 1999) where a skin color map was designed

using a histogram approach based on a given set of

training images. Chai and Ngan observed that the Cr

and Cb distributions of skin color falls in the ranges

[133, 173] and [77, 127], respectively, regardless the

skin color variation in different races.

The Cr

max

parameter is calculated dynamically,

taking into account the histogram of the pixels with

Cr values in the range [Cr

min

, 183], looking for the

maximum value of Cr associated with at least 0.1%

of pixels in the image. The same applies to Cb

min

taking the histogram with Cb values in the range

[77, Cb

max

]. Y

and Y

(shorter base of the upper trape-

zoid) are, respectively, the 5th and 95th percentile of

the luminance values associated with the pixels of the

image with Cr = Cr

max

. A similar procedure is used

to ﬁnd the values of the shorter base of the other trape-

zoid, Y

and Y

(see Fig. 2 for an example).

The correlation rules between the chrominance

components P

and P

of a pixel P are deﬁned as:

• the minimum difference between the values P

and P

, denoted I

;

• an estimated value of P

, namely P

;

• the maximum distance between the points

, P

) and (P

, P

), denoted J

Therefore, to determine if P is skin, the following

equations must hold:

− P

≥ I

(1)

− P

| ≤ J

(2)

In (Brancati et al., 2017) this rate is reported to be equal

to 10%. However, in the distributed source code we found

the value 0.1%, that we are using in the experiments.

Combined Correlation Rules to Detect Skin based on Dynamic Color Clustering

311

Figure 2: Computation of Cr

max

= 162 based on Cr values

histogram of a 724 x 526 image.

The estimated value P

is given by

= Cb

max

− dP

(3)

where

= α · dP

(4)

= P

−Cr

min

(5)

The coordinates of the points [P

, H

)] and

, H

)] in one of the legs of the trapezoid

are useful for the calculation of α. We ﬁrst com-

pute the distances ∆

) and ∆

) between the

points (P

, H

)), (P

, H

)) and the base of

the trapezoids:

∆

) = H

) −Cr

min

(6)

∆

) = Cb

max

− H

) (7)

Next, the distances are normalized with respect to

the difference in size of the trapezoids:

∆

) =

(

∆

) ·

YCb

YCr

if A

YCr

≥ A

YCb

∆

) otherwise

(8)

∆

) =

(

∆

) if A

YCr

≥ A

YCb

∆

) ·

YCr

YCb

otherwise

(9)

where A

YCr

and A

YCb

are the areas of trapezoid T

YCr

and T

YCb

, respectively.

is the distance between the points (P

, P

) and

, Cb

max

) in the YCb subspace, calculated on the basis of

, observing the inversely proportional behavior of the

components. α is the rate between the normalized heights

of the trapezoids in relation to the P

value.

is the distance between (P

, P

) and (P

, Cr

min

)

points in the YCr subspace.

Then, the value of α is given by:

α =

∆

)

∆

)

(10)

Finally, I

and J

are given by:

= s f · [(∆

) − dP

) + (∆

) − dP

)]

(11)

= dP

+ dP

∆

) + ∆

)

(12)

where:

s f =

min((Y

−Y

), (Y

−Y

))

max((Y

−Y

), (Y

−Y

))

(13)

3.2 Extended Method

The hypothesis deﬁned in the original method is

based on rules that an estimated value of the point

, namely P

, must hold in order for the correla-

tion to be valid. On the basis of the inversely propor-

tional behavior of the chrominance components, we

will rewrite the correlation rules with respect to the

point.

Thus, we have to refactor the correlation rules to

put them in terms of the estimated value of P

, that

we denote as P

= dP

+Cr

min

(14)

where

= α · dP

(15)

= Cb

max

− P

(16)

Next, the constraints given by I

and J

in the Eq.

11 and 12 respectively, can be redeﬁned as:

= s f · [(∆

) − dP

) + (∆

) − dP

)]

(17)

= dP

+ dP

∆

) + ∆

)

(18)

Therefore, to determine if the pixel P is skin, we

have to modify the conditions given by Eq. 1 and 2:

− P

≥ I

(19)

− P

| ≤ J

(20)

is the distance between the points (P

, P

) and

, Cr

min

) in the YCr subspace, calculated on the basis of

, observing the inversely proportional behavior of the

components. α is the rate between the normalized heights

of the trapezoids in relation to the P

value.

is the distance between (P

, P

) and (P

, Cb

max

)

points in the YCb subspace.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

312

Doing this simple extension, we are now able to

apply the method to the same sets of images to eval-

uate, in fact, the inversely proportional behavior of

the chrominance components. More than that, we can

combine all these constraints, given by the pair equa-

tions 1 and 2, 19 and 20, to reinforce the ﬁrstly deﬁned

hypothesis.

3.3 Neighborhood Extended Method

Both methods presented in Sec. 3.1 and 3.2 can be

applied to detect skin pixels, either separated or in a

conjunction rule. However, skin pixels do not usually

appear isolated and we can improve the method using

neighbor pixels information, when evaluating a pixel

P, in order to decide if P represents human skin, or

not. Let N

−

(P) the 8-connected neighbors of P that

can be reached before P when scanning the image in

raster order (blue points in Fig. 3).

Thus, we classify P as skin in the following man-

ner: if the constraints given by the pair of equations

1 and 2, as well as 19 and 20 hold, then P is classi-

ﬁed as skin. When only one of conditions is satisﬁed,

then we check the decision in N

−

(P). If three or more

pixels are skin, then P will also be classiﬁed as a skin

pixel.

Figure 3: Neighbors evaluation with respect to P. If the im-

age is scanned in raster order, N

−

(P) is the set of points that

can be reached before P in a 8-connected neighborhood.

4 EXPERIMENTS

In this section we present some experimental evalua-

tions of the proposed extensions along with the orig-

inal method in three widely known datasets: SFA,

Pratheepan and HGR.

4.1 Datasets

The SFA is a set of images of frontal faces obtained

from two other color image databases: the FERET,

created by (Phillips et al., 1996), and the AR proposed

by (Mart

ınez and Benavente, 1998), which provided

876 and 242 images each, respectively. It is important

to notice that AR images have a white background

and small variations of skin color. In other words,

the environment is more controlled than the images in

FERET (Casati et al., 2013).

The images in the Pratheepan dataset were down-

loaded randomly from Google for human skin detec-

tion search. There are 78 images of family and face

captured with a range of distinct cameras using dif-

ferent color enhancement and under different illumi-

nation conditions (Tan et al., 2012).

The last dataset is the HGR for hand gesture

recognition which contains the gestures from Polish

and American Sign Language. There are 1,558 im-

ages acquired in different conditions of background,

dimensions and lightening (Kawulok et al., 2014).

4.2 Evaluation Measures

Precision, Recall, Speciﬁcity and F-measure have

been used as evaluation metrics. They are the same

used in (Brancati et al., 2017) to compare the perfor-

mance with state-of-the-art methods.

4.3 Results and Discussion

The original method was compared with six well

known rule-based methods in literature using four dif-

ferent datasets, two of them, HGR and Pratheepan,

have also been used here.

Because the method had the best F-measure in the

HGR and Pratheepan datasets in comparison with the

other six methods and, in addition, because it per-

formed the top ﬁrst Precision in HGR and second in

Pratheepan, we decided to compare the proposed ex-

tensions only to the original method.

Table 1 shows quantitative result metrics of the

experiments. Column 1 refers to the dataset used.

Column 2 refers to the method being experimented:

Original for the original hypothesis; Reversed refers

to the reverse hypothesis with respect to P

param-

eter; Combined refers to the combination of both of

the former methods (see Sec. 3.2); Neighbors refers

to the extension of the method using the neighborhood

approach.

As one can see, the reverse hypothesis performed

better than the original method and achieved the best

Recall in HGR and SFA. It also achieved the best F-

measure in SFA with a 0.8125 rate, which gave almost

0.25 in gain compared to the original.

In general, the reverse method increased the Re-

call but did not perform well in Precision and Speci-

ﬁcity measures. When we combined both methods,

the best Precision and Speciﬁcity were achieved for

all datasets but it loses some performance in Recall.

However, it has very high F-measure rates.

The combined method along with the neighbor-

hood approach achieved the best F-measure in HGR

Combined Correlation Rules to Detect Skin based on Dynamic Color Clustering

313

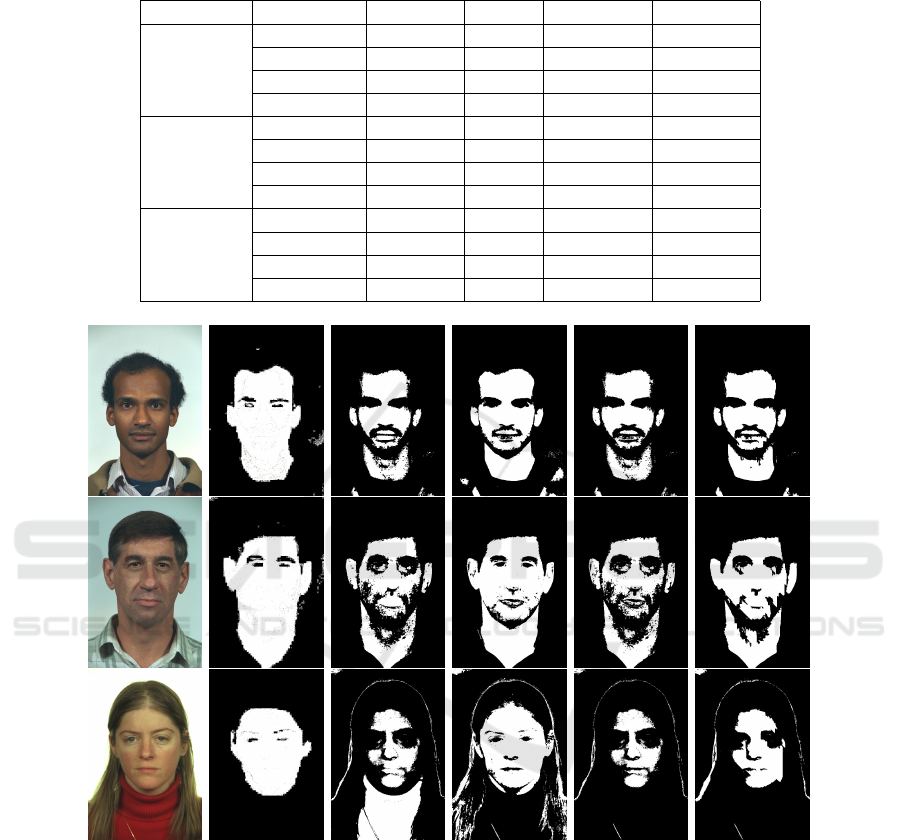
Table 1: Quantitative result metrics of the methods. For each dataset, we have four different applications: the original

hypothesis with respect to P

, the reverse hypothesis with respect to P

, the one which combines both, and the extension

using the neighborhood approach.

Dataset Hypothesis Precision Recall Speciﬁcity F-measure

HGR

Original 0.8938 0.7664 0.9274 0.8252

Reverse 0.7929 0.8429 0.8337 0.8171

Combined 0.8994 0.6952 0.9390 0.7843

Neighbors 0.8818 0.7935 0.9211 0.8353

Pratheepan

Original 0.5513 0.8199 0.8230 0.6592

Reverse 0.5249 0.7326 0.8188 0.6116

Combined 0.6681 0.6683 0.9164 0.6682

Neighbors 0.6280 0.7515 0.8871 0.6843

SFA

Original 0.8636 0.4214 0.9692 0.5664

Reverse 0.8563 0.7730 0.9381 0.8125

Combined 0.9288 0.3958 0.9894 0.5551

Neighbors 0.9176 0.5111 0.9826 0.6565

(a) (b) (c) (d) (e) (f)

Figure 4: Image samples with the results of each method in SFA dataset: (a) original image (b) ground truth (c) original

method (Brancati et al., 2017) (d) reverse method (e) combined method (f) neighbors method.

and Pratheepan. Moreover, the other metrics still are

in a very high rate for all datasets, being in the top

second in almost cases.

Therefore, the combined and extended approaches

are very competitive compared to the original method.

Furthermore, all the variations of the original method

are still computed in quadratic time, maintaining the

desired computational efﬁciency that are useful in dif-

ferent application domains, mainly near real time sys-

tems (processing time of about 10ms for a typical im-

age of dimensions 300x400).

Figures 4, 5, and 6, present some image sam-

ples in column (a) along with the results for each

method tested. Column (b) presents the respective

ground truth for each image in column (a), column (c)

presents the original method (Brancati et al., 2017)

results, column (d) presents the respective reverse

method results, column (e), the combined method

results and column (f) the extended neighborhood

method.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

314

(a)

(b)

(f)

Figure 5: Image samples with the results of each method in Pratheepan dataset: (a) original image (b) ground truth (c) original

method (Brancati et al., 2017) (d) reverse method (e) combined method (f) neighbors method.

(a)

(b)

Figure 6: Image samples with the results of each method in HGR dataset: (a) original image (b) ground truth (c) original

method (Brancati et al., 2017) (d) reverse method (e) combined method (f) neighbors method.

5 CONCLUSIONS

Human skin segmentation is still a unsolved problem,

mainly for real time applications. In (Brancati et al.,

2017), a surprisingly simple and clever method has

been presented and it established a new tier. We re-

produced the original experiments and also checked if

the same patterns were presented in RGB, HSV, and

Lab color spaces, or other applications as ﬁnding tree

leaves but the results were not consistent as the origi-

nal approach for human skin using YCbCr space.

In this paper, we introduced two extensions based

on a hypothesis that the original rule could be reversed

and also taking in consideration that a human skin

pixel does not appear isolated. Both extensions are

simple and do not hurt the efﬁciency of the original

method.

We tested the extensions in three standard public

datasets and the experiments show that our methods

improve the accuracy of skin detection, even when

there exists a huge variation in ethnicity and illumi-

nation. Moreover, our approach proved to be very

Combined Correlation Rules to Detect Skin based on Dynamic Color Clustering

315

competitive, outperforming alternative state-of-the-

art work.

Our results conﬁrm that skin color is an extremely

powerful cue for detecting human skin in uncon-

strained imagery. Other local properties can be ex-

perimented to be used in a future work, along with

the methods presented here, such as texture, shape,

geometry, and other neighborhood operations.

In the future, we will explore further the connec-

tivity of the skin pixels and, because there is so far no

explanation why the original method works so well,

we plan to statistically analyse the shape of the trape-

zoids on the YCbCr space and try to correlate with the

classiﬁcation accuracy.

Our intuition, based on the experimental results,

says that trapezoids features such as size, area, sym-

metry and others, could be used to establish a relation

with the classiﬁcation accuracy. Moreover, if this re-

lationship exists, the shape of the trapezoids could be

previously processed, for instance by ﬁltering image

illumination, to obtain better classiﬁcation results.

ACKNOWLEDGEMENTS

The authors thanks CAPES and FAPESP (#

2015/01587-0) for ﬁnancial support.

REFERENCES

Albiol, A., Torres, L., and Delp, E. J. (2001). Optimum

color spaces for skin detection. In International Con-

ference on Image Processing, pages 122–124.

Bergasa, L. M., Mazo, M., Gardel, A., Sotelo, M. A., and

Boquete, L. (2000). Unsupervised and adaptive gaus-

sian skin-color model. Image and Vision Computing,

18(12):987–1003.

Brancati, N., Pietro, G. D., Frucci, M., and Gallo, L. (2017).

Human skin detection through correlation rules be-

tween the YCb and YCr subspaces based on dynamic

color clustering. Computer Vision and Image Under-

standing, 155:33–42.

Casati, J. P. B., Moraes, D. R., and Rodrigues, E. L. L.

(2013). SFA: A human skin image database based

on FERET and AR facial images. In IX workshop de

Vis

ao Computational.

Chai, D. and Ngan, K. N. (1999). Face segmentation us-

ing skin-color map in videophone applications. IEEE

Trans. on Circ. and Sys. for Video Tech., 9(4):551–

564.

Chaves-Gonz

alez, J. M., Vega-Rodr

ıguez, M. A., G

omez-

Pulido, J. A., and S

anchez-P

erez, J. M. (2010). De-

tecting skin in face recognition systems: A colour

spaces study. Digital Signal Processing, 20(3):806–

823.

Fleck, M. M., Forsyth, D. A., and Bregler, C. (1996). Find-

ing naked people. In European conference on com-

puter vision, pages 593–602. Springer.

Jayaram, S., Schmugge, S., Shin, M. C., and Tsap, L. V.

(2004). Effect of colorspace transformation, the illu-

minance component, and color modeling on skin de-

tection. In Proceedings of the 2004 IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition, volume 2, pages 813–818. IEEE.

Jones, M. J. and Rehg, J. M. (2002). Statistical color mod-

els with application to skin detection. International

Journal of Computer Vision, 46(1):81–96.

Kakumanu, P., Makrogiannis, S., and Bourbakis, N. (2007).

A survey of skin-color modeling and detection meth-

ods. Pattern recognition, 40(3):1106–1122.

Kaur, A. and Kranthi, B. V. (2012). Comparison between

YCbCr color space and CIELab color space for skin

color segmentation. International Journal of Applied

Information Systems, 3(4):30–33.

Kawulok, M., Kawulok, J., Nalepa, J., and Papiez, M.

(2013). Skin detection using spatial analysis with

adaptive seed. In 2013 IEEE International Conference

on Image Processing, pages 3720–3724. IEEE.

Kawulok, M., Kawulok, J., Nalepa, J., and Smolka, B.

(2014). Self-adaptive algorithm for segmenting skin

regions. EURASIP Journal on Advances in Signal

Processing, 2014(170):1–22.

Kovac, J., Peer, P., and Solina, F. (2003). Human skin color

clustering for face detection, volume 2. IEEE.

Kumar, A. and Malhotra, S. (2015). Performance analysis

of color space for optimum skin color detection. In

2015 Fifth Int. Conf. on Communication Systems and

Network Technologies, pages 554–558. IEEE.

Mahmoodi, M. R. and Sayedi, S. M. (2016). A comprehen-

sive survey on human skin detection. Int. Journal of

Image, Graphics and Signal Processing, 8(5):1–35.

Mart

ınez, A. and Benavente, R. (1998). The AR face

database. Technical report, Purdue University.

Naji, S. A., Zainuddin, R., and Jalab, H. A. (2012). Skin

segmentation based on multi pixel color clustering

models. Digital Signal Processing, 22(6):933–940.

Phillips, P. J., Wechsler, H., Huang, J., and Rauss,

P. J. (1996). The facial recognition technology

(FERET) database. https://www.nist.gov/programs-

projects/face-recognition-technology-feret.

Shaik, K. B., P., G., Kalist, V., Sathish, B. S., and Jenitha, J.

M. M. (2015). Comparative study of skin color detec-

tion and segmentation in HSV and YCbCr color space.

Procedia Computer Science, 57:41–48.

Tan, W. R., Chan, C. S., Yogarajah, P., and Condell, J.

(2012). A fusion approach for efﬁcient human skin

detection. IEEE Trans. on Ind. Inf., 8(1):138–147.

Vezhnevets, V., Sazonov, V., and Andreeva, A. (2003). A

survey on pixel-based skin color detection techniques.

In IN PROC. GRAPHICON-2003, pages 85–92.

Yogarajah, P., Condell, J., Curran, K., McKevitt, P., and

Cheddad, A. (2011). A dynamic threshold approach

for skin tone detection in colour images. International

Journal of Biometrics, 4(1):38–55.

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

316